Estimating causal effects of air quality regulations using principal stratification for spatially correlated multivariate intermediate outcomes

Abstract

Methods for causal inference regarding health effects of air quality regulations are met with unique challenges because (1) changes in air quality are intermediates on the causal pathway between regulation and health, (2) regulations typically affect multiple pollutants on the causal pathway towards health, and (3) regulating a given location can affect pollution at other locations, that is, there is interference between observations. We propose a principal stratification method designed to examine causal effects of a regulation on health that are and are not associated with causal effects of the regulation on air quality. A novel feature of our approach is the accommodation of a continuously scaled multivariate intermediate response vector representing multiple pollutants. Furthermore, we use a spatial hierarchical model for potential pollution concentrations and ultimately use estimates from this model to assess validity of assumptions regarding interference. We apply our method to estimate causal effects of the 1990 Clean Air Act Amendments among approximately 7 million Medicare enrollees living within 6 miles of a pollution monitor.

1. INTRODUCTION

Despite the well-established link between long-term exposure to air pollution and health (Zeger and others, 2008;Pope and others, 2009), understanding of how air quality regulations causally affect health outcomes is still evolving. Despite the heightened interest on the part of the US Environmental Protection Agency (EPA) and other stakeholders, methods for conducting health outcomes research in air quality management (also called “accountability research”) are scarce, especially for large-scale regulatory strategies that target the entire nation and are expected to have subtle effects on pollution and health unfolding over several years (Chay and others, 2003;Health Effects Institute, 2010).

One reason for the sparse literature on long-term accountability research is the presence of several unavoidable challenges. First, because the health outcomes thought to be influenced by exposure to air pollution can also be affected by other factors (e.g. advances in medical care), it is difficult to determine the extent to which postregulation changes in health are indeed caused by the regulation, as opposed to being affected by concurrent trends in factors unrelated to the regulation. Second, the consequences of a regulation may extend beyond effects on ambient air pollution, presenting the challenge of parsing regulation effects on health that are associated with improvements in air quality from regulation effects on health that are due to other regulation-induced changes such as changes in behavior or in economic activity. Finally, although large-scale regulations typically target one specific pollutant, they likely affect sources that emit multiple pollutants that may interact in complex ways to impact health.

Facing these challenges, we develop a framework for accountability research designed to distinguish causal regulation effects on health that are associated with causal regulation effects on air quality from causal regulation effects on health that are associated with other causal pathways. Viewing pollution measures as intermediates on the causal pathway between regulation and health implies that standard statistical adjustments entail conditioning on a posttreatment concomitant variable, which has been shown to distort estimation of causal effects (Rosenbaum, 1984). Alternatively, our proposed method is predicated on the potential outcomes method of principal stratification (Frangakis and Rubin, 2002), which allows us to determine whether regulation-induced improvements in health are most pronounced in locations where the regulation also reduces pollution.

The methodological contributions of this article are designed to address several fundamental challenges in accountability research for air quality regulations. First, while existing methods for principal stratification appear in settings where the intermediate variable is univariate, we provide an extension to accommodate a continuously scaled multivariate intermediate response vector. This extension to a multipollutant approach is particularly germane in light of recent reports of the National Research Council and other research groups that have questioned whether current approaches that establish regulations separately for individual pollutants are adequately protective of population health and recommended the development of multipollutant approaches (National Research Council Committee on Air Quality Management in the United States, 2004; Dominici and others, 2010).

Another methodological contribution of this article is the integration of recent methods for modeling point-referenced spatial data into potential outcomes methods for causal inference. Specifically, we capitalize on the spatially correlated nature of air pollution and incorporate a spatial hierarchical model that allows prediction of unobserved potential pollution concentrations based in part on relationships with pollution in surrounding locations. Viewing pollution as correlated across locations reflects a belief that regulations in a given location could affect pollution in nearby locations, that is, it reflects a violation of the standard “no interference” or stable unit treatment value assumption that typically underlies potential outcomes approaches (Rubin, 1980). To our knowledge, ours is the first application of spatial models to potential outcomes methods for causal inference.

The regulatory action we examine in this article is a particular feature of the 1990 Clean Air Act Amendments (CAAA) that induced the EPA to designate areas in violation of the National Ambient Air Quality Standards (NAAQS) as “nonattainment,” inducing these areas to take actions to improve air quality. We use our proposed methodology to estimate the causal effects of the 1991 nonattainment designations for particulate matter with aerodynamic diameter <10 μm (PM₁₀) on ambient concentrations of both PM₁₀ and ozone (O₃) during the period 1999–2001 and on all-cause mortality in the Medicare population in 2001.

Section 2 of this paper describes the CAAA and the construction of a data set linking information from several national sources. Section 3 addresses the assumptions pertaining to interference, formalizes the use of principal stratification as a framework for conducting accountability research, and extends the ideas to accommodate multivariate intermediate outcomes. Section 4 presents our modeling strategy for air pollution and health outcomes, including specification of the multivariate spatial hierarchical model for pollution concentrations. Section 5 details our Bayesian estimation strategy, and Section 6 summarizes results from using our method for the CAAA. We conclude with a discussion.

2. THE CAAA AND DATA FOR ACCOUNTABILITY RESEARCH

As a consequence of the CAAA, the EPA (in 1991) designated counties as “nonattainment” with regard to the 1987 NAAQS for PM₁₀ if (1) at least one pollution monitor in the county indicated a violation of the NAAQS for PM₁₀ during the years 1987–1989 or (2) part of the county was thought to contribute to a violation of the NAAQS for PM₁₀ in another area during 1987–1989. County nonattainment designations compelled states to implement strategies to achieve the NAAQS by the end of 2001. We refer to locations in nonattainment counties as “regulated.” All other counties are considered in attainment and we refer to these counties as “unregulated,” as no specific air quality actions were required.

To characterize causal effects of the 1991 nonattainment designations on pollution and health, we focus on 3-year average ambient concentration of PM₁₀ and O₃ during the period 1999–2001 and on all-cause mortality in 2001 among Medicare beneficiaries living in the vicinity of an air pollution monitor. To this end, we compile data from several national sources. From the EPA Air Quality System (AQS) database, we obtain 3-year average ambient concentrations of PM₁₀ and O₃ during the preregulation period (1987–1989) and the 3 years leading up to the target date for attainment of the NAAQS (1999–2001). From the Center for Medicare and Medicaid Services Medicare enrollee file, we obtain all-cause mortality information in 2001 for all Medicare enrollees living within 6 miles of a pollution monitor, as well as basic demographic characteristics such as age, gender, and ethnicity. From the 2000 US Census, we obtain county-level demographic characteristics such as population size and income characteristics. From the Centers for Disease Control and Prevention Behavioral Risk Factor Surveillance System, we obtain county-level smoking rates in 2000. Table 1 summarizes the available data.

Table 1.

Summary of data available for accountability assessment of the CAAA

Source	Data	Spatial resolution	Year(s)
EPA	Preregulation PM10†, ‡, preregulation O3†, ‡	Monitor	1987–1989, 1999–2001
	postregulation PM10, postregulation O3
US Federal Register	PM10 attainment status	County	1991
Center for Medicare	All-cause mortality, age†, ‡,	Individual beneficiary	2001
and Medicaid Services	sex†, ‡, race/ethnicity‡
Centers for Disease Control and Prevention Behavioral Risk Factor Surveillance System	Smoking rate†, ‡	County	2000
Census	Population†, ‡, %urban†, ‡, 5-year migration†, ‡,	County	2000
	median income†, ‡, %high school grad†, ‡,
	%female†, ‡, race/ethnicity†

^†denotes variables included as covariates in the model for air pollution.

^‡denotes variables included as covariates in the model for mortality.

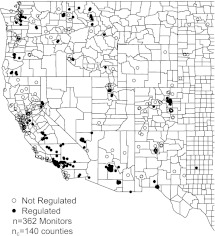
The observational units of the analysis are the locations of air pollution monitors in AQS having data available for PM₁₀ and/or O₃ during either the pre- or postregulation years. We used volume 56, number 51, of the US Federal Register to determine which of these monitors fell within initial PM₁₀ nonattainment areas. Next, we determined all Medicare enrollees living in US zip codes having geographic centroids within a 6-mile radius of a pollution monitor and assigned these enrollees pollution exposure measured from that monitor. We restrict the analysis to monitor locations in the western United States having at least 50 Medicare enrollees because almost all initial PM₁₀ nonattainment areas fell in this region. The resulting data set consists of ambient pollution measurements at 362 pollution monitor locations (of which 200 lie in regulated counties), county-level characteristics on 140 counties, and basic characteristics and mortality information for 6 926 338 Medicare beneficiaries. Figure 1 displays the monitor locations.

Fig. 1.

Map of the monitor locations for PM₁₀ and O₃ used to estimate the causal effects of the CAAA.

3. POTENTIAL OUTCOMES AND MULTIDIMENSIONAL PRINCIPAL STRATA

For any hypothetical allocation of nonattainment designations, let A≡[A(s_i)]_{i = 1}ⁿ be the vector of indicators denoting whether each of n = 362 locations would fall in a nonattainment county, with A(s_i) = 1 denoting nonattainment for the ith location. Note that there are n_c = 140 counties, and that all locations within a county have the same designation. We refer to the entire vector A as a regulation program, and note that, at least hypothetically, there are 2^n_c different possible regulation programs of which only one is observed. We denote a specific regulation program with A = a and the observed program for the CAAA with A = a^obs. Furthermore, let ℛ^aobs and 𝒰^aobs respectively denote the set of 200 regulated and 162 unregulated locations under the program A = a^obs. Our goal was to estimate causal effects of a regulation program that enacts regulations in all locations versus a program that enacts regulations in no locations. For simplicity, we denote these programs with A = 1,0, respectively.

Let Y_a(s) denote the number of deaths in 2001 (10 years postregulation) at location s that would potentially occur under regulation program A = a. Let X_a(s) denote the q-dimensional vector of average concentrations of q pollutants that would potentially be observed during 1999–2001 under regulation program A = a. Our analysis of the CAAA considers q = 2, representing concentrations of PM₁₀ and O₃. Note that the only observed potential outcomes are (X_a^obs(s),Y_a^obs(s)); all others are considered missing data. Throughout, we use Z(s) to denote time-invariant and location-specific covariates.

3.1. Assumptions about interference between locations

Mortality outcomes and pollution levels are only observed under the program A = a^obs. Therefore, we require assumptions to relate observed potential outcomes to those that would have been observed under programs A = 0,1. Typically, this would be achieved with the assumption of no interference between observational units (or SUTVA), which states that potential outcomes for a given location are unrelated to regulation designations of all other locations. This assumption implies that there are exactly 2 sets of potential outcomes for each location: pollution and mortality if that location is regulated and pollution and mortality if that location is unregulated. Thus, with no interference, potential outcomes under any hypothetical program A = a could be considered on a location-by-location basis, with (X_a(s),Y_a(s)) = (X_a^obs(s),Y_a^obs(s)) as long as a and a^obs entail the same regulation status for location s.

In studies of air pollution, however, the assumption of no interference does not likely hold because regulations at a given location likely impact air quality at nearby locations. Thus, knowing the observed potential outcomes at location s under A = a^obs does not imply knowledge of the potential outcomes under any other A = a because potential outcomes for s can differ when regulations are allocated differently to other locations. In fact, with no assumptions regarding interference, potential outcomes for each location are distinctly defined for each of the 2^n_c different possible regulation programs because changing the regulation designation of any location could impact potential outcomes at all other locations.

We liken investigation of the CAAA to previously considered problems of “partial interference” (Sobel, 2006) where observations within a clearly defined group (e.g. residents of a particular neighborhood) interfere with one another, but observations in different groups (e.g. residents of distant neighborhoods) do not. Unlike previously considered partial interference settings, there are no clearly defined interference sets for analyzing the CAAA (e.g. assuming no interference between locations in different counties might be too restrictive, especially for observations near county borders). We argue that a unique feature of the CAAA is that nonattainment designations were “assigned” with some implicit regard to interference because one criterion for a nonattainment designation was contribution to an NAAQS violation in a nearby area. That is, if weather patterns or mere proximity led pollution in one location to affect pollution in another location, the EPA ensured that these 2 locations shared the same regulation designation.

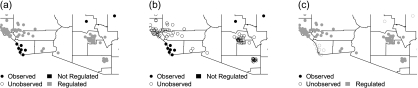
We adopt what we term the “assignment group interference assumption (AGIA)” to reflect the notion that locations within ℛ^aobs do not interfere with those in 𝒰^aobs. Thus, changing the regulation designation of any location in 𝒰^aobs would not change the potential outcomes of locations in ℛ^aobs (and vice versa). A consequence of this assumption is that (X₁(s),Y₁(s)) = (X_a^obs(s),Y_a^obs(s)) for s∈ℛ^aobs and (X₀(s),Y₀(s)) = (X_a^obs(s),Y_a^obs(s)) for s∈𝒰^aobs. Figure 2 graphically depicts the implication of AGIA. In practice, this assumption implies that, in all locations observed to be regulated (ℛ^aobs), observed potential outcomes are the same as those that would have been observed if the EPA had additionally regulated all other locations. Analogously, AGIA also implies that in all unregulated locations (𝒰^aobs), observed potential outcomes are the same as those that would have occurred if the EPA had regulated no locations. We discuss assessment of this assumption in Section 4.3.

Fig. 2.

Structure of potential outcomes for different regulation programs under the AGIA. Points represent monitor locations in counties contained in portions of California and Arizona. (a) A = a^obs. The observed regulation program determines 𝒰^aobs and ℛ^aobs. All pollution and mortality outcomes are observed under this program. (b) A = 0. Pollution and mortality outcomes are observed for locations in 𝒰^aobs and unobserved for those in ℛ^aobs. (c) A = 1. Pollution and mortality outcomes are observed for locations in ℛ^aobs and unobserved for those in 𝒰^aobs.

3.2. Regulation ignorability assumption

In addition to AGIA, we assume that the EPA regulation designations are strongly ignorable conditional on covariates. In other words, there is no unmeasured confounding in the sense that Z(s) contains all factors that tend to differ between regulated and unregulated locations and that also impact potential pollution and mortality outcomes. Note that Z(s) will include preregulation pollution measurements from year(s) before the designations that are used in the EPA decision process, as well as demographic characteristics of the population surrounding location s (see Table 1). Note that this assumption is unverifiable, and that employing any causal inference method with observational data requires some form of ignorability assumption. We revisit this assumption in Section 7.

3.3. Principal strata and principal causal effects

We confine attention to the regulation programs A = 0 and A = 1 and define the monitor-level causal effect of A on the kth pollutant as the comparison between the potential pollution concentration of that pollutant under the regulated program, [X₁(s)]_k, and the potential concentration of that pollutant under the unregulated program, [X₀(s)]_k. We similarly define the causal effect of regulation on mortality for location s as the comparison between Y₁^r(s) and Y₀^r(s), where Y_a^r(s) denotes the mortality rate per 1000 Medicare beneficiaries.

Principal strata are defined by the joint vector of potential pollution concentrations for all q pollutants under both possible regulation programs, (X₀(s),X₁(s)) (e.g. the regulated and unregulated concentrations of both PM₁₀ and O₃). A location's principal stratum indicates the causal effect of the regulation on pollution for that location; strata with [X₀(s)]_k = [X₁(s)]_k for k = 1,…,q represent locations where regulation does not causally affect air pollution, while strata with [X₀(s)]_k≠[X₁(s)]_k for at least one k represent locations where regulation causally affects at least one pollutant. Causal regulation effects on mortality within principal strata (or unions of principal strata), called “principal effects,” can indicate the extent to which regulation effects on mortality coincide with regulation effects on pollution.

Towards this end, we use principal stratification to define regulation effects on mortality as associative or dissociative with regulation effects on pollution. An “associative effect” is a causal regulation effect on mortality in locations where there is a causal regulation effect on pollution. A “dissociative” effect is a causal regulation effect on mortality in locations where there is no causal regulation effect on pollution. To formally extend these definitions to settings with multivariate X_a(s), define K to be a subset of the q pollutants, which could represent an individual pollutant or any combination of pollutants. For example, in our application with q = 2, K can be PM₁₀}, {O₃}, or {PM₁₀, O₃}. We define 𝒦-associative effects as mortality comparisons within strata where the regulation causally affects the pollutant(s) in 𝒦, that is, as comparisons between Y₁^r(s) and Y₀^r(s) in strata where [X₀(s)]_K≠[X₁(s)]_K. Similarly, K-dissociative effects are defined as comparisons between Y₁^r(s) and Y₀^r(s) in strata where the regulation does not causally affect the pollutant(s) in K, that is, in strata with [X₀(s)]_K = [X₁(s)]_K.

In general, average causal effects on mortality can be defined for any combination of principal strata. In order to characterize average dissociative and associative effects in practice, interest may lie in average effects on mortality in (a) locations where the regulation does not meaningfully affect pollution and (b) locations where the regulation meaningfully reduces pollution. To summarize such quantities, we define expected K-dissociative effects (EDE_K) and expected K-associative effects (EAE_K) as:

(3.1)

(3.2)

where C_K^A denotes a vector of thresholds beyond which a change in each pollutant in 𝒦 is deemed scientifically meaningful, and C_K^D is a vector of thresholds below which changes in these pollutants are considered inconsequential. The > and < signs represent component-wise comparisons between vectors. For example, with K = {PM₁₀, O₃}, EAE_K could estimate the average causal effect on mortality in locations where the regulation-induced reduction of PM₁₀ exceeds 4 μg/m³ and the regulation-induced reduction on O₃ exceeds 0.005 ppm.

Large 𝒦-associative effects relative to small 𝒦-dissociative effects would indicate that the regulation has the strongest effect on mortality in locations where the regulation causes improvements in air quality. K-associative and K-dissociative effects of equal magnitude wound indicate that the regulation effect on mortality is the same regardless of whether the regulation improved air quality, which would suggest some important causal pathways through which the regulation impacts mortality without reducing pollution.

4. MODELS FOR AIR POLLUTION AND MORTALITY

Conditional on observed covariates, Z(s), we factor the joint density of all potentially observable quantities at each location as a model for air pollution and a model for mortality conditional on pollution: f(X₀(s),X₁(s)|Z(s))f(Y₀(s),Y₁(s)|X₀(s),X₁(s),Z(s)). Note that without further assumptions, a model for this full joint density will not be identified from observed data because of the lack of information on the following pairwise associations between quantities that are never jointly observed at the same location:

• (Ai) Pollution under opposite regulations: [X₀(s)]_k,[X₁(s)]_k^′|Z(s) for k = 1,…,q and k^′ = 1,…,q.

• (Aii) Mortality counts under opposite regulations: Y₀(s),Y₁(s)|Z(s),X₀(s),X₁(s).

• (Aiii) Mortality counts under a given regulation and pollution under the opposite regulation: Y_a(s),X_a^′(s)|Z(s),X_a(s) for a,a^′ = 0,1 and a≠a^′.

Resulting from the lack of observed data pertaining to these associations, modeling the full joint density requires assumptions pertaining to the associations in 1–3. We put forward one set of assumptions.

4.1. Spatial hierarchical model for air pollution

For f(X₀(s),X₁(s)|Z(s)), we propose the following spatial hierarchical model:

(4.3)

where X(s) = (X₀^T(s),X₁^T(s))^T is the 2q-dimensional vector of potential pollution concentrations (q pollutants under each of 2 regulations), W(s) is a vector of spatially varying random intercepts, and ϵ(s) represents nonspatial “nugget” error (e.g. measurement error). We assume ϵ(s)∼MVN(0,Ψ) and Ψ diagonal. Z^T(s) is a 2q×p matrix of time-invariant covariates, where p = Σ_kp_k and p_k is the number of covariates pertaining to the kth pollutant at location s (including an intercept).

The spatial correlation structure follows from specifying W(s) as a realization from a multivariate Gaussian Process with cross-covariance function K(s_i,s_j;ν) being the 2q×2q matrix of covariances between the 2q potential pollution concentrations measured at locations s_i and s_j. For example, [K(s_i,s_j;ν)]_1,2 denotes the covariance between PM₁₀ at location s_i and O₃ at location s_j, both under A = 0, and [K(s_i,s_j;ν)]_2,3 denotes the covariance between O₃ at location s_i under A = 0 and PM₁₀ at location s_j under A = 1. The parameter ν = (ν₁,…,ν_2q) indexes functions that characterize the spatial decay of correlations between pollution measurements across space. Note that when i = j, K(s_i,s_j;ν) = K(s,s) is in fact a covariance matrix characterizing the relationships among the 2q potential pollution concentrations within a location.

The mechanics of model (4.3) rely on separating K(s_i,s_j;ν) into 2 distinct features: (1) K(s,s) and (2) functions for the decay of correlations between each pollution concentration across space. Decomposing the cross-covariance in this way yields computational feasibility for model (4.3), but it also has the nice feature that it isolates the part of the model representing the nonidentifiable associations between pollution measurements under opposite regulation programs, that is, the associations in 1. Specifically, the q×q diagonal blocks of K(s,s) represent the relationships among pollutants under the same regulation and are identified from observed data. The off-diagonal blocks of K(s,s) represent relationships among pollutants measured under opposite regulations within a location (i.e. between X₀(s) and X₁(s)). These off-diagonal blocks are nonidentified from observed data and will be specified with a sensitivity parameter in the next section. For the second feature of K(s_i,s_j;ν) capturing the spatial decay of correlations across space, we assume isotropic exponential correlation functions that depend on the Euclidean distance between locations s_i and s_j (||s_i − s_j||), with ρ_k(s_i,s_j) = e ^{− ν_k||s_i − s_j||}, for k = 1,…,2q. The ν_k will be informed by observed data and have important implications for AGIA because they determine the estimated correlation between measurements at different locations. Details of this model specification appear in Appendix A of the supplementary material available at Biostatistics online and also in Banerjee and others (2008).

4.2. Sensitivity parameter for the associations between pollutants under opposite regulations

To isolate the nonidentifiable quantities in model (4.3), write: 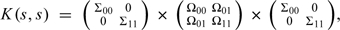, where Σ_aa represents a q×q diagonal matrix of standard deviations and Ω_aa represents a correlation matrix for q pollutants measured at the same location under program A = a, all of which are informed by observed data. The q×q matrix Ω₀₁ represents the nonidentified correlations between q pollutants measured at the same location under opposite designations, pertaining to association 1.

We adopt a strategy that specifies Ω₀₁ and varies this specification to assess sensitivity to assumptions about these nonidentifiable associations. Specifically, we define the q×q matrix Ω_avg, the entries of which are the averages of the values from the corresponding observable entries of Ω₀₀ and Ω₁₁, and set Ω₀₁ = ω×Ω_avg, where ω is a scalar-valued sensitivity parameter. This strategy implies that the correlation between the same pollutant under opposite regulation programs is ω, and that the correlation between different pollutants under opposite programs is an attenuated (by a factor of ω) version of the correlation observed separately under each program. For example, if the correlation between PM₁₀ and O₃ observed in 𝒰^aobs is 0.4, and the analogous correlation observed in ℛ^aobs is 0.6, then this specification implies that the assumed correlation between PM₁₀ under A = 0 and O₃ under A = 1 is $\omega \times \frac{0.4+0.6}{2}$.

4.3. Interference and the spatial model

High values of ν from K(s_i,s_j;ν) represent fast spatial decay, implying correlations only among potential pollution measurements at nearby locations, whereas low values of ν represent slow spatial decay. Values of ν that suggest correlation between locations in ℛ^aobs and 𝒰^aobs would suggest a possible violation of AGIA because there would be correlation among pollution at locations assumed to not interfere. For example, if ν implies that observations located d units apart remain correlated and if any location in ℛ^aobs is located within d units of a location in 𝒰^aobs, then there is evidence of a violation of AGIA.

4.4. Log-linear model for mortality

For f(Y₀(s),Y₁(s)|X₀(s),X₁(s),Z(s)), we make use of 2 assumptions regarding the associations in 2 and 3. In regard to 2, we assume conditional independence of potential mortality outcomes, conditional on covariates and air pollution: Y₀(s)╨Y₁(s)|X₀(s),X₁(s),Z(s). Estimates of EDE_K and EAE_K that pertain to average mortality rate differences are expected to be robust assumptions about the association between Y₀(s) and Y₁(s). Regarding 3, we assume that under a given regulation, after conditioning on pollution under that regulation (and covariates), mortality outcomes are independent of pollution under the opposite regulation: f(Y_a(s)|X₀(s),X₁(s),Z(s)) = f(Y_a(s)|X_a(s),Z(s)), for a = 0,1. This assumption reflects a belief that knowledge of both (X₀(s),X₁(s)) does not contribute any information pertaining to Y_a(s) above and beyond that contained in X_a(s) alone. As a result of these assumptions, we write f(Y₀(s),Y₁(s)|X₀(s),X₁(s),Z(s)) = ∏_{a = 0}¹f(Y_a(s)|X_a(s),Z(s)) and model the terms of this product with the following log-linear models:

(4.4)

where a = 0,1, N(s) is the total number of Medicare enrollees living near location s, α₁^a captures mortality relative risks associated with differences in Z(s) under regulation program A = a, and α₂^a captures mortality relative risks associated with differences in postregulation ambient pollution concentrations under regulation program A = a.

5. BAYESIAN ESTIMATION

Recall that X(s) = (X₀(s)^T,X₁(s)^T)^T and let Y(s) = (Y₀(s)^T,Y₁(s)^T)^T. The full joint density of the data can be written as:

(5.5)

where θ is a generic parameter with prior distribution p(θ). Distinguishing between the missing (mis) and observed (obs) quantities in X(s) and Y(s), the posterior distribution of θ is proportional to:

(5.6)

Inference from (5.6) is difficult because of the integration over missing potential outcomes, leading us to focus instead on the following joint posterior distribution:

(5.7)

which is convenient for its proportionality to the standard posterior distribution of θ had all the potential outcomes been observed (Jin and Rubin, 2008). Thus, our computational strategy consists of a Monte Carlo Markov chain (MCMC) data augmentation algorithm that iteratively samples missing potential outcomes conditional on observed data and parameters, then samples parameters and calculates the EDE_K and EAE_K conditional on “complete” data with identified principal strata. Appendix A of the supplementary material available at Biostatistics online contains details of our MCMC strategy.

6. ACCOUNTABILITY RESEARCH FOR THE CAAA

We apply our method to analyze the CAAA and estimate causal effects of the 1991 EPA nonattainment designations on average ambient concentrations of PM₁₀ and O₃ (q = 2) during the period 1999–2001 and on all-cause mortality in the Medicare population in 2001. We use model (4.3) with X_a(s) representing log-transformed potential pollution concentrations and consider Z(s) to be the same for each pollutant and under both regulations. We model the mortality outcomes using the model defined in (4.4). The variables included in Z(s) for the pollution and mortality models are denoted in Table 1.

Analysis of the CAAA entails 3 types of missing data. First are the unobserved potential pollution and mortality outcomes. Second are missing pollution outcomes in 1999–2001 that result from having colocated monitors for PM₁₀ and O₃ for only 108 monitor locations. All these missing outcomes are imputed throughout the MCMC, with uncertainty propagated into estimates of causal effects. Finally, we are confronted with pollution monitors that were not in operation during the 1987–1989 period, yielding 179 missing preregulation PM₁₀ concentrations and 228 missing preregulation O₃ concentrations. Since these are important baseline covariates in our analysis, missing preregulation pollution concentrations were imputed from a 2D spatial model analogous to (4.3) fit to observed pollution values during 1987–1989 without the complication of potential outcomes or nonidentifiable associations. These imputed covariate values are treated as fixed for our analysis.

We allow different nugget errors (Ψ) and spatial decay parameters (ν) for PM₁₀ and O₃ but assume that, for a given pollutant, these quantities are the same under A = 0 and A = 1. For the sensitivity parameter characterizing the within-location correlation between the same pollutant measured under opposite regulation programs, we consider ω = (0.0,0.3,0.6,0.9). Details of the prior specification appear in Appendix A of the supplementary material available at Biostatistics online, and an analysis using simulated data appears in Appendix B of the supplementary material available at Biostatistics online to illustrate proof of concept.

6.1. Results

The estimated overall average causal effect of the regulation program on mortality was 1.76 fewer deaths per 1000 Medicare beneficiaries after adjusting for the aforementioned covariates with a Poisson regression model (posterior mean [sd] deaths/1000: 63.41 [0.29] vs. 65.17 [0.34]). However, our proposed method estimated that this regulation effect on mortality was due in large part to causal pathways not involving average ambient concentrations of PM₁₀ and/or O₃ during the period 1999–2001. The threshold values C_K^A,C_K^D defining meaningful changes in pollution concentrations are 4, 4 for K = {PM₁₀}; 0.005, 0.005 for K = {O₃}; and (4, 0.005), (4, 0.005) for K = {PM₁₀, O₃}. These values of C_K^A,C_K^D were chosen to represent roughly 10% of the average pollution concentrations in 1987–1989.

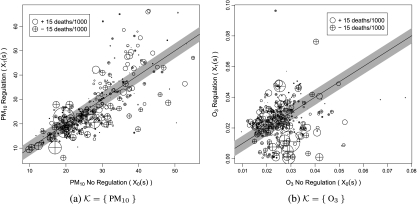
Posterior summaries of all model parameters appear in Appendix C of the supplementary material available at Biostatistics online. To summarize regulation effects, Figure 3 examines estimated causal effects on mortality as a function of estimated causal effects on air quality. The size and plotting symbol of the points indicate the magnitude and direction of the estimated causal effect on mortality for each location (Y₁^r(s) − Y₀^r(s)). The shaded region represents a causal effect on air pollution below the threshold C_K^D, meaning that points lying in the shaded region represent locations that are estimated to have essentially no casual effect on the pollutant in K. The area below the shaded region represents a causal effect on pollution in excess of the threshold C_K^A, meaning that points lying below the shaded region represent locations where we estimate a meaningful causal reduction in pollution. This illustration uses mean posterior predictive values of unobserved potential outcomes for the analysis with ω = 0.6. Analogous plots for other values of ω were similar and are not pictured.

Fig. 3.

Depiction of causal effects on mortality as a function of causal effects on pollution for K = PM₁₀ and K = O₃ for ω = 0.6. Values of X_a(s) represent observed or posterior predictive mean values. Size and plotting symbol of point indicates the posterior mean causal effect on mortality for that location. Points in shaded area represent areas with [X₀(s)]_K − [X₁(s)]_K < C_K^D. (a) K = {PM₁₀} and (b) K = {O₃}.

For K = {PM₁₀}, we see in Figure 3(a) that points within the shaded area tend to indicate a decrease in mortality, that is, the regulation reduces mortality when it does not causally effect PM₁₀ (negative dissociative effect). Similarly, we see that points below the shaded area also tend to indicate decreases in mortality, indicating that the regulation reduces mortality when it causally reduces PM₁₀ (negative associative effect). A similar pattern is evident in Figure 3(b) for K = {O₃} but with points more evenly dispersed along the line [X₀(s)]_K = [X₁(s)]_K (shaded area).

Figure 4 shows boxplots of posterior distributions of EDE_K and EAE_K across different values of the sensitivity parameter. For K = {PM₁₀}, the similar magnitude of the associative and dissociative effects suggests that the regulation caused a similar decrease in mortality regardless of whether the regulation decreased the average ambient concentration of PM₁₀ during 1999–2001. For K = {O₃}, estimates of EAE_K and EDE_K appear more sensitive to assumptions about ω, with the dissociative effect always estimated to be slightly more pronounced than the associative effect, although both effects are estimated near 0. For K = {PM₁₀, O₃}, the analyses with ω = 0.6 or 0.9 estimate more pronounced associative effects than dissociative effects, with EDE_K = − 0.95 or − 1.31 and EAE_K = − 1.29 or − 1.88 deaths per 1000 Medicare beneficiaries. This provides some evidence that the regulation causally reduced mortality most when it causally reduced average ambient concentrations of both PM₁₀ and O₃ during 1999–2001.

Fig. 4.

Posterior summaries of EDE_K and EAE_K for different values of the sensitivity parameter (ω). (a) K = {PM₁₀}}, (b) K = {O₃}, and (c) K = {PM₁₀}, O₃}.

To assess AGIA, we use posterior estimates of ν to compute the estimated correlations between pollution at locations in 𝒰^aobs and pollution at locations in ℛ^aobs. Using the lowest estimate of ν for each pollutant (from analyses with different ω), we found correlations >0.25 between 30 (54) PM₁₀ (O₃) measurements at locations in different interference sets. Thus, there is evidence of a violation of AGIA, but relatively, few locations exhibit correlations greater than 0.25. Further detail of the assessment of AGIA appears in Appendix D of the supplementary material available at Biostatistics online.

6.2. Additional sensitivity analyses

Appendix E of the supplementary material available at Biostatistics online provides additional detail of our treatment of missing outcome and covariate data. We found that our model for covariate imputation yielded reasonable out-of-sample predictions for preregulation pollution. We also calculated EDE_K and EAE_K using only locations with observed preregulation pollution. This analysis suggested very similar results for K = {PM₁₀}} and more pronounced effects on health for K = {O₃} and K = {PM₁₀}, O₃}, with all estimates exhibiting increased uncertainty. Appendix F of the supplementary material available at Biostatistics online investigates sensitivity to the choice of C_K^D and C_K^A and indicates that substantive conclusions are fairly robust to the choice of these thresholds.

7. DISCUSSION

We have provided an innovative causal inference framework for estimating the health effects of air pollution regulatory actions. Amid the growing demand for a shift from a single pollutant to a multipollutant approach, we extended existing methods for principal stratification to accommodate a continuously scaled multivariate intermediate response vector. We also introduced what we believe to be the first application of potential outcomes methods for causal inference in settings with spatially correlated data.

Our analysis of the CAAA estimated that 1991 nonattainment designations for PM₁₀ did causally reduce Medicare mortality in 2001, and that there are important causal pathways through which this effect occurred without affecting average ambient concentrations of PM₁₀ or O₃ during 1999–2001. Other pollution measures (e.g. average daily maximum) and other time periods deserve investigation, and this analysis is not without limitations. As with any causal analysis with observational data, the possibility of unmeasured confounding persists. Our results are predicated on the belief that after adjusting for demographic characteristics in 2000–2001 (see Table 1) and preregulation pollution levels, there are no unmeasured factors relevant to air quality and mortality that differ systematically between attainment and nonattainment areas. Strategies to collect additional data, possibly at a finer spatial or resolution or with better temporal alignment, would bolster confidence in the ignorability assumption of Section 3.2.

In order to estimate causal effects of a program that would regulate all areas versus a program that would regulate no areas, we made use of an assumption about interference, namely, AGIA. However, our estimates can be viewed as approximate in the sense that there is evidence of a violation of AGIA, although relatively few locations suggest a substantial violation. Furthermore, we used a relatively restrictive (exponential) spatial decay function that was indexed by a single parameter, but more flexible (e.g. anisotropic) spatial covariance functions could provide better fit to pollution data and should be explored. To ease interpretability, we also incorporated a single sensitivity parameter (ω) to characterize nonidentifiable pollution correlations but additional sensitivity parameters could be included.

Finally, the data used for our analysis entail limitations that are often unavoidable when combining heterogenous data sources on a large scale. With limited individual-level data, we must rely on aggregate summaries at different spatial resolutions. Furthermore, our models relied on demographic variables from 2000 and 2001 to estimate the causal effects of regulations enacted in 1991. Because we consider potential pollution and mortality outcomes in 1999–2001, we believe that demographic information from this time period provides the most sound strategy for predicting unobserved potential outcomes. We also believe that any long-term demographic changes occurring between 1991 and 2001 would not be substantial enough to alter our assumptions about EPA regulatory decisions in 1991. Previous studies of long-term air pollution exposure have indicated that using this type of multisource national data does not alter substantive conclusions (Eftim and others, 2008;Zeger and others, 2008;Greven and others, 2011). Finally, our linked data set contained missing preregulation pollution during 1987–1989. We imputed these missing covariate values from a separate model and treated these imputations as fixed for the final analysis, which does not reflect imputation uncertainty. However, we illustrated the predictive ability of our imputation model, and a sensitivity analysis that calculated EDE_K and EAE_K using only locations with observed preregulation pollution concentrations did not provide substantively different estimates for K = {PM₁₀}} and indicated more pronounced health effects associated with changes in O₃.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

USEPA (RD83479801, R83622, RD83241701); the National Institutes of Health (5T32ES007142-28, R01ES012044).