Semiparametric Stochastic Modeling of the Rate Function in Longitudinal Studies

Abstract

In longitudinal biomedical studies, there is often interest in the rate functions, which describe the functional rates of change of biomarker profiles. This paper proposes a semiparametric approach to model these functions as the realizations of stochastic processes defined by stochastic differential equations. These processes are dependent on the covariates of interest and vary around a specified parametric function. An efficient Markov chain Monte Carlo algorithm is developed for inference. The proposed method is compared with several existing methods in terms of goodness-of-fit and more importantly the ability to forecast future functional data in a simulation study. The proposed methodology is applied to prostate-specific antigen profiles for illustration. Supplementary materials for this paper are available online.

1 Introduction

This paper focuses on semiparametric stochastic modeling of rate functions for functional data in a multi-subject setting, where the data consists of a set of subjects, and for each subject, the observations are discrete samples from a curve with additive measurement errors. The rate function describes the functional rate of change or slope with respect to time, and has been of recent interest in longitudinal biomedical studies (Mungas et al., 2005; Lloyd-Jones et al., 2007; Strasak et al., 2008; Kariyanna et al., 2010). For example, from subject-matter knowledge it may be the rate of change, rather than the level of some biomarker, that can explain and predict the disease outcomes. One challenge in this research is to model the rate function without making a strong parametric assumption. Further challenges include modeling the rate functions across the subjects and allowing it to depend on the covariates of interest.

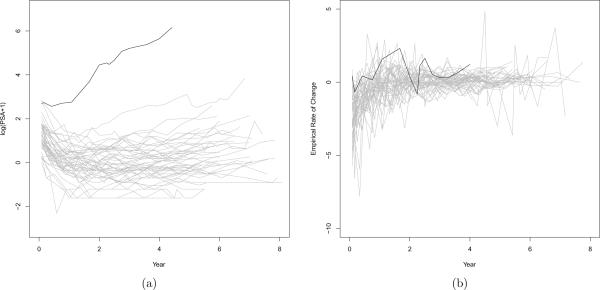
Our development has been largely motivated by a longitudinal study in prostate cancer patients (Proust-Lima et al., 2008), where prostate-specific antigen (PSA) profiles were collected for patients who received external beam radiation therapy (EBRT). PSA is roughly proportional to the prostate tumor size, and its rate of change has been shown to be associated with the recurrence of prostate cancer (Sartor et al., 1997). Figure 1(a) shows the log-transformed PSA level over time after EBRT treatment for 50 selected patients, and Figure 1(b) illustrates individual empirical rates of change, one for each subject. Figure 1(b) suggests that the individual rate of change of PSA roughly follows a common pattern. That is, it begins with a negative value caused by the EBRT, decreases over time in magnitude as the rate of tumor shrinkage gets lower, and eventually reaches a certain stable level. It is also apparent that rates of change vary considerably from this common pattern. For example, for the subject highlighted in black in Figure 1(b), his empirical rate of change fluctuates around zero and his PSA level appears very different from the others. Hence it is desirable to model the rate of change semiparametrically by incorporating empirical evidence or prior knowledge through a parametric function of time while accounting for deviation from the common pattern nonparametrically. Additionally, it is clear that for some subjects the long term stable rates of change are near zero, while for others they are positive. It is thus appealing not only to model a common stable rate of change across the subjects but also to let it follow a distribution, say a normal distribution with its mean depending on some baseline covariates. This flexibility will benefit the forecasts of future observations.

Figure 1.

PSA plots of (a) the raw data, (b) the empirical rate of change, which is defined as $\frac{\Delta Y_{ij}}{\Delta t_{ij}}=\frac{Y_{ij}-Y_{i,j-1}}{t_{ij}-t_{i,j-1}}$, for the give subject i with observation Y_ij at time t_ij. All profiles are plotted as the gray solid lines, except one profile highlighted in black color.

A number of methods have been used to study the rate of change in longitudinal studies. A popular approach is through a parametric linear mixed model (Laird and Ware, 1982; Diggle et al., 2002; Verbeke and Molenberghs, 2009), for example the random intercept and slope mixed model for disease progression (Zhang et al., 2008). This model assumes the subject's mean function follows a straight line with constant rate of change, which in turn is dependent on the covariates. In contrast to parametric models, the mean function have been modeled nonparametrically (Rice and Silverman, 1991; Wang and Taylor, 1995; Zeger and Diggle, 1994; Zhang et al., 1998; Verbyla et al., 1999). For these approaches, the rate function, as the first order derivative of the mean function, does not have any parametric form, and usually is not dependent on covariates. For other relevant literature that considers population dynamic models with multiple subjects see Wang et al. (2008), Paul et al. (2009) and Müller and Yao (2010). Additionally, in a time-varying coefficient model (Hastie and Tibshirani, 1993; Hoover et al., 1998) or functional mixed model (Guo, 2002; Morris and Carroll, 2006), the mean function U_i(t) of the ith subject is specified as $U_i\left(t\right)={\Sigma }_{k=0}^K{X}_{ik}{\beta }_k\left(t\right)$. Hence, U_i(t) is a linear combination of several arbitrary smooth functions β_k(t) with covariates X_ik as the weights and depends on covariates linearly. Thus there seems to be a need for a model that allows flexible relationships between the rate function and covariates. Moreover, note that except for few approaches (Qin and Guo, 2006; Welham et al., 2006), nonparametric approaches seldom incorporate any prior knowledge from the subject-matter science, if available, in the modeling of the shape of the rate function.

Our goal is to develop a semiparametric stochastic model for the analysis of the rate function, which is called in this paper a semiparametric stochastic velocity model (SSVM). A key feature of SSVM is to utilize a stochastic process as a prior for the rate function, in a similar spirit to the work of Wahba (1978) and Zhu et al. (2011) for functional data in a single-subject setting. Formally, for each rate function $V_{x_i}\left(t\right)\in \mathbb{R}$ for subject i ε N = {1, 2, …, n} and time $t\in {\mathcal{T}}_s=[0,\infty )$, its prior is assumed to be a Gaussian process, conditional on x_i = (x_i0, x_i1, …, x_ip)′, the vector of covariates for the ith subject. As an important special case of the proposed SSVM, we consider $V_{x_i}\left(t\right)=f_{x_i}\left(t\right)+{\sigma }_{\xi }{W}_i\left(t\right)$, where f_xi(t) has a pre-specified parametric functional form dependent on covariates x_i and ${\sigma }_{\xi }{W}_i\left(t\right)$ is a scaled standard Wiener process. Hence, E{V_xi(t)} = f_xi(t) implies that V_xi(t), the rate function of the ith subject, is expected to be centered about f_xi(t), while the second term ${\sigma }_{\xi }{W}_i\left(t\right)$ allows deviations from the parametric functional expectation f_xi(t).

The remainder of the paper is organized as follows. Section 2 first presents the model and then is devoted to an important special case with the Ornstein-Uhlenbeck process as the prior for the rate function. Section 3 develops MCMC based methods for posterior inference and forecasting. Section 4 applies the methods to analyze the data of PSA profiles. Section 5 presents simulation results to evaluate and compare the performance of the proposed method with other existing methods. The paper concludes with a discussion in Section 6. Some supplementary materials related to the technical details of the proof of Theorem 1 are available online.

2 Semiparametric Stochastic Velocity Model

2.1 Model Specification

Suppose that Y_i(t_ij), j = 1, 2, …, m_i, i = 1, 2, …, n, is the response of the ith subject at time t_ij and satisfies the following hierarchical model, SSVM:

$$Y_i\left(t\right)=U_{{\mathit{x}}_i}\left(t\right)+{\epsilon }_i\left(t\right),t\in {\mathcal{T}}_{\mathit{io}}=\{t_{\mathit{ij}}:t_{i1}<t_{i2}<\cdots <t_{{\mathrm{im}}_i}\},$$ (1)

$${\mathrm{dU}}_{{\mathit{x}}_i}\left(t\right)=V_{{\mathit{x}}_i}\left(t\right),\mathit{dt},t\in {\mathcal{T}}_s=[t_0,\infty ),$$ (2)

$${\mathrm{dV}}_{{\mathit{x}}_i}\left(t\right)=a\{V_{{\mathit{x}}_i}\left(t\right);{\mathit{x}}_i,{\varphi }_i\}\mathit{dt}+b\{V_{{\mathit{x}}_i}\left(t\right);{\mathit{x}}_i,{\varphi }_i\}{\mathit{dW}}_i\left(t\right),t\in {\mathcal{T}}_s,$$ (3)

where U_xi(t) is the mean function for the ith subject's outcome curve, V_xi(t) is the corresponding rate function and W_i(t) denotes the standard Wiener process. Note that in this specification, although the mean function is defined at continuous time ${\mathcal{T}}_s$, it is observed at discrete times ${\mathcal{T}}_{io}$ only and is subject to measurement error. Equation (3) may be regarded as a prior for the rate function V_xi(t), in which the behavior of V_xi(t) is governed by a stochastic differential equation (SDE), with drift term a{V_xi(t); x_i, ϕ_i} and diffusion term b{V_xi(t); x_i, ϕ_i}, where x_i and ϕ_i are the covariate vector and subject-specific parameter vector. We assume that the initial values $[U_{x_i}\left(t_0\right),V_{x_i}\left(t_0\right)]\prime \stackrel{\mathrm{iid}}{~}{\mathcal{N}}_2(0,{\sigma }_0^2{\mathit{I}}_2)$ with large value of variance ${\sigma }_0^2$ to make it non-informative, and that the measurement error ${\epsilon }_i\left(t\right)\stackrel{\mathrm{iid}}{~}\mathcal{N}(0,{\sigma }_{\epsilon }^2)$. Here I_k is the k×k identity matrix and ${\mathcal{N}}_k(m,\Sigma )$ denotes the k-dimensional normal distribution with mean vector m and covariance matrix Σ. Furthermore, [U_xi(t₀), V_xi(t₀)]′, ε_i(t) and W_i(t) are assumed mutually independent.

The SDE in equation (3) gives rise to a general class of Markovian Gaussian processes (Feller, 1970; Grimmett and Stirzaker, 2001). In our model, this stochastic process is considered as the prior for the rate function V_xi(t). According to the specific research interest or context of a given study, we can choose different forms for a{V_xi(t); x_i, ϕ_i}, which measures the instantaneous mean or the expected conditional acceleration, and for b²{V_xi(t); x_i, ϕ_i}, which reflects the instantaneous variance of the rate process. In particular, we have the SSVM-W, when a{V_xi(t); x_i, ϕ_i} = 0 and b{V_xi(t); x_i, ϕ_i} = σ_ξ, and the prior for V_xi(t) is the Wiener process. The resulting mean function takes the form $U_{x_i}\left(t\right)=U_{x_i}\left(t_0\right)+V_{x_i}\left(t_0\right)(t-t_0)+{\sigma }_{\xi }{\int }_{t_0}^{t}W\left(s\right)\mathit{ds}$, which is the partially integrated Wiener process leading to a smoothing spline (Wahba, 1978; Wecker and Ansley, 1983; Ansley and Kohn, 1986) for a given subject. Note that this prior is independent of covariates.

For the PSA data analysis given in Section 4, we specify $a\{V_{x_i}\left(t\right);x_i,{\varphi }_i\}=-\rho \{V_{x_i}\left(t\right)-{\stackrel{‒}{\nu }}_i(x_i,\beta )\}$ and b{V_xi(t); x_i, ϕ_i} = σ_ξ. This specification corresponds to an Ornstein-Uhlenbeck (OU) process for V_xi(t), and the resulting rate function is given by $V_{x_i}\left(t\right)=f_{x_i}\left(t\right)+{\sigma }_{\xi }{W}_i\left(t\right)=V_{x_i}\left(t_0\right)-{\int }_{t_0}^t\rho \{V_{x_i}\left(s\right)-{\stackrel{‒}{\nu }}_i(x_i,\beta )\}\mathit{ds}+{\sigma }_{\xi }{W}_i\left(t\right)$. More details and properties of the OU process can be found in Section 2.2 below. We refer to this specification as SSVM-OU. For the PSA data analysis, it is of interest to estimate the stable rate ${\stackrel{‒}{\nu }}_i(x_i,\beta )$, since V_xi(t) will eventually stabilize and fluctuate around the level given by ${\stackrel{‒}{\nu }}_i(x_i,\beta )$, which describes the long term rate of tumor growth after radiation treatment. In addition, to address the relationship between the long term tumor growth rate ${\stackrel{‒}{\nu }}_i(x_i,\beta )$ and the patients' baseline characteristics, we propose a linear model ${\stackrel{‒}{\nu }}_i(x_i,\beta )={\nu }_i+x_i^{\prime }\beta$, where β = (β₀, β₁, …, β_p)′ is the vector of fixed effect parameters and ${\nu }_i\stackrel{\mathrm{iid}}{~}\mathcal{N}(0,{\sigma }_{\nu }^2)$ are random effects. This subject-specific SSVM-OU is very useful to understand the dynamics of tumor growth, to assess the effect of covariates, and to predict a patient's future PSA values using the baseline covariate information.

2.2 The OU and IOU Processes

The OU process was first proposed as a physical model for the velocity of a particle suspended in a fluid (Uhlenbeck and Ornstein, 1930). It describes a homeostasis system that fluctuates around some stable level and has been applied in biology (Trost et al., 2010), finance (Nicolato and Venardos, 2003) and engineering (Kulkarni and Rolski, 2009), among many others. In the statistics literature, Aalen and Gjessing (2004) studied the first-passage time of an OU process, and Taylor and Law (1998) modeled the serial correlation in a linear mixed model by an integrated OU (IOU) process with mean zero. The OU process is particularly suitable for the PSA profiles considered in this paper, where the rate function of tumor growth reaches a stable level that potentially depends on baseline covariates.

Now we present some properties for both the OU and IOU processes. For ease of exposition, we suppress the subject index i in the discussion. Let U_j := U(t_j) and V_j := V(t_j). The IOU and OU processes are given by, respectively,

$$\mathit{dU}\left(t\right)=V\left(t\right)\mathit{dt},$$ (4)

$$\mathit{dV}\left(t\right)=-\rho \{V\left(t\right)-\stackrel{‒}{\nu }\}\mathit{dt}+{\sigma }_{\xi }\mathit{dW}\left(t\right).$$ (5)

Theorem 1 For IOU and OU processes at time t_j, conditional on the values at time t_j−1and parameters $\stackrel{‒}{\nu }$, ρ, σ_ξ, the transition distribution is given by

$$U_j,V_j\mid U_{j-1},V_{j-1},\stackrel{‒}{\nu },\rho ,{\sigma }_{\xi }\sim {\mathcal{N}}_2({\mathit{m}}_j,{\Sigma }_j),$$

δ_j = t_j − t_j−1, with conditional mean and covariance matrix given, respectively, by,

$${\mathit{m}}_j={\left[U_{j-1}+\stackrel{‒}{\nu }{\delta }_j+\{V_{j-1}-\stackrel{‒}{\nu }\}\left\{\frac{1-\text{exp}(-\rho {\delta }_j)}{\rho }\right\},\stackrel{‒}{\nu }+\{V_{j-1}-\stackrel{‒}{\nu }\}\text{exp}(-\rho {\delta }_j)\right]}^{\prime },$$

$${\Sigma }_j={\sigma }_{\xi }^2\left[\begin{array}{cc}\hfill \frac{{\delta }_j}{{\rho }^2}+\frac{1}{2{\rho }^3}\{-3+4\text{exp}(-\rho {\delta }_j)-\text{exp}(-2\rho {\delta }_j)\}\hfill & \hfill \frac{1}{2{\rho }^2}\{1-2\text{exp}(-\rho {\delta }_j)+\text{exp}(-2\rho {\delta }_j)\}\hfill \\ \hfill \frac{1}{2{\rho }^2}\{1-2\text{exp}(-\rho {\delta }_j)+\text{exp}(-2\rho {\delta }_j)\}\hfill & \hfill \frac{1}{2\rho }\{1-\text{exp}(-2\rho {\delta }_j)\}\hfill \end{array}\right].$$

The proof is included in the supplementary materials.

Corollary 1 For δ_j → ∞ and fixed ρ > 0, such that exp(−ρδ_j) = o(1), then the conditional mean and variance in Theorem 1 can be approximated by,

$${\mathit{m}}_j={[U_{j-1}+\stackrel{‒}{\nu }{\delta }_j,\stackrel{‒}{\nu }]}^{\prime }+{\mathit{R}}_{m_j}\left(1\right),$$

$${\Sigma }_j={\sigma }_2^{\xi }\left[\begin{array}{cc}\hfill \frac{{\delta }_j}{{\rho }^2}-\frac{3}{2{\rho }^3}\hfill & \hfill \frac{1}{2{\rho }^2}\hfill \\ \hfill \frac{1}{2{\rho }^2}\hfill & \hfill \frac{1}{2\rho }\hfill \end{array}\right]+{\mathit{R}}_{{\Sigma }_j}\left(1\right),$$

where the errors in the approximation are ${\mathit{R}}_{m_j}\left(1\right)=[\mathrm{o}\left(1\right),\mathrm{o}\left(1\right)]\prime$ and ${\mathit{R}}_{{\Sigma }_j}\left(1\right)=\left[\begin{array}{cc}\hfill \mathrm{o}\left(1\right)\hfill & \hfill \mathrm{o}\left(1\right)\hfill \\ \hfill \mathrm{o}\left(1\right)\hfill & \hfill \mathrm{o}\left(1\right)\hfill \end{array}\right]$. The proof is straightforward by noting that ρδ_j → ∞ as δ_j satisfies exp (−ρδ_j) = o(1).

Corollary 2 For OU and IOU processes with ρ > 0 and δ_j = o(1), the approximate transition density denoted by $\prec U_j,V_j\mid U_{j-1},V_{j-1},\stackrel{‒}{\nu },\rho ,{\sigma }_{\xi }\succ$ is given by,

$$\begin{array}{c}\hfill \prec U_j,V_j,\mid U_{j-1},V_{j-1},\stackrel{‒}{\nu },\rho ,{\sigma }_{\xi }\succ =\prec V_j\mid V_{j-1},\stackrel{‒}{\nu },\rho ,{\sigma }_{\xi }\succ \delta (U_j-U_{j-1}-V_{j-1}{\delta }_j)\hfill \\ \hfill =\varphi ({\tilde{m}}_j,{\tilde{\Sigma }}_j)\delta (U_j-U_{j-1}-V_{j-1}{\delta }_j)\hfill \end{array}$$

where $\varphi ({\tilde{m}}_j,{\tilde{\Sigma }}_j)$ is the normal density with mean ${\tilde{m}}_j=V_{j-1}-\rho \{V_{j-1}-\stackrel{‒}{\nu }\}{\delta }_j$ and variance ${\tilde{\Sigma }}_j={\sigma }_{\xi }^2{\delta }_j$, and δ(·) is the Dirac Delta function.

This corollary can be proved by taking the component-wise first-order Taylor approximation of m_j and Σ_j in Theorem 1 with respect to δ_j.

3 Inference and Forecasting

3.1 Posterior Distribution Approximation

In this section, we present Bayesian estimation for the mean function U_xi(t), the rate function V_xi(t) and parameters ϕ_i and σ_ε for i = 1,2, –, n. Let [· | ·] denote the exact conditional density, $\prec \cdot \mid \cdot \succ$ the approximate conditional density and $\mathit{U}=[{\mathit{U}}_1^{\prime },{\mathit{U}}_2^{\prime },\cdots ,{\mathit{U}}_n^{\prime }]\prime$ where ${\mathit{U}}_i=[{\mathit{U}}_{i1},{\mathit{U}}_{i2},\cdots ,{\mathit{U}}_{{\mathrm{im}}_i}]\prime$. Similar notation is used for V, Y and x. For the model specified by equations (1), (2) and (3), we first consider the posterior density [ϕ | U, V, Y, x] for ϕ, where $\varphi =[{\varphi }_1^{\prime },{\varphi }_2^{\prime },\cdots ,{\varphi }_n^{\prime }]\prime$. The posterior distribution is given by

$$[\varphi \mid \mathit{U},\mathit{V},\mathit{Y},\mathit{x}]\propto \prod _{i=1}^n\prod _{j=1}^{m_i}[U_{ij},V_{ij}\mid U_{i,j-1},V_{i,j-1},{\varphi }_i,{\mathit{x}}_i][U_0,V_0]\left[{\varphi }_i\right],t\in {\mathcal{T}}_{io}$$ (6)

where [U_ij, V_ij | U_i;j−1M, V_i;j−1, ϕ_i, x_i] is the exact transition density derived from the SDE in equation (3) and [U₀, V₀] and [ϕ_i] are non-informative prior densities. Unfortunately, except for a very few specific forms for the drift and diffusion terms in equation (3), [U_ij, V_ij | U_i;j−1, V_i;j−1, ϕ_i, x_i] is usually analytically intractable. Even when the exact transition density does have a closed form, as is the case for the OU and IOU processes, for which the exact transition density is given in Theorem 1, the posterior density for ϕ still does not have an explicit form. Hence, we will use the Euler approximation to approximate the exact transition density, while applying the method of data augmentation (Tanner and Wong, 1987) to minimize the error in this approximation.

The strategy of combining data augmentation and Euler approximation to approximate the exact transition density has been discussed by Elerian et al. (2001), Eraker (2001), Roberts and Stramer (2001) and Durham and Gallant (2002), in the context of estimating parameters in the SDE for a single diffusion process observed at discrete times without measurement errors. Our approach is related to theirs, but with an important distinction that instead of being partially observed, both processes V_xi(t) and U_xi(t) are completely unobserved, and will be sampled as part of an MCMC algorithm. In this manner, we will estimate the processes V_xi(t), U_xi(t) and the parameters ϕ. It is worth pointing out that although augmentation only needs to take place for the latent process, augmenting the data themselves will facilitate the operation of the simulation smoother, as this algorithm requires observations (either observed or augmented) available at each corresponding time. In addition, the data augmentation allows us to create augmented longitudinal data with a common set of time points, and consequently this method enables us to handle longitudinal data with irregularly spaced times which may vary across the subjects.

To carry out the data augmentation and the Euler approximation, we first specify time points at which data would be augmented. Let ${\mathcal{T}}_{\mathit{ia}}=\{t:t=t_{ij}+k{\tau }_{ij},{\tau }_{ij}=\frac{t_{i,j+1}-t_{ij}}{M_{ij}}<{\tau }_c,t\in (t_{ij},t_{i,j+1}),k=1,2,\dots ,M_{ij,j}=1,2,\dots ,m_i-1\}$ denotes the set of augmentation times for the ith subject. Consequently, the time interval τ_ij between adjacent data points, either observed or augmented, is less than τ_c. In addition, let $\mathcal{T}={\cup }_{i=1}^n({\mathcal{T}}_{io}\cup {\mathcal{T}}_{ia})=t:t_j,j=1,2,\dots ,m$ denote the set of all possible time points of the observed and augmented data across subjects. With further data augmentation at times $t\in {\mathcal{T}}_{im}=[t:t\in \mathcal{T},t\notin {\mathcal{T}}_{io},t\notin {\mathcal{T}}_{ia}]$, each subject would have either observed or augmented data ${\tilde{Y}}_i=[Y_{i1},Y_{i2},\cdots ,Y_{im}]\prime$ at the common time set $\mathcal{T}$. The Euler approximation to equations (2) and (3) for $t\in \mathcal{T}$ leads to the following difference equations:

$$U_{ij}=U_{i,j-1}-V_{i,j-1}{\delta }_j,$$ (7)

$$V_{ij}=V_{i,j-1}+a\{V_{i,j-1};{\mathit{x}}_i,{\varphi }_i\}{\delta }_j+b\{V_{i,j-1};{\mathit{x}}_i,{\varphi }_i\}(W_j-W_{j-1}),$$ (8)

where $W_j-W_{j-1}\sim {\mathcal{N}}_1(0,{\delta }_j)$ and j = 1, 2, …, m. Thus, the conditional posterior density for ϕ is approximated by,

$$\prec \varphi \mid \tilde{\mathit{U}},\tilde{\mathit{V}},\tilde{\mathit{Y}},\mathit{x}\succ \propto \prod _{i=1}^n\prod _{j=1}^m\prec U_{\mathit{ij}},V_{\mathit{ij}},\mid U_{i,j-1},V_{i,j-1},{\varphi }_i,{\mathit{x}}_i\succ [U_0,V_0]\left[{\varphi }_i\right],$$ (9)

where $\tilde{\mathit{U}}=[{\tilde{\mathit{U}}}_1^{\prime },{\tilde{\mathit{U}}}_2^{\prime },\dots ,{\tilde{\mathit{U}}}_n^{\prime }]\prime$ with ${\tilde{\mathit{U}}}_i=[U_{i1},U_{i2},\dots ,U_{im}]\prime$ and similarly for $\tilde{V}$ and $\tilde{Y}$. Note that the approximate transition density ≺ U_ij, V_ij | U_i,j−1, V_i,j−1, ϕ_i, x_i ≻ in equation (9) is given by,

$$\prec U_{\mathit{ij}},V_{\mathit{ij}}\mid U_{i,j-1},V_{i,j-1},{\varphi }_i,{\mathit{x}}_i\succ ={\mathcal{N}}_1(V_{i,j-1}+a\{V_{i,j-1};{\mathit{x}}_i,{\varphi }_i\}{\delta }_j,b^2\{V_{i,j-1};{\mathit{x}}_i,{\varphi }_i\}{\delta }_j)\times \delta (U_{\mathit{ij}}-U_{i,j-1}-V_{i,j-1}{\delta }_j),$$ (10)

which is derived from equations (7) and (8). This implies that it is feasible to directly sample from the posterior distribution of ϕ, if the conjugate priors for ϕ are chosen.

With regard to the posterior samples of U_xi(t) and V_xi(t) for $t\in {\mathcal{T}}_{s_1}$, we follow equations (7) and (8) to come up with their approximations, denoted by $U_{x_i}^{\left(m\right)}$(t) and $V_{x_i}^{\left(m\right)}$(t), with linear interpolation for t between t_j−1 and t_j for j = 1, 2, …, m. Bouleau and Lepingle (1992) showed that under some regularity conditions, with constant C_i, the L_p-norm of the approximation error for V_xi(t) is bounded at the rate of $\sqrt{\frac{\text{log}m}{m}}$; that is,

$${\parallel \underset{t\in {\mathcal{T}}_{s_1}}{\text{sup}}\mid V_{{\mathit{x}}_i}\left(t\right)-V_{{\mathit{x}}_i}^{\left(m\right)}\left(t\right)\mid \parallel }_p\le C_i{\left(\frac{1+\text{log}m}{m}\right)}^{1∕2},1\le p<\infty ,$$

where ∥f∥_p = {∫_Ω |f(z)|^pdμ(z)}^1/p for a real function f on the space (Ω, $\mathcal{A}$) with measure μ on random variable z. This indicates that if m is sufficiently large, then $V_{x_i}^{\left(m\right)}$(t) will approach to its continuous counterpart V_xi(t) with arbitrary precision. Similar arguments hold for $U_{x_i}^{\left(m\right)}$(t). Note that we will sample m instead of m_i data points for $U_{x_i}^{\left(m\right)}$(t) and $V_{x_i}^{\left(m\right)}$(t) with possibly m ≫ m_i. Hence, the benefit of introducing augmented data is two fold: (i) it reduces the error of approximation, when $U_{x_i}^{\left(m\right)}$(t) or $V_{x_i}^{\left(m\right)}$(t), instead of $U_{x_i}^{\left(m\right)}$(t) or $V_{x_i}^{\left(m\right)}$(t), is used to replace U_xi(t) or V_xi(t); (ii) it gives a more accurate approximation to the exact transition density, as shown by Pedersen (1995), which benefits estimation of model parameters ϕ. Under the assumption that m is large enough such that the approximation error is small, for the ease of exposition, we still use V_xi(t) instead of $V_{x_i}^{\left(m\right)}$(t) throughout the rest of the paper. U_xi(t) is treated similarly.

In the MCMC algorithm to update the values of U_xi(t) and V_xi(t) for $t\in t_0\bigcup \mathcal{T}$, we draw samples from

$$\prec U_0,V_0,\tilde{\mathit{U}},\tilde{\mathit{V}}\mid \tilde{\mathit{Y}},\mathit{x},\varphi ,{\sigma }_{\epsilon }^2\succ \propto \prod _{i=1}^n\prod _{j=1}^m[{\tilde{Y}}_{\mathit{ij}}\mid U_{\mathit{ij}},{\sigma }_{\epsilon }^2]\prec U_{\mathit{ij}},V_{\mathit{ij}}\mid U_{i,j-1},V_{i,j-1},{\varphi }_i,{\mathit{x}}_i\succ \times [U_0,V_0],$$ (11)

where $[{\tilde{Y}}_{ij}\mid U_{ij},{\sigma }_{\epsilon }^2]=\varphi (U_{ij},{\sigma }_{\epsilon }^2)$, ≺ U_ij, V_ij | U_i,j−1, ϕ_i, x_i ≻ is given in equation (10) and [U₀, V₀] is a non-informative prior. Equivalently, the posterior density (11) may be derived from a state space model representation (Durbin and Koopman, 2001), which is a useful reformulation of the SSVM in equations (1), (2) and (3) when it is discretized using the Euler approximation and data augmentation.

Consider an example where V_xi(t) follows the OU process and ≺ U_ij, V_ij | U_i,j−1, ϕ_i, x_i ≻ is given in Corollary 2. Let ${\tilde{Y}}_j=[{\tilde{Y}}_{1j},{\tilde{Y}}_{2j},\dots ,{\tilde{Y}}_{nj}]\prime$ denote the observed or augmented data for n subjects at time t_j, and let $\theta =[{\theta }_{1j}^{\prime },{\theta }_{2j}^{\prime },\dots ,{\theta }_{nj}^{\prime }]\prime$ be the latent states with ${\theta }_{ij}=[U_{x_i}\left(t_j\right),V_{x_i},\stackrel{‒}{\nu }({\mathit{x}}_i,\beta )]\prime$. The corresponding SSVM can be expressed as a state space model, given as follows:

$${\tilde{\mathit{Y}}}_j=\mathit{F}{\prime }_j{\theta }_j+{\epsilon }_j,{\epsilon }_j\sim {\mathcal{N}}_n(0,{\sigma }_{\epsilon }^2{\mathit{I}}_n)$$

$${\theta }_j={\mathit{G}}_j{\theta }_{j-1}+{\xi }_j,{\xi }_j\sim {\mathcal{N}}_{3n}(0,{\sigma }_{\xi }^2{\mathit{I}}_n\otimes {\Sigma }_j)$$

where F_j = I_nI ⊗ F_ij, G_j = I_n ⊗ G_ij, F_ij = [1, 0, 0]′ with ⊗ denoting Kronecker product,

$${\mathit{G}}_{\mathit{ij}}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill {\delta }_j\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1-\rho {\delta }_j\hfill & \hfill \rho {\delta }_j\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],{\Sigma }_j=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\delta }_j\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$$

Likewise, when V_xi(t) follows a Wiener process, the corresponding reformulation as a state space model can be obtained in a similar manner.

In this paper we have adopted the MCMC method for Bayesian inference. In the literature other likelihood-based or sampling-based methods have also been developed for nonlinear and/or non-Gaussian state space models, including Kitagawa's (1987) numeric algorithm using piecewise linear approximation, Durbin and Koopman's (1997) simulated maximum likelihood estimation, Jørgensen et al.'s (1999) Kalman estimating equations and some recent work on sequential Monte Carlo methods using particulate filtering (Gordon et al., 1993; Pitt and Shephard, 1999; Liu, 2008; Andrieu et al., 2010), among others.

3.2 MCMC Algorithm

Under the state space model formulation, Gibbs sampler was first developed to sample one latent state θ_j at a time, this was later improved by various algorithms that use simultaneous block-based sampling schemes (e.g. Frühwirth-Schnatter 1994; Carter and Kohn 1994). The simulation smoother proposed first by de Jong and Shephard (1995) and later improved by Durbin and Koopman (1997) provides a remarkably efficient sampling tool. It draws samples of θ_j through sampling independent innovations ξ_j, rather than realizations of a Markov process, so the entire sampling is based on very low dimensional distributions and free of autocorrelation. Thus, the rate of mixing and moreover burn-in can be achieved quickly. We will use the simulation smoother in our implementation.

The proposed MCMC algorithm iterates through the following steps.

1. Draw augmented data according to $Y_i\left(t\right)\sim \mathcal{N}(U_{x_i}\left(t\right),{\sigma }_{\epsilon }^2)$ at times $t\in {\mathcal{T}}_{ia}\bigcup {\mathcal{T}}_{im}$ for the ith subject, i = 1, 2, …, n.

2. Update latent states U_xi(t) and V_xi(t) for $t\in t_0\bigcup \mathcal{T}$ from the posterior density (11) by using the simulation smoother.

3. Update ϕ by sampling from the posterior density (9). In particular, when V_xi(t) follows an OU process and is discretized through the Euler approximation, the collection of equations (8) can be equivalently reformulated as a linear mixed model,

   $${\mathit{Y}}_j^{\ast }={\mathit{X}}_j^{\ast }{\beta }^{\ast }+{\mathit{Z}}_j^{\ast }{\mathit{b}}^{\ast }+{\xi }_j^{\ast },$$

   where ${\mathit{Y}}_j^{\ast }=\frac{V_j-V_j-1}{\sqrt{{\delta }_j}}$, ${\mathit{X}}_j^{\ast }=[\mathit{X}\sqrt{{\delta }_j},{\mathit{V}}_{j-1}\sqrt{{\delta }_j}]$, ${\mathit{Z}}_j^{\ast }=-\sqrt{{\delta }_j}{\mathit{I}}_n$ with V_j = [V_1j, V_2j, …, V_nj and $\mathit{X}=[x_1^{\prime },x_2^{\prime },\dots ,x_n^{\prime }]\prime$. Further, β* = [ρβ′, −ρ]′, b* = ρν, ν = [ν₁, ν₂, …, ν_n]′, ${\xi }_j^{\ast }\sim {\mathcal{N}}_n(0,{\sigma }_{\xi }^2{\mathit{I}}_n)$, $\mathit{b}\ast \sim {\mathcal{N}}_n(0,{\rho }^2{\sigma }_{\nu }^2{\mathit{I}}_n)$. As a result, the set of model parameters is $\varphi \ast =[\beta \ast ,\mathit{b}\ast ,{\sigma }_{\xi }^2,{\rho }^2{\sigma }_{\nu }^2]\prime$, can be sampled straightforwardly by using the standard Gibbs sampler in the linear mixed model (Ruppert et al., 2003, Chap. 16) with non-informative conjugate priors, $\beta \ast \sim {\mathcal{N}}_{p+2}(0,{\sigma }_{\beta \ast }^2{\mathit{I}}_{p+2})$, ${\sigma }_{\xi }^2\sim \mathcal{IG}(a_{\xi },b_{\xi })$, and ${\rho }^2{\sigma }_{\nu }^2\sim \mathcal{IG}(a_{\sigma },b_{\sigma })$. Here $\mathcal{IG}(a,b)$ denotes the inverse gamma distribution with shape parameter a and scale parameter b.
4. Update ${\sigma }_{\epsilon }^2$ by sampling from the following posterior distribution

   $$[{\sigma }_{\epsilon }^2\mid \tilde{\mathit{U}},\tilde{\mathit{V}},\tilde{\mathit{Y}},\mathit{x}]\sim \mathcal{IG}(a_{\epsilon }+\frac{1}{2}\mathit{mn},b_{\epsilon }+\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^m{(Y_i\left(t_j\right)-U_{\mathit{xi}}\left(t_j\right))}^2),$$

   where the prior distribution for ${\sigma }_{\epsilon }^2$ is $\mathcal{IG}(a_{\epsilon },b_{\epsilon })$.

3.3 Bayesian Posterior Forecasting

The proposed model is useful to forecast processes of interest, including U_xi(t), V_xi(t) and Y_i(t), for $t\in {\mathcal{T}}_{S2}=\{t:t>t_m\}$. With the availability of posterior samples for U_xi(t), V_xi(t), ϕ_i and σ_ε with i = 1, 2, …, n and $t\in \mathcal{T}$, it is straightforward to derive Bayesian posterior forecasting. Note that the posterior forecasting distributions are,

$$[U_{\mathit{xi}}\left(t\right),V_{\mathit{xi}}\left(t\right)\mid \mathit{Y},\mathit{x}]=\int \int \int [U_{\mathit{xi}}\left(t\right),[V_{\mathit{xi}}\left(t\right)\mid U_{\mathit{xi}}\left(t_m\right),V_{\mathit{xi}}\left(t_m\right),{\varphi }_i,\mathit{x}]\times [U_{\mathit{xi}}\left(t_m\right),V_{\mathit{xi}}\left(t_m\right),{\varphi }_i\mid \mathit{Y},\mathit{x}]{\mathit{dU}}_{\mathit{xi}}\left(t_m\right){\mathit{dV}}_{\mathit{xi}}\left(t_m\right)d{\varphi }_i,$$

and

$$[Y_i\left(t\right)\mid \mathit{Y},x]=\int \int \int [Y_i\left(t\right)\mid U_{\mathit{xi}}\left(t\right),{\sigma }_{\epsilon }^2][U_{\mathit{xi}}\left(t\right),V_{\mathit{xi}}\left(t\right)\mid \mathit{Y},\mathit{x}]\times [{\sigma }_{\epsilon }^2\mid \mathit{Y},\mathit{x}]{\mathit{dU}}_{\mathit{xi}}\left(t\right){\mathit{dV}}_{\mathit{xi}}\left(t\right)d{\sigma }_{\epsilon }^2,$$

Thus, we draw $U_{x_i}^r\left(t\right)$, $V_{x_i}^r\left(t\right)$ and $Y_i^r\left(t\right)$ from $[U_{x_i}^r\left(t\right),V_{x_i}^r\left(t\right)\mid U_{x_i}^r\left(t_m\right),V_{x_i}^r\left(t_m\right),{\varphi }_{is}^r,x]$ and $[Y_i^r\left(t\right)\mid U_{x_i}^r\left(t\right),{\sigma }_{\epsilon }^{2r}]$ for r = 1,2, …, where $U_{x_i}^r\left(t_m\right)$, $V_{x_i}^r\left(t_m\right)$, ${\varphi }_{is}^r$ and ${\sigma }_{\epsilon }^{2r}$ are the rth posterior samples from the MCMC algorithm. If [U_xi(t), V_xi(t) | U_xi(t_m), V_xi(t_m), ϕ_i, x] does not have a closed form, the approximate transition density ≺ U_xi(t), V_xi(t) | U_xi(t_m), V_xi(t_m), ϕ_i, x ≻ could be used instead along with data augmentation.

4 Application to the PSA Data

We apply the proposed SSVM-OU to analyze the PSA data discussed in Section 1. The prior of the rate function V_xi(t) is assumed to be the OU process with $a\{V_{x_i}\left(t\right);x_i,{\varphi }_i\}=-\rho \{V_{x_i}\left(t\right)-{\stackrel{‒}{\nu }}_i({\mathit{x}}_i,\beta )\}$ and b{V_xi(t); x_i, ϕ_i} = σ_ξ in equation (3). A total of 739 observations are obtained for 50 subjects. The number of observations for each subject varies from 13 to 24. The initial observation for all subjects is at one month (0.083 years) after EBRT treatment, and the time for the last observation ranges from 3.833 to 8.083 years, with the average of 6.050 years. To reduce the approximation error discussed in Section 3.1, we further augment the data to let the time interval between adjacent data points, either observed or augmented, be less than 0.0208 years. The appropriateness of this choice of time interval is confirmed using the simulation studies in Section 5. We investigate the association of the pretreatment covariates (i.e. baseline PSA, Gleason score and T-stage) with the stable PSA rate via the model ${\stackrel{‒}{\nu }}_i({\mathit{x}}_i,\beta )={\nu }_i+{\beta }_0+{\beta }_1{X}_{Pi}+{\beta }_2{X}_{Ti}+{\beta }_3{X}_{Gi}$, where ${\nu }_i\sim {\mathcal{N}}_1(0,{\sigma }_{\nu }^2)$ is a random effect; X_Pi denotes the log-transformed baseline PSA for the ith subject, centered around the mean of 2.3; X_Gi is equal to 1 if Gleason score is above or equal to level 7, and is 0 otherwise; X_Ti takes the value of 1 if T-stage is at level 2 or higher, and is 0 otherwise. We leave out the last observation for each subject as well as the observations after year 5 as validation data to assess the forecasting ability of the model.

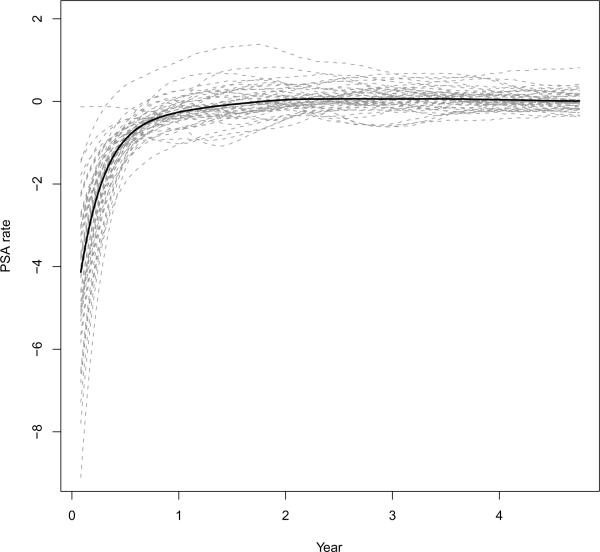
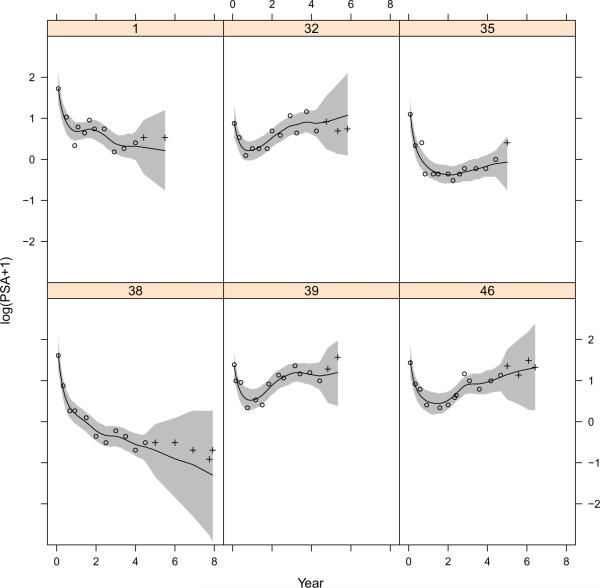
The posterior draws are obtained from the proposed MCMC algorithm with 20,000 iterations, discarding the first 10,000 as the burn-in stage and subsequently saving every 10th draws. The trace plots suggest the algorithm converges fast and mixes well. Table 1 presents the posterior summary statistics for the parameters. Baseline PSA and T-stage are found to have significant effect on the PSA stable rate. This result suggests that Baseline PSA and T-stage are predictive of the long term rate of change for PSA, which is in agreement with the finding by Lieberfarb et al. (2002). Figure 2 displays E[V_xi(t) | Y], the posterior means of the rate function for each subject (shown as dashed lines), and E[V (t) | Y] = E[E[V_xi(t) | Y]], the posterior mean of the rate function in the population (shown as a solid line). It is clear that although the rate function for the population is smooth and may be specified by a parametric form, the individual rate functions are much more wiggly, vary significantly across subjects and would be difficult to model parametrically. Figure 3 shows the posterior means and credible intervals of U_xi(t) for six randomly selected subjects, including the forecasted U_xi(t) after year 5. Note that the width of the forecasted credible intervals is comparable to the theoretical results given in Corollary 1.

Table 1.

PSA data: Posterior means and quantiles of parameters for the SSVM-OU and LMM.

Model	Parameter	Mean	SD	2.5%	50%	97.5%
SSVM-OU	${\sigma }_{\epsilon }^2$	0.044	0.004	0.037	0.044	0.053
	${\sigma }_{\xi }^2$	1.365	0.297	0.921	1.320	2.108
	ρ	3.721	0.360	3.101	3.690	4.464
	${\sigma }_{\nu }^2$	0.054	0.015	0.031	0.051	0.089
	β 0	−0.171	0.085	−0.335	−0.169	−0.004
	β 1	0.139	0.072	0.001	0.139	0.277
	β 2	0.242	0.095	0.060	0.237	0.438
	β 3	0.061	0.103	−0.157	0.064	0.269
LMM	β 20	0.061	0.066	−0.072	0.058	0.200
	β 21	0.116	0.056	0.008	0.117	0.225
	β 22	0.260	0.076	0.116	0.260	0.411
	β 23	0.046	0.078	−0.105	0.046	0.193

Figure 2.

Posterior means of V_xi(t) for each subject as gray dashed lines and the population-level rate function V (t) as black solid line

Figure 3.

Plots of training data points (ο), validation data points (+), posterior means (−) and 95% credible intervals (gray shades) of U_xi(t) for six randomly selected subjects.

For comparison, we also analyze the PSA data using smoothing splines and a parametric linear mixed-effects model(LMM). The model fits are evaluated by the Deviance Information Criterion (DIC, Speigelhalter et al., 2003). Note that $\mathit{DIC}=\stackrel{‒}{D}+p_D$, where the posterior mean deviance $\stackrel{‒}{D}$ measures the goodness of fit and the “effective number of parameters” p_D measures the model complexity. According to Speigelhalter et al. (2003), DIC may be regarded asymptotically as a generalization of the Akaike information criterion (AIC). Similar to AIC, a smaller value of DIC indicates a better trade-off between the fit to the data and the complexity of model. We further compare the forecasting ability of these three models on the validation data points. For the smoothing spline approach, we obtain the estimates of V_xi(t) from the SSVM-W with a Wiener process as the prior for V_xi(t), where a{V_xi(t); x_i,ϕ_i} = 0 and b{V_xi(t); x_i,ϕ_i} = σ_ξ in equation (3). As mentioned in Section 2.1, the estimation of V_xi(t) from this model, is equivalent to estimation by a smoothing spline with a common smoothing parameter $\lambda =\frac{{\sigma }_{\xi }^2}{{\sigma }_{\xi }^2}$. The exact transition density in this SSVM-W, is given by Wecker and Ansley (1983) as

$$[U_i,V_j\mid U_{j-1},V_{j-1},{\sigma }_{\xi }]\sim {\mathcal{N}}_2({\mathit{m}}_i,{\mathit{V}}_j),$$

with

$${\mathit{m}}_j=[U_{j-1}+V_{j-1}{\delta }_j,V_{j-1}]\prime ,$$

$${\mathit{V}}_j={\sigma }_{\xi }^2\left[\begin{array}{cc}\hfill \frac{{\delta }_j^3}{3}\hfill & \hfill \frac{{\delta }_j^2}{2}\hfill \\ \hfill \frac{{\delta }_j^2}{2}\hfill & \hfill {\delta }_j\hfill \end{array}\right],$$

and is used in the proposed MCMC algorithm. The forecasting of future observations is outlined in Section 3.3 for the SSVM-OU and SSVM-Ws. The parametric linear mixed model is similar to the one given by Proust-Lima et al. (2008),

$$\begin{array}{cc}\hfill Y_i\left(t_{\mathit{ij}}\right)& =U_{{\mathit{x}}_i}\left(t_{\mathit{ij}}\right)+{\epsilon }_i\left(t_{\mathit{ij}}\right)\hfill \\ \hfill & =U_{{\mathit{x}}_i}^0\left(t_{\mathit{ij}}\right)+U_{{\mathit{x}}_i}^1\left(t_{\mathit{ij}}\right)+U_{{\mathit{x}}_i}^2\left(t_{\mathit{ij}}\right)+{\epsilon }_i\left(t_{\mathit{ij}}\right)\hfill \\ \hfill & =({\beta }_{00}+{\nu }_{0i}+{\beta }_{01}{X}_{\mathit{Pi}})+({\beta }_{10}+{\nu }_{1i}+{\beta }_{11}{X}_{\mathit{Pi}}+{\beta }_{12}{X}_{\mathit{Ti}})f_1\left(t_{\mathit{ij}}\right)+({\beta }_{20}+{\nu }_{2i}+{\beta }_{21}{X}_{\mathit{Pi}}+{\beta }_{22}{X}_{\mathit{Ti}}+{\beta }_{23}{X}_{\mathit{Gi}})f_2\left(t_{\mathit{ij}}\right)+{\epsilon }_i\left(t_{\mathit{ij}}\right),\hfill \end{array}$$ (12)

where the mean function U_xi(t) consists of three parts: (i) post-therapy level $U_{x_i}^0\left(t\right)$, (ii) short-term evolution $U_{x_i}^1\left(t\right)$, and (iii) long-term evolution $U_{x_i}^2\left(t\right)$. In addition, f₁(t) = (1 + t)^−1.5 − 1 and f₂(t) = t; the fixed effects ${\beta }_{\mathit{lmm}}=[{\beta }_{00},{\beta }_{01},{\beta }_{10},{\beta }_{11},{\beta }_{12},{\beta }_{20},{\beta }_{21},{\beta }_{22},{\beta }_{23}]\prime \sim {\mathcal{N}}_9(0,{\sigma }_{\beta ,\mathit{lmm}}^2{\mathit{I}}_9)$ a non-informative prior with large value of ${\sigma }_{\beta ,\mathit{lmm}}^2$; the random effects $[{\nu }_{0i},{\nu }_{1i},{\nu }_{2i}]\prime \sim {\mathcal{N}}_3(0,{\Sigma }_{2\nu ,\mathit{lmm}}^2)$ where Σ_ν,lmm is a diagonal matrix with its main diagonal entries ${\nu }_{\mathit{lmm}}=[{\sigma }_{0\nu ,\mathit{lmm}}^2,{\sigma }_{1\nu ,\mathit{lmm}}^2,{\sigma }_{3\nu ,\mathit{lmm}}^2]\prime$; measurement error ${\epsilon }_i\left(t_{ij}\right)\sim {\mathcal{N}}_1(0,{\sigma }_{\epsilon ,\mathit{lmm}}^2)$. We further assume noninformative prior distributions $\mathcal{IG}$ with small values of a and b for ${\sigma }_{\beta ,\mathit{lmm}}^2$, ${\sigma }_{0\nu ,\mathit{lmm}}^2$, ${\sigma }_{1\nu ,\mathit{lmm}}^2$, ${\sigma }_{2\nu ,\mathit{lmm}}^2$, and ${\sigma }_{\epsilon \nu ,\mathit{lmm}}^2$ respectively. The MCMC algorithm for the linear mixed model (Ruppert et al., 2003, Chap. 16) is applied to draw the posterior samples with the same burn-in stage and thinning scheme as for the MCMC algorithm for the SSVM-OU. Table 1 presents the posterior summary of the parameters β₂₀, β₂₁, β₂₂, and β₂₃, which are involved in the long-term evolution $U_{x_i}^2\left(t\right)$ in equation (12). Note that these parameters in the LMM are designed to measure the association between the long term stable level and the covariates of the interest, similar to the parameter β₀, β₁,β₂, and β₃ in the SSVM-OU. Given the rth samples ${\beta }_{\mathit{lmm}}^r$, ${\nu }_{\mathit{lmm}}^r$ and ${\sigma }_{\epsilon ,\mathit{lmm}}^{2r}$, the forecasts of PSA at time t for the ith subject can be drawn from $Y_i^r\left(t\right)\sim \mathcal{N}(U_{x_i}^r\left(t\right),{\sigma }_{\epsilon ,\mathit{lmm}}^{2r})$, where $U_{x_i}^r\left(t\right)=({\beta }_{00}^r+{\nu }_{0i}^r+{\beta }_{01}^r{X}_{Pi})+({\beta }_{10}^r+{\nu }_{1i}^r+{\beta }_{11}^r{X}_{Pi}+{\beta }_{12}^r{X}_{Ti})f_1\left(t\right)+({\beta }_{20}^r+{\nu }_{2i}^r+{\beta }_{21}^r{X}_{Pi}+{\beta }_{22}^r{X}_{Ti}+{\beta }_{23}^r{X}_{Gi})f_2\left(t\right)$.

The values of DIC for SSVM-OU and SSVM-W are 71.809 and 119.400 respectively, both of which are significantly lower than that of LMM (151.048). Thus, SSVM-OU fits the data best among these three models. This implies that the parametric LMM is less able to capture longitudinal dynamics of subject's trajectories than the other two SSVMs. Next, to compare the prediction capability among these three models, we predict the 164 validation data points and evaluate their posterior predictive ability. Table 2 presents relative bias and mean squared error (MSE) of the point forecast based on the posterior mean, as well as corresponding coverage rate and averaged length of credible interval. For the 69 validation data points within 1 year distance from the last training data points, the SSVM-OU performs best, with the smallest MSE. For the remaining validation data points at later times, the SSVM-W outperforms the other two in terms of relative bias and MSE. However, for the coverage rate, the SSVM-OU intervals are closest to the nominal 95% level, whereas those from the SSVM-W are too wide to be clinically useful. This may be due to the nonstationary variance of the latent process of SSVM-W.

Table 2.

PSA data: Posterior forecasting of the validation data points. The relative bias is defined as $E(\tilde{Y}∕Y-1)$ for $\tilde{Y}$ the posterior mean of validation data point Y.

Method	Type	Relative Bias	MSE	Coverage Rate	Interval Length
SSVM-OU	≤ 1 year	−0.143	0.076	1	1.403
	> 1 year	−0.913	0.581	0.966	2.356
	All	−0.644	0.404	0.912	2.023
SSVM-W	≤ 1 year	−0.047	0.098	1	2.379
	> 1 year	0.031	0.403	1	8.329
	All	0.040	0.296	1	6.250
LMM	≤ 1 year	0.205	0.108	0.899	1.226
	> 1 year	0.387	0.568	0.672	1.610
	All	0.323	0.407	0.748	1.476

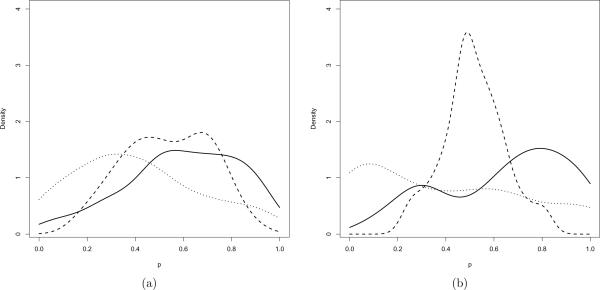
Besides evaluation of the point forecasts and the corresponding credible intervals, we further use the probability integral transform (PIT, Dawid, 1984; Gneiting et al., 2007) value to assess the predictive performance of the probabilistic forecasts. This forecast can be expressed as the posterior predictive cumulative distribution functions (CDFs) F_ij(Y), where Y is the forecasted validation data point at time t_ij for the ith subject and is assumed to be generated from the true unknown CDF G_ij(Y). For the observed validation data point Y_ij, the PIT value p_ij = F_ij(Y_ij) should have a uniform distribution, if F_ij(Y) = G_ij(Y) for every i and j. We estimate F_ij(t) by the empirical CDF ${\tilde{F}}_{ij}\left(Y\right)$, which is based on the Bayesian posterior forecasting draws for the three models. The corresponding smoothed density plots of ${\tilde{p}}_{ij}$ are displayed in Figure 4. The density of ${\tilde{p}}_{ij}$ for the SSVM-OU is left skewed, indicating the forecasts are slightly under predicted, while the density for the linear mixed model is right skewed and the forecasts are slightly over predicted. The density for the SSVM-W is hump-shaped, implying the posterior predictive distribution is over dispersed and the credible intervals are too wide on average. While none of the models gives the ideal PIT plots, the plots of SSVM-OU and the LMM are reasonably close to a uniform density..

Figure 4.

PIT density plots for (a) t_ij ≤ 1 year, (b) t_ij > 1 year of SSVM-OU (−), SSVM-W (- - -), LMM (⋯)

5 A Simulation Study

We carry out a simulation study to (i) assess the performance of the proposed MCMC algorithm in estimating the model parameters and stable rates ${\stackrel{‒}{\nu }}_i({\mathit{x}}_i,\beta )$ and (ii) compare the performance of the proposed SSVM-OU with the other two methods for forecasting future observations. We generate 100 replicated datasets from the SSVM-OU with the model parameter set close to those estimated from the analysis of the PSA data. Each dataset includes 20 subjects each with 13 observations and three validation data points per subject. The observations are equidistantly spaced with time interval 0.416, equal to the median of time intervals in the PSA data. The three validation data points are at 0.08, 0.5 and 1 years after the last observation, respectively. To investigate the influence of data augmentation on the estimation of the model parameters, we analyze the same dataset using the proposed MCMC algorithm without data augmentation, and with 9 and 19 augmented data points between the consecutive observed data points. The corresponding time interval between the adjacent data points, either observed or augmented, decreases from 0.416 in the original datasets to 0.0416 and 0.0208 for the MCMC algorithm with 9 and 19 augmented data points between neighboring observations.

Table 3 presents simulation results for the estimation of model parameters, assessed by relative bias, MSE of posterior means, coverage rate and average length of credible interval. All results indicate clearly that the data augmentation is critical to obtain proper estimates of the second moment parameters, ${\sigma }_{\epsilon }^2$, ${\sigma }_{\xi }^2$, ${\sigma }_{\nu }^2$ and ρ. Their relative biases and MSEs decrease significantly even by adding 9 data points between adjacent observations. For example, the relative bias of ρ reduces from 0.47 to 0.052 and the MSE drops from 2.704 to 0.0360. Augmentation with 19 data points can further improve the relative bias in the estimation of parameters ${\sigma }_{\xi }^2$ and ρ, and no additional improvement results from more aggressive augmentation (the results not shown here). The data augmentation, however, has little effect on the relative bias for the estimation of parameters of interest, β₁, β₂ and β₃, implying that the consistent estimation for these parameters may be obtained using observed data. Yet, the data augmentation has noticeable effects on the coverage rates, because it affects the variance of posterior distributions.

Table 3.

Simulation results on the estimation of SSVM-OU parameters. The relative bias is defined as $E(\tilde{\varphi }∕\varphi -1)$ for $\tilde{\varphi }$ the posterior mean of the parameter ϕ.

Data Augmented	Parameter	Truth	Relative Bias	MSE	Coverage Rate	Interval Length
0	${\sigma }_{\epsilon }^2$	0.05	−0.202	1.294e−04	0.678	0.026
	${\sigma }_{\xi }^2$	1.00	−0.408	1.689e−01	0.044	0.461
	ρ	3.50	−0.470	2.704e+00	0.000	0.101
	${\sigma }_{\nu }^2$	0.05	2.101	1.123e−02	0.211	0.299
	β 0	−0.15	0.03	1.992e−02	1.000	1.150
	β 1	0.15	0.139	3.140e−02	1.000	1.307
	β 2	0.25	−0.006	1.693e−02	1.000	1.120
	β 3	0.10	−0.105	1.995e−02	1.000	1.166
9	${\sigma }_{\epsilon }^2$	0.05	0.012	2.952e−05	0.967	0.024
	${\sigma }_{\xi }^2$	1.00	−0.041	2.253e−02	0.967	0.800
	ρ	3.50	−0.052	3.596e−02	0.256	0.273
	${\sigma }_{\nu }^2$	0.05	0.548	9.410e−04	0.989	0.133
	β 0	−0.15	0.035	2.033e−02	0.978	0.647
	β 1	0.15	0.135	3.133e−02	0.956	0.739
	β 2	0.25	0.005	1.673e−02	0.989	0.634
	β 3	0.10	−0.099	2.006e−02	0.956	0.660
19	${\sigma }_{\epsilon }^2$	0.05	0.013	3.921e−05	0.956	0.024
	${\sigma }_{\xi }^2$	1.00	0.007	2.497e−02	0.967	0.802
	ρ	3.50	−0.018	8.104e−03	0.911	0.288
	${\sigma }_{\nu }^2$	0.05	0.494	7.960e−04	0.989	0.126
	β 0	−0.15	0.022	2.013e−02	0.967	0.625
	β 1	0.15	0.138	3.135e−02	0.944	0.713
	β 2	0.25	0.003	1.686e−02	0.978	0.612
	β 3	0.10	−0.113	1.980e−02	0.978	0.635

For the data simulated from the SSVM-OU, we further forecast the validation data points by the SSVM-OU, SSVM-W and LMM (12). Table 4 compares the forecasting ability of the posterior mean and credible intervals for the three models, evaluated by the relative bias, MSE, coverage rate and interval length. As we expected, the relative biases of posterior means of the forecasting draws from the SSVM-OU are smaller than those from the other models and the corresponding interval lengths are narrower. Furthermore, it is of interest to study the sensitivity of the forecasting ability of SSVM-OU. We simulate another 100 datasets from the LMM specified as equation (12) in which the parameters are the same as those obtained from the PSA data analysis. In addition, the number of subjects, and the number of observations and the validation data points, are set identical to those used to generate datasets from the above SSVM-OU. The forecasting results are given in the second part of Table 4. We find that SSVM-OU has comparable performance to the LMM (for the short-term forecast at time 0.08), with smaller relative bias but slightly larger MSE and wider interval length. For the long-term forecast at time 0.5 or 1, SSVM-OU performs worse than the LMM but is better than SSVM-W.

Table 4.

Simulation results on forecasting by three models

Simulation Model	Fitted Model	Year Distance	Relative Bias	MSE	Coverage Rate	Interval Length
SSVM-OU	SSVM-OU	0.08	0.010	0.162	0.949	1.116
		0.5	0.019	0.232	0.951	1.336
		1	0.011	0.343	0.951	1.639
	SSVM-W	0.08	0.008	0.270	0.957	1.455
		0.5	−0.144	6.700	1	9.640
		1	−0.024	39.430	1	23.974
	LMM	0.08	−0.165	1.508	0.994	3.465
		0.5	−0.061	2.206	0.936	3.547
		1	−0.303	3.442	0.742	3.661
LMM	SSVM-OU	0.08	0.001	0.034	0.915	0.483
		0.5	0.077	0.069	0.974	0.781
		1	0.092	0.155	0.996	1.249
	SSVM-W	0.08	−0.021	0.046	0.920	0.565
		0.5	0.075	0.384	1.000	2.152
		1	−0.040	1.905	1.000	5.085
	LMM	0.08	−0.007	0.028	0.943	0.456
		0.5	0.026	0.030	0.943	0.478
		1	−0.006	0.034	0.952	0.510

6 Discussion

This paper considers modeling and inference for the rate functions in longitudinal studies with an application in the analysis of PSA biomarker profiles. For a given subject, the rate of change is described by a rate function whose prior is assumed to follow a Gaussian process conditional on the covariates. A key feature of this approach is that the Gaussian process is specified by an SDE and is expected to be centered on a pre-specified parametric function, while allowing significant deviations from this functional expectation nonparametrically. We have focused on the case where the rate function follows an OU process, motivated by analyzing PSA profiles. The same modeling strategy and inference method should be widely useful in the setting when we aim to model the rate function semiparametrically.

One can extend our model to discrete outcomes and to include the covariates in equation (1). Moreover, a similar modeling and inference approach can be applied to analyze the acceleration function, which is the second-order derivative of the mean function. In addition, for simplicity, we assume the stable rates depend on the covariates through a parametric distribution, which could potentially be replaced by a nonparametric distribution with a stick-breaking process as its prior.

The MCMC algorithm is currently programmed in R (R Development Core Team, 2008). For the PSA application with 50 subjects and 225 observed or augmented data points per subject, it took about 4 hours per 1000 MCMC iterations on a PC with 2.93GHz Intel(R)Core(TM)2Duo CPU. In contrast, it took about 15 minutes per 1000 MCMC iterations if the model was fit with only observed data. One way to speed up computation is to develop a C or C++ program for the proposed method, which is one of our future research tasks. Our computation-related experiences have suggested that the computation time is approximately linearly proportional to the number of subjects. Hence, we anticipate that with fast computation software this algorithm can be applied to handle studies with relatively large sample sizes.