Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2011 Dec 16;40(5):e35. doi: 10.1093/nar/gkr1221

Maximizing signal-to-noise ratio in the random mutation capture assay

Suresh Kumar Poovathingal, Jan Gruber 1, Li Fang Ng 1, Barry Halliwell 1, Rudiyanto Gunawan 2,*
PMCID: PMC3300001  PMID: 22180539

Abstract

The ‘Random Mutation Capture’ assay allows for the sensitive quantitation of DNA mutations at extremely low mutation frequencies. This method is based on PCR detection of mutations that render the mutated target sequence resistant to restriction enzyme digestion. The original protocol prescribes an end-point dilution to about 0.1 mutant DNA molecules per PCR well, such that the mutation burden can be simply calculated by counting the number of amplified PCR wells. However, the statistical aspects associated with the single molecular nature of this protocol and several other molecular approaches relying on binary (on/off) output can significantly affect the quantification accuracy, and this issue has so far been ignored. The present work proposes a design of experiment (DoE) using statistical modeling and Monte Carlo simulations to obtain a statistically optimal sampling protocol, one that minimizes the coefficient of variance in the measurement estimates. Here, the DoE prescribed a dilution factor at about 1.6 mutant molecules per well. Theoretical results and experimental validation revealed an up to 10-fold improvement in the information obtained per PCR well, i.e. the optimal protocol achieves the same coefficient of variation using one-tenth the number of wells used in the original assay. Additionally, this optimization equally applies to any method that relies on binary detection of a small number of templates.

INTRODUCTION

Mutations in nuclear and mitochondrial DNA are associated with congenital disorders, diseases (e.g. cancer) and ageing (1). An accurate determination of tissue level DNA mutation abundance is challenging, but critical for understanding the impact of these mutations on cellular and tissue physiology (2–4). Furthermore, the ability to sensitively detect the frequency of random spontaneous mutations of DNA is necessary to define critical parameters like the mutation rate, which is essential for understanding the role of genomic mutagenesis in human diseases and ageing.

Many procedures have been developed based on quantification of point mutation frequency by PCR amplification of short fragments of DNA. However these methods have recently come under criticism, because mis-incorporation of nucleotides due to the intrinsic error rate of polymerase enzymes will result in introduction of spurious mutations during the initial PCR step. Upon cloning, these mutations become indistinguishable from true mutations and may provide an overestimation of the mutation load (5). These artifactual mutations may be at frequencies exceeding actual in vivo mutation frequencies, especially when measuring low-level spontaneous DNA mutations (~10−6 bp−1) (6).

In 2005, Bielas and Loeb (3) developed a novel assay for quantifying low levels of spontaneous random mutations in DNA. This method, known as the ‘Random Mutation Capture’ (RMC) assay, is based on PCR detection of mutations that render the target sequence resistant to restriction enzyme digestion (2,4). Following complete restriction digest, digest resistant mutant templates are quantified by real-time PCR amplification after dilution to single molecule level (5). This approach avoids the need for pre-amplification and associated artifactual mutations due to polymerase error that have confounded previous methods (2).

Given these advantages, it is not surprising that the RMC assay has been widely applied. Since it was first described in 2005 (3), 17 studies reporting original data based on the RMC method have been published. Data based on the RMC assay has also been central to some very high impact results. For example, RMC data on the point mutation and deletion burden in the mtDNA of polymerase gamma ‘mutator mice’ has been cited over 190 times (7,8). Also, application of the RMC assay to the determination of the mutation frequency in mitochondrial DNA (mtDNA) of ageing wild-type mice (7) has resulted in values about two orders of magnitude lower than the previous estimates (9,10), a result that has wide reaching implication in the context of ageing (11). The RMC assay itself has been widely discussed, with over 21 additional articles and reviews discussing it (see Supplementary Table S2).

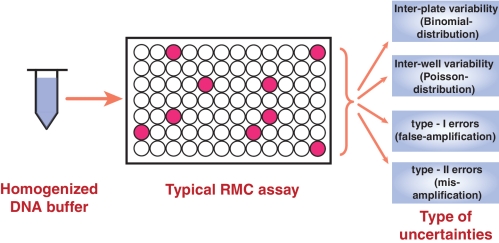
The RMC assay is based on quantification of mutation burdens by real-time PCR following dilution to single molecule level (Figure 1). The advantage of this approach is that each PCR-amplified well results from only single mutant molecules because the likelihood of finding more than a single mutant in a well is negligible (3,5). However, while at the population level, low sample size has been shown to negatively affect the conclusion drawn from DNA mutation studies (12), here we show that statistical aspects related to protocols necessitating such high dilution (down to single molecule level) can also introduce significant noise in the mutation frequency estimates. Unfortunately, the statistics associated with the discrete molecular nature of such assays can become non-trivial, an aspect that was overlooked in the original protocol and subsequent applications. In this work, a novel optimization of the RMC assay has been developed based on statistical modeling techniques. These statistical techniques are used to investigate the impact of high dilution endpoints in the RMC assay on the accuracy of mutation frequency measurements.

Figure 1.

Figure 1.

Open in a new tab

Statistical aspects associated with the RMC assay. There are primarily four sources of variability that are important for the sensitive estimation of DNA mutation load using the RMC assay, including: (i) the number of PCR (un)amplified wells among independent RMC trials (inter-plate variability) even when each PCR well receives same number of DNA templates, (ii) the random molecular count of mutant DNA in different wells of a single plate (inter-well variability), (iii) false amplification (Type I error) and (iv) mis-amplification (Type II errors).

The statistically optimized RMC assay developed in this work not only significantly reduces the extent of measurement variability, facilitating better hypothesis testing, but also increases the amount of information returned per sample. Additionally, most PCR assays involving single molecular dilution protocol, other than the RMC assay, such as the digital PCR (dPCR) (13–15) or digital RT-PCR (16) and single molecular PCR (smPCR) (6,17,18), utilize a DNA template dilution factor of ~50% (one in two wells amplifying). The selection of this dilution factor is chosen to yield ‘single’ DNA template per PCR well and with the intention of maximizing information return per well by assuming Binomial statistics. However, the analysis in this work demonstrates that this end-point dilution, while better than the higher dilution of the RMC assay, may also be suboptimal with respect to measurement variability. A more careful and rigorous mathematical analysis, such as the one presented here, will therefore not only benefit the RMC assay but may also be equally applicable to other single molecule assays.

METHODS

Statistical optimization of the RMC assay

The conventional RMC assay (3,5,7) is based on PCR amplification of a single mutant molecule (restriction enzyme digest resistant) in the presence of excess copy numbers of wild-type sequences (digest sensitive). The mutation frequency is calculated by dividing the fraction of PCR wells that are amplified by the amount of DNA per well (3,7). In the conventional RMC assay, intrinsic variability arises due to the well-to-well and plate-to-plate variability that can arise from non-uniform sampling of DNA content to PCR wells at single molecule level dilutions and from the random number of amplified/non-amplified wells in a plate, respectively (Figure 1). The other sources of error (bias) in this protocol are associated with (i) the assumption that each amplified well only contains a single mutant molecule, (ii) false PCR amplification due to contamination or incomplete digestion (Type I), and (iii) failed PCR amplification (Type II). Each of these factors contributes in a non-trivial manner to the statistics of the mutation frequency data, and has not been addressed previously.

To arrive at the optimal protocol, two types of statistical analyses were performed. The first involved a linearized variance propagation of functions of random variables arising from the variability due to the non-uniform sampling of DNA content to PCR wells, while the second used a Monte Carlo approach involving the function of random variables, that simulates the protocol a large number of times (n = 10 000). The optimization was then performed to minimize the coefficient of variation, by changing the amount of DNA molecules that were sampled into each well. The details of each analysis are outlined below.

First order uncertainty propagation analysis

Assuming that the DNA homogenate for which mutation frequency is to be determined is well mixed, the probability of sampling x number of mutant molecules into a PCR well, which is associated with the well-to-well variability, can be described by the Poisson distribution with a mean of λ. This mean is the quantity of interest in this assay as the point mutation frequency (per bp) can be calculated by dividing λ with the total amount of DNA in a well. Using the Poisson density function, the probability of sampling zero mutant template into an PCR well, denoted by p0, is given by:

graphic file with name gkr1221m1.jpg (1)

Furthermore, assuming that p0 is constant and ignoring the Type I and II errors described earlier, the number of wells n0 that are not PCR-amplified among a total of nwells wells is an outcome of Bernoulli trials, similar to coin flipping. While the number of unamplified wells (n0) has an expectation value of nwells × p0, the outcome from a particular RMC assay follows a random Binomial distribution, giving rise to the plate-to-plate variability. In this case, we can only obtain an estimate of p0, which is calculated as 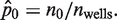Inline graphic Here, we show that the quality of estimating λ depends in non-trivial ways on p0.

An estimate of λ can be calculated from 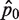Inline graphic by rearranging Equation (1), such that:

graphic file with name gkr1221m2.jpg (2)

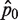Since Inline graphic is an unbiased estimator of p0 (i.e. the expected value of 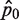Inline graphic is equal to p0), the variance of 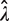Inline graphic can approximated by using a Taylor series expansion of Equation (2) and the coefficient of variation (CV) of 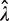Inline graphic is given by (see Supplementary Data for a detailed derivation):

graphic file with name gkr1221m3.jpg (3)

Using the above function, the minimum CV is attained at 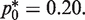Inline graphic That is, the optimal (smallest) CV results from choosing a template dilution where 80% of wells amplify. Note that the mutation burden here is computed from the fraction of PCR wells that are not amplified, as opposed to counting wells that are PCR-amplified in the conventional RMC assay and other types of single molecular dilution assays. However, a similar optimization based on the fraction of amplified wells gave the same optimal sampling protocol.

Our analysis shows that all methods involving single molecule protocol relying on binary reading (e.g. amplified or not amplified), such as the RMC assay, dPCR and smPCR, are fundamentally quite different from traditional biochemical assays. In particular we find that their statistical properties are not trivial. What the optimal protocol, e.g. in terms of information-return-per-well and robustness with respect to errors, should be is not obvious without a thorough statistical analysis, such as one carried out in this article. It is intuitively clear that the ideal percentage of amplified wells should lie somewhere between zero amplified wells (no information gained) and 100% of wells amplified (also no information gained). One could further argue that counting the number of non-amplified wells is equivalent to counting the number of amplified wells (since both arise from the same Bernoulli trials), and it might therefore be expected that the maximum information per well should correspond straightforwardly to the points when half of the wells are amplified (or not amplified). However, a further careful and detailed analysis shows that this is not the case. The reason for this lies in the Poissonian random sampling of DNA templates into the PCR wells. This leads to 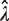Inline graphic being a logarithmic function of p0 [Equation (2)]. The logarithmic function is significantly non-linear near 0 and hence, any small differences in the measured 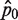Inline graphic near 0 will be disproportionately magnified in the Inline graphic estimates (Figure 2A). Consequently, the SD of 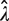Inline graphic increases dramatically at high dilution [see the numerator of Equation (3)]. On the other hand, increasing the average number of amplifiable templates per well beyond the optimal level comes with a diminishing return in reducing the CV of 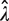Inline graphic. In this case, the benefit of reducing variance by increasing p0 is counterbalanced by the corresponding decrease in the mean of 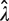Inline graphic. This tradeoff thus explains the skewed optimal point for CV at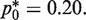 Inline graphic

Figure 2.

Figure 2.

Open in a new tab

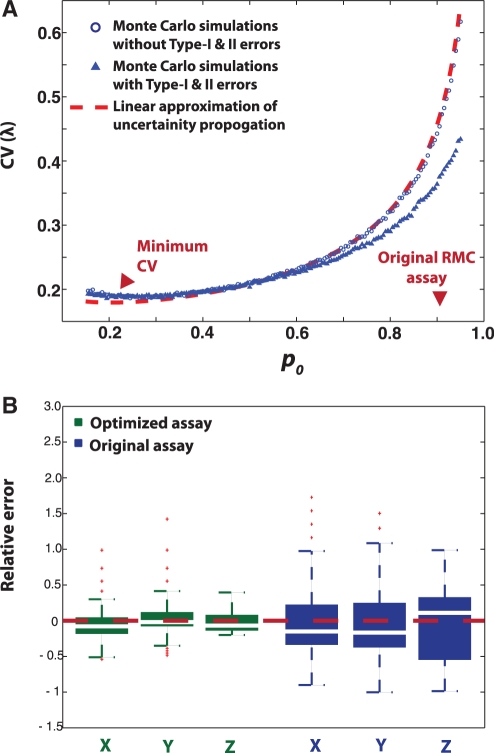
Optimized RMC assay. (A) Coefficient of variation (CV) of DNA mutant frequency as a function of p0 (the mean fraction of unamplified wells) as predicted by MC simulations and statistical analysis using assay with 48 wells. The parameter p0 relates to the DNA template dilution factor, where higher dilution increases p0 (fewer DNA templates per PCR well). The CV has a minimum value around p0 = 0.20, as opposed to the conventional RMC assay of p0 ≈ 0.91. The lower CV in simulations with Type I and Type II errors comes at the cost of lower accuracy due to bias. (B) Comparison of the relative errors between optimized and conventional RMC assays in (X and Y) simulation and (Z) experiment; (nwells = 48, see also Table 1). MC simulations (n = 10 000 realizations) were performed (X) with and (Y) without Types I and II errors. The Types I and II errors were determined based mock RMC repeats (n = 100 PCR wells, Supplementary Table S1). For the original RMC assay, Type II error rate was the same as above, but Type 1 frequency was set to zero, since existence of mutant DNA in amplified wells is confirmed by sequencing. Both MC simulations and experimental data confirmed the superiority of the optimized protocol in terms of CV reduction and accuracy improvement.

Monte Carlo analysis

The analytical treatment discussed earlier does not consider false positives and false negatives (Type I or Type II errors) as described in Figure 1. To better understand the influence of these errors on the mutation frequency estimates, we have also performed Monte Carlo (MC) simulations of the conventional RMC assay and the proposed alternative protocol (i.e. counting non-amplified PCR wells) with and without these errors. When PCR amplified wells contain exactly 1 mutant molecule, sequencing of the PCR product can eliminate false positives and at the same time provide the mutational spectra. Using a high dilution factor, the conventional RMC assay assures that most, if not all, of the wells contain 0 or 1 mutant molecule and in this case, Type I error can be made negligible by sequencing. Consequently, the Type I error rate was set to zero in the MC simulations of the original RMC protocol. In the case of the proposed optimized RMC assay, since some PCR wells have more than a single DNA template, the likelihood of finding more than a single type of allele is higher compared to the conventional RMC assay. Also, each PCR amplified wells of the optimized assay would, on an average, contain two DNA templates (for 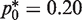Inline graphic). While this does not preclude the usage of sequencing or other more advanced technologies to exclude Type I errors in the case of proposed optimal RMC assay, it does make these controls slightly more challenging. Thus, for the MC simulations of the optimized assay, we have considered both the Type I and Type II errors. Type I and Type II error frequencies for the MC simulations were estimated from experimental data (see Supplementary Table S1). It should further be noted that setting Type I errors to zero in the simulations of the traditional but not the optimized RMC assay is conservative (favoring the traditional RMC assay).

Each MC simulation emulated the statistical random sampling of DNA material into each PCR well on a plate and the PCR amplification experiment. In this case, such a simulation was performed a large number of times to obtain the statistics of the mutation frequency estimates, such as the mean and CV. The pseudo-codes for the MC algorithms are given in Supplementary Data. The Monte Carlo algorithms were implemented in C++ on a Linux Platform [CentOS; GNU C++ compiler (v4.1.1)] using a combination of a long period random number generator (19) and a multiple independent streams generator (20). In addition, non-uniform random numbers were generated using algorithms described elsewhere (21,22). The codes will be made available upon request.

Validation of RMC optimization

The performance of the proposed optimized protocol was compared against experimental data from a mock RMC assay to validate theoretical and simulation predictions. Briefly, we generated a plasmid containing the target sequence and a matching TaqMan probe/primer set based on the TaqMan MGB Probe with 5′-6FAM and 3′-MGBNFQ dye technology (Applied Biosystems, Calif.). The plasmids were serially diluted to approximately either 0.1 or 1.6 molecules per microliter. The former corresponds to the dilution used in the single molecule amplification of the original RMC assay (3), while the latter represents the suggested dilution of the optimized assay 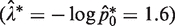Inline graphic. A 1-µl sample of either the high or the low copy number dilutions were added to a 19 µl of standard TaqMan UDP master-mix (TaqMan Universal PCR Master Mix, Applied Biosystems, CA, USA) to each well of a 96-well plate PCR plate (Applied Biosystems). The wells were subsequently subjected to PCR amplification and detected using an Applied Biosystems 7500 real-time PCR system running 60 cycles of PCR of a modified universal amplification profile (50°C for 2 min, 95°C for 10 min followed by 60 cycles of: 95°C for 45 s, 55°C for 45 s and 72°C for 90 s). Amplification was monitored at 520 nm (FAM Dye) and under these conditions single molecules are found to be reliably amplified (data not shown).

Conceptually, the RMC assay comprises two stages. During the first stage WT DNA templates are removed with high efficiency by complete restriction digest, leaving only low copy numbers mutant templates. In the second stage (‘quantification stage’), these mutant templates are further diluted to single molecule level (limiting dilution) and quantified using the discrete RT-PCR step (only information regarding amplification or no amplification is used). The first ‘digest’ stage of the RMC protocol involves methodological challenges of its own, including digestion efficiency of restriction enzymes, star activity and template degradation. However, these will vary from one application to another and can be minimized without the use of a rigorous statistical analysis. Our analysis is concerned purely with the second stage, in particular with the effect of randomness and sampling due to the single molecule sampling step. Much of the aspects in the quantification stage of the assay can be captured by preparing limiting dilution series using plasmids containing the mutant sequence. In terms of validation of our modeling claim, the use of plasmids is preferable because the copy number of plasmids can be very accurately determined beforehand and identical samples can be generated each time. The use of whole genome samples, while possible, would significantly complicate the protocol without adding additional insight into the question explored here. In practice, the use of higher mutant templates per well, as suggested by the optimization, will concomitantly increase competing WT DNA copies, which may possibly affect single molecule detection efficacy. Detection limit should therefore be validated using appropriate control experiments such as spiking pre-digested WT samples with mutant or uncut WT DNA at known copy number. Such control should in any case be a part of assay calibration together with controls to ensure that only WT sequences are cut during restriction digestion.

RESULTS AND DISCUSSION

Following the derivation in the Method section, the optimal protocol involves (i) preparation of DNA sample such that about 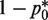Inline graphic fraction of the wells will be amplified by adjusting the dilution factor and (ii) the mutation frequency estimate 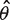Inline graphic (mutations per base pairs) can be computed according to

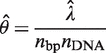graphic file with name gkr1221m4.jpg (4)

where nDNA is the total number of DNA molecules in a single PCR well and nbp is the length restriction site [nbp = 4 for TaqI recognition site (7)]. Figure 2 shows that the results of statistical optimization using the linearized analysis and MC approach, and from the RMC validation experiments. In particular, Figure 2A and Supplementary Figure S1 suggests that the minimum CV can be achieved by diluting DNA sample such that 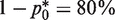Inline graphic of the wells are PCR amplified, which corresponds to 1.6 mutant molecules per well. This is in contrast to the original RMC assay that prescribes end-point dilution down to 0.1 mutant molecules per well. Importantly, the optimized protocol offers a significant improvement of the accuracy in mutation estimates compared to the conventional RMC assay. For example, Monte Carlo (MC) simulations of RMC assays (n = 10 000) on 48 PCR wells (nwells = 48) predicted a 53% reduction in coefficient of variation (CV) (from 40% to 19% CV) by using the optimal protocol in place of the original (Figure 2B). Furthermore, this protocol provides a more robust estimate of λ than the traditional RMC assay, where the CV is approximately constant for the values of p0 between 0.1 and 0.4, even in the presence of experimental artifacts (false positive and false negative errors) (Figure 2A, Supplementary Figure S1). Even at much higher false amplification and non-amplification errors (Type I and Type II errors up to 30%), the optimized protocol could still provide a significant reduction in the CV and better overall accuracy of mutation burden estimates over the conventional RMC assay (Supplementary Figures S2 and S3).

We tested the theoretical predictions experimentally by conducting a mock RMC assay using plasmid DNA (see Method). As expected, at the optimal dilution factor of 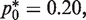Inline graphic this protocol provides a substantial reduction of variability with an actual CV reduction of 68% (from 57% to 18% CV) (Figure 2B and Table 1). In other words, the optimal RMC protocol offers the same information as the original protocol using only 1/10 the number of wells and provides significantly higher accuracy. The high variability due to the discrete molecular nature of the original assay can lead to a significant uncertainty in measurement estimates. These findings highlighted that in the quantification of low-level DNA mutations, the manner in which samples are prepared for analysis can contribute non-trivially to the statistics of the measurement data. Given the increasing utilization of the RMC and similar limiting dilution assays (8,17), we feel that this insight is important to maximize information and minimize measurement uncertainty when using these types of assays.

Table 1.

Mock RMC experimental results using the optimized and original protocol

Optimized protocol (λ = 1.6)
 Original protocol (λ = 0.1)
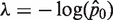
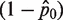
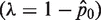
Fraction of amplified wells Inline graphic Average mutant molecules per well Inline graphic Fraction of amplified wells Inline graphic Average mutant molecules per well Inline graphic
Run # 1 36/48 1.39 Run # 1 1/48 0.02
Run # 2 39/48 1.67 Run # 2 6/48 0.13
Run # 3 38/48 1.57 Run # 3 10/48 0.23
Run # 4 35/48 1.31 Run # 4 7/48 0.16
Run # 5 36/48 1.39 Run # 5 6/48 0.13
Run # 6 42/48 2.08 Run # 6 3/48 0.06
Average (molecule per well) 1.5668 Average (molecule per well) 0.1146
SD (molecule per well) 0.2854 SD (molecule per well) 0.0656
CV 0.1822 CV 0.5721
Open in a new tab

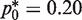At Inline graphic a great majority (>98%) of the amplified wells still contain at most four DNA templates. Although the conventional sequencing techniques are best applied to only single DNA template, the sequencing of up to four mutant molecules in a single well of the RMC assay should not pose much difficulty, especially considering that different templates are present at high and approximately equal number post-PCR amplification. In addition, as the typical applications of RMC assay involve point mutation frequencies of 10−6–10−4 bp−1, the probability of having multiple mutations in a single 4-bp restriction site is negligible. Thus, by assuming that each mutant molecule contains only a single point mutation, the sequence of each DNA template in the PCR well can be uniquely and straightforwardly identified from multiple chromatogram traces in the sequencing output (23). Alternatively, if more accuracy is required, a clone and sequence approach can be followed (23). Finally, more advanced RT-PCR techniques for allelic discrimination exist that can be used to confirm if any WT alleles are present in the wells (24).

Additionally, it should be noted that the CV is not a strong function of the fraction of amplified wells between 30% to 80% positives (0.2 ≤ p0 ≤ 0.7, see Figure 2A). Using a value of p0 in this range, it is possible to obtain improved accuracy of the mutation burden, while resolving the complexity of DNA sequencing, if this is desirable. For instance, at a dilution giving 30% amplified wells (0.35 molecules per well, p0 = 0.7), a great majority of amplified wells (four out of five) will contain only a single DNA template per well and 99% of amplified wells contain at most two DNA templates. While the corresponding CV is suboptimal, this level of dilution can still provide 50% reduction in CV from the conventional RMC assay and also make sequencing easier (see Figure 2A). Therefore, if determining mutation spectra is of a major interest, an intermediate dilution factor can be chosen and Figure 2A can be used to estimate the trade off in information loss.

Applications of the RMC assay in the past have been for quantifying DNA mutation burden in numerous cell types and in different organisms (see Supplementary Table S2). A majority of these applications has been concerned with age-dependent mutation burden in mitochondrial DNA. Most of these applications have been used predominantly in the original form. While a modification of the RMC assay was recently proposed (25), the modified protocol still used the original DNA dilution and sampling procedure and did not address the issues highlighted earlier. Experimental data in the proposed work (25) shows that their modified RMC assay using the same DNA homogenates still exhibited high degree of noise with half of the repeats having >50% differences and a quarter have >100% deviations [see Figure 5 in (25)]. As the measurement of each DNA homogenate was only repeated once, it is statistically difficult to conclude further about the reproducibility of their modified assay. To elucidate the impact of the optimal protocol developed in this work in reducing the measurement noise and further improving the quality of data on age-dependent mtDNA mutation accumulation, we have further performed Monte Carlo simulations of low-level accumulation of mtDNA mutations during ageing and their measurements using the RMC assay with the original and the optimal protocol.

Briefly, based on our earlier work (26), the in silico mouse model tracks for the accumulation of mtDNA point mutations during two stages of mouse life: development and post-development. The model simulates two mtDNA-related maintenance processes: mitochondrial turnover, comprising of relaxed replication and degradation of mitochondrial DNA, and de novo point mutation during the mtDNA replication. In development, the replication of the mtDNA during the symmetric binary cell divisions is simulated, starting with a single progenitor cell. In the post-natal stage, however, relaxed replication of the mtDNA in a post-mitotic cardiomyocyte is simulated (more details are included in Supplementary Data).

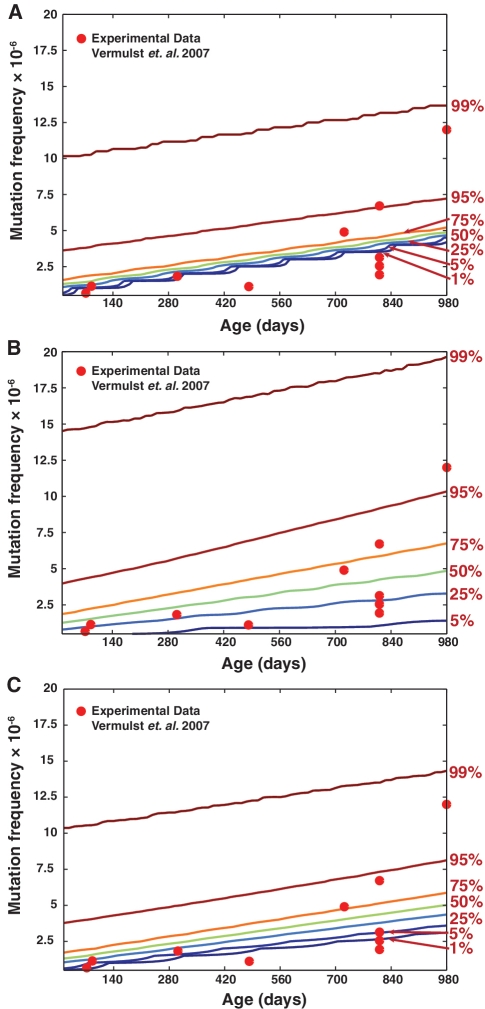
Figure 3A shows the intrinsic variability in the levels of mtDNA mutations among heart tissues from a population of mice that may arise from random drift of mtDNA point mutations. The underlying density function of this uncertainty is represented as g(θ) where θ is the mtDNA mutation frequency. The variability of RMC mutation burden data in this population is a combination of the intrinsic variability above and the uncertainty associated with the RMC assay protocol (original and optimized), which can be calculated by:

graphic file with name gkr1221m6.jpg (5)

where f(m|θ) is the probability of obtaining a mutation burden reading of m by RMC assay, when the true mutation frequency is θ (26, 27). When using the original RMC assay, the additional variability (noise) from suboptimal sampling of the original RMC assay prevents any definitive conclusion regarding the dynamics of mtDNA mutation accumulation, as shown in Figure 3B. On the other hand, the reduction in the sampling variability offered by the optimal protocol provides a much more definitive insight into the mutation dynamics (Figure 3C), which is important in deducing mechanisms of age-related mtDNA mutations (26).

Figure 3.

Figure 3.

Open in a new tab

Variability in the point mutation frequency in mouse heart tissues. Point mutation burden in a wild-type mouse population (n =  1000 mice) as predicted by a random drift model (26). Actual experimental RMC data are shown in red circles (7). The simulated percentile curves in the plots give the maximum mutation frequency that a given percentage of the mouse population harbors (e.g. 99% of the mouse population harbor mutation frequency up to and including the level indicated by the 99th percentile line). The percentiles of point mutation frequency distribution in mouse heart tissues as a result of (A) random drift of mtDNA mutation; (B) random drift and sampling variability from the original RMC assay; and (C) random drift and sampling variability from the optimized RMC protocol. The comparison of overall data variability indicates that the optimized protocol developed in this work provides a substantial reduction in the measurement variability and provides a better estimate of the underlying age-dependent mtDNA mutation accumulation dynamics.

CONCLUSIONS

Methods for quantifying extremely low levels of mutation frequency (~10−6 bp−1), like the RMC assay (3), represent an important technological advance. Our findings reveal that the statistics associated with the sample preparation in these assays are of great importance, but often overlooked. Consequently, sampling protocols need to be carefully designed to maximize signal-to-noise ratio. Here we show that a sensitive and more robust estimate of mutation frequency can be obtained by a simple modification of the original assays (3,5,7) based on statistical analysis. While the original procedure prescribes a dilution factor of about 0.1 molecules of mutant per well and the counting of amplified wells, we found, however, that the maximum signal-to-noise ratio corresponds to a lesser dilution factor of 1.6 molecules per well and quantifying the fraction of unamplified wells. The optimized assay is predicted and confirmed by experimental data, to substantially reduce the measurement variability, and thus provide significantly more accurate estimates of mutation frequency, for instance in age-dependent mutation dynamics. While the work developed here pertains to the RMC assay, the statistics related to sample preparation and sampling protocol maybe more generally applicable to other DNA quantification techniques requiring high dilution to obtain single molecule end point dilutions.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Methods, Supplementary Tables 1 and 2, Supplementary Figures 1–3 and Supplementary References [3,7,26–55].

FUNDING

Singapore Ministry of Education Grants [AcRF Tier 1, FRC Grant (R279000299112 to S.K.P. and R.G.) and AcRF Tier 2, (MOE2010-T2-2-048 to S.K.P., J.G., N.L.F. and B.H.)] and ETH Zurich (to R.G.). Funding for open access charge: ETH Zurich.

Conflict of interest statement. None declared.

Supplementary Material

Supplementary Data
supp_40_5_e35__index.html (864B, html)

ACKNOWLEDGEMENTS

The authors would like to thank, Dr Ce-Belle Chen, Dr Sebastian Schaffer, Mr Srinath Sridharan and Mr Thanneer Malai Perumal for their helpful and insightful comments during the manuscript preparation.

REFERENCES

  • 1.Wallace DC. Mitochondrial DNA mutations and neuromuscular disease. Trends Genet. 1989;5:9–13. doi: 10.1016/0168-9525(89)90005-x. [DOI] [PubMed] [Google Scholar]
  • 2.Bielas JH, Heddle JA. Proliferation is necessary for both repair and mutation in transgenic mouse cells. Proc. Natl Acad. Sci. USA. 2000;97:11391–11396. doi: 10.1073/pnas.190330997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Bielas JH, Loeb LA. Quantification of random genomic mutations. Nat. Methods. 2005;2:285–290. doi: 10.1038/nmeth751. [DOI] [PubMed] [Google Scholar]
  • 4.Greaves LC, Beadle NE, Taylor GA, Commane D, Mathers JC, Khrapko K, Turnbull DM. Quantification of mitochondrial DNA mutation load. Aging Cell. 2009;8:566–572. doi: 10.1111/j.1474-9726.2009.00505.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Vermulst M, Bielas JH, Loeb LA. Quantification of random mutations in the mitochondrial genome. Methods. 2008;46:263–268. doi: 10.1016/j.ymeth.2008.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Kraytsberg Y, Nicholas A, Caro P, Khrapko K. Single molecule PCR in mtDNA mutational analysis: genuine mutations vs. damage bypass-derived artifacts. Methods. 2008;46:269–273. doi: 10.1016/j.ymeth.2008.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Vermulst M, Bielas JH, Kujoth GC, Ladiges WC, Rabinovitch PS, Prolla TA, Loeb LA. Mitochondrial point mutations do not limit the natural lifespan of mice. Nat. Genet. 2007;39:540–543. doi: 10.1038/ng1988. [DOI] [PubMed] [Google Scholar]
  • 8.Vermulst M, Wanagat J, Kujoth GC, Bielas JH, Rabinovitch PS, Prolla TA, Loeb LA. DNA deletions and clonal mutations drive premature aging in mitochondrial mutator mice. Nat. Genet. 2008;40:392–394. doi: 10.1038/ng.95. [DOI] [PubMed] [Google Scholar]
  • 9.Kujoth GC, Hiona A, Pugh TD, Someya S, Panzer K, Wohlgemuth SE, Hofer T, Seo AY, Sullivan R, Jobling WA, et al. Mitochondrial DNA mutations, Oxidative stress, and Apoptosis in mammalian aging. Science. 2005;309:481–484. doi: 10.1126/science.1112125. [DOI] [PubMed] [Google Scholar]
  • 10.Trifunovic A, Wredenberg A, Falkenberg M, Spelbrink JN, Rovio AT, Bruder CE, Bohlooly YM, Gidlof S, Oldfors A, Wibom R, et al. Premature ageing in mice expressing defective mitochondrial DNA polymerase. Nature. 2004;429:417–423. doi: 10.1038/nature02517. [DOI] [PubMed] [Google Scholar]
  • 11.Khrapko K, Vijg J. Mitochondrial DNA mutations and aging: a case closed? Nat. Genet. 2007;39:445–446. doi: 10.1038/ng0407-445. [DOI] [PubMed] [Google Scholar]
  • 12.Wonnapinij P, Chinnery PF, Samuels DC. Previous estimates of mitochondrial DNA mutation level variance did not account for sampling error: comparing the mtDNA genetic bottleneck in mice and humans. Am. J. Hum. Genet. 2010;86:540–550. doi: 10.1016/j.ajhg.2010.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Sykes PJ, Neoh SH, Brisco MJ, Hughes E, Condon J, Morley AA. Quantitation of targets for PCR by use of limiting dilution. Biotechniques. 1992;13:444–449. [PubMed] [Google Scholar]
  • 14.Vogelstein B, Kinzler KW. Digital PCR. Proc. Natl Acad. Sci. USA. 1999;96:9236–9241. doi: 10.1073/pnas.96.16.9236. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Zimmermann BG, Grill S, Holzgreve W, Zhong XY, Jackson LG, Hahn S. Digital PCR: a powerful new tool for noninvasive prenatal diagnosis? Prenat. Diagn. 2008;28:1087–1093. doi: 10.1002/pd.2150. [DOI] [PubMed] [Google Scholar]
  • 16.Warren L, Bryder D, Weissman IL, Quake SR. Transcription factor profiling in individual hematopoietic progenitors by digital RT-PCR. Proc. Natl Acad. Sci. USA. 2006;103:17807–17812. doi: 10.1073/pnas.0608512103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Kraytsberg Y, Khrapko K. Single-molecule PCR: an artifact-free PCR approach for the analysis of somatic mutations. Expert Rev. Mol. Diagn. 2005;5:809–815. doi: 10.1586/14737159.5.5.809. [DOI] [PubMed] [Google Scholar]
  • 18.Kraytsberg Y, Kudryavtseva E, McKee AC, Geula C, Kowall NW, Khrapko K. Mitochondrial DNA deletions are abundant and cause functional impairment in aged human substantia nigra neurons. Nat. Genet. 2006;38:518–520. doi: 10.1038/ng1778. [DOI] [PubMed] [Google Scholar]
  • 19.Matsumoto M, Nishimura T. Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 1998;8:3–30. [Google Scholar]
  • 20.LeCuyer P, Simard R, Chen EJ, Kelton WD. An object-oriented random-number package with many long streams and substreams. Oper. Res. 2002;50:1073–1075. [Google Scholar]
  • 21.Stadlober E. Sampling from Poisson, binomial and hypergeometric distributions: ratio of uniforms as a simple and fast alternative. Math. Statist. Sekt. 1989;303:1–93. [Google Scholar]
  • 22.Stadlober E. The ratio of uniforms approach for generating discrete random variates. J. Comput. Appl. Math. 1990;31:181–189. [Google Scholar]
  • 23.Fakhrai-Rad H, Zheng J, Willis TD, Wong K, Suyenaga K, Moorhead M, Eberle J, Thorstenson YR, Jones T, Davis RW, et al. SNP discovery in pooled samples with mismatch repair detection. Genome Res. 2004;14:1404–1412. doi: 10.1101/gr.2373904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Applied Biosystems. TaqMan allelic discrimination - demonstration Kit 57, Applied Biosystems. 2000. California. [Google Scholar]
  • 25.Wright JH, Modjeski KL, Bielas JH, Preston BD, Fausto N, Loeb LA, Campbell JS. A random mutation capture assay to detect genomic point mutations in mouse tissue. Nucleic Acids Res. 2011;39:e73. doi: 10.1093/nar/gkr142. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Poovathingal SK, Gruber J, Halliwell B, Gunawan R. Stochastic drift in mitochondrial DNA point mutations: a novel perspective ex silico. PLoS Comput. Biol. 2009;5:e1000572. doi: 10.1371/journal.pcbi.1000572. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Montgomery DC, Runger GC. Applied Statistics and Probability for Engineers. New York: Wiley; 2006. [Google Scholar]
  • 28.Iborra FJ, Kimura H, Cook PR. The functional organization of mitochondrial genomes in human cells. BMC Biol. 2004;2:9. doi: 10.1186/1741-7007-2-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Satoh M, Kuroiwa T. Organization of multiple nucleoids and DNA molecules in mitochondria of a human cell. Exp. Cell Res. 1991;196:137–140. doi: 10.1016/0014-4827(91)90467-9. [DOI] [PubMed] [Google Scholar]
  • 30.Chen H, Chan DC. Emerging functions of mammalian mitochondrial fusion and fission. Hum. Mol. Genet. 2005;14(Suppl 2):R283–R289. doi: 10.1093/hmg/ddi270. [DOI] [PubMed] [Google Scholar]
  • 31.Halliwell B, Aruoma OI. DNA damage by oxygen-derived species. Its mechanism and measurement in mammalian systems. FEBS Lett. 1991;281:9–19. doi: 10.1016/0014-5793(91)80347-6. [DOI] [PubMed] [Google Scholar]
  • 32.Kunkel TA. DNA replication fidelity. J. Biol. Chem. 1992;267:18251–18254. [PubMed] [Google Scholar]
  • 33.Gillespie DT. Markov Processes: An Introduction for Physical Scientists. San Diego: Academic Press; 1991. [Google Scholar]
  • 34.Gardiner CW. Handbook of Stochastic Methods: for Physics, Chemistry and the Natural Sciences (Springer Series in Synergetics) Berlin: Springer; 2004. [Google Scholar]
  • 35.Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
  • 36.Steuerwald N, Barritt JA, Adler R, Malter H, Schimmel T, Cohen J, Brenner CA. Quantification of mtDNA in single oocytes, polar bodies and subcellular components by real-time rapid cycle fluorescence monitored PCR. Zygote. 2000;8:209–215. doi: 10.1017/s0967199400001003. [DOI] [PubMed] [Google Scholar]
  • 37.Elliott K, O'Connor M. Embryogenesis in mammals (Ciba Foundation symposium; 40) Amsterdam: Elsevier; 1976. [Google Scholar]
  • 38.Piko L, Taylor KD. Amounts of mitochondrial DNA and abundance of some mitochondrial gene transcripts in early mouse embryos. Dev. Biol. 1987;123:364–374. doi: 10.1016/0012-1606(87)90395-2. [DOI] [PubMed] [Google Scholar]
  • 39.Larsson NG, Wang J, Wilhelmsson H, Oldfors A, Rustin P, Lewandoski M, Barsh GS, Clayton DA. Mitochondrial transcription factor A is necessary for mtDNA maintenance and embryogenesis in mice. Nat. Genet. 1998;18:231–236. doi: 10.1038/ng0398-231. [DOI] [PubMed] [Google Scholar]
  • 40.Cao L, Shitara H, Horii T, Nagao Y, Imai H, Abe K, Hara T, Hayashi J, Yonekawa H. The mitochondrial bottleneck occurs without reduction of mtDNA content in female mouse germ cells. Nat. Genet. 2007;39:386–390. doi: 10.1038/ng1970. [DOI] [PubMed] [Google Scholar]
  • 41.Moraes CT. What regulates mitochondrial DNA copy number in animal cells? Trends Genet. 2001;17:199–205. doi: 10.1016/s0168-9525(01)02238-7. [DOI] [PubMed] [Google Scholar]
  • 42.Sissman NJ. Developmental landmarks in cardiac morphogenesis: comparative chronology. Am. J. Cardiol. 1970;25:141–148. doi: 10.1016/0002-9149(70)90575-8. [DOI] [PubMed] [Google Scholar]
  • 43.Karatza C, Stein WD, Shall S. Kinetics of in vitro ageing of mouse embryo fibroblasts. J. Cell. Sci. 1984;65:163–175. doi: 10.1242/jcs.65.1.163. [DOI] [PubMed] [Google Scholar]
  • 44.Cervantes RB, Stringer JR, Shao C, Tischfield JA, Stambrook PJ. Embryonic stem cells and somatic cells differ in mutation frequency and type. Proc. Natl Acad. Sci. USA. 2002;99:3586–3590. doi: 10.1073/pnas.062527199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Dubec SJ, Aurora R, Zassenhaus HP. Mitochondrial DNA mutations may contribute to ageing via cell death caused by peptides that induce cytochrome c release. Rejuvenation Res. 2008;11:611–619. doi: 10.1089/rej.2007.0617. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Miller FJ, Rosenfeldt FL, Zhang C, Linnane AW, Nagley P. Precise determination of mitochondrial DNA copy number in human skeletal and cardiac muscle by a PCR-based assay: lack of change of copy number with age. Nucleic Acids Res. 2003;31:e61. doi: 10.1093/nar/gng060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Wiesner RJ, Ruegg JC, Morano I. Counting target molecules by exponential polymerase chain reaction: copy number of mitochondrial DNA in rat tissue. Biochem. Biophys. Res. Commun. 1992;183:553–559. doi: 10.1016/0006-291x(92)90517-o. [DOI] [PubMed] [Google Scholar]
  • 48.Clayton DA. Replication of animal mitochondrial DNA. Cell. 1982;28:693–705. doi: 10.1016/0092-8674(82)90049-6. [DOI] [PubMed] [Google Scholar]
  • 49.Shadel GS, Clayton DA. Mitochondrial DNA Maintenance in vertebrates. Annu. Rev. Biochem. 1997;66:409–435. doi: 10.1146/annurev.biochem.66.1.409. [DOI] [PubMed] [Google Scholar]
  • 50.Terman A, Brunk UT. Autophagy in cardiac myocyte homeostasis, ageing, and pathology. Cardiovasc. Res. 2005;68:355–365. doi: 10.1016/j.cardiores.2005.08.014. [DOI] [PubMed] [Google Scholar]
  • 51.Davis AF, Clayton DA. In situ localization of mitochondrial DNA replication in intact mammalian cells. J. Cell. Biol. 1996;135:883–893. doi: 10.1083/jcb.135.4.883. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Collins ML, Eng S, Hoh R, Hellerstein MK. Measurement of mitochondrial DNA synthesis in vivo using a stable isotope-mass spectrometric technique. J. Appl. Physiol. 2003;94:2203–2211. doi: 10.1152/japplphysiol.00691.2002. [DOI] [PubMed] [Google Scholar]
  • 53.Taylor RW, Turnbull DM. Mitochondrial DNA mutations in human disease. Nat. Rev. Genet. 2005;6:389–402. doi: 10.1038/nrg1606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Zhang D, Mott JL, Chang SW, Denniger G, Feng Z, Zassenhaus HP. Construction of transgenic mice with tissue-specific acceleration of mitochondrial DNA mutagenesis. Genomics. 2000;69:151–161. doi: 10.1006/geno.2000.6333. [DOI] [PubMed] [Google Scholar]
  • 55.Limson M, Jackson CM. Changes in the weights of various organs and systems of young rats maintained on a low-protein diet. J. Nutr. 1931;5:163–174. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_40_5_e35__index.html (864B, html)
supp_gkr1221_nar-01509-met-k-2011-File005.pdf (3.2MB, pdf)

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES