Strong physical constraints on sequence-specific target location by proteins on DNA molecules

Abstract

Sequence-specific binding to DNA in the presence of competing non-sequence-specific ligands is a problem faced by proteins in all organisms. It is akin to the problem of parking a truck at a loading bay by the side of a road in the presence of cars parked at random along the road. Cars even partially covering the loading bay prevent correct parking of the truck. Similarly on DNA, non-specific ligands interfere with the binding and function of sequence-specific proteins. We derive a formula for the probability that the loading bay is free from parked cars. The probability depends on the size of the loading bay and allows an estimation of the size of the footprint on the DNA of the sequence-specific protein by assaying protein binding or function in the presence of increasing concentrations of non-specific ligand. Assaying for function gives an ‘activity footprint’; the minimum length of DNA required for function rather than the more commonly measured physical footprint. Assaying the complex type I restriction enzyme, EcoKI, gives an activity footprint of ∼66 bp for ATP hydrolysis and 300 bp for the DNA cleavage function which is intimately linked with translocation of DNA by EcoKI. Furthermore, considering the coverage of chromosomal DNA by proteins in vivo, our theory shows that the search for a specific DNA sequence is very difficult; most sites are obscured by parked cars. This effectively rules out any significant role in target location for mechanisms invoking one-dimensional, linear diffusion along DNA.

INTRODUCTION

Cellular DNA is always partially covered with DNA-binding proteins such as transcription factors, polymerases, repair enzymes, methyltransferases, histones and, in prokaryotes, histone-like proteins, to name but a few (1–6). These binding proteins are in a constant state of flux, competing with each other for binding to the DNA and to perform their function. The histones and histone-like proteins comprise the vast majority of these DNA-binding proteins and they bind, with little specificity, to any DNA sequence. This general binding results in the coating of the DNA and its wrapping up into higher-order structures. In addition, numerous small molecules, such as polyamines (4,7), are also competing to bind to the DNA. It is intuitively obvious that such an environment, where the DNA is randomly coated with ligands, should reduce the likelihood that a sequence-specific protein can find an accessible copy of its target sequence. For example, Hildebrandt and Cozzarelli (8), by examining rates of recombination in vivo, showed that the effective concentration of the recombination target sites was lowered by occlusion of those sites by non-specifically bound proteins. They suggested that this was a general mechanism of gene regulation.

To introduce mechanistic details for the problem of site-specific binding, consider binding of a single restriction endonuclease molecule to a single copy of its target sequence residing within a long piece of DNA, Figure 1. The enzyme will approach the target site either by three-dimensional diffusion or by some form of lower-dimensional facilitated diffusion such as hopping (transient dissociation and re-association), inter-segment transfer (if for the sake of argument, the enzyme had two DNA-binding sites) or by random sliding along the DNA (one-dimensional sliding following the helical path or two-dimensional sliding over the whole DNA surface) [e.g. see reviews (9–12)]. The actual manner of the enzymes' arrival near its target site is not important here. In a simple test tube experiment with purified components, the endonuclease will diffuse to the vicinity of its DNA target, make its final approach over the last 1 or 2 nm to contact the DNA and then bind without any hindrance. In vivo however, the endonuclease will arrive in the vicinity of its target site where it is likely to find that other proteins are already totally or partially covering its target site, Figure 2. Given sufficient time and the right conditions, these other proteins will dissociate from the DNA allowing the endonuclease to compete with these proteins and other nearby proteins for binding to the now unobstructed segment of DNA containing the target sequence. This competition for binding will certainly reduce the efficiency of sequence-specific binding and subsequent function of the endonuclease just as was found in the recombination experiments (8). During different stages of the cell growth cycle, the likelihood of the endonuclease (or other site-specific protein) finding its target sequence free of obstructions will vary as the concentrations of other DNA-binding proteins varies and the higher order structure of the DNA varies. In the case of invading bacteriophage DNA, which is the normal target for a restriction endonuclease and which will initially be relatively free of bound proteins (the vast majority will be bound to the chromosome), the likelihood of the target sequence being free of obstructions should be higher than on the chromosomal DNA.

Figure 1.

Diffusion mechanisms for a protein (oval) to reach its DNA target site (black rectangle) on a segment of DNA (open rectangle). The leftmost protein is using linear diffusion (sliding) to randomly search along the DNA molecule for the target. The middle protein is using multiple dissociation/association (hopping) events. It takes two random steps towards the target but then hops away from the target and then onto another DNA segment. The rightmost protein has two DNA-binding sites and can bridge between different DNA segments during its search for the target.

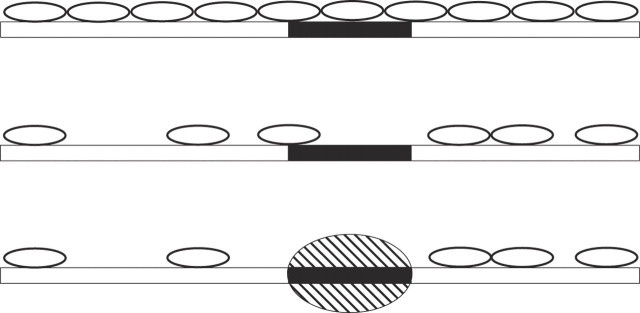
Figure 2.

Non-specific DNA-binding ligands (small ovals) bind to a DNA segment (open rectangle) containing a target site (black rectangle) for a site-specific protein (large shaded oval). The small ligands cover n base pairs of DNA and the large protein covers g base pairs. The upper DNA molecule is coated with perfectly ‘parked’ ligands and the target site for the site-specific protein is blocked. The middle panel shows sub-optimal parking as gaps between consecutive ligands that are not multiples of n. Complete coverage of this DNA molecule with ligands is impossible and one of the ligands is obstructing the target site of the site-specific protein. The lower panel shows sub-optimal coverage by the small ligands but the site-specific protein has been able to bind to its unobstructed target site.

Our objectives in this article are first to put a quantitative limit on the probability that at any given instant, a large enough segment of DNA is free from obstructing non-specifically bound proteins to allow binding and function of a protein which operates on a specific DNA target sequence within that DNA segment. Our theory gives this probability as a function of saturation of the DNA with non-specific binding proteins. It is important to note that our theory assumes that the non-specific binding proteins do not alter their position on the DNA, in other words they bind irreversibly (or at least for very much longer than the sequence-specific protein), and we are therefore ignoring all kinetic effects. This is of course an entirely unrealistic situation as life would not be possible without movement of proteins on DNA but the assumption is extremely useful for several reasons. Namely, that the problem has an exact mathematical solution and is therefore entirely general to all site-specific binding processes in all cells, it represents the worst possible scenario for a site-specific protein and therefore sets an upper limit or constraint on this process (in other words it constrains qualitative discussions of site-specific binding within strict limits) and finally, the calculation does not appear to have been presented previously.

Second, we show that if one assays the sequence-specific enzyme by measuring its enzyme activity, then one has a means of determining how long a segment of unobstructed DNA is required for not only sequence recognition but also for function. In other words, we can determine an ‘activity footprint’. This contrasts with other footprinting methods, such as exonuclease III and DNase footprinting, used to study DNA-binding proteins (13). They reveal only the physical size of the DNA region covered by the bound protein. As an example, we use our theory to determine the activity footprint of the EcoKI type I restriction endonuclease [reviewed in (14,15)] with an intercalating dye molecule playing the role of the non-specific binding ligand. We find that the activity footprint required for EcoKI activity on DNA is larger than the physical footprint determined previously (16,17), in agreement with the general finding that enzymatic activity of DNA-binding proteins often requires some ‘elbow room’ on the DNA next to the protein's target sequence (12).

Last, we explore the implications of the theory for the general problem of site-specific binding of proteins to chromosomal DNA in vivo and conclude that such binding is going to be extraordinarily difficult if, as is often assumed (10,11), the sequence-specific protein scans along the DNA looking for its target sequence. In other words, the location of specific target sequences on chromosomal DNA by proteins using a one-dimensional diffusional sliding mechanism over distances greater than a few tens of base pairs appears to be neither physically feasible nor relevant in vivo. This is in agreement with considerations based upon many experiments and the polymer physics of DNA which indicate that it takes n² steps to locate a specific site by sliding but only n^1/2 steps to locate the target by three-dimensional diffusion [reviewed in (12)]. However, it should be noted that sliding can be observed under non-physiological conditions in vitro on naked DNA [reviewed in (10) and (11)]. Our theory strongly suggests that, when other ligands are also bound on the same DNA molecule, only higher dimensional diffusion mechanisms or energy-driven DNA translocation processes are suitable for moving on DNA and for locating specific DNA sequences.

THEORY

General parking problems

The binding of a ligand to a DNA molecule can be considered abstractly as a ‘parking problem’ with the DNA acting as a lattice to which ligands can adsorb. Random sequential adsorption is the mathematical term for processes in which such parking problems are the point of interest. They occur in many contexts and have been considered extensively (18,19). For example, by equating non-sequence-specific DNA-binding ligands with cars, McGhee and von Hippel developed a straightforward theory that describes the coverage (saturation) of DNA by parked cars (20). They showed that it was virtually impossible to saturate the DNA for any physically reasonable size of car (a ligand covering >1 bp). As the number of parked cars increased, an increasing number of the gaps between consecutive cars were too small to allow another car to bind within the gap. They also examined the case of two different types of non-sequence-specific cars binding randomly and considered cooperative binding of cars. Cooperativity allowed a higher degree of saturation because cars tended to ‘bunch up’ (group together) without leaving intervening gaps. Their theory has proved very successful for studying experimentally such non-specific binding processes (21–23). Even simpler formulations result if one can experimentally determine the number and location of the cars (24).

The problem of site-specific target location by a protein in the presence of non-specific DNA-binding ligands is akin to parking a truck at a specific site (e.g. a loading bay) on the side of a road where cars are also allowed to park. If a parked car blocks the loading bay, even partially, the truck cannot park at the loading bay to deliver its goods. This problem does not appear to have been previously considered in the context of protein-DNA interactions. In the present article we derive an exact formula describing the probability that a specific DNA sequence (the loading bay for the sequence-specific molecule or ‘truck’) is free from obstructing parked cars. The latter are non-sequence-specific and non-cooperative DNA-binding ligands which bind randomly to the DNA. The size of the load-ing bay is a parameter of the theory with unknown value and is determined from the concentration of parked trucks as a function of car concentration.

Derivation for site-specific parking

We define our DNA lattice to be N base pairs in length on which are parked B cars, each of length n base pairs. Hence, the fractional coverage of the DNA lattice by cars is nB/N = nv. On this lattice there is one loading bay of g base pairs in length. In the Supplementary Data we show that the probability of the truck's loading bay being completely free of parked cars is

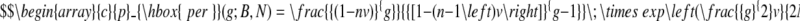1

In other words, this equation gives the probability that a specific binding site sequence, g base pairs in length, is free from non-specifically bound ligands. As the size of the loading bay for the truck increases or as the number of parked cars increases, there is a lower probability that the loading bay is not obstructed.

The pre-exponential factor can be rewritten as shown

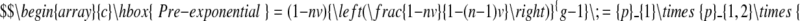2

and reveals that it is the product of the probability, p₁, that the first base pair of the loading bay site is free (1 − nv or in other words, one minus the probability that a base pair chosen at random is occupied by a car) multiplied by the conditional probabilities that sufficient successive base pairs are also free. The term in brackets is the conditional probability, p_i−1,i, that the i-th base pair is free if the preceding (i − 1) base pair is free, as calculated by McGhee and von Hippel (20), and this term is raised to the power g − 1 to give a total of g consecutive base pairs free of cars.

If the DNA molecule is large (N > 1000) and values of g are of order 100 or less, then further simplifications can be made to Equation 1. As shown in the supporting material, it transpires that for all nB/N with physically reasonable values of g up to order 100 bp, that the pre-exponential factor alone is an accurate description of the probability p_per(g; B, N) where this probability is non-negligible. In other words,

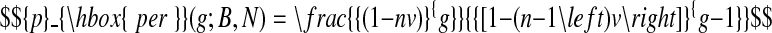3

Thus, Equation 3 can be used to explore the probability of site-specific binding by trucks as a function of the size of the cars and the size of the loading bay.

In the above equations, we assume that the cars cannot be displaced by the truck and that they are physically able to block the parking of the truck. We also ignore any time-dependence of the binding process where the cars and trucks would have some mean residence time on the DNA. Kinetic processes for the association and dissociation of cars and trucks from the lattice would eventually allow a truck to park at its loading bay. For simplicity, we also assume that the cars do not interact with each other but all park independently. Interactions between cars would be equivalent to cooperative binding of the car proteins to the DNA. Such effects are obviously important in the real world and would require our theory to be extended to consider a car size dependent upon the concentration of the cars, a situation considered by McGhee and von Hippel and others (20,25,26). If cooperativity existed in the binding of cars in our theory then, at higher car concentrations, the cars cluster together to essentially act as larger cars. The larger the cars then the greater is the probability that the loading bay would be clear for any given lattice saturation.

Behaviour of Equation 3

A typical non-specific DNA-binding protein would be a histone in eukaryotes or a histone-like protein in prokaryotes. These proteins are all small in size and as a crude approximation we can say that each such protein can be represented by a car of size n = 10 bp. The size of the site-specific truck is varied from an unrealistic 1 bp up to a more realistic 100 bp which could represent a large protein complex such as a polymerase.

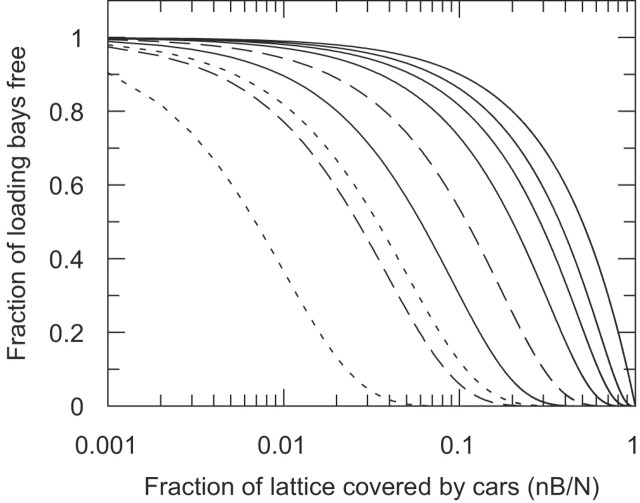
It is apparent from Figure 3, that even low coverage of the DNA, of the order of 10% of the total number of base pairs (nB/N = 0.1), significantly reduces the probability of a specific site, of order 10 or more base pairs in length, being available for binding by the site-specific protein truck. If the truck has a footprint of ∼100 bp then it will find the majority of its binding sites occupied by obstructing cars even when cars cover only 5–10% of the DNA.

Figure 3.

Theoretical curves for the probability, p_per(g; B, N), of a gap of g base pairs completely encompassing the loading bay for the truck as a function of the fractional coverage (nB/N) of the DNA lattice by cars, calculated using Equation 3. There are B cars bound to a lattice of N = 4000 bp. The solid lines are for car size n = 10 bp and loading bay gap size, g, varying from 100, 20, 10, 5 and 1 bp from left to right. The dashed lines are for n = 4 with g = 100 (left-hand curve) and 20 (right-hand curve). The dotted lines are for n = 1 with g = 100 (left-hand curve) and 20 (right-hand curve). (Note that complete saturation of the lattice is reached at B/N = 0.1 for n = 10 as nB/N = 1 and in general at 1/n. Curves for g = 1 are independent of n.)

DNA is also often studied and visualized by the addition of small fluorescent dye molecules, e.g. ethidium bromide or YOYO, or targeted by small drug molecules, e.g. cisplatin, so we also consider such small molecules with a car of size n = 4 bp. Figure 3 shows that smaller cars with n = 4 (or an unrealistic n = 1) are more effective at blocking the loading bay than the cars with n = 10. This is physically reasonable as, for any given fractional coverage of the DNA, there are more of the small cars than of the large cars and hence a higher chance for any one of them to be obstructing the loading bay.

RESULTS AND DISCUSSION

An example of ‘activity footprinting’ using experimental data

It is apparent that Equations 1 and 3 could be used to determine the size of a loading bay for any site-specific truck if the extent of truck binding or truck activity could be measured as a function of saturation of the DNA with non-specific cars. The equations would be valid if the cars were assumed to be bound irreversibly. This assumption would be most reliable if, when measuring truck activity, one used single turnover conditions so that the non-specific cars had no chance to re-arrange themselves during the measurement. This would represent a novel method for footprinting site-specific DNA-binding proteins. Footprinting methods normally measure the length of DNA required for protein binding. However, with our equations one can also measure a parameter such as the enzyme activity of the truck and determine an ‘activity footprint’; the length of loading bay required for function as opposed to merely binding.

As an example, we use the type I DNA restriction endonuclease, EcoKI, which recognizes the long DNA target sequence 5′-AACNNNNNNGTGC-3′ [reviewed in (14,15)] in the role of the truck and the bis-intercalating dye, YOYO, in the role of the car. EcoKI will cut DNA containing its target sequence if it lacks methylation at the N6 position of both adenine bases at the underlined positions in the target sequence. In stark contrast to commercial restriction endonucleases (type II restriction enzymes), type I enzymes do not cut the DNA at a defined location at or near their target sequence. Instead, they initiate ATP hydrolysis to drive motors within the enzyme. The enzyme remains at its target sequence and these motors reel in the DNA towards the enzyme extruding large loops of DNA as they operate. Initiation of the translocation is a slow event presumably because the enzyme must introduce a large distortion into the DNA to start loop extrusion (27). DNA cleavage occurs when the motor-driven translocation stalls at locations often thousands of base pairs distant from the target sequence (28–30). After cleavage, ATP hydrolysis continues, and the enzyme apparently remains bound to the DNA and so does not turn over in the restriction reaction. The large size of the EcoKI enzyme, 440 kDa, equivalent to an idealized 10 nm diameter sphere, leads to a large physical ‘footprint’ on DNA when bound to its target sequence (17). This footprint is 45 bp (15.3 nm) in length in the absence of ATP, and changes to 30 bp (10.2 nm) in the presence of ATP (17). This change in footprint size is not due to dissociation of any subunits from the enzyme, but reflects some structural re-arrangement. The enzyme must alternate between these two footprint sizes as it hydrolyses ATP and translocates the DNA. This oscillation in size may represent the ‘power stroke’ of the motors. Given the large size of EcoKI and the complexity implied by the translocation mechanism, it is possible that the enzyme needs a much longer DNA substrate to display activity than it does merely to bind to the target sequence.

Figure 4 shows the fractional decrease in the experimental rate constants for ATP hydrolysis and DNA cleavage as a function of increasing saturation of the DNA lattice with parked YOYO (31). In our experiments, the absence of turnover coupled with the effectively irreversible binding of YOYO on the time scale of our assays, gives each EcoKI molecule only one chance to display activity and the neglect of the kinetics of car parking in our theory is not a problem. YOYO will, like all intercalators, affect the supercoiling of the circular DNA plasmids used in our assays. DNA topology by itself does not appear to completely prevent the ATPase, translocation and cleavage reactions of the type I restriction enzyme EcoAI (32) and we assume that EcoKI will behave similarly. We note that YOYO still had an inhibitory effect on EcoKI activity when linear DNA, which has no topoisomers, was used (31). Therefore, we believe that the effects we observe in the presence of YOYO are primarily due to parking effects rather than topology effects. Furthermore, YOYO has only weak sequence preference when compared with the highly specific restriction enzyme (31) so we assume that it binds randomly.

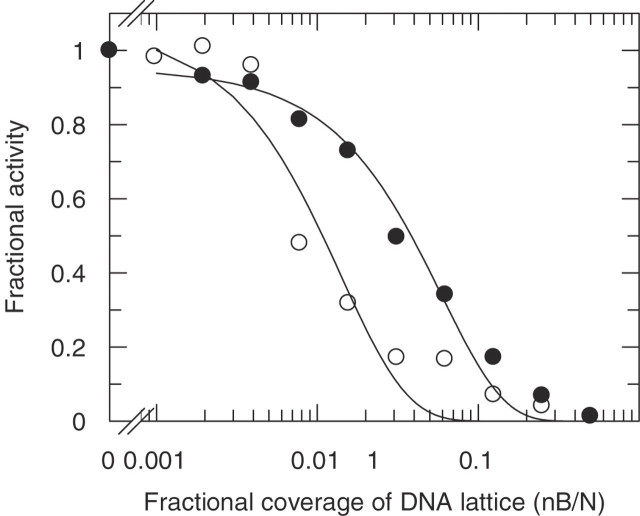
Figure 4.

Activity footprint determination, using Equation 3 and the law of mass action (Supplementary Data, Equation S18), for the inhibition of EcoKI activity on circular plasmid DNA as a function of saturation of the plasmid with the intercalating dye molecule YOYO. The ordinate axis shows the experimental rate constants for ATP hydrolysis (filled circles) and DNA cleavage (open circles) expressed as fractions of the rate constants measured in the absence of YOYO. The DNA (N = 4361 bp) has one target site for the enzyme and YOYO is assumed to be a car binding irreversibly with n = 4 bp. The binding affinity, K_d, of EcoKI for its target was fixed at 2 nM (17) with [EcoKI] = 67 nM and [DNA] = 50 nM. The only variables in fitting were the loading bay gap size, g, and an ordinate scaling factor which deviated <15% from the expected value of 0.02 (given by 1/[DNA]). Data at high saturation are taken from Keatch et al. (31); data at low saturation have been added using the same experimental methods as used previously (31).

As described in the Supplementary Data, Equation 3 can be incorporated into the solution to the equilibrium mass action equation for the interaction of EcoKI with its target sequence and this can then be fitted to experimental data describing the rate of ATP hydrolysis and of DNA cleavage by EcoKI as function of saturation of the DNA with parked cars. By allowing the loading bay size to vary we find that the best fit to the ATP hydrolysis data gives an EcoKI loading bay size, g, of 66 ± 12 bp, a figure similar in magnitude to that determined by more traditional methods. However, it is immediately apparent from the data for DNA cleavage that the parked cars have a greater effect on cleavage than on ATP hydrolysis. Fitting our equation to the data for DNA cleavage we obtain a loading bay size, g, of 293 ± 45 bp. This is an enormous length of DNA around the EcoKI target sequence which apparently must be kept clear of parked cars to allow the enzyme to perform the complex restriction reaction. This enormously large activity footprint strongly suggests some extreme structural distortion in the DNA around the EcoKI target as the enzyme commences loop extrusion and DNA translocation.

One may ask whether the large activity footprint observed in vitro is relevant to the function of EcoKI and related enzymes in vivo? From these large activity footprint values and our general discussion below, it is apparent that EcoKI will find it virtually impossible to not only locate its target on chromosomal DNA but also commence its translocation/restriction reaction. This is a fortunate state of affairs as occasionally unmethylated target sites occur on the chromosomal DNA during times of cell stress and concomitant DNA damage (33). If such sites triggered a successful restriction reaction, they could lead to cell death. Not only do such sites occur with very low probability, Escherichia coli can invoke a phenomenon called restriction alleviation when such sites are formed. Restriction alleviation involves proteolysis of the restriction subunit only when it is attempting to translocate on unmodified chromosomal DNA but not on unmodified foreign DNA (33–35). Translocation on chromosomal DNA is greatly hindered by non-specifically bound ligands, at least in vitro (31,36), but rapid on essentially naked foreign DNA [in vivo translocation rates of up to 200 bp/s have been measured (29), similar to rates measured in vitro (28)]. The normal function of the restriction enzyme is to identify and destroy invading foreign DNA such as that from a bacteriophage. Such DNA will enter the cell essentially naked without any cars parked upon it [and in fact EcoKI can facilitate DNA entry in some circumstances, see (29)]. This unobstructed DNA is a suitable substrate for the enzyme to perform ATPase-driven DNA translocation and DNA cleavage. The foreign DNA will not remain free of non-specifically bound proteins for more than a few seconds, however, since at least some fraction of the cytoplasmic population of EcoKI appears to be associated with the inner membrane (35,37), it will be able to restrict the foreign DNA before the predominantly nucleoid-associated proteins (38) described below can dissociate from the nucleoid, diffuse to the incoming DNA and begin to hinder the action of EcoKI.

The implications of the parking theory for site location in vivo

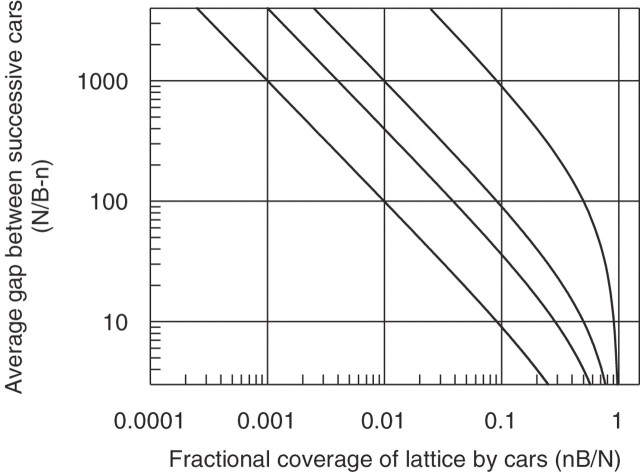
We wish to conclude with a general discussion of the implications of Equations 1 and 3 in relation to the problem of location of specific target sequences on DNA in vivo. To make the implications of the equations clearer we calculate the average distance between successive cars as function of saturation. It is obvious that N/B is the space on the lattice per car and we know that each car occupies n sites. So the average space between cars is the remainder, N/B − n sites. Figure 5 shows this average gap size as a function of car size and saturation, nB/N. It shows the same features as the previous graphs: for a given saturation of the lattice with cars, large cars leave larger regions of the lattice clear of obstructions and hence there is more chance that the truck can locate an unobstructed loading bay.

Figure 5.

The average size (N/B − n), in base pairs, of a gap between consecutive cars as a function of lattice (N = 4000) saturation with cars of different sizes. The curves from left to right have cars sizes of n = 1, 4, 10 and 100. The E.coli chromosome has a fractional coverage varying between 0.1 and 0.5 depending upon growth conditions.

It is abundantly clear from Figure 5 that it is, as realized by McGhee and von Hippel (20), almost impossible to saturate a lattice with cars of size greater than n = 1 as gaps smaller than the car accumulate between successive parked cars; an effect frequently and frustratingly encountered in the macroscopic world when attempting to park a car on a crowded street. If, as we have assumed, the cars are irreversibly parked and do not interact with each other, then it is highly likely that the truck will be unable to bind at all to its target sequence or ‘loading bay’.

In vivo, enzymes whose function depends on the recognition of a specific DNA target sequence have to operate on host chromosomal DNA predominantly covered by histone proteins in eukaryotes and histone-like proteins, such as HN-S, in prokaryotes. These proteins are very abundant and cover ∼10 bp of DNA each. In E.coli, Azam et al. (39) have determined that in the logarithmic growth phase there are 215 000 proteins associated with the 4.6 × 10⁶ bp of chromosomal DNA. Six types predominate, Fis, Hfq, HN-S, HU, IHF and StpA. Of these, HN-S, StpA, HU and IHF are uniformly distributed throughout the nucleoid (40) and total of ∼105 000 molecules. We will take this value as our absolute minimum number of bound proteins. In stationary phase, the Dps protein predominates with 180 000 copies plus ∼50 000 other proteins giving 230 000 bound proteins as our absolute maximum number. Electron microscopy has shown a highly condensed nucleoid structure (41). If we consider nucleoid-associated proteins as our cars each covering 10 bp (n = 10) and use the total abundances ranging from 105 000 to 230 000 proteins, then the coverage of the 4.6 × 10⁶ bp in the chromosome will range from roughly nB/N = 0.217–0.5. However, we must not forget that during rapid growth, it has been determined that E.coli has ∼2.13 chromosomes or 9.8 × 10⁶ bp (4). If we again take 105 000 proteins evenly spread over this amount of DNA, we get a value of nB/N = 0.107. These nB/N values, ranging from 0.107 to 0.5 (agreeing with early estimates in 1 and 2), are noteworthy; most of the DNA lattice is covered with cars getting in the way of site-specific trucks! Examination of the curves in Figure 5 shows that for a site-specific protein to find its target site completely free of parked cars with n = 10, then its footprint cannot be larger than ∼80 bp in log phase and 10 bp in stationary phase. It can of course be argued from the structure of the nucleosome that the cars should have n of order 100 bp or more. For a given coverage of the DNA, these larger cars are spaced more widely and the average separation between parked cars increases to 100 or more base pairs. As these gaps are now very large, one might conclude that parking the truck at the loading bay will be simple. However, whatever car size and saturation one chooses, these are average gap sizes and do not take into account the probability of the gap being at the correct location encompassing the loading bay. Such considerations reduce the probability of site-specific truck binding to very low levels (the effect is to shift the curves given in Figure 5 to the left so that they intercept the abscissa, with g = 0, when nB/N = 1 − p_per(g; B, N). In other words, the effective concentration of a single site, p_per(g; B, N) [DNA], will be very much lower than [DNA]. Using these rough experimental constraints, one can conclude that large site-specific DNA-binding proteins have a low probability of being able to bind to their DNA targets in log phase. This conclusion was also reached from experiments studying recombination in vivo which indicated that the effective concentration of DNA in vivo was much lower than the chemical concentration determined from mass/volume (8). During the stationary phase, when proteins such as Dps almost completely coat the DNA, site-specific proteins will be unable to find their targets at all. Whilst these calculations have been applied to the nucleoid of E.coli, they are equally applicable to the chromosomes of other organisms.

Our calculations would appear to imply that, whilst large gaps can exist on the DNA, they are unlikely to encompass the loading bay and hence location of a specific target sequence in the chromosome will often be impossible. This would clearly make life impossible. However, we have not considered kinetic effects in our theory but have only calculated the parking situation which might be found at any instant on the DNA. It is clear that the histones and related proteins acting as cars do not spend all of their time bound to DNA but transiently dissociate and move around on the second to minute time scale (42–44). Thus eventually, any specific DNA target site will become open for the site-specific protein to bind. As an example, it has been demonstrated that transient partial dissociation, driven by thermal energy, of some of the DNA from the histone core complex in a nucleosome can expose a target site for the LexA repressor protein. It was estimated that at any instant 2–10% of the nucleosomes contained a suitable unobstructed loading bay to allow access of LexA (45). Kinetic effects have been considered in other formulations of the problem of site location but they have generally ignored or grossly underestimated the effects of the density of parked cars on DNA in vivo (46–49). An extension of the theory presented in this paper to include kinetic effects should ultimately be possible but is likely to sacrifice the general nature of our formulation.

In addition to random dissociation events by cars transiently exposing loading bays and allowing truck binding, some DNA-binding enzymes, such as RNA polymerases and chromatin remodeling factors are capable of translocating along DNA and of exerting considerable force as they move (43,50,51). Such enzymes should be able to push parked cars out of the way to reach their target site or even to drag or push other protein complexes to a specific target site. Such directed, energy-requiring processes offer an efficient alternative solution to the problem of locating a specific DNA site.

Notwithstanding kinetic considerations or energy-driven processes, we have shown that location of a target site on DNA which is not obstructed by other proteins is surprisingly rare. It is believed that DNA-binding proteins locate their targets by various forms of facilitated diffusion. Riggs et al. (52) originally proposed linear diffusion (sliding) along the DNA with the protein following the helical path of the substrate as a way of accounting for the rapid diffusion of the lac repressor to its target sequence. Such one-dimensional diffusion pathways have been demonstrated as feasible in vitro on naked DNA for several enzymes [see reviews (10) and (11)] but it has been strongly argued that such mechanisms are not relevant in vivo (12). Several additional methods for target location, including two-dimensional sliding over the surface of the DNA duplex, hopping and longer range three-dimensional diffusion between DNA sites by successive dissociation-association steps, and inter-segment transfer by DNA looping, have been put forward and supported experimentally (9,10,12,53–55). Given the experimentally determined density of nucleoid-associated proteins on DNA (39) and our theory, it is clearly impossible, in vivo, for any protein to rapidly conduct random one-dimensional diffusional sliding along DNA over a distance exceeding a few tens of base pairs and that the other site-location methods must be the primary mechanisms for target site location on chromosomal DNA. In the absence of an energy-driven motor, sliding can only be relevant on invading foreign DNA which is likely to be largely free of protein as it enters the cell.

SUPPLEMENTARY DATA

Supplementary data including full derivations of equations are available at NAR Online.