Orientation selectivity and noise correlation in awake monkey area V1 are modulated by the gamma cycle

Abstract

Gamma-band synchronization adjusts the timing of excitatory and inhibitory inputs to a neuron. Neurons in the visual cortex are selective for stimulus orientation because of dynamic interactions between excitatory and inhibitory inputs. We hypothesized that these interactions and hence also orientation selectivity vary during the gamma cycle. We determined for each spike its phase relative to the gamma cycle. As a function of gamma phase, we then determined spike rates and their orientation selectivity. Orientation selectivity was modulated by gamma phase. The firing rate of spiking activity that occurred close to a neuron's mean gamma phase of firing was most orientation selective. This stimulus-selective signal could best be conveyed to postsynaptic neurons if it were not corrupted by noise correlations. Noise correlations between firing rates were modulated by gamma phase such that they were not statistically detectable for the spiking activity occurring close to a neuron's mean gamma phase of firing. Thus, gamma-band synchronization produces spiking activity that carries maximal stimulus selectivity and minimal noise correlation in its firing rate, and at the same time synchronizes this spiking activity for maximal impact on postsynaptic targets.

Rhythmic neuronal synchronization has been described in numerous brain systems, species, and under many different conditions. A prominent proposal is that rhythmically synchronized spikes have an enhanced impact on target neurons. This consequence of synchronization might stem from direct feed-forward triggering of coincidence detection mechanisms, from the entrainment of target neurons, or from both mechanisms in conjunction (1–4). This proposal has been detailed in several computational studies (5, 6) and has received substantial experimental support (7–11).

Here, we ask a complementary, yet central question: Does the rhythmically synchronized spiking activity, besides its enhanced impact, also carry an enhanced representation of, e.g., a sensory stimulus in its firing rate? One of the best-studied cases of neuronal stimulus selectivity is the orientation selectivity of neurons in primary visual cortex. We recorded from several sites in awake monkey primary visual cortex while it was stimulated with patches of drifting grating that varied in orientation. Those stimuli induced strong gamma-band synchronization. We sorted spikes based on the phase in the gamma cycle at which they occurred, and we tested whether orientation selectivity varied as a function of phase in the gamma cycle.

Stimulus-selective neuronal responses signal a stimulus to postsynaptic target neurons most effectively when they are not corrupted by so-called correlated noise. The term “noise” is often used to denote variance in neuronal activity that is not explained by variance in the sensory stimulus. This so-called noise might well be fully determined, just by brain processes that are not determined by the stimulus. This noise could be averaged out if it were uncorrelated across neurons. However, numerous studies have reported moderate (12, 13) to weak (14, 15) correlations among the noisy response fluctuations of simultaneously recorded neurons. Because we hypothesized that stimulus selectivity was modulated by the gamma phase, we investigated whether gamma phase modulated noise correlations.

Results

Orientation Selectivity as a Function of Phase in the Gamma Cycle.

We recorded spikes and local field potentials (LFPs) from 94 sites in primary visual cortex, V1, of three awake macaque monkeys (32, 26, and 36 sites in monkeys JE, LI, and NI, respectively). The sites were activated by the presentation of gratings moving within a circular aperture for 0.8–1.4 s per trial. Across trials, eight different orientations were presented at random. The different orientations induced systematically varying firing rates in most of the recorded single units (Fig. S1A). The first 0.25 s after stimulus onset were characterized by strong transients, the following period by sustained firing. We focused on the sustained period because it allows the assumption that the data are approximately stationary, and because stimuli that are stationary or smoothly moving occupy most of natural viewing time, whereas sudden stimulus onsets are rare. During the sustained period (0.25 s after stimulus onset until end of trial), we quantified spike-field locking with a metric that is not biased by the number of spikes—namely, the pairwise phase consistency (PPC) (16). Spikes were, on average, phase locked to LFP oscillations in the gamma-frequency band (Fig. S1) and to LFP components <5 Hz (Fig. S2). We first focus on the gamma band and later turn to the low frequencies. Across monkeys, gamma-frequency bands differed, as has previously been found in monkeys (17–21) and humans (22–24) (Fig. S1 B–D)—a phenomenon partly due to genetic factors (25). We were interested in whether orientation selectivity and/or noise correlation varied systematically during the gamma cycle. The gamma cycle is only meaningfully defined within each monkey's individual gamma band. We therefore focused on the induced gamma band of each individual monkey.

From the 94 recording sites at which we recorded spiking and LFP activity, we were able to obtain 77 well-isolated single units. Of those 77 single units, 52 showed statistically significant spike-field locking in the gamma band (Rayleigh test, P < 0.05, on average 206 ± 13 SEM trials per unit). We focused the further analysis on those 52 significantly gamma-locked single units, because only for them could the mean gamma phase of firing and thereby the gamma phases relative to this mean phase be reliably determined. For each single unit, we then determined the mean gamma phase of firing across all spikes recorded from that unit. Across the 52 single units, the mean gamma phases were tightly clustered (Fig. S1E). During sustained activation, these units showed an average firing rate of 22.9 ± 3.2 Hz (SEM).

As set out in the introduction, we hypothesized that the orientation selectivity carried in the firing rate of spiking activity is modulated as a function of the phase at which the spiking activity occurs in the gamma cycle. Orientation selectivity is a well-studied phenomenon that can be quantified using standard metrics such as the orientation selectivity index (OSI; SI Methods) (26). Typically, orientation selectivity is determined using average firing rates computed per stimulus orientation separately. Averaging is performed across trials, and also across time in trials, and thereby disregards, e.g., the phase of the gamma-band rhythm at which a spike occurs. Here, we preprocessed the spike trains before determining orientation selectivity. We sorted a given spike train into multiple virtual spike trains, such that for a given virtual spike train, all its spikes had occurred within a limited range of the gamma cycle, (i.e., within a specific gamma-phase bin). Across the different virtual spike trains, all phases of the gamma cycle were covered. For each of these virtual spike trains, we then averaged across time and trials to determine the standard OSI index (see Fig. 1 for an example neuron). Across the different gamma-phase bins, this gave the phase-dependent OSI. In short, to obtain virtual spike trains, we determined the gamma phase for each individual spike, and we used this phase to sort the spikes into eight nonoverlapping gamma-phase bins, constructing eight sets of virtual spike trains. For each gamma-phase bin and neuron separately, we quantified the orientation-dependent variation of spike rates by computing the OSI. The OSI is defined as 1 − the circular variance of the responses—(i.e., as the circular resultant vector length) (Fig. S3 and SI Methods). We found that orientation selectivity was particularly strong for firing rates computed for spiking activity that occurred close to the mean gamma phase, and decreased for spiking activity at differing gamma phases (Fig. 1 B and C).

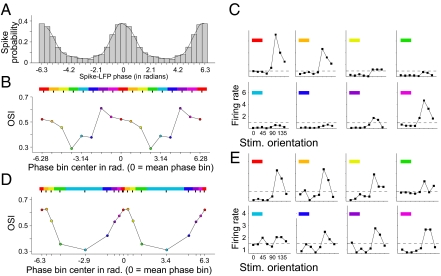
Fig. 1.

Example of gamma phase-dependent orientation selectivity based on equal-width phase bins, and phase bins with equal number of spikes. (A) Spike probability (y axis) as a function of the phase of the LFP (x axis, 0 = mean phase). (B) Bars show the equally wide and nonoverlapping phase bins. Average spike rate (y axis) across stimulus orientations (x axis) for each phase bin (in different panels). The dashed horizontal line denotes the average spike rate across orientations. The panels show that orientation tuning becomes apparent only for spike distributions around the mean phase. (C) OSI [1 − circular variance] (y axis) for phase-dependent spike counts across phase bins (x axis). The color of the rectangle in each panel denotes the phase bin from Fig. 1B from which the phase-dependent spike counts were used to compute the OSI. (D and E) Same format and example neuron as in B and C, but now for phase bins containing identical number of spikes. The color of the rectangle in each panel denotes the phase bin from Fig. 1D from which the phase-dependent spike counts were used to compute the OSI.

There may be one potential confound in this analysis, namely, the bins around the mean gamma phase have the highest spike count. Hence, the higher spike counts rather than the extraction of spikes occurring at particular gamma phases might be responsible for the observed differences in orientation selectivity across the different phase bins. However, the OSI metric is invariant to spike rate (SI Methods) and positively biased by low spike count (Fig. S4). Low spike count was observed opposite to the mean gamma phase, where we found the lowest OSI values. Thus, the spike count-dependent OSI bias reduced, rather than produced, the observed effects. To directly remove the variation in spike counts across gamma-phase bins, and thereby any potential confound, we introduced phase bins of varying width, such that we kept spike counts constant across the different phase bins. For each neuron, one bin was centered at the mean gamma phase across all spikes of this neuron. Seven additional bins were then adjusted such that they fully covered the gamma cycle without overlap, and all bins contained the same number of spikes. The results confirmed those from the other binning regimes (Fig. 1 D and E). Orientation selectivity of firing rates was particularly pronounced for the spiking activity that occurred close to the neuron's mean gamma phase of firing.

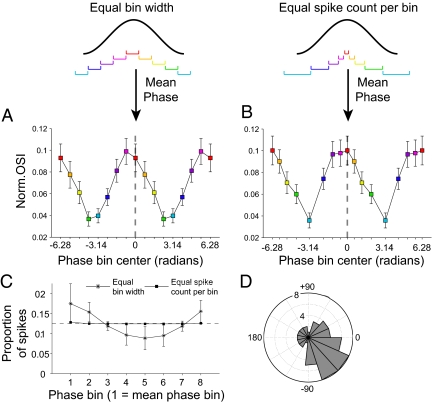
The effect described above for an example neuron was consistent across the population of neurons (Fig. 2 A and B). To obtain the population results, we first determined, for each neuron separately, the gamma phase-dependent OSI values, and subsequently averaged them across the 52 neurons. For both ways of binning, average orientation selectivity of firing rates degraded significantly when using spikes that occurred away from the neurons’ mean gamma phases (Fig. 2 A and B). Note that normalizing the OSI curves (Fig. 2 A and B) does not alter their modulation depth, as can be appreciated from the raw OSI curves in Fig. S5, but merely removes the across-cell variance and highlights the across-phase bins variance in OSI values.

Fig. 2.

Population results for gamma phase-dependent orientation selectivity. (A and B) Normalized OSI for phase-dependent spike counts for each phase-binning type. OSI was normalized by subtracting the minimum OSI across phase bins for each cell separately, before group averaging. The x axes denote the phase bin center. Arrows indicate the mean phase bin. For the binning with equal bin widths and equal spike counts per bin, the x axis replicates the gamma cycle twice to illustrate the cyclic modulation. For all panels, error bars denote SEM. (C) Proportion of spikes across phase bins with the two types of phase binning illustrated in A and B. Dashed line shows the 12.5% level reflecting equal distribution of spikes across phase bins. (D) Across-cell distribution of gamma phases at which orientation selectivity was estimated to be highest.

Fig. 2 A and B suggest that the gamma phase at which the OSI peaked was, on average, slightly advanced relative to the mean gamma phase, (i.e., the phase at which spike density was highest). To examine this directly, we estimated, for each neuron separately, at which gamma phase OSI was highest. To this end, the OSI values as a function of gamma phase were fitted with a cosine function, separately for each neuron. The cosine function provided a good model (mean explained variance R² = 0.49, P < 0.001, permutation test). Cosine fits were significant for 42.3% of the cells (at P = 0.05, permutation test) and for those cells the average peak-to-through cosine amplitude was 0.18 ± 0.016 (SEM), corresponding to an average 56.8 ± 7.9% (SEM) change relative to the cells’ average OSI. We then determined the gamma phases at which the cosine fits reached their respective maxima (Fig. 2D). These phases had a significant (Rayleigh test, P < 0.001, resultant vector length = 0.38) circular mean direction of −31.9 ± 26.9° [95% confidence interval (CI)], preceding (P < 0.01, test on confidence interval) the mean gamma phase (defined as 0°). Across animals, the (cosine) modulation of OSI as a function of gamma phase was roughly confined to the gamma-frequency band that characterized each of the three monkeys. However, an additional lower (monkeys JE and NI) or higher (monkey LI) gamma-band peak was also visible (Fig. 3).

Fig. 3.

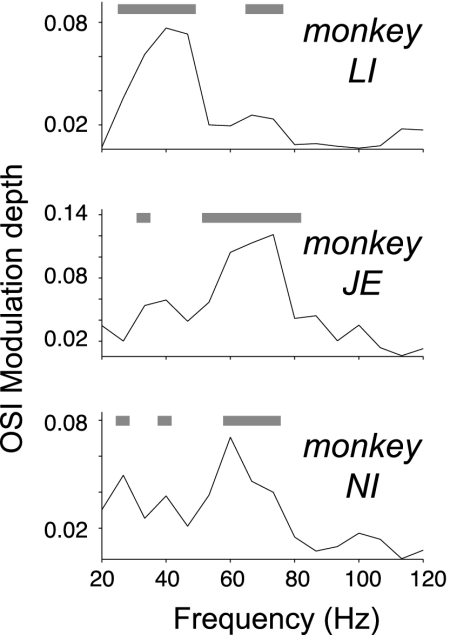
Frequency specificity of gamma phase-dependent orientation selectivity. Modulation of phase bin-dependent changes of OSI (y axis) across frequencies (x axis) for the binning, ensuring equal spike counts per bin (Fig. 2B). Modulation depth indexes the peak-to-trough modulation depth of a cosine fit to the OSI across phase bins per frequency. Gray bars on top of each graph highlight frequencies with statistically significant phase bin-dependent tuning (see Methods for details).

Taken together, these analyses demonstrate that orientation selectivity of firing rates is modulated with gamma phase, with highest orientation selectivity occurring slightly before the mean gamma phase. We repeated the analysis for the low-frequency bands showing significant spike-field locking. We observed significant phase-dependent orientation tuning in a frequency band of 1–3 Hz in both monkeys (SI Results and Fig. S2).

Relationship Between Orientation Selectivity and Strength of Phase Locking.

We found that, for a given neuron, orientation selectivity of firing rates was strongest for the spiking activity that occurred close to the mean gamma phase. A similar relationship may hold across neurons. We hypothesized that firing rates are highly orientation selective for neurons that fire relatively many spikes close to their respective mean gamma phase. We tested this hypothesis by linearly relating the cells’ PPC values to their respective OSI values. A potential confound is that average PPC values differed between monkeys (Fig. S1). We thus Z-score transformed the PPC values across cells separately for each monkey. We found a positive correlation between Z-score–transformed PPC values and the OSI across cells (Fig. 4; for all units: R = 0.65, P < 0.001; for the 52 significantly gamma phase-locking cells: R = 0.65, P < 0.001).

Fig. 4.

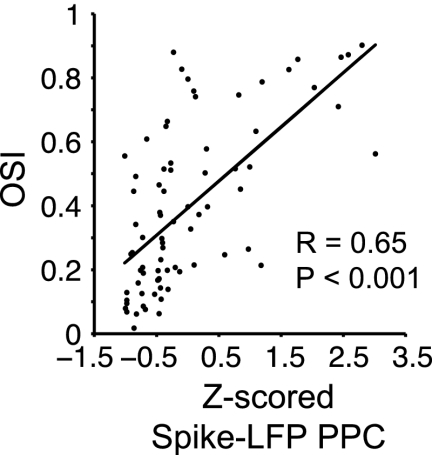
Relationship spike-LFP phase locking and orientation selectivity. Raw OSI values (y axis) as function of Z-score–transformed PPC values. Every dot represents a cell.

Relationship Between Phase Shifting, Orientation Tuning of Spike-LFP Locking, and Phase-Dependent Orientation Selectivity.

Previously, we found that the gamma phase of spiking is a few milliseconds advanced for preferred orientations relative to nonpreferred orientations (27). We were interested if any relationship exists between this gamma-phase shifting and the phase-dependent orientation tuning described here. We tested this as follows: for each neuron separately, we computed the gamma phase difference between the two most preferred and the four least preferred orientations (the different numbers of orientations were chosen to reduce the imbalance in spike counts) (see ref. 27 for more detail). A negative gamma-phase difference value indicated an advance of gamma phase for preferred orientations (27). We observed a positive linear correlation between the absolute value of this gamma-phase difference and the amplitude of the cosine fit to the OSI vs. gamma phase (Pearson R = 0.25, P < 0.05). Thus, cells with larger gamma-phase shifts as a function of orientation displayed a stronger modulation of orientation selectivity with gamma phase. For neurons whose spike gamma phase was advanced for preferred orientations, we observed highest orientation selectivity before the mean phase, at −50.0 ± 22.1° (95% CI; P < 0.001). In contrast, for neurons whose spike gamma phase was lagging for preferred orientations (against the average shift), we observed highest orientation selectivity after the mean gamma phase, at +27.2 ± 26.9° (95% CI; P < 0.05).

We also examined the relationship between phase-dependent OSI and the orientation tuning of the spike-LFP PPC. For every neuron, we computed the linear correlation between firing rates and the spike-LFP PPC across the eight orientations, called rate-PPC cotuning. Across neurons, we found a positive average rate-PPC cotuning (mean ± SEM of Pearson R = 0.2 ± 0.06, P < 0.01, two-sided t test). However, rate-PPC cotuning was significant for only 7 of 52 individual cells. By contrast, phase-dependent OSI was significant for 22 of 52 cells, such that for a substantial proportion of cells (28.8%, 15 of 52), we observed phase-dependent OSI without rate-PPC cotuning. When we directly correlated the strength of phase-dependent OSI with rate-PPC cotuning, this relation was not significant (Pearson R = 0.24, P = 0.08). Finally, rate-PPC cotuning is symmetric with respect to the mean gamma phase (because the PPC quantifies the concentration of phases around the mean gamma phase), whereas the OSI peaked before the mean gamma phase. Together, these findings suggest that the phenomenon of phase-dependent OSI is only weakly related to the orientation tuning of the spike-LFP PPC.

Orientation Selectivity as a Function of Gamma Power.

Because the phase in the gamma cycle influences orientation selectivity, one might expect that the strength of population gamma-band synchronization, reflected in absolute gamma-band power, might also have an effect. To examine this possibility, we sorted the trials according to the gamma-band power in the LFP. Power was averaged across all LFPs recorded from different electrodes other than the electrode providing the single unit. We then performed, separately for each stimulus orientation, a median split of power across trials. Subsequently, we compared orientation selectivity in the trials with strong gamma and trials with weak gamma. Trials with strong gamma-band power had an average OSI that was 0.025 ± 0.0083 (SEM; P < 0.01, Wilcoxon signed rank test) higher than trials with weak gamma-band power, corresponding to an average increase of 11.6 ± 3.7% (SEM).

Noise Correlation as a Function of Phase in the Gamma Cycle.

As mentioned in the introduction, neuronal activity fluctuates in part independently of the stimulus. This so-called noise can be averaged across a group of neurons, in case it is uncorrelated across the neurons of the group. We have found that neurons, as they move through the gamma cycle, modulate their stimulus selectivity. The resulting stimulus-selective responses could signal a stimulus to postsynaptic neurons best if noise correlations were low at the gamma phase with strong stimulus selectivity. Therefore, we investigated noise correlation as a function of gamma phase.

Noise correlations were always computed for each of the 16 stimulus directions separately, by linearly correlating the respective spike counts of the two recording sites across trials. Subsequently, correlation values were averaged across stimulus directions. This procedure ensured that stimulus direction was excluded as a source of rate correlations. The average noise correlation for all unit pairs (86 pairs) was small, but significantly greater than zero (0.028 ± 0.0122, P < 0.05), comparable to a recent report by Ecker et al. (15). Though an average noise correlation of such small magnitude may at first glance seem insignificant for neural processing, it likely does have a substantial impact on information processing (15). Noise correlations were positively related to the product of firing rates (Pearson R = 0.26, P = 0.0162); however, they did not depend on the strength of gamma phase-locking, because we observed no statistically detectable correlation between the sum of the (pair's) Z-scored (within animal) gamma-band PPC values and noise correlations (P = 0.23, t = −1.2, multiple linear regression with firing rate as covariate).

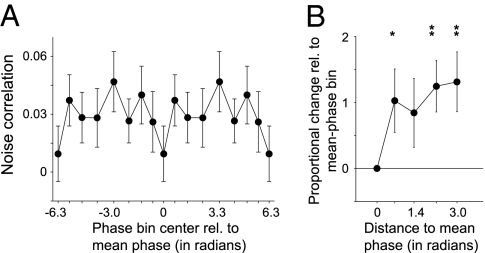
Typically, noise correlations are computed disregarding the phase of the gamma-band rhythm at which spiking activity occurs. Similar to the phase-dependent OSI analysis above, we preprocessed the spike trains before determining noise correlation, sorting a given spike train into multiple virtual spike trains, such that for a given virtual spike train, all its spikes had occurred within a limited range of the gamma cycle, (i.e., within a specific gamma-phase bin). To investigate the dependence of noise correlation on gamma phase, it is critical that spike counts do not differ across gamma-phase bins, because noise correlations may be dependent on the number of spikes (14). To achieve this, we used the adaptive binning strategy that yielded constant spike counts across bins, as in Fig. 2B. For a given pair of simultaneously recorded neurons from different electrodes, we then determined the noise correlation between the trial-wise firing rates computed for the spiking activity occurring in every individual phase bin separately. Across all units, the average noise correlation across phase bins equaled 0.0115 ± 0.0068 (86 pairs), only slightly exceeding the level of statistical detection (P < 0.05, one-sided t test). This value is smaller than the one reported above, because noise correlations were now calculated on the basis of shorter windows, and it is known that noise correlations (and likewise their SEs) are reduced by computing them over smaller windows (14). We found that noise correlation was modulated with gamma phase. Noise correlation was lowest when considering the trial-wise firing rates computed for spiking activity occurring closest to the mean gamma phase of firing (Fig. 5A; 46 pairs of significantly gamma phase-locking cells) and increased >100% for spikes away from the mean phase (Fig. 5B). Thus, the spiking activity that occurs close to a neuron's mean gamma phase of firing exhibits the highest stimulus selectivity in its firing rate, and, at the same time, its signal conveyed to postsynaptic target neurons is least corrupted by correlated noise.

Fig. 5.

Gamma phase modulates noise correlation. (A) Noise correlation (y axis) as a function of gamma phase (x axis) at which the spikes occurred relative to the LFP. Zero denotes the mean phase. Phase bins contained an equal number of spikes (Fig. 2C). (B) Proportional change in noise correlation relative to the mean phase bin (y axis) as a function of the distance of the bin centers to the mean phase. *P < 0.05; **P < 0.01; error bars show SEM.

Noise Correlation as a Function of Gamma Power.

So far, we found that spiking activity occurring close to a neuron's mean gamma phase of firing carries the highest stimulus selectivity and lowest noise correlation. Therefore, we tested whether also overall higher gamma-band synchronization results in lower noise correlation. For each recording site, we assessed per trial the LFP gamma-band power as a measure of overall gamma-band synchronization. For each stimulus direction separately, we then performed a median split of the trials into strong and weak gamma trials. For strong and weak gamma trials separately, we calculated noise correlations between the firing rates of pairs of single neurons. Notably, noise correlations were significantly reduced for trials with strong gamma compared with weak gamma (Wilcoxon signed rank test, P = 0.02). With weak gamma, the average noise correlation was 0.1. By contrast, with strong gamma, noise correlations were on average not significantly different from zero (r = −0.006, not significant). A potential concern is that firing rates may differ between high and low gamma-band power trials. However, the ratio of firing rates for these two sets of trials was 0.99 ± 0.017, not differing significantly from one.

Discussion

Implications for Decoding of Orientation Signals and Phase Coherence.

Gamma-band synchronization focuses within a few milliseconds the spiking activity that carries the highest stimulus selectivity in its firing rate. This focusing will increase the impact of that spiking activity onto postsynaptic target neurons, because the latter act as coincidence detectors (1, 4, 6, 28, 29). When those target neurons get entrained to the input rhythm, they will undergo correlated excitability fluctuations and this will likely further increase the impact of the most gamma-locked spikes. In the present study, we show that the synchronized spiking activity is not only particularly effective, but that its firing rate is also particularly stimulus selective. Thus, the same mechanism of synchronization appears to enhance the impact of the synchronized spiking activity and the selectivity of its firing rate.

Mechanisms Accounting for Gamma Phase-Dependent Orientation Selectivity.

The gamma cycle creates windows of opportunity for spiking through a tight coordination of excitatory and inhibitory inputs (30, 31), with excitation leading inhibition in the gamma cycle (5, 32–34). This tight coordination between excitation and inhibition generates steep membrane potential slopes at particular phases of the gamma cycle. Those fast membrane depolarizations are crucial in triggering postsynaptic spikes (1, 28) and thereby crucial in closing a reverberant cortical loop. It is important to note that the tight coordination of excitation and inhibition quenches noisy slow fluctuations in synaptic input (35) and thereby reduces the noise in the cell's output and most likely also the noise correlation among neighboring cells. This finding is consistent with our observation that the spiking activity occurring close to a neuron's mean gamma phase of firing carried the lowest noise correlations in its firing rate. These mechanisms are likely closely related to the findings by Azouz and Gray (1, 28), who observed, in anesthetized cat V1, higher orientation selectivity of the membrane potential's gamma-band power compared with its low-frequency power. Azouz and Gray (1, 28) also found a stronger correlation of output spike rates with membrane potential gamma-band power than with low-frequency power. These findings from intracellular recordings are consistent with LFP recordings in awake monkeys (36), which demonstrated stronger tuning of the gamma-band component of the LFP compared with its low-frequency component. The stronger tuning of gamma power might be at the same time cause and consequence within the above-mentioned reverberant loop in which gamma exerts its impact during phases of maximal membrane potential slope. As a consequence of the enhanced tuning of the membrane potential gamma band, the spiking activity that occurs close to a neuron's mean gamma phase of firing may be the most orientation selective, as observed in the present study; the same would apply to those neurons most strongly phase locking to the LFP gamma rhythm.

Another putative mechanistic account for phase-dependent OSI is that stimulus-related spikes are inserted into otherwise random firing preferentially around the mean gamma phase. Responses to preferred stimuli would then contain relatively more spikes close to the mean gamma phase than responses to nonpreferred stimuli. However, our data argue against this possibility. First, we found that, across orientations, spike-LFP locking strength was only weakly related to firing rate, and that this relationship was significant for only the minority of neurons for which phase-dependent OSI was observed. Second, we found that the strength of phase-dependent OSI was not significantly related to the amount of PPC-rate cotuning, (i.e., the correlation between firing rate and spike-LFP locking strength across orientations).

Relationship Between Phase-Dependent Rate Code and Phase Code.

Recently, we published a related finding (using largely the same dataset as here), namely that stronger activation makes neurons spike earlier in the gamma cycle (27). This gamma-phase shifting was also found for the different activation levels induced in primary visual cortex neurons by different stimulus orientations. Stimulus orientation was thus represented by the mean phase of spiking in the gamma cycle (figure 2b in ref. 27). In short, we demonstrated a gamma-phase code. By contrast, in the present paper, we demonstrate a gamma phase-dependent rate code. Most previous studies that investigated the phase of spikes relative to the LFP were concerned with phase codes (37, 38), rather than with phase-dependent rate codes. In the rodent hippocampus, e.g., the phase of spikes relative to the theta oscillation (4–8 Hz) can contain information about the animal's position (37, 39, 40). Similarly, in the monkey auditory cortex, the phase of spikes relative to stimulus evoked low-frequency LFP fluctuations can contain stimulus information (41). Though those earlier phase-code studies were concerned with relatively low frequencies, we demonstrated a phase code (27) and now a phase-dependent rate code for neuronal gamma-band synchronization.

Changing Views on Noise Correlation.

We found that not only orientation selectivity is modulated dynamically, but also noise correlation. The dynamic nature of noise correlation might inform us about its underlying mechanisms. Noise correlation has been modeled as the consequence of synaptic input that is common to the noisily correlated neurons (42). This common structural input results in individual synaptic inputs that are precisely synchronous between the neurons. The precisely synchronous inputs result in an enhanced probability of precisely synchronous output spikes, [i.e., a sharp central peak in the cross-correlation histogram (CCH) between the two neurons’ spike trains (figure 8 in ref. 42)]. Similarly sharp peaks in the CCH were among the first reported signs of gamma-band synchronization (43). It is probably this similarity that led some investigators to assume a close link between neuronal gamma-band synchronization and noise correlation, as if those were reflecting the same mechanism. As explained above, noise correlation degrades the signal that a neuronal population can send and, correspondingly, it has been argued that gamma-band synchronization is detrimental for neuronal processing. Our current results demonstrate that this reasoning is most likely incorrect. We show that noise correlation is enhanced when gamma-band synchronization is weak, but that it is absent (i.e., not significantly different from zero) when gamma-band synchronization is strong. We furthermore show that noise correlation is weakest among the firing rates of the spiking activity that occurs closest to the mean gamma phase.

There has been a recent debate about the correct estimation of noise correlation in primary visual cortex (14, 15). It has been argued that noise correlation estimates are very low when cells are optimally isolated and recordings are performed in awake animals. The noise correlation values found in this study are much lower than the ones reported in most previous studies, and close to the ones found by Ecker et al. (15) who used tetrode recordings for optimal cell isolation. We note that the effects of gamma power and gamma phase on noise correction, which we describe here, are orthogonal to potential effects of cell isolation.

Gamma Phase-Dependent Stimulus Selectivity, Noise Correlation, and Attention.

Our finding of reduced noise correlation around the mean gamma phase and with generally enhanced gamma power is consistent with several recent studies relating either gamma-band synchronization or noise correlation to attention. When attention is directed to a behaviorally relevant stimulus, neurons in area V4 that are driven by this stimulus show enhanced gamma-band synchronization (7, 8, 10, 19, 44, 45–47). We demonstrate here that enhanced gamma-band synchronization co-occurs with reduced noise correlation. Reduced noise correlation has recently been found among V4 neurons driven by the attended stimulus (48, 49). It remains to be investigated whether the reduced noise correlation with attention might be due to a mechanistic link between noise correlations and gamma-band synchronization.

Methods

A detailed description of methods is provided in SI Methods. Experiments were performed as described in detail in Vinck et al. (27) on three awake adult monkeys. Recordings were performed in area V1 using 2–5 tungsten/platinum electrodes. Monkeys passively viewed drifting gratings of varying orientations (16 directions in steps of 22.5°). Spike-LFP phase was determined by fast Fourier transforming a Hanning-tapered LFP segment around each spike. The consistency of spike-LFP phases was quantified using the PPC (16). We quantified orientation selectivity as the OSI by considering the neuronal response variation across all orientations by calculating [1 − circular variance]. This measure reflects the resultant vector length of the spike rates across orientations and has been validated in previous studies (26, 50, 51). The OSI is invariant to any scaling effect of the firing rate. We calculated noise correlations as the linear (Pearson) correlation coefficient between the firing rates of the units at different electrodes. All noise correlations were computed for trials with identical stimuli (direction of moving grating).