Abstract
In this article, a nonlinear mathematical model is developed based on the physiology of the cochlea of the guinea pig. The three-dimensional intracochlear fluid dynamics are coupled to a micromechanical model of the organ of Corti and to electrical potentials in the cochlear ducts and outer hair cells (OHC). OHC somatic electromotility is modeled by linearized piezoelectric relations whereas the OHC hair-bundle mechanoelectrical transduction current is modeled as a nonlinear function of the hair-bundle deflection. The steady-state response of the cochlea to a single tone is simulated in the frequency domain using an alternating frequency time scheme. Compressive nonlinearity, harmonic distortion, and DC shift on the basilar membrane (BM), tectorial membrane (TM), and OHC potentials are predicted using a single set of parameters. The predictions of the model are verified by comparing simulations to available in vivo experimental data for basal cochlear mechanics. In particular, the model predicts more amplification on the reticular lamina (RL) side of the cochlear partition than on the BM, which replicates recent measurements. Moreover, small harmonic distortion and DC shifts are predicted on the BM, whereas more significant harmonic distortion and DC shifts are predicted in the RL and TM displacements and in the OHC potentials.
Introduction
The mammalian cochlea exhibits a compressive nonlinearity that extends the dynamic range of hearing. An active feedback mechanism, called the cochlear amplifier and driven by outer hair cell (OHC) motility, selectively amplifies the basilar membrane (BM) vibrations. The BM is highly sensitive and sharply tuned close to its characteristic frequency (CF) in response to a low-level acoustic stimulus and is less sensitive and less sharply tuned in response to more intense acoustic stimuli (1–4). Nonlinearity and frequency selectivity of OHC extracellular and intracellular electrical potentials (5,6) have also been observed. In addition to this compressive nonlinearity, moderate even- and odd-order harmonic distortion have been measured, both in the BM displacement or velocity (4,7,8) and in the intracochlear fluid pressure (9). A DC shift has been recorded in the OHC transmembrane potential (5) and in the organ of Corti mechanics (10–12) (moderate at the base and more dramatic at the apex (12)). The objective of this article is to develop a comprehensive mathematical model that simultaneously predicts the different characteristics of the nonlinear steady state response of the base of the cochlea to a single tone (frequency selectivity, compressive nonlinearity, harmonic distortion, and DC shift).
Two different mechanisms have been proposed to underlie nonlinear cochlear amplification (13): somatic electromotility (14,15) and hair-bundle (HB) motility (16). We have recently predicted using a linear model of the cochlea (17) that amplification is primarily due to somatic electromotility at the base of the cochlea. The main source of nonlinearity in the cochlea has been hypothesized to be the saturating nonlinearity of the transduction current (18) that depolarizes the OHC and drives electromotility. In the model developed here, HB motility is neglected and somatic electromotility is explicitly modeled and coupled to nonlinear HB mechanoelectrical transduction.
The BM response to a single tone has been predicted by many mathematical models of the cochlea (reviewed in de Boer (19)). However, most previous cochlear models have made some simplifications that limit their predictive capability. For example, some of them are based on highly simplified one- or two-dimensional models of the intracochlear fluids (18,20–22), have reduced the cochlear partition to a single degree of freedom (20,23,24) or have neglected the effect of structural longitudinal coupling. However, three-dimensional fluid effects (25), the complex mode of deformation of the cochlear partition (26,27), and longitudinal coupling in the BM or TM mechanics (28–30) have been shown to be important for cochlear mechanics. Furthermore, most cochlear models do not explicitly couple electrical potentials to the mechanical vibrations or use phenomenological assumptions in their description of OHC activity (regarding the magnitude or phase of the electromechanical OHC force). Comprehensive nonlinear models that include all the details mentioned above are still needed. A linear mechanical-electrical-acoustical model of the cochlea has been developed by Ramamoorthy et al. (31) and Meaud and Grosh (28). This model couples the three-dimensional fluid dynamics to explicit models of the micromechanics of the organ of Corti and of the electrical domain of the cochlea (to represent the potentials in the scalae of the cochlea and the intracellular OHC potential).
In this article a nonlinear physiologically based mathematical model of the cochlea is developed by extending the previously developed linear model (28,31). The different aspects of the nonlinear response of the cochlea to a single tone are predicted using a single set of parameters. The validity of our cochlear model is tested by comparing its predictions to available in vivo measurements of the response of the cochlea to acoustic stimulation.
Methods
Micromechanical model
As described in previously developed linear models (28,31), the fluid domain of the cochlea is modeled by a box geometry with a three-dimensional representation of the intracochlear fluid pressure coupled to a micromechanical model of the organ of Corti (Fig. 1). As in our previous work (28), structural longitudinal coupling is included in the BM and TM mechanics. The radial dependence of the BM displacement is assumed to be similar to the experimental data from Cooper (32) and is integrated out to reduce the BM deformation to one degree of freedom at each cross section (31). The HB deflection relative to the RL, uhb/rl, is a linear function of the BM, TM shear, and TM bending displacements. The HB rotation relative to the reticular lamina (RL), θhb/rl, is then given by
where Lhb is the length of the HB.
Figure 1.
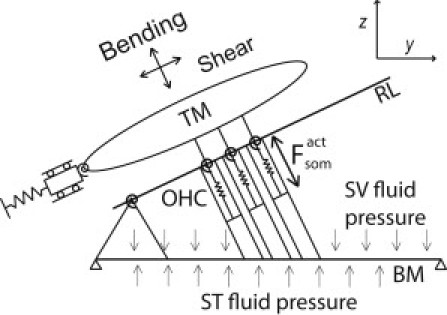
Micromechanical model of a cross section of the cochlear partition (modified from Meaud and Grosh (17)). There are three structural degrees of freedom at each cross section: the BM displacement and the displacements of the TM bending and shearing modes. Due to the kinematic assumptions of the model (31), the displacement of the reticular lamina (RL) in the direction perpendicular to the RL is the same as the displacement of the TM bending mode. The fluid pressure is coupled to the BM displacement. More details can be found in Ramamoorthy et al. (31).
Nonlinear transduction channel model
The transduction channel is modeled as a nonlinear two-state channel, based on the gating spring theory of HB mechanotransduction (33). The open probability of the channel, P0, is modeled by a first-order Boltzmann function of the HB rotation relative to the RL, θhb/rl (see Fig. 2),
| (1) |
where X0 and ΔX are constant displacements and Lhb is the length of the HB. Based on the gating-spring theory (33), ΔX is given by
| (2) |
where fgs is the single channel gating force in the tip link direction (given by fgs = kgs d, where kgs is the gating spring stiffness and d is gating swing), kB is the Boltzmann constant, T is the temperature and γ is the geometrical gain factor, that relates the displacement of the HB in a direction perpendicular to the HB to its displacement along the tip link direction (33). The transduction channel conductance, Ghb(θhb/rl), is assumed to be proportional to the open probability of the channel,
| (3) |
where is the maximum saturating conductance of the HB (34). Note that in this model we do not solve for the steady-state operating point of the cochlea in the absence of stimuli but only for the change from the operating point. We chose the resting probability of the transduction channel, , to be 0.4 so as to predict DC shifts and second-order harmonic distortions that are similar to experimental data (see Fig. 2).
Figure 2.
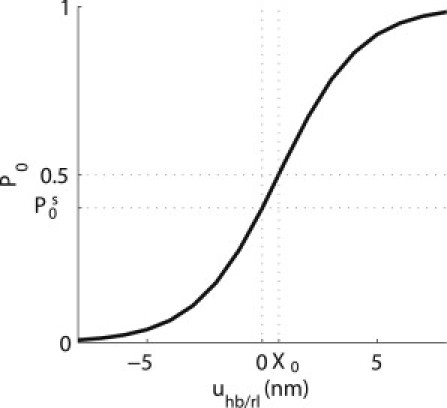
Open probability of the MET channel, P0, as a function of the HB deflection, uhb/rl, at the 16 kHz BP modeled as a first-order Boltzmann function. The slope of the probability function is given by P0(1P0)/(ΔX). The open probability is equal to 0.5 when uhb/rl = X0. To predict even-order harmonic distortion and a DC shift toward the scala vestibuli, we chose the resting probability, , to be different from 0.5, using a nonzero value for X0 (so that the second derivative of the probability with respect to the HB displacement is nonzero when uhb/rl = 0).
The difference between the potential in the scalia media, Vsm, and the intracellular OHC potential, Vohc, is defined as ΔVhb. The value ΔVhb can be written as
| (4) |
where is the resting value of the potential difference and Δϕhb(t) is the perturbation from its resting value at time t. In the time domain, the current flowing through apical end of the OHC, Ia, is given by
| (5) |
where Ca is the apical OHC capacitance. The perturbation in the apical OHC current, ia, from its resting value, is given by the equation
| (6) |
where is the resting value of the HB conductance. In the results from simulations shown in this article, the last term in Eq. 6,
was not included (because we found that it does not have a significant effect on the results). In this model, the effects of channel gating on the HB force (nonlinear gating compliance (33)) and of adaptation of the transduction current (35) are neglected (in contrast to our previous work (17)).
OHC somatic electromechanical force and piezoelectric current
OHC somatic electromotility is modeled using a time domain version of the linear piezoelectric model that was used in Ramamoorthy et al. (31). The perturbations in the somatic electromechanical force, fohc, and current, iohc, from their resting values can be written as
| (7) |
| (8) |
where Δϕohc is the perturbation in the OHC transmembrane potential away from its resting value (difference between the perturbation in the OHC extracellular potential and the perturbation in the extracellular potential), the OHC compression, ϵ3 is the electromechanical coupling coefficient, Gm is the basolateral conductance of the OHC, and Cm is its capacitance. The parameters of the model (such as the HB conductance (34)), the OHC somatic electromechanical coupling coefficient (15), or the OHC basolateral capacitance and conductance (36)) are based on biophysical single cell measurements (see the Supporting Material).
Nonlinear finite element formulation
The equations governing the dynamics of the cochlea are discretized using Bubnov-Galerkin finite elements methods (37,38). In the time domain, the equations governing the nonlinear dynamics of the cochlea have the matricial form
| (9) |
where M, C, and K are the mass, damping, and stiffness matrices, respectively; d is the vector of the degrees of freedom (displacement of the BM, TM shearing and TM bending modes, fluid pressures, and potentials); nl(d) is a vector that is a nonlinear function of the vector d (due to the nonlinearity of HB mechanoelectrical transduction); and F is the external force vector (due to the vibrations of the stapes). In this model, the middle ear is not explicitly modeled (in contrast to cochlear models such as Liu and Neely (39)). However, the frequency dependence of the stapes vibrations is taken into account, as described in the Supporting Material.
The nonlinear equation, Eq. 9, is transformed into a set of frequency domain equations given by
| (10) |
where m is the index that identifies the harmonic component (m = 0 correspond to the DC component, m = 1 to the fundamental, m = 2 to the second harmonic, …), the Fourier components of any variable x are denoted as Xm, and ω0 is the radian frequency of the stimulus. An iterative alternating frequency/time scheme (40), similar to the method used by Nobili and Mammano (18), is used. Only a finite number of Fourier components, Nh, is used for the computation, so that Nh nonlinear systems have to be solved. At each iteration of the algorithm, the inverse Fourier transform is applied to this estimate of the harmonic components of the solutions so as to compute the nonlinear forcing terms in the time domain, nl(t). The Fourier component of the nonlinear forcing term, NLm, is then computed by applying the Fourier transform to the transduction current. The algorithm is described in more detail in the Supporting Material.
Results
In this section, the nonlinear stationary response of the cochlea in response to a single tone is simulated using a single set of parameters and the model presented in the Methods.
Fundamental of the BM displacement at basal locations
The magnitude of the fundamental of the BM displacement relative to the stapes is plotted as a function of frequency at the 16 kHz best place (BP) in Fig. 3 a. The model predictions are in good agreement with the measured magnitude of the BM gain to acoustic stimulation by Zheng et al. (41). At low intensity, the response is highly sensitive and sharply tuned to 16 kHz, the characteristic frequency (CF). As the intensity of the stimulation is increased, the response peak shifts to a lower frequency and the response is less sharply tuned and less sensitive, as seen in the experimental data. At frequencies significantly lower than the CF, the response is linear because the gain is independent of the intensity of the stimulus.
Figure 3.
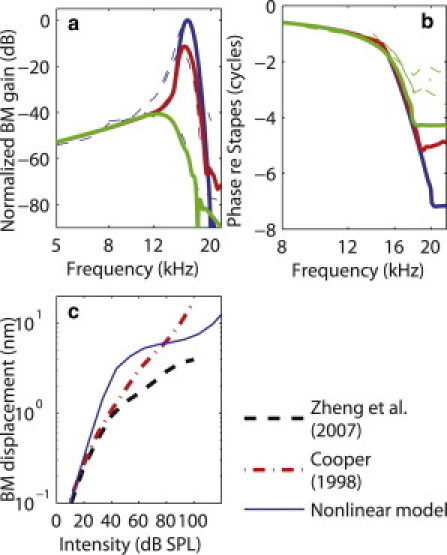
Fundamental of the BM displacement at the 16 kHz BP in response to a single tone. (a) Magnitude of the gain at the 16 kHz BP in response to a single tone, plotted as a function of frequency and normalized to the maximum gain at 4 dB SPL. (b) Phase of the fundamental of the BM displacement (relative to the stapes) at the 16 kHz BP in response to a single tone, plotted as a function of frequency. (a and b, solid lines) Model predictions (for a 4 dB SPL, 54 dB SPL, and 104 dB SPL stimulation. (Dashed lines) Experimental data from Cooper (4) (for 10 dB SPL, 50 dB SPL, and 100 dB SPL sounds. (c) Magnitude of the BM displacement as a function of the intensity of stimulation at 16 kHz. (Solid line) Model predictions. (Dotted-dashed line) Data from Cooper (4). (Thick dashed line) Data from Zheng et al. (41).
The dependence of the magnitude of BM response on the intensity of stimulation at CF (16 kHz) is quantitatively analyzed and compared to experimental data from Zheng et al. (41) and Cooper (4) in Fig. 3 c. In contrast to both sets of experimental data that show nonlinearity from the lowest intensity (10 dB SPL) to the highest measured intensity (100 dB SPL), the model predicts a linear BM response at very low intensity (up to ∼30 dB SPL) and a compressive nonlinearity from 30 dB to 120 dB SPL. The BM response is predicted to exhibit a linear dependence on sound intensity above 120 dB SPL. At moderate intensity, the slope of the curve (the rate of growth (8)) is lower than in experimental data (0.06 dB/dB compared to 0.45 dB/dB in the data from Cooper and 0.2 dB/dB in the data from Zheng et al. (41)), which indicates a more compressive response. Moreover, the magnitude of the displacement at moderate intensity is higher than in the experimental data.
In the plot of the phase of the BM displacement relative to the stapes as a function of frequency (shown in Fig. 3 b), the slope of the phase curve at CF becomes less steep and the value of the phase lag at CF becomes slightly lower when the intensity of stimulation is increased (the phase lag is 2.35 cycles at 4 dB SPL and 2.2 cycles at 104 dB SPL). As can be seen from the figure, the predicted and measured values of the phase at CF and of the slope of the phase at CF are similar. Compared to the experimental data, the phase accumulation at frequencies higher than CF is predicted to be higher (∼7 cycles at the lowest intensity) than in the measurements (∼3 cycles). However, the difference between our predictions and the measurements could be due to 2π phase ambiguity at high frequency (3). Overall, the predictions of the phase of the BM match commonly observed trends in measurements of the BM response to acoustic stimulation (2,4,41).
Harmonic distortion and DC shift on the BM at basal locations
Harmonic distortion (4,7,8,11), as well as small DC shifts (11), have been reported in the BM response to acoustic stimulation at the base of the cochlea. The DC shift in the BM displacement represents a change in the baseline position of the BM (compared to its resting position in the absence of a stimulus) during dynamic loading. In the model, the nonlinearity of the MET channel generates odd-order harmonic distortion. The generation of even-order distortion and of a DC shift requires the operating point of the MET channel to be noncentered around zero (X0 is not zero in Eq. 1, see Fig. 2). A nonzero value of X0 is consistent with the data from Frank and Kössl (42) who showed that the effect of acoustical and electrical biases on distortion product otoacoustic emissions could be explained by a small asymmetric position of the OHC resting probability.
The magnitudes of the fundamental, second harmonic and third harmonic and of the DC shift in the BM displacement in response to a single tone are plotted as a function of the stimulus frequency in Fig. 4, a and b, at the 16 kHz best place for an intensity of stimulation of 64 dB SPL (Fig. 4 a) and 94 dB SPL (Fig. 4 b). At 64 dB SPL, the peak frequency of the fundamental is ∼15.7 kHz. The second harmonic exhibits two peaks (at a stimulus frequency of 16 kHz close to CF and at a stimulus frequency close of 8.1 kHz close to CF/2) whereas the third harmonic exhibits three peaks (for stimulus frequencies close to CF, CF/2, and CF/3). Note that at 94 dB SPL the peak of the second harmonic close to CF/2 has a higher magnitude than the peak close to CF. These model predictions are in good qualitative agreement with the experimental data for the second harmonic from Cooper at the base of the guinea pig cochlea (4). As seen in our predictions, Cooper observed two peaks in the frequency response of the second harmonic for stimulus frequencies close to CF and CF/2. The number of peaks for the third harmonic is not clear in the experimental data, possibly due to the lower level of the third harmonic and to the noisiness of the data for the third harmonic.
Figure 4.
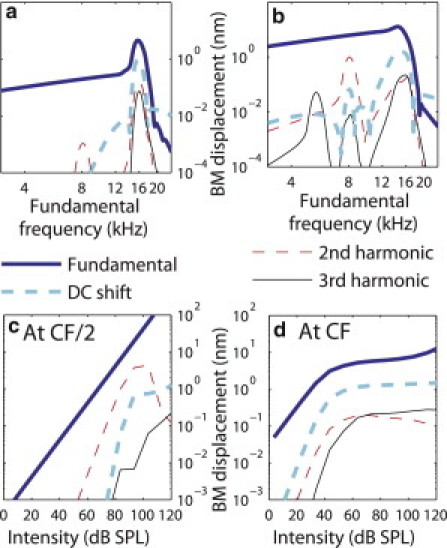
Magnitude of the fundamental, harmonic distortion components and DC shift of the BM displacement at the 16 kHz BP: (a) as a function of frequency for a 64 dB SPL single tone, (b) as a function of frequency for a 94 dB tone, (c) as a function of the intensity of stimulation for a 8.0 kHz single tone, and (d) as a function of the intensity of stimulation for a 16 kHz single tone. (Thick solid line) Fundamental. (Thin dashed line) Second harmonic. (Thin solid line) Third harmonic. (Thick dashed line) DC shift.
The dependence of the magnitudes of the fundamental, DC shift, and harmonic distortion components on the intensity of stimulation is analyzed in Fig. 4, c and d, at the 16 kHz BP. At this location, for a fundamental frequency of 8 kHz (Fig. 4 c), the response of the fundamental is linear whereas the second and third harmonics exhibit an expansive nonlinearity at moderate intensities (with a slope of 2 dB/dB for the second harmonic and 3 dB/dB for the third harmonic, as would be seen in a simple single degree of freedom nonlinear system). When the intensity of the stimulus is further raised, the magnitude of the second harmonic decreases (which could be due to suppression of this component by the fundamental) and the growth rate of the third harmonic is lower than at low intensity. As observed experimentally (4), the magnitude of the second harmonic relative to the fundamental is predicted to be high for a stimulus frequency equal to CF/2: the second harmonic component is within 15 dB of the fundamental at 94 dB SPL; Cooper (4) measured a second harmonic within 11 dB of the fundamental at 60 dB SPL. The magnitude of the second harmonic relative to the fundamental is lower for a 16 kHz stimulus frequency, as it is predicted to be within 30 dB of the fundamental at 60 dB SPL (Fig. 4 d). For a 16 kHz stimulus frequency, the second and third harmonics are also predicted to have a growth rate of 2 dB/dB and 3 dB/dB at low intensity of stimulation. Above ∼60 dB SPL, the third harmonic grows very slowly with respect to the intensity of stimulation, and the magnitude of the second harmonic decreases. In the data from Cooper (4), for stimulus frequencies close to the CF, the second and third harmonics are above the noise floor only for moderate and high SPLs and grow slowly as the level of stimulation is increased.
As observed in Cooper and Rhode (11), the model predicts a small DC shift of the BM toward the scala vestibuli, with a magnitude lower than the fundamental and higher than the second harmonic at CF (Fig. 4, a, b, and d). At CF, the DC shift is predicted to be very small at low intensity of stimulation (with a magnitude of 10−1 nm at 30 dB SPL) and is below the noise floor in experimental measurements (11). The DC shifts increases with a growth rate of 2 dB/dB as the intensity of stimulation is raised from 4 dB to 50 dB SPL. At 100 dB SPL the magnitude of the DC shift is ∼1 nm compared to 7 nm for the fundamental. At CF/2 the magnitude of the DC shift is below the magnitude of the second harmonic except above 100 dB SPL.
Organ of Corti micromechanics: large vibrations and DC shifts of the TM bending mode
As described in the Methods, this cochlear model has degrees of freedom for the BM, TM bending, and TM shearing modes at each cross section. The predictions for the fundamental in the BM, TM shearing, and TM bending modes are shown in Fig. 5 a at the 16 kHz BP. At low intensity of stimulation (4 dB SPL), the three degrees of freedom are approximately tuned to the same frequency, the CF. The magnitude of the TM shear displacement is ∼0.7 dB higher than the magnitude of the BM displacement whereas the displacement of the TM bending mode has a magnitude that is 9 dB higher than the displacement of the BM. At higher intensity of stimulation (94 dB SPL), the three modes are approximately tuned to the same frequency and the magnitudes of the three modes are within 2 dB of each other. In addition to the different magnitude of the fundamental of the BM and TM bending modes, the DC shifts of these modes are also predicted to have different magnitudes, as shown in Fig. 5 b. At high intensity of stimulation (94 dB SPL), the magnitude of the DC shift reaches ∼1.6 nm on the BM, <10−2 nm on the TM shearing mode, and ∼11 nm on the TM bending mode. The relative magnitude of the DC shift is much higher on the TM bending mode than on the BM: the DC shift in the TM bending displacement is within 2 dB of the fundamental of the TM bending displacement, whereas the DC shift in the BM displacement is 18 dB lower than the fundamental of the BM displacement.
Figure 5.
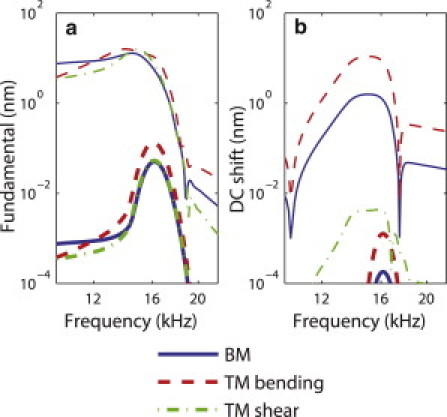
Fundamental and DC shift on the BM (solid lines), TM bending mode (dashed lines), and TM shearing mode (dotted dashed lines). (a) Magnitudes of the fundamental at 4 dB SPL (thick lines) and 94 dB SPL (thin lines) as a function of frequency. (b) DC shifts at 4 dB SPL (thick lines) and 94 dB SPL (thin lines).
OHC intracellular and extracellular potential
Because of the coupling between the mechanical and electrical domains in this mechanical-electrical-acoustical model of the cochlea, the magnitude and phase of the intracellular and extracellular OHC potentials are predictions of the model that can be compared to in vivo experimental measurements (5,6) to validate the model. The extracellular and intracellular potentials exhibit a similar frequency tuning as the BM, as shown in Fig. 6, a and b. At low intensity, the intracellular potential, and to a lesser extent the extracellular potential, are sharply tuned. As the intensity of stimulation is increased, the potentials have a lower quality factor (Q10dB), and are tuned to a lower frequency. At moderate intensity (34 dB SPL in Fig. 6 b), the intracellular and extracellular potentials have slightly lower Q10dB values than the BM (with a quality factor, Q10dB, of 7.0 for the intracellular potential, 6.6 for the extracellular potential, and 7.3 for the BM), as observed by Fridberger et al. (6). The peak frequencies are 16.1 kHz for the intracellular potential and for the BM displacement and 15.9 kHz for the extracellular potential. In contrast to our predictions, Fridberger et al. (6) observed that the extracellular potential was tuned to a slightly higher frequency than the BM. These difference might be due to the three-dimensional architecture (24) of the organ of Corti that has not been taken into account in our model.
Figure 6.
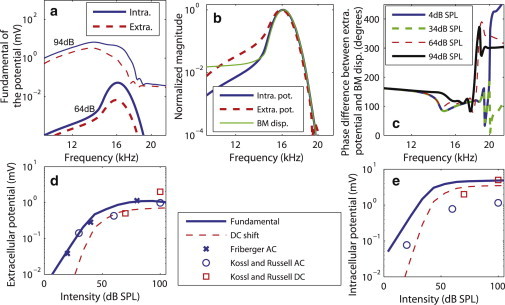
Intracellular and extracellular OHC potential. (a) As a function of the frequency for a 4 dB SPL and a 94 dB SPL single tone. (b) Normalized magnitude of the intracellular and extracellular potentials and of the BM displacement. (c) Phase difference between the extracellular potential and the BM displacement. (d) Model predictions for the fundamental and DC shift at CF in the extracellular potential as a function of intensity, compared to experimental data from Fridberger et al. (6) and Kössl and Russell (5) (e) Fundamental and DC shift at CF in the intracellular potential as a function of intensity, compared to the data from Kössl and Russell (5).
The phase of the extracellular potential relative to the BM is plotted in Fig. 6 c. The predictions are consistent with the measurements from Fridberger et al. (6). Well below the CF, the phase difference is approximately constant (∼155°) and independent of the intensity of stimulation. Just below CF, the phase lead of the potential relative to the BM decreases at low intensity of stimulation (up to 64 dB SPL). Above the CF, there are rapid changes in the phase difference, as seen in the experiment.
As seen in Fig. 6, d and e, the OHC intracellular and extracellular potentials are also predicted to exhibit a compressive nonlinearity at CF. Note the excellent agreement between our predictions and the data from Kössl and Russell (5) and Fridberger et al. (6) for the extracellular potential. The magnitude of the intracellular potential is predicted to be higher than the extracellular value. The predicted value is ∼5 times higher than measured in Kössl and Russell (5). However, this measurement might underestimate the physiological value of the potential, as the piercing of the OHC with a microelectrode could cause a leakage current that would reduce the intracellular potential (see discussion in Meaud and Grosh (17)). Nonnegligible DC shifts (similar to the values of the fundamental) are predicted in the intracellular and extracellular potential (Fig. 6, d and e), at high intensity. The intracellular and extracellular values are predicted to be 3.5 mV and 0.7 mV, respectively, for a 100 dB SPL stimulus (similar to the measured values of 5 mV and 2 mV (5), respectively).
Comparison of harmonic distortion of the OHC transmembrane potential and of the BM and TM bending displacements
For a stimulus frequency that matches the CF (Fig. 7 a), the relative magnitudes of the second harmonic (normalized to the fundamental) of the OHC transmembrane potential and BM displacement are similar (within ∼30 dB of the fundamental at 60 dB SPL) whereas the relative magnitude of the second harmonic of the TM bending mode is lower (within 45 dB of the fundamental at 60 dB SPL). However, for a stimulus frequency that matches CF/2 (Fig. 7 b), the second harmonic component is within 15 dB of the fundamental at 90 dB SPL (as shown in Fig. 4) whereas the second harmonic in the TM bending displacement is within 1 dB of the fundamental and the OHC transmembrane potential is ∼7 dB higher than the fundamental.
Figure 7.
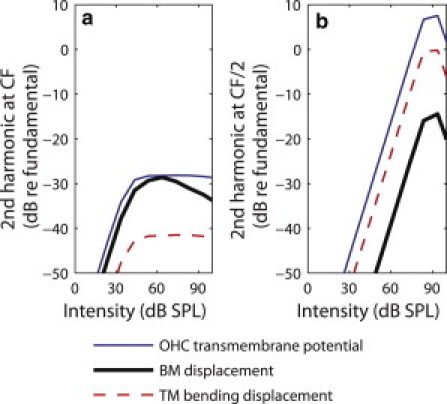
Magnitude of the second harmonic of the BM displacement, TM bending displacement, and OHC transmembrane potential, relative to the fundamental, at the 16 kHz best place: (a) for a 16 kHz stimulus frequency and (b) for a 8 kHz stimulus frequency.
Discussion
Compressive nonlinearity at the base of the cochlea
In this model, deflection of the HB causes a transduction current (Eq. 6) and thereby alters the OHC transmembrane potential. The transmembrane potential is then converted into an electromechanical somatic force (Eq. 8) that amplifies the vibrations of the organ of Corti in response to low level sounds. As recently observed by Chen et al. (27), amplification is predicted to be more pronounced on the RL (and TM bending mode) than on the BM. Because of the saturating nonlinearity of the MET channel (Eq. 1) a compressive nonlinearity is observed in the OHC potentials and in the BM and TM displacements.
As in other models of the cochlea (18,39), the nonlinearity of the somatic force with respect to the voltage (43) has been neglected. However previous models were based on a low RC cutoff frequency due to the basolateral impedance of the OHC (44). Here the recent measurements of Johnson et al. (36) were used to set the values of the basolateral conductance, Gm, and capacitance, Cm (see Table S1 in the Supporting Material). Despite a significantly higher RC cutoff frequency (36) than previously reported (44), the transmembrane potential is predicted to be relatively small during acoustic stimulation (the fundamental and DC shifts are <∼5 mV even at the highest intensity of stimulation). The electromechanical force is approximately a linear function of the voltage over a 100-mV transmembrane potential range (15). Therefore neglecting the nonlinearity of the somatic force and current with respect to the voltage is a valid approximation.
In our model (as in many other models (18,23)) the BM is predicted to respond linearly at low levels (up to ∼30 dB SPL or to BM displacements of ∼1 nm) and to exhibit a highly compressive nonlinearity at moderate levels and up to 120 dB SPL. However, in some sensitive experimental data (2,4,41), the BM responds nonlinearly even at the lowest intensity of stimulation (even for BM displacements <0.1 nm). Moreover, the growth rate measured in the BM response of the guinea pig at moderate intensity (4,41) is higher than in our predictions. However, note that there are significant differences regarding the response at moderate intensity between the two sets of experimental data shown in Fig. 3 c and that the rate of growth predicted by our model is similar to the values reported by Rhode (8) in the most sensitive chinchillae. The proximity of the cochlea system to a Hopf bifurcation has been proposed to explain the nonlinear behavior at low levels seen in measurements (45). Other potential explanations for the nonlinearity at low levels includes a higher value of the single channel gating force, fgs, than used here (causing saturation of the MET channels for lower HB deflection than in our model), or a significantly higher magnitude of the HB deflection relative to the BM displacement than predicted by the micromechanical model of the organ of Corti.
Apical cochlear mechanics
The model parameters have been tuned to predict the response of the cochlea at locations in the basal turn and up to the 5 kHz best place. Because of the complexity of the model, the choice of parameters that result in reasonable responses at more apical locations is challenging. With the parameters used here, the response at the most apical locations is linear, as there is no amplification and harmonic distortion and the DC shift are small (see Fig. S3 in the Supporting Material). There are contradictory experimental data for apical cochlear mechanics, as some studies found no amplification and a negative feedback (46) whereas others found limited amplification with significant harmonic distortion and DC shift (47). A large DC shift in the Hensen's cell region of the organ of Corti has been measured by Cooper and Dong (12) at the apex of the cochlea (∼100 nm at 100 dB SPL for a 0.5 kHz CF). Our model predicts a similar DC shift on the TM bending displacement for the 6.5 kHz CF but the value predicted at the most apical locations is very low (10−2 nm). Other mechanisms, not included in our model, such as HB motility, coiling of the cochlear ducts (48), or changes in the mode of deformation of the organ of Corti a low frequencies (49), might play an important role at apical locations and might be needed to model apical cochlear mechanics.
Generation and amplification of harmonic distortion at the base of the cochlea
The model predictions for the intensity and frequency dependence of harmonic distortion on the BM are in good qualitative agreement with the in vivo data from Cooper (4). The highest distortion component is the second harmonic, which is prominent in the response to stimulus frequencies close to CF and close to CF/2. The level of distortion both on the BM and in the OHC transmembrane potential relative to the fundamental are low at CF and more significant at CF/2. Moreover, for stimulus frequencies close to CF/2, the TM bending displacement and OHC potential are predicted to be more distorted than the BM.
The peak of the second-harmonic component for a stimulus frequency of F0 equal to CF/2 is due to what Cooper has called “amplified distortion” (4). This peak results from the amplification of the second harmonic (because the frequency of the 2F0 component matches the CF of the location for a tone of frequency F0 = CF/2). The peak of amplified distortion has also been observed in the BM response of the chinchilla (8) and in pressure measurements in the gerbil (9). In our cochlear model, amplification is due to somatic electromotility while filtering is due to the micromechanics of the organ of Corti. Although the prediction of the fundamental close to CF depends mostly on the amplification, nonlinearity, and filtering at CF, the predictions of the second harmonic for stimulus frequencies close to CF/2 depends simultaneously on all these factors at CF/2 (for the generation of the distortion) and at CF (for the amplification of the distortion). Because of this dependence on many factors, the prediction of the magnitude of the distortion at CF/2 is a good test of the model.
Indeed, as discussed in How et al. (50) where a phenomenological model is used, cochlear models that predict reasonable fundamental in response to a single tone do not necessarily predict accurate harmonic distortion. Harmonic distortion has been previously predicted in cochlear models (18,21,23). However, predictions for a CF/2 stimulus frequency were not shown in Nobili and Mammano (18) and Chadwick (21), and predictions in Lim and Steele (23) do not exhibit two peaks in the second-harmonic response. The predictions shown here emphasize that this model, and in particular the filtering by the micromechanical model of the organ of Corti, are consistent with the measurements of distortion in the cochlea (4). Cochlear models that rely on another mechanism for amplification and filtering (such as HB motility at the base of the cochlea in Reichenbach and Hudspeth (22)) could be tested by comparing the predictions of harmonic distortion to experimental data.
DC shifts at the base of the cochlea
Despite the observation of significant DC shifts in the OHC potentials in response to high levels sounds (5), the DC shifts that have been measured on the BM are small (11) at the base of the cochlea. In the model, the noncentering of the nonlinearity of the MET channel around the operating point (see Fig. 2) results in the generation of a significant DC shift in the OHC intracellular and extracellular potential (see Fig. 6). However, using the same set of parameters, the level of the DC shift on the BM is predicted to be low (∼0.7 nm for a CF of 25 kHz; see Fig. S3) at the most basal locations, which is similar to measurements (a DC shift of <1 nm toward to the scala vestibuli for a 100 dB SPL sound at the 30 kHz best place (11)). The reason for the low DC shift on the BM is that the somatic electromechanical force pushes both on the stiff BM and on the more compliant RL and TM bending mode. Hence the DC shift in the OHC potential results in small DC shifts on the BM and more significant DC shifts on the RL and TM bending mode (see Fig. 5, b and d, and Fig. 7 b).
Conclusions
The model developed here couples the somatic electromechanical force and the nonlinear HB mechanoelectrical transduction current to a micromechanical model of the organ of Corti embedded in a three-dimensional model of the intracochlear fluids. Using a single set of parameters, this physiologically based approach results in reasonable predictions of the major characteristics of the nonlinear response of the base of the cochlea to a pure tone: compressive nonlinearity, harmonic distortion, and DC shifts in the displacements of the BM, TM, and in the electrical potentials. If in vivo recording techniques of the macromechanical and micromechanical response of the cochlea to acoustic stimulation continue to improve (such as Chen et al. (27)), some predictions of the model that have not been tested due to lack of experimental measurements (such as the significant DC shifts on the RL and TM) could be used to further test this theoretical model.
Acknowledgments
The authors thank Y. Li for her helpful discussions about the manuscript.
This research was supported by National Institutes of Health grant No. NIH-NIDCD R01-04084.
Supporting Material
References
- 1.Rhode W.S. Observations of the vibration of the basilar membrane in squirrel monkeys using the Mössbauer technique. J. Acoust. Soc. Am. 1971;49:1218–1231. doi: 10.1121/1.1912485. [DOI] [PubMed] [Google Scholar]
- 2.Nuttall A.L., Dolan D.F. Steady-state sinusoidal velocity responses of the basilar membrane in guinea pig. J. Acoust. Soc. Am. 1996;99:1556–1565. doi: 10.1121/1.414732. [DOI] [PubMed] [Google Scholar]
- 3.Ruggero M.A., Rich N.C., Robles L. Basilar-membrane responses to tones at the base of the chinchilla cochlea. J. Acoust. Soc. Am. 1997;101:2151–2163. doi: 10.1121/1.418265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cooper N.P. Harmonic distortion on the basilar membrane in the basal turn of the guinea-pig cochlea. J. Phys. (Lond.) 1998;509:277–288. doi: 10.1111/j.1469-7793.1998.277bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kössl M., Russell I.J. The phase and magnitude of hair cell receptor potentials and frequency tuning in the guinea pig cochlea. J. Neurosci. 1992;12:1575–1586. doi: 10.1523/JNEUROSCI.12-05-01575.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fridberger A., de Monvel J.B., Nuttall A. Organ of Corti potentials and the motion of the basilar membrane. J. Neurosci. 2004;24:10057–10063. doi: 10.1523/JNEUROSCI.2711-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Parthasarathi A.A., Grosh K., Nuttall A.L. Effect of current stimulus on in vivo cochlear mechanics. J. Acoust. Soc. Am. 2003;113:442–452. doi: 10.1121/1.1519546. [DOI] [PubMed] [Google Scholar]
- 8.Rhode W.S. Basilar membrane mechanics in the 6–9 kHz region of sensitive chinchilla cochleae. J. Acoust. Soc. Am. 2007;121:2792–2804. doi: 10.1121/1.2718397. [DOI] [PubMed] [Google Scholar]
- 9.Olson E.S. Harmonic distortion in intracochlear pressure and its analysis to explore the cochlear amplifier. J. Acoust. Soc. Am. 2004;115:1230–1241. doi: 10.1121/1.1645611. [DOI] [PubMed] [Google Scholar]
- 10.LePage E.L. Frequency-dependent self-induced bias of the basilar membrane and its potential for controlling sensitivity and tuning in the mammalian cochlea. J. Acoust. Soc. Am. 1987;82:139–154. doi: 10.1121/1.395557. [DOI] [PubMed] [Google Scholar]
- 11.Cooper N.P., Rhode W.S. Basilar membrane mechanics in the hook region of cat and guinea-pig cochleae: sharp tuning and nonlinearity in the absence of baseline position shifts. Hear. Res. 1992;63:163–190. doi: 10.1016/0378-5955(92)90083-y. [DOI] [PubMed] [Google Scholar]
- 12.Cooper N.P., Dong W. Sound-evoked changes in the baseline position of the cochlear partition at the apex of the guinea-pig cochlea. J. Phys. (Lond.) 2000;527:90P–91P. [Google Scholar]
- 13.Ashmore J., Avan P., Canlon B. The remarkable cochlear amplifier. Hear. Res. 2010;266:1–17. doi: 10.1016/j.heares.2010.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brownell W.E., Bader C.R., de Ribaupierre Y. Evoked mechanical responses of isolated cochlear outer hair cells. Science. 1985;227:194–196. doi: 10.1126/science.3966153. [DOI] [PubMed] [Google Scholar]
- 15.Iwasa K.H., Adachi M. Force generation in the outer hair cell of the cochlea. Biophys. J. 1997;73:546–555. doi: 10.1016/S0006-3495(97)78092-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hudspeth A.J., Martin P., Choe Y. Cochlear amplification by active hair-bundle movements. J. Phys. (Lond.) 2000;523:14S–15S. [Google Scholar]
- 17.Meaud J., Grosh K. Coupling active hair bundle mechanics, fast adaptation, and somatic motility in a cochlear model. Biophys. J. 2011;100:2576–2585. doi: 10.1016/j.bpj.2011.04.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nobili R., Mammano F. Biophysics of the cochlea. II. Stationary nonlinear phenomenology. J. Acoust. Soc. Am. 1996;99:2244–2255. doi: 10.1121/1.415412. [DOI] [PubMed] [Google Scholar]
- 19.de Boer E. Mechanics of the cochlea: modeling efforts. In: Dallos P., Popper A., Fay R., editors. The Cochlea. Springer-Verlag; New York: 1996. pp. 258–317. [Google Scholar]
- 20.Kanis L.J., de Boer E. Self-suppression in a locally active nonlinear model of the cochlea: a quasilinear approach. J. Acoust. Soc. Am. 1993;94:3199–3206. doi: 10.1121/1.407225. [DOI] [PubMed] [Google Scholar]
- 21.Chadwick R.S. Compression, gain, and nonlinear distortion in an active cochlear model with subpartitions. Proc. Natl. Acad. Sci. USA. 1998;95:14594–14599. doi: 10.1073/pnas.95.25.14594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Reichenbach T., Hudspeth A.J. A ratchet mechanism for amplification in low-frequency mammalian hearing. Proc. Natl. Acad. Sci. USA. 2010;107:4973–4978. doi: 10.1073/pnas.0914345107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lim K.M., Steele C.R. A three-dimensional nonlinear active cochlear model analyzed by the WKB-numeric method. Hear. Res. 2002;170:190–205. doi: 10.1016/s0378-5955(02)00491-4. [DOI] [PubMed] [Google Scholar]
- 24.Yoon Y.J., Steele C.R., Puria S. Feed-forward and feed-backward amplification model from cochlear cytoarchitecture: an interspecies comparison. Biophys. J. 2011;100:1–10. doi: 10.1016/j.bpj.2010.11.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kolston P.J. The importance of phase data and model dimensionality to cochlear mechanics. Hear. Res. 2000;145:25–36. doi: 10.1016/s0378-5955(00)00067-8. [DOI] [PubMed] [Google Scholar]
- 26.Gummer A.W.G., Hemmert W., Zenner H.P. Resonant tectorial membrane motion in the inner ear: its crucial role in frequency tuning. Proc. Natl. Acad. Sci. USA. 1996;93:8727–8732. doi: 10.1073/pnas.93.16.8727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen F., Zha D., Nuttall A.L. A differentially amplified motion in the ear for near-threshold sound detection. Nat. Neurosci. 2011;14:770–774. doi: 10.1038/nn.2827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Meaud J., Grosh K. The effect of tectorial membrane and basilar membrane longitudinal coupling in cochlear mechanics. J. Acoust. Soc. Am. 2010;127:1411–1421. doi: 10.1121/1.3290995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Russell I.J., Legan P.K., Richardson G.P. Sharpened cochlear tuning in a mouse with a genetically modified tectorial membrane. Nat. Neurosci. 2007;10:215–223. doi: 10.1038/nn1828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ghaffari R., Aranyosi A.J., Freeman D.M. Longitudinally propagating traveling waves of the mammalian tectorial membrane. Proc. Natl. Acad. Sci. USA. 2007;104:16510–16515. doi: 10.1073/pnas.0703665104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ramamoorthy S., Deo N.V., Grosh K. A mechano-electro-acoustical model for the cochlea: response to acoustic stimuli. J. Acoust. Soc. Am. 2007;121:2758–2773. doi: 10.1121/1.2713725. [DOI] [PubMed] [Google Scholar]
- 32.Cooper, N. P. 2000. Radial variation in the vibrations of the cochlear partition. In Proceedings of the International Symposium on Recent Developments in Auditory Mechanics, 1999, Sendai. World Scientific, Singapore. 109-115.
- 33.Howard J., Hudspeth A.J. Compliance of the hair bundle associated with gating of mechanoelectrical transduction channels in the bullfrog's saccular hair cell. Neuron. 1988;1:189–199. doi: 10.1016/0896-6273(88)90139-0. [DOI] [PubMed] [Google Scholar]
- 34.He D.Z.Z., Jia S.P., Dallos P. Mechanoelectrical transduction of adult outer hair cells studied in a gerbil hemicochlea. Nature. 2004;429:766–770. doi: 10.1038/nature02591. [DOI] [PubMed] [Google Scholar]
- 35.Fettiplace R., Ricci A.J. Adaptation in auditory hair cells. Curr. Opin. Neurobiol. 2003;13:446–451. doi: 10.1016/s0959-4388(03)00094-1. [DOI] [PubMed] [Google Scholar]
- 36.Johnson S.L., Beurg M., Fettiplace R. Prestin-driven cochlear amplification is not limited by the outer hair cell membrane time constant. Neuron. 2011;70:1143–1154. doi: 10.1016/j.neuron.2011.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hughes T.J.R. Dover, Mineola; NY: 2000. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. [Google Scholar]
- 38.Parthasarathi A.A., Grosh K., Nuttall A.L. Three-dimensional numerical modeling for global cochlear dynamics. J. Acoust. Soc. Am. 2000;107:474–485. doi: 10.1121/1.428352. [DOI] [PubMed] [Google Scholar]
- 39.Liu Y.W., Neely S.T. Distortion product emissions from a cochlear model with nonlinear mechanoelectrical transduction in outer hair cells. J. Acoust. Soc. Am. 2010;127:2420–2432. doi: 10.1121/1.3337233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cameron T.M., Griffin J.H. An alternating frequency/time domain method for calculating the steady-state response of nonlinear dynamic systems. J. Appl. Mech. T. ASME. 1989;56:149–154. [Google Scholar]
- 41.Zheng J.F., Deo N., Nuttall A.L. Chlorpromazine alters cochlear mechanics and amplification: in vivo evidence for a role of stiffness modulation in the organ of Corti. J. Neurophysiol. 2007;97:994–1004. doi: 10.1152/jn.00774.2006. [DOI] [PubMed] [Google Scholar]
- 42.Frank G., Kössl M. Acoustical and electrical biasing of the cochlea partition. Effects on the acoustic two tone distortions f2-f1 and 2f1-f2. Hear. Res. 1997;113:57–68. doi: 10.1016/s0378-5955(97)00131-7. [DOI] [PubMed] [Google Scholar]
- 43.He D.Z.Z., Dallos P. Somatic stiffness of cochlear outer hair cells is voltage-dependent. Proc. Natl. Acad. Sci. USA. 1999;96:8223–8228. doi: 10.1073/pnas.96.14.8223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Housley G.D., Ashmore J.F. Ionic currents of outer hair cells isolated from the guinea-pig cochlea. J. Physiol. 1992;448:73–98. doi: 10.1113/jphysiol.1992.sp019030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hudspeth A.J., Jülicher F., Martin P. A critique of the critical cochlea: Hopf—a bifurcation—is better than none. J. Neurophysiol. 2010;104:1219–1229. doi: 10.1152/jn.00437.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zinn C., Maier H., Gummer A.W. Evidence for active, nonlinear, negative feedback in the vibration response of the apical region of the in-vivo guinea-pig cochlea. Hear. Res. 2000;142:159–183. doi: 10.1016/s0378-5955(00)00012-5. [DOI] [PubMed] [Google Scholar]
- 47.Cooper N.P., Rhode W.S. Nonlinear mechanics at the apex of the guinea-pig cochlea. Hear. Res. 1995;82:225–243. doi: 10.1016/0378-5955(94)00180-x. [DOI] [PubMed] [Google Scholar]
- 48.Cai H.X., Manoussaki D., Chadwick R. Effects of coiling on the micromechanics of the mammalian cochlea. J. R. Soc. Interface. 2005;2:341–348. doi: 10.1098/rsif.2005.0049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jacob S., Pienkowski M., Fridberger A. The endocochlear potential alters cochlear micromechanics. Biophys. J. 2011;100:2586–2594. doi: 10.1016/j.bpj.2011.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.How J.A., Elliott S.J., Lineton B. The influence on predicted harmonic and distortion product generation of the position of the nonlinearity within cochlear micromechanical models. J. Acoust. Soc. Am. 2010;127:652–655. doi: 10.1121/1.3279812. [DOI] [PubMed] [Google Scholar]
- 51.Gummer A.W., Johnstone B.M., Armstrong N.J. Direct measurement of basilar membrane stiffness in guinea pig. J. Acoust. Soc. Am. 1981;70:1298–1309. [Google Scholar]
- 52.Liu S., White R.D. Orthotropic material properties of the gerbil basilar membrane. J. Acoust. Soc. Am. 2008;123:2160–2171. doi: 10.1121/1.2871682. [DOI] [PubMed] [Google Scholar]
- 53.Richter C.P., Emadi G., Dallos P. Tectorial membrane stiffness gradients. Biophys. J. 2007;93:2265–2276. doi: 10.1529/biophysj.106.094474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zwislocki J.J., Cefaratti L.K. Tectorial membrane. II. Stiffness measurements in vivo. Hear. Res. 1989;42:211–227. doi: 10.1016/0378-5955(89)90146-9. [DOI] [PubMed] [Google Scholar]
- 55.Strelioff D., Flock A., Minser K.E. Role of inner and outer hair cells in mechanical frequency selectivity of the cochlea. Hear. Res. 1985;18:169–175. doi: 10.1016/0378-5955(85)90009-7. [DOI] [PubMed] [Google Scholar]
- 56.Fernandez C. Dimensions of the cochlea (guinea pig) J. Acoust. Soc. Am. 1952;24:519–523. [Google Scholar]
- 57.Gavara N., Chadwick R.S. Collagen-based mechanical anisotropy of the tectorial membrane: implications for inter-row coupling of outer hair cell bundles. PLoS ONE. 2009;4:e4877. doi: 10.1371/journal.pone.0004877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Beurg M., Nam J.H., Fettiplace R. The actions of calcium on hair bundle mechanics in mammalian cochlear hair cells. Biophys. J. 2008;94:2639–2653. doi: 10.1529/biophysj.107.123257. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


