Calcium-based plasticity model explains sensitivity of synaptic changes to spike pattern, rate, and dendritic location

Abstract

Multiple stimulation protocols have been found to be effective in changing synaptic efficacy by inducing long-term potentiation or depression. In many of those protocols, increases in postsynaptic calcium concentration have been shown to play a crucial role. However, it is still unclear whether and how the dynamics of the postsynaptic calcium alone determine the outcome of synaptic plasticity. Here, we propose a calcium-based model of a synapse in which potentiation and depression are activated above calcium thresholds. We show that this model gives rise to a large diversity of spike timing-dependent plasticity curves, most of which have been observed experimentally in different systems. It accounts quantitatively for plasticity outcomes evoked by protocols involving patterns with variable spike timing and firing rate in hippocampus and neocortex. Furthermore, it allows us to predict that differences in plasticity outcomes in different studies are due to differences in parameters defining the calcium dynamics. The model provides a mechanistic understanding of how various stimulation protocols provoke specific synaptic changes through the dynamics of calcium concentration and thresholds implementing in simplified fashion protein signaling cascades, leading to long-term potentiation and long-term depression. The combination of biophysical realism and analytical tractability makes it the ideal candidate to study plasticity at the synapse, neuron, and network levels.

Numerous experiments have shown how synaptic efficacy can be increased [long-term potentiation (LTP)] or decreased [long-term depression (LTD)] by the relative spike timing [spike timing dependent plasticity (STDP)] (1–4) and firing rate of pre- and postsynaptic neurons (5, 6). Studies in different brain regions and under varying experimental conditions have revealed a plethora of different types of STDP (7). Experimental protocols using a diversity of spike patterns have furthermore highlighted the complexity and nonlinearity of plasticity rules in different systems (6, 8–11). However, how the diversity and nonlinearity of plasticity results emerge from the interplay between the underlying biochemical synaptic machinery and activity patterns remains elusive.

Molecular studies have identified two key elements for the induction of synaptic plasticity in hippocampus and neocortex. First, postsynaptic calcium entry mediated by NMDA receptors (NMDARs) (12) and voltage-dependent Ca²⁺ channels (VDCCs) (13–15) has been shown in many cases to be a necessary (15–17) and sufficient (18–20) signal for the induction of synaptic plasticity. Second, calcium, in turn, triggers downstream signaling cascades involving protein kinases (mediating LTP) and phosphatases (mediating LTD) (10, 21–23). Another G protein-coupled LTD induction pathway involves retrograde signaling by endocannabinoids (15, 24), whose efficiency is greatly modulated by postsynaptic calcium (15, 25, 26). Depending on type of synapse, age, and induction protocol, different types and combinations of signaling cascades provide the link between the activity-dependent postsynaptic calcium signal and expression mechanisms of synaptic plasticity, such as number and/or phosphorylation level of postsynaptic AMPA receptors or changes in presynaptic transmitter release probability (12).

Despite the large amount of modeling studies on abstract and detailed implementations of biochemical signaling cascades (review in ref. 27), a mechanistic understanding of whether and how the calcium signal, combined with the multitude of identified signaling cascades, can give rise to the observed phenomenology of synaptic plasticity is still lacking. To make progress on this issue, we followed the path pioneered by Shouval et al. (28) and devised a biologically plausible but simplified calcium-based model that provides a link between stimulation protocols, calcium transients, protein signaling cascades, and evoked synaptic changes. The model implements in a schematic fashion two opposing calcium-triggered pathways mediating increases of synaptic strength (LTP; i.e., protein kinase cascades) and decreases of synaptic strength (LTD; i.e., protein phophatase cascades or G-protein cascades). The model is shown to be able to account for a wide range of experimental plasticity outcomes in hippocampal cultures and hippocampal as well as neocortical slices. Fitting this data quantitatively allows us to predict differences in the underlying calcium dynamics between these different studies.

Results

Synaptic Efficacy Changes Induced by Calcium.

We consider a model of a single synapse submitted to trains of pre- and postsynaptic action potentials (APs). The model represents the state of a synapse as a synaptic efficacy variable, ρ (t), whose temporal evolution is described by a first-order differential equation (Eq. 1):

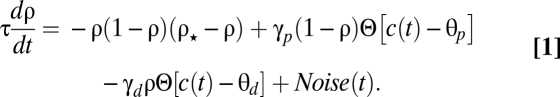In Eq. 1, τ is the time constant of synaptic efficacy changes happening on the order of seconds to minutes. The first term on the right-hand side describes the dynamics of the synaptic efficacy in the absence of pre- and postsynaptic activity. Here, we choose a cubic function of ρ that endows the synapse with two stable states at rest: one at ρ = 0, a DOWN state corresponding to low efficacy, and one at ρ = 1, an UP state corresponding to high efficacy. ρ_⋆ = 0.5 is the boundary of the basins of attraction of the two stable states. This bistable behavior is consistent with some experiments (29–31) as well as some biochemically detailed models (32, 33). It could be easily modified to account for more stable states or even a continuum of states without qualitatively modifying most of the results reported below.

The next two terms in Eq. 1 describe (in a highly simplified fashion) calcium-dependent signaling cascades leading to synaptic potentiation (e.g., kinases) and depression (e.g., phosphatases or G protein-coupled pathways), respectively (similar to Wittenberg)*. The synaptic efficacy variable tends to increase or decrease when the instantaneous calcium concentration, c(t), is above the potentiation (θ_p) or depression threshold (θ_d), respectively (Θ denotes the Heaviside function: Θ[c − θ] = 0 for c < θ and Θ[c − θ] = 1 for c ≥ θ). γ_p /γ_d measures the rates of synaptic increase/decrease when potentiation/depression thresholds are exceeded. The last term in Eq. 1 is an activity-dependent noise term, 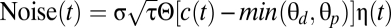, where σ measures the amplitude of the noise, η(t) is a Gaussian white noise process with unit variance density, and the Θ function gives an activity dependence to noise (it is present whenever calcium is above the potentiation and/or depression thresholds). This term accounts for activity-dependent fluctuations stemming from stochastic neurotransmitter release, stochastic channel opening, and diffusion.

Changes in the synaptic efficacy are induced by the calcium concentration, c(t), which is simply the linear sum of individual calcium transients elicited by pre- and postsynaptic APs. The calcium concentration makes a jump of size C_pre after each presynaptic spike (with a delay D) and then decays exponentially with time constant τ_Ca, which is on the order of milliseconds, modeling calcium influx induced by NMDAR activation (34) (Fig. 1A). Likewise, a calcium transient triggered by a postsynaptic spike mediated by VDCC activation is described by a jump of size C_post followed by an exponential decay with the same time constant as for the presynaptic spike, τ_Ca (SI Appendix, Simplified Calcium Model). For simplicity, we neglect the NMDA nonlinearity, finite rise times, and different decay time constants for NMDA- and VDCC-mediated calcium transients here, and their impact on the model results is discussed in SI Appendix.

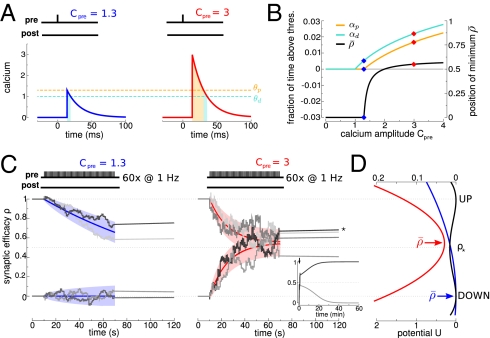
Fig. 1.

Repeated calcium transients induce transitions between the two stable states of synaptic efficacy. (A) A presynaptic spike at time t = 0 ms induces a postsynaptic calcium transient of amplitude C_pre after a delay D = 13.7 ms. Left and Right show transients with two different amplitudes that are indicated above the panels. The times spent above the depression (turquoise) and potentiation (orange) thresholds are indicated by shaded regions. (B) The higher the induced calcium transient, C_pre, the more time is spent above the depression (turquoise) and potentiation (orange) thresholds (left-hand y axis). Depression and potentiation together determine the average asymptotic value of synaptic efficacy (black; right-hand y axis) (SI Appendix). The two examples from A are indicated (◆). (C) Repeated calcium transients of high amplitude can lead to a transition from the DOWN to the UP state. The dynamics of ρ are shown in response to 60 presynaptic spikes at 1 Hz inducing calcium transients of low (Left) and high (Right) amplitude. ρ resides initially in the UP or DOWN state. Two instances of noise are shown for each initial condition (gray lines). ★, A DOWN to UP transition occurs for this case (Right). Inset shows the temporal evolution of ρ on a longer time scale for the two cases starting at the DOWN state in Right. The dynamics of the mean (colored line) and SD (shaded area) for the corresponding Ornstein–Uhlenbeck processes are depicted for each stimulation protocol and the two initial conditions. (D) During stimulation, the potential of the synaptic efficacy is approximately quadratic and has a single minimum at 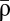(indicated by a colored arrow and shown for the two cases of C; scale at the bottom). In the absence of activity, the potential has two minima (the black line corresponds to two stable states; scale at the top). Note the different scales of the potential during (scale at the bottom) and in the absence of (scale at the top) synaptic activity (because γ_p, γ_d ≫ 1; see text).

Importantly, the calcium-induced fast (approximately milliseconds) changes in the synaptic efficacy depend on the relative times spent by the calcium trace above the potentiation and depression thresholds. Increasing the evoked calcium amplitude increases the time spent above both thresholds (Fig. 1B). Repetitive presentations of the same calcium transients lead to the accumulation of changes in ρ caused by the slow time scale of ρ in the absence of activity (Fig. 1C, Inset). When calcium amplitudes and γ_p are sufficiently large, these accumulated changes provoke a transition from the DOWN to the UP state with high probability (that is, they induce LTP). Such a transition occurs stochastically because of the noise in the model (Fig. 1C). Also, the protocol has to be long enough for the variable ρ to have a chance to cross the unstable fixed point.

In the model, synaptic activity induces small but fast changes (within milliseconds) in the efficacy variable. In the absence of activity, the synaptic activity slowly decays to one of the stable steady states on a time scale of minutes (Fig. 1C, Inset). Slow dynamics after the induction protocol are seen in many experiments (3, 6, 10) but not experiments involving putative single synaptic connections (29, 31) that are consistent with abrupt changes between two discrete states. This discrepancy could be reconciled by a simple modification of the model, in which the synaptic efficacy would be determined by applying a threshold-nonlinearity to the ρ-variable.

The model is simple enough, so that the probabilities to induce LTP and LTD can be calculated analytically. The analytical results reproduce the model behavior under two assumptions: (i) single calcium transients induce small changes in the synaptic efficacy (Fig. 1C), and (ii) the depression and potentiation rates (γ_d and γ_p) are sufficiently large so that one can neglect the cubic term in Eq. 1 during synaptic stimulation (Fig. 1D, note the different scales for quadratic and double-well potentials). These assumptions reduce Eq. 1 to an Ornstein–Uhlenbeck process for which the potential of ρ during stimulation is quadratic with the minimum at 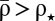(Fig. 1 B and D and SI Appendix). The outcome of a particular plasticity protocol will be largely determined by whether 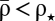is above or below the unstable fixed point ρ_⋆ = 0.5. LTP tends to be induced if 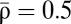(Fig. 1C, Right), whereas LTD tends to be induced if 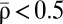(Fig. 1C, Left).

Spike Pair Stimulation Can Evoke a Plethora of Different STDP Curves.

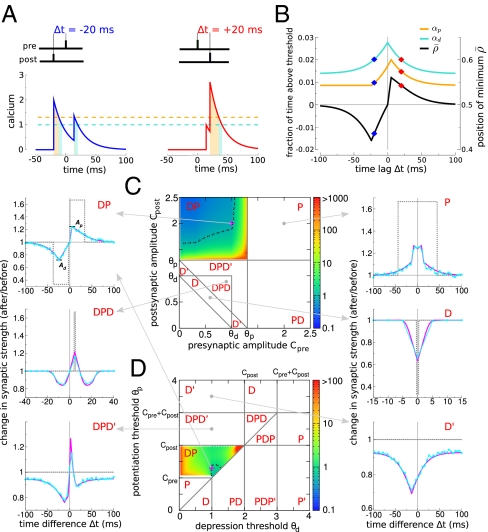
We start by explaining how the model reproduces the classical STDP curve (that is, depression for post-pre pairs and potentiation for pre-post pairs). Such a curve can be obtained when the potentiation threshold is larger than the depression threshold (θ_p > θ_d, consistent with ref. 22), the amplitude of the postsynaptic calcium transient is larger than the potentiation threshold (C_post > θ_p), and the amplitude of the presynaptic transient is smaller than the potentiation threshold (C_pre < θ_p). In addition, we impose that spike pairs with a large time difference should not evoke efficacy changes, which is the case if potentiation and depression rates balance on average during the protocol (i.e., 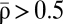) (SI Appendix). These conditions yield the classical STDP curve (Fig. 2B).

Fig. 2.

Diversity of STDP curves in response to spike pair stimulation. (A) Compound calcium transients evoked by a pair of pre- and postsynaptic spikes for two values of Δt (indicated on top of the panels) for C_pre = 1 and C_post = 2. (B) Fraction of time spent above the depression (turquoise line) and potentiation thresholds (orange) and average asymptotic value of the synaptic efficacy (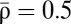; black) as a function of Δt for the parameters of A. The two examples from A are indicated (◆). (C and D) The shape of the STDP curve varies as a function of the pre- and postsynaptic calcium amplitudes C_pre and C_post (C; shown for θ_d = 1 and θ_p = 1.3) and the depression and potentiation thresholds θ_d and θ_p (D; shown for C_pre = 1 and C_post = 2). We identify a total of 10 qualitatively different regions with respect to the occurrence of depression, D, and potentiation, P, along the Δt axis. The changes in synaptic strength for six representative parameter sets (parameters in SI Appendix, Table S1) are shown in Left and Right in the presence and absence of noise (simulations in the presence of noise are in cyan and analytical results are in magenta; analytical results without noise, σ = 0, are in dotted gray). For some of the cases, changes are exclusively driven by noise (DPD′, DPD, and D′), whereas the presence of noise smoothes out the transitions and reduces the maximal potentiation and depression amplitudes for the DP, DPD, P, and D cases. The color codes in both DP regions depict the ratio of the maximal potentiation, A_p, and the maximal depression, A_d, amplitudes (Top Left; dotted black line indicates a ratio = 1). All changes in synaptic strength in this figure are in response to the presentation of 60 spike pairs at 1 Hz.

For large Δt, pre- and postsynaptic calcium transients do not interact, and contributions from potentiation (because of the postsynaptic spike) and depression (because of the post- and presynaptic spikes if C_pre > θ_d) cancel each other, leading to no synaptic changes on average. For short negative Δt, the presynaptically evoked calcium transient rises above the depression threshold. Consequently, depression increases, whereas potentiation remains constant, which brings the potential minimum closer to the DOWN state (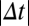) and leads to LTD induction (Fig. 2 A and B). For short positive Δt, however, the postsynaptically evoked calcium transient rides on top of the presynaptic transient and increases activation of both depression and potentiation. This brings the potential minimum closer to the UP state (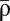) and in turn, gives rise to potentiation, because the rate of potentiation is larger than the rate of depression (γ_p > γ_d) (Fig. 2 A and B). As observed in experiments, the transition from maximal potentiation to maximal depression occurs within a small range of time lags. Furthermore, in the case C_pre ≤ θ_d, no synaptic changes are evoked if presynaptically evoked calcium transients are blocked, reproducing the NMDA dependence of synaptic plasticity (3, 15). Extending the model to account for the NMDAR nonlinearity for pre-post spike pairs furthermore renders LTP VDCC-independent, as seen in experiments (3, 15) (SI Appendix).

We now turn to discuss how STDP curves change when amplitudes of calcium transients or thresholds for potentiation and depression are varied. We find that a total of 10 qualitatively different STDP curves can be observed: D, D′, DP, DPD, DPD′, P, P′, PD, PDP, and PDP′, where D refers to depression and P refers to potentiation (Fig. 2 C and D) depending on parameters. For example, in region D, depression occurs at all values of Δt, whereas region DPD means that, when one increases Δt from large negative values, one first sees depression, then potentiation, and again depression. We impose no synaptic changes for large Δt (i.e., ) in regions where potentiation and depression are activated by individual calcium transients (P, DP, and PD). That requirement fixes the ratio γ_p/γ_d (SI Appendix). A prime (e.g., D′) means that, in the corresponding region, potentiation and depression cannot be balanced for large Δt. This lack of balance occurs when single calcium transients cross the depression but not the potentiation threshold (and vice versa). Furthermore, we choose γ_p and γ_d to yield both potentiation and depression in the DPD, PDP, DPD′, and PDP′ regions. For example, in the DPD′ region, D′ behavior can also be observed if γ_p is not large enough.

In Fig. 2C, these regions are plotted in the C_pre-C_post plane for fixed values of the potentiation and depression thresholds (θ_p = 1.3, θ_d = 1). Starting from the already discussed DP region (Fig. 2C, classical STDP curve), we see that decreasing the amplitude of postsynaptic calcium transients leads to the DPD′ and DPD regions, in which a second LTD window appears at positive Δt. Decreasing C_pre and C_post more so that their sum is below the potentiation threshold leads to the D and D′ regions (depression occurs at all Δt). If both calcium transients are individually larger than the potentiation threshold, then only potentiation occurs (P region). Finally, exchanging pre and post leads to an inversion of the curves along the Δt axis (for example, C_pre > θ_p > C_post leads to an STDP curve that is inverted PD compared with the classical one DP, which is seen, for example, in ref. 35 in a cerebellum-like structure in fish). The different states are also represented in the θ_d-θ_p plane for fixed values of C_pre = 1 and C_post = 2, revealing additional types of curves (Fig. 2D). For example, a DPD curve occurs if both thresholds are crossed by interacting calcium transients only, a region originally described in ref. 28.

The diversity of STDP curves emerges solely from a combination of linear superpositions of calcium transients from pre- and postsynaptic spikes followed by the potentiation/depression threshold nonlinearities. Note that taking into account the temporal dynamics of the calcium concentration variable is crucial in the model to determine the plasticity outcome as in more detailed models (27, 36). In fact, the maximal amplitude of the calcium transient alone does not predict whether a synapse will potentiate or depress. In other words, potentiation and depression can be seen for the same maximal calcium amplitude in an intermediate range (SI Appendix, Fig. S1), which was seen in the experiments in ref. 15.

Pairings with Postsynaptic Spikes and Bursts.

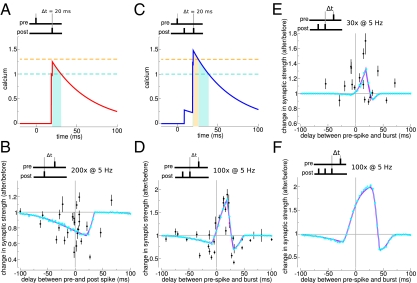
The next challenge for the model is to account for a set of experimental data obtained under the same experimental conditions but with different stimulation protocols. We show here that the model can reproduce the data shown in ref. 11 from CA3-CA1 slices. In this preparation, pairs of single pre- and postsynaptic spikes repeated at θ-frequency yield LTD only (similar to our D region), whereas pairing a single presynaptic spike with a burst of two postsynaptic spikes yields curves that are similar to our DPD or P region, depending on the duration of the protocol.

We find that all of the results of this experiment can be reproduced by our model (Fig. 3) provided that the parameters of the model are such that it is located in the D region for single spike pairs at low frequency (SI Appendix, Fig. S2). In this region, the model naturally reproduces the results shown in ref. 11 for the protocol in which the postsynaptic neuron emits a single spike (Fig. 3 A and B). Adding a second postsynaptic spike with a short interspike interval between the two leads to a pronounced increase in the amplitude of the compound calcium trace (Fig. 3C), giving rise to LTP at short positive Δt (DPD curve) provided that the potentiation rate γ_p is large enough (Fig. 3D). Interestingly, the model then produces a faster induction of LTP than LTD (37), which explains why only potentiation is seen when the duration of the protocol is reduced (Fig. 3E). The model parameters can be fitted quantitatively to the data of ref. 11 (SI Appendix and Table S2). The model can then be used to predict the plasticity outcomes for arbitrary protocols in the same experimental setting. For example, we predict that adding a third spike in the burst would yield broader and stronger LTP at positive Δt and short negative Δt (Fig. 3F).

Fig. 3.

Numbers of postsynaptic spikes and repetitions of the stimulation motif qualitatively change the STDP curve. (A) Compound calcium trace evoked by a spike pair for C_pre = 1, C_post = 0.276, and Δt = 20 ms. For these parameter values, the calcium trace remains below the potentiation threshold (θ_p = 1.3, θ_d = 1). (B) For the parameters of A, spike pair simulation induces synaptic depression for small positive and negative values of Δt. (C) Adding a postsynaptic spike, resulting in a postsynaptic burst with an interburst interval of 11.5 ms, leads to crossing of the potentiation threshold. (D) Prespike and postburst stimulation results in a DPD curve. (E) Reducing the number of prespike and postburst motif presentations from 100 to 30 turns the DPD curve into a PD curve exhibiting potentiation, with little depression at positive Δt. (F) Prespike and postburst stimulation with three postsynaptic spikes amplify potentiation at short positive Δt values. All data points are taken from plasticity experiments in hippocampal slices (mean ± SEM) (11). Analytical results of changes in synaptic strength are shown in magenta, and simulation results are shown in cyan (see SI Appendix, Table S2 for parameters).

Spike Triplets and Quadruplets.

We now show that our synapse model naturally reproduces nonlinearities of spike triplet and quadruplet experiments if calcium amplitudes of pre- and postsynaptically evoked transients have different amplitudes. In those experiments from hippocampal cultures, post–pre-post triplets and post–pre-pre-post quadruplets are shown to evoke LTP, whereas pre–post-pre triplets and pre–post-post-pre quadruplets induce no synaptic changes (or little potentiation) (10).

We fitted the synapse model to experimental plasticity results from protocols with spike triplets and quadruplets (SI Appendix, Fig. S3) (10). The resulting parameter sets are located in the DP region, consistent with the experimental results on spike pairs in hippocampal cultures (3, 10). The fit consistently yields a large, postsynaptically evoked calcium amplitude C_post > C_pre (Discussion and SI Appendix, Fig. S3A). Consequently, post–pre-post triplets lead to stronger activation of potentiation compared with pre–post-pre triplets (SI Appendix, Fig. S3B). Together with a potentiation rate that is larger than the depression rate (γ_p > γ_d), this model creates an imbalance in plasticity outcomes between pre–post-pre and post–pre-post triplets (SI Appendix, Fig. S3 C and D). The model is also able to fit the quadruplet data (SI Appendix, Fig. S3E), again because of the pronounced difference between pre- and postsynaptically evoked calcium transients. Finally, parameters that best fit triplet and quadruplet data also reproduce the pair data (SI Appendix, Fig. S3F).

Plasticity Vs. Firing Rate.

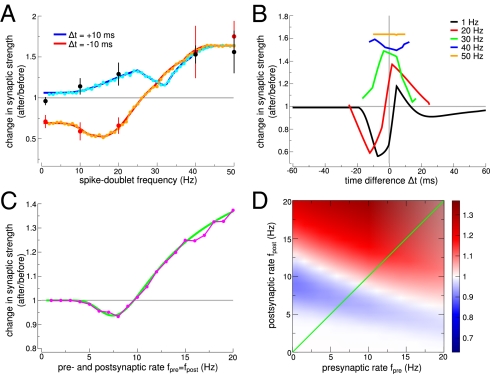
Here, we show that the firing rate dependence of plasticity results emerges naturally in the model because of interactions between successive calcium transients. In visual cortex slices, spike pairs at very low frequency induce no significant changes for short positive Δt (Δt = 10 ms) (1, 6), whereas pronounced LTD is obtained for short negative Δt (Δt = −10 ms). However, pairings at high frequency induce LTP only (6).

We successfully fitted the synapse model to data obtained with pre-post (Δt = 10 ms) and post-pre spike pairs (Δt = −10 ms) presented at frequencies ranging from 0.1 to 50 Hz (Fig. 4) (6). The fit results reside in the DPD and DPD′ regions (SI Appendix, Fig. S2) and lead to STDP curves for low frequencies, which are biased to depression for the small 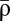except for short positive Δt values at which no or little potentiation is evoked (Fig. 4B). Increasing the stimulation frequency naturally leads to an increase in time spent by the calcium trace above the potentiation threshold, because successive calcium transients start to interact with each other, which progressively leads to LTP at all time differences, consistent with the information in ref. 6 (Fig. 4A; compare Fig. 4B with figure 7 in ref. 6). Our model, furthermore, qualitatively reproduced experimental plasticity results in response to random firing in which spike times of both pre- and postsynaptic neurons are jittered and LTD is evoked at low frequencies, whereas high frequencies elicit LTP (SI Appendix, Fig. S4) (6).

Fig. 4.

Plasticity vs. firing frequency. (A) Periodic pre-post pairs (Δt = 10 ms) evoke no change at low-presentation frequencies and LTP at high frequencies, whereas post-pre pairs (Δt = −10 ms) lead to depression at low frequencies and potentiation at high frequencies. Data points are taken from plasticity experiments in cortical slices (6) (mean ± SEM). Analytical results of changes in synaptic strength are shown in blue and red, and simulation results are shown in cyan and orange. (B) Change in synaptic strength as a function of Δt for various frequencies f (as indicated). Low presentation frequencies (black line) of spike pairs lead to a DPD curve with a narrow LTP region. Potentiation is recruited when consecutive calcium transients start to interact at high frequencies, leading to potentiation only above 29 Hz for all Δt. (C) Pre- and postsynaptic Poisson firing at equal rates (f_pre = f_post) evokes no synaptic changes at low rates, LTD at intermediate rates, and LTP at high rates. Analytical results of changes in synaptic strength are shown in green, and simulation results are shown in magenta. (D) The change in synaptic strength (analytical results) in response to Poisson stimulation is shown for all combinations of pre- and postsynaptic rates. The green diagonal illustrates the values depicted in C (see SI Appendix, Table S2 for parameters).

The above-studied deterministic spike patterns are at odds with experimentally recorded spike trains in vivo, which show a pronounced temporal variability similar to a Poisson process. We, therefore, turn to investigate the model in response to uncorrelated Poisson spike trains of pre- and postsynaptic neurons (SI Appendix, Fig. S10). The synapse model predicts that pre- and postsynaptic firings contribute in a similar way to synaptic efficacy changes in visual cortex: no change for low pre- and post rates, LTD for intermediate rates, and LTP for high rates (Fig. 4 C and D). The model also predicts that LTP occurs for purely postsynaptic activity at high frequency. Such a behavior could, however, be prevented through a frequency-dependent attenuation of the postsynaptically induced calcium transients, modeling failure in backpropagating consecutive APs at high frequencies.

Synaptic Plasticity and Dendritic Location.

While fitting our model to the plasticity results above, we have so far neglected any influence of dendritic filtering such as attenuation of the backpropagating AP. We show here that the model reproduces the switch from LTP, for proximal layer 5 to layer 5 synapses, to LTD for distal neocortical layer 2/3 to layer 5 synapses, since attenuation of AP backpropagation leads to reduced calcium influx (38).

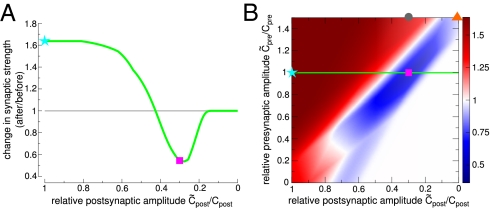
Using the parameter set obtained from fitting our model to plasticity outcomes at proximal cortical synapses (Fig. 4) and varying only the evoked calcium amplitudes reproduces a bulk of experimental data on the location dependence of plasticity. (i) LTP turns into LTD at distal synapses when the postsynaptic calcium amplitude drops to 30%, which is in agreement with the experimentally observed magnitude of calcium influx reduction at distal dendrites (Fig. 5, magenta square). (ii) Large excitatory postsynaptic potentials (EPSPs) induced experimentally by extracellular stimulation or boosting of single synaptic inputs, leading to higher presynaptically evoked calcium influx (C_pre) paired with APs, rescue LTP at distal dendrites (Fig. 5B, gray circle). (iii) Strong distal presynaptic input alone evokes LTD (Fig. 5B, orange triangle). All these results are naturally explained by the dependence of the amplitude of the calcium transient on dendritic location, and no parameter tuning is needed to reproduce them.

Fig. 5.

LTP turns into LTD at distal synapses because of reduced calcium influx. (A) Reducing the postsynaptically evoked calcium amplitude because of the attenuation of the backpropagating AP turns LTP into LTD (magenta square, reduction to 30%). (B) Change in synaptic strength as a function of deviations of the pre- and postsynaptically evoked calcium amplitudes from the parameters used in Fig. 4 (SI Appendix, Table S2). The green line illustrates the dependence of plasticity on the postsynaptic amplitude as in A. LTP can be rescued by boosting presynaptic stimulation (gray circle), but strong presynaptic stimulation alone evokes LTD (orange triangle).

Another study on dendritic location dependence of plasticity in the somatosensory cortex showed that proximal LTP turns into LTD at distal synapses for pre-post pairing, whereas proximal LTD turns into distal LTP for post-pre pairings (39). These results can be explained in the framework of our model by a DPD plasticity window that shifts to negative Δt at distal synapses because of delayed NMDAR activation.

Discussion

The model presented here posits that synaptic changes are driven by calcium transients evoked by pre- and postsynaptic spikes through potentiation and depression thresholds that represent (in a simplified fashion) protein signaling cascades leading to LTP and LTD. This model allows us to analytically compute plasticity outcomes as a function of model parameters for deterministic as well as stochastic protocols. This feature enabled us to fully characterize the behavior of the model in response to standard STDP protocols and show its ability to fit a large set of experimental data in different preparations. Because of the properties of calcium transients, our synaptic learning rule (as the experimental data) is naturally sensitive to both spike timing and firing rates of both pre- and postsynaptic neurons. The model illustrates that the calcium trace together with the nonlinear calcium-dependent activation of signaling cascades are potentially sufficient to explain the diversity and nonlinearity of plasticity outcomes.

Our model makes several predictions. We predict how Poisson stimulation shapes synaptic plasticity in cortical slices, hippocampal cultures, and hippocampal slices and predict that the plasticity results exhibit very different overall behaviors (Fig. 4D and SI Appendix, Fig. S10 C and D). For Poisson stimulation in cortical slices, we predict that decreasing calcium amplitudes (e.g., by partially blocking calcium intracellularly) shift the threshold for LTP induction to higher frequencies (SI Appendix, Fig. S5B). Conversely, boosting calcium amplitudes (e.g., by increasing extracellular calcium concentrations) should move the threshold to lower frequencies. We predict, furthermore, that reproducing the classical STDP curve (DP) requires single postsynaptic calcium transients to activate both potentiation and depression cascades. Contributions from both pathways cancel for single postsynaptic spikes, whereas blocking potentiating or depressing cascades should disrupt that balance and reveal LTD or LTP, respectively, for postsynaptic stimulation alone.

The model also allows us to infer information about the calcium transients using the stimulation protocol and the observed plasticity outcomes. For example, AP backpropagation seems to be more efficient (e.g., through less attenuation or broader APs) in hippocampal cultures, because only a single postsynaptic spike is required to elicit LTP as opposed to the requirement for postsynaptic bursts in hippocampal and cortical slices (11, 15). In line with that observation, fitting our model to hippocampal culture data yields a larger, postsynaptically evoked calcium amplitude for single APs (SI Appendix, Fig. S2). Furthermore, cortical slice parameters show that the maximal calcium amplitude does not predict the direction of synaptic changes, which was seen in cortical slice experiments (compare SI Appendix, Fig. S1 with ref. 15). We predict that synaptic changes should be much more correlated with the times spent above specific calcium thresholds than with the amplitudes of the calcium transients. Conversely, the model provides a tool to predict changes in synaptic strength when the calcium dynamics or stimulation protocols are varied. In particular, we have shown that it naturally reproduces the dependence of synaptic plasticity on dendritic location (Fig. 5).

The model bears similarities with a number of previous synaptic plasticity models (28, 40–42). Shouval et al. pioneered the study of calcium-based models and showed how such models can reproduce a variety of experimental protocols (28). Our model can be seen as an additional simplification of this model, which allows us to (i) analytically compute plasticity outcomes and (ii) find that the standard STDP curve (DP in our terminology) can naturally be reproduced without any need for additional detectors of synaptic activity other than calcium. Brader et al. introduced bistability in a calcium-based model but did not attempt to fit experimental data with such a model (41). Additionally, the works of Pfister et al. (40) and Clopath et al. (42) use a similar approach as our approach of fitting a variety of experimental protocols to a simplified model. However, in contrast to our model, the works in refs. 40 and 42 use a purely phenomenological model (based on adding triplet terms and a voltage dependence to a simple STDP rule) that cannot be easily related to the biophysical properties of the synapse. Furthermore, such models fail to produce the plethora of STDP curves (Fig. 2) and the nonlinear summation of synaptic changes seen when changing the number of motif presentations (Fig. 3). The strength of the calcium-based approach used here is the fact that we can investigate how synaptic plasticity is affected when biophysical parameters, such as the calcium amplitudes, are varied (Fig. 5).

Finally, we emphasize that our model could easily be generalized in various directions. One of such directions is the implementation of a Bienenstock-Cooper-Munro (BCM)-like sliding threshold as shown in SI Appendix, Fig. S5. A second generalization would be to include the effects of various neuromodulators that are known to affect synaptic plasticity (43). One simple way of implementing neuromodulation would be to add neuromodulatory dependence to specific model parameters as the thresholds or rates. Such an implementation could potentially lead to a more biophysical ground of reinforcement learning theories.

To conclude, our synaptic learning rule provides a bridge between activity patterns, the calcium signal, biochemical signaling cascades, and plasticity results. Its simplicity and analytical tractability make it an ideal candidate for investigating the effects of learning at the network level.

Materials and Methods

Analytical solution for transition probabilities.

The behavior of the model is governed by α_p and α_d, the fraction of time the calcium concentration spends above the potentiation and depression thresholds, respectively. α_p and α_d can be computed analytically for all the stimulation protocols considered here. The probability for a DOWN-to-UP transition, , and for the reverse transition, , can then be computed analytically using the Fokker-Planck formalism (SI Appendix, Eqs. S13 and S15).

Synaptic strength, change in synaptic strength and simulations.

We take the synaptic strength linearly related to ρ as w = w₀ + ρ(w₁ − w₀), where w₀/w₁ is the synaptic strength of the DOWN/UP state. We assume that, before a stimulation protocol, a fraction β of the synapses are in the DOWN state. We consider the change in synaptic strength as the ratio between the average synaptic strengths after and before the stimulation, i.e. ([(1 − )β + (1 − β)] + b[β + (1 − )(1 − β)])/(β + [1 − β]b), where b = w₁/w₀.

Fitting the synapse model to experimental data.

Fitting procedures are described in SI Appendix and parameters are summarized in SI Appendix, Table S2.