Bitrophic interactions shape biodiversity in space

Abstract

Ecologists and conservation biologists often study particular trophic groups in isolation, which precludes an explicit assessment of the impact of multitrophic interactions on community structure and dynamics. Network ecology helps to fill this gap by focusing on species interactions, but it often ignores spatial processes. Here, we are taking a step forward in the integration of metacommunity and network approaches by studying a model of bitrophic interactions in a spatial context. We quantify the effect of bitrophic interactions on the diversity of plants and their animal interactors, and we show their complex dependence on the structure of the interaction network, the strength of interactions, and the dispersal rate. We then develop a method to parameterize our model with real-world networks and apply it to 54 datasets describing three types of interactions: pollination, fungal association, and insect herbivory. In all three network types, bitrophic interactions generally lead to an increase of plant and animal spatial heterogeneity by decreasing local species richness while increasing β-diversity.

Two major frameworks in biodiversity research are network and metacommunity theories. The metacommunity theory highlights the role of spatial processes in community dynamics (1), while the theory of ecological networks highlights the role of multitrophic interactions (2, 3). Metacommunity studies focus generally on one particular trophic group like plants (4–7), whereas network studies consider larger communities across several trophic groups but are generally local (7). From the metacommunity perspective, accumulating evidence suggests that ecological interactions impact community composition (8–10). From the network perspective, it is unclear whether the reported effects of network architecture on species richness (7) stand in spatially extended systems coupled through dispersal. In short, we need to add a spatial component to network studies or a network component to metacommunity studies (11–14).

In recent years, a number of studies have begun the integration of spatial processes and multispecies interactions by exploring community modules of two or three species (15, 16). These studies have shown that dispersal can stabilize pairwise trophic interactions (15), tritrophic food chains (11), and competitive interactions (17). Similarly, another source of multispecies stability is induced by the action of predators (18, 19).

Models at the module level have been very useful at providing a bridge between the complexity of entire communities and the simplicity of pairwise interactions (20). To go a step farther into closing the circle, a few theoretical papers have begun to study the role of spatial processes in models of entire ecological networks (13, 14, 21, 22). Here, we follow the same avenue, focusing on bitrophic ecological networks such as those networks describing pollination or herbivory between plants and insects. Our aim is to understand to what degree network structure affects the metacommunity dynamics of the two interacting groups.

We will use the neutral metacommunity model in the work by Hubbell (4) as our baseline reference. This minimal model encapsulates the combined role of dispersal limitation and stochasticity in metacommunity dynamics. Next, we will extend this framework by adding a deterministic component emerging from the nonrandom structure of bitrophic interaction networks. Comparing the outputs of the extended model and the neutral one will allow us to assess the impact of bitrophic interactions on the composition and dynamics of the metacommunity.

When they act differentially among community members, bitrophic interactions induce fitness differences among individuals. For instance, if pollinators preferentially pollinate flowers with short corollas, flowers with long corollas will tend to produce fewer seeds and will be progressively filtered out of the plant community. Phrased in the terms of metacommunity theory, bitrophic interactions act as an environmental filter for some community members if these members suffer greater damages from antagonists or benefit less from mutualists than their competitors (23–25). Bitrophic interactions should, thus, decrease species richness.

However, bitrophic interactions can stabilize the coexistence of different species if different community members partition biotic resources (mutualists) or threats (antagonists) by having different specialized interactions. For instance, assume that plant species A is locally abundant and sustains a large population of herbivore species B. If such species B exclusively feeds on plants of species A, then individuals of a rare plant species C may have a competitive advantage against individuals of species A in suffering less from herbivory (18, 26, 27). Herbivory should now stabilize the coexistence of the two plant species. Inversely, the diversity of plants creates a diversity of food sources for the animals. This diversity can also increase the likelihood of coexistence of different animal species (28). More generally, bitrophic interactions are likely to affect the composition of a trophic group (e.g., plants) just like abiotic conditions (29). Their overall effect on community richness will depend on a balance between their filtering and stabilizing (niche partitioning) effects. This overall impact of bitrophic interactions on community richness is, thus, likely to depend on the architecture of the interaction network, just as the heterogeneity in the abiotic environment contributes to the assembly of each trophic group.

Here, we first perform extensive individual-based simulations to explore how interactions between two trophic groups can alter their composition and dynamics (Box 1). We consider two types of interactions independently: mutualistic (e.g., plants and their pollinators) and antagonistic (e.g., plants and their insect herbivores). Each trophic group experiences stochastic lottery-like dynamics (30) in a lattice of patches connected by dispersal. Interactions between the trophic groups are controlled by two trait-based rules used in isolation or combined: a threshold rule and a matching rule (31) (Box 1). Exploring a wide range of combinations of model parameters, we investigate under which circumstances bitrophic interactions have an overall positive or negative effect on community richness and other community characteristics.

After assessing the potential range of effects of bitrophic interactions, we confront our theoretical findings to real data of ecological networks. We, hence, develop a statistical method based on approximate Bayesian computation (ABC) (32, 33) (Box 2) to fit our model to 54 bipartite networks (23 plant–pollinator networks, 16 plant–fungi networks, and 15 plant–insect herbivore networks) (SI Appendix). This procedure consists in simulating the model with a wide range of parameter values and retaining the parameter values that produce interaction networks that are closest to real ones. The combination of our theoretical exploration and empirical testing enables us to determine the likely impact of community-wide bitrophic interactions on community structure in nature and pinpoint knowledge gaps where efforts should be concentrated in the near future.

Box 1. Description of the Model

We model the dynamics of two trophic groups: plants and animals. The groups occupy a regular grid of l × l patches. Each patch contains N_p plants and N_a animals and follows stochastic dynamics with dispersal from the four neighboring patches at rates m_p and m_a and long distance dispersal from a pool of species at rates μ_p and μ_a (SI Appendix, Fig. S1). We consider that the patches are constantly saturated, and therefore at each generation, N_p and N_a descendants are drawn at random in a lottery manner (30) and replace their parents. For plants (similarly for animals replacing subindex p by a), the descendants of a patch P can come from either the present patch P, from one of the four neighboring patches, or from the regional pool. The respective probabilities of these three scenarios are 1/(1 + m_p + μ_p), m_p/(1 + m_p + μ_p), and μ_p/(1 + m_p + μ_p), respectively. We use regional pools of 300 species with equal species regional abundances. Immigrants from the regional pool, hence, belong to a randomly drawn species (of 300). Immigrants from the neighboring patches have the species identity of a randomly drawn individual in the neighboring patches. Descendants coming from the local patch have a species identity drawn at random with a probability proportional to the product of the local species abundance and its seed (egg) production. This seed (egg) production is affected, in part, by the local interaction with the other group as defined next.

Case 1: Mutualistic Interactions.

For the group of plants (animals), the seed (egg) production f_i^p (f_i^a) of an individual of species i is equal to

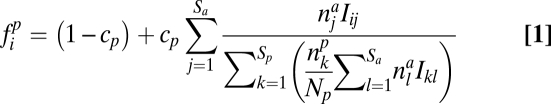and

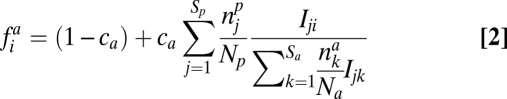where c_p (c_a) is the component of seed (egg) production that depends on the interaction with the other trophic group, 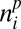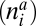is the number of individuals of species i in the group of plants (animals), and I_ij is the interaction strength between plant i and animal j.

For plants, the term 1 − c_p in Eq. 1 means that seed production is partially uncoupled from the interaction with animals (e.g., because of selfing). Eq. 1 also describes that plants compete to attract animals: a plant i interacts with animals at a total rate of 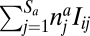. It will then receive a fraction of plant–animal interactions proportional to the term after c_p.

For animals, Eq. 2 is similarly constituted of two terms: the uncoupled egg production 1 − c_a and the coupled one, where the term after c_a describes the competition among animals to obtain the reward offered by plants. An animal i will receive from a plant j a fraction of its reward proportional to 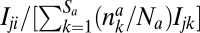. This animal i will, thus, obtain a total reward from the plants given by the term after c_a (SI Appendix).

If c_p and c_a equal zero or if interactions between plants and animals are equivalent among species (i.e., I_ij is constant), the dynamics of plants and animals are purely neutral and uncoupled.

Case 2: Antagonistic Interactions.

For antagonistic interactions, the seed production f_i^p is similarly modeled by

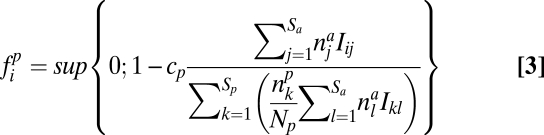where sup{0; x} equals zero if x < 0 and x otherwise. 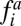is given by Eq. 2.

Interaction Rules.

Each species has a set of T independent trait values randomly drawn from the interval [0, 1] according to a uniform probability density function. These trait values determine the interaction strength between plants and animals. For each of the T traits, one of two interaction rules is used.

The first interaction rule is a threshold rule: an animal j with trait value 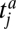can interact with a plant i with trait value 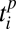only if 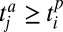. This rule increases the nestedness of the network: animals with low trait values are more specialist and interact with the subset of plants that have low trait values, whereas animals with large trait values are more generalist and interact with a larger subset of plants having both low and large trait values (45). Similarly, plants with large trait values are specialists and interact only with animals with large trait values, whereas plants with low trait values interact with a larger subset of animals.

The second interaction rule is a matching rule: an animal j with trait value t_j^a interacts with a plant i with trait value t_i^p with a probability proportional to 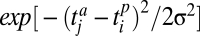, where σ is a parameter measuring the specificity of the interaction. This rule increases the specificity of plant–animal interactions: plants and animals interact more if they have similar trait values. Consequently, plants (animals) with different trait values tend to interact with different subsets of animals (plants). In this rule, the smaller σ is, the more specific the interactions will be; with these two interaction rules and less than four independent traits, various topological properties of real ecological networks can be reproduced as shown by ref. 31.

Our model formulation presents several advantages (directly comparable with a neutral model, simulation speed, and control of community size) (SI Appendix), but it also makes a number of assumptions that need to be taken into account (Discussion).

Results

In this section, we will use the term animal to designate a plant's interactor, although it can be a fungus in the datasets studied.

Model Results.

Our simulations show that mutualistic and antagonistic interactions can either increase or decrease local plant and animal species richness (Fig. 2 and SI Appendix, Fig. S4) depending on the balance between biotic filtering and niche partitioning. This balance, in turn, depends on the model parameters describing the structure of the interaction network, the dispersal rate across patches (m_p and m_a), and the strength of the interactions (i.e., the component of seed or egg production—c_p and c_a, respectively—accounted by the interaction with the other trophic group) (SI Appendix, Tables S1 and S2).

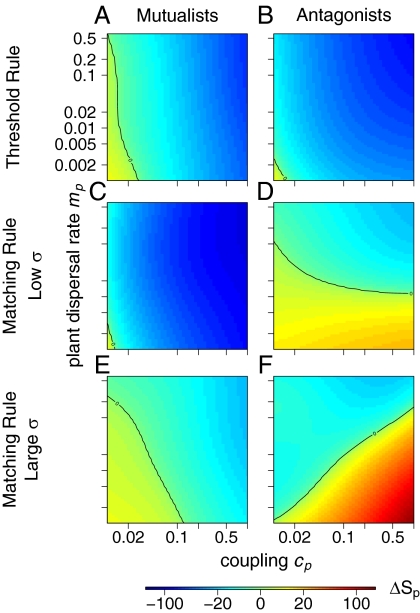
Fig. 2.

Relative variation (in percentage) of plant α-diversity between trophically coupled and uncoupled communities. α-Diversity is measured as the local plant species richness S_p. A positive value means that trophically coupled communities are species-richer than uncoupled ones. Different panels show results for the threshold model with one trait (A and B), the matching model with one trait and σ = 0.015 (C and D), and the matching model with one trait and σ = 1 (E and F). A, C, and E correspond to mutualistic interactions, whereas B, D, and F correspond to antagonistic interactions. Parameter values are μ_p = μ_a = 0.004, m_a = 0.625, and c_a = 0.16.

The stabilizing effect (34) of bitrophic interactions is induced, for plants, by the heterogeneity among animals in their plant preferences and for animals, by the diversity of plant resources. It can be detected by looking at the variance in trait values among community members. Communities tend to gain species with overdispersed traits during the coupled dynamics (SI Appendix, Variance Test).

The other effect of bitrophic interactions is to filter out community members by producing fitness differences among individuals. We detect this filtering effect by computing the average interaction strength between plant and animal individuals. When mutualistic interactions have a negative impact on plant (animal) species richness, the average interaction strength increases compared with the neutral case. The surviving plants (animals) are those plants that encounter more mutualists. For antagonistic interactions, the average interaction strength decreases (increases) for plants (animals) when bitrophic interactions have a negative impact on plant (animal) species richness. The surviving plants are those plants that encounter fewer antagonists, whereas the surviving animals are those animals that have many interactions (SI Appendix, Coupling Test).

Bitrophic interactions, however, principally affect rare species: in 96% of the cases, the similarity in species composition between trophically coupled and uncoupled plant sets is larger when an abundance-weighted measure is used (SI Appendix).

Fig. 2 illustrates how the net effect of bitrophic interactions on local plant richness S_p depends on the plant dispersal rate m_p and the component of seed production dependent on bitrophic interactions c_p. In Fig. 2, various extremes of network structure are illustrated. These contrasting network architectures are produced with a threshold rule, a matching rule with high trait specificity, and a matching rule with low trait specificity, respectively. They result in nested, specialized, and generalized networks, respectively (Box 1 has details on these interaction rules and the resulting network structures).

Two points arising from Fig. 2 are worth mentioning. First, in the limits of low dispersal (low m_p) and weak interactions (low c_p), we recover the results shown in the work by Bastolla et al. (35)—namely, that nested networks tend to increase plant local richness (Fig. 2A, bottom left). Second, there is a strong interaction in the effect of the different model parameters on the outcome of bitrophic interactions. This finding means that, with such a relatively simple model, one can already produce very complex outcomes, and therefore, the effects of bitrophic interactions on metacommunity structure and dynamics are likely to be case-specific. A detailed interpretation of the patterns observed in Fig. 2 as well as the effect on bitrophic interactions on other community characteristics, including the animal group, can be found in SI Appendix.

Box 2. ABC Procedure

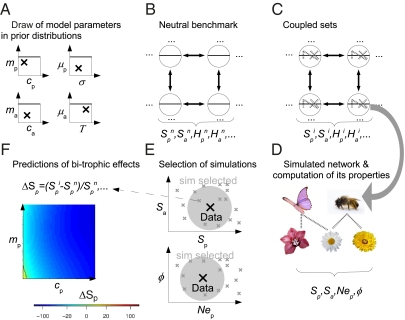
We compared our model to real data using an approximate Bayesian computation (ABC) (32, 33). The ABC procedure is represented in Fig. 1. It consists in replacing the computation of the model likelihood by simulations of this model (SI Appendix). This approximation is useful when likelihood formulas are unavailable as in the present case.

Fig. 1.

Approximate Bayesian computation (ABC) procedure. (A) Model parameter values (symbolized by ×) are randomly drawn in flat prior distributions (symbolized by rectangles). (B) A neutral metacommunity is simulated to form the benchmark. A grid of patches (circles) is connected by dispersal (arrows). Plants and animals (lower and upper semicircles, respectively) coexist in the patches, but they do not interact. Various community statistics are computed in this neutral benchmark . (C) The metacommunity dynamics are pursued including the bitrophic interactions (dotted lines between the half circles) this time. Various community statistics are computed in this coupled metacommunity 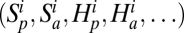. (D) A network of bitrophic interactions is simulated in a randomly chosen patch of the metacommunity, and its properties are computed (S_p, S_a, Ne_p, φ). (E) The properties of the simulated networks (small gray ×) are compared with those properties of the real data (large black ×), and the simulations with the best match are selected (gray circles). (F) Selected simulations are used to assess the effect of bitrophic interactions. This assessment is done by comparing the final metacommunity structure in the simulation (C) with the one of the neutral benchmark (B). These bitrophic effects are plotted against the two model parameters explaining the bulk of their variation: m_p and c_p for plants and m_a and c_a for animals.

The ABC procedure consists in simulating the model multiple times. For each one of these replicates, we draw the parameter values in prior (here flat) distributions (Fig. 1A and SI Appendix, Table S5). At the end of each simulation, a network of interactions between plants and animals is simulated (Fig. 1D). To this end, we first choose at random a patch out of the l × l simulated patches. In this patch, N_n animals are drawn at random, and for each of them, the plant with which it interacts is also drawn at random with probability proportional to 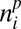I_ij, where 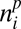is the abundance of plant species i in the patch and I_ij is the interaction strength between plant species i and animal species j.

Four network properties are then computed: the number of both plant 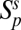and animal 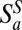species sampled by this procedure, the nestedness index of plants Ne_p (35), and an index of specialization φ defined as φ = 1 − H_i/ < H_i >, where 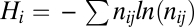and n_ij is the number of interactions between plant i and animal j divided by the total number of interactions (< H_i > is the average of H_i computed in 100 randomized networks). The null model used consists in randomly drawing an interaction network with the same total number of plants, animals, and interactions and having each interaction independently placed between a plant i and an animal j with probability 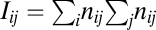. Note that 1 − φ is close to the 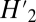value in the work by Blüthgen et al. (46), but the null model used here is different in that it does not constrain the number of interactions per plant and animal species. We use these last two indices to capture the effect of the different interaction rules on network structure: threshold rules tend to increase Ne_p, whereas matching rules tend to increase φ.

The properties of the simulated network are then compared with the ones of the real network, and therefore, the closest simulations according to these properties are retained (Fig. 1E).

These retained simulations are then used to quantify the impact of bitrophic interactions on the composition and dynamics of the plant and animal groups. This quantified effect depends on badly fitted model parameters, mainly on m_p (m_a) and c_p (c_a), which are not well-fitted because of the limited information content of the data used (Figs. 1F and 3 and SI Appendix, Figs. S7–S9). Note that we used the ABC procedure to perform an approximate Bayesian model averaging. The goal here is neither to compare the different interaction rules (with threshold and/or matching rules) nor obtain precise model parameter estimates but constrain our simulations so that they fit observed network properties.

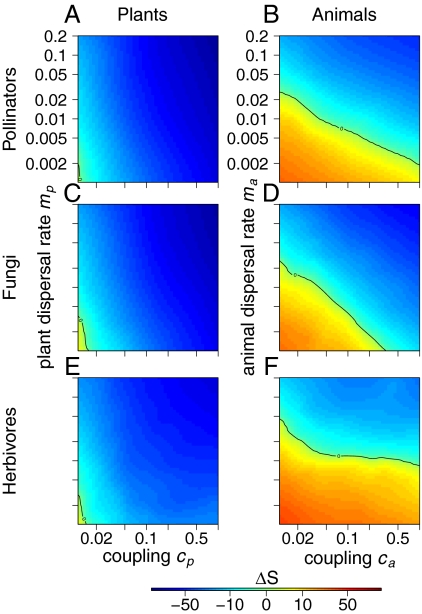
Fig. 3.

Variation of plant and animal local species diversity between trophically coupled and uncoupled communities in simulations that best fit observed network structure in real datasets. (A, C, and E) Relative variation of plant α-diversity measured as local plant species richness S_p; 70%, 64%, and 45%, respectively, of the variance is explained by the interpolation on average in each dataset. (B, D, and F) Relative variation of animal α-diversity measured as local animal species richness S_a; 33%, 40%, and 30%, respectively, of the variance is explained by the interpolation on average in each dataset. (A and B) Plant–pollinator datasets (n = 23). (C and D) Plant–fungi datasets (n = 16). (E and F) Plant–insect herbivore datasets (n = 15).

Application to Real Networks.

Because the theoretical exploration of our model revealed a rich variety of possible outcomes, we proceeded by assessing what specific patterns would emerge when the model was fitted to real data. We, therefore, developed a statistical technique to fit our bitrophic metacommunity model to local networks compiled in the literature. This fitting procedure is based on ABC (32, 33) (Box 2). The information available in the data was not sufficient to fully parameterize our metacommunity model and hence, precisely quantify the effect of bitrophic interactions on plant and animal richness in these datasets. It was, however, sufficient to greatly constrain our simulations, and therefore, the remaining variation in bitrophic effects on plant (animal) richness was highly dependent on two noninferred parameters: the plant (animal) dispersal rate between patches m_p (m_a) and the proportion of seed (egg) production c_p (c_a), which depends on trophic interactions (average R² = 61% and 23%, respectively) (Fig. 3).

We found that bitrophic interactions are likely to decrease local plant species richness in the three types of networks (Fig. 3 A, C, and E), producing an increase in β-diversity (SI Appendix, Fig. S2). The sole exception is for very weak interactions and very low dispersal rates, where our model predicts an increase in local diversity. In plant–pollinator networks, we can estimate c_p with the index of pollen limitation, which compares the fruit set of freely pollinated flowers with the fruit set of encapsulated flowers. The average of reported indices of pollen limitation for angiosperms in the metaanalysis in the work by Larson and Barrett (36) is c_p = 0.4. This value is an order of magnitude higher than the value required for a positive effect of pollinators on local richness (c_p < 0.02). In plant–fungi and plant–herbivore networks, c_p is more difficult to relate to any direct empirical measure. However, even in these cases, we can use available information to set up some general limits to the potential range of variability in this parameter. In the case of herbivores, for example, defoliation, flower, and fruit consumption attributable to insects represent above 5% each of the corresponding biomass (37). It is then likely that c_p is generally well above 0.02 in real settings.

From the animals’ perspective, our model predictions are more dependent on the precise value of c_a and m_a (Fig. 3 B, D, and F). A combination of larger c_a and m_a is required for bitrophic interactions to lead to an increase in animal spatial structure. Because animal interactors feed on plants, c_a would likely be at least equal to 0.1 in real settings, whereas animal dispersal rates should be, in general, larger than those rates for plants. It is, consequently, likely that bitrophic interactions lead in general to an increase of animal spatial structure, although this result might be more context-dependent than for plants. Overall, our results suggest that, in the majority of real scenarios, bitrophic interactions will decrease local plant and animal species richness, while increasing plant and animal β-diversity. These predictions were qualitatively similar across the different empirical networks (SI Appendix, Figs. S11–S16) and when looking at local diversity using Shannon's index H (SI Appendix, Fig. S7).

Discussion

We have shown theoretically that bitrophic interactions can both decrease or increase local plant and animal species richness, whereas regional richness is far less affected or not affected at all (SI Appendix). This effect of bitrophic interactions was found to principally affect rare species. This finding implies that community ecologists may be safe while ignoring bitrophic interactions when looking at general trends in community composition. Nevertheless, if they want to truly understand the composition and dynamics of entire groups—not just of the most abundant species—it may be essential to take bitrophic interactions into account.

Our integrative framework confirms the importance of network structure for species richness, and it is in agreement with other recent approaches (35, 38) (SI Appendix). Similarly, our study supports recent calls for looking at bitrophic interactions to understand plant community assembly and dynamics (10, 39). At the same time, however, our results show that knowing the structure of the interaction network is insufficient to fully predict the magnitude of this biotic filter: a large source of variation is explained by the properties of each trophic group and the proportion of fitness impacted by bitrophic interactions (Fig. 3).

For the same network structure, the decrease in local species richness is likely to be greater for less dispersal-limited systems (large m_p or m_a) and stronger coupling between plants and animals (large c_p or c_a). Our results suggest that dispersal rate and the strength of bitrophic coupling play similar roles in explaining variation in species richness.

By means of a computer-intensive statistical technique, we were able to relate this complex model to real world data. We have shown that, for realistic network structure, both mutualistic and antagonistic interactions are likely to reduce local plant and animal species richness and that the decrease in local species richness and associated increase in β-diversity can be substantial (Fig. 3 and SI Appendix, Fig. S10). Because our datasets encompass many different interaction types and geographical locations, our results are likely to be general and highlight the filtering role of bitrophic interactions at local scales. Neutral processes have already been shown to produce spatial community turnover (40). As shown here, this neutral spatial structuring can be amplified with realistic architectures of bitrophic interactions, with which different local assemblages will filter different local community members. These results are consistent with the recent analysis in the work by Pellissier et al. (41) showing that plant sets in the Swiss Alps present evidence of spatial structuring in traits related to pollination.

To be able to fit our model to available network data, we have made a number of simplifications that need to be acknowledged. First, we did not consider any spatial heterogeneity in the abiotic environment. Including this factor would add a new source of spatial structure in the plant and animal groups.

Second, another related simplification of our model was to ignore any kind of tradeoffs, such as those tradeoffs between the plant's resistance to herbivory and its growth rate and competitive ability (42). In the presence of such tradeoffs, trophic interactions would increase plant biodiversity by equalizing the fitness of otherwise unequal competitors (27, 34).

Third, we assumed that interactions had symmetrical effects on the plant and animal interactions. This assumption, which is not supported by real data on interaction networks, might be relaxed in future studies. To this goal, we need additional data on the fitness consequences of ecological interactions.

Fourth, our model ignored any variation in community size of plants and animals. In particular, year to year variation in animal community sizes could increase their impact on the plant set. Indeed, the competition among flowers to attract pollinators should be exacerbated in years of low pollinator abundance. Similarly, the impact of herbivores on the plant set should be maximal in years of high herbivore abundance. Again, a detailed analysis would be required to explore such possibilities.

Fifth, our lottery-like modeling framework is rather atypical in the literature on ecological networks (27, 43). The pros and cons of such a choice are detailed in SI Appendix. It would certainly be worth examining whether similar results were obtained with other modeling approaches, such as Lotka–Volterra-like equations, although this method would require solving additional challenges (SI Appendix). The fact that we recover the results from the work by Bastolla et al. (35) in the limit of low migration and coupling is reassuring and suggests that this finding might be the case.

We have pointed out a number of directions worth pursuing to better understand the combined effects of dispersal and trophic interactions on metacommunity dynamics in real world communities. Our study represents only a first step in this direction. Despite the limitations of our approach, it illustrates how complex questions and models can be statistically compared with real world data through an ABC approach. It also points out that, to elaborate and test more complicated models of spatial network dynamics, new types of data should be concurrently gathered, informing us on the mechanisms of network assembly, the dispersal rates of organisms, and the impact of trophic interactions on organisms’ fitness.

Materials and Methods

Model Outputs.

The two trophic groups are initialized fixing c_p and c_a to zero. They are, thus, at a neutral dispersal–drift dynamic equilibrium that can be simulated quickly by coalescence (44). The coalescence procedure consists of tracing backward in time the genealogy of the individuals in the present. Because all individuals ultimately have a unique common ancestor, the number of individuals to simulate progressively decreases, making the computation quicker. Starting from this reference neutral point obtained by coalescence, the trophically coupled dynamics of the two groups are simulated forward in time during 100 generations (with c_p and c_a different from zero). Species richness in both a single patch (local) and all of the patches together (metacommunity) and species diversity (measured as Shannon's index) are recorded for both plants and animals and both before and after coupling the two trophic groups. The turnover in plant and animal composition from one generation to the next is also recorded (SI Appendix, Temporal Turnover). We measure the effect of the bitrophic interactions by the relative variation of plant and animal species richness between the coupled and uncoupled scenarios 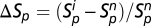and 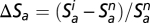(the superscripts i and n indicate with and without trophic interaction, respectively). We also monitor the relative variation of the other summary statistics in the same way.

Effect of the Interactions and Role of the Different Parameters.

We performed simulations on a grid of parameter values: μ_p and μ_a in {0.0005, 0.004}, m_p and m_a in {0.001, 0.005, 0.025, 0.125, 0.625}, and c_p and c_a in {0.01, 0.04, 0.16, 0.64, 1}. Eight different interaction rules were used based on a combination of zero, one, or two threshold rules and zero, one, or two matching rules, and each rule applies to independent and uncorrelated traits (hence, the number of traits T ranged between one and four depending on the interaction rule). Matching rules were used with σ in {0.015, 0.125, 1, 8}. For each interaction rule and set of parameter values, 10 independent communities were simulated, leading to a total of 1,300,000 simulations. We used l = 5, N_p = 1,000, and N_a = 200. The results were qualitatively similar with other choices of N_a and l (SI Appendix). Simulations were run with periodic boundary conditions. Results were similar in simulations with zero-flux boundary conditions and lost migrants at the boundary (SI Appendix). A detailed analysis of the effect of each model parameter as well as some community properties on the impact of bitrophic interactions are provided in SI Appendix.

To assess the robustness of our results to the specific choice of the component of seed (egg) production because of the trophic interaction, we studied an additional model where Eq. 2 is similar to Eq. 1, finding similar results (SI Appendix).

Compilation of Ecological Networks.

Datasets were included based on two criteria: they had to be quantitative and built from a single study site (7). In the majority of cases, there is little information on the spatial dimension of these sampled networks, and here, we will be assuming that they correspond in our model to a single patch.