Identifying malignant transformations in recurrent low grade gliomas using high resolution magic angle spinning spectroscopy

Abstract

Objective

The objective of this study was to determine whether metabolic parameters derived from ex vivo analysis of tissue samples are predictive of biologic characteristics of recurrent low grade gliomas (LGGs). This was achieved by exploring the use of multivariate pattern recognition methods to generate statistical models of the metabolic characteristics of recurrent LGGs that correlate with aggressive biology and poor clinical outcome.

Methods

Statistical models were constructed to distinguish between patients with recurrent gliomas that had undergone malignant transformation to a higher grade and those that remained grade 2. The pattern recognition methods explored in this paper include three filter-based feature selection methods (chi-square, gain ratio, and two-way conditional probability), a genetic search wrapper-based feature subset selection algorithm, and five classification algorithms (linear discriminant analysis, logistic regression, functional trees, support vector machines, and decision stump logit boost). The accuracy of each pattern recognition framework was evaluated using leave-one-out cross-validation and bootstrapping.

Materials

The population studied included fifty-three patients with recurrent grade 2 gliomas. Among these patients, seven had tumors that transformed to grade 4, twenty-four had tumors that transformed to grade 3, and twenty-two had tumors that remained grade 2. Image-guided tissue samples were obtained from these patients using surgical navigation software. Part of each tissue sample was examined by a pathologist for histological features and for consistency with the tumor grade diagnosis. The other part of the tissue sample was analyzed with ex vivo nuclear magnetic resonance (NMR) spectroscopy.

Results

Distinguishing between recurrent low grade gliomas that transformed to a higher grade and those that remained grade 2 was achieved with 96% accuracy, using areas of the ex vivo NMR spectrum corresponding to myoinositol, 2-hydroxyglutarate, hypo-taurine, choline, glycerophosphocholine, phosphocholine, glutathione, and lipid. Logistic regression and decision stump boosting models were able to distinguish between recurrent gliomas that transformed to a higher grade and those that did not with 100% training accuracy (95% confidence interval [93%–100%]), 96% leave-one-out cross-validation accuracy (95% confidence interval [87%–100%]), and 96% bootstrapping accuracy (95% confidence interval [95%–97%]). Linear discriminant analysis, functional trees, and support vector machines were able to achieve leave-one-out cross-validation accuracy above 90% and bootstrapping accuracy above 85%. The three feature ranking methods were comparable in performance.

Conclusions

This study demonstrates the feasibility of using quantitative pattern recognition methods for the analysis of metabolic data from brain tissue obtained during the surgical resection of gliomas. All pattern recognition techniques provided good diagnostic accuracies, though logistic regression and decision stump boosting slightly outperform the other classifiers. These methods identified biomarkers that can be used to detect malignant transformations in individual low grade gliomas, and can lead to a timely change in treatment for each patient.

1. Introduction

Ever year, approximately 17,000 adults in the United States are diagnosed with glioma, which is one of the most aggressive types of brain tumor [1]. Approximately 10,000 adults per year die from this disease [1]. Gliomas have a complex evolution process which is characterized by a high degree of biological and clinical diversity. Thus, despite major advances over the last two decades, the prognosis for patients with high grade lesions is poor. Survival depends on the tumor type and grade of malignancy, and has a median of 7–10 years for grade 2 tumors, 2–5 years for grade 3 tumors, and less than 1 year for grade 4 tumors [1]. Significant progress in the diagnosis, treatment and prevention of these tumors will require both the timely harnessing of the advances in basic and clinical brain tumor research, and a continuing effort to increase the understanding of brain tumor biology.

Recent oncology research shows that the evaluation of cellular metabolism can be very helpful for the diagnosis and assessment of treatment effects for patients with brain tumors. High resolution magic angle spinning (HRMAS) spectroscopy provides detailed metabolic data of whole biopsy samples for investigating tumor biology (see Figures 1, 2, 3). Analysis of such data can lead to identification of metabolites that may be used as biomarkers for discriminating different types of cancer, for grading tumors, and for assessing their evolution. The identification of ex vivo metabolites can also inform the acquisition of in vivo magnetic resonance spectroscopy (MRS), which can lead to a non-invasive assessment of tumor biology.

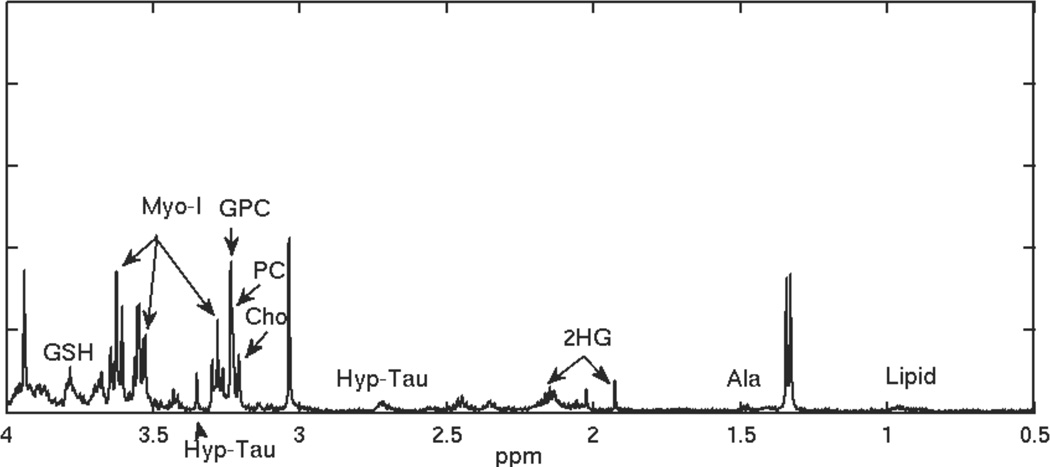
Figure 1.

HRMAS spectrum for a recurrent grade 2 glioma.

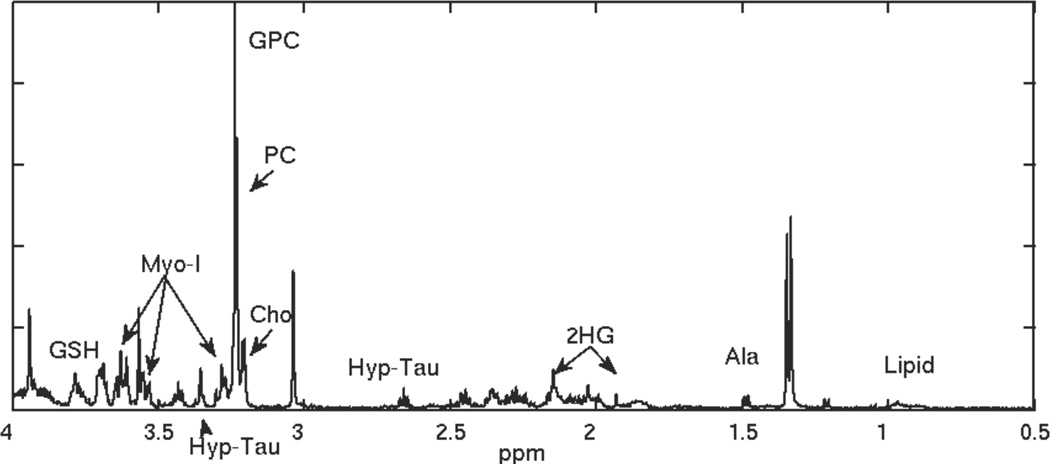
Figure 2.

HRMAS spectrum for a recurrent low grade glioma that transformed to grade 3.

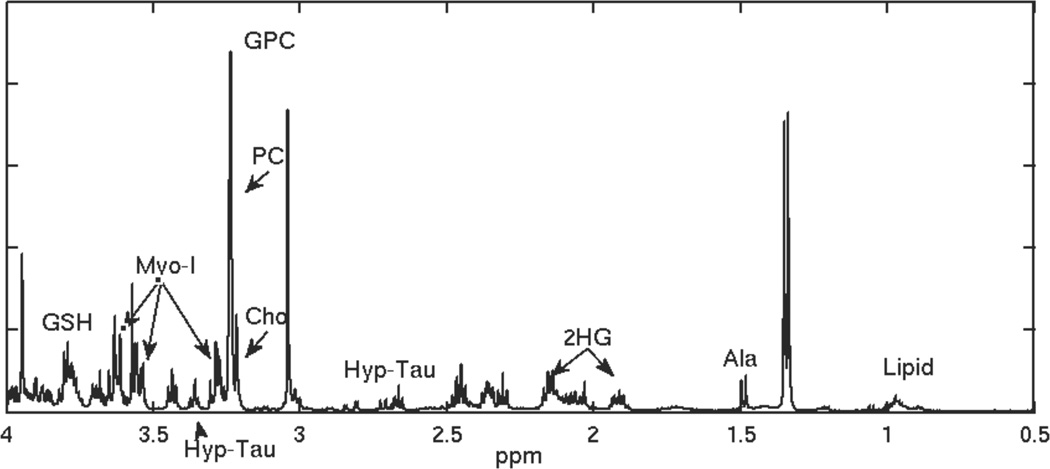
Figure 3.

HRMAS spectrum for a reccurent low grade glioma that transformed to grade 4.

Low grade gliomas (LGGs) include a diverse group of tumors, with distinct characteristics, patterns of occurrence, response to treatment, and survival timelines. The objective of this study is to determine whether quantitative metabolic parameters derived from HRMAS data are predictive of the biologic behavior of recurrent low grade gliomas. This is an important clinical question because of the need to determine whether a lesion has transformed to a more malignant phenotype and to treat each patient with the therapy that is most likely to be effective for their particular lesion. Thus, the goal of this study was to explore multivariate pattern recognition methods to generate statistical models of the metabolic characteristics of recurrent LGGs that correlate with aggressive biology and poor clinical outcome. These models can be used for the early detection of malignant transformations in individual low grade gliomas, and can lead to a timely change in treatment for each patient.

2. Related work

The clinical presentation of brain tumors varies greatly depending on tumor type and location. There is a growing body of evidence that MRS contributes to the clinical evaluation of a number of pathologies and therapeutically induced changes in tumor biochemistry [2–28].

MRS provides information on the metabolic processed occurring within an area of tissue. By comparing the relative concentration of metabolites in MRS data, clinicians can evaluate neuronal viability, neurotoxins, and membrane turnover within the volume of interest and, therefore, characterize the underlying pathology [2]. The clinical impact of MRS in medicine has been reviewed by Hollingworth et al. [2], Nelson [3, 4], and Smith et al. [5], and shows promise as a method to complement routine diagnostic investigation.

In vivo MRS suffers from some internal and external limitations. In particular, the restrictions on in vivo spectral resolution lead to the presence of overlapping peaks and ambiguity in identifying resonances, which lower the signal to noise ratio. Even among metabolites that are detectable with in vivo MRS, subtle differences in the concentrations of metabolites between normal and pathological tissue can go unnoticed and result in a diagnostic error. HRMAS techniques make it possible to examine the biochemical composition of tissue by spectroscopic analysis directly from tissue specimens [29]. HRMAS offers improved spectral resolution over the standard in vivo nuclear magnetic resonance (NMR) spectroscopy techniques. It is a non-destructive technique that can be applied to tissue prior to immunohistochemical analysis, thus providing a link between metabolite concentrations, pathology, and in vivo magnetic resonance imaging and spectroscopy. To this end, a large body of research tried to identify biomarkers for brain tumor characterization and typing using HRMAS [6, 7, 30–33]. The quest for biomarkers usually involves analyzing the behavior of single metabolites or ratios of two metabolites in different groups of patients, but does not exploit the relationship between large numbers of metabolites. In contrast, multivariate pattern analysis methods exploit the potential of ex vivo and in vivo NMR spectroscopy for a series of applications, such as the separation between normal brain and brain tumors [6, 34, 35] as well as for the characterization of different types and degrees of malignancy in tumors [7–17, 36–46]. Recent work using HRMAS for brain tumors showed that it is possible to classify spectroscopy samples according to tumor histological type [8, 12, 16, 18, 20, 22, 27, 44, 46] and grade [10, 12, 14, 16, 27, 46, 47] using multivariate methods such as linear discriminant analysis [14, 16], support vector machines [12, 14, 16], logistic regression [10, 47], partial least squares discriminant analysis [8], and multi-layer perceptrons [12]. Moreover, HRMAS multivariate studies successfully revealed the status of tumor microheterogeneity [9, 13, 15, 17] and detected alterations in tumor metabolism before changes in morphology occurred [12]. These studies combined dimensionality reduction methods such as principal component analysis [14, 20, 22] and metabolite quantification [10, 14–17, 22, 30, 47] with the robust classification methods listed above. Many of the dimensionality reduction methods and classifiers employed combine the data in such a way that the extracted components lack physical meaning. For example, in principal component analysis, the entire spectra may participate in the principal components, and the linear combination may mix both positive and negative weights, which might partly cancel each other out, thus making the results difficult to interpret. On the other hand, quantification methods such as LCModel [48], QUEST[49], and AQSES [50] quantify previously known chemicals in NMR spectra by incorporating prior knowledge about the set of frequencies that resonate for each chemical, the relative area of the various resonance peaks, and the shape of chemicals’ spectra. These methods could potentially overlook important information in the spectrum, such as the presence of previously unquantified metabolites. In addition, methods that search for metabolites independently based on their shape cannot distinguish between low levels of a chemical or bad fits. In order to avoid some of these disadvantages, this study explored whole-spectrum analyses with statistical feature selection methods that maintain a link to the biological meaning of the features. Robust feature selection and classification methods were combined to obtain accurate classifications with parsimonious and interpretable sets of features. The features identified can be used to inform in vivo MRS acquisition, and thus to better categorize tumor properties non-invasively.

In comparison to other multivariate studies, this work examines the metabolic transformations occurring in tumors that were previously of the same category, thus gaining insight into malignant transformations in low grade gliomas that are undergoing standard-of-care treatment. It also includes a relatively large number of gliomas of each grade compared to previous studies.

3. Data acquisition

This study involved 53 patients who had previously been diagnosed with World Health Organization (WHO) grade 2 gliomas and were presenting for surgical resection due to suspected disease recurrence. The patients had received prior standard-of-care treatment with surgical resection, radiation, or chemotherapy. Table 1 provides information about the patient baseline characteristics and treatment prior to recurrence, broken down by grade of recurrence. The differences in baseline characteristics and prior treatment between patients with gliomas that recurred at different grades were not statistically significant.

Table 1.

Characteristics of recurrent low grade glioma patients enrolled in the study and treatment received prior to recurrence, tabulated according to the tumor grade at recurrence.

Characteristic	Grade 2	Grade 3	Grade 4	Total
Male	9	13	4	26
Female	13	11	3	27
Mean age (years)	37.6	49.5	46	44.4
Biopsy	22	24	7	53
Resection	17	18	5	40
Chemotherapy	10	14	1	25
Radiation	4	6	1	11
Total	22	24	7	53

Pre-surgical in vivo MR examinations enabled the planning of targeted biopsies for sampling tissue from patient lesions. Imaging parameters derived from post-processed data helped guide the designation of small (5 mm³), putative tumor regions. Regions of suspected tumor located in relatively homogenous areas of the MR images were designated as targets for tissue sampling using surgical navigation software.

Tissue samples were divided into two parts. One part was flash-frozen in liquid nitrogen and the other was fixed using conventional pathological techniques. The fixed component was examined by a pathologist for histological features and for consistency with the tumor grade diagnosis. Only tissue samples that contained tumor cells and that were consistent with the diagnosis were included in the analysis. Histological analysis of tissue samples collected from the patients revealed that 7 tumors transformed to grade 4, 24 transformed to grade 3, and 22 remained grade 2.

The frozen part of the tissue sample was analyzed with ex vivo HRMAS. Tissue samples weighing between 0.78 and 28.14 mg (mean = 9.56 mg) were loaded into a 35-µl zirconium rotor (custom-designed by Varian) with 3 µl of 99.9% atom-D deuterium oxide containing 0.75 wt% 3-(trimethylsilyl) propionic acid (TSP) for chemical shift referencing. Data were acquired at 11.7 T, 1°C, 2250 Hz spin rate in a 4-mm gHX nanoprobe with a Varian INOVA 500 MHz multi-nuclear spectrometer. The nanoprobe gHX is an inverse probe, optimized for the direct detection of protons and the indirect detection of X-nuclei (e.g., 13C, 31P, 15N), and was equipped with a magic-angle gradient coil. A rotor-synchronized 1D CPMG pulse sequence was run with TR/TE=4s/144 ms, 512 scans, 40,000 acquired points, and 20 KHz spectral width for a total time of 35 minutes. The 180° hard pulses were spaced 888 ms apart and synchronized to two turns of the rotor, resulting in 162 pulses.

4. Analysis

Pattern analysis methods were used to build models capable of distinguishing between patients with recurrent low grade gliomas that transformed to a higher grade and those that remained low grade.

The development of pattern recognition systems involves four major steps that can be identified as follows: preprocessing the data, reducing the data dimensionality, and selecting relevant features, constructing a classifier, and predicting its performance on previously unseen data.

4.1. Preprocessing

The raw free induction decay HRMAS signal was preprocessed using jM-RUI [51]. The original time domain representation of the signal was transformed into the frequency domain using the fast Fourier transform. The frequency domain signal was shifted using TSP as a reference, and phased using zero-order phase correction. Residual water signal was then removed using Hankel-Lanczos singular value decomposition. Each data sample in the frequency domain was normalized using the electronic reference to access in vivo concentrations (ERETIC) method [52] and the tissue weight of each sample.

The preprocessed data were grouped into frequency bins of widths 5, 10, 15, 20, and 25 samples to account for the fact that different metabolites have different linewidths. The value used for each bin was obtained using trapezoidal numerical integration for the 5, 10, 15, 20, or 25 samples corresponding to that bin. This resulted in an input vector with 18,266 dimensions. This method is equivalent to identifying areas of parts of the spectrum, and is therefore less susceptible to noise than using all the spectral data points.

4.2. Dimensionality reduction

Because one of the goals of this project was to obtain parsimonious models that can be easily interpreted biologically, non-linear dimensionality reduction methods or methods that transform the original features into a smaller set of mathematically related features that combine information from all the available data (such as PCA) were not employed. Instead, the dimensionality of the data was reduced by identifying regions in the HRMAS spectrum that have a mutual association with disease stage or tumor grade, using three feature ranking metrics that lead to easily interpretable results. The three measures of association between features and classification output that we compared are based on the value of the chi-squared statistic with respect to the class [53], the information gain ratio with respect to the class [54], and a conditional probability-based technique that measures the mutual association between class decisions and feature values based on conditional probabilities [55]. The forty highest-ranked features in the HRMAS spectra were obtained for each of the three association metrics, for each classification problem. Selecting forty features was a heuristic loose enough to include most features with high and moderate levels of association, while keeping the second feature selection step computationally tractable.

A second feature selection step was performed in order to obtain a stable, parsimonious model capable of diagnosing new patients. A wrapper-based feature selection method was used to evaluate the suitability of subsets of features as a group, not just individually. The wrapper-based method [56] used genetic algorithms [57] to search through the space of possible feature sets and evaluate each subset of features by determining its performance when used in conjunction with a classification method. The genetic algorithm represented a solution as a binary vector that encoded whether a feature was included in the subset or not. Leave-one-out cross-validation accuracy was used to measure the fitness of a possible solution. At first, fifty individual solutions were randomly generated to form an initial population. During each successive iteration, a subset of the population was chosen to breed a new generation of solutions. Fitter solutions were more likely to be selected to breed. The new generation of solutions was obtained from pairs of parent solutions by combining the two parents using cross-over and mutation. Fifty iterations were performed, after which the highest ranked solution was selected.

4.3. Classification

The classification methods used to build diagnostic models were linear discriminant analysis [58] (which attempts to express the target class as a linear combination of predictors), logistic ridge regression [59] (which models the probability of occurence of an event by fitting the data to a logit function), functional trees [60] (which use decision nodes with multivariate tests and leaf nodes that make predictions using linear functions), support vector machines with a polynomial kernel [61] (which project the data into a different space and separate positive and negative examples using a hyperplane with maximum margin), and logit boost decision stumps [62] (which sequentially apply decision stump classification to re-weight versions of the training data and then take a weighted majority vote of the sequence of classifiers thus produced). These methods were chosen because of their popularity and ease of interpretation.

Parsimonious diagnostic models based on very few relevant features were obtained after data preprocessing, dimensionality reduction, and model learning. The features chosen as part of the most discriminative subset for each model were then traced back to metabolites that are known to appear in the chemical shift range corresponding to the regions that were identified. These metabolites correspond to the best set of discriminatory features and their in vivo acquisition would be beneficial for assessing glioma grade non-invasiveley.

4.4. Validation

For classification problems, it is natural to measure a classifier’s performance in terms of the accuracy. The classifier predicts the class of each instance: if it is correct, it is counted as a success; if not, it is an error. The accuracy is just the proportion of correct classifications over a whole set of instances, and it measures the overall performance of the classifier. The classifier’s likely future performance on new data is, of course, more interesting than its past performance on old data. To predict the performance of the classifier on new data, the classification accuracy needs to be assessed on a test set that played no role in the formation of the classifier. When a large amount of data is available, a model can be learned based on a large training set, and evaluated based on another large test set. Once the accuracy has been determined, it is acceptable to produce a final classifier for actual use based on both the training and the test data [63].

When the amount of labeled data is limited, the question becomes how to make the most of the limited data set. From this dataset, a certain amount is held out for testing, and the remaining is used for training. The more data are used for the training, the better the classifier. The more data are used for testing, the better the accuracy estimate. Cross-validation and bootstrapping are techniques for dealing with this dilema. Among these, bootstrapping is probably the evaluation method of choice in most practical limited-data situations [63].

Cross-validation reserves a certain amount of data for testing and uses the remainder for training, but in order to mitigate any bias caused by a particular set being chosen for holdout, the whole process is repeated, training and testing, several times, with different random samples. The initial data set is split into a fixed number of partitions, or folds. Each partition is in turn used for testing while the remainder of the data is used for training. The accuracy estimates obtained during the different iterations are averaged to yield the overall accuracy. Leave-one-out is a special case of cross-validation, in which each fold contains only one data sample; thus one sample is in turn held out for testing, while the rest of the data is used for training. This procedure is attractive because it uses the greatest possible amount of data in each case, and no random sampling is involved. Thus, leave-one-out offers the chance to make the most out of a small data set and to obtain as accurate an estimate of the classifier’s performance on unseen data as possible [63].

Cross-validation methods provide unbiased, but high variance estimates of a classifier’s prediction accuracy. This means that if the whole validation process were to be repeated, cross-validation estimates could vary significantly. Bootstrapping, on the other hand, provides nearly unbiased estimates of the prediction accuracy that are relatively low in variance, by repeating the validation process several times on different samples of the data, thus also avoiding overfitting. Bootstrapping is based on the statistical procedure of sampling with replacement. The data set is sampled with replacement to form a training set. For this, a data set with N instances is sampled N times, with replacement, to give another data set of N instances. Because some elements in this second data set will very likely be repeated, there must be some instances in the original data set that have not been picked - the test instances. For a reasonably large data set, the test set will contain about 36.8% of the instances, and the training set will contain about 63.2% of them [63], leading to the name 0.632 bootstrapping. Some instances will be repeated in the training set, bringing it up to a total size of N, which is the same as the original data set. The accuracy estimate obtained by training a classifier on the training set and calculating its accuracy on the test set will be a pessimistic estimate of the true prediction accuracy of a model on new data drawn from the sampling distribution, because even though the training set has size N, it only contains 63.8 % of the original data, which is far less than the amount used in leave-one-out cross-validation. To compensate for this, the accuracy on the test sample is combined to that of the training sample, to give an unbiased estimate of the overall accuracy:

$$\mathit{\text{accuracy}}=0.632\times {\mathit{\text{accuracy}}}_{\mathit{\text{test}}}+0.368\times {\mathit{\text{accuracy}}}_{\mathit{\text{training}}}.$$ (1)

Then, the whole bootstrap procedure is repeated several times, with different replacement samples for the training set, and the results are averaged.

The bootstrap procedure offers the best way to estimate prediction accuracy for very small data sets [63]. The estimate of the accuracy represents an unbiased estimate of the performance of the classifier on new data drawn from the sampling distribution [63]. However, before a model can be used with confidence in clinical practice, it is necessary to validate it on a completely independent data set, because the sampling distribution may not always accurately summarize the population distribution.

In this study, both leave-one-out cross-validation and 0.632 bootstrapping with 200 repetitions [64] were used in order to evaluate the ability of the pattern recognition methods employed to generalize to unseen examples drawn from the sampling distribution. The pseudo-code for these methods is provided in Algorithms 1 and 2. Thus, the data set given as input to these algorithms contains 53 samples. The cross-validation algorithm calls Algorithm 3 using only 52 of the original samples each time. The bootstrapping algorithm calls Algorithm 3 using 53-sample data sets obtained by resampling the original data set. Algorithm 3 calls the wrapper-search algorithm (Algorithm 5) using the reduced or resampled data set. The wrapper-search algorithm, in turn, calls the cross-validation or bootstrapping algorithms respectively in the Evaluate step, thus ensuring that all of the prediction accuracy estimates are based on data that was left out during the model building.

Algorithm 1.

Leave-One-Out Cross-Validation(D)

Require: D = {(x1, y1), … (xN, yN)}

1: for i = 1 to N do

2:    Di ← D{(xi, yi)}.

3:    Mi ← BuildModel(Di)

4:    errori ← |Mi(xi) − yi|

5: end for

6: return $\mathit{\text{accuracy}}=1-\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\mathit{\text{error}}}_i$

Algorithm 2.

Bootstrapping(D)

Require: D = {(x1, y1), … (xN, yN)}

1: for i = 1 to N do

2:  for b = 1 to NFOLDS do

3:    Si ← Resample(D)

4:    errorb = 0

5:    totalb = 0

6:    if (xi, yi) ∉ Si then

7:      Mi,b ← BuildModel(Si)

8:      errori,b ← |Mi,b(xi) − yi|

9:      errorb ← errorb + errori,b

10:      totalb ← totalb + 1

11:      errorb ← errorb/totalb

12:    end if

13:  end for

14: end for

15: ${\mathit{\text{accuracy}}}_b\leftarrow 1-\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\mathit{\text{error}}}_b$

16: M ← BuildModel(D)

17: ${\mathit{\text{accuracy}}}_t\leftarrow 1-\frac{1}{N}{\displaystyle \sum _{i=1}^N}|M(x_i)-y_i|$

18: return accuracy ← 0.632 × accuracyb + 0.368 × accuracyt

Algorithm 3.

BuildModel(S)

Require: S = {(x1, y1), … (xK, yK)}

1: S′ ←Filter(S)

2: S* ←WrapperSearch(S′).

3: M ← TrainClassifier(S*)

4: return M

Algorithm 5.

WrapperSearch(S*)

Require: S = {(x1, y1), … (xK, yK)}

1: i ← 0

2: while Stopping criterion not met do

3:    Si = Generate Feature Subset(S)

4:    accuracyi = Evaluate(Si)

5: end while

6: return ${\mathit{\text{argmax}}}_{S_i=\{(x_1^{\prime },y_1)\dots (x_K^{\prime },y_K)\}}\{{\mathit{\text{accuracy}}}_i\}$

5. Results

5.1. Classification

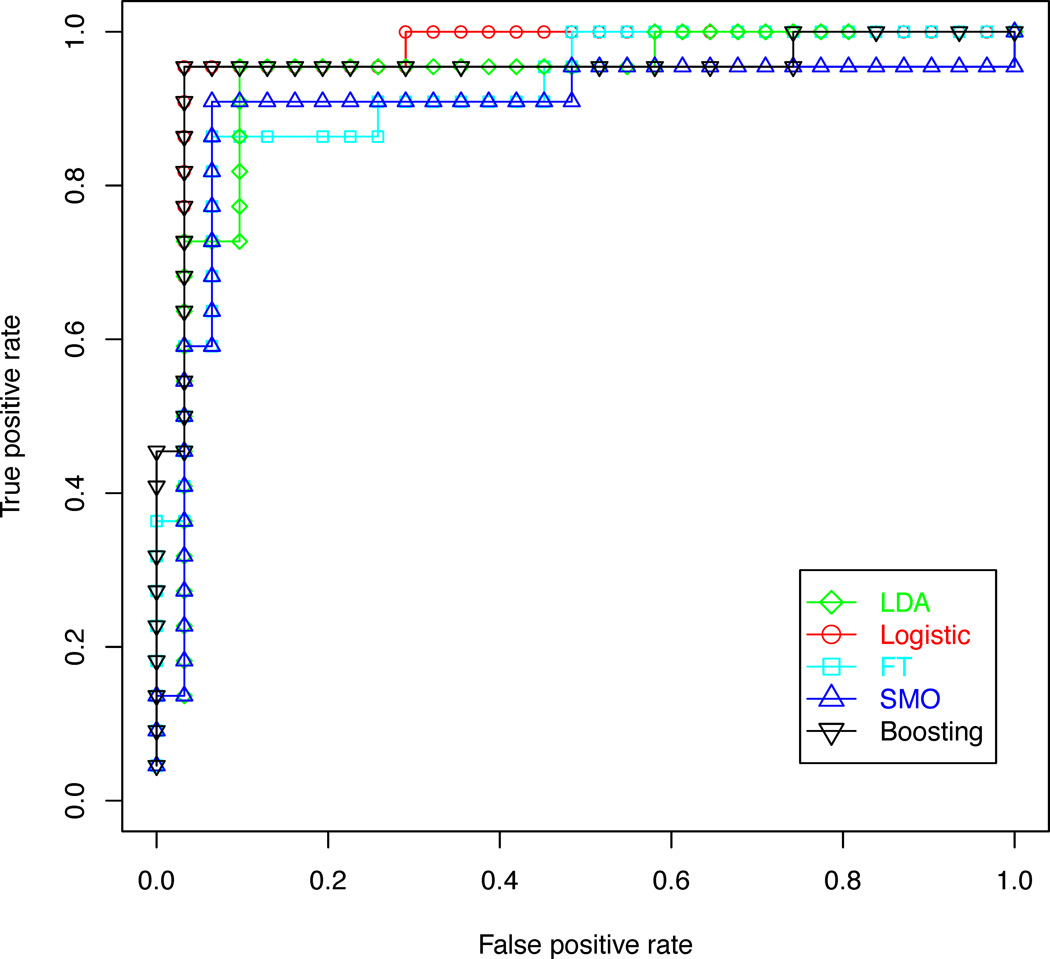
In order to determine whether quantitative metabolic parameters derived from HRMAS data are predictive of malignant transformations in recurrent low grade gliomas, the performance of diagnostic models for distinguishing between patients with recurrent gliomas that transformed to a higher grade and those that remained grade 2 were compared. The results of this analysis are illustrated in Tables 2 and 3. Logistic regression and decision stump boosting models were able to distinguish between recurrent gliomas that transformed to a higher grade and those that did not with 100% training accuracy, 96% leave-one-out cross-validation accuracy, and 96% bootstrapping accuracy. Linear discriminant analysis, functional trees and support vector machines were able to achieve leave-one-out cross-validation accuracy above 90% and bootstrapping accuracy above 85%. The three feature ranking methods were comparable in performance. The pattern recognition methods for this classification task were further compared using a plot of precision and recall, illustrated in Figure 4, and receiver operating characteristic (ROC) curves, illustrated in Figure 5. These curves show that the five classification methods are comparable, but the logistic regression and decision stump boosting methods have a slight advantage. The difference in performance between logistic regression and decision stump boosting and the other three methods is statistically significant, as can be seen from the non-overlapping 95 % confidence intervals of the bootstrapping accuracy presented in Table 3.

Table 2.

Accuracy for distinguishing between recurrent low grade gliomas which transformed to a higher grade and those that did not using five classifiers trained on HRMAS features selected using three feature selection methods.

Accuracy	Features	LDA	Logistic	FT	SVM	Boosting
Training	Chi-square Gain ratio Conditional	0.93 0.85 0.94	1.00 1.00 1.00	0.93 0.93 0.92	0.94 0.94 0.94	1.00 1.00 0.98
Cross-Valid	Chi-square Gain ratio Conditional	0.94 0.93 0.98	0.94 0.96 0.91	0.91 0.91 0.93	0.94 0.93 0.94	0.96 0.94 0.91
Bootstrap	Chi-square Gain ratio Conditional	0.87 0.84 0.89	0.96 0.96 0.95	0.89 0.89 0.89	0.85 0.83 0.83	0.96 0.94 0.94
ROC AUC	Chi-square Gain ratio Conditional	0.94 0.99 1.00	0.9 1.00 0.99	0.95 1.00 1.00	0.92 1.00 0.99	0.94 1.00 0.97
Precision	Chi-square Gain ratio Conditional	0.92 0.98 0.99	0.92 1.00 0.98	0.90 0.99 0.99	0.92 1.00 0.99	0.90 0.99 0.98
Recall	Chi-square Gain ratio Conditional	0.91 0.98 0.99	0.92 1.00 0.98	0.9 0.99 0.99	0.92 1.00 0.99	0.90 0.99 0.98
F Measure	Chi-square Gain ratio Conditional	0.91 0.98 0.99	0.92 1.00 0.98	0.9 0.99 0.99	0.92 1.00 0.99	0.90 0.99 0.98

Table 3.

95% confidence intervals for accuracy results (presented in Table 2) for distinguishing between recurrent low grade gliomas which transformed to a higher grade and those that did not using five classifiers trained on HRMAS features selected using three feature selection methods.

Accuracy	Features	LDA	Logistic	FT	SVM	Boosting
Training	Chi-square Gain ratio Conditional	0.82–0.98 0.72–0.93 0.84–0.99	0.93–1 0.93–1.00 0.93–1.00	0.84–0.99 0.84–0.99 0.82–0.99	0.84–0.99 0.84–0.99 0.84–0.99	0.93–1.00 0.93–1.00 0.90–1.00
Cross-valid	Chi-square Gain ratio Conditional	0.84–0.99 0.82–0.98 0.90–1.00	0.84–0.99 0.87–1.00 0.79–0.97	0.79–0.97 0.79–0.97 0.82–0.98	0.84–0.99 0.82–0.98 0.84–0.99	0.87–1.00 0.84–0.99 0.79–0.97
Bootstrap	Chi-square Gain ratio Conditional	0.86–0.88 0.83–0.85 0.88–0.90	0.95–0.97 0.95–0.97 0.94–0.96	0.88–0.90 0.88–0.90 0.88–0.90	0.84–0.86 0.82–0.84 0.82–0.84	0.95–0.97 0.93–0.95 0.93–0.95
ROC AUC	Chi-square Gain ratio Conditional	0.88–1.00 0.96–1.00 1.00–1.00	0.82–0.98 1.00–1.00 0.96–1.00	0.89–1 1.00–1.00 1.00–1.00	0.85–0.99 1.00–1.00 0.96–1.00	0.88–1.00 1.00–1.00 0.93–1.00
Precision	Chi-square Gain ratio Conditional	0.78–0.98 0.89–1.00 0.89–1.00	0.78–0.98 0.89–1.00 0.89–1.00	0.74–0.98 0.89–1.00 0.89–1.00	0.78–0.98 0.89–1.00 0.89–1.00	0.74–0.98 0.89–1.00 0.89–1.00
Recall	Chi-square Gain ratio Conditional	0.71–0.99 0.85–1.00 0.85–1.00	0.77–0.99 0.85–1.00 0.85–1.00	0.71–0.97 0.85–1.00 0.85–1.00	0.77–0.99 0.85–1.00 0.85–1.00	0.71–0.97 0.85–1.00 0.85–1.00
F measure	Chi-square Gain ratio Conditional	0.75–0.99 0.87–1.00 0.87–1.00	0.78–0.99 0.87–1.00 0.87–1.00	0.72–0.98 0.87–1.00 0.87–1.00	0.78–0.99 0.87–1.00 0.87–1.00	0.72–0.98 0.87–1.00 0.87–1.00

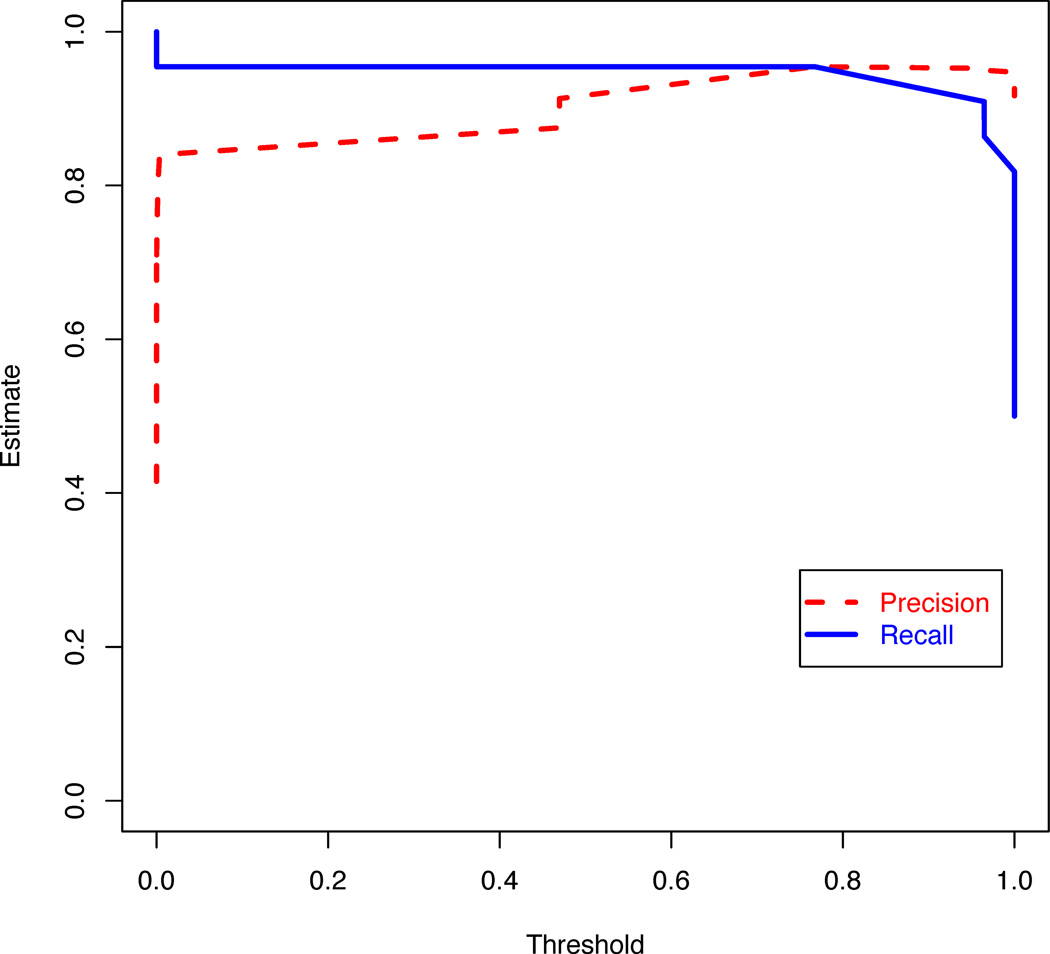
Figure 4.

Plot of specificity and sensitivity for different thresholds of the logistic regression model with features selected using the gain ratio filter and a genetic search wrapper-based method. The response variable is whether the tumor transformed to a higher grade or not.

Figure 5.

ROC curves comparing five classification methods used to distinguish between gliomas that transformed to a higher grade and those that did not, based on features selected using the gain ratio filter and a genetic search wrapper-based method.

An additional validation experiment was performed in order to address the concern that the high classification accuracies obtained may be due to overfitting caused by the large number of features explored. Transformed/not transformed labels were randomly assigned to the HRMAS spectra, and bootstrapping accuracy results were obtained using the same methods that generated the best model in the previous analysis. Logistic regression models were built based on the data with random labels. The features were filtered using information gain ratio. The best subset of features was then selected using a genetic wrapper-based search. The experiment was repeated one hundred times, for different random generations of the labels. The average bootstrapping classification accuracy was 63% with a 95% confidence interval of [49%–77%] (range 42%–81%), significantly lower and more variable than the 96% bootstrapping accuracy with a 95% confidence interval of [95%–97%], obtained using the true labels. The random labels of the data sets that resulted in bootstrapping accuracies in the high end of the range actually had a significant number of labels that matched the true labels.

In order to assess the ability to distinguish between different degrees of disease malignancy based on HRMAS data, two other comparisons were performed. Statistical models were built to distinguish between recurrent low grade gliomas that upgrade to grade 3 and those that remained grade 2 (100% training accuracy, 96% cross-validation and bootstrapping accuracy), and between recurrent low grade gliomas that transformed to grade 4 and those that transformed to grade 3 (100% training accuracy, 98% cross-validation and bootstrapping accuracy). These comparisons also show a slight advantage when using logistic regression and decision stump boosting.

Overall, the results suggest that metabolic parameters derived from HRMAS are predictive of malignant transformations in low grade gliomas. Models that were built based on these parameters are specific and sensitive enough to be used for diagnosing individual patients, and do not merely reflect average differences between different patient groups. All classification and feature selection methods exhibit good performance, with logistic regression and decision stump boosting slightly outperforming the other classification methods.

5.2. Feature selection results

Although the direct identification of metabolites that are predictive of malignant transformations is not necessary to distinguish those patients who exhibit malignant transformations, analyzing the different metabolites that lead to high classification accuracy can lead to the detection of metabolic biomarkers and to the better understanding of tumor metabolism. Thus, one of the goals of this study was to model the metabolic transformations in gliomas in such a way that the results are easy to interpret biologically, and able to inform in vivo data acquisition. To this effect, feature selection results are presented. The features in this study represent normalized concentrations found in small chemical shift ranges. In order to interpret these features, their chemical shift ranges were linked to metabolites typically found in those spectral regions using the QUEST [49] quantification algorithm.

There was significant overlap in the forty highest-ranking features selected using the chi-squared statistics, the information gain ratio, and the conditional probability-based association techniques. These features corresponded to nine metabolites, listed in Table 5. The highest-ranking of the forty features were very similar across the three measures, even though the ranks differed slightly. Parameters corresponding to My-I, 2HG, Hyp-Tau, and Cho compounds were identified among the forty highest-ranking features by all three association techniques, while parameters corresponding to GSH and Ala were identified only by some of the methods.

Table 5.

Abbreviations for metabolites found to be useful in detecting malignant transformations in recurrent low grade gliomas.

Abbreviation	Metabolite
My-I	myoinositol
2HG	2-hydroxyglutarate
Hyp-Tau	hypo-taurine
Cho	choline
PC	phosphocholine
GPC	glycerophosphocholine
Lip	lipid
GSH	glutathione
Ala	alanine

Table 4 shows the percentage of times each metabolite was identified by the logistic regression genetic search wrapper-based feature subset selection algorithm as being part of the feature subset which was best at discriminating between tumor grades, during the bootstrapping process. Thus, for each comparison, up to 200 models were built on resampled versions of the original data set, and the percentage of times certain features were selected as part of these models is reported in Table 4, grouped by corresponding metabolite.

Table 4.

Percentage of time each feature was selected in one of the models for distinguishing between low grade tumors that recurred at different grades.

Metabolite		Transformed vs. not			Transf. to grade 3 vs. 2			Transf. to grade 4 vs. 3
Name	Range	Gain ratio	Chi-sq.	Cond.	Gain Ratio	Chi-sq.	Cond.	Gain ratio	Chi-sq.	Cond.
My-I	3.51–3.54 3.61–3.68	100% 96%	13% 94%	78% 85%	75% 15%	48% 0%	76% 0%	33% 0%	0% 0%	0% 0%
2HG	1.75–1.87 2.24–2.3	100% 70%	78% 92%	63% 87%	26% 67%	80% 89%	54% 28%	21% 0%	64% 0%	48% 0%
Hyp-Tau	2.62–2.69 3.35–3.39	57% 95%	99% 99%	77% 63%	75% 95%	100% 33%	100% 45%	100% 67%	94% 73%	100% 9%
Cho/PC/GPC	3.21–3.29 3.69–3.71	96% 0%	100% 53%	100% 48%	78% 26%	100% 100%	100% 50%	0% 0%	75% 0%	15% 0%
Lip	0.96–1.00	100%	19%	100%	89%	0%	65%	0%	0%	0%
GSH	3.79–3.81	0%	97%	36%	100%	15%	100%	100%	78%	100%
Ala	1.4–1.5	0%	17%	0%	0%	57%	0%	88%	0%	3%

Distinguishing between recurrent low grade gliomas that transformed to a higher grade and those that remained grade 2 was possible using areas of the ex vivo NMR spectrum corresponding to myoinositol (My-I), 2-hydroxyglutarate (2HG), hypo-taurine (Hyp- Tau), choline (Cho), glycerophosphocholine (GPC), phosphocholine (PC), glutathione (GSH), and lipid (Lip). The abbreviations used in the table are linked to their corresponding metabolites in Table 5. On average, the relative levels of My-I parameters were 56% lower in gliomas that transformed to a higher grade compared to those that remained grade 2. The gliomas that transformed to a higher grade also had 2HG levels in the [2.24–2.3] chemical shift range that were 120% higher, 2HG levels in the [1.75–1.87] range that were 30% higher, Hyp-Tau levels in the [2.62–2.69] range that were 137% higher, Hyp-Tau levels in the [3.35–3.39] range that were 57% higher, Cho compound levels in the [3.21–3.29] range were 26% higher, Cho compound levels in the [3.69–3.71] range were 83% higher, Lip levels that were 53% higher, GSH levels that were 39% higher, and Ala levels that were 25% higher.

Distinguishing between recurrent low grade gliomas that transformed to grade 4 and those that recurred as grade 3 was possible using features corresponding to Hyp-Tau, GSH, alanine (Ala), and Cho. Another predictive feature shows increased activity in the 3.79 chemical shift range, where metabolites are very hard to quantify. Levels of Hyp-Tau, GSH, Cho, My-I, and 2HG were useful in distinguishing between gliomas that transformed to grade 3 and those that remained grade 2.

While some of the differences in metabolite levels between tumors that transformed to a higher grade and those that remained grade 2 are very large, individual metabolites are not sensitive or specific enough to distinguish between the two groups of lesions. Pattern recognition methods were able to objectively combine the information provided by all of these metabolites into a model that can accurately identify lesions that have undergone malignant transformations.

6. Discussion

The methods presented in this study were able to accurately detect malignant transformations in recurrent low grade gliomas based on small sets of metabolites, without any prior knowledge. While the bootstrapping accuracies of the models created are very promising, the confidence in the models could be further strengthened by performing validation on an independent data set.

Distinguishing between low grade gliomas that recurred at different grades was possible based on features corresponding to My-I, 2HG, Hyp-Tau, Cho compounds, GSH, Lip, and Ala. The fact that some features were selected in very different percentages of the models when using different filtering methods shows that that the features are highly correlated. Including all of these features in a model would be superfluous. In fact, the models created during the bootstrapping phase were based on three to eight features each. This also explains why some metabolites identified as important biomarkers in the literature were not selected as features in these models. There are two reasons why a feature may not be selected by the algorithm: either because it is not well correlated with the outcome, or because it is highly correlated with some of the other features already in the model and it does not provide any additional information for the classification. Thus, the features identified by the pattern classification methods are a parsimonious set of metabolites that are specific and sensitive enough to lead to a quantitative formula that can be used to diagnose individual patients and can be applied to unseen data.

This analysis identified 2HG as a metabolite whose increased concentration is highly predictive of malignant transformations in recurrent low grade gliomas, but whose concentration is generally low in newly diagnosed grade 4 gliomas. Recent studies have demonstrated that cancer-associated IDH1 mutations lead to the accumulation of 2HG [65]. These mutations have also been reported in Acute Myeloid Leukemia (AML) [65], suggesting that a common mechanism may underpin both these AML and secondary grade 4 glioma malignancies. These studies offer novel opportunities to develop tumor directed therapeutic strategies.

Several of the metabolites selected by the pattern recognition methods for their discriminative power, such as Cho, Lip, and My-I, can be acquired using current in vivo MRS methods, implying that using pattern recognition methods in conjunction with in vivo spectroscopy may be successful in determining whether patients with recurrent low grade gliomas have transformed to a more malignant phenotype without the need for a tissue diagnosis. Lip, lactate, Cho, NAA and creatine are already being acquired in in vivo patient studies. My-I is one of the most important metabolites in terms of its discriminative power in all of the models explored. This metabolite can be acquired in vivo, and the results in this study lead us to believe that it should be included in future in vivo acquisition protocols.

7. Conclusion

This study demonstrates the feasibility of using quantitative pattern recognition methods for the metabolic assessment of tissue samples obtained from brain tumor biopsies. The findings in this study enhance the knowledge obtained from previous HRMAS and MRS classification studies, because they suggest that it is possible to obtain high classification accuracy by using only a few spectral features obtained without any prior knowledge. The pattern recognition methods described in this paper identified biomarkers of importance in detecting malignant transformations in low grade gliomas. Most of the metabolite parameters revealed by this method can be acquired in vivo. The use of MRS at high magnetic fields and with a robust classification approach should improve the characterization, typing, and prognostication of brain tumors. It can also be applied to assist in stratifying patients for appropriate therapeutic protocols and in the monitoring of new therapies.

Algorithm 4.

Fliter(S′)

Require: S = {(x1, y1), … (xK, yK)}

Require: length(xi) = F

1: for i = 1 to F do

2:    Rank(feature i, S)

3: end for

4: S′ = (Highest Ranked Features(X), Y)

5: return S′