Modeling DNA Double-Strand Break Repair Kinetics as an Epiregulated Cell-Community-Wide (Epicellcom) Response to Radiation Stress

Abstract

The multicellular signaling model (MULTISIG1) was recently introduced to simulate the kinetics of repair of DNA double-strand breaks (DSBs) that were induced in confluent (non-dividing) cultured cells by a very low radiation dose where at most a single induced DSB would be expected in a given cell nucleus. The repair kinetics was modeled as representing what is now called an epigenetically-regulated (epiregulated) cell-community-wide (epicellcom) response to radiation stress. DSB repair initiation is assumed to require a threshold number of cells with DSBs participating in intercellular stress-response signaling. The MULTISIG1 model is extended in this study to apply to moderate doses where several DSBs can occur on the same DNA molecule. The repair of multiple breaks on the same molecule is treated as sequential stochastic events. For cells of differing genetic characteristics and epigenetic statuses, relationships are provided for evaluating the relative susceptibility (RS) for DSB induction, relative repair capacity (RRC) for DSB repair, and relative epiapoptosis capacity (REC), for epigenetically regulated apoptosis. The modified MULTISIG1 model is used to characterize the expected repair kinetics for confluent, human lung fibroblasts (MRC-5 line) briefly exposed in vitro to 90-kV x-rays. Possible application of the model to biological dosimetry is also discussed.

INTRODUCTION

The integrity of the human genome is continuously challenged in our bodies by both endogenous and exogenous DNA damaging agents (Dinant et al. 2008). Ionizing radiation from external and internal sources induces a variety of DNA lesions, among which double-strand breaks (DSBs) are considered the most significant (Asaithamby and Chen 2009). Misrepair of DSB can lead to genomic instability, mutations, neoplastic transformation, and cancer (Tan 1991; Ganesh et al. 1993; Löbrich et al. 1995; Scott 2005; Scott et al. 2009; Falk et al. 2010). Thus, considerable research has been conducted related to understanding DNA DSB repair signaling pathways and how they are influenced by exposure to radiation and other genotoxic agents (Jeggo 1998; Löbrich et al. 2000; Daboussi et al. 2002; Rothkamm and Löbrich 2003; Rothkamm et al., 2003, 2007; Ishizaki et al. 2004; Kühne et al. 2004; Kohn and Prommier 2005; Löbrich et al. 2005; Ataian and Krebs 2006; Bouquet et al. 2006; Friedberg et al. 2006; Hamada et al. 2006; Han et al. 2007; Prise et al. 2007; Qi et al. 2007, 2008; Wei et al. 2007; Escargueil et al., 2008; Haley et al. 2009; Dickey et al. 2009; Grudzenski et al. 2010; Wilson et al., 2010). DNA damage signaling appears to be essential for coordinating DSB repair pathways with their associated cell cycle and apoptosis regulatory pathways (Daboussi et al. 2002).

Multiple pathways have evolved for repairing DSBs, the most important which are as follows: homologous recombination (HR), single strand annealing (SSA) and nonhomologous end joining (NHEJ). With the HR pathway, repair is achieved by retrieving genetic information from an undamaged homologue (sister-chromatid or homologous chromosome), and this requires DNA sequence homology. For the SSA pathway, repair is achieved through annealing of complementary sequences on both sites of the break (mostly repetitive sequences) and thus also needs the presence of DNA sequence homology. For the NHEJ pathway, repair is achieved via direct ligation of the DNA ends without any requirement for sequence homology. While HR ensures essentially error-free repair, NHEJ is almost always mutagenic due to misrepair (Dudáš and Chovanec 2004). Possibly, many of the mutations are silent (i.e., do not cause a change in the sequence of amino acids encoded by a gene) (Conrad et al. 1983; Gorlov et al. 2006).

The indicated repair mechanisms have been conserved through evolution and therefore operate in a wide range of organisms, including prokaryotes and eukaryotes (Dudáš and Chovanec 2004). In somatic cells of mammals in the G1 phase, DSBs are repaired via NHEJ. HR occurs mainly in the late S/G2 phases (Anderson et al. 2010).

Mansour et al. (2008) have proposed a hierarchical DSB repair model which is dominated by the protein Ku80. Because of its abundance and high affinity, Ku80 occupies all DNA ends and initiates high fidelity end-joining. Without Ku80, NHEJ shifts to an error-prone mode, which either relies on the remaining NHEJ core proteins or involves and alternative end-joining pathway. Further, homology-mediated recombinational repair pathways (SSA and gene conversion [HR]) can partly substitute for NHEJ and rescue repair proficiency. According to Mansour et al. (2008), the available data imply that the most mutagenic repair pathway (SSA) is the least desirable option for the cell, because it is suppressed by both Ku80 and Rad51.

An important step during the cellular response to radiation induced DSBs is the phosphorylation of the nuclear-DNA-associated histone H2A variant (H2AX) at the break site, giving rise to discrete nuclear γ-H2AX foci that can be detected. The dissolution of the foci over time is considered to reflect the associated DNA repair kinetics since a one-to-one relationship between the γ-H2AX foci and DSBs has been established (Rothkamm and Löbrich 2003). This has allowed use of the kinetics of γ-H2AX foci dissolution to evaluate DNA DSB repair kinetics. The DNA DSB repair kinetics simulated in this paper is based on in vitro studies of the temporal variation of γ-H2AX foci per surviving cell after x-ray exposure.

In a separate related paper (Scott 2010), the author introduced the novel systems-biology-related Multicellular Signaling (MULTISIG1) model in which DNA DSB repair kinetics was treated as representing what is now called an epigenetically-regulated cell-community-wide (epicellcom) response to radiation stress. Under the MULTISIG1 model, DNA DSB repair arises as an epicellcom process requiring intercellular stress-response signaling involving a threshold number of cells with DSBs, which occurs only after a threshold absorbed radiation dose T. For in vitro studies of DNA damage response using confluent cells, the threshold absorbed dose for initiating DSB repair as an epicellcom process (i.e., throughout the irradiated cell community) can be evaluated using the following equation (Scott 2010):

$$T=(B_T-B_0)/\alpha .$$ (1)

The parameter α is the slope of the presumed linear-no-threshold (LNT), dose-response function for induced DSBs per surviving cell; B₀ is the spontaneous DSBs per surviving cell (an average) and the parameter B_T is the total (radiation-induced and spontaneous) DSBs per surviving cell (an average) at the threshold absorbed radiation dose T. According to the MULTISIG1 model, B_T also represents the on average residual breaks per cell (asymptotic value at late times) after completion of DSB repair among the cell community and therefore can be estimated from DNA repair kinetics information as is done in this study. Because of the one-to-one relationship between DSB and γ-H2AX foci, the kinetics of the dissolution of the foci can be used to indirectly evaluate DSB repair kinetics (Rothkamm and Löbrich 2003) as already indicated. The observed average spontaneous foci per cell (F₀) estimates B₀ and the minimum (F_min) of the average residual foci per cell tens of hours after radiation exposure estimates B_T.

The MULTISIG1 model was developed for low radiation doses whereby at most a single DSB would be expected to be induced on a given DNA molecule. Because repair of radiation-induced DSB is assumed to represent a Poisson process (Cox and Isham 1980; Ross 1995), an exponential distribution of post irradiation repair times (after brief exposure at a high rate) was employed with the mean time to repair a DSB given by the dose-independent parameterβ (Scott 2010). The exponential distribution allows for fast, intermediate and slow repair events even though data for individual DSB repair times are not available. The average repair rate per break is given by μ = 1/β and the repair halftime (for break rejoining) is given by 0.6931β.

For moderate and high radiation doses, multiple breaks can occur on the same DNA molecule, with breaks over the DNA molecules among the target cell population assumed to have a Poisson distribution (Scott 2010). Analytical solutions are provided below for the expected DNA DSB repair kinetics when n DSBs (spontaneous and radiation-induced) are present on a given DNA molecule in the cell nucleus shortly after a radiation dose D > T to confluent cells in culture. The solutions apply to brief high-dose-rate exposure. For D ≤ T, an LNT function with spontaneous (B₀) and radiation-induced breaks (α D) per cell is used to be consistent with notation used elsewhere (Scott 2010).

The fraction of cells with persistent residual breaks (B_T ≥ B₀) is given here by Y_∞, with the subscript ∞ indicating after a long follow-up time. The distributions of times to DSB repair developed in the following section apply to the proportion of the faction (1 - Y_∞) of the irradiated cells that survive radiation exposure. For the remaining surviving cells (from the Y_∞ fraction), an infinite time to DSB repair completion can be assigned (i.e., incomplete repair).

If cells are allowed to proliferate after developing residual DSBs, some cells with residual breaks may be eliminated via epigenetically regulated apoptosis (epiapoptosis) (Scott et al. 2009), which also is considered an epicellcom process, based on findings of others (Bauer 2007; Portess et al. 2007). The average proportion of cells removed via epiapoptosis can be expressed as a protection factor (PROFAC), which depends on the type of radiation and likely also on the type of cells (Scott 2004, 2005). Intracellular signaling during epiapoptosis involves reactive oxygen and nitrogen species and may involve biological agents such as transforming growth factor beta (Portess et al. 2007) and interleukin-6 (IL-6) (Mariotti et al. 2010).

The LNT damage induction feature of the MULTISIG1 model is used to evaluate the average DSB per DNA molecule (BPM) shortly after brief high dose-rate exposure of confluent cells in culture to low linear-energy-transfer (LET) photon radiation (e.g., x-rays, gamma rays). This average is then used to estimate the number distribution of DSBs over different DNA molecules after irradiation of cells in culture, assuming a Poisson-distribution-related mass function, poisson(n, BPM ), for n breaks per molecule when the average over the irradiation cell population is given by BPM.

POSTULATES RELATED TO THE MULTISIG1 MODEL

The original version of MULTISIG1 model is based on six systems-biology-related postulates (Scott 2010) which have been updated as follows:

• Postulate 1: DSB induction by brief exposure to ionizing radiation at a high rate occurs shortly after radiation energy is deposited in the cells so that the kinetics of DSB production can be ignored when modeling DSB repair kinetics.

• Postulate 2: DSB damage to multiple cells leads to stress-response-related intercellular signaling with an intensity that depends on the number of cells with DSBs.

• Postulate 3 (epicellcom response initiation): The required signaling intensity for triggering cell-community-wide up-regulation of DNA DSB repair genes after exposing cells to ionizing radiation occurs only when a threshold number of cells have DSBs (which occurs at absorbed dose T).

• Postulate 4 (epicellcom response implementation): Epigenetic changes (epiactivation of stress-response genes) occur shortly after the threshold dose for DSB repair is delivered, facilitating DNA damage repair, which occurs at a constant cell-genetic-characteristics- and epigenetic-status-based rate for a given break as long as DSB repair genes remain up-regulated.

• Postulate 5 (epicellcom response termination): After DSB repair has been ongoing among damaged cells for a period of time, stress signaling intensity among cells declines proportionally to the decline in cells with DSBs, and DSB repair genes are down-regulated (silenced) via epigenetic changes (or other mechanisms) when the number of cells with DSB falls just below the number associated with the threshold dose T for initiating cell-community-wide DSB repair.

• Postulate 6: DNA DSBs (spontaneous and radiation induced) have a dose- and time-dependent Poisson distribution after low to moderate doses of ionizing radiation and when the average number of breaks/cell < 4.0, most cells do not have more than 1 DSB on a given nuclear DNA molecule.

The dose- and time-dependent functions presented in the next section are based on the above postulates. The details of intercellular and intracellular signaling related to DSB repairs are not modeled. Rather, the complex signaling and related biological changes are presumed to lead to the DSB repair (for a given damaged molecule) as a Poisson Process. This implicates an exponential distribution of times for repairing DSBs when only one break occurs on a given molecule, as already indicated. For sequential repairs of multiple breaks on the same molecule, the expected distribution of the times to repair completion (for all breaks on a molecule) can be calculated as demonstrated in the section on Dose-and Time-Dependent Functions.

EPICELLCOM-PROCESS-RELATED INTERCELLULAR SIGNALING

Clues about potential intercellular signaling pathways and signaling agents related to DNA DSB repair as an epicellcom process can be obtained from the literature on stress-response-related, cell-to-cell communications and radiation bystander effects (Leach et al. 2001; Burdak-Rothkamm et al. 2008; Mariotti et al. 2010). Bystander effects occur in unirradiated cells that are close to irradiated cells (Mothersill and Seymore 2002; Hall 2003). In the context of evaluating DNA DSBs as an epicellcom process, references to bystander effects relate to circumstance where many cells have radiation hits but some nearby cells are not hit and communications between hit and un-hit cells occurs, thus being essentially a cell-community-wide phenomenon.

It is likely that multiple signaling pathways are involved in bystander effects as has been found for apoptosis of transformed cells resulting from intercellular communications between transformed and non-transformed cells (Bauer 2007; Portess et al. 2007). Constitutive nitric oxide has been proposed (Hei et al. 2008) to have an essential early signaling roll for communications between cells hit by radiation and bystander un-hit cells that develop DSBs. The detection of DSBs in the bystander cells has been based on markers such as γ-H2AX.

A unifying conceptual bystander signaling model was proposed by Hei et al. (2008) and is summarized here. After radiation exposure, expression/secretion of inflammatory cytokines increase (a stress response). Membrane-associated or secreted forms of cytokines (e.g., tumor necrosis factor α [TNFα]) activate IκB kinase (IKK)-mediated phosphorylation of IκB, which then causes the release of nuclear factor (NF)-κB. NF-κB enters the nucleus and functions as a transcription factor for the COX-2 gene and the inducible nitric oxide (NO) synthase (iNOS) gene. TNFκ also activates mitogen activated protein (MAP) kinases pathways (extracellular signal related kinase (ERK), c-Jun N-terminal kinase (JNK) and p38) which through the activation of protein (AP)-1 transcription factor, also up-regulate expression of COX-2 and iNOS, which then stimulates production of NO. Mitochondrial damage facilitates the production of hydrogen peroxide (H₂O₂) (Leach et al. 2001), which migrates freely across plasma membranes and is subjected to antioxidant-based elimination. Because H₂O₂ has a relatively long half-life compared to other reactive oxygen and nitrogen species, it may have an important role in long-distance (several cell diameters) communications between cells.

Other signaling agents that may participate in the bystander signaling include the following (Hei et al. 2008): interleukins (IL-1, IL-8), peroxynitrite anions (ONOO-), prostaglandin E2, transforming growth factor beta, and TNF-related apoptosis-inducing ligand (TRAIL). In the conceptual model of Hei et al. (2008), activation of COX-2 provides a continuous supply of reactive radicals and cytokines for the propagation of intercellular signaling to bystander cells. The signaling can be either via gap junctions or the medium. The pathways and signaling agents may be involved in DNA DSB repair when it occurs as a community wide phenomenon (i.e., the presumed epicellcom process).

Given the complexities of the intercellular signaling pathways between hit and bystander cells and the resulting cellular responses, it is reasonable to assume that the time to occurrence of DSB repair is stochastic and reflective of a Poisson process. A Poisson process is a stochastic process in which statistically independent events occur continuously. While a deterministic (i.e., fixed) time to repair completion could be more easily modeled, it is not considered a plausible model given observed DNA DSB repair kinetics profiles. A distribution of time to repair completion is implicated rather than a single fixed (deterministic) time.

DOSE- AND TIME-DEPENDENT FUNCTIONS

Induced Double Strand Breaks per Cell and per DNA Molecule

For cells exposed to a low, moderate, or high radiation doses delivered at a high rate in a short time, DNA DSB induction is modeled as being an LNT function of the radiation dose (called specific energy z) to the cell’s nucleus. The dose z to the microscopic-sized nucleus is called a microdose. The expected yield B(z) of DSBs per cell, given specific energy z to the cell nucleus, is given by (Scott 2010):

$$B(z)=B_0+\alpha z.$$ (2)

Because z is stochastic (i.e., has a probability distribution), one has to evaluate the expectation (average) value of B(z) over the probability distribution for z. Because the expectation value for z is identical to the macroscopic absorbed dose D (radiation energy deposited per unit mass of the biological target) (Feinendegen et al. 2007), Equation 2 can be replaced with the following equation (Scott 2010):

$$B(D)=B_0+\alpha D.$$ (3)

Equation 3 represents the average number of DSBs per surviving cell shortly after exposing a population of homogeneous confluent cells (e.g., in culture) to an ionizing radiation absorbed dose D delivered at a high rate and is the basis for Equation 1. Fluctuations in B(D) as measured in experimental data will in part relate to variability in z. For D > T, Equation 3 can be re-expressed as follows (Scott 2010):

$$B(D)=B_T+\alpha (D-T).$$ (4)

B_T equals B₀ + α T. According to the MULTISIG1 model, the threshold T is associated with an epicellcom adaptive response to radiation stress and is evaluated as indicated in Equation 1. For confluent human cells in culture, each which has m = 46 DNA molecules (same as the number of chromosomes) per cell nucleus, the corresponding equation for the average BPM (breaks per molecule) among the m molecules in a cell nucleus is given by:

$$\mathit{BPM}(D)=(B_T/m)+\alpha (D-T)/m.$$ (5)

The term B_T/m is the average DSB per DNA molecule (spontaneous and radiation-induced) in a cell nucleus at the threshold dose T for activating DSB repair and the remaining term is the average radiation-induced DSB per DNA molecule in a cell nucleus induced by the excess dose, D - T, above T. The distribution of DSBs among different DNA molecules can be evaluated using the Poisson probability mass function poisson(j, BPM(D)) with mean BPM(D) and j DSBs on the same molecule. The indicated function can be evaluated in Excel using the function POISSON(j, k, false), with k set equal to BPM(D). The term false informs Excel to return the probably mass for j events when the population mean is k. For example, the assignment POISSON(4, 1, false) for 4 DSB on a DNA molecule in the nucleus when the average is 1 break per molecule over the irradiated cell population returns the frequency 0.0153 (rounded) for exactly 4 DSB on the same DNA molecule.

For the fraction of nuclear DNA molecules with exactly 1 DSB at the beginning of the infinitesimal post-irradiation time interval (t, t + dt), the expected fractional (differential) repair completions per unit time is given by the exponential distribution function (Scott 2010):

$${\varphi }_1(t)=[\text{exp}(-t/\beta )]/\beta .$$ (6)

As already indicated, β is the average time for repairing (rejoining) a DSB. The distribution in Equation 6 allows for a wide range of repair times. For n ≥ 2 breaks on a given DNA molecule in the nucleus, the corresponding distribution function ϕ_n (t) can be obtained via evaluating the following convolution relationship:

$${\varphi }_n(t)=\underset{0}{\overset{t}{\int }}{\phi }_1(\tau ){\phi }_{n-1}(t-\tau )d\tau .$$ (7)

Analytical solutions are provided below for some useful endpoints related to the repair of multiple DSB on the same DNA molecule.

Distribution Function for Repairing n Breaks per DNA Molecule

The analytical solution for Equation 7 is as follows (a gamma distribution):

$${\varphi }_n(t)=\frac{{(\beta )}^{-n}{t}^{n-1}}{(n-1)!}\text{exp}(-t/\beta ).$$ (8)

The solution applies for n = 1, 2, ... Model parameters (B₀, B_T, α, β) can be estimated from γ-H2AX dissolution kinetics data as summarized in Table 1.

TABLE 1.

Estimates of MULTISIG1 model parameters, variables, and functions based on data for γ-H2AX foci per cell.^a

Parameter, Variable, or Function	Estimate
RB(t, D)	Ft: experimentally determined average residual γ-H2AX foci per cell at time t after exposure to dose D
BT	Fmin: minimum of measured values for average γ-H2AX foci per cell at late times after exposure when repair is completed
α	Calculated slope of the dose-response curve for average γ-H2AX foci per cell obtained shortly after exposure (before repair occurs)
B0	F0: observed average spontaneous γ-H2AX foci per cell
T	d = (Fmin- F0)/slope
β	b = - t / ln{(Ft– Fmin) / [slope (D - d)]}
μ	b−1
Repair halftime	b ln (2)

^aEstimates of model parameters can also be obtained by fitting the MULTISIG1 model to dose-response data for γ-H2AX foci per cell using a Bayesian approach.

For confluent human-derived lung fibroblasts (MRC-5) exposed to 90-Kv x-rays (study by Rothkamm and Löbrich 2003), T has been estimated to be 1.4 mGy (Scott 2010), a dose associated with on average, about 1 electron track (from ionizations) per cell nucleus. B_T has been estimated to be 0.1 break per cell, based on the asymptotic value for residual γ-H2AX foci per cell (F_min in Table 1) reported by Rothkamm and Löbrich (2003) and they also reported an estimate of 0.035/mGy for the slope α of the dose-response curve for induced foci per cell. The average time to repair a single DSB (on a given molecule) for the indicated cell culture assay has been estimated to be β =2.5 h (Scott 2010), assuming an exponential distribution ϕ₁(t) for the repair times for single DSB breaks per cell. The indicated estimate is based on γ-H2AX foci dissolution data (Rothkamm and Löbrich 2003).

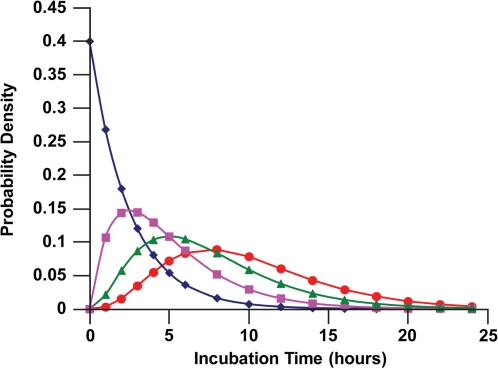
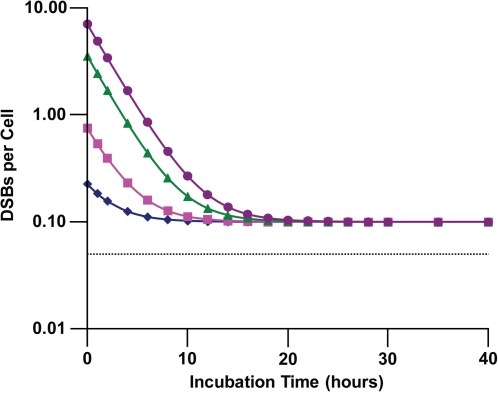
Figure 1 shows the calculated distributions (reflecting the expected DNA DSB repair kinetics) for ϕ₁(t), ϕ₂(t), ϕ₃(t), and ϕ₄(t) for 1, 2, 3, or 4 DSBs per DNA molecule (nuclear) among human fibroblasts (MRC-5 line). For surviving cells with up to 4 DSBs on one or more DNA molecules, up to about 25 h are expected for repair of all of the repairable breaks.

FIGURE 1.

Expected time distributions ϕ_n(t) (probability densities) for nuclear DNA DSB repairs among confluent human lung fibroblast (MRC-5 line) briefly exposed in culture at a high rate to 90-kV x-rays: diamonds, ϕ₁(t); squares, ϕ₂(t); triangles, ϕ₃(t); circles, ϕ₄(t). Data points indicate where calculations were perform rather than actual measured data.

Attributions to the Repair Kinetics Profile

It is useful to consider the relative contributions of the different repair kinetics in Figure 1 to the expected overall repair kinetics profile after exposure of human lung fibroblasts in culture to a given x-ray dose. This can be assessed via assigning the weight, poisson(n, BPM(D)), to the average time to DSB repair for each value n (i.e., n = 1, 2, ...). This allows evaluating the expected attribution (Att_n(D)) (percent contribution of ϕ_n(t)) to the overall repair kinetics profile. The dose-dependent attribution Att_n(D) to the DSB repair kinetics profile is given by:

$${\mathit{Att}}_n(D)=100n\beta [\mathit{poisson}(n,\mathit{BPM}(D))]/\sum _{j=1}^{\infty }i\beta [\mathit{poisson}(j,\mathit{BPM}(D))].$$ (9)

The product nβ in the numerator is the average time (expectation value) for repairing n DSBs on the same DNA molecule when ϕ_n(t) is given by Equation 8. The denominator in Equation 9 represents the average time to DSB repair completion, when multiple breaks per molecule are involved. Equation 9 reduces to the following:

$$\begin{array}{c}{\mathit{Att}}_n(D)=100n\beta [\mathit{poisson}(n,\mathit{BPM}(D))]/[\beta (\mathit{BPM}(D))]\\ =100n[\mathit{poisson}(n,\mathit{BPM}(D))]/\mathit{BPM}(D)\end{array}$$ (10)

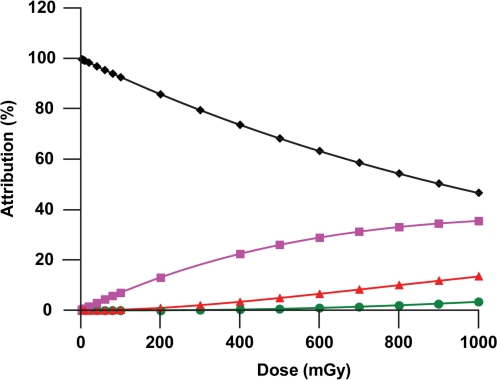
It follows that the average time for DSB repair after a dose D is given by the product β [BPM(D)]. Figure 2 shows calculated results obtained for Att₁(D), Att₂(D), Att₃(D), and Att₄(D) for human lung fibroblasts (MRC-5 line) exposed to 90-Kv x-rays for doses up to 1000 mGy. For doses < 10 mGy, Att₁(t) > 99%, so that essentially all of the repair kinetics profile is expected to be accounted for by the kinetics associated with repairing DNA molecules that have only 1 DSB. For a dose of 1000 mGy, about 47 % of the repair activities is expected to be associated with repairing two breaks on the same DNA molecule (Att₂(D) = 46.7%). At the same dose Att₃(D) = 13.6% (rounded) and Att₄(D) = 3.4% (rounded). For much higher doses repair of multiple breaks per DNA molecule would be expected to predominate over repairing only a single break per molecule. The indicated results apply to surviving cells; however, cell killing is not presently addressed in the modeling undertaken. Thus, there is an implied assumption that cells with several DSBs per nucleus are not preferentially lost relative to those with a single DSB for confluent cells, which may not be a case when D is as large as 1000 mGy.

FIGURE 2.

Expected attributions to DNA repair kinetics for x-ray exposed confluent human lung fibroblasts (MRC-5 line) irradiated in culture: diamonds, Att₁(D); squares, Att₂(D); triangles, Att₃(D); and circles, Att₄(D). Data points indicate where calculations were perform rather than actual measured data.

Cumulative Distribution Functions for DSB Repair

The cumulative distribution function, Ψ_n(t) for the time to repair n DSBs on the same DNM molecule during an epicellcom response to radiation stress is obtained by integrating ϕ_n(x)dx from zero up to time t which yields the following result (cumulative gamma distribution):

$${\mathrm{\Psi }}_n(t)=1-\sum _{j=0}^{n-1}\frac{{(t/\beta )}^j}{j!}\hspace{0.17em}\text{exp}(-t/\beta ).$$ (11)

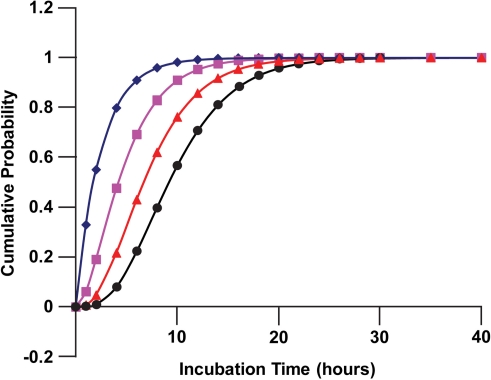
Figure 3 shows application of Equation 11 to human lung fibroblasts (MCR-5 line) for a subset of DNA molecules which have the same number of DSBs (1, 2, 3, or 4 breaks). To obtain a cumulative distribution function for the time to DNA DSB repair completion after radiation exposure where a different number of breaks occur on different molecules, it is necessary to average Equation 11 over the dose-dependent Poisson distribution of the n breaks for the initial (induced and spontaneous) DSBs on DNA molecules. This can be achieved by assigning the weight poisson(n, BPM(D)) to Ψ_n(t) for each value of n ( i.e., n = 1, 2, ..., ∞). The weighted average is indicated by Cum(t, D), where:

$$\mathit{Cum}(t,D)={\sum }_{j=1}^{\infty }[\mathit{poisson}(n,\mathit{BPM}(D)){\mathrm{\Psi }}_n(t)/\mathrm{\Omega }(D)].$$ (12)

FIGURE 3.

Cumulative distributions for the corresponding probability densities presented in Figure 1: diamonds, Ψ₁(t); squares, Ψ₂(t); triangles, Ψ₃(t); circles, Ψ₄(t). Data points indicate where calculations were perform rather than actual measured data.

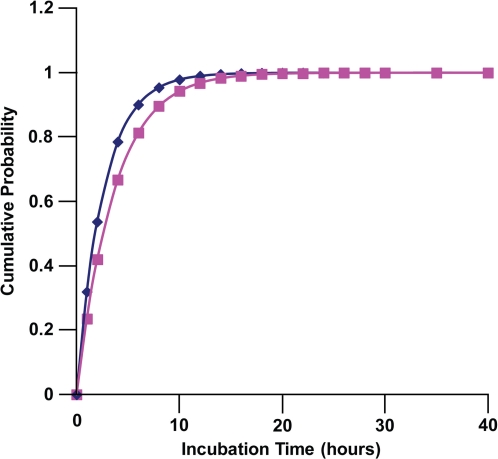
The normalization function Ω(D) is just the sum from 1 to ∞ of the probability mass poisson(n, BPM(D)), which equals 1 – exp(– BPM(D)). The function Cum(t, D) is the expected cumulative probability for repair of the DSBs by time t post radiation exposure. Equation 12 has been used to evaluate the dose-dependent expected cumulative probability for repair of DSBs among human lung fibroblasts (MRC-5 line) that were briefly exposed in culture at a high rate to 90-kV x-rays. Results obtained for doses in the range 2 to100 mGy were essentially the same (not presented), with Cum(t, D) being almost identical to poisson(1,BPM(D))Ψ₁(t)/Ω(D) as expected. This is just a reflection of single DSBs per DNA molecule being the most common induced lesion expected after low doses, so that mainly only one induced break per molecule needs to be repaired. Results obtained for D =100 and 1000 mGy are presented in Figure 4.

FIGURE 4.

Poisson-probability-mass weighted expected cumulative distribution of time to DSB repair after brief exposure at a high rate of human lung fibroblasts (MRC-5) in culture to 90-kV x-rays: diamonds, Cum(t, 100 mGy); squares, Cum(t, 1000 mGy). Data points indicate where calculations were perform rather than actual measured data.

Characterizing Residual DSBs vs. Time after Radiation Exposure

Equation 12 can be used to modify the MULTISIG1 model-based equation (Scott 2010) for characterizing the residual DSBs at time t after brief in vitro exposure of confluent cells at a high rate. The previously derived equation (Scott 2010) applies only to low doses where the decline in DSB is according to dose-independent exponential exp(– t/β). Now this function can be replaced with (1 – Cum(t, D)) yielding the following equation for the residual breaks per cell (RB) which applies not only to low but also to moderate radiation doses:

$$\mathit{RB}(t,D)=B_T+\alpha (D-T)(1-\mathit{Cum}(t,D)).$$ (13)

The parameter B_T gives the residual breaks per cell after tens of hours of follow-up at which point the DSB repair is completed for all repairable breaks. Equation 13 applies to D > T so that B_T is also a biological marker for the corresponding threshold dose for the epicellcom process that involves stress-response related DSB repair among the targeted cell population. Low dose experimental data for DSB repair kinetics (e.g., based on γ-H2AX foci dissolution) and information in Table 1 can be used to estimate the MULTISIG1 model parameters. For low doses 1 - Cum(t, D) in Equation 13 can be replaced with exp(– t / β) facilitating estimation of β.

Figure 5 shows simulated repair kinetics based on Equation 13 for x-ray exposed confluent MRC-5 cells in vitro for does of 0, 5, 20, 100, and 200 mGy. Estimates of MULTISIG1 model parameters, variables, and functions are based on Table 1 and Rothkamm and Löbrich (2003), except for the parameterβ. Parameter estimates are as follows: B_T = 0.1 (Rothkamm and Löbrich 2003), α = 0.035/mGy (Rothkamm and Löbrich 2003), and T = 1.4 mGy were used as was done elsewhere (Scott 2010). The central estimate of the parameter β is 2.5 h as already indicated. The estimate was obtained by systematically changing the value of β until simulated residual breaks per cell closely matched γ-H2AX foci per cell reported in figures presented in Rothkamm and Löbrich (2003). Based on this analysis, a subjective uncertainty range for β of between 0.5 h (subjective lower bound) and 4.5 h (subjective upper bound) was obtained. New research is needed to improve on these estimates.

FIGURE 5.

Predicted residual DNA DSBs per cell as a function of follow-up time for human lung fibroblasts (MRC-5 line) exposed briefly in culture to 90 kV x-rays: diamonds, 5 mGy; squares, 20 mGy; triangles, 100 mGy; circles, 200 mGy; horizontal dashed line, 0 mGy. Data points indicate where calculations were perform rather than actual measured data.

Results obtained in Figure 5 for the 5 and 20 mGy groups compare favorably to those reported by Rothkamm and Löbrich (2003), although a logarithmic scale is used here. For x-ray doses less than T = 1.4 m Gy, no repair of DSBs is expected under the MULTISIG1 model which employs a deterministic threshold (Scott 2010). Future research will explore the possibility of a stochastic threshold (Scott 2005) that varies over replicate studies and the possibility of a delay before the start of repair. For cases for which D < T, the expected DSBs per cell can be evaluated using Equation 3, irrespective of follow-up time. For example, for D = 0.1 mGy, Equation 3 yields 0.0535 DSBs per cell which is just above the horizontal line (0.05 DSB per cell (Rothkamm and Löbrich 2003)) presented in Figure 5 for controls.

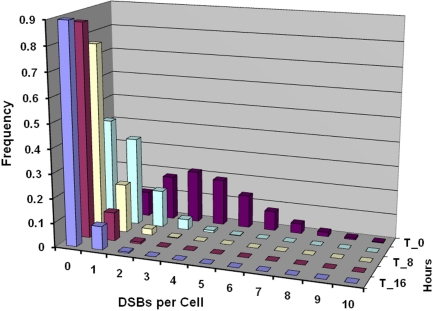
Figure 6 shows expected residual DNA DSBs per cell for different follow-up times after an x-ray dose of 100 mGy, based on results presented in Figure 5. Follow-up times considered were 0, 4, 8, 12, and 16 h post exposure of MRC-5 cells.

FIGURE 6.

Predicted residual DSBs per cell for confluent human lung fibroblast (MRC-5 line) exposed briefly in culture to 100 mGy of 90-kV x-rays. Predictions are for follow-up times (from front to back) of 16 (T_16), 12, 8 (T_8), 4, and 0 (T_0) h post exposure.

Characterizing Residual DSBs per DNA Molecule

Based on Equations 5 and 13, it follows that residual breaks per DNA molecule (RBM) is given by the following:

$$\mathit{RBM}(t,D)=\mathit{RB}(t,D)/m.$$ (14)

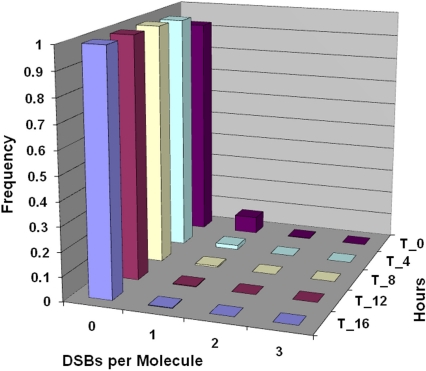
Figure 7 shows corresponding results to those in Figure 6 for DSBs per DNA molecule and implicate repair of a single break on a given molecule, rather than repairs of multiple breaks on the same molecule when the dose is of the order of 100 mGy or smaller.

FIGURE 7.

Predicted residual DSBs per DNA molecule for confluent human lung fibroblast (MRC-5 line) exposed briefly in culture to 100 mGy of 90-kV x-rays. Follow-up times considered were (from front to back) 16 (T_16), 12 (T_12), 8 (T_8), 4 (T_4), and 0 (T_0) h post exposure (same as for Figure 6).

Equation for residual γ-H2AX foci per cell (RF) or per DNA molecule (RFM) can be obtained from Equations 13 and 14 by replacing RB(t, D) with RF(t, D), replacing B_T with F_T, and replacing RBM(t, D) with RFM(t, D).

Systems Biology Perspective for Parameters μ and β

The average rate μ of DSB repair will be influenced by the contributions to repair from the related competing processes NHEJ, SSA, HR and other pathways. This can be addressed quantitatively via representing μ as the following repair-pathway-weighted average:

$$\begin{array}{c}\mu =p\{\mathit{NHEJ}\}\mu (\mathit{NHEJ})+p\{\mathit{SSA}\}\mu \{\mathit{SSA}\}\\ +p\{\mathit{HR}\}\mu \{\mathit{HR}\}+p\{\mathit{other}\}\mu \{\mathit{other}\}.\end{array}$$ (15)

The functions p{.} are probabilities for the different repair pathways (NHEJ, SSA, HR, and other) and the parameters μ{.} are the corresponding pathway-specific average repair rates per DSB. If necessary the term for the other pathway can be replaced by corresponding multiple terms: other₁, other₂, other₃, etc. Equation 15 is expected to be valid even when a single repair pathway (e.g., NHEJ) predominates. The corresponding solution for β is as follows:

$$\begin{array}{c}\beta ={[p\{\mathit{NHEJ}\}/\beta \{\mathit{NHEJ}\}+p\{\mathit{SSA}\}/\beta \{\mathit{SSA}\}+p\{\mathit{HR}\}/\beta \{\mathit{HR}\}+p\{\mathit{other}\}/\beta \{\mathit{other}\}]}^{-1}\end{array}$$ (16)

Note the reciprocal relationships (−1 power) on the right-hand side of Equation 16.

OTHER APPLICATIONS OF THE MULTISIG1 MODEL

There are a number of other possible applications of the MULTISIG1 model. These include the following: (1) predicting the results of cell culture media transfer studies; (2) application to relative comparison studies; (3) application to DNA-damage-related, cell-sensitization studies; (4) application to in vivo biological dosimetry.

Predicted Results of Cell Culture Media Transfer Studies

The MULTISIG1 model can be used to predict the expected results of media transfer studies involving confluent cells. Examples follow below:

• Because the intercellular signals are present in the cell culture media shortly after radiation exposure to a dose D > T, transferring media to unirradiated cultures is predicted to stimulate and epicellcom process involving up-regulation of DSB repair pathways with subsequent repair of DSBs that are already present and those occurring spontaneously or otherwise in the cell culture samples.

• When the radiation dose is < T, DSB repair pathways are predicted not be to be influenced by the media transfer.

The indicated predictions can be tested by specific experiments using confluent cells and x- or gamma rays.

Applications to Relative Comparison Studies

The genetic characteristics and epigenetic status of the irradiated cell population can influence the response to radiation exposure. It is therefore useful to consider model parameters as depending on such characteristics. Thus, for cells of a given type it is convenient to re-express the model parameters α and β as α{a, b} and β{a, b}, respectively, for cells with genetic characteristic a (e.g., wild type characteristic) and epigenetic status b (e.g., wild-type status). For other cells with genetic characteristics c (e.g., having a specific DNA repair gene polymorphism) and epigenetic status d (e.g., having a specific DNA repair gene epigenetic characteristic), the relative susceptibility (RS) for radiation-induced DSBs is given by the following equation for cells with genetic characteristic c and epigenetic status d, relative to cells with genetic characteristic a and epigenetic status b:

$$\mathit{RS}\{c,d|a,b\}=\alpha \{c,d\}/\alpha \{a,b\}.$$ (17)

Similarly the relative repair capacity (RRC) for repair of radiation-induced DSBs for cells with genetic characteristic c and epigenetic status d, relative to cells with genetic characteristic a and epigenetic status b is given by:

$$\mathit{RRC}\{c,d|a,b\}=\beta \{a,b\}/\beta \{c,d\}.$$ (18)

The different indicators in the numerators (right-hand side) of Equations 17 (c, d) and 18 (a, b) relate to susceptibility to DSBs increasing as α increases while DNA repair capacity decreases as β increases since β is inversely related to the rate μ of DSB repair.

The statistics RS{c, d | a, b} and RRC{c, d | a, b} could be linked to findings from epigenetic, genomics, and proteomics studies designed to elucidate the biological bases for the different values for MULTISIG1 model parameters α and β. Where necessary, a, b, c, and d can be replaced by corresponding covariate vectors a, b, c, and d, allowing for multiple genetic characteristics and for a multiple epigenetic statuses for a given cell type. When the genetic characteristics and epigenetic statuses are not known, less formal notation can be used, e.g., RS{cell type 2 | cell type 1}, for relative susceptibility of cells of type 2 relative to cells of type 1. Corresponding relationships would also apply to RRC, i.e., RRC{cell type 2 | cell type 1}. These less formal statistics can be used for comparing a tumor cell line vs. a normal cell type (wild type), or for comparing neoplastically transformed cells vs. normal cells, or for comparing lung fibroblast vs. lung epithelial cells, or for comparing other cell types.

For human lung fibroblasts lines exposed in vitro as confluent cultures, α has been estimated to be 0.035/mGy (Rothkamm and Löbrich 2003) for the MRC-5 cell line and 0.021/mGy for the HSF1 cell line. Thus, the RS{MRC-5 | HSF1 } is estimated to be (0.035/mGy)/(0.021/mGy) or 1.7 (rounded). Correspondingly, RRC{MRC-5 | HSF1 } is estimated as 4.5 h/2.5 h or 1.8. The value β = 2.5 h (a rough estimate) for MRC-5 cells is based on an analysis of data from Rothkamm and Löbrich (2003). The value of β = 4.5 h (a rough estimate) for HSF1 cells is based on an analysis of data from Grudzenski et al. (2010). The results obtained suggest that RS to genomic damage induction and RRC may be similar. However, new focused research is needed to address such issues.

The PROFAC can also be represented as PROFAC{a, b} for cells with genetics characteristics a and epigenetic status b and can be considered a measure of epiapoptosis capacity (EC). This allows for evaluating the relative epiapoptosis capacity (REC) for cells with genetic characteristics c and epigenetic status d relative to cells with corresponding genetic characteristics a and epigenetic status b using the following:

$$\mathit{REC}\{c,d|a,b\}=\mathit{PROFAC}\{c,d\}/\mathit{PROFAC}\{a,b\}.$$ (19)

PROFACs against spontaneous neoplastic transformation have been previously estimated for different photon radiations sources, based on the NEOTRANS₂ and NEOTRANS₃ dose-response models (Scott et al. 2004; Scott 2005). Less formal representations of the REC can also be used where appropriate, e.g., REC{cell type 2| cell type 1}. For example, based on estimates of PROFAC values for low-dose, gamma-ray suppression of spontaneous neoplastic transformation of C3H 10T1/2 cells and HeLa x skin fibroblast human hybrid cells in culture (Scott et al. 2004), REC{C3H 10T1/2 | HeLa x skin fibroblasts} = 0.071/0.32 or 2.2 (central estimate). Thus, the C3H 10 T1/2 cells appear to have about twice as much epiapoptosis capacity on average as do HeLa x skin fibroblast human hybrid cells.

Application to Cell Sensitization Studies

Grudzenski et al. (2010) demonstrated that prior exposure of human lung fibroblasts (HSF1 line) in vitro to low doses of H₂O₂ that produced single-strand breaks but not DSBs altered the kinetics of DSB repair (based on γ-H2AX foci dissolution) after x-ray exposure. This observation can be explained using the MULTISIG1 model in that the H₂O₂ exposure would be expected to possibly alter the genetic characteristic and epigenetic status of the target cells. If so, it is also possible that the threshold T for inducing DSB repair as an epicellcom process and the related parameter β may both be reduced by prior exposure to H₂O₂. This can be formally addressed by assigning values T{a, b} and β {a, b} for genetic characteristic a and epigenetic status b when no prior exposure to H₂O₂ occurs and assigning corresponding values T{c, d} and β {c, d} when prior exposure to low-level H₂O₂ occurs. For such scenarios, T{c, d} ≤ T{a, b} and β {c, d} ≤ β {a, b} might be expected.

Application to Biological Dosimetry

The MULTISIG1 model could also be used to develop calibration relationships for biodosimetry applications for individuals exposed to low-dose radiation. Calibration curves could be established based on γ-H2AX foci per cell for peripheral blood lymphocytes (Rothkamm et al. 2007). This would involve developing dose-response curves for γ-H2AX foci per cell vs. radiation dose that were for specific follow-up times (e.g., 12 h after exposure, 24 h after exposure, etc.). Electronic and/or hard copy tables could then be made available that convert a given value for foci per cell measured at a given time after radiation exposure to an estimated whole-body radiation dose. The tables would vary for the different types of radiation. This will be addressed in more detail in follow-on research.

CONCLUSIONS

The following conclusions apply to x-ray exposure of cultures of confluent human lung fibroblasts (MRC-5) when the exposure is brief, the dose rate is high, and the dose is low or moderate:

• For D < T (i.e., 1.4 mGy), DNA DSB repair as an epicellcom process is not expected to occur. Rather, DSBs are expected to be produced in accordance with the LNT hypothesis and persist until cells are allowed to proliferate, at which time some cells with residual DSB may be removed via epiapoptosis.

• For T < D ≤ 100 mGy, the DSB repair kinetics are expected to arise as an epicellcom process reflecting the kinetics of the repair of DNA molecules each with a single DSB, with the initial number of broken molecules increasing with dose. The average repair time for this dose range is given by β.

• For x-ray doses as large as 1000 mGy or larger multiple DSBs per DNA molecule are expected to occur and to be repaired as an epicellcom process that requires longer repair times because of the multiple breaks per DNA molecule. For repair of n breaks on a given DNA molecule, the average repair time under the current version of the MULTISIG1 model is nβ.

• Exposure of cells to a low-level of single-strand break inducing agents other than radiation (e.g., H₂O₂) could alter the DSB repair kinetics after exposure to radiation via lowering the threshold for activating DSB repair as an epicellcom process and via facilitating faster implementation of DSB repair pathways.

• The novel statistics RS{c, d | a, b}, RRC{c, d | a, b}, and REC{c, d | a, b} are expected to be useful for quantifying differences in cellular responses to radiation (and other DNA damaging agents) that relate to genetic characteristics and epigenetic statuses of the target cell populations.