Virtual Genomes in Flux: An Interplay of Neutrality and Adaptability Explains Genome Expansion and Streamlining

Abstract

The picture that emerges from phylogenetic gene content reconstructions is that genomes evolve in a dynamic pattern of rapid expansion and gradual streamlining. Ancestral organisms have been estimated to possess remarkably rich gene complements, although gene loss is a driving force in subsequent lineage adaptation and diversification. Here, we study genome dynamics in a model of virtual cells evolving to maintain homeostasis. We observe a pattern of an initial rapid expansion of the genome and a prolonged phase of mutational load reduction. Generally, load reduction is achieved by the deletion of redundant genes, generating a streamlining pattern. Load reduction can also occur as a result of the generation of highly neutral genomic regions. These regions can expand and contract in a neutral fashion. Our study suggests that genome expansion and streamlining are generic patterns of evolving systems. We propose that the complex genotype to phenotype mapping in virtual cells as well as in their biological counterparts drives genome size dynamics, due to an emerging interplay between adaptation, neutrality, and evolvability.

Introduction

Recent efforts to reconstruct the ancestral gene contents at various evolutionary depths have provided evidence for the existence of universal patterns in the evolution of genome size. An initially surprising outcome of phylogenetic reconstructions is the rich ancestral gene content inferred for archaea (Snel et al. 2002; Csűrös and Miklós 2009; David and Alm 2010), bacteria (Snel et al. 2002), and eukaryotes (Makarova et al. 2005; Zmasek and Godzik 2011) as well as for a hypothetical last universal common ancestor (Ouzounis et al. 2005). Although a large genome of Eden (Doolittle et al. 2003) is generally considered an unwelcome artifact of denying the importance of horizontal gene transfer, accounting for such events (Snel et al. 2002; Cordero and Hogeweg 2007) and using different methodologies (Ouzounis et al. 2005; Tuller et al. 2010) has upheld the notion of large ancestral genomes that are on a par with those of present-day descendants. Complementing the results of gene-rich ancestors is the finding that ongoing gene loss on diverging branches is a major contributor to genome evolution (Snel et al. 2002; Makarova et al. 2006; Csűrös and Miklós 2009; David and Alm 2010).

It has been proposed that evolution can act in two fundamentally different modes (Koonin 2007). Extensive new gene and functional repertoires originate in rapid inflationary phases of evolution, while subsequent cooling phases are characterized by divergence of species and a slowing down of genome dynamics.

Although extensive genetic exchange has played a crucial role in almost all inflations leading to major transitions in evolution (e.g., the emergence of a repertoire of catalytic RNAs and protein folds and protocells), other forms of genetic turbulence, such as rapid genome expansions, may not be fundamentally different in their dynamics. Rapid genomic and intronic expansion was most likely the driving force behind the radiation of the eumetazoan lineage (Putnam et al. 2007; Harcet et al. 2010; Srivastava et al. 2010), playing out at an intermediate evolutionary depth. In multiple plant species, whole genome duplications have been associated with drastic changes in the environment (Blanc and Wolfe 2004; Van de Peer et al. 2009), potentially enabling these species to survive.

Looking at even shorter evolutionary distances, lineage-specific expansions in eukaryotes and prokaryotes suggest that amplification of certain gene families plays an important role in the adaptation of individual lineages (Jordan et al. 2001; Lespinet et al. 2002; Dujon et al. 2004; Demuth and Hahn 2009; Ames et al. 2010). There are, for example, many cases known of fast adaptation toward novel resources and toxins in bacteria through the rapid increase in copy number of specific genes (for an extensive review, see Andersson and Hughes (2009)). Francino (2005) stresses that an amplification and divergence model is a favorable alternative to sub- and neofunctionalization models for the evolution of genetic novelty because it can account for prolonged retention of multiple gene copies due to the direct adaptive advantage of increased dosage. Amplification of an, initially, low-efficiency enzyme consequently broadens the scope for adaptive mutations to arise in the enzymatic function in any of the gene duplicates. Once the efficiency of a particular copy of the gene increases due to some adaptive mutations, redundant copies may be removed by a streamlining process.

Notwithstanding these adaptive effects of duplications on short evolutionary timescales, long-term evolutionary patterns of genome complexification, as seen most evidently in multicellular eukaryotes, have been attributed to neutral accumulation of excess DNA due to the increased power of drift in populations with low effective population sizes (Lynch and Conery 2003a, 2003b; Lynch 2006a, 2007), although strong deletion biases in prokaryotes (Kuo and Ochman 2009) may be a confounding factor in these analyses.

Through computational modeling, important insights have been gained in some of the driving forces behind genome size dynamics. Knibbe, Coulon, et al. (2007) showed that organisms with spatial genomes can adapt to a given mutation rate by changing their genome size and coding density, whereas de Boer and Hogeweg (2010) found that early genome expansion, limited by the per base mutation rate, determines the success rate of evolving abstract pathways for resource consumption. At the microscopic level, folding stability of essential proteins and the toxic effects of misfolding can severely limit genome size under high mutation rates (Zeldovich et al. 2007; Chen and Shakhnovich 2009), providing an explanation for differences in proteome stability distributions of viruses and bacteria (Chen and Shakhnovich 2010).

A second type of modeling has focused on the evolution of gene regulatory networks (GRNs), letting fitness depend on the network state relative to a given environment. Environmental heterogeneity can feed back on the network structure, for example, due to the evolution of modularity (Parter et al. 2008) and ultimately on the spatial structuring of the genome itself (ten Tusscher and Hogeweg 2009). In a simple model of a signaling network, complexity remained significantly above the minimum required due to neutral evolution of robustness, avoiding lethal deletion of network components (Soyer and Bonhoeffer 2006).

The above studies clearly show the need for simulating genome dynamics explicitly in order to enhance our understanding of general structuring mechanisms acting on cells. So far, few models have combined an explicit genome structure with the evolution of a plausible biological function. A notable exception is the model by Neyfakh et al. (2006), who studied the evolution of homeostasis in virtual cells. Fitness is attributed to genotypes in a natural way by taking into account gene regulation and enzyme kinetics. This model strikes a nice balance between a sufficiently low level of description on the one hand and computational feasibility and analyzability on the other hand.

Modeling a Virtual Cell

We adapted the model by Neyfakh et al. (2006) because its natural definition of phenotypes combined with the explicit coding of the genotype make it particularly suitable to answer questions about genome size dynamics in general. In particular, we used it to find mechanistic explanations for the apparent complexity of early ancestors and the patterns of fast genome expansion and steady streamlining that emerge from the phylogenetic data.

In the virtual cell model, individuals have to maintain homeostasis in two essential molecules under highly variable environmental conditions. At their initial randomized creation, cells invariably perform very poorly at the task of reaching and maintaining the target concentrations for the resource molecule, A and the energy carrier, X. Subsequently, populations evolve a wide variety of network structures with performance ranging from poor to near perfect homeostasis in a wide range of environmental conditions. Both point mutations and large-scale duplications, deletions and rearrangements occur, affecting among others the dosage and efficiency of enzymes and rewiring the regulatory network. This results in a large degree of flexibility of the evolving genotype–phenotype mapping enhancing the evolvability of the system. The details of the model can be found below in Materials and Methods.

Materials and Methods

Model Overview

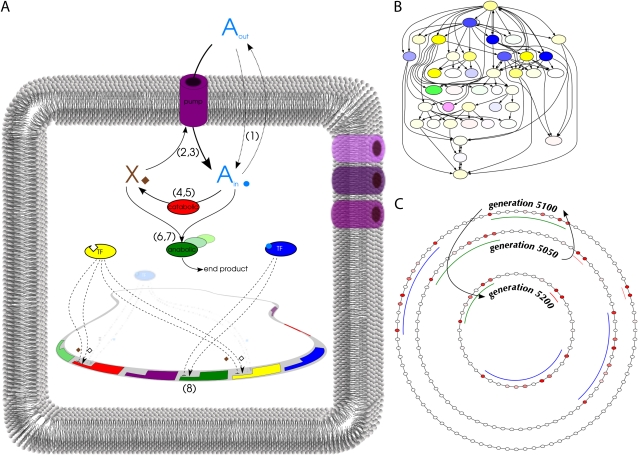
In the virtual cell model, genes code for five basic protein types (see fig. 1A). These proteins regulate the uptake and conversion of two types of simple molecules. A resource (A) that is present in the environment can be a source of energy when it is enzymatically converted into the energy carrier molecule X and can alternatively be made available as a cellular building block in a second type of enzymatic reaction. Both these reactions are carried out by specialized types of enzymes. The resource diffuses passively over the membrane of a cell and can additionally be transported inward by the action of pump proteins which requires the consumption of X. Two protein types are transcription factors (TFs) that can modulate gene transcription and that are distinguished by their ligand, A and X, respectively. Binding of a TF to a gene regulatory region requires a match between the binding sequence of the TF and the operator region of that particular gene. A TF may either upregulate or downregulate its downstream genes, and it can have a different effect in its ligand bound form from the ligand-free form (see fig 1B for an example of an evolved GRN).

FIG. 1.—

Schematic view and representations of the genome of virtual cells. (A) A permeates through the membrane (1) depending on relative concentrations inside and outside of the cell. Pumps consume X (2) to pump in A from the environment (3). Catabolic enzymes can convert A (4) into X (5) in a 1:4 ratio. Anabolic enzymes consume A (6) and X (7) to produce an unspecified end product. Protein expression (8) depends on the promoter strength and additional regulation of upstream TFs of the corresponding genes. The regulatory effect of a TF changes upon binding of its ligand (either A or X). (For reaction equations, see Materials and Methods). (B) GRN representation of a cell. Gene colors indicate the type as in (A), whereas color intensity indicates basal expression rate. (C) Circular genome representation of cells at three time points in evolution. Intensity of the red coloring of genes corresponds to fitness loss upon knockout of the gene. Colored arcs indicate syntenic regions that contain essential genes at different generation time points. Several genomic regions have been duplicated and deleted in the line of descent between the time points. The network in (B) corresponds with the middle circular genome at time = 5,050.

The cellular dynamics are modeled by ordinary differential equations (see below). Ligand-TF and TF-operator binding are assumed to be fast processes and set to quasi steady state.

Fitness of cells is a measure of their ability to maintain homeostasis at predefined target concentrations of intracellular X and A. Deviations from the targets for [A_in] and [X_in] will result in a fitness penalty. Because cells live in a variable environment where fluctuates, cells can increase their competitiveness by evolving regulatory circuitry that accommodates this variation. The lifetime fitness of an individual cell is a function of fitness measurements taken at three time points. Between these time points, the [A_out] changes with a probability of 0.4 to a new value chosen randomly from an exponential distribution that ranges over four orders of magnitude.

Genotypes are subjected to two distinct types of mutations. The first type alters the parameters of individual genes and is comparable to a point mutation. Affected parameters are the rate and binding constants of enzymes and binding sequences of TFs and promoter regions as well as the ligand that TFs have. The second type of mutation affects stretches of the genome that can span multiple genes (e.g., see fig. 1C). Duplications, deletions, and excision insertion mutations may affect up to half of the total length of the genome with an average of one quarter of the genome per mutational event.

In a default run of the model, a population of 1,024 cells is allowed to evolve for 10,000 generations. At initialization, genomes contain a collection of genes with randomly assigned parameter values, with an average size of ten genes. Mutational parameters are chosen such that individual genes are equally affected by point mutations, duplications, deletions, and rearrangements. We thus do not impose any explicit mutational bias toward increasing or decreasing genome size.

Cellular Dynamics

Cellular dynamics are governed by the following ordinary differential equations that correspond to the various cellular processes (see fig. 1):

diffusion over the membrane

(1)

pumping

(2)

(3)

catabolism

(4)

(5)

anabolism

(6)

(7)

protein expression and degradation

(8)

The two small molecules A and X act as a resource and an energy carrier, respectively. Five basic protein types play a role in the described cellular processes. Their respective behaviors within the network depend on the values of several parameters that determine, for example, basal transcription rate, substrate binding constants, and TF binding sequence. All types encode an operator sequence (o), represented by an integer value, that determines which TFs can regulate its respective expression. All genes encode a promoter strength (Pr) determining basal transcription rate that can be modulated by TF regulation (see below).

Pump enables the uptake of A from the environment by using the energy stored in X.

• Genes encoding pumps define the following binding and rate parameters:

• Ka_p binding constant for A_out: inverse of [A_out] where half of the pumps are bound by A,

• Kx_p binding constant for X_in: inverse of [X_in] where half of the pumps are bound by X,

• $\mathbf{V}{\mathbf{max}}_{\text{p}}$ rate constant determining maximum influx of A through the pump.

Catabolic enzyme converts resource A into energy carrier X.

• Ka_c analogous to Ka_p,

• $\mathbf{V}{\mathbf{max}}_{\text{c}}$ determines maximum flux through the enzyme.

Anabolic enzyme synthesizes an unspecified building block, consuming A and X.

• Ka_a analogous to Ka_p,

• Kx_a analogous to Kx_p,

• $\mathbf{V}{\mathbf{max}}_{\text{a}}$ determines maximum flux through the enzyme.

TF two types exist that have A or X as their ligand, respectively. A TF regulates the expression of a set of downstream genes.

• b A binding sequence type that determines binding to downstream genes,

• K_d constant of dissociation, inverse concentration at which half of the TFs ligand is bound to it (see below),

• K_b binding constant that describes the TFs affinity for the downstream operators that it binds to, inverse [TF] where half of the available binding sites are bound (see below),

• Eff_apo regulatory effect that the TF has in the ligand-free state,

• Eff_bound regulatory effect that the TF has in the ligand-bound state.

The conversion ratio (N) determines the yield in X of one molecule of A. In our default simulations, it is set to 4. All proteins are degraded with the same fixed rate (Degr) 0.1. Regulation (Reg) of gene expression is a function of all the TFs that can bind that genes operator sequence and calculated as follows:

(9)

(10)

(11)

(12)

Here, W gives the fraction of TF molecules that is bound to or free from its ligand. V is the fraction of time that an operator is bound by one particular TF out of all possible TFs with a corresponding binding sequence (n_o). “states” are the ligand-bound and ligand-free form of TFs. Reg for a particular gene with operator o is the sum of all regulatory effects of upstream TFs in their respective states according to the fraction of time they are bound to this operator + the basal transcription effect (1.) when it is not TF bound.

All differential equations are solved by simple Euler integration, either until an equilibrium steady state is reached or a maximum number of time steps (default = 1,000) have passed.

Population Initialization

We initialize each run with 32² = 1024 individual cells. Individual genomes are randomly initiated with sizes distributed normally around 10. TFs are twice as abundant as the pumps and enzymes in randomly created cells. All binding parameters are bounded between 0.1 and 10 and initialized as 10^a with a normally distributed between −1 and 1. All randomly initialized operators and binding sequences $\in \left\{1,\hspace{0.17em}2,\dots ,10\right\}$.

Environmental Change

In our simulations, cells are essayed in three environments every generation. Per environment the [A_out] changes to a new value with a probability of 0.4, making the chance that [A_out] remains constant during one generation 0.6 · 0.6 = 0.36. [A_out] takes on values 10^r with r drawn from a normal distribution over $[-1.5\dots 1.5)$, thus ranging over three orders of magnitude.

Fitness Evaluation and Reproduction

As is described above, between one and three different environments are encountered per generation, which leads to a sparse evaluation of fitness. Fitness of cells is calculated according to their ability to reach steady-state levels of [A_in] ([A_eq]) and [X_in] ([X_eq]) that approach predefined target concentrations [A_TARGET] = 1. and [X_TARGET] = 1.. When no steady state is reached within a maximum number of time steps, a cell is assigned a fitness of 0. Otherwise, the differences relative to the targets are recorded as $\text{Δ}\left[A\right]=\frac{\left|\left[A_{\text{eq}}\right]-\left[A_{\text{TARGET}}\right]\right|+\left[A_{\text{TARGET}}\right]}{\left[A_{\text{TARGET}}\right]}$ and similarly for Δ[X]. The performance of a cell in an environment i is given by $f_i=\frac{1}{\text{Δ}{\left[A\right]}_i·\text{Δ}{\left[X\right]}_i}.$ Its fitness potential $F_{\text{p}}={\displaystyle {\prod }_i^n{f}_i}$ given the set of environments n seen it has seen. A cells fitness, defining its reproductive chances, is the nondecreasing function $2^{F_P}-1$. Every generation all cells reproduce with a chance proportional to their fitness, until the offspring completely replaces the previous population.

Mutation

After replication, the new cells are subjected to a round of mutation, applying the different mutational operators in a chance process, according to their relative rates. The genome is subjected to point mutations, affecting individual parameters, as well as major mutations that act on stretches of genes. We define an overall mutation rate per gene and specify the relative ratio at which point mutations, duplications, deletions, and rearrangements take place. In our default settings, where the overall genic mutation rate is set to 0.05 and the fractions are equal for rearrangements, duplications, deletions, and point mutations, we expect $0.05·\frac{1}{4}$ oint mutations per gene per round of mutation, etc. Point mutations alter the various constants (c) with the function $c_{\text{new}}=c_{\text{old}}^s$ with s drawn from a normal distribution over $[0.1,\dots ,10)$. The minimum and maximum values that c can take on, however, are 0.1 and 10. Operators and binding sequences, when mutated, take on a new value $\in \left\{1,\mathrm{2..10}\right\}$.

The different large-scale mutations occur at most once per generation and affect stretches of up to half the total genome size with an average stretch size of one quarter of the genome. The probability of an event is scaled to match the per gene mutation rate.

Parameter Choices

We took a pragmatic approach in determining parameter settings. For example, balancing the rate of gene duplications and deletions and choosing not to impose an explicit penalty on genome size allowed for a transparent assessment of factors contributing to the evolution of genome size. We converged on parameters that gave good results in terms of adaptation to homeostasis. Given the open-ended and time-consuming nature of our simulations, we could not be exhaustive in the search for optimal evolutionary parameters.

We chose to maintain the conversion (N = 4) and degradation (Degr = 0.1) parameters as they appear in the original model by Neyfakh et al. (2006). Sparse fitness evaluation in the form of a stochastically changing sparsely sampled environment significantly increases the success rate of evolutionary runs in comparison with the original static scheme, which evaluated just the three standard environments ([A_out] = 0.1, 1, and 10). However, the rate with which [A_out] changes in our setup makes a difference for the ease with which populations adapt and gave the best results when the chance of moving to a new environment was 0.4.

The chance that a gene is affected by a mutation is 0.05. This rate is then equally divided between point mutations, duplications, deletions, and rearrangements. The rates of the per genome, large-scale duplication, deletion, and rearrangement events are scaled to arrive at the prescribed per gene mutation rates. Several things can be noted when changing the form and the relative frequencies of these large-scale mutations. In the first place, when large-scale mutations are made less frequent relative to point mutations, the genome expansion is less pronounced and the success rate is lower. Second, when the mechanism of mutations is changed such that only single genes are affected by duplication or deletion, but keeping the per gene mutation rates as they were, we also see less pronounced genome expansions and a lower success rate. These same shifts occur when we impose a bias toward the deletion of genes. It is important to note, however, that these parameters can be varied upon within a fairly large range, without losing the characteristic patterns that we report. We will elaborate on the effects of these parameters in the Discussion.

Results

Evolution of Fitness and Genome Size

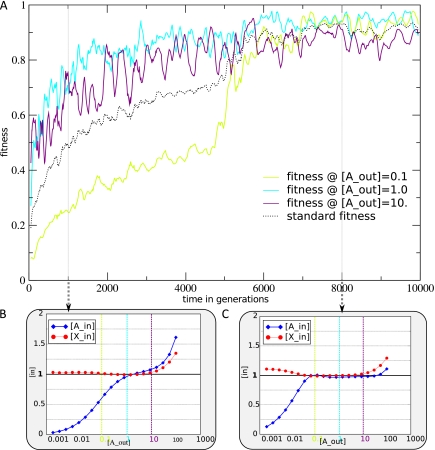
Figure 2 shows the fitness increase in a typical evolutionary simulation reaching a high fitness state (>0.85). Here, the fitness is measured within the line of descent using three standard environments, where the outside concentrations of A ([A_out]) are 0.1, 1, and 10, respectively. This measurement is different from a cell's lifetime fitness, which determines its reproductive success and depends on the stochastically changing environmental [A_out] conditions that it encounters. The standardized fitness is used to have a consistent readout of performance of cells. Figure 2B and C shows two snapshots at generations 1,000 and 8,000 of response curves of [A_in] and [X_in] as a function of [A_out]. At the later time point, regulation has evolved to bring [A_in] and [X_in] much closer to the target at 1. The increase in fitness in the standard environments (fig. 2A) reflects this increase in regulatory fine tuning. The displayed run is typical in that the initial fitness gain is fast and plateaus at an intermediate fitness level. From there, a new round of adaptation brings it close to the target optimum.

FIG. 2.—

Typical evolution of fitness in the line of descent of a run reaching a high fitness state. (A) Evolution of fitness in each standard environment separately (colored lines). The dotted black line is the standard fitness when the three environments are combined. (B and C) Snapshots of the regulatory response of the network for individuals at generations 1,000 (B) and 8,000 (C) in a log-log scale. Plotted are [A_in] and [X_in] as a function of [A_out]. For reference, the dashed vertical lines depict the [A_out] of the standard environments. The colors of reference lines correspond to those of the fitness lines in the upper graph. Genome size evolution of this run is depicted in figure 3, third graph from the back.

In our simulations, adequate regulation in the resource poor environment ([A_out] = 0.1) is invariably last to evolve, as can also be seen in figure 2. In our default setting, but using different random seeds per run, approximately half of the populations evolve a high fitness (>0.85), comparable to the example. We will refer to these runs as the fit set. Almost all populations evolve some level of meaningful regulation.

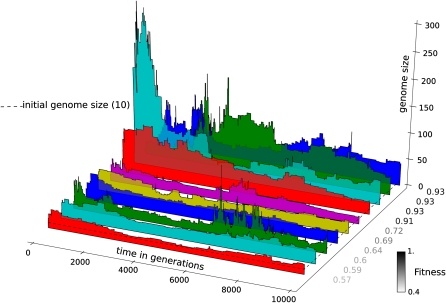
Figure 3 shows the evolution of genome size along the line of descent for ten independent runs, ordered according to final fitness. The dashed line shows the average initial genome size for this set of runs (see Materials and Methods). A striking pattern is the very rapid expansion of the genome well within the first thousand generations. In a larger set of 74 completed runs (out of a total of 80 initialized runs), we found that this increase is on average 8.3-fold (standard deviation [SD] 6.7) within the first 1,000 generations, relative to the genome size of the first common ancestor. A second pattern that is visible in several runs is a comparatively slow genomic streamlining after the initial genome expansion. The set of 74 runs shows that there is on average a 4.7-fold (SD 2.6) maximum decrease in the remainder of the run. A third pattern that can be observed several times in the later phases of evolution is the gain and loss of substantial amounts of genes in quick succession, an example of which can be seen in the second half of the third run from the front. The latter dynamics are more erratic than the coordinated early expansions. The graphs in figure 3 are ordered according to the maximum fitness attained in each run. There is an intriguing trend of fitter runs showing larger initial genome expansions (see below and table 1).

FIG. 3.—

An example of ten independent runs to illustrate the evolution of genome size. Plotted is the genome size in the line of descent. In the y-direction, the graphs of individual runs are ordered according to the fitness that the lineages have reached at the end of the run (fitness values in gray scale). The dashed line marks the average genome size of ten genes in the initial populations of all runs. There is a trend for the runs with larger initial genome expansions to be ordered toward the back.

Table 1.

Larger Size But Not Higher Fitness in Fit Runs Compared with Unfit Runs

Fitness		Size
1–100	101–200	1–100	101–200
=(P> 0.1)	=(P> 0.1)	+(P < 0.05)	+(P < 0.05)

Note.—Equal signs denote a lack of significant difference in the fitness during early evolution of runs in the fit set compared with unfit runs. Two cohorts are defined, of generations 1–100 and 101–200, respectively. Plus signs indicate that in early evolution, runs in the fit set have significantly larger genomes compared with unfit runs (Mann–Whitney U test).

The patterns that our model generates have a high variability in onset, duration and magnitude, due to the many degrees of freedom in the mapping from genotype to phenotype. We nevertheless set out to find common mechanisms for each of the trends identified above. In the following sections, we will first look at the causes and consequences of early genome expansion. In particular, we examined how the local fitness landscape around the initial population shapes subsequent evolution. Next, we focus on the effects of long-term evolution on genome structure. We investigated the causes of streamlining and size fluctuations by analyzing how the distribution and magnitude of mutational load in the GRN evolves. Finally, by integrating the findings in these experiments, we explore the relationship between expansion dynamics, neutrality, and evolutionary potential. We asked how adaptive and neutral processes interact and how this shapes the evolutionary outcome.

Early Genome Expansion

Characterizing the Early Fitness Landscape

Many of the randomly created genomes of individuals in the first population contain at least one copy of all enzymatic gene types and are thus equipped to perform all necessary cellular functions. However, initial production of enzymes can be expected to be low, given randomized expression rates of genes, potentially allowing copy number increases to have immediate adaptive effects and explaining the observed rapid expansions. To test if genome expansion can be explained by a bias toward positive duplications relative to deletions, we constructed mutational landscapes of cells in the line of descent separating duplication and deletion mutants.

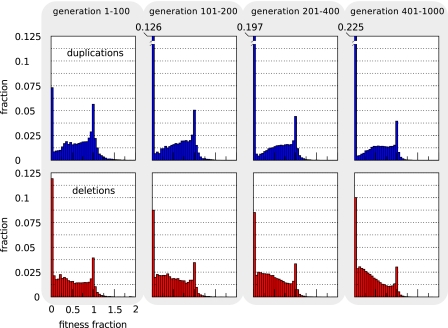
In figure 4, a distribution of the relative fitnesses of mutants with a duplication (upper panels) and deletion (lower panels) in four subsequent periods. As individuals get fitter over time, mutants are less likely to retain full fitness or increase their fitness, which is visible as the lowering of the peak at 1 and less pronounced right tails of the distribution, for both types of mutations in the later time intervals. The fraction of lethal mutants, however, initially decreases for deletions, whereas it monotonically increases over all intervals for duplications.

FIG. 4.—

Large-scale duplication and deletion fitness landscapes. Mutant fitness data for 80 independent runs are created at 20 generation intervals during the first 1,000 generations of simulation. At these time points, 50 deletion and 50 duplication mutants are created for all 80 lineages and their fitnesses recorded in standard environments. Data of all runs are combined and lumped together into four time intervals (generations 1–100, 101–200, 201–400, and 401–1,000). Single duplication (deletion) events typically involve a stretch of adjacent genes of which we measure the net effect. The upper, blue histograms are duplications showing the fraction of mutants per fitness bin. Fitness values are the fractions of wild-type fitness that the mutants retain. For the lethal duplication mutants (fitnesses approaching 0), we annotate fractions separately in the last three time intervals. Lower, red histograms are deletions.

Except for the first interval, lethality of deletions remains far below that of duplications. Lethality is due to cells not reaching a steady state in all internal molecules before the end of their life. Deletions may have drastic effects on the cellular dynamics when the GRNs of cells are small, as is still the case in the first time interval, because the small networks are prone to lose all genes of a given type, potentially losing the ability to reach a steady state in time. This can cause a relatively high fraction of deletions to be lethal in the first interval. In the second time interval, the lethality of deletions decreases, most likely because redundancy is higher due to the duplication of genes. Because in some runs genome streamlining sets in as early as in the 401–1,000 generation interval, lethality of deletions increases again in this last interval, due to the loss of redundant coding.

For duplications, the story is quite different. Lethality in the first interval is lower in the duplication mutants compared with the deletion mutants because essential genes cannot be lost in a duplication. Duplications can, however, cause drastic increases in enzymatic products that can prevent timely equilibration of the cellular dynamics. As cells adapt, regulation tends to be strengthened by an increase in the basal expression levels of many genes in the network (data not shown). This can explain the steady increase in lethality of duplications because they cause more severe overexpression.

The record of duplications and deletions that have been fixed in surviving lineages (supplementary fig. S1, Supplementary Material online) is largely in agreement with the general shape of the early fitness landscapes, to the extent that there is a surplus of duplications in early evolution whose effects are more often slightly positive than negative. There are, however, also large-scale mutations that become fixed, despite fitness losses of up to 50%. Their survival can be explained by the sparse evaluation of fitness in our model, causing periods of relatively lenient environmental conditions that allow for an extended period of time for compensatory mutations to arrive (see supplementary fig. S2, Supplementary Material online).

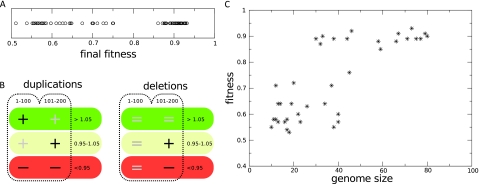
Predicting Fitness Evolution by the Shape of the Fitness Landscape

We found that there is a sharp divide in fitness values between lineages that either have a very good overall homeostasis response or a response that is lacking in the low resource regime (see fig. 5A). There appears to be a relationship between the extent of genome expansion in the first generations of a lineage and the maximum fitness that a lineage can reach during evolution. Therefore, we wondered if certain features of the fitness landscape of the early ancestors could be a predictor for the future success of lineages. More specifically, we hypothesized that lineages in the fit set (final fitness > 0.85) have higher fractions of duplications leading to fitness increase (and lower fractions of mutants with decreased fitness). We tested for significance of such over (under) representation in fitness classes in a simplified representation of the previously introduced fitness landscapes, where the fitness effects are condensed into three bins. The results are shown in figure 5B. Indeed, for lineages in the fit set, the early fitness landscape is biased toward positive duplications. Neutral duplications are also overrepresented, while deleterious duplications are found less in the local fitness landscape. For deletions, biases in the landscape are a secondary effect of the increased genome sizes in the fit set, resulting in a larger proportion of neutral deletions in the second time interval.

FIG. 5.—

Relationship between fitness, size, and the early fitness landscape. (A) The distribution of fitness values in 74 independent runs. (B) Biased fitness landscapes for future fit lineages. Runs were classified as fit if their final fitness exceeded 0.85. Fitness landscapes for mutants with duplications and deletions, respectively, were constructed for individuals in the line of descent during early evolution. At 20 generation intervals, 50 deletion and 50 duplication mutants of the lineages were created, and the fitness effects expressed as a fraction of the ancestral fitness. Fitness landscapes of fit and unfit lineages were combined and the time points lumped into two time intervals: generations 1–100 and 101–200, respectively. Plus and minus signs denote over- and underrepresentation of a class of fitness effects in a given time interval for the fit set, as measured with Mann–Whitney U tests. Dark signs are significant (P < 0.05) and grayed signs denote a bias under a lower threshold (P < 0.1), whereas equal signs denote no bias. (C) (early) genome size affects late fitness. In 40 runs with a fixed genome size (see main text for details), the late fitness is plotted as a function of the genome size.

Having observed these differences in shape of early fitness landscapes for fit and unfit runs, we wanted to know if the future fit lineages capitalized on the subtle differences in the landscape immediately, in other words, if future fit runs are fitter from the start. Table 1 shows that this is not the case. The lifetime fitness and standard fitness do not become significantly elevated. Interestingly, the two sets can be clearly distinguished on genome size even in the first time interval. We thus see that the higher likelihood of positive duplications in future fit lineages promotes the expansion pattern, providing the building blocks for their successful future adaptation. Put differently, the fitness landscape of the early ancestors of lineages that become very fit much later in evolution promotes adaptation by dosage increases, which initially causes larger genome expansions that only secondarily increase their adaptive success.

Genome Size and Evolvability

To study the effect of genome size on the evolutionary potential more directly, we created populations with different initial genome sizes and disabled the duplication and deletion of genomic stretches. For average genome sizes of 10, 20, 40, and 80 genes, respectively, we created ten populations each and let them evolve. Figure 5C shows that the final fitness correlates strongly with the number of genes in the genome, where larger fixed genome sizes lead to higher final fitnesses. Clearly, the evolutionary potential is positively influenced by having a larger initial genome size in the population. When gene stretches are allowed to be duplicated and deleted, as is the case in our default setup, this evolutionary potential increases as a consequence of the expansion phase, that is, largely driven by positive dosage increases and duplicated genes that hitchhike on the positive effects. Evolution via dosage effects can thus accelerate subsequent adaptation and innovation by increasing the evolvability of organisms.

The analyses of the early fitness landscape and the consequences of genome complexity for evolvability of lineages show that the evolution of fit lineages depends on immediate as well as secondary effects of genome expansion. When the early fitness landscape harbors more adaptive duplications, genome expansions will tend to have a larger magnitude. The increased gene content, in turn, improves further adaptation of homeostasis.

Long-term Evolution

Genome expansion is a relatively short-term evolutionary pattern, predominantly occurring within, although not strictly limited to the first 2,000 generations of evolution. Mostly, size dynamics will slow down at the end of a period of fitness increase, giving way to long-term evolutionary dynamics. However, the exact timing of the onset and duration of these expansion patterns is variable, complicating a statistical analysis over multiple runs of the long-term evolutionary dynamics. Therefore, we resorted to analyzing individual runs and report on a typical run that displays the characteristic that we wished to describe in a clear way. Because we aimed to explain phylogenetic patterns of extant lineages that have, de facto, been successful on earth, we also selected lineages from our simulations that were successful in evolving homeostasis.

Streamlining

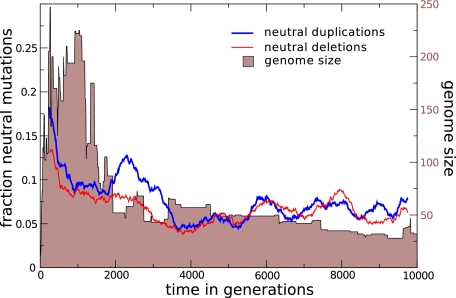
Mostly, we observed that after a rapid growth of the genome in early evolution, the ensuing dynamics slowed down and shifted to a clear downward trend. Because no explicit bias in the rates of gene adding and removing mutations exists in our full model, we wondered whether a bias in the fitness landscape toward neutral deletions, relative to neutral duplications could be causing the streamlining pattern. This would imply that the bias changes in the opposite direction of that during genome expansion. To test this, we extended the analysis of the fitness landscape to the timescale of the whole run. In figure 6, we plot the fractions of neutral duplications and deletions, respectively. We do not observe that deletions are neutral more often than duplications during the streamlining period. Counter to expectation, the most significant size decrease (generations 1,000–3,000) occurs when the fraction of neutral duplications is consistently above that of neutral deletions. Thus, for the run under investigation, there is no bias in the neutrality of major mutations that could explain the downward trend in genome size. In the following sections, we investigate other factors that could bring about the streamlining pattern.

FIG. 6.—

Fractions of neutral duplications and deletions in random mutation essays. The fraction of mutants with either duplication or deletion mutations that show no fitness effect is plotted over evolutionary time in the line of descent at ten generation intervals, as a 50 point running average. For reference, the genome size is plotted in the background.

Specialization of Genes

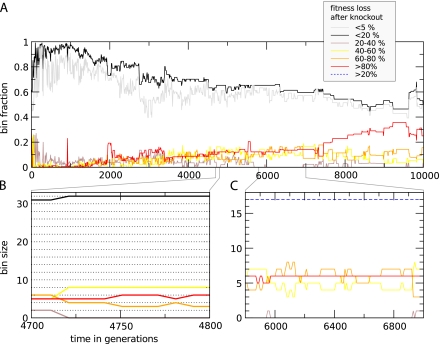
We examined how functionality is distributed through the GRN to see how evolution toward a more compact coding in combination with streamlining takes place. As a proxy for the contribution of individual genes, we measure the effect of their knockouts. The genes are then assigned to contribution bins according to the residual fitness fraction of their respective knockout mutants. Note that these contributions cannot be considered additive because fitness is a network property. In figure 7, we plotted the fractions (a) and sizes (b, c) of a set of contribution bins. Several large-scale trends can be identified when we look at the fractions of genes in the depicted bins in figure 7A over evolutionary time. First, the bulk of genes (over 90%) constituting the early expansion contribute only marginally (<5%) to fitness, but this fraction then decreases to about 0.5 at the end of the run. In the first half of the run, the fraction of genes in the <20%-bin are significantly higher than that of the subset <5%-bin. However, in the second half of the run, the bins increasingly overlap, indicating that the fitness contributions of genes in the <20%-bin are slowly marginalized. At the same time, highly essential genes (>80%) slowly start to dominate the GRN at the expense of the intermediate classes (20–80%).

FIG. 7.—

Specialization of genes in the GRN. Genes have been assigned to bins according to the fitness loss of the cell after knockout of the gene. Five main bins exist for all 20% fitness partitions. The <5%-bin (gray line) is a subset of the <20%-bin (black line). (A) shows fractions that the respective bins take up in the whole network. (B and C) show the actual bin sizes in numbers of genes. In (B), between generation 4,700 and 4,725, we see that one gene moves to the <20%-bin (black) from the 20%- to 40%-bin (brown), whereas a second gene from the brown bin increases its contribution, moving into the 40%- to 60%-bin (yellow). At the same time, two genes from the 60%- to 80%-bin (orange) also move down to the yellow bin. In (C), the >20%-bin (blue dashed line) sums over all main bins that have a higher than 20% fitness loss. This remains constant, whereas the contributions of individual genes are continuously changing.

Together, these trends constitute a process in which the network functionality evolves from being widely distributed over many, mostly lowly contributing genes to a state with a confined, highly specialized subset of genes performing the network function. This results in an increase in lethality of mutations that target essential network components but can at the same time serve to decrease the amount of ongoing mutations due to deletion of neutral genes.

Figure 7B illustrates the discrete changes of gene contributions in more detail. From generation 4,700–4,725 we see that, while the total gene number remains constant, several genes move at the same time to different contribution classes. By a constant stream of point mutations, there can be a restructuring of the contributions that individual genes have in the network, something that has been observed in real regulatory circuits of various yeast species (Ihmels et al. 2005; Tsong et al. 2006; Martchenko et al. 2007; Lavoie et al. 2010). Genes that move into the low contribution bins (black and gray) during this resorting process risk being irreversibly removed from the network by a deletion. Figure 7C is further testimony that function drift is a continuous process with an apparently neutral character on the intermediate timescale.

Mutational Load

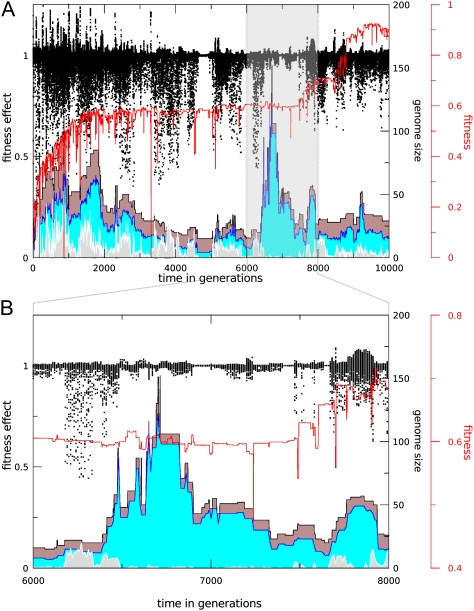
Because duplication and deletion rates of genes are equal in our full model, we considered the role of mutational load in the occurrence of the streamlining pattern. To visualize how mutational load evolves in the redundant part of our networks, we performed additional mutational analysis on surviving lineages. Using knockout analysis as described above, we focused on the neutral contribution class of genes with less than 5% fitness loss. For this gene set, we created 50 mutants per gene with a point mutation. In figure 8, we plot all individual fitness scores of these mutants next to a simple measure of mutational load, being the sum of the average residual fitnesses over all neutral genes, overlayed on the total genome size and size of the neutral gene pool. It can be clearly seen that the spread of the mutant fitness values as well as the load measure decrease toward the end of the simulation.

FIG. 8.—

Evolution of the mutational load associated with neutral genes. (A) Individual mutant fitness fractions (black dots), illustrating the breadth of mutational effects, and a simple mutational load measure (gray graph) are shown together with the total genome size (brown graph) and the set of neutral genes (cyan). (B) The corresponding evolution of the fitness of the ancestor (red) and that of the population as a whole (orange, averaged).

Also, the size of the neutral gene set seems to roughly correlate with the mutational load, showing a similar trend to decline toward the end of the simulation. However, mutational load can fluctuate quite strongly when the neutral gene set is more or less stable (e.g., between generations 6,500 and 7,000). This illustrates that mutational load can vary due to changes in the genetic background and that individual genes that drift in and out of the set of neutral genes by traversing the 5% essentiality cutoff can have strongly differing contributions to mutational load. These effects are exacerbated in the early generations, when adaptive evolution is the dominant mode and temporary drops in standard fitness occur relatively frequently, due to short-term selection pressures in particular (extreme) lifetime environments. However, it is still clear that the high levels of mutational load associated with early genome expansion (generations 1–1,000) are alleviated by subsequent streamlining (generations 1,000–2,000).

The fact that the average fitness in the population increases while the fitness does not increase in the line of descent (fig. 8B, generations 3,800–9,000) indicates that robustness is evolving neutrally in the population (van Nimwegen et al. 1999). Streamlining, by decreasing the mutational load of neutral genes, contributes directly to this increase of robustness.

Population Size Effects and Neutral Size Fluctuations

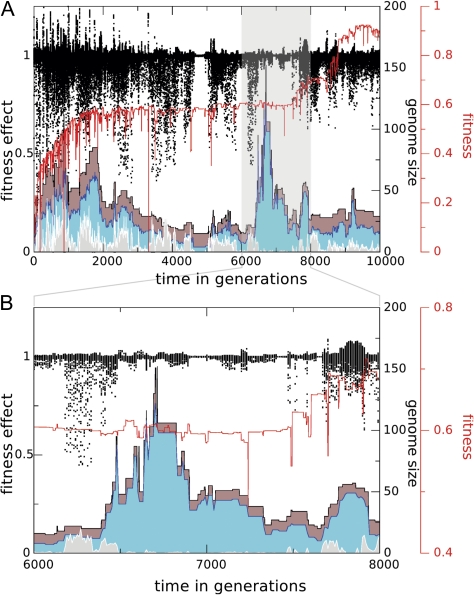
Streamlining is a robust pattern that appears to be most pronounced in high fitness populations and has slow dynamics relative to the timescale of a simulation. In some runs, we see a radically different pattern overlayed on the slow dynamics of streamlining, characterized by fast erratic fluctuations in genome size, generally in the absence of variation in fitness. Upon close inspection, these transient fluctuation patterns derive from highly neutral stretches of the genome that can be duplicated and deleted without fitness effect (see fig. 9). The potential to be duplicated without costs stems from the very low mutational load from the (stretches of) neutral genes. In fact, the streamlining pattern and the generation of highly neutral elements contribute to the neutral evolution of robustness. In the case of these transiently fluctuating genomic stretches, neutral genes, instead of being eliminated by a deletion, are rendered “harmless” by a suppressing point mutation that quenches the effect of most subsequent point mutations of the neutral gene. These elements are then free to drift to higher copy numbers. Since we consider only tandem duplications in our full model, the process has the potential to create an expanding stretch of highly neutral elements.

FIG. 9.—

Neutral genome fluctuations. As in figure 8, A shows mutational load of neutral genes (black dots), total genome size (brown), the subset of neutral genes (cyan), and the mutational load measure (gray), but this time overlayed with fitness in the line of descent (red). In the highlighted area (seen in more detail in B), fitness remains initially constant, whereas the neutral gene complement increases drastically. The most significant size increases occur after the mutational load has gone down a very low level. Subsequently, when the genome has shrunk but is still at a significantly higher level than before the sudden increase, fitness starts to go up, eventually reaching the high fitness regime after a 1,500 generation phase of adaptive evolution. It appears that the new adaptive phase is triggered by the initially neutral genome size fluctuations.

If size fluctuations are indeed an effect of the indirect evolution of robustness, it could be expected that larger population sizes enhance both the streamlining and the fluctuation pattern. To test this, we first performed additional simulations where population size was increased 2-fold. Of ten large population runs, seven reached high fitness within 5,000 generations, providing enough time for streamlining, whereas 23 runs in the standard set met the same criteria. The average of minimum genome sizes in the 10-fold larger populations was significantly lower than that for populations in the standard set (22 vs. 37, P < 0.05, Mann–Whitney U test). On the other hand, the ancestor in three of seven large population runs reaches a maximum genome size above 200, subsequent to reaching the size minimum, whereas in only 1 of 23 standard runs, this maximum lies above 100. This shows that larger effective population sizes enhance not only the efficiency of streamlining but also the, apparently, opposite pattern of neutral size fluctuations (e.g., see supplementary fig. S3, Supplementary Material online). The explanation lies in the mechanism of mutational load reduction that was explained above.

As may be expected, when we reduced population size 10-fold, relative to the standard runs, a much lower percentage of runs reached the high fitness regime. When we increased the simulation time for these populations by 10-fold, the percentage of runs crossing the threshold (0.85) to be in the fit set approximated that of the standard set (≈50%). In small populations, ancestor lineages that belong to this, the fit have slightly but significantly lower fitness than those in the standard populations. An average 2-fold higher standard variation in the running fitness of ancestors further illustrates that small populations have more difficulty in maintaining their high fitness. Nevertheless, we see the same trend of streamlining and neutral fluctuation in small populations but on a much longer timescale. While after 5,000 generation streamlining, average minimum genome size is significantly higher than in the standard runs (59 vs. 37, P < 10⁻², Mann–Whitney U test), after increasing evolutionary time for the small populations by 10-fold, streamlining is even more effective, and neutral fluctuations are more pronounced compared with the standard runs (minimum: 21 vs. 37, P < 10⁻³ and maximum: 126 vs. 45, P < 0.05, Mann–Whitney U test). Thus, more effective selection, either by increasing population size or increasing evolutionary time, leads first to minimal size genomes, which than can expand and shrink by neutral processes.

Evolution of Robustness

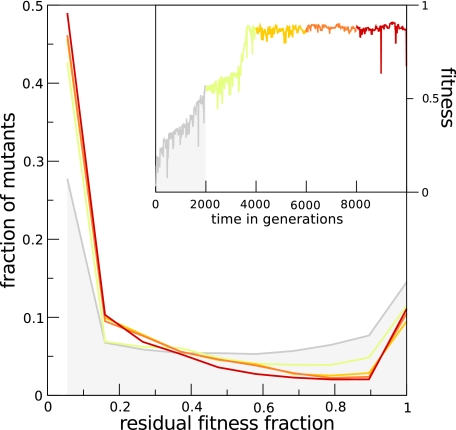
What are the effects of long-term evolutionary process on the fitness landscape along the line of descent? Up until now, we have considered various mutational protocols to highlight particular aspects of the mutational landscapes for cells along the line of descent. On the one hand, specialization of genes suggests that lethality of mutations can increase in long-term evolution, whereas on the other hand, the slow increase of population fitness when adaptation has halted indicates that robustness is increasing. We saw that an increase in robustness is facilitated by removal of load generating neutral genes. Figure 10 shows how rounds of random mutations, identical to those experienced in the full model, but with 10-fold increased mutation chance, affect the fitness of mutants created along the line of descent. For all of the ancestors at ten generation intervals, we created 50 mutants and measured their residual fitness. We plotted distributions that are lumped together for 2,000 generation intervals. We indeed see an increase in the lethality, both during adaptive and neutral evolution. Meanwhile, the fraction of near neutral mutants is remarkably constant after the first interval, despite an increase in fitness of over 50% (from 0.56 to 0.87) in the second interval. The compensatory mechanism by which increasing lethality can coincide with steady neutrality seems to be a decrease of the number of near neutral mutants. This leads to the interesting observation that the selection coefficient increases over time, which in turn facilitates the maintenance of the fittest phenotype in the population. Although our modeling was not aimed at accurately predicting the shape of an organism's mutational landscape, to our surprise we found a remarkable correspondence with in vitro data of this distribution in the yeast Saccharomyces cerevisiae (Wloch et al. 2001; fig. 5A) (Sliwa 2005; Hall and Joseph 2010). Although in our simulations intermediate effects diminish over time, the u-shape of the distribution is even more pronounced in the experimental results, suggesting that the absence of intermediate effects is an evolving property of the underlying genotype to phenotype mapping.

FIG. 10.—

Long-term fitness landscape evolution. A set of averaged fitness landscapes of 2,000 generation intervals in the line of descent of a single run is plotted. Fitness landscapes are constructed by inducing rounds of mutations in individuals in the lineage at ten generation intervals. The mutation scheme is identical to that used in standard evolutionary runs, except that a 5-fold higher mutation rate is used, resulting in a 0.5 chance for all mutational operators to affect an individual gene. Colors of graphs correspond to the colored section in the inset, showing the evolution of fitness.

Discussion

Large ancestral genomes, genome expansion, and differential loss of genes are some of the most striking recurring observations from a rapidly growing body of phylogenetic reconstruction studies. All three trends arise within a framework of populations of organisms whose structured genomes are shaped by, and at the same time dictate adaptive and neutral evolutionary processes within a changeable environment. A suitable modeling approach can give vital insights into the generic patterns that can be generated in biological evolving systems. To this end, we evolved populations of virtual cells with structured genomes and a flexible genotype to phenotype mapping and studied the evolution of their genomes.

It has been extensively shown that an interplay between neutral and adaptive evolution is an important property of complex genotype–phenotype maps (Huynen et al. 1996; van Nimwegen et al. 1999; Soyer and Bonhoeffer 2006; Ciliberti et al. 2007a, 2007b; Aldana et al. 2007) and that given a high degree of freedom in the mapping, the coding structure itself will evolve adaptive features (Crombach and Hogeweg 2007, 2008; Knibbe, Coulon, et al. 2007; Knibbe, Mazet, et al. 2007; de Boer and Hogeweg 2010). In our virtual cell model, which exhibits a high degree of flexibility in the evolving genotype to phenotype mapping, it proved crucial to analyze the interplay between adaptive and neutral evolutionary processes in detail in order to understand the evolutionary dynamics of genome structuring and the evolutionary potential of the different lineages.

In our model, we observe dynamic patterns of genome structuring that operate on different evolutionary timescales. We have found the following scenario for a typical evolutionary run of our model: A population of cells that starts out ill-adapted goes through a phase of fast adaptation that is initially accompanied by a large increase in genome size and that is generally followed by rounds of adaptive gene loss. After this fast adaptive phase, the evolution takes on a neutral character, with long periods of fitness stasis. During this phase, mutational load due to secondary effects of neutral genes is alleviated. Streamlining but also quenching of the mutational effects of neutral genes are important in load reduction. As a consequence, the average fitness but not the maximum fitness in the population steadily increases due to the neutral evolution of mutational robustness (van Nimwegen et al. 1999). When the evolving neutrality of the genome structure leads to the formation of highly neutral stretches of genes, this improves the evolvability of the system by providing a flexible repertoire of potentially adaptive genes.

This scenario mimics the major patterns in gene content evolution, inferred from phylogenetic analysis. Because we showed that these patterns emerge as generic properties of evolving populations of cells with structured genomes and a flexible functional mapping, our scenario gives a possible unifying explanation for the observations in the data. We argue that genome complexification followed by gene loss is to be expected and is achieved by an alternation of rapid bursts of duplications during adaptive phases and long phases with slow streamlining dynamics.

A striking feature of our model of genome size evolution is the highly predictable occurrence of genome expansions during early adaptive evolution. Although size variation in our model is a governed by duplication patterns of a limited set of gene types, our observation can help explain the remarkably large gene complements of common ancestors of the major kingdoms (Snel et al. 2002; Makarova et al. 2005; Ouzounis et al. 2005; Csűrös and Miklós 2009; David and Alm 2010; Zmasek and Godzik 2011). The expansion dynamics that we describe are in agreement with big bang dynamics during the major transitions in evolution (Koonin 2007, 2010). Within the big bang hypothesis of evolution, fast inflationary dynamics are a generic property of an evolutionary process that exploits unparalleled new levels of complexity. There are indications that big bang type events have been triggered by dramatic changes in environmental conditions (De Bodt et al. 2005; Fawcett et al. 2009; David and Alm 2010). Specifically in eukaryotes, whole genome duplication events have been linked to the occupation of new niches (Scannell et al. 2006; Van de Peer et al. 2009; van Hoek and Hogeweg 2009) and the survival of lineages during drastic environmental changes (De Bodt et al. 2005). Taken together, the pattern that we observe in our model and that has been postulated by Francino (2005) as an important mechanism for short-term adaptation, appears to be generic and occurring on many different evolutionary timescales.

Our virtual cells can also be seen as rising to the challenge of a drastic change in the environment for which they start out ill-equipped. We found that a combination of adaptive and neutral aspects of genome complexification explains why inflationary dynamics are prevalent in successful surviving lineages. A bias in the early fitness landscape of ill-adapted cells with small genomes accounts for a net fixation of duplications in the line of descent. Moreover, lineages stemming from an early common ancestor with a larger bias toward beneficial duplications have larger genome expansions. Lineages that had the largest early expansions had the best chance to adapt fully. An important contributing factor to the future success of lineages in our simulations is extensive hitchhiking to higher copy numbers of genes that are adjacent to the primary targets of dosage increasing duplications on the genome. Indeed, results of runs where duplications and deletions have been implemented as mutations affecting individual genes instead of connected stretches, but otherwise equal mutation rates, show almost no expansion pattern and a much lower success rate (further discussed below). This suggests that the hitchhiking due to spatial linkage in gross chromosomal rearrangements ( GCRs) is crucial in supplying the building blocks for successful adaptation. Interestingly, a mechanism of short-term adaptation by GCRs in yeast (Ferea et al. 1999; Dunham et al. 2002) has been explained by structuring of the genome on an evolutionary timescale (Crombach and Hogeweg 2007).

Although we assume no explicit bias in the rate of gene deletion compared with duplication, loss of genes is a prominent feature in our model, occurring in an adaptive as well as a neutral context. Differential gene loss following species radiation is an often observed pattern in phylogenies (Scannell et al. 2006; Zmasek and Godzik 2011), although the mechanisms behind it are not well understood. Convergent gene loss is particularly prominent in the evolutionary histories of obligate endosymbionts (van Ham et al. 2003; Sakharkar et al. 2004; Khachane et al. 2007) and is usually ascribed to a manifestation of Muller's ratchet. In contrast, in our model, gene loss does not necessarily entail a loss of functional capacity. This is illustrated in our networks, where streamlining always proceeds with full preservation of fitness. Even genes with significant fitness contributions can later drift to redundancy and become subject to streamlining due to compensatory effects.

In computational modeling, choosing reasonable parameters for simulations is an important issue. In the case of evolutionary modeling, one can make a distinction between the parameters of the model universe, invariant conditions that the system evolves to cope with, and those parameters that bear on the problem that is being studied, in our case mutational parameters. The former type of parameters, such as resource conversion rate, protein degradation rate, etc., have been kept constant in all simulations. By performing additional simulations, varying mutational parameters in an informative way, we found that our main results of the inflation and streamlining pattern remain valid when we varied the rates of mutations but could not be fully reproduced when the nature of genome scale mutations was changed from targeting stretches of genes to single genes, (See supplementary table S1, Supplementary Material online). The lack of adaptive success when the spatial structure of duplications and deletions is ignored, underlines the importance of the hitchhiking mechanism in our standard runs for the rapid expansion pattern as well as its long-term adaptive effect.

Another issue in computational modeling is the question to which extent simplifications may influence the observed phenomena. In order to focus on regulatory mechanisms in cells, we have ignored microscopic processes like protein stability, which has the potential to restrain genome size, due to toxic effects of misfolding. We have shown that in our model, strong negative selection on longer genomes is present, due to the associated mutational load, triggering a streamlining process. Only after prolonged evolution does neutrality evolve, which sometimes leads to neutral size fluctuations. In our opinion, adding protein stability would not qualitatively (although possibly quantitatively) alter the pattern of expansion and streamlining that we have presented in this work.

Focusing on population size, the scenario that we presented has pronounced differences as well as interesting parallels with theories that consider the lower efficacy of purifying selection in organisms with small population sizes to be the primary cause of the expansion of their genomes (Lynch and Conery 2003a, 2003b; Teichmann and Babu 2004; Lynch 2006b, 2007). Instead of a gradual increase in genome size as a result of a reduced selection against slightly deleterious mutations, we see sudden expansions due to rounds of duplications of adaptive, as well as hitchhiking, neutral genes. Counter to the expectation from the latter theory that an increase in selective power should necessarily lead to streamlined genomes, we found that in 10-fold larger populations neutral size fluctuations occur more frequently and are much more pronounced. In agreement, however, streamlining prior to these large fluctuations proceeds significantly faster in larger populations. Small populations, on the other hand, have similarly enhanced streamlining and fluctuation trends when evolutionary time is increased.

Taking a leap of faith, we may attempt to understand the specific case of the genomic complexity in the eukaryotic kingdom in the light of the scenario that we have outlined. Endosymbiogenesis undoubtedly presented a major adaptive challenge to the functional capacities of the newly fledged symbiotic organism. It is telling that the gene content of the last eukaryotic common ancestor was estimated to have increased to almost twice the size of the first common ancestor of eukaryotes by extensive paralogization (Makarova et al. 2005). At least two more inflation events have been characterized in the eukaryotes at the roots of eumetazoa and vertebrata, respectively (Zmasek and Godzik 2011). At the same time, streamlining is an ongoing process in eukaryotes.

Typically, timescales of eukaryotic diversification are much shorter than those of prokaryotes (Sheridan et al. 2003; Battistuzzi et al. 2004; Chernikova et al. 2011). For example, the ancestor of mitochondria is inferred to cluster within the α-proteobacteria within close range of rickettsiales (Sicheritz-Pontén et al. 1998; Kurland and Andersson 2000), which, given a minimal age of the eukaryotic lineage of 1 G years (Chernikova et al. 2011) amounts to a divergence time that is in stark contrast to the, in evolutionary terms, extremely short divergence times of the large mammalian divisions of approximately 100 Myr (Archibald 1999). We have stressed that streamlining is a slow process compared with genome expansion. For eukaryotic evolution, the possible implication is that inflationary bouts have come in such quick succession that not enough time has passed to bring eukaryotic gene content back to the levels seen in prokaryotes. On the other hand, similar to the evolution of neutral size diversity in a subset of our simulations, eukaryotes appear to have evolved a coding structure that supports a high level of neutrality in genome size variation, with closely related species showing many fold differences in genome size (Gregory 2005, p. 12–24) and evidence for significant levels of within-species variation (Redon et al. 2006).

Concluding Remarks

An interplay of adaptive and neutral evolutionary processes leads to a characteristic pattern of genome expansion and gradual streamlining of genomes. More specifically, genome structuring and evolutionary adaptation in a population of cells to a fluctuating environment feed back on each other to accommodate robustness to ongoing mutations as well as evolvability in terms of genetic variability on a population level. A perfect example of this interplay is the evolution of neutral genetic material that serves as potential building blocks in subsequent adaptive evolution. Early expansions, although driven by adaptations to environmental conditions, increase evolutionary potential due to neutral hitchhiking of stretches of genes. No biases in large-scale mutations nor explicit costs on genome size were assumed, leading to the conclusion that patterns are entirely dependent on the interplay of the adaptive and neutral processes described above. This interplay depends crucially on a flexible mapping that yields a high degree of freedom for the evolving coding structure.

Our work makes the case for sufficiently complex models to study a problem that is as large and as far reaching as the evolution of genome sizes. At the same time, it should be possible to fully analyze and interpret the mechanisms that lead to pattern formation in silico. Here, we find general principles of evolving biological systems that can be used to interpret a range of remarkable patterns found in phylogenetic data.

The challenges in future modeling efforts lie in facilitating true species radiation and niche occupation in our model without sacrificing the possibility for detailed analysis. Succeeding in this approach can link our work even closer to specific standing puzzles, such as the unparalleled diversification of species during the Cambrian explosion, multifurcating patterns of radiation of the eukaryotic phyla, and the impact of drastic environmental changes on rates of genome evolution.

Supplementary Material

Supplementary tables S1 and figures S1–S3 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).