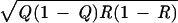The optimal measure of allelic association

Abstract

Allelic association between pairs of loci is derived in terms of the association probability ρ as a function of recombination θ, effective population size N, linear systematic pressure v, and time t, predicting both ρ_rt, the decrease of association from founders and ρ_ct, the increase by genetic drift, with ρ_t = ρ_rt + ρ_ct. These results conform to the Malecot equation, with time replaced by distance on the genetic map, or on the physical map if recombination in the region is uniform. Earlier evidence suggested that ρ is less sensitive to variations in marker allele frequencies than alternative metrics for which there is no probability theory. This robustness is confirmed for six alternatives in eight samples. In none of these 48 tests was the residual variance as small as for ρ. Overall, efficiency was less than 80% for all alternatives, and less than 30% for two of them. Efficiency of alternatives did not increase when information was estimated simultaneously. The swept radius within which substantial values of ρ are conserved lies between 385 and 893 kb, but deviation of parameters between measures is enormously significant. The large effort now being devoted to allelic association has little value unless the ρ metric with the strongest theoretical basis and least sensitivity to marker allele frequencies is used for mapping of marker association and localization of disease loci.

Dependence of alleles at two loci is called allelic association, gametic association, or linkage disequilibrium (LD). It has long been of interest for evolutionary genetics (1) and now has become a focus for genetic epidemiology. Its applications include localizing genes of unknown sequence (positional cloning), determining whether a particular allele is descended from a single founder (monophyletic), identifying regions of unusually high or low association that may reflect variations in recombination or a selective sweep, and recognizing effects of population structure and history. Many metrics have been used for LD, for most of which there is no genetic theory (2, 3). Some measure statistical significance and are therefore sensitive to sample size. All metrics are sensitive to variations in marker allele frequencies, and some are acutely sensitive in comparisons of expected and simulated LD. This variability has become increasingly important as many researchers explore LD in different chromosome regions and populations. Their observations are ineffectual unless they use the metric with the strongest theoretical basis and least sensitivity to marker allele frequencies. Fortunately, the two optima coincide. Here we derive genetic and statistical theory and examine the performance of alternative metrics on large samples of random haplotypes.

Genetic Theory

Let the four haplotype frequencies in a random sample for two diallelic loci, A and B, be arranged as in Table 1 with π₁₁ π₂₂ ≥ π₁₂ π₂₁, π₁₂ ≤ π₂₁, and Q ≤ R, 1 − Q. These constraints can always be satisfied by exchanging rows and columns. As Q/R decreases, the probability increases that A¹ is the youngest allele that by chance arose in a gamete carrying B¹. Because π_ij is a linear function of ρ ≥ 0, Table 1 may be written as a commingling of two tables

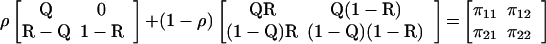1

with 0 ≤ ρ ≤ 1 defined as the association probability. Given the observed haplotype frequencies, all other measures of association are functions of Q, R, and ρ. Under certain conditions to be examined, ρ is an estimate of the probability that a random haplotype has descended without recombination from a founder population in which π₁₂ was zero, whereas the complementary class with frequency 1 − ρ has undergone at least one crossover between the loci and so the alleles are independent. When ρ = 0, there is linkage equilibrium. When ρ = 1, there is complete disequilibrium. However, this limit was not reached for the founder population if the A¹ B² haplotype was polyphyletic because of gene conversion, population admixture, or recurrent mutation.

Table 1.

Haplotype frequencies in a random sample

Locus A	Locus B		Allele frequency
	Allele 1	Allele 2
Allele 1	π11 = Qρ + QR(1 − ρ)	π12 = (1 − ρ)Q(1 − R)	Q = π11 + π12
Allele 2	π21 = (R − Q)ρ + R(1 − Q)(1 − ρ)	π22 = (1 − R)ρ + (1 − Q)(1 − R)(1 − ρ)	1 − Q = π21 + π22
Allele frequency	R = π11 + π21	1 − R = π12 + π22	1

Population genetics theory provides the expected association ρ_t in the tth generation after founders. Association between loci plays the same role as identity by descent in kinship theory, except that it deals with one gamete instead of two and the initial value ρ₀ need not be zero. For loci A and B, a random haplotype in generation t is identical by descent from a specified haplotype in t − 1 with probability 1/2N_t−1, where N_i is the effective population size in the ith generation. In the complementary event, the probability that a random haplotype in t − 1 has undergone no recombination since the founder generation is ρ_t−1. Therefore the association probability is

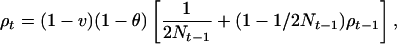2

where v is the linear pressure toward linkage equilibrium from migration and mutation and θ is the recombination frequency. The role of N is to describe stochastic variation, and the role of v is to ensure that over many generations the allele frequencies remain realistically close to their present values. This recurrence satisfies

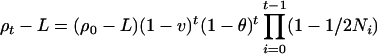where L is the association as t → ∞.

As implied by Crow and Kimura (4), we may equate Π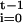 (1 − 1/2N_i) to e^−t/2N, where N is the unknown effective size over the unknown sequence N₀, N₁, … , N_t−1. This is a definition of N, not an approximation, and so the N_i may be constant, randomly varying, exponentially increasing, or an arbitrary sequence, for a change in the order of the N_i does not alter ρ_t. Because t is large relative to v and θ, we may take (1 − v)^t (1 − θ)^t = e^−(v+θ)t. Rearranging, we finally obtain

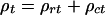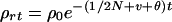3

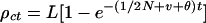where ρ_rt is residual kinship that declines from ρ₀ in founders, and ρ_ct is the increasing kinship caused by drift from founders. As t increases, ρ_rt → 0 and ρ_ct → L. If N is constant,

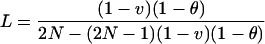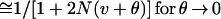4

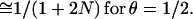Whether N is constant, ρ_t may be expressed as

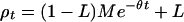5

where M = (ρ₀ − L)e^−(v+1/2N)t/(1 − L).

The exponential term in M is nearly zero if v + 1/2N ≪ 1/t, and then M = 1 if ρ₀ = 1. A value of M not significantly less than 1 is consistent with monophyletic inheritance and a relatively short history. A value of M significantly less than 1 is evidence for ρ₀ < 1, and in that sense for polyphyletic origin. Mutation and gene conversion are not negligible over large t, and so polyphyletic origin is likely for a common marker in a large population.

Most population genetics theory deals not with a single path between generation t and the founders but with a double path from founders to two gametes in t (e.g., ref. 4, equation 6.6.2). Sved (5) derived a theory for kinship ϕ, the probability that locus B is identical by descent (ibd), conditional on ibd for locus A. This double path replaces 1 − θ by (1 − θ)², the term e^−t/2N remaining the same. For constant N, the limit of ϕ_t as t approaches infinity is 1/(1 + 4Nθ) for small θ, and 1/(1 + 6N) for θ = 1/2 (ref. 5, equations 6 and 7). Because kinship does not have a simple relation to LD, we shall not pursue it.

Association as a function of time is not observable except in replicate populations simulated over large t. The theory becomes much more useful when time is transformed into distance along the chromosome, replacing θt by ɛd where ɛ is assumed constant for a specified region and d is the distance between loci on the genetic scale as centimorgans (cM) or on the physical scale as kilobases (kb). The association at distance d is predicted as

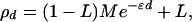6

which is the Malecot equation for isolation by distance (ref. 6, p. 84; ref. 7, p. 75; and ref. 8, equation 3). Let z be the number of distance units per morgan, or 100 if d is expressed in cM and the genetic map is accurate. If the physical scale is used, distance is more precise but proportionality of the genetic and physical scales is assumed and the value of z is uncertain. The rule of thumb that equates megabases (Mb) with cM predicts z = (100 cM/morgan) (1,000 kb/Mb) = 10⁵ if z is expressed in kb, but there is as much variability in z as in mutation rates. The estimated duration is zɛ generations, and the swept radius over which M is reduced by e⁻¹ and LD is useful for positional cloning is 1/ɛ. Whether the Malecot equation is expressed in terms of t, cM, or kb, the L parameter predicts association between unlinked loci, and so provides an efficient alternative to the transmission disequilibrium test that requires family data and makes no use of homozygous parents and their children (9).

The Malecot equation or other realistic model for LD has several advantages. The parameters are meaningful and they illuminate differences among populations and chromosome regions. Oligogenes with effects on a particular phenotype large enough to be detectable by current methods have a density less than 1 per morgan. If the model is fitted to n markers in such a large region to test the null hypothesis that ɛ = 0, there is no need for a Bonferroni correction that would increase the critical logarithm of odds (lod) from 3 to at least 3 + log n if the markers were tested individually (10). Therefore, testing each marker individually has low efficiency by comparison with the Malecot model.

Statistical Theory

An estimate ψ̂ of an association metric with expected value ψ has an amount of information, K_ψ, that allows for simultaneous estimation of Q and R but not for the evolutionary variance that accumulated over time. If n independent samples are tested and m parameters are estimated, the composite likelihood is exp [−∑_i(ψ̂_i − ψ_i)²K_ψi/2], where the quadratic form has a χ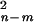 distribution under a true hypothesis. Several of the alternatives to ρ are of the form ψ = D/C, where C is a function of Q and R only and so C = ∂D/∂ψ and K_ψ = C²K_D. They include the covariance D, the correlation r, the frequency difference f, and the regression b (Table 2). Other alternatives to ρ are of a more complicated form in which ∂D/∂ψ is a function of D. Examples of this class are D²/C, δ, and the Yule (12) metric y (two or more other symbols have been used for all these metrics). If ψ = D²/C, then ∂D/∂ψ = C/2D, a function of association that is indeterminate under the null hypothesis. Therefore metrics like ρ², r², and f² should be avoided. The δ metric approaches ρ as Q → 0 and is invariant under case-control sampling. It is defined as δ = |π₁₁ π₂₂ − π₁₂ π₂₁|/Q π₂₂ = D/[Q (1 − R − Q + RQ + D)]. The efficiency of δ relative to ρ decreases as Q increases. The asymptotic standard error for ln(1 − δ) (11) implies K_δ = 0 if π₂₁ = 0. For determinacy and comparability, we take D = Cψ, ∂D/∂ψ = C²/[C − D(∂C/∂D)], and K_ψ = K_D(∂D/∂ψ)². On the null hypothesis, ∂D/∂ψ = C, and χ² = δ² K_δ. Yule's measure (12) is y = (π₁₁ π₂₂ − π₁₂ π₂₁)/(π₁₁ π₂₂ + π₁₂ π₂₁) = D/[2Q (1 − Q) R(1 − R) + D (1 − 2Q)(1 − 2R) + 2D²]. Yule (12) gave the information in an expression that is quartic in y and goes to zero if any of the π_ij is zero. This problem can be solved in the same way as for δ. Table 2 provides ψ̂ and K_ψ, distinguishing between the predicted covariance D and its estimate D̂.

Table 2.

Measures of allelic association ψ in random haplotypes

Definition	Symbol	Estimate ψ̂ = D̂/C
Covariance	D	D̂= |π11π22 − π12π21|
Association	ρ	D̂/Q(1 − R)
Correlation	r	D̂/
Regression	b	D̂/R(1 − R)
Frequency difference	f	D̂/Q(1 − Q)
Delta	δ	D̂/Q(1 − R − Q + RQ + D)
Yule	y	D̂/[2Q(1 − Q)R(1 − R) + D(1 − 2Q)(1 − 2R) + 2D2]

D̂ is an estimate with expected value D and information K_D. 

K_D = n/[Q(1 − Q)R(1 − R) + D(1 − 2Q)(1 − 2R) − D²] (ref. 34, equation 3.8). 

If there is no doubt about a candidate region, K_ψ should be evaluated under the null hypothesis that D = 0, but this is not optimal once a candidate region has been demonstrated and the goal is to obtain the most accurate estimates of the Malecot parameters, perhaps including the location S of a gene affecting a quantitative trait or disease. Under H₁, both ψ and K_ψ depend on D. The allass program has an option to estimate ψ and K_ψ simultaneously (http://cedar.genetics.soton.ac.uk/public_html). We find that this refinement has little effect on estimates and standard errors, and does not increase the relative efficiency of alternatives to ρ₀.

Under the Malecot model, as many as four parameters may be estimated: M, L, ɛ, and S, the location of a disease locus as a function of distance (13). The most general model may be rejected because of a type I error, significant evolutionary variance, nonindependence of samples, variable recombination, map error, or other departure from the model. Then subhypotheses may be tested by using the quadratic form as an error sums of squares with n − m degrees of freedom. The optimal metric consistently minimizes the sums of squares. Because the optimum is chosen on general considerations and not on the sample in hand, confidence intervals are not invalidated by choice of an extremum (14).

Materials and Methods

We applied these methods to several large samples of haplotypes. Two studies observed X chromosomes in males, the other inferred autosomal haplotypes. Ennis et al. (15) studied more than 7,000 haplotypes for 8 markers in the FRAX region, spanning 790 kb (1.36 cM) on chromosome Xq27–q28. They include two trinucleotide repeats (FRAXA and FRAXE) that were the focus of the study, 5 dinucleotide repeats (DXS548, FRAXAC1, FRAXAC2, DXS1691, and DXS6687), and a single-nucleotide polymorphism (SNP), ATL1. Nontransmitted haplotypes in mothers of typed males were inferred, assuming no crossover in transmission to the son. This assumption was supported in pedigrees and has minimal error in mother–child pairs. Pre- and full-mutation haplotypes and haplotypes identical by descent from a pedigree founder were excluded to make the gametes representative of the Wessex population. Each common allele or set of alleles of similar size was tested against the other markers to reduce the data to 2 × 2 tables by an algorithm that works well with major loci (13, 16). Taillon-Miller et al. (17) studied 39 SNPs in three populations: an outbred European sample (CEPH) and the more isolated populations of Finland and Sardinia. The SNPs were selectively in two small regions of 1 Mb in Xq25 and 340 kb in Xq28 that suggested strong LD. Eaves et al. (18) reported 21 microsatellites in a 6.5-cM interval on chromosome 18q31, with multiple alleles dichotomized around their modes. Families in four populations were studied (U.K., U.S.A., Finland, and Sardinia), yielding 800 unrelated haplotypes for each. Although the families were selected through insulin-dependent diabetes, the putative IDDM6 locus has a very small relative risk and ascertainment bias was not evident in comparison with affected family-based controls.

For each sample, we fitted the Malecot model with information evaluated under the null hypothesis and then estimated simultaneously. The general model for ɛ, M, and L gives a residual variance for testing the subhypothesis L = 0, which was often tenable over small intervals (<1 Mb). However, over much larger intervals, L was significantly greater than zero, often far too great to be attributed to a small effective population size and almost entirely because of bias in estimating association, which is constrained to be positive, because negative values have no useful interpretation. The bias for ψ is approximately 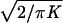, where K is the mean information per marker pair. Because the bias is relatively large when K_ψ is small, and K_ψ is proportional to sample size, the small samples tolerated by coalescence theory are unsatisfactory for allelic association. Ideally, L would be estimated in each study as the mean association for pairs of unlinked loci. All tests and standard errors are adjusted for the residual variance when it exceeded 1. Efficiency of ψ relative to ρ was estimated as the ratio of the residual variance for ρ to the residual for ψ. Goodness of fit to association parameters was determined by the χ² test. We analyzed ρ beginning with ML estimates for ψ, giving −2 ln lk = A. Then we estimated M (if M̂ < 1 for ρ) and L (if L̂ > 0 for ρ) to give −2 ln lk = B. Then, if the joint ML estimates for ρ give −2 ln lk = C with k = n − m degrees of freedom and C/k > 1, we took (A − B)/(C/k) as a χ² with 1 or 2 degrees of freedom testing goodness of fit of M, L, and (B − C)/(C/k) as χ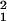 for goodness of fit of ɛ. These tests are conservative, because they treat ɛ̂, M̂, L̂ for ρ as parameters rather than as estimates for a correlated trait in the same sample.

Results

Estimates of ɛ for ρ range from 0.0011 to 0.0026, corresponding to swept radii of 893 and 385 kb, respectively (Table 3). M is estimated to be 1 in the chromosome 18 sample of microsatellites, which was dichotomized so as to conserve major modes and is therefore nearly monophyletic. On the contrary, the FRAX sample distinguished antimodal alleles that are known to be polyphyletic, and this is reflected in the smallest estimate of M, which has no genetic interpretation for metrics other than ρ. Earlier work established that L is not significantly different from zero in this 710-kb region (15). Estimates of L are greatest in samples with small values of information, K_ρ.

Table 3.

Estimates of parameters for association ρ under H₀ (distance in kb)

Sample	ɛ	σɛ	M	σM	L	σL	1/ɛ, kb
Xq, Wessex	0.00238	0.00012	0.604	0.013	0	—	420
Xq, CEPH	0.00255	0.00027	0.793	0.041	0.1276	0.0067	392
Xq, Finland	0.00204	0.00022	0.782	0.039	0.1215	0.0083	490
Xq, Sardinia	0.00112	0.00031	0.675	0.026	0.1300	0.0578	893
18, U.K.	0.00253	0.00014	1	—	0.0342	0.0104	395
18, U.S.A.	0.00260	0.00014	1	—	0.0320	0.0095	385
18, Finland	0.00212	0.00012	1	—	0.0515	0.0118	472
18, Sardinia	0.00234	0.00013	1	—	0.0331	0.0103	427

The six measures alternative to ρ provide 48 tests in the eight samples. In no case was the error variance as small as for ρ. Efficiency relative to association is extremely low for D and b and intermediate for r, corresponding to a loss of more than 20% of the information for f, d, and y and more than 70% for D and b (Table 4). This inefficiency was anticipated by the pilot study of Collins et al. (19), which found a relative efficiency of less than 60% for r. Relative efficiency of alternatives to ρ is exceptionally low in the FRAX sample from Wessex when information is estimated under H₁. Excluding this sample, there is little difference from the estimates under H₀. Convergence under H₁ is slower and the estimates and their standard errors are robust. This lack of improvement under H₁ is not surprising, because the evolutionary variance that exceeds the sampling variance is not modeled. All these metrics are confounded seriously with the gene frequencies Q and R (2). Devlin and Risch (3) simulated case-control samples from a population with initial frequency Q₀ = 0.01. We take δ as a benchmark, because this metric approaches ρ as Q approaches 0 and is then a surrogate for ρ. When the average variance among replicates within initial allele frequencies is used, δ has the highest efficiency, followed by |D′|_max, which equals ρ under random sampling but not in case-control samples (13). Goodness of fit to association parameters under H₀ is extremely poor (Table 5). Clearly, different measures are not equivalent, either for estimates or for error variances.

Table 4.

Efficiency relative to association ρ

Source	D	r	b	f	δ	y	|D′|max
Devlin and Risch (3),* H0	—	0.417	—	0.389	1.000	0.793	0.822
Collins et al. (19), H0	—	0.576	—	—	—	—	—
This study, H0	0.262	0.481	0.277	0.773	0.786	0.665	—
This study, except Wessex	0.476	0.610	0.505	0.703	0.652	0.540	—
This study, H1	0.134	0.231	0.141	0.278	0.449	0.372	—
This study, except Wessex	0.466	0.571	0.490	0.642	0.757	0.623	—

^*Case-control sampling. 

Table 5.

χ² goodness of fit to association parameters under H₀

Source	df	D	r	b	f	δ	y
M, L	11	8961	2024	3841	2656	609	3025
ɛ	8	48	32	87	32	170	316

Discussion

Classical population genetics considered D_ij for an arbitrarily specified haplotype, ij. If p_i, p_j are the corresponding allele frequencies, D_ij lies in the ± p_i p_j interval. Defined in this way, D_ij is as likely to be decreased as increased by genetic drift. This model leads to D_t = (1 − θ)^t D₀, which approaches zero as t increases, and does not attempt to explain the initial disequilibrium measured by D_t. The more perceptive geneticists recognized that genetic drift during population contraction was a likely cause, although selection and hybridization between previously isolated populations are not excluded. Hill and Robertson (20) remarked that “any restriction of population size may cause disequilibrium as a result of genetic sampling, and the return to equilibrium will be slow if the loci are tightly linked.” Sewall Wright (21) characteristically incorporated this reality into his evolutionary theory:

This bottleneck effect is greatest in cases in which the total population consists of small demes, each likely to become extinct after a few generations but, if so, always replaced sooner or later by a few stray migrants from populations that have persisted. In this way, every deme at any given time has a history of passage through a great many bottlenecks of small numbers on being traced back from place to place, and since a few momentarily flourishing demes may be the source from which many new colonies are founded, large areas or even the whole species may, in the course of time, trace to a single deme that has passed through many bottlenecks… .

The expected value of D_t is D₀ e^{−(1/2N+θ)t} in a closed population without mutation (22). This forward equation encounters allele fixation, which led Hill and Robertson (20) to conclude that the expected value of D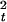 reaches a maximum and then declines to 0. Fixation is obviously irrelevant to a sample polymorphic in generation t, and Sved (5) noted that “the derivation of the recurrence relation is a backward calculation, since the value of [LD] is calculated conditional on the observed genotypic distribution in the present generation.” Sved was able to show that genetic drift can increase as well as decrease conditional identity by descent, which traces back to the founders and down to the current generation. This seminal result is not directly applicable to allelic association. However, partition of association into a decreasing term (ρ_rt) and an increasing term (ρ_ct) is made plausible by abandoning D_ij in favor of the probability ρ, which in random samples for two diallelic loci (but not for case-control samples) equals |D′_ij|_max, where D_ij was defined by Lewontin (23) as a maximum or minimum, without implying a probability. Limitation of ρ to the 0, 1 interval has the same effect as tracing a double path or taking E(D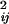), introducing a positive value of ρ_ct, as in Eq. 3. As with other evolutionary processes, LD now is modeled as the outcome of stochastic and systematic forces.

Whereas classical theory was preoccupied with change in time, current interest lies in change with distance along the chromosome. For the nominal equivalence of 1 cM to 1 Mb, nearly 700 generations (14,000 years) are required to go halfway to equilibrium at 100 kb (Table 6). For much smaller distances, the halfway time is large relative to duration of our species. Therefore, equilibrium is unlikely for distances less than 100 kb, and doubtful for greater distances.

Table 6.

Time to go halfway to equilibrium if θ ≫ v + 1/2N

Recombination, θ	cM	Nominal kb	Generations, t = (ln 2)/θ	Years, 20t
10−6	0.0001	0.1	693,147	13,862,940
10−5	0.001	1	69,315	1,386,294
10−4	0.01	10	6,931	138,629
10−3	0.1	100	693	13,863
10−2	1	1,000	69	1,386
10−1	10	10,000	7	139

During the last 2 years, less parsimonious models have been introduced, selecting the estimate that is closest to known location (14, 24, 25). The overparametrized Bayesian variant (26) uses a parameter termed “penetrance” that has no relation to that genetic concept or other biological property. The proportion 1 − M of disease alleles not derived from the major founder is miscalled penetrance, with the claim that “previous approaches fail to explicitly allow for this in their association models.” The best estimates of location by these methods agree with the Malecot model, but estimation with hindsight is not feasible for an unknown location, and haplotype-based methods are not applicable to genes with effects too small to be reliably assigned to a haplotype.

Estimation of time back to founders is central to coalescence theory but peripheral to allelic association. However, when time in number of generation can be inferred correctly from other evidence, it may be used in the Malecot model to estimate ɛ as t/z, where z is the number of distance units per morgan. If M = 1 and L = 0, a single marker with association ρ to a disease locus provides an estimate of distance as (−ln ρ̂)/ɛ. For example, the DSTST locus for diastrophic dysplasia was cloned positionally from this information (27). Because the disease is distributed evenly in Finland with a frequency of Q = 0.008, it was assumed that the mutation was present among the first Finnish settlers (t = 100). The integrated map available at that time, and currently, is consistent with z = 10⁵ kb/morgan and therefore with ɛ = 0.001. Association for restriction fragment length polymorphisms within CSF1R increases toward the centromere (28). The most proximal marker is EcoRI with ρ̂ = 0.94, about 64 kb away from the DSTST mutation with an error of about 8 kb. This precision was lucky, because the information about ρ under H₀ is K_ρ = χ²/ρ̂² = 268, and so the standard error is about 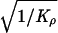/ɛρ̂ = 65 kb. The Malecot model under these simplifying assumptions is equivalent to the Luria–Delbruck model but is more general. For example, the three points, BT1, CSF1R/EcoRI, and CSF1R/TAGA, are consistent with ɛ = 0.001 and localize DSTST 88 kb proximal to the EcoRI marker with a standard error of 44 kb. No method has been demonstrated to have higher power than the association probability ρ under the Malecot model.

Turning now to marker × marker evidence, it is clear that most genomic regions have swept radii much greater than the 3 kb suggested by a recent simulation (29). Results in Table 3 are consistent with other reports of significant disequilibrium extending to several hundred kb (15, 19, 30–32). However, some small regions have much less or greater LD, which may be caused by a recombination hotspot, selection, or chance. Whatever the cause, an LD map can make positional cloning more efficient by adjusting the density of SNPs to be proportional to ɛ. Each SNP has its own value of ɛ, estimated by fitting the Malecot equation to ρ for all pairs with syntenic markers. Then, if two adjacent SNPs at distance d₁₂ have estimates ɛ₁, ɛ₂, their midpoint contributes [(ɛ₁ + ɛ₂)](d₁₂/2) to the LD map, the midpoint of the ɛ₂, ɛ₃ pair at distance d₂₃ contributes [(ɛ₁ + ɛ₂)](d₁₂/2) + [(ɛ₂ + ɛ₃)](d₂₃/2), and so on. Collins et al. (33) have shown how ɛ estimated for each SNP delineates the same transition from low to high LD in two populations, confirming the reliability of this approach. Our evidence on relative efficiency of association measures suggests that heterozygosity and other weakly correlated surrogates will give less reliable estimates than ρ in this application as in others.

Abbreviations

LD

linkage disequilibrium (= allelic association)

SNP

single-nucleotide polymorphism

cM

centimorgan