Model-based Confirmation of Alternative Substrates of Mitochondrial Electron Transport Chain

Background: There are alternative substrates to the mitochondrial respiration.

Results: Data-driven model-based analysis renders predictions of alternative substrates to the mitochondrial respiration.

Conclusion: Metabolomics data in conjunction with flux-based models can discriminate among hypotheses based on enzymology alone.

Significance: This analysis provides a basic framework for in silico studies of alternative pathways in metabolism.

Abstract

Discrimination of metabolic models based on high throughput metabolomics data, reflecting various internal and external perturbations, is essential for identifying the components that contribute to the emerging behavior of metabolic processes. Here, we investigate 12 different models of the mitochondrial electron transport chain (ETC) in Arabidopsis thaliana during dark-induced senescence in order to elucidate the alternative substrates to this metabolic pathway. Our findings demonstrate that the coupling of the proposed computational approach, based on dynamic flux balance analysis, with time-resolved metabolomics data results in model-based confirmations of the hypotheses that, during dark-induced senescence in Arabidopsis, (i) under conditions where the main substrate for the ETC are not fully available, isovaleryl-CoA dehydrogenase and 2-hydroxyglutarate dehydrogenase are able to donate electrons to the ETC, (ii) phytanoyl-CoA does not act even as an indirect substrate of the electron transfer flavoprotein/electron-transfer flavoprotein:ubiquinone oxidoreductase complex, and (iii) the mitochondrial γ-aminobutyric acid transporter has functional significance in maintaining mitochondrial metabolism. Our study provides a basic framework for future in silico studies of alternative pathways in mitochondrial metabolism under extended darkness whereby the role of its components can be computationally discriminated based on available molecular profile data.

Introduction

The development of mathematical models of metabolic processes is based on accurate gene annotations and functional characterization of the involved enzymes. However, the systems biology paradigm has already recognized that an accurate description of metabolism involves more than a mere enumeration of its components (i.e. enzymes and metabolites). The promise of mathematical modeling lies in its potential to quantitatively encompass the multitude of scenarios under which a given biological process may operate and, as a result, elucidate which components contribute to the emerging behavior (1–8). For this purpose, the spatial separation of metabolites and biochemical reactions into their cellular compartments is an important feature to provide an accurate assessment of energetic limitations that may be lost in decompartmentalized models (9, 10). Nevertheless, the predictive power of decompartmentalized models can be increased by providing more realistic constraints and objectives (10). To this end, high throughput data from the recently established metabolomics profiling technologies have already proven invaluable in positing hypotheses related to the underlying mechanisms of investigated processes (11, 12). However, the usage of (time-resolved) high throughput data in devising and discriminating between models that can precisely capture not only a single environmental condition but also various internal and external perturbations is still in its nascent stages and strongly depends on the employed computational approaches.

Metabolic network analysis has provided numerous approaches for in silico probing of biological processes in order to elucidate, to understand, and, ultimately, to control the underlying biochemical mechanisms (13, 14). For instance, flux balance analysis (FBA),³ as one of the prominent computational approaches, facilitates the analysis of steady-state fluxes in metabolic networks assumed to operate toward optimizing an objective (e.g. biomass yield) under the constraints captured by the stoichiometric matrix (2, 15–19). However, perturbed metabolic networks, altered by removing reactions, may not obey the assumptions inherent to FBA. To determine the flux distributions in a perturbed metabolic network, the minimization of metabolic adjustment (MOMA) approach has been proposed, based on the hypothesis that fluxes undergo a minimal redistribution compared with those of the unperturbed network (20). Nevertheless, FBA and MOMA are based on the steady-state assumption and, thus, preclude the analysis of the dynamics of metabolite levels and flux (re)distribution.

The dynamics of metabolic networks has traditionally been investigated by methods rooted in ordinary differential equations, which require a large amount of information for simulating the temporal changes of metabolite concentrations/levels and reaction fluxes (21, 22). To this end, the phenomenological parameters of specific enzyme kinetics (e.g. mass action, Michaelis-Menten, or Hill) have to be determined by accurate measurements of enzyme activities and data fitting to experimentally obtained data, constraining the application of these methods to well studied systems of moderate size and complexity.

In contrast, dynamic FBA (DFBA) offers an alternative to predicting time-resolved metabolic profiles with limited knowledge of enzyme kinetics (23). Moreover, DFBA has been combined with MOMA, resulting in the so-called M-DFBA approach based on the hypothesis of minimal fluctuation of the dynamic profile of metabolite levels over time (24, 25). Unlike the analyses based on FBA, which focus on the steady-state behavior, DFBA and M-DFBA offer the means to analyze transient (non-steady) states. M-DFBA has recently been employed in predicting time-resolved metabolite concentrations and flux (re)distributions in photosynthetic metabolism under different CO₂ and water conditions (25) and in reconstructing the network of the myocardial energy metabolism under normal and ischemic conditions (24). However, although these approaches have resulted in establishing viable hypotheses related to the system's dynamics (here represented by stoichiometry-constrained polynomial-based approximation), to our knowledge, their quantitative accuracy with respect to experimental data has not yet been tested. Therefore, further investigations of the capacity of constraint-based approaches to pose and validate data-driven hypotheses in a dynamic setting are required, particularly with respect to recently raised issues related to the effect of different optimization criteria (26, 27).

In plants, like other organisms, the functional involvement of the electron transfer flavoprotein-electron transfer flavoprotein:ubiquinone oxidoreductase (ETF-ETFQO) complex has recently been demonstrated (28). It participates in an important mechanism by which the cell can sustain respiration under conditions in which carbon supply is severely compromised (1, 28). In fact, detailed enzymological studies, broad metabolite profiling, and isotope tracer studies of a range of Arabidopsis t-DNA knock-out mutants have ultimately led to the elucidation of the pathways linking the alternative plant substrates to the mitochondrial electron transport chain (ETC) (1, 29, 30). Furthermore, it has been demonstrated that alternative pathways are not constitutively active (1) and that they are coordinated with a general increase in protein and amino acid degradation (31).

In this study, we devise and apply an extension of M-DFBA to 12 different model variants of the mitochondrial ETC in Arabidopsis thaliana during dark-induced senescence in order to elucidate alternative substrates of this important pathway. This is achieved by statistically sound model discrimination based on determining the likeliest model complying with the experimental measurement of metabolite levels. Moreover, the model is validated not only for the wild type but also for four mutant lines (see Fig. 1). We opt for A. thaliana as opposed to other microbial or mammalian models due to the availability of data across a relatively broad time scale (1). That said, variations on these varying inputs are conserved across kingdoms; indeed, genetic defects in paralogous inputs to the Arabidopsis system are responsible for multiple mammalian diseases (32–35), indicating the broad physiological importance of these alternative inputs into the key respiratory pathway catalyzed by the mitochondrial ETC (36). Our findings demonstrate that the coupling of the proposed extended M-DFBA approach and time-resolved metabolomics data results in an accurate description of the dynamic behavior of metabolite levels following the onset of dark-induced senescence in Arabidopsis thaliana. The predictions from the modeling are in line with the experimental data despite the simplification regarding metabolite compartmentalization (i.e. the mitochondrial and extramitochondrial pools are considered to be in equilibrium). However, this is perhaps not surprising given the size and substrate diversity of the mitochondrial carrier family (37) alongside the physiological evidence of rapid metabolite exchange across the mitochondrial membranes (38). Furthermore, we show that the integration of metabolomics data facilitates the discrimination between different model alternatives in the case when only pathway stoichiometry is known. Finally, by using the experimentally validated M-DFBA models, we provide computational model-based confirmation that (i) under carbon starvation, isovaleryl-CoA dehydrogenase (IVDH) and 2-hydroxyglutarate dehydrogenase (D2HGDH) feed electrons into the ETC; (ii) phytanoyl-CoA does not act as a substrate of the ETF-ETFQO complex; and (iii) the γ-aminobutyric acid (GABA) transporter is of functional significance in maintaining normal mitochondrial metabolism in A. thaliana in conditions of extended darkness.

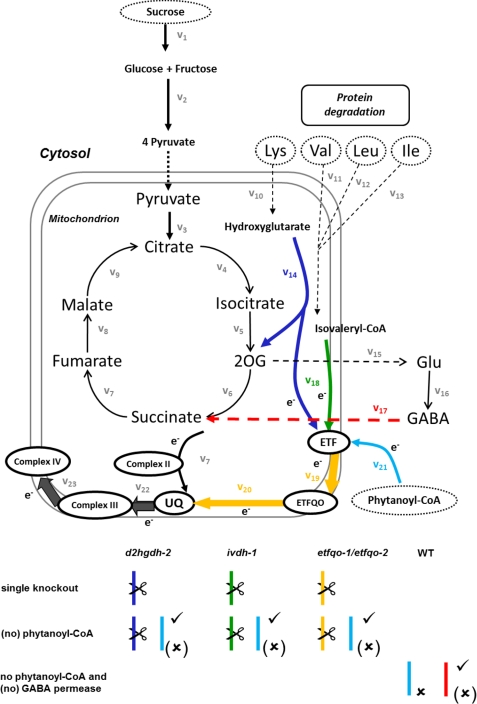
FIGURE 1.

Simplified electron transport chain network together with the considered model variants. The model variants for the single knock-out mutant lines are given in dark blue for d2hgdh-2, green for ivdh-1, and yellow for both etfqo-1 and etfqo-2, resulting in four alternatives. The model variants of the single knock-out mutant lines with exclusion of phytanoyl-CoA are highlighted in light blue followed by x. Analogously, the model variants of the wild type with exclusion of GABA permease are given in red followed by x. A check mark next to an enzyme denotes inclusion of the corresponding reaction in the investigated model variants.

MATERIALS AND METHODS

Experimental Data of Metabolite Levels

Metabolite profiles of wild type and mutant lines (ivdh-1, d2hgdh1–2, etfqo-1, and etfqo-2) during dark-induced senescence were obtained from a previous study (1). Metabolites were measured using the ninth to twelfth leaves of 4-week-old, short day (8 h light/16 h dark) grown Arabidopsis plants after treatment for 0, 3, 7, 10, and 15 days in extended darkness. The values for the absolute levels of metabolites used in modeling are the means obtained from six independent plants per genotype (see supplemental Table 2). Absolute levels were estimated based on concentration curves of authentic standard compounds that were run side by side with the samples.

Dynamic Flux Balance Analysis Based on Minimization of Metabolic Adjustment

DFBA has been developed to overcome the main drawback of the classical FBA which, due to the steady-state assumption, precludes the analysis of the network dynamics. Computationally, the DFBA approach involves optimization over a given time period to obtain time-resolved flux rates and metabolite levels. The optimization problem is rendered computationally tractable by parameterizing the dynamic equations with the help of orthogonal collocation on finite elements (39). To this end, the time period of interest is divided into a finite number of intervals, named finite elements. Furthermore, the metabolite concentrations/levels and flux rates are parameterized at the roots of an orthogonal polynomial (e.g. Legendre polynomial) within each finite element (23). A description of how this algorithm works is provided in the supplemental material.

The combination of MOMA with DFBA has been formulated by the objective function of minimizing the Euclidean distance between metabolite levels at adjacent orthogonal roots. Consequently, the objective function of the basic M-DFBA is defined as follows,

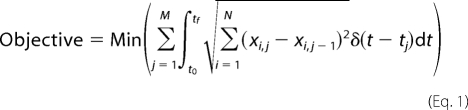where x_i,j represents the level of the metabolite i at the time point given by the orthogonal root j, and δ is the Dirac delta function (40).

Here, we extend the basic M-DFBA by including a minimization of the simulated data to experimentally obtained metabolite levels in order to improve the possibility of comparing the considered model alternatives (41). As a result, the objective function is expanded by the sum of the Euclidean distance between predicted levels and experimentally obtained values for all K measured metabolites over L time points. Note that, due to the particular experimental setting and the collocation points used in the parameterization, it always holds that K ≤ M and L ≤ N; in other words, it may be the case that the levels of few metabolites are measured at some collocation points. The nonlinear program used in solving this extended M-DFBA approach is then formulated as follows,

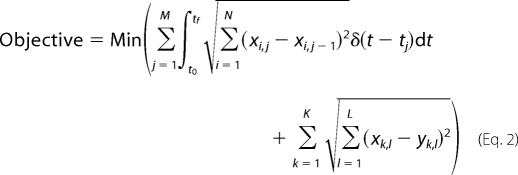subject to dX/dt = S·v, v_min ≤ v ≤ v_max, X_min ≤ X ≤ X_max, and X(t₀) = X₀, where X and v are vectors of metabolite levels and reaction fluxes over time, S denotes the stoichiometric matrix (with rows corresponding to metabolites and columns to reactions of the metabolic network described by S), and t is the time. Experimentally measured levels of metabolite k at time point l are denoted by y_k,l. The minimum and maximum allowable fluxes of each reaction and metabolite levels are defined by v_min and v_max and X_min and X_max, respectively. The vector X₀ gives the initial level for the set of metabolites.

Statistical Analysis

Let y_i,j represent the experimentally obtained level of the ith metabolite at time point (collocation point) j, and let x_i,j represent the level predicted by M-DFBA. In addition, let the number of time points, in our case collocation points, be given by M. We validate the results for the metabolite levels predicted by the modified M-DFBA with experimental data by using statistics based on the residual sum of squares (RSS). For the ith metabolite, this statistic is given by the following.

Experimental data for each orthogonal root are obtained by a cubic spline interpolation of the mean of measurements of six replicates for each plant at the five given time points. The residual sum of squares is only determined for the metabolites that are present in all modeling variants and for which experimental data are available.

The RSS statistics for the different metabolites do not provide a single value to denote how well the entire model fits the data. Moreover, these statistics strongly depend on the actual range in which metabolite levels may vary. Therefore, they cannot be used for a meaningful and fair comparison of models.

The most common method for model discrimination is performed by means of the F-test. However, the F-test can only be used if the compared models are nested (i.e. one is a simplification of the other). Moreover, the existing methods can be used to compare two models only when both of them are fitted to exactly the same data. In our setting, we do not have nested models for all pair-wise comparisons; in addition, we do not use the same data for any pair of mutants (see Fig. 2). Furthermore, a statistical analysis is only useful for these metabolites for which measured values are available, whereas only the metabolites that are present in all model alternatives lead to a significant comparison. Therefore, this setting of our analysis does not justify the usage of the F-test.

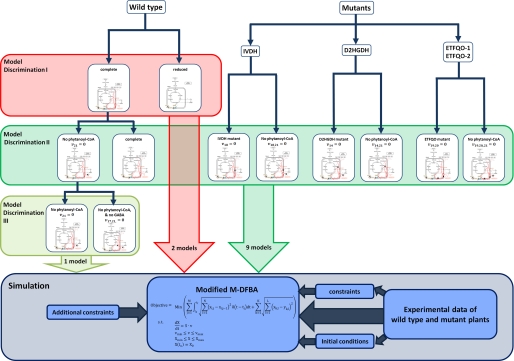
FIGURE 2.

Overall process of model analysis and discrimination. Model discrimination is initially carried out for the complete and the reduced model variants. The better performing model is subjected to two additional steps of model discrimination, each with the help of a different data set. The extended version of M-DFBA is used in conjunction with the available data sets at every level of model discrimination.

Another alternative for comparison of modeling alternatives is given by R-squared measures (R²), known as coefficients of determination. However, many R-squared measures strongly depend on the number of considered reactions and/or metabolites and, consequently, on the complexity of the compared models (42, 43).

Here, we use the explained sum of squares (R_exp²) for each metabolite defined as follows.

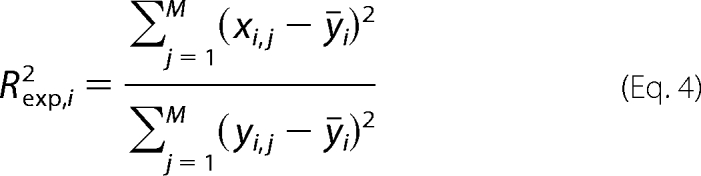Due to the usage of a nonlinear objective in the extended M-DFBA, the predicted values for the metabolite levels and flux rates may not linearly depend on the measured data. Consequently, the value of R_exp,i² may exceed unity in small samples; however, it does not need to increase due to an increasing model complexity. As a result, for model comparison, we used a modified R_exp,i², whereby in the numerator, the sample mean of experimental data, ȳ_i, is replaced by the sample mean of the fitted values x̄_i (42, 43).

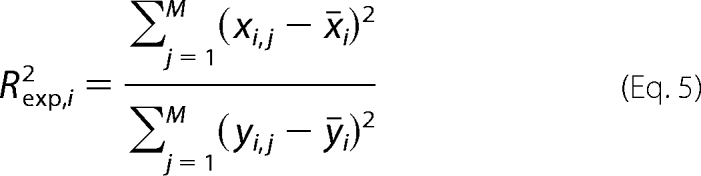The value of R_exp² for the entire model is the average of R_exp,i² over all considered metabolites; a larger value indicates better correspondence between model predictions and experimental observations.

Implementation

All mathematical programming approaches are implemented in MATLAB 7.8.0, R2009a with the optimization platform TOMLAB version 7.6 (44). We use SNOPT to solve nonlinear programming problems.

RESULTS

Modeling of Mitochondrial Electron Transport Chain of A. thaliana

Here we have constructed a simplified model of the ETC in the mitochondria of A. thaliana to formally describe the metabolic responses in plants under conditions of extended dark conditions and examined it by using different model variants. The model considers the basic tricarboxylic acid (TCA) cycle reactions as well as the involvement of other enzymes, such as IVDH and D2HGDH, which can supply electrons and carbon skeleton to the TCA cycle during dark-induced senescence in order to supply electrons to the ETC. Although it is clear that not only the classical phosphorylating pathways but also several non-phosphorylating pathways, involving NAD(P)H dehydrogenases, the alternative oxidase, and active uncoupling protein, have an effect on the mitochondrial metabolism (45), there is no evidence for alteration in their function in the analyzed mutants. It is also important to mention that sugars, the substrate of the main pathway of electron transfer, are almost fully consumed within a few days of darkness, whereas paradoxically some of the TCA cycle intermediates increase (1), indicating that they are not greatly catabolized, making the usage of alternative substrates such as those considered here essential for plant survival.

The process of the model analysis is divided into two parts: (i) model discrimination and (ii) simulation, depicted in Fig. 2. It should be noted that the experimentally obtained metabolite levels included in the modeling process belong to different cell types of the leaves and are not resolved with respect to subcellular levels. Therefore, the model is set up on a leaf rather than on a cell level. As a simplification of this leaf-based model, other substrates, such as NAD, are excluded. However, we point out that during dark-induced senescence, the main respiratory substrates are completely consumed within few days of stress (1, 29, 30, 46), making the presence of alternative pathways an essential condition to maintain respiratory rates, which further justifies the exclusion of other substrates of the ETC in the modeling.

Altogether, the model of the ETC in the mitochondria of A. thaliana during dark-induced senescence consists of 30 metabolites biochemically transformed via 39 reactions. Six of the metabolites, including phytanoyl-CoA, lysine, valine, leucine, isoleucine, and sucrose, are considered as external (depicted as dashed ovals in Fig. 1). Reactions 1 and 2 (v₁ and v₂) capture the transformation of sucrose into pyruvate, which then enters the TCA cycle (reactions 3–9 (v₃–v₉)). Reactions 15–17 (v₁₅–v₁₇) model the transport (from mitochondria to cytosol) and transformation of 2-oxoglutarate into glutamate, its subsequent conversion into GABA, and the experimentally confirmed transport (from cytosol to mitochondria) (47) and transformation of GABA into succinate. Reactions 14–23 (v₁₄–v₂₃) model the transport of electrons, whereas reactions 10–13 (v₁₀–v₁₃) model the import of the four (external) amino acids. From the 39 reactions included in the model, 29 are set as irreversible, with an unbounded maximal flux rate (see supplemental Table 1). Furthermore, as common practice in stoichiometry-based modeling, the reversible reactions are split into two irreversible reactions (48, 49).

As a central part of our study, the electron transfer between different metabolites (referring also to the proteins participating in this process) is modeled with the help of coupled reactions. Each metabolite involved in electron transfer can exist in two states, with or without a bound electron (e⁻), denoted by the subscripts c and p, respectively. To illustrate, the reaction modeling the transfer of an electron from ubiquinone (UQ) to complex III is modeled as follows,

where the subscript c denotes that both ubiquinone and complex III are with a bound e⁻. Because ubiquinone can also exist in a state without a bound electron, an additional reversible reaction is added, whereby the following is true.

The maximum allowable levels for the metabolites in a c state as well as for the e⁻ are unconstrained. On the other hand, in absence of data concerning the temporal behavior of metabolites in state p, the levels for the metabolites in this state are assumed to remain constant during the modeled time period. Such reaction coupling fully captures the mechanism of electron transfer. Finally, for every metabolite for which experimental measurements are available, the initial level at time point t₀ = 0 (X₀), is defined to be the mean of the available data (marked in red in supplemental Table 2); X₀ for pyruvate is set to 5000 μmol mg⁻¹ fresh weight; for the remaining metabolites, the initial levels are set to 1 μmol mg⁻¹ fresh weight.

By applying the extended M-DFBA approach, we model the metabolite levels and flux rates over a time period of 16 days, corresponding to the experimental design (1). This time period is divided into eight finite elements, and the metabolite levels and flux rates within each finite element (spanning 2 days) are predicted at five time points, corresponding to the collocation points. Therefore, altogether, the metabolite levels and flux rates at 40 time points are considered in the computational investigation.

Whereas the stoichiometric coefficients of the network are fixed by the biochemical reactions (see “Materials and Methods”), the bounds for the metabolite levels are adjusted by using the available experimental data (see supplemental Table 2). To this end, the minimum and maximum metabolite levels measured over the considered time interval were used as lower and upper bounds (X_min and X_max), respectively, for the internal and external metabolites. In addition, for the external metabolites, the metabolite level bounds at the orthogonal roots, coinciding with the measured time points, are set to the corresponding minimum and maximum measured levels. Moreover, the levels measured at the fourth time point, corresponding to 10 days, are used as constraints for the orthogonal root (collocation point) at 10.0938 days as a root of closest value. The levels of metabolites for which no experimental data are available were assumed to be ≥0 μmol mg⁻¹ fresh weight.

Model-based Confirmation of Posited Hypotheses

The predictions obtained from the model by using the proposed M-DFBA approach are in turn used to discriminate between different modeling alternatives representing the possible behaviors under dark-induced senescence. The model variant that predicts time-resolved metabolite levels closest to the experimental data will be considered as the likeliest model that can explain the electron transfer under the investigated conditions.

First, we focus on the behavior of the A. thaliana wild type during dark-induced senescence. Here, we discriminate between two different model variants: the first consisting of all considered components, including 30 metabolites and 39 reactions, and the second excluding the reactions 10–14 as well as 18–21, given in Fig. 1. Clearly, the exclusion of reactions 10–14 and 18–21 results in a submatrix of the stoichiometric matrix of the complete model.

The average residual sum of squares (RSS) for each metabolite is employed to demonstrate that the predictions for the metabolite levels are close to the experimental data, as summarized in the first and second row of Table 1, corresponding to the two investigated model variants. From the 11 metabolites for which RSS can be computed, the levels of the following four are closest to the time-resolved experimental data: GABA, glutamate, 2-oxoglutarate, and succinate. Larger discrepancies can be observed for glucose, fructose, sucrose, and malate. Taken together, the range of the values for RSS for both model variants confirms that M-DFBA can closely predict the time-resolved metabolite levels.

TABLE 1.

Average residual sum of squares (RSS) for each metabolite in the 12 considered model variants

Shown are the values of RSS for 11 metabolites whose levels have been experimentally measured: sucrose (suc), glucose (gluc), fructose (fru), citrate (cit), 2-oxoglutarate (2OG), succinate (succ), fumarate (fum), malate (mal), glutamate (glu), and GABA. The complete model includes all 30 metabolites and 39 reactions, whereas the reduced model variant excludes reactions 10–14 and 18–21, shown in Fig. 1. The model variant “No phyt-CoA” excludes phytanoyl-CoA as the electron donor via the ETF-ETFQO complex, whereas the model variant “No phyt-CoA and no GABA” excludes in addition the GABA permease (reaction 17) from the complete model. Values for RSS closer to zero indicate a better agreement between time-resolved predictions of metabolite level and the employed experimental data.

	Model	suc	gluc	fru	cit	iso	2OG	succ	fum	mal	glu	GABA
WT	Complete	159.02	221,230.76	191,918.84	48.34	9.38	28.93	5.57	0.82	103,723.82	26.95	0.95
WT	Reduced	1529.96	3005.61	2307.22	59.57	11.93	43.70	5.90	0.19	43,305.98	104.27	0.62
WT	No phyt-CoA	3415.16	5506.61	4338.30	58.51	8.42	52.44	6.09	0.04	44,943.25	285.25	0.95
WT	No phyt-CoA & no GABA	477.47	2065.20	819.33	19.48	0.99	14.69	1.42	0.02	43,507.80	24.90	0.08
d2hgdh1-2	Complete	488.61	135,187.01	155,327.49	122.87	2.57	0.63	19.18	207.76	127,850.79	1.22	1.51
d2hgdh1-2	No phyt-CoA	890.94	2482.94	947.50	165.81	64.27	2.79	28.58	307.95	852,055.93	5.02	1.56
etfqo-1	Complete	408.56	2943.75	1138.70	176.00	24.93	2.27	54.46	15.17	469,183.19	17.96	5.55
etfqo-1	No phyt-CoA	146.95	1354.74	583.71	14.16	31.34	0.91	46.62	14.74	657,855.62	3.96	2.89
etfqo-2	Complete	803.83	3524.91	1268.16	863.69	26.61	4.26	64.24	28.35	1,256,949.23	31.93	2.48
etfqo-2	No phyt-CoA	813.56	3136.59	1403.67	793.27	23.84	3.49	60.90	28.17	1,253,703.10	36.66	1.58
ivdh-1	Complete	976.12	5556.01	4530.74	115.37	122.38	0.89	16.64	9.37	719,997.15	4.39	0.73
ivdh-1	No phyt-CoA	1163.52	5959.82	4884.76	79.20	89.29	0.31	16.59	7.70	701,012.11	4.26	0.95

Averaging the values of RSS over all metabolites, however, cannot be used for selecting the model that best fits the experimental data (see “Materials and Methods”). To discriminate between the two model variants, we used the modified explained sum of squares (R_exp²), presented in Table 2. The value of 0.89 for the R_exp² in the case of the complete model is higher than that for the reduced model variant (0.8118). This finding indicates that the first model variant, which includes all considered reactions, provides the best fit to the data. As a result, we are able to not only ascertain the experimental data but also provide modeling support in confirming the hypotheses concerning the feeding of electrons into the ETC from IVDH and D2HGDH during dark-induced senescence (1). However, it should be noted that, although these pathways are particularly prominent during dark-induced senescence (1, 46), recent evidence suggests that they also operate in the dark period of a normal light-dark cycle in the photosynthetic tissue of Arabidopsis (50, 51).

TABLE 2.

Explained residual sum of squares (RSS) for each metabolite together with its mean and variance for the 12 considered model variants

Shown are the values of RSS for 11 metabolites whose levels have been experimentally measured: sucrose (suc), glucose (gluc), fructose (fru), citrate (cit), 2-oxoglutarate (2OG), succinate (succ), fumarate (fum), malate (mal), glutamate (glu), and GABA. The complete model includes all 30 metabolites and 39 reactions, whereas the reduced model variant excludes reactions 10–14 and 18–21, shown in Fig. 1. The model variant “No phyt-CoA” excludes phytanoyl-CoA as electron donor via the ETF-ETFQO complex, whereas the model variant “No phyt-CoA and no GABA” excludes in addition the GABA permease (reaction 17) from the complete model. A larger value for the mean RSS indicates a model with higher explanatory power.

	Model	suc	gluc	fru	cit	iso	2OG	succ	fum	mal	glu	GABA	Mean RSS	Variance RSS
WT	Complete	0.95	0.02	0.02	0.53	1.34	0.75	1.75	2.71	0.11	0.81	0.80	0.8900	0.6544
WT	Reduced	0.62	0.52	0.62	0.66	1.37	0.63	1.82	0.72	0.00	0.88	1.09	0.8118	0.2292
WT	No phyt-CoA	1.92	1.53	1.83	0.82	1.41	1.33	1.69	1.42	0.00	1.72	1.44	1.3736	0.2954
WT	No phyt-CoA and no GABA	0.88	0.69	0.82	0.60	1.12	0.75	1.38	0.94	0.01	1.07	0.95	0.8373	0.1224
d2hgdh1-2	Complete	0.87	0.33	0.36	0.91	1.02	0.95	1.42	0.86	0.68	1.06	0.85	0.8464	0.0951
d2hgdh1-2	No phyt-CoA	0.80	0.72	0.79	0.95	1.06	0.81	1.63	0.85	0.00	0.99	0.95	0.8682	0.1436
etfqo-1	Complete	1.31	1.09	1.51	0.84	1.14	0.82	1.49	1.41	0.04	0.78	0.64	1.0064	0.1949
etfqo-1	No phyt-CoA	1.06	0.91	1.26	1.07	1.12	1.01	1.59	1.36	0.01	1.07	0.84	1.0273	0.1579
etfqo-2	Complete	0.81	0.63	0.84	0.78	1.15	0.70	1.33	1.90	0.00	0.91	0.99	0.9127	0.2203
etfqo-2	No phyt-CoA	0.80	0.65	0.86	0.75	1.14	0.74	1.35	1.93	0.00	0.93	1.04	0.9264	0.2266
ivdh-1	Complete	0.70	0.48	0.51	0.92	0.82	0.77	0.97	0.80	0.00	0.93	1.02	0.7200	0.0876
ivdh-1	No phyt-CoA	0.67	0.45	0.48	0.88	0.80	0.87	0.95	0.80	0.01	1.00	0.98	0.7173	0.0897

Knowing that the complete model performs better, in the next step, we use it to predict the metabolite levels for four different mutant lines, namely ivdh-1 (green), d2hgdh1-2 (blue), and etfqo-1/etfqo-2 (yellow), described in the legend to Fig. 1. In this context, it should be mentioned that a metabolic model is only useful as long as it can explain not only wild type data but also data coming from different environmental and/or genetic scenarios. For this purpose, the maximum allowable flux rate is set to zero for reactions that are knocked out in the different mutants. By employing the submatrix of stoichiometries, corresponding to each of the four model variants, as input to M-DFBA, we observe that the resulting RSS values indicate a good agreement between the obtained predictions and experimental data (1). More specifically, GABA, 2-oxoglutarate, glutamate, sucrose, glucose, and fructose exhibit a small RSS, whereas moderate discrepancies between predictions and experimental data are observed for all other metabolites. The exception is malate, whose RSS in all model variants has a value higher than 40,000.

Moreover, the values for the modified explained sum of squares (R_exp²) of 0.72 and 0.8464 for the ivdh-1 and d2hgdh1-2 mutant lines, respectively, indicate that both IVDH and D2HGDH play an important conditional role in feeding electrons to the mitochondrial ETC in many diverse species (28, 31). Analogous conclusions can be elicited for the etfqo-1 and etfqo-2 mutant lines, whose model variants exhibit R_exp² of 1.0064 and 0.9127, respectively. That said, the fact that phytanoyl-CoA, as the chlorophyll breakdown intermediate, accumulates both in knock-out mutants of ETF-ETFQO complex and of IVDH following dark-induced senescence (1) suggests that it may also serve as a plant-specific substrate for this pathway.

For this reason, in the subsequent modeling steps, we analyze the barely explored influence of phytanoyl-CoA in transferring electrons into the ETC during dark treatment. For each mutant line, two model variants are considered in M-DFBA-based analysis: with and without electron feeding from phytanoyl-CoA. Interestingly, our findings demonstrate that phytanoyl-CoA does not act as a substrate of the ETF-ETFQO complex in A. thaliana during dark-induced senescence, a hypothesis put forth by Araújo et al. (46). This claim is quantitatively supported by the larger values for the R_exp² of the model variants without phytanoyl-CoA acting as substrate compared for three of the four model variants, corresponding to the mutant lines, namely d2hgdh1-2, etfqo-1, and etfqo-2. The computational findings presented in Table 2 indicate that the value of R_exp² for the ivdh-1 model variant with phytanoyl-CoA is larger by 0.0027 compared with that of the model variant without phytanoyl-CoA. Although this small discrepancy may still be indicative of phytanoyl-CoA acting as alternative substrate, closer inspection of RSS in Table 1 shows that for all metabolites, the model variant without phytanoyl-CoA results in predictions of metabolite levels that are consistently closer to the used experimental data. Additionally, these results are in good agreement with the recent finding that ivdh-1/d2hgdh1−2 double mutants have a phenotype similar to that of mutants of the ETF-ETFQO complex (46). Moreover, our findings suggest that alternative pathways of plant respiration occur independently of phytanoyl-CoA 2-hydrolase and its substrate, phytanoyl-CoA. It is important to mention that the maximum capacity of this alternative pathway is theoretically much lower than the respiratory rate in leaves.

Iterative Refinement of Confirmed Hypotheses

Our finding that phytanoyl-CoA does not act as a substrate of the ETF-ETFQO complex in plant mitochondrial metabolism holds true in the model variants for the four investigated mutant lines. In the following, we refine this confirmed hypothesis and show that it is also valid for the complete wild type model of plant mitochondrial metabolism (including all considered components). To this end, we compare the explained sum of squares R_exp² and RSS between the two variants of the complete model: with and without phytanoyl-CoA as alternative electron donor via the ETF-ETFQO complex. The computational findings presented in Table 2 indicate that the value of R_exp² for the model variant without phytanoyl-CoA is larger by 0.4836 compared with that of the model variant with phytanoyl-CoA.

Finally, we investigate the extent to which our computational results depend on the inclusion of GABA transport in the model without phytanoyl-CoA. Although recent experimental evidence suggests that mitochondrial GABA permease plays a functional role in plants (47), its contribution to the maintenance of mitochondrial metabolism is not fully understood yet. Here we compare two variants of the model without phytanoyl-CoA: with and without GABA transport into the mitochondria (reaction 17). In the latter, an additional reaction is included that allows the usage of GABA in further reactions. The value of 0.8373 for R_exp² demonstrates that the model variant without GABA transport has less explanatory power compared with the model variant in which the GABA transport into the mitochondria is present. Therefore, these findings confirm the existence of GABA flux into the mitochondrion, deemed necessary for maintaining the experimentally observed levels of this metabolite. It should be noted, however, that the GABA permease is certainly not the only protein capable of catalyzing mitochondrial GABA uptake.

DISCUSSION

In mammals, the ETFQO is a component of the mitochondrial ETC, which, together with ETF, forms a short pathway able to transfer electrons from at least 11 different mitochondrial flavoprotein dehydrogenases to the ubiquinone pool (28). By sharp contrast, in plants, only two major donors, IVDH and D2HGDH, have been characterized to date (1). In the same study, the authors provide compelling evidence for a conditional role of those enzymes in the maintenance of mitochondrial respiration under conditions of carbon starvation and indicate alternative pathways as an essential role for the maintenance of respiratory rates.

Here, by using a computational approach, we aid in the elucidation of plant-specific substrates that donate electrons to the ubiquinone pool. We show that the presented model predictions and the experimentally observed behavior in A. thaliana are in excellent agreement, supporting the claim that both lysine and 2-hydroxyglutarate are the major substrates supplying electrons to the mitochondrial ETC under carbon limitation conditions. Moreover, our modeling approach provides compelling evidence that the phytanoyl-CoA breakdown does not contribute to the electron donation via the ETF-ETFQO complex, as suggested very recently on the basis of experimental data (46).

Although the metabolic significance of GABA in plants and animals has not yet been fully understood (47), considerable advances in our understanding will probably be achieved by studying the dynamics of GABA distribution and transport. Here, we provide model-based evidence that GABA transport plays a functional role in augmenting the TCA cycle and maintaining of a normal metabolism (47). This claim is experimentally supported by demonstrating the existence of GABA flux into the mitochondrion in rat brain (52, 53) as well as the recently demonstrated presence and (albeit relatively minor) functional role of a mitochondrial GABA permease (AtGABP) in both primary carbon metabolism and growth as well as its importance in ensuring proper GABA-mediated respiration in plants (47). It is important to mention that it is currently not experimentally possible to produce a mutant fully deficient in GABA uptake because we do not know the molecular nature of additional mitochondrial transporters. On the other hand, this renders the use of modeling approaches, such as the one reported here, an essential tool for characterizing the metabolic system.

The agreement between the main biochemical properties observed in previous experimental studies and our computational predictions further implies that the M-DFBA approach is a suitable method to study complex metabolic networks. M-DFBA captures smooth changes over time (by the Euclidean distance); thus, internal perturbations are reduced, which arise due to temporal changes of the metabolic state characterized by the coupling of metabolite concentrations and flux distributions. For instance, even with the assumption of the simplest kinetic law, namely, mass action kinetics whereby a reaction flux rate is proportional to the product of the concentrations of the participating reactants (54), a change in metabolite concentrations may affect flux rates. The change in fluxes, in turn, as a result of the mass balances, has an effect on the concentrations. In addition, our findings demonstrate that the combination of the extended M-DFBA approach with the explained sum of squares provides the means for model discrimination, which can be used for model-based confirmation of hypotheses. We believe that the model discrimination in which no parameter values are allowed to change between modeling scenarios represents the most objective setting for model selection. In accordance with our claims, here, the (sub)stoichiometries, flux boundaries, and polynomials used to obtain the collocation points remain unchanged for the 12 considered model variants, further confirming the strength of stoichiometry-based modeling.

Altogether, the data-driven model-based confirmation of alternative substrates to the mitochondrial ETC highlights the potential of molecular profiling data in the development of models consistent with previously described observations under changing conditions. We believe that this information is of high relevance for our basic understanding of plant respiration and its alternative pathways. In fact, our computational study indicates that the proposed model in conjunction with M-DFBA has the potential to probe various in silico scenarios that are in line with in vivo plant mitochondrial metabolism. Therefore, this study provides a basic framework for future in silico studies of mitochondrial metabolism under carbon limitation conditions, through which hypotheses related to the role of its components can be tested. Although the present study relies on data from model plant species, we believe that any data set of a similar quality could be analogously interrogated.