Structure-based model of allostery predicts coupling between distant sites

Abstract

Allostery is a phenomenon that couples effector ligand binding at an allosteric site to a structural and/or dynamic change at a distant regulated site. To study an allosteric transition, we vary the size of the allosteric site and its interactions to construct a series of energy landscapes with pronounced minima corresponding to both the effector bound and unbound crystal structures. We use molecular dynamics to sample these landscapes. The degree of perturbation by the effector, modeled by the size of the allosteric site, provides an order parameter for allostery that allows us to determine how microscopic motions give rise to commonly discussed macroscopic mechanisms: (i) induced fit, (ii) population shift, and (iii) entropy driven. These mechanisms involve decreasing structural differences between the effector bound and unbound populations. A metric (ligand-induced cooperativity) can measure how cooperatively a given regulated site responds to effector binding and therefore what kind of allosteric mechanism is involved. We apply the model to three proteins with experimentally characterized transitions: (i) calmodulin-GFP Ca²⁺ sensor protein, (ii) maltose binding protein, and (iii) CSL transcription factor. Remarkably, the model is able to reproduce allosteric motion and predict coupling in a manner consistent with experiment.

Allostery involves coupled motion of a functionally important regulated site to effector binding at a distant allosteric site (1). Allostery is important, for example, in the regulation of biological pathways, drug induced inhibition, and protein biosensors. Hemoglobin was one of the first identified allosteric systems (2, 3). Researchers discovered that oxygen binds hemoglobin’s four subunits cooperatively, and consequently allostery was thought for many years to occur solely in systems with symmetric quaternary structures. Later, proteins with only single subunits, such as myoglobin (4), were also shown to demonstrate allostery (4).

Allostery is a special case of protein dynamics. Protein dynamics, including protein folding and binding, has been well described using an energy landscape perspective (5). An energy landscape describes relative stabilities of all conformations as well as the barriers that separate them (6, 7). Any unique chemical species has a specific landscape that spans all the degrees of freedom of the system. A minor chemical perturbation will change the landscape and can give rise to dramatic changes in the relative stabilities of the conformations. Myoglobin, for instance, can exist in a ligand bound or ligand unbound form (4), and cytochrome c can exist in distinct states due to ionization of amino acid side chains in solvents with varying pH (8). Allostery is yet another example of a small chemical perturbation, one that results in potentially large structural and dynamic changes at a distant regulated site in response to binding of a ligand at an allosteric site.

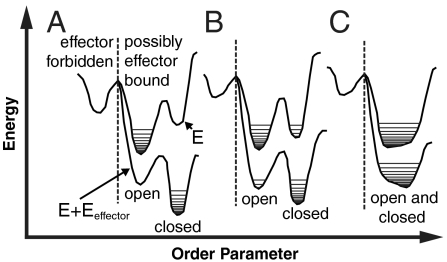
To describe allostery, we draw a landscape for the effector bound and unbound states (Fig. 1). For both landscapes, the configurations of the protein are assigned to open and closed substates, depending on the configuration of the regulated site. An open substate occurs if the regulated site configuration is closer to that in the effector unbound crystal structure than to that of the effector bound crystal structure; a substate is closed otherwise. Three commonly discussed “macroscopic” mechanisms can be defined by the relative stabilities between the open and closed substates, the barriers between the substates, and the structural difference between the substates. The induced fit mechanism results when there is a significant energy difference between the open and closed substates and/or large barriers between them; the large energy change is associated with a significant effector-induced structural transition (Fig. 1A). A population shift mechanism results when the energy difference between the open and closed substates is small compared to the ligand binding energy, resulting in a shift of the population triggered by effector binding (Fig. 1B). An entropy (or dynamically) driven mechanism occurs when there is not a significant change of structure upon effector binding, but there is an exchange of entropy between local regions of the protein (9) (Fig. 1C).

Fig. 1.

General landscapes of allostery. In an approximation, energy landscapes can be projected onto an “order parameter” that separates conformations of the system based on the structure of the regulated site. There are two landscapes pertaining to the effector bound (E + E_effector) and unbound (E) states. Within each state there is an open substate, which occurs if the regulated site configuration is closer to that in the effector unbound crystal structure than to that of the effector bound crystal structure, and a closed substate, which occurs otherwise. The horizontal lines indicate different populated structures in each basin. Different proteins may have dissimilar landscapes, in terms of the relative heights of the barriers and basins as well as the entropy within each basin. There are three general scenarios: (A) induced fit, (B) population shift, and (C) entropy driven. For allosteric proteins, conformations not consistent with effector binding (left of the dashed line) must be less stable than bound conformations (right of the dashed line).

Experimental studies of allostery frequently focus on determining the residues that propagate the allosteric signal (i.e., the allosteric network) (10, 11). Most approaches to mapping an allosteric network rely on introducing point mutations into the studied system (12). Even a single mutation, however, can have multiple effects on protein structure and/or stability, thus causing difficulty when interpreting these experiments in terms of an allosteric network. For instance, mutation of a residue that is not part of the allosteric network can stabilize regions of the energy landscape that forbid effector binding, thereby decreasing the observed effect at the regulated site (Fig. 1). In such a case, the site may be assigned as part of the allosteric network even though the residue does not play a role in transmitting the allosteric signal. Theoretical analysis and simulation methods are often used to construct detailed models of allostery for systems of known structure (13–16). Computational approaches, such as elastic network models that extrapolate dynamics from a native structure, can sometimes successfully predict motions relevant to allostery (17). Molecular dynamics studies have been used to predict allosteric coupling (18, 19), but are limited to systems with relatively small and rapid motions.

Here, we integrate an energy landscape perspective with atomistically detailed comparative protein structure modeling to construct a model of allostery. The model can sample the conformational transitions sufficiently well to accurately link microscopic motions to macroscopic allosteric phenomena. In particular, the model is able to reproduce allosteric motion and predict coupling in a manner consistent with experiment for three allosteric proteins.

Results and Discussion

The model is defined by pairs of potential energy functions (i.e., energy landscapes) corresponding to the effector bound and unbound states. Each landscape has pronounced minima corresponding to the effector bound and unbound crystal structures and can therefore be described as a dual structure-based/dual 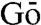model (20, 21). Our landscapes are smooth because they lack ruggedness from interactions that must be formed and broken as the protein switches from one substate to another. Despite having only two basins, the model allows structural permutations that can result in many conformations of similar energy. The landscapes are sampled by molecular dynamics, allowing us to map the interconversion between the allosteric substates (Fig. S1). Similar models are commonly used to study long timescale processes, such as protein folding (20, 22, 23). More recently, they have also been applied to study ligand binding (21).

For a given protein, the allostery model defines several effector bound and unbound landscapes that differ by the size of the allosteric site. Varying the size of the allosteric site mimics the ligand binding reaction in a manner related to capillarity growth in protein folding (24). The energy function that defines each landscape is a sum of nonbonded distance terms that control the attractive interactions between atoms and bonded terms that maintain proper stereochemistry. The nonbonded distance terms determine the efficient sampling of the allosteric transition and vary with the size of the allosteric site. The allosteric site, defined as residues within a radius of the effector ligand (r^AS), involves pairwise atomic interactions with a single energy minima corresponding to distances in either the bound or unbound crystal structure (Fig. 2A). The remaining interactions between atoms have two energetically equivalent minima corresponding to distances from both crystal structures (Fig. S2). Varying r^AS changes how the distance energy is distributed across the structure, thereby driving the simulation to sample different regions of the conformational space relevant to the allosteric transition. An order parameter for allostery is obtained by changing r^AS while restraining the allosteric site first to the unbound and then to the bound structure. In other words, changing r^AS allows interpolation between the effector bound and unbound landscapes (Fig. 1).

Fig. 2.

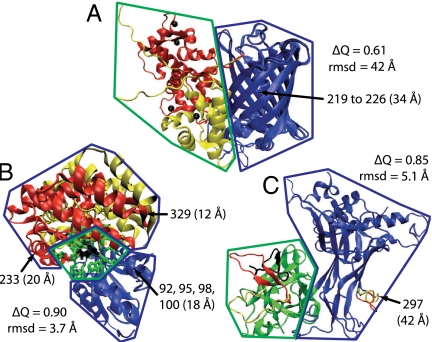
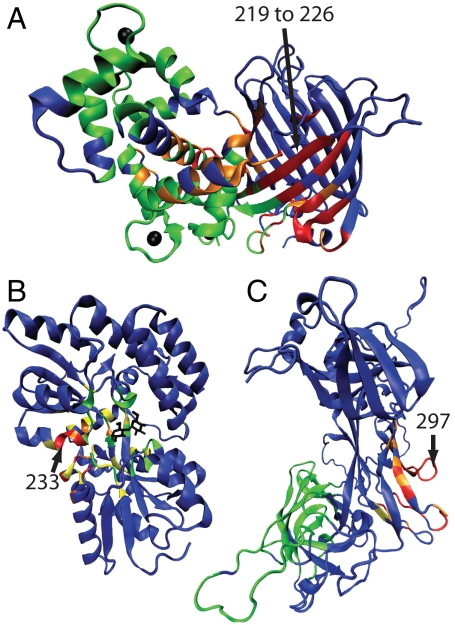
Allosteric and regulated sites. The crystal structures for (A) CaGFP, (B) MBP, and (C) CSL. The parts of the effector bound and unbound structures that differ from each other are shown in red and yellow, respectively. The effector ligand is shown in black. A radius around the effector ligand (r^AS) defines the allosteric site (green). The regulated region is shown in blue. Also shown for each structure are the distance(s) between the regulated and allosteric sites, the C^α rmsd between the bound and unbound crystal structures, and the similarity measure ΔQ between the bound and unbound crystal structures. The regulated site for CaGFP is a stretch of the sequence responsible for fluorescence (residues 219–226).

The robustness and accuracy of the model is assessed by varying the parameters. The depth and width of the attractive, nonbonded distance interaction was parameterized to reproduce folding temperatures (SI Text). The depth of the distance interaction was chosen to be 2 to 3 times the energy required to rotate a backbone dihedral angle, which allows the protein to interconvert between allosteric states. The width of the distance interaction is small to strongly restrain atoms in the backbone, but is given systematically larger values for interactions involving side chains and for interactions involving residues whose atoms are not determined in the crystal structures. We varied a number of parameters within a wide range, without affecting our conclusions based on the simulations; the absolute rates of motions within the simulation change but the relative rates of motions remain similar (Fig. 3 and Fig. S3). Monitoring the variability of results as a function of r^AS, which provides an order parameter for allostery, allows an estimate for how well each landscape is sampled.

Fig. 3.

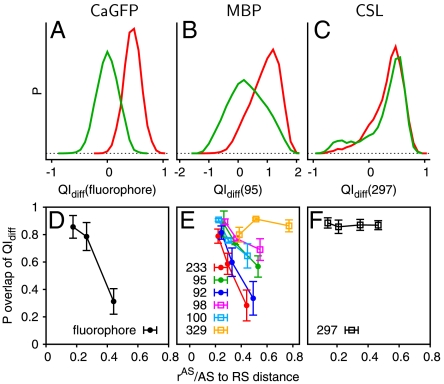
Coupling of distant sites. (A–C) The probability distributions of QI_diff for the regulated sites corresponding to a large r^AS (approximately half the distance between allosteric and regulated sites) for the effector bound (red, QI_diff > 0) and effector unbound (green, QI_diff < 0) simulations. (D–F) The P_overlap (overlapping area between the distributions) is shown as a function of r^AS, normalized by the distance between each regulated site and the allosteric site. The regulated sites experimentally demonstrated to be highly coupled to effector binding in solution are shown as lines with closed circles and other sites are shown as lines with open squares. Error bars represent the standard deviation calculated by randomly dividing the set of simulations into thirds.

Constant temperature molecular dynamics (300 K) is used to sample the landscapes. The trajectories are then analyzed using local structural measures that reference the crystal structures. For example, QI_diff is a residue-specific, pairwise distance similarity metric that is positive if a residue’s configuration is close to the effector bound substate and is negative if the configuration is close to the effector unbound substate. The metric provides a microscopic view of the structural distributions in the effector bound and unbound states. We use these microscopic structural measures to differentiate macroscopic allosteric mechanisms. The model can therefore be used to predict what residues are responsible for transmitting the signal between the allosteric and regulated sites (i.e., the allosteric network).

Cooperative Allostery in CaGFP and Maltose Binding Protein (MBP).

CaGFP is composed of two proteins, neither protein allosteric independently, in which a fluorescent GFP domain is inserted into the sequence of a calcium-binding calmodulin domain (Fig. 2B). Four calcium ions act as effector ligands that induce a partial folding transition in the calmodulin domain, which is mostly unstructured in the apo crystal structure (25). The calmodulin domain forms a well-packed interface with GFP and protects the fluorophore from solvent exposure, increasing fluorescence when calcium is bound. The simulations similarly indicate that the calmodulin domain forms a well-structured interface with GFP if the calcium is bound. QI_diff, which monitors the local structure around the fluorophore, shows that the calcium bound conformations in the simulation are consistent with the crystal structure of the fluorescent protein (Fig. 3A). The simulated calcium unbound conformations are similar to the crystal structure of the nonfluorescent protein. Thus, the simulations for CaGFP nontrivially reproduce the structure of the regulated site based on the structure of the allosteric site, even though the allosteric signal is transmitted over a rather long distance (34 Å).

Allostery in MBP involves more subtle motions than the partial folding transition of CaGFP. Crystal structures as well as residual dipolar coupling measurements suggest that maltose binding coincides with a closed hinge between two domains (26). In the absence of maltose, the domains themselves are similar to the holo structure but the interdomain hinge is fully open. Paramagnetic NMR measurements in the absence of maltose suggest the presence of a minor species (5–10%), corresponding to a partially closed configuration that is in rapid equilibrium with the fully open species (27). The allostery model predicts that the most populated component in the bound and unbound simulations is similar to the bound and unbound crystal structures, respectively (Fig. 3B). The simulations of the apo structure also indicate transient fluctuations to a partially closed configuration (Fig. S1C), in agreement with experiment. This transient intermediate may aid the allosteric transition because it allows partial formation of the effector binding site.

The simulations also agree with experiment on the residue level. We define residues coupled to the effector binding as those whose local structure and/or dynamics are sensitive to effector binding, based on a comparison of the populations for the effector bound and unbound states. Computationally, we predict coupled residues by assessing the local structural difference QI_diff between the bound and unbound crystal structures (Fig. 3E). As the size of the allosteric site (r^AS) is increased in the simulation, the effector bound and unbound landscapes become more dissimilar, resulting in structural and dynamic changes for a subset of residues. These coupled residues will have different QI_diff distributions for the effector bound and unbound simulations. Experimentally, coupled residues are inferred from mutation experiments. As coupled residues are influenced by effector binding, a perturbation of a coupled site can, but does not necessarily, affect the effector binding site. Coupled residues in MBP are thus inferred by monitoring the effector binding affinity with and without mutation (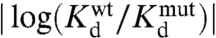). In agreement with the experiment, simulations suggest that residues 233, 95, and 92 are coupled and residues 98, 329, and 100 are less coupled (10). Given that residue 329 is rather close to the allosteric site, the coupling is not simply related to the residue distance to the effector binding site. The mutation sites were chosen because their local environments are different in the bound and unbound crystal structures, yet not all residues are allosterically linked to maltose binding. Protein motions observed in the simulation, not obvious upon inspection of the static structures, are therefore needed to rationalize allostery in this case (Fig. S4).

Entropy-Driven Allostery in CSL.

CSL is a DNA binding protein that is part of a large transcription complex. Studies have shown that binding of a peptide at the allosteric site results in docking of a helical protein over 40-Å away. Crystal structures of CSL demonstrate that a protruding loop at the regulated site inhibits docking of the helical protein in the effector unbound conformation (28). The global structural differences between the two allosteric structures are small compared to those in CaGFP and MBP (Fig. 2). The simulations likewise show only subtle changes in the dynamics upon effector binding. The effector peptide binds and causes folding of a loop, likely producing a significant entropy decrease that can drive allostery through regions that are nearly identical in the effector bound and unbound crystal structures. Consistent with experimental results, the loop at the regulated site is approximately three times more likely to protrude in the effector unbound simulations compared to the effector bound simulations (Fig. 3C).

The simulation results for CSL are consistent with entropy-driven allostery. The mechanism of entropy-driven allostery has been proposed based on molecular dynamics simulations and experimental evidence for systems other than CSL (29, 30). A key feature of this type of allostery is that the structure of the two allosteric substates is almost the same, although the dynamics are different. Allosteric signaling consequently occurs due to changes in the entropy of local regions triggered by effector binding.

Three pieces of evidence are consistent with the highly dynamical behavior of CSL. First, the CSL complex has been observed to be highly dynamic due to rather weak association of the domains that are sometimes unstructured in crystallographic electron density maps (31). Second, the dynamic behavior of CSL is evident because binding of an ankyrin-repeat protein to a third site on CSL allows binding at the regulated site, thereby eliminating the need for effector binding (28). Third, the allostery model predicts that effector binding allows docking at the regulated site loop of CSL by decreasing the rapid interconversion between protruding and nonprotruding conformations.

Other allosteric mechanisms for CSL, although not directly supported by experimental evidence, may be possible in a different variation of the model. A small structural difference between the two loop structures makes it difficult to estimate their relative stabilities by our model. Indeed, in a study of systems related to CSL, accuracy was improved by including more finely detailed energy functions (21). Further difficulties to predict the dynamics of loop structures arise because conformational ensembles at biological temperatures can vary significantly from low temperature crystal structures (20, 32).

Predicting Microscopic Details of Allosteric Motions.

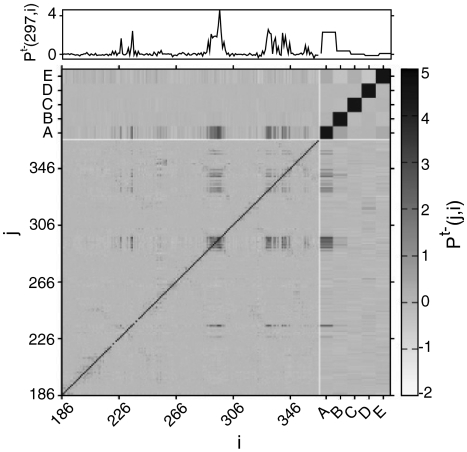
Analysis of correlated motions from simulation trajectories suggests how dynamic signals are transmitted through proteins. Examples include analyses of covariance matrices of atomic positions and energy contributions by subregions of the protein (18, 33). Here, we introduce a simple method to analyze simulations in which the system interconverts between two states of interest, which we call pseudocorrelation (Materials and Methods). All residues are classified using QI_diff, in a binary fashion, as being in one or the other allosteric substate. By analyzing the simulated structural ensemble, we can estimate the likelihood that a residue i will be in a certain substate given the substate of another residue j. A pseudocorrelation map [i.e., PC(j,i)] (Fig. 4) shows that only some of the contacts in CSL participate in transmitting the allosteric signal, which involves regions far apart in sequence. The regulated site loop (residues 295–299) moves in a cooperative manner and is well correlated with several other regions of the protein.

Fig. 4.

Pseudocorrelation map. A pseudocorrelation map [PC^t-(j,i)] for the allosteric site (AS), regulated site (RS), and C-terminal (CT) domains of CSL is obtained by assigning all residues (or subsets of residues) into the effector bound or effector unbound substate using QI_diff. (Upper) The row corresponding to the regulated site, for PC^t-(297, i). A–C represent pseudocorrelations of single domains: Q_diff (RS), Q_diff (AS), and Q_diff(CT), respectively. D and E represent pseudocorrelations for contacts at the interface between domains, QI_diff(AS to RS) and QI_diff (CT to RS), respectively.

Pseudocorrelation can be used to predict the residues involved in the allosteric network. By identifying residues correlated with the regulated site, we can determine what regions help transmit the allosteric signal distant from the effector binding site (Fig. 5 and Table S1). The allosteric signal in CSL propagates through loop structures in the most direct path between the allosteric and regulated sites (Fig. 5C). In contrast, rather than transmitting a signal from the allosteric site to the regulated site in a linear path, the allosteric network for MBP is scattered across the interface of the domains (Fig. 5B). Both CSL and MBP have a small number of residues in the allosteric network as compared to CaGFP, which involves many residues at the interface between the two domains (Fig. 5A).

Fig. 5.

Allosteric networks. The allosteric networks are shown for (A) CaGFP, (B) MBP, and (C) CSL. Residues are colored red when in contact and well correlated with the regulated site (labeled with arrows). A residue is considered correlated if PC^t+(regulated site, i) has a value greater than two standard deviations above the mean PC^t+ (Z score > 2). Residues colored orange and yellow are in contact and well correlated with red and orange residues, respectively. The remaining residues are either colored green if they are in the allosteric site (within the r^AS radius) or blue if they are in the regulated region.

To support our model of allostery, we compare the simulation results to a mutational study of CaGFP designed to improve its calcium sensing functionality. Nineteen mutations were made at nine sites with the aim to increase the fluorescence change triggered by calcium binding (25) (Table S1). Three mutated sites showed the desired increase in the calcium-induced change of fluorescence (residues 116, 303, and 381); three other sites led to a decrease in the change of fluorescence (residues 120, 140, and 380). Of these six coupled sites, four are predicted to be highly correlated to the fluorophore structure, including two that increase fluorescence (Table S2). Of the three sites that are demonstrated not to be allosterically coupled (residues 81, 219, and 377), two are predicted not to be correlated with the fluorophore environment (Table S2). We correctly predict the allosteric role for six out of the nine residues, suggesting that our allostery model may aid the design of allostery into a given protein structure.

The pseudocorrelation map also qualitatively agrees with coupling inferred from MBP mutation experiments. The value of PC^t+(regulated site, allosteric site) for different regulated site residues can be compared to the observed coupling value from mutation experiments (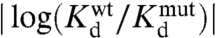). Highly coupled residues 233, 95, and 92 have coupling values of 0.8, 0.5, and 0.4 and PC^t+ values of 1.6, 0.6, and 1.4, respectively. Residues 98, 100, and 329 that are not well coupled have coupling values of 0.2, 0.1, and 0.1 and PC^t+ values of 0.4, 0.2, and 0.3, respectively. Therefore, there is indeed a strong correlation between the observed coupling values and the predicted pseudocorrelation (Fig. S4).

Ligand-Induced Cooperativity.

Allostery requires an effector ligand to stabilize interactions in the closed substate over those in the open substate, yet the open substate must be accessible for binding. Because most allosteric transitions involve well-folded structures, the average energy and entropy are similar in both substates, likely not differing more than a few k_BT. In such a case, the allostery model suggests that the effector shifts the distribution of local energies and entropies for many residues (ligand-induced cooperativity), although not necessarily changing the total energy and entropy significantly. These ligand-induced motions involve only a small subset of the total degrees of freedom and are therefore distinct from cooperativity related to folding. In contrast, large changes in total energy and entropy can occur if the allosteric mechanism involves a partial folding/unfolding transition, such as for CaGFP.

To study allosteric mechanisms further, we introduce a metric to quantify ligand-induced cooperativity (LIC). The metric is useful because allosteric mechanisms can be distinguished using LIC values more accurately than evaluation of static crystal structures. Effector bound and unbound crystal structures may contain structural differences that are random and not induced by the ligand. LIC is large if a residue’s local environment differs significantly between the effector bound and unbound simulations (small P_overlap of QI_diff in Fig. 3). Monitoring the coupling of residues along an order parameter for allostery, from low to high r^AS, provides a measure of ligand-induced cooperativity: 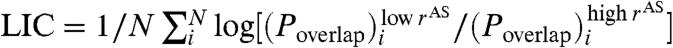, where N is either the total number of residues in the protein or one (corresponding to a single residue), a low r^AS is defined as the smallest radius sampled (typically 5 Å), and a high r^AS is the value that spans approximately half the distance to the regulated site. LIC, in which N is the protein length, estimates the fraction of residues that participate in the allosteric transition. Note that LIC ranks CSL lower than MBP and CaGFP, whereas ΔQ and rmsd do not.

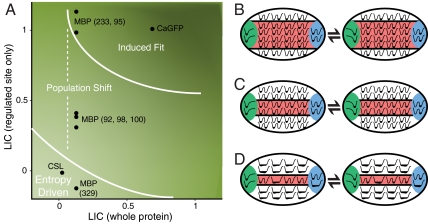
Allosteric mechanisms cannot be determined by a single LIC calculation because several sites on the same protein may be coupled to the allosteric site to drastically different degrees. An allosteric mechanism is therefore a function of the LIC over the whole protein and the LIC calculated for a single residue in the regulated site (Fig. 6A). The lines in Fig. 6A do not indicate a sharp transition between two allosteric mechanisms. We are unaware of any evidence to suggest a sharp boundary; rather, the transition between allosteric mechanisms is likely to be continuous. For the induced fit mechanism, there is a significant amount of structural change triggered by effector binding and therefore high LIC for most residues. Highly cooperative motions imply that many spatially distributed residues are in the allosteric network that links the allosteric site to the regulated site (Fig. 6B). For the entropy-driven mechanism, the protein does not significantly change in structure. The allosteric network is therefore small and can be very dispersed because the motions that transmit the allosteric signal are minimal (Fig. 6D). The population shift mechanism is between these two extremes. To the right of the dotted line in Fig. 6A, effector binding induces cooperative allosteric transitions between two substates with similar stabilities, not much unlike induced fit (Fig. 6C). The allosteric network is smaller for proteins toward the left in the diagram because residues in the structure have low ligand-induced cooperativity. The allosteric network involved with a moderately cooperative population shift is likely dispersed and may involve a small number of residues. LIC therefore helps to describe how microscopic structural distributions are connected to macroscopic allosteric mechanisms.

Fig. 6.

Allosteric mechanisms. (A) Diagram that qualitatively differentiates between allosteric mechanisms. LIC averaged over the whole protein (x axis) and LIC of the regulated site (y axis) are shown for CaGFP, MBP, and CSL. Points are shown for residues in the regulated site, which are defined by experimental studies, including six for MBP. Diagrams that show energy landscapes for a subset of residues in a protein are shown: (B) induced fit, (C) population shift, and (D) entropy-driven mechanisms. The arrows represent the equilibrium between the unbound (Left) and bound (Right) landscapes. The protein is divided in an allosteric site (green), regulated site (blue), allosteric network (red), and the rest (white). The sum of the contributions of individual interactions for the mechanisms in B–D results in landscapes shown in Fig. 1 A–C, respectively. Higher LIC values across the whole protein often coincide with a large allosteric network and involve the cooperative motions of many residues between the allosteric site and the regulated site.

Allosteric Mechanisms.

An interesting question to consider is how often natural proteins exhibit each of these allosteric mechanisms. All of the discussed allosteric mechanisms appear to be robust to mutation (34). A highly cooperative allosteric mechanism with a large allosteric network can easily tolerate individual mutations without significantly affecting function. A less cooperative allosteric mechanism can tolerate individual mutations if there are many independent pathways that allow allosteric communication, provided that hindering one pathway by mutation triggers compensation by another pathway. It is conceivable that an entropy-driven mechanism can evolve rather easily by mutation because few residues are in the allosteric network. Entropy-driven allostery can serve as an evolutionary bridge between a nonallosteric sequence and a highly cooperative and robust induced fit mechanism. The issue is further complicated because a protein’s allosteric mechanism may be affected by the solvent conditions because of solvent-induced traps in the energy landscape (i.e., chemical frustration), which can drastically affect structure and dynamics (35).

We proposed a description of the energy landscape for proteins as well as a tool that can accurately link microscopic motions to macroscopic allosteric phenomenon. The energy landscape is defined by two known allosteric states of a protein. Despite its simplicity, the model successfully predicts the relative changes in structure and dynamics that occur due to effector binding in three rather different proteins. These landscapes are not dominated by specific, high-energy interactions and therefore require local regions of the protein move concertedly. The model suggests how these cooperative motions are connected to macroscopic allosteric mechanisms in terms of ligand-induced cooperativity metrics. The model is also able to predict the role of specific residues in allosteric coupling, which is not attainable by casual observation of the crystal structures alone. The model may therefore aid in the rational design of allosteric proteins.

Materials and Methods

Allostery Model.

In our allostery model, a landscape is given by a potential energy function that is a sum of bonded and nonbonded terms implemented using MODELLER (36): E_i = E_bonded + E_nonbonded (SI Text). Correct stereochemistry is achieved by the same terms MODELLER uses for standard comparative modeling: E_bonded = E_bond + E_angle + E_dihedral + E_{improper dihedral}. To induce allostery, we add a truncated Gaussian distance term to the soft-sphere atom overlap term, to obtain total nonbonded energy: E_nonbonded = E_soft sphere + E_distance. This distance term is given by a sum over all heavy atom pairs more than two residues apart in sequence and less than 11-Å apart in distance. The energy function for a single atom pair has one or two minima depending on the distance to the effector, r^AS (Fig. S2). For interactions less than r^AS from the effector, the function has one energetic minimum corresponding to the distance in either the effector bound or unbound structure. For all other interactions, the function has two minima corresponding to the distances in the bound and unbound structures.

Molecular dynamics simulations are used to sample many landscapes (E_i) for each protein, including the effector bound and unbound landscapes with different r^AS. Thirty simulations were run for each landscape. The system is first equilibrated and then simulated for 6 ns using 3 fs time steps and velocity rescaling every 200 steps.

Structural Analysis.

We compare structures from simulations to crystal structures using pairwise distance similarity scores (5, 21). For a given structure, an overall fold similarity to any other structure t is given by Q^t, reflecting the fraction of similar contacts (SI Text). To determine if a simulated structure is more similar to the effector bound (t+) or the effector unbound (t-) crystal structures, we calculate Q_diff = (Q^t+ - Q^t-)/(1 - ΔQ) where ΔQ is the structural similarity (Q^t) between the two allosteric crystal structures. Restricting the calculation to a subset of contacts, such as Q_diff(X), results in a score for region X. Also, QI_diff(X) refers to a score of the interface between X and the remaining protein and QI_diff(X to Y) refers to a score of the interface between X and Y.

Pseudocorrelation maps are used to determine which subsets of residues have correlated motions (Fig. 4 and Fig. S5). We first analyze the simulation trajectories, for all values or r^AS, and classify residues or their subsets into the effector bound or unbound substate using QI_diff. Pseudocorrelation is determined using the log odds ratio of the probability that a residue (or subset of residues) j is in the effector unbound substate (t-) if another residue (or subset) i is also in substate t-, given by P(j is t - |i is t - ), to the probability given by P(j is t - |i is t + ). This expression gives a likelihood that j will be affected by the substate of i: PC^t-(j,i) = log[P(j is t - |i is t - )/P(j is t - |i is t + )].