The Elastic Basis for the Shape of Borrelia burgdorferi

Abstract

The mechanisms that determine bacterial shape are in many ways poorly understood. A prime example is the Lyme disease spirochete, Borrelia burgdorferi (B. burgdorferi), which mechanically couples its motility organelles, helical flagella, to its rod-shaped cell body, producing a striking flat-wave morphology. A mathematical model is developed here that accounts for the elastic coupling of the flagella to the cell cylinder and shows that the flat-wave morphology is in fact a natural consequence of the geometrical and material properties of the components. Observations of purified periplasmic flagella show two flagellar conformations. The mathematical model suggests that the larger waveform flagellum is the more relevant for determining the shape of B. burgdorferi. Optical trapping experiments were used to measure directly the mechanical properties of these spirochetes. These results imply relative stiffnesses of the two components, which confirm the predictions of the model and show that the morphology of B. burgdorferi is completely determined by the elastic properties of the flagella and cell body. This approach is applicable to a variety of other structures in which the shape of the composite system is markedly different from that of the individual components, such as coiled-coil domains in proteins and the eukaryotic axoneme.

Introduction

Spirochetes constitute a unique group of motile bacteria, with some members being highly virulent in humans. Although the flagella of these bacteria are structurally similar to those of other species, they are encased within the periplasmic space, which lies between the cell wall complex (i.e., cell cylinder) and the outer membrane. Although spirochetes vary tremendously with respect to habitat, size, number of periplasmic flagella attached at each end, and their mechanics of swimming, DNA sequence analysis indicates that they all evolved from a primordial protospirochete (1–3). Depending on the species, the final shape of a spirochete is either helical or a flat wave. As in other bacteria, the flagella serve an obvious motile function as they are driven by rotary motors at their base, but, in spirochetes, these organelles rotate between the outer membrane and cell cylinder (3). Species such as Spirochaeta aurantia and Treponema primitia swim by a mechanism in which the flagella do not deform the cell cylinder and do not influence cell shape (4,5). In contrast, in other species, such as Leptospira interrogans and Borrelia burgdorferi (B. burgdorferi), the flagella are also skeletal organelles; cells lacking flagella or with straight flagella have altered shapes, and these mutants are also nonmotile (6–10). Moreover, several models of spirochete locomotion indicate that the skeletal function of the periplasmic flagella is essential for their motility (3,6,11–13).

In these species of spirochetes, where the flagella serve both skeletal and motile functions, shape and motility are intimately connected. In addition, mounting evidence suggests a substantial link between motility and virulence in B. burgdorferi. For example, preliminary results with two B. burgdorferi targeted mutants isolated independently in the periplasmic flagellar protein encoded by flaB found the following: the flaB mutants were not infectious in mice at an infectious dose 50 (ID₅₀) of 5 × 10³ cells/mouse. Reisolation of B. burgdorferi from the flaB inoculated mice tissues also failed even when the animals received 200 times the ID₅₀ (M. Motaleb, P. Stewart, A. Bestor, P. Rosa, and N. Charon, unpublished). Artificially infected Ixodes scapularis ticks were also unable to transmit the mutant organism from their intestines to experimental mice. These results, although preliminary, indicate that motility is required for infection in vivo, irrespective of their route of infection (M. Motaleb, P. Stewart, A. Bestor, P. Rosa, and N. Charon, unpublished). These results are also consistent with the results of Botkin et al. (14), who found that a putative flagellar motor mutant was less infectious than that of wild-type cells. Taken together, because the flaB mutants are nonmotile and are rod shaped, and the wild-type cells have a flat-wave morphology and are motile, we expect that the overall shape of the cells, which is tied to motility, is an important factor for virulence.

A complete picture for how spirochetes create and maintain their shape is lacking. In some spirochete species, genetic evidence indicates that the helical cell shape of the cell is associated with the cell wall and is independent of the periplasmic flagella (3,6,8–10,15). However, in others, the final shape of the entire cell is due to complex interactions between the cell cylinder and the periplasmic flagella. Specifically, the Lyme disease spirochete B. burgdorferi, and possibly the syphilis spirochete Treponema pallidum (16), have flat-wave morphologies. B. burgdorferi has a periodically undulating, nearly planar shape ( Fig. 1, a, b, e, f). Remarkably, cells lacking FlaB, the primary constituent of the left-handed flagellar filament, are rod-shaped (3,7,12,17) (Fig. 1, c and g). Thus, the periplasmic flagella play a major role in creating the flat-wave morphology in this species. Yet, the physics of how this flat-wave morphology arises is not clear. Because T. pallidum is unable to be continuously cultured in vitro, we know very little about the factors that influence its shape.

Figure 1.

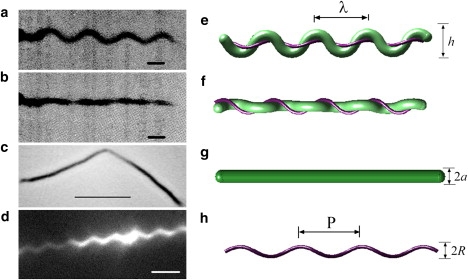
The morphology and architecture of B. burgdorferi, which has a planar, flat-wave morphology. (a, e) When viewed from one perspective, the cell body appears wave-like; (b, f) When rotated by 90°, the cell shape appears straight. (e, f) Schematic of the cell construction of B. burgdorferi. The cell cylinder is shown in green and the perplasmic flagellar bundle in purple. The outer membrane sheath is not shown. The flagella wrap around the cell body, inducing a flat-wave shape, with a wavelength of λ and amplitude h. The shapes shown here were produced by the mathematical model with parameters a = 0.2 μm and A = 5. (c) Mutants lacking FlaB do not produce flagella, and the cells are rod-shaped. Scale bar, 5 μm. Figure originally published in (3) and reproduced with permission. (g) Schematic of the cell cylinder. The radius of the cell cylinder is a. (d) Darkfield image of purified flagella from B. burgdorferi. Scale bar, 2 μm. Image courtesy of S. Goldstein. (h) Purified flagella are helical with a pitch, P and diameter 2R. (a, b) Scale bars, 1 μm. Figures originally published in (12).

The morphology and motility of B. burgdorferi has been characterized in detail. High-voltage electron microscopy (13) has been used to determine the typical cell dimensions: the cell cylinder radius (a = 0.17 μm), length (10–20 μm), wavelength (λ = 2.83 μm), and undulation amplitude (h = 0.78 μm) (12,13). Attached subterminally to the ends of the cell are between 7 and 11 flagellar filaments with a diameter of 20–24 nm (13,18). Each filament is connected to a rotary motor anchored in the inner membrane of the cell. Spirochete flagellar motors, including those of B. burgdorferi, are similar to the motors found in other bacterial species (19,20). Rotation of the periplasmic flagella of B. burgdorferi induces traveling-wave deformations of the cell cylinder, which provide the thrust that drives the swimming of these bacteria (12). Periplasmic flagella that are not constrained by the cell cylinder have been observed to be left-handed helical filaments with a helix radius R = 0.14 μm and pitch P = 1.48 μm (21) (Fig. 1, d and h). In situ, the periplasmic flagella shape is dramatically different, due to its interaction with the cell cylinder. Although the flagella remain left-handed, they wrap about the cell cylinder in a right-handed sense and are stretched with R = 0.19–0.20 μm, and with a helical pitch of P = 2.83 μm (note that P = cell's λ) (13).

These observations suggest a model for the development of the flat-wave morphology in B. burgdorferi. Enclosing the flagella inside the periplasmic space causes an elastic deformation of the cell cylinder, which in turn exerts a force back onto the periplasmic flagella, causing them to deform as well. To explore whether this conceptual picture is sufficient to explain the flat-wave morphology, we developed and tested a mathematical model that treats the cell cylinder and the periplasmic flagella as filamentary elastic objects, because the cell cylinder and the flagella are much longer than they are wide. This approximation assumes that the cross sections of the filaments do not change appreciably during deformation, which is typically valid for long, thin objects that bend on length scales much longer than their diameter. As the flat-wave shape is observed even in nonmotile cells, we explore the static configurations of the model that is developed here.

Materials and Methods

Bacterial strains

We used the high-passage B. burgdorferi senso stricto strain B31A, which has been previously described (7,22).

Cell cylinder preparation

To remove the outer membrane of cells for use with the optical trapping experiments, we centrigued 25 mL of late logarithmic phase cells (1 × 10⁸/mL) of B. burgdorferi senso stricto strain B31A at 6000 × g for 20 min. The cells were then washed in 20 mL of 150 mM phosphate buffered saline, pH 7.4 (PBS) and then centrifuged again at 6000 × g for 15 min. We resuspended the pellet in 10 mL of PBS with myristate detergent (final concentration 1%), and the solution was shaken in a 37°C water bath for 12 min and then centrifuged at 6000 × g for 15 min, washed, and recentrifuged at 6000 × g for 15 min. Finally, the pellet was resuspended in 2–3 mL of water and a pipette was used to disperse the cells.

Measurement of the cellular morphology

Darkfield images of B. burgdorferi strain B31A with and without the outer membrane were taken using a Zeiss Axioscope 2 (100 × oil immersion objective) connected to a Hamamatsu digital camera (C4742-95). The peak-to-peak amplitude and wavelength were measured using the “line tool”' in Volocity 4 software (Improvision Inc., Coventry, UK). At least 8–12 individual cells were measured.

Purification of the periplasmic flagella

Periplasmic flagella were purified using a method similar to that given in (19). Approximately 250 mL of late logarithmic phase cells were centrifuged at 6000 × g for 20 min (all centrifuation was done at 4°C). The pellet was washed in 30 mL of sucrose solution (0.5M sucrose, 0.15M Tris-HCl, pH 8) and recentrifuged at 6000 × g for 15 min. The pellet was then resuspended in 15 mL sucrose solution and stirred on ice for 10 min, 0.15 mL of lysozyme (10 mg/mL) was slowly added, and then the solution was stirred on ice for 5 min. 1.5 mL EDTA (stock 20 mM) was added to a final concentration of 2 mM, and the solution was then stirred on ice for 20 min, and then stirred at room temperature for 40 min. Approximately 1.5 mL myristate detergent (stock 10% in PBS) was added to a final concentration of 1%, and then it was stirred at room temperature for 1 h. 0.3 mL MgSO₄ (stock 0.1 M) was added and then the solution was stirred at room temperature for 5 min. 0.3 mL EDTA (stock 0.1 M) was added, then the solution was stirred for 5 min and centrifuged at 17,000 × g for 15 min. The supernatant was taken, and 2 mL PEG solution (stock 20% PEG in 1M NaCl) was added, and then it was put on ice for 30 min. The solution was centrifuged at 27,000 × g for 20 min. The pellet was resuspended in 5 mL H₂O and then recentrifuged at 85,000 × g for 30 min, and the pellet was resuspended in 1 mL H₂O and stored at 4°C.

Coverslip preparation

Two-micrometer-diameter polystyrene spheres were coated with poly-L-lysine and placed in a 100 mM NaCl solution. The 2 μm spheres were then flowed into a flowcell and let stand for ∼10 min to allow them to settle and stick to the surface of the coverslip to provide reference points and spacers in the experiment. The fluid was then exchanged with dionized H₂O to remove excess, nonstuck spheres from the flowcell. The experimental assay was then flowed into the chamber.

Optical trapping experiments

Our optical trapping system was constructed using an 800mW NdYg laser (Santa Few Laser Co.) and a Nikon 60X 1.4 NA oil objective on a TE-2000 Nikon microscope. The average spring constant for the trap was 0.25 pN/nm.

The flagellar assay consisted of a dilution of purified flagella from B. burgdorferi and 1 μm silica spheres coated with poly-L-lysine in 0.6% methylcellulose solution with 100 mM NaCl.

The cell cylinder assay consisted of a dilution of spirochete cell cylinders and 1 μm silica spheres coated with poly-L-lysine in 0.6% methylcellulose solution with 50 mM NaCl added. The solution was pH adjusted to 7.5–8.9 using NaHCO₃.

For individual flagellum measurements, the sample was searched for bead flagellum pairs with one end of the flagellum spontaneously adherent to the surface. The tethered bead was trapped and brought to a height of 0.8 μm off the surface of the coverslip. In the case of surface tethered flagella, the y position was adjusted to triangulate the point of attachment and determine the length of the flagella.

For cell cylinder measurements, cells were found that had a 1 μm sphere attached somewhere along the length. This sphere was attached to the surface. A second bead was attached to the distal end of the cell and was brought to a known height off the surface of the coverslip.

The piezo stage (MadCity Labs, Nano-H100) was driven with a triangle wave (Agilent 33220A). The y position of the stage was adjusted such that the stretching of the flagella or cell was purely in the x direction. The amplitude, frequency, and offset position of the stage were adjusted so that the stretching event occurred at an appropriate rate for tracking and to ensure that the event included the unstressed configuration of the cell or flagellum (nominally 50–100 mV, at 0.25 Hz).

A quadrant photodiode was used to image the trapped bead in the back focal plane of the condenser and was used to monitor and adjust the position of the bead in the trap. Trap calibration was done by taking 10 sets of 500 images of the trapped bead (at a specified height) with a 1 ms physical shutter for calibration of the trap (Photometrics, Quantex 57). This exposure time was necessary to match the characteristic time of a bead in the trap and minimize overestimation of the trap stiffness. The calibration images were reduced to remove optical and electronic noise (23) using Image J (24). The positions of the beads were then tracked using “Track Particles” in Metamorph (Molecular Devices) following the guidelines set out by Carter et al. (25). The bead tracks were then used to calibrate the trap stiffness, K, using the equipartition method (26).

The stiffness K was calculated for each bead in the calibration set and averaged. The weighted average of all of the beads was then calculated giving the average trap stiffness. In the case of surface stretching experiments where the “test” bead could not be calibrated directly, the optical trap stiffness was determined by the weighted average of all the K values for a given height in a given experiment (n = ∼10).

The stretching angle in z was taken into account for determining the cell/flagellum lengths and in the force calculations.

The composite two-filament model for B. Burgdorferi

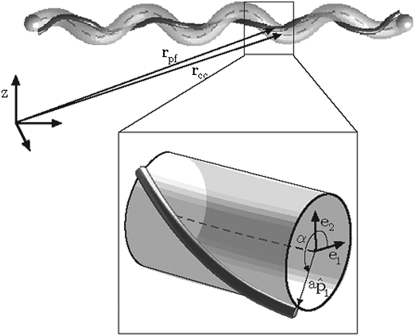
In B. burgdorferi, the periplasmic flagella reside at the surface of the cell cylinder. Therefore, there is a relationship between the centerline coordinates of the cell cylinder and those of the periplasmic flagella. Because the cell cylinder and the periplasmic flagella are much longer than they are wide, we treat them both as filamentary objects with circular cross-sections. There are typically between 7 and 11 periplasmic flagella per end in B. burgdorferi (18). The flagella form a ribbon-like structure when observed using cryoelectron tomography (27). Because the flagella are circumferentially localized, we treat the flagellar ribbon as a single filament, for simplicity. We define the centreline of the cell cylinder as r _c(s), where s is the arclength along the centreline ( Fig. 2). Likewise, r _f(s _f) is the centreline position of the periplasmic flagella, where s _f is the arclength along the flagellar ribbon (Fig. 2).

Figure 2.

Schematic diagram showing a B. burgdorferi cell. The cell cylinder is gray and the periplasmic flagella are treated as a single helical filament, shown in black. The centerline of the cell cylinder, described by the vector, r_c, is depicted by the dashed line. r_f is the vector describing the centreline of the periplasmic flagella. (Inset) A close up view of a short segment of the cell. ${\hat{\mathbf{e}}}_1$ and ${\hat{\mathbf{e}}}_2$ are unit vectors that point to the surface of the cell cylinder. The flagella are located at a point a${\hat{\mathbf{p}}}_1$ from the centreline. α is the angle from ${\hat{\mathbf{e}}}_1$ to ${\hat{\mathbf{p}}}_1$.

At all points along the centerline of the cell cylinder, we define an orthonormal triad $\left\{{\hat{\mathbf{e}}}_1,{\hat{\mathbf{e}}}_2,{\hat{\mathbf{e}}}_3\right\}$, with ${\hat{\mathbf{e}}}_3=\partial {\mathbf{r}}_c/\partial \mathit{s}$ the tangent vector of the cell cylinder. The unit vectors ${\hat{\mathbf{e}}}_1$ and ${\hat{\mathbf{e}}}_2$ point to material points on the surface of the cell cylinder (Fig. 2). Curvature and twist of the cell cylinder causes the material frame to rotate (28):

$$\frac{\partial {\hat{\mathbf{e}}}_{\mathit{i}}}{\partial \mathit{s}}=\mathbf{\Omega }\times {\hat{\mathbf{e}}}_{\mathit{i}},$$ (1)

where i = 1,2,3. The vector Ω = {Ω₁, Ω₂, Ω₃} is the strain vector, which describes the bending and twisting strain at a given point. Ω₁ and Ω₂ give the curvature of the cell cylinder, and Ω₃ is the twist density of the cell cylinder about its tangent vector.

Because the periplasmic flagella lie at the surface of the cell cylinder, we can describe the position of the flagella in terms of r _c (Fig. 2),

$${\mathbf{r}}_f={\mathbf{r}}_c+\mathit{a}\cos \alpha {\hat{\mathbf{e}}}_1+\mathit{a}\sin \alpha {\hat{\mathbf{e}}}_2,$$ (2)

where a is the radius of the cell cylinder and α is the angular position of the periplasmic flagella with respect to ${\hat{\mathbf{e}}}_1$. Using Eq. 2, it is possible to write the curvature and twist of the periplasmic flagella in terms of Ω, α, and a rotational angle for the flagella, β. A complete description of this derivation is given in the Supporting Material.

When the flagella are not present, the cell cylinder has a straight, rod-shaped morphology (3,7,12). As mentioned above, the flagella are helical with a helix radius, R = 0.14 μm and pitch P = 1.48 μm (21). Therefore, we treat the cell cylinder as a straight filament with no preferred curvature or twist. Using the empirically determined helix radius and pitch, the preferred curvature and torsion of the periplasmic flagella are

$$\begin{array}{l}{\kappa }_0=\frac{\mathit{R}}{\left({\mathit{R}}^2+{\left(\frac{\mathit{P}}{2\pi }\right)}^2\right)}=1.86\mu {\text{m}}^{-1}\\ {\tau }_0=\frac{\left(\mathit{P}/2\pi \right)}{\left({\mathit{R}}^2+{\left(\frac{\mathit{P}}{2\pi }\right)}^2\right)}=3.14\mu {\text{m}}^{-1}\end{array}\text{.}$$ (3)

The internal elastic stresses of the cell cylinder exert a force F ^c and a moment M ^c on the cross section at s. Balancing the forces and moments of an element of the rod of length ds leads to (28)

$$\begin{array}{l}\frac{\partial {\mathit{F}}^c}{\partial \mathit{s}}+\mathit{K}=0,\\ \frac{\partial {\mathit{M}}^c}{\partial \mathit{s}}+{\hat{\mathbf{e}}}_3\times {\mathit{F}}^c=0,\end{array},$$ (4)

where K is the force per length that the periplasmic flagella exert on the cell cylinder. Likewise, the elastic stresses of the periplasmic flagella exert a force F ^f and a moment M ^f on the cross section of the flagella that lies at s. Force and moment balance on an element of the periplasmic flagella of length $\sqrt{g}$ ds, where $\sqrt{g}$ is the ratio of an infinitesimal length of the flagella to that of the cell cylinder, leads to

$$\begin{array}{l}\frac{1}{\sqrt{g}}\frac{\partial {\mathit{F}}^f}{\partial \mathit{s}}-\frac{1}{\sqrt{g}}\mathit{K}=0,\\ \frac{1}{\sqrt{g}}\frac{\partial {\mathit{M}}^f}{\partial \mathit{s}}+{\hat{\mathbf{\varepsilon }}}_3\times {\mathit{F}}^f=0,\end{array}$$ (5)

where ${\hat{\mathbf{\varepsilon }}}_3$ is the tangent vector of the periplasmic flagella.

We use linear elasticity theory to define the constitutive relations that define the elastic restoring moments to the strain vectors. Therefore, the bending moments are linearly related to the curvatures, and the twisting moments depend linearly on the twist density. Because the cell cylinder prefers to be straight and the periplasmic flagella prefer to be helical,

$$\begin{array}{l}{\mathit{M}}^c={\mathit{A}}_c{\Omega }_1{\hat{\mathbf{e}}}_1+{\mathit{A}}_c{\Omega }_2{\hat{\mathbf{e}}}_2\mathit{+}{\mathit{C}}_c{\Omega }_3{\hat{\mathbf{e}}}_3,\\ {\mathit{M}}^f={\mathit{A}}_f\left({\omega }_1-{\kappa }_0\right){\hat{\mathbf{\varepsilon }}}_1+{\mathit{A}}_f{\omega }_2{\hat{\mathbf{\varepsilon }}}_2\mathit{+}{\mathit{C}}_f\left({\omega }_3-{\tau }_0\right){\hat{\mathbf{\varepsilon }}}_3,\end{array}$$ (6)

where A _c and A _f are the bending moduli for the cell cylinder and periplasmic flagella, respectively. C _c and C _f are the twisting moduli for the cell cylinder and periplasmic flagella. Here ${\hat{\mathbf{\varepsilon }}}_1$ and ${\hat{\mathbf{\varepsilon }}}_2$ are orthogonal unit vectors that are perpendicular to the tangent vector of the periplasmic flagella, and ω is the strain vector for the periplasmic flagella.

The force and moment balance equation (Eqs. 5 and 6) along with the relationships between the cell cylinder material frame and the periplasmic material frame comprise a system of 12 equations in 12 unknowns. In the Supporting Material (Eqs. S25 and S38), we show that there are a number of conserved quantities that can be used to simplify the system of equations, and we discuss the method of solution that is used to solve for the equilibrium morphology of B. burgdorferi.

Results

B. burgdorferi periplasmic flagella are polymorphic

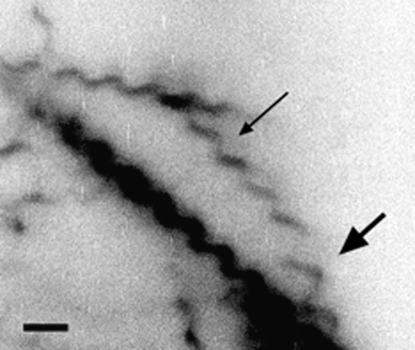
In samples of purified flagella, we observed two different morphologies of the flagella. Roughly 90% of the flagella had a helix pitch of 1.4 ± 0.1 μm and helix diameter of 0.4 ± 0.1 μm, which is comparable to the published values (21). The other flagella were observed to have a larger helix pitch and diameter with values of 2.0 ± 0.1 μm and 0.8 ± 0.1 μm, respectively. This alternative conformation of the periplasmic flagella was independently discovered by S. Shibata and S-I. Aizawa (S. Aizawa, University Hiroshima, personal communication, 2008), and our measurement of the helix pitch and helix diameter was confirmed using dark-field microscopy (S. Goldstein, University Minnesota, personal communication, 2008). This larger waveform of flagella has preferred torsion and curvature of 1.2 μm⁻¹ and 1.5 μm⁻¹. In some circumstances, a flagellum was observed to have both morphologies in different regions along its length ( Fig. 3). Therefore, like the flagella of other bacteria, the periplasmic flagella of B. burgdorferi are polymorphic (29). We denote the smaller waveform as the normal form and the larger waveform as the wide form.

Figure 3.

Polymorphism of the flagella of B. burgdorferi. A B. burgdorferi periplasmic flagellum with one end in the normal helical form (small arrow) and the other end in the wide form (large arrow). Other flagella are shown that are in the normal form. Scale bar, 2 μm. Image courtesy of S. Goldstein.

Theoretical model

The energy required to twist or bend a filamentary elastic object is determined by the two elastic moduli, which are each determined by a material property such as the Young's modulus and the radius of the filament. Using the force and moment balance equations described previously (Eqs. 5 and 6), the equilibrium shape of the composite system of cell cylinder and flagella can be determined. Our model assumes that the flagella are localized at one position about the circumference of the cell cylinder and that they are free to slide. A similar model was used previously to describe the shape and dynamics of the Leptospiraceae (30); however, this model ignored the effects of the finite radius of the cell cylinder, which are necessary to describe the shape of B. burgdorferi.

For most materials, the ratio of the twisting to bending modulus is between 2/3 and 1 (28). Therefore, we assume that the ratios C _c/A _c = C _f/A _f = 1. Then, there is only one free parameter in the model, the ratio A = A _f/A _c, which was varied to determine the range of shapes predicted by the model. In addition, we used the model to examine the cell morphology for the two different observed flagellar conformations.

We began by examining the morphologies that are predicted by the model using the preferred curvature and torsion of the normal form of the periplasmic flagella. When the cell cylinder is much stiffer than the flagella, the cell is nearly straight and the flagella wrap about it with a pitch that is larger than P. As the ratio A increases, the cell cylinder deforms into a flat-wave shape whose deformation amplitude increases while the wavelength decreases ( Fig. 4, a and d). In this flat-wave shape, the model predicts that the periplasmic flagella should wrap about the cell cylinder in the opposite sense of their own handedness; i.e., a left-handed flagellum should wrap about the cell cylinder in a right-handed fashion, which agrees with previous experimental measurements (13). In addition, for values of A larger than 1.0, there can be a noticeable axial rotation of the flat-wave morphology (Fig. 4 a), a precession about the cell axis that is often observed (12). The extent of precession depends on the relative positions of flagellar attachment points at the two ends. However, we find that the amplitude and wavelength of the flat-wave shape are always less than those observed experimentally. The largest value of the wavelength is ∼2.0 μm, which occurs at small values of A. When A is equal to 3, we find an amplitude of 0.54 μm and a wavelength of 1.7 μm (Fig. 4 d). At larger values of A, the amplitude increases slightly, but the wavelength decreases, and as A goes to infinity the wavelength goes to the pitch of the normal form of the flagella. We also found that the shape of the cell did not depend strongly on the values of the twisting moduli (results not shown). Therefore, using the parameters for the normal form of the periplasmic flagella, there is no value of A that reproduces the observed amplitude and wavelength of the flat-wave shape.

Figure 4.

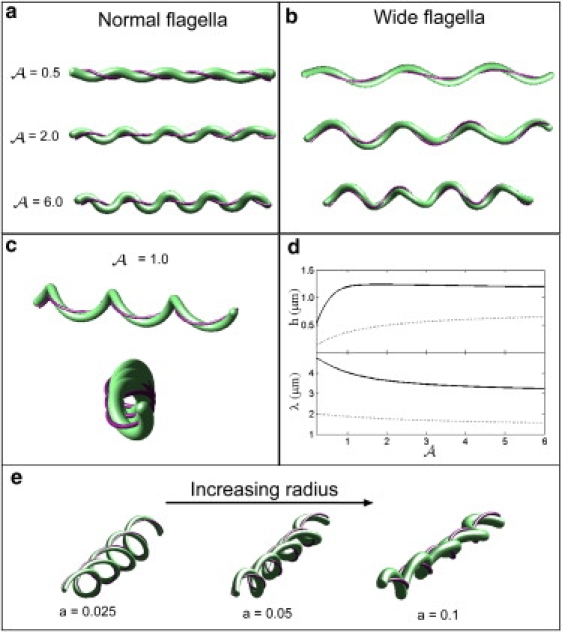
Predictions of the mathematical model. (a) The shape of the cell when the flagella are deformed with respect to the normal form for A = 0.5, 2, and 6. Increasing the stiffness of the periplasmic flagella leads to larger deformations of the cell cylinder. When A is between 1 and 5, the flat-wave shape precesses about the long axis of the cell morphology, which leads to a nonplanar waveform (bottom figure). (b) The shape of the cell when the flagella are deformed with respect to the wide form for A = 0.5, 2, and 6. (c) For the larger waveform of the periplasmic flagella, the morphology is not a true flat wave, but rather is a flattened-helical form. Top panel shows a side view of the shape with A = 1 and the bottom panel shows an end-on view. (d) The model predicts that increasing the ratio A leads to a decrease in the wavelength of the cell cylinder deformation, λ, and an increase in the amplitude, h. The solid line shows the results for the wide form of the flagella and the dashed line is the results for the normal form. (e) Effect of changes in the cell radius. For small values of the cell radius, a, the shape of the cell is helical. As the cell radius increases, the shape becomes more flattened. Here, values for a are given in microns.

Using the helix parameters for the wide form of the periplasmic flagella, we find good agreement with the experimentally observed flat-wave shapes. When A = 2, we found an amplitude of 1.2 μm and a wavelength of 3.6 μm (Fig. 4 b), which agrees well with the value of the amplitude and wavelength that we measure for cells with the outer membrane removed (see below). As A increases, the amplitude remains roughly constant, and the wavelength decreases. When the flagella are in this larger waveform configuration, the shape of the cell is not a true flat wave, but rather is a flattened-helical form (Fig. 4 c). Indeed, for values of A > 6, the shape becomes much more helical and does not resemble a flat wave. As A gets larger, the shape becomes more helical and there is a larger precession of the shape about the central axis (Fig. 4 b). Thus the model implies that the ratio A is between 2 and 6.

The flat-wave shape of B. burgdorferi is due to a matching between the helical radius and pitch of the flagella and the radius of the cell cylinder. If the flagella are stretched, then this matching depends on the current configuration of the flagella, not their preferred shape. Our mathematical model suggests that the flat-wave shape arises when the radius of the cell cylinder, a, times the square of the torsion of the periplasmic flagella is roughly equal to the curvature of the flagellum: aτ² ∼ κ (see Eq. S52 in the Supporting Material). For the normal form of B. burgdorferi periplasmic flagella, we find that this relation is satisfied for the preferred torsion and curvature, τ ₀ and κ ₀. Therefore, we expect that for large values of A, the flat-wave shape should arise when the flagella are in the normal form, which is what is predicted by the model. To illustrate how the cell shape depends on this matching condition, we treated the cell radius a as a free parameter and examined the shape of the cell when the flagella are in the normal form. When the cell cylinder's radius is much smaller than that of the flagella, the cell is also helical (Fig. 4 e). Increasing the radius of the cell leads to a flatter morphology (Fig. 4 e).

The preferred shape of the cell cylinder

Our mathematical model assumes that the shape of the cell cylinder is a straight rod when the flagella are not attached. This assumption is based on the finding that B. burgdorferi cells that are lacking FlaB (the primary constituent of the flagellar filament) are rod-shaped (7,12,17). However, this result does not preclude the possibility that the presence of the periplasmic flagella alters cell wall growth such that the cell cylinder takes on a nonrod-shaped morphology. Therefore, we treated cells with detergent to remove their outer membrane and then treated cells with low pH buffer (pH 2.8–3.2) to dissociate the periplasmic flagella into monomer. These cells became rod-shaped, which confirms the hypothesis that the preferred shape of the cell cylinder is a straight rod.

Measurement of the elastic parameters of the cell cylinder and the periplasmic flagella

To test the mathematical model, we measured the stiffness of the cell cylinder and the periplasmic flagella using optical trapping methods. For studies of the cell cylinder, detergent was used to remove the outer membrane of cells of B. burgdorferi senso stricto strain B31A, which exposes the cell wall. With the outer membrane removed, the flagella often remain intertwined about the cell cylinder. To determine whether removing the outer membrane plays a significant role in determining the cell morphology, we measured the cell morphology before and after detergent treatment. Before detergent treatment, we measured the cell wavelength to be 3.2 ± 0.2 μm and the amplitude was 1.0 ± 0.1 μm, which is comparable to what has been measured previously (12,13). After detergent treatment, the wavelength was 3.6 ± 0.2 μm and the amplitude was 1.3 ± 0.1 μm. Therefore, the presence of the outer membrane has a small effect on the morphology of the cells, but the gross morphology is not altered. Presumably, removing the outer membrane allows the flagella to pull away slightly from the cell cylinder.

Polylysine-coated silica beads (1 μm diameter) were attached to two points along the length of the purified cell cylinder. One of the beads was then anchored to a coverslip by attachment to another bead ( Fig. 5 a). The second bead was positioned in an optical trap. A quadrant photodiode was used to measure and align the position of the bead in the optical trap as well as to calibrate the spring constant of the trap; all calibrations were done in Metamorph using video tracking of trapped beads imaged with very short (1 ms) shutter speeds (26). The microscope stage was oscillated and the displacement of the trapped bead with respect to the position of beads affixed to the coverslip was measured. Using this procedure, the force required to stretch the cell cylinders was determined (Fig. 5 b). The shape of B. burgdorferi is roughly sinusoidal (12,13), and the force-displacement curves are well-fit by assuming that the cell cylinder behaves like an elastic sine wave (see Sec. 2 in the Supporting Material for more details). The effective bending modulus found using this fitting procedure is 42 ± 24 pN μm². We attribute the significant uncertainty in this fit to arise mostly due to variation in the number of periplasmic flagella per cell. By stretching the cell cylinder, bent regions where the periplasmic flagella are still wrapped about the cell body are straightened. Therefore, this bending modulus accounts for the combined effect of the cell cylinder and the periplasmic flagella. Our mathematical model predicts that the bending modulus that is measured by this experiment is A _c + 0.6A _f (see Eq. S37 in the Supporting Material).

Figure 5.

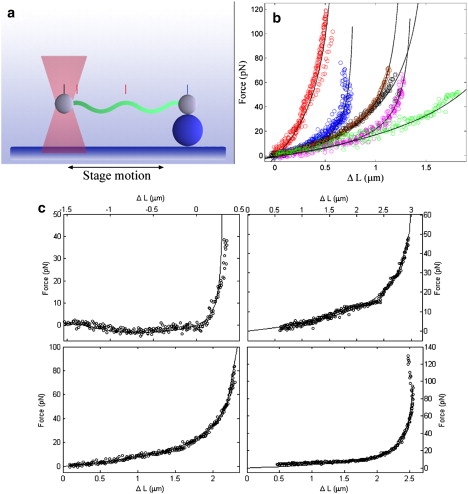
Experimental measurement of the stiffness of the cell cylinder and the periplasmic flagella. (a) Schematic of the experimental setup. Polystyrene beads are attached to two points on the cell cylinder of Triton-X treated cells or a purified flagellum. One of the beads is anchored to the coverslip via adhesion to another bead. The other bead is trapped in an optical trap. Oscillation of the microscope stage deforms the cell cylinder or flagellum. A quadrant photodiode detector is used to measure displacement of the bead in the trap. Video images are used to measure the displacement of the trapped bead with respect to fixed beads on the surface of the coverslip. (b) Six representative plots of the force vsersus displacement of the cell cylinder (see Experimental Procedure in text as well as in Supporting Material). Different colors represent data from different experiments. The black lines show the fits to the data. The parameters used to fit the data ranged from A = 21 pN μm² to 91 pN μm². (c) Four representative experiments for stretching purified flagella. Black circles are the experimental data. Solid lines show the fits to a model for deforming a linear elastic helix. The parameters used for these fits are A = 1.1 pN μm² (top left), 7.7 pN μm² (top right), 11.6 pN μm² (bottom left), and 5.8 pN μm² (bottom right).

Using a similar experimental procedure, we attached polylysine coated microspheres to single, purified flagella and measured the stiffness of the periplasmic flagella using our optical trap. Fig. 5 c shows four representative force-displacement curves. We fit these data to theoretical curves generated numerically for stretching and compressing an elastic helix. From these fits, the bending modulus for the periplasmic flagellum was estimated to be 6.7 ± 3.7 pN μm². This value is of the same order as measurements of the bending modulus of flagellar filaments from Salmonella enterica serovar Typhimurium performed using quasielastic scattering of light (31), extensional flow (32,33), and optical trapping experiments using repolymerized flagellar filaments (34). Using a flagellar diameter of 20 nm, we estimate the Young's modulus of the flagellum to be 700 MPa. Therefore, if there are 8 periplasmic flagella along the length of B. burgdorferi, A _f would be ∼53 pN μm². From this result and the results from the cell stretching experiments, we can conclude that the bending modulus for the cell cylinder is no more than a few 10s of pN μm². For an elastic tube, such as the cell wall, the Young's modulus, E, is related to the bending modulus as A ∼ πEa³t. Here t is the thickness of the cell wall, which we estimate to be ∼6 nm based on cyoelectron tomography (27). Therefore, the Young's modulus of the cell wall of B. burgdorferi is no larger than 0.5 MPa, which is comparable to that measured for Magnetospirillum gryphiswaldense (35) and Myxococcus xanthus (36) but substantially lower than what has been estimated for Escherichia coli and Bacillus subtilis (37,38). As this Young's modulus is on the low end of what has been measured for bacteria, we expect that the actual Young's modulus is not significantly less than a 100 KPa. Using this value, we estimate the bending modulus of the cell cylinder to be ∼10 pN μm², which implies that A ≈ 5, in good agreement with the results from the mathematical model.

Discussion

We have shown that the mechanical coupling of the helical periplasmic flagella to the rod-shaped cell cylinder is sufficient to determine the flat-wave morphology of B. burgdorferi. Interestingly, we find that to match the experimentally observed amplitude and wavelength of the flat-wave morphology, the flagella must be in a wide form configuration that is only observed in a small percentage of purified flagella. In addition, we have measured the elastic parameters of both of these structures. Coupling of helical flagellar filaments to a rod-shaped cell cylinder naturally leads to a flat-wave shape. Even though both the helix and the cell cylinder have axial symmetry, the breaking of this symmetry arises from the fact that the flagella are not evenly distributed about the circumference of the cell cylinder. Therefore, the attachment point of the flagella breaks this axial symmetry and can produce a planar morphology. As we showed in the Results section, as the radius of the cell cylinder goes to zero the shape becomes more helical, and, indeed, the equilibrium shape when the cell cylinder radius is zero is a helix.

In spirochetes, because the interaction between the periplasmic flagella and cell cylinder is quite intimate, these organelles may have coevolved to achieve optimal motility and for survival in nature. It is not clear why some spirochete species are helical and others are flat waves. However, there are two obvious advantages to being a spirochete. First, all known spirochetes can swim efficiently in highly viscous gel-like media that slow down or stop other species of bacteria (3,39,40). Second, because the periplasmic flagella are intracellular, these organelles are protected from harsh environments including specific antibodies (3). Evidently, each species evolved in a manner that maintained these attributes to best adapt to its specific ecological niche.

If the shape and dynamics of B. burgdorferi have evolved to allow for optimal motility and/or the ability to invade host tissue, then it is interesting to speculate about the physical consequences of our findings. Our results suggest that there are two major factors that can be adjusted to modify B. burgdorferi's cell morphology, the geometric parameters of the helical flagella and the ratio of the stiffness of the periplasmic flagella to that of the cell cylinder. We find that the stiffness of an individual flagellum of B. burgdorferi is comparable to the stiffness that has been measured in other species, such as Salmonella enterica serovar Typhimurium (31–33). Therefore, it may be that bacterial flagellar stiffness is not evolutionarily tunable. However, some bacterial flagella have a sheath around the flagellum or have glycosylated or sulfated residues on the flagellum, which could be a method for increasing flagellar stiffness, but the stiffnesses of these flagella have not yet been measured (41–45).

The other ways that a spirochete could modify the stiffness ratio would be to alter the number of the flagella or the stiffness of the cell cylinder. Indeed, bacterial cell wall stiffness varies dramatically between bacterial species, as does the number of periplasmic flagella in spirochetes. Comparison of our measurements of the stiffness of the B. burgdorferi cell cylinder to theoretical estimates for Leptonema illini suggests that B. burgdorferi's cell cylinder is considerably less stiff than that of L. illini (30). Because the stiffness of a group of periplasmic flagella should increase with the number of filaments, this is another parameter that can be varied between species. If this line of reasoning is correct, then an individual spirochete could adjust its number of flagella in response to physical parameters of the environment to optimize its motility. Although other explanations are possible, this hypothesis could explain why in vitro culturing of Borrelia garinii results in a decreased number of periplasmic flagella and decreased motility in gel-like media (46). In fact, the flagella could even act as the regulatory sensor. In Vibrio parahaemolyticus, the polar flagellum acts as a mechanosensor that is sensitive to fluid viscosity and triggers lateral flagella synthesis for efficient swimming in highly viscous environments and on surfaces (43,47).

Morphology of B. burgdorferi is implicitly connected with motility. Moreover, motility is likely to be essential for these organisms to cause disease (3,14,46). How rotation of the flagella produces the undulating motions that drive motility and enables translocation through host tissues remains unknown. However, the description of the physical interaction between the flagella and the cell cylinder developed here provides a basis for a quantitative model of the mechanism of motility in B. burgdorferi and will likely serve as a foundation for eventually understanding the motility of T. pallidum.

Many biological structures are composed of interconnected filamentary objects. At the single protein level, α helices often intertwine into helix bundles, such as the coiled-coil structure (48), and many receptor and motor proteins have large coiled-coil domains. At the molecular level, DNA, F-actin, microtubules, and the bacterial flagellum are all composed of multiple connected polymer strands or protofilaments. And, at the cellular level, the axoneme, which is the primary component of eukaryotic cilia and flagella, is composed of a cylindrical array of nine microtubule doublets, crosslinked by dynein motors (49,50). The mathematical model that is presented here describes the complex physics of conjoined elastic filaments and should therefore be applicable to many of these structures. Indeed, simplified models have already been used to describe the dynamics of cilia (51), the configuration of the bacterial flagellum (52), and the structure of alpha-helical bundle proteins (53,54).