Rapid Sample Size Calculations for a Defined Likelihood Ratio Test-Based Power in Mixed-Effects Models

Abstract

Efficient power calculation methods have previously been suggested for Wald test-based inference in mixed-effects models but the only available alternative for Likelihood ratio test-based hypothesis testing has been to perform computer-intensive multiple simulations and re-estimations. The proposed Monte Carlo Mapped Power (MCMP) method is based on the use of the difference in individual objective function values (ΔiOFV) derived from a large dataset simulated from a full model and subsequently re-estimated with the full and reduced models. The ΔiOFV is sampled and summed (∑ΔiOFVs) for each study at each sample size of interest to study, and the percentage of ∑ΔiOFVs greater than the significance criterion is taken as the power. The power versus sample size relationship established via the MCMP method was compared to traditional assessment of model-based power for six different pharmacokinetic and pharmacodynamic models and designs. In each case, 1,000 simulated datasets were analysed with the full and reduced models. There was concordance in power between the traditional and MCMP methods such that for 90% power, the difference in required sample size was in most investigated cases less than 10%. The MCMP method was able to provide relevant power information for a representative pharmacometric model at less than 1% of the run-time of an SSE. The suggested MCMP method provides a fast and accurate prediction of the power and sample size relationship.

INTRODUCTION

Clinical drug development contains both learning and confirming activities as outlined by Sheiner (1). Confirming phases are most predominant in the proof-of-concept stage, to inform decisions regarding the possible start of full development, and at the end of the Phase III trials. Most often, the confirmatory evidence is generated through testing an alternative hypothesis against a null hypothesis by traditional statistical methods (2). Pharmacometric models (3–5) are increasingly expanding in drug development and can provide advantages over traditional methods (e.g. T-test, ANOVA) for example with respect to power (6). In traditional analysis, the information content is often truncated with pairwise comparison of a single dose group (often at the highest dose) against the placebo group and a drug effect evaluated at a specific time point (i.e. end of study), hence leading to a loss of power. In a pharmacometric approach, a higher power is achieved primarily by the possibility to perform a longitudinal analysis, incorporating each subject’s measurement on several occasions and e.g. integrating a drug effect across time and/or dose levels.

A critical element to be addressed in the planning phase of a confirmatory trial is to estimate the required size of the study for answering the primary research question. While such sample size calculations are relatively straightforward and fast for traditional methods (7,8), a multitude of methods have been suggested for linear models (9–12) and nonlinear mixed-effects models, each of which comes with some drawbacks. The binary covariate approach using the Wald’s hypothesis-testing method (13–17) has been proposed for sample size calculation. This approach assumes a symmetrical uncertainty distribution around the parameter estimate and an accurate prediction of the parameter precision. Other analytical solutions (18–20) have also been suggested on the use of confidence intervals. The standard for making inference based on nonlinear mixed-effects models are however not Wald test but the likelihood ratio test (LRT). Power calculation for the LRT has been described based on multiple simulations and re-estimations (21–23). Sample size calculations by repeated stochastic simulations and estimations (SSE) remain however time-consuming and computer-intensive (many replicated datasets for one tested sample size) and embed drawbacks such as the assumption of both the correct degrees of freedom for the hypothesis variable in consideration (e.g. the degree of freedom for a random effect) and the distribution shape around the null hypothesis (i.e. if the chi-squared distribution is achieved). A need for correction for type I error inflation has been demonstrated by Wählby et al. (24,25) to be necessary for small sample sizes.

This paper intends to propose a new power calculation method—the Monte Carlo Mapped Power (MCMP)—using a nonlinear mixed-effects approach that allows a complete mapping of the power curve without the main impediments of run-time intensity and need for Type I error correction, as mentioned for the SSE methods. The approach adopted here attempts to extend the same simulation and hypothesis-testing settings as proposed previously but to only one single step of simulation and estimation from a large simulated data set. This reduction of computation workload and time is based on the use of the objective function value of each included subjects in the study.

METHODS

Nonlinear Mixed-Effects Model

The nonlinear mixed-effects modelling approach used in population PK/PD studies allows recognition of multi-level random variation present in the data. A nonlinear mixed-effects model can be described as follows:

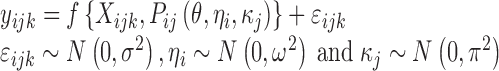1

where y_ijk denotes the kth (k = 1,…,n_i) observation at jth occasion in ith individual (i = 1,…,N). y_ijk is described by a function of individual PK/PD parameters described by 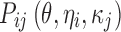in which θ is the typical value of the parameter P and η_i and κ_j are the random effects that quantify the difference between the typical and the individual-specific and occasion-specific parameter values. It is also described by X_ijk (i.e. time, dose and exposure, demographic covariates) a vector of independent variables. The residual error ε_ijk describes the deviation between the individual prediction and the observation. In Eq. 1, the residual error is an additive residual error model. Other residual error models exist where the deviation is described for example as proportional or as a combination of additive and proportional. The random effects η_i, κ_j and ε_ijk are assumed to be normally distributed with mean 0 and variance–covariance matrices Ω, Π and ∑.

Principle of the MCMP Method

In NONMEM version 7.1.2 (26), the overall objective function value (OFV) of a model for a given dataset, which is approximately proportional to minus twice the natural logarithm of the likelihood of the data, can be easily outputted as individual objective function values (iOFV), such as:

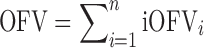2

where iOFV_i denotes the ith individual contribution to the overall OFV.

The MCMP method as outlined in Fig. 1 tests the hypothesis of a possible drug/covariate effect using the substitution of the overall OFV value by the summation of iOFV values in the LRT. Given a defined study design of n individuals per study group, a large simulated dataset is first computed from a model containing the tested drug/covariate effect. The generated data are then estimated with a single full and a single reduced model (i.e. including or not the test drug/covariate effect, respectively), providing a large pool of iOFV values for the full model, denoted as iOFV_FULL and for the reduced model, denoted as iOFV_REDUCED. In the LRT, the difference in the overall objective function value (ΔOFV) between two nested models can be redefined in each individual, such as:

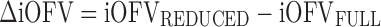3

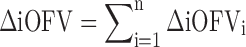4

Fig. 1.

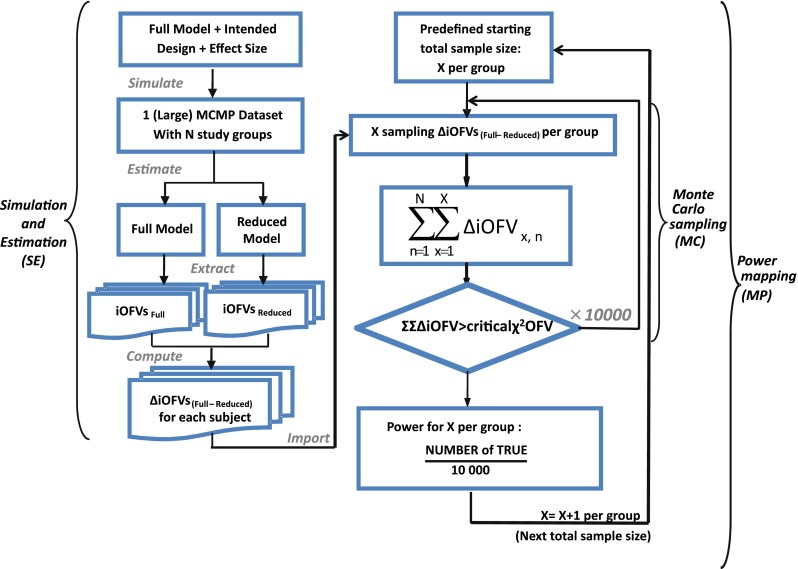
A schematic representation of the MCMP method illustrating the three consecutive steps of one simulation and estimation (SE), multiple Monte Carlo samplings (MC) and power mapping (MP) for each increment of sample size according to an intended design with a specific effect size

In the MCMP method, the total summation of n ΔiOFV values (ΣΔiOFV) is used instead of the overall ΔOFV for statistical inference in the LRT. This ΣΔiOFV is significant (i.e. confirming the improvement in data fit caused by the addition of the covariate or drug effect) when it is higher to the theoretical value obtained from the χ² distribution with degrees of freedom corresponding to the difference in number of parameters between the two contending models and with an assigned significance level (i.e. 3.84 in ΔOFV for nominal significance level of 0.05 with df = 1).

To map the whole power versus sample size relationship up to a predefined sample size, this procedure is repeated 10,000 times for each sample size of the power curve by randomly sampling the sum of all ΔiOFV (e.g. in increments of one subject per study group). This value of 10,000 was selected to provide a low error contribution from sampling noise. At each current design (i.e. each sample size), the power is assessed as the percentage of ∑ΔiOFVs out of 10,000 times that is greater than the significance level criterion defined by the LRT.

Method Evaluation

In order to evaluate the newly implemented method, the power versus sample size relationship established via the MCMP method was compared to traditional assessment of model-based power via the SSE method for a selection of sample sizes and models. For each sample size selected for power assessment using SSE, 1,000 replicates were simulated from the full model and both full and reduced models were fitted to the simulated data. For each replicate, the difference in the OFV was computed and submitted to the hypothesis χ² test. The number of replicates where the difference results indicated a significant subgroup effect was counted. The ratio of this number over the total number of replicates provides the estimated power of the study for the tested sample size N. The process was carried out repeatedly for a range of sample sizes to cover different areas of the power curve obtained by the MCMP method.

Simultaneously, to correct for the difference between the actual and nominal type I error due to the deviation of the LRT from its properties at small sample sizes (24), a systematic type I error calibration was applied to the critical ΔOFV value obtained from the SSE: 10,000 replicates of the same design used in the SSEs were simulated from the reduced model and both the full and reduced models were fitted to the simulated data. The ΔOFV for each replicate was calculated and ranked to determine the nominal cut-off OFV from the fifth percentile. This new, empirically determined, OFV cut-off is used to reassess the power for the present sample size: the percentage of ΔOFV greater than the new cut-off OFV is taken as the power for the current sample size. The type I error corrected SSE determined power, further referred as calibrated SSE, was compared to the power obtained from the MCMP method.

MCMP Dataset Size

The relation between the MCMP dataset size and imprecision in estimated sample size needed to reach 90% power (N_90%) was explored. Several MCMP dataset sizes (n = 250, 500, 1,000, 2,000, 4,000, 8,000 and 10,000) were investigated in the MCMP simulation step by simulating 1,000 replicates each from a one-compartment infusion model with a binary covariate effect on the clearance for four samples per individual. Each replicate was then estimated under the full and reduced models. For each MCMP dataset size, 1,000 MCMP curves were obtained and used to compute the relative standard error, the mean and the standard deviation in N_90%.

Number of SSEs for Equivalent Relative Standard Error in MCMP Power Prediction

For each dataset size described in the previous section, a relative standard error (RSE) in power predicted by MCMP is calculated based on the 95% confidence interval derived from the same 1,000 MCMP curves simulated from the previous infusion model. The number of SSE (n_SSE) replicates for equivalent RSE was computed from the following relationship for the power of interest of :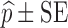

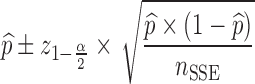5

Simulation Models and Designs

All modelling and both graphical and statistical evaluations were performed using the MCMP tool implemented both in PsN version 3.2.12 (27) and MATLAB R2009b, NONMEM version 7.1.2 (26) and run on a Linux cluster with a Red Hat 9 operating system using OpenMosix and a G77 Fortran compiler. For run-time comparisons, a dedicated node was used.

To compare the performance of the proposed MCMP method with traditional SSE evaluations, PK/PD datasets were simulated from different models and study designs. The default model parameters and design conditions used for simulation are summarized in Table I. Two basic pharmacokinetic models were used as proof-of-concept to map the power versus sample size relationship. The first example involves a one-compartment intravenous (IV) bolus model with first order elimination, with typical CL and V values being 10 L/h and 100 L, respectively. The inter-individual variability (IIV) in CL and V were assumed to be log-normally distributed and the residual error was assumed to be proportional. The second example involves a one-compartment model with first-order elimination and zero-order absorption where steady state conditions were assumed, with typical CL and dosing rate values being 10 L/h and 1 mg/h, respectively. The inter-individual variability was also assumed to follow a log-normal distribution and the residual error was assumed to be additive.

Table I.

Parameter Values (i.e. Structure and Magnitude of the Random Effects) and Design Settings (i.e. Number of Subjects in the MCMP Large Dataset, Number of Samples Per Subject, Sample Spacing, Magnitude of the Tested Drug/Covariate Effect) Used in the Models Simulation Step of Both MCMP and SSE Methods

Models	No. of subjects in MCMP simulated data sets	No. of samples per subject	Sample spacing	Effect size of drug/covariate	Model for η	Inter-individual variability (ω2)	Model for residual error (ε)	Residual error (σ)
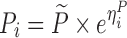
One-compartment, IV bolus model	1,000	4	1.75/3/7/12 h	−25% on CL		0.09	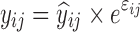b	0.1
						0.09
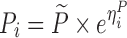
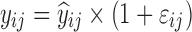
One-compartment, zero-order input model	1,000	4	1.75/3/7/12 h	−20%c and -35% on CL		0.09		0.1
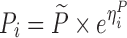
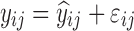
Linear disease, slope effect model	1,000	4	1.75/3/7/12 h	-20% on slope		0.01		0.1
						0.09
						0.09
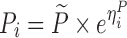
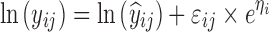
Indirect transit compartment model (FPG-HbA1c) (28)	2,000	4	2/4/8/12 weeks	−27,5% on FPG K out		0.09		0.0964
						0.01
						0.0184
						0.00345		0.0495
						0.131a
						0.0684a
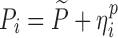
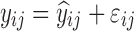
HIV viral load, bi-exponential model (29)	10,000	6	1/3/7/14/28/56 days	−26.2% on first decay rate		0.3		0.0042
						0.3
						0.3
						0.3
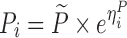
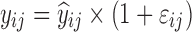
Digoxin two-compartment, linear effect model (30,31)	10,000	5	0/2/6/12/16 h	−10.3% on baseline heart rate		1.507984		0.09
						0.031329

^aVariability on the residual error as described in the error model of the FPG-HbA1c model

^bHeteroscedastic exponential error model

^cEffect size tested but not reported in the “RESULTS” section

The implemented new method was also tested on four distinctly different PK/PD models of varying complexity: a linear disease model with a drug effect on the slope and log-normal distributed IIVs on baseline, slope and effect parameters, a nonlinear mixed-effects model in Type 2 Diabetes Mellitus (28) describing the mechanistic relationship between tesaglitazar exposure, fasting plasma glucose (FPG), glycosylated hemoglobin (HbA1c) and aging red blood cell (RBC) with drug effect added on the rate of elimination (K_out) of FPG, a nonlinear mixed-effects model describing the decrease of viral load in HIV-infected patients after initiation of antiretroviral treatment (29) and a nonlinear mixed-effects base model with no original covariate inclusion, describing the relationship between the plasma concentration of digoxin, the estimated concentration at the effect site and the reduction in heart rate during atrial fibrillation with a drug effect linearly added on the heart rate baseline value (30,31).

The hypothesis of a possible covariate/drug effect in all performed models was tested by introducing in the simulated model, a covariate/drug effect relationship to a parameter P described as follows:

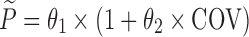6

where θ₁ represents the population mean value of the parameter and θ₂ the fraction deviated from the mean parameter value θ₁ altered by the inclusion of the categorical covariate COV (i.e. value of 0 or 1 according to a predefined allocation design). In each example cited above, two nested models (i.e. the full and the reduced models) were used to fit the simulated dataset from the full model containing this covariate or drug effect relationship. The estimation method used in all examples was the First-Order Conditional Estimation method with Interaction (FOCEI).

Impact of η-Shrinkage on MCMP Power Prediction

To evaluate the impact of η-shrinkage, the one-compartment IV bolus model was re-run using the MCMP method with a reduced number of samples per subject (i.e. 2 versus 4 samples per subject) and a residual error increased up to 30%. The total sample size resulting in 90% power from the MCMP method was selected for power assessment using a calibrated SSE. Power predictions from both methods were then compared.

RESULTS

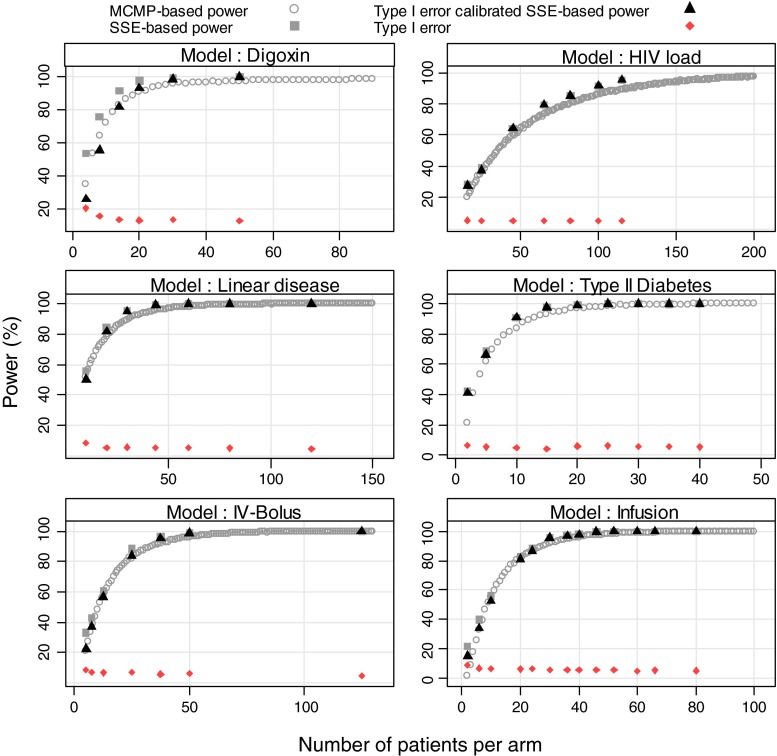
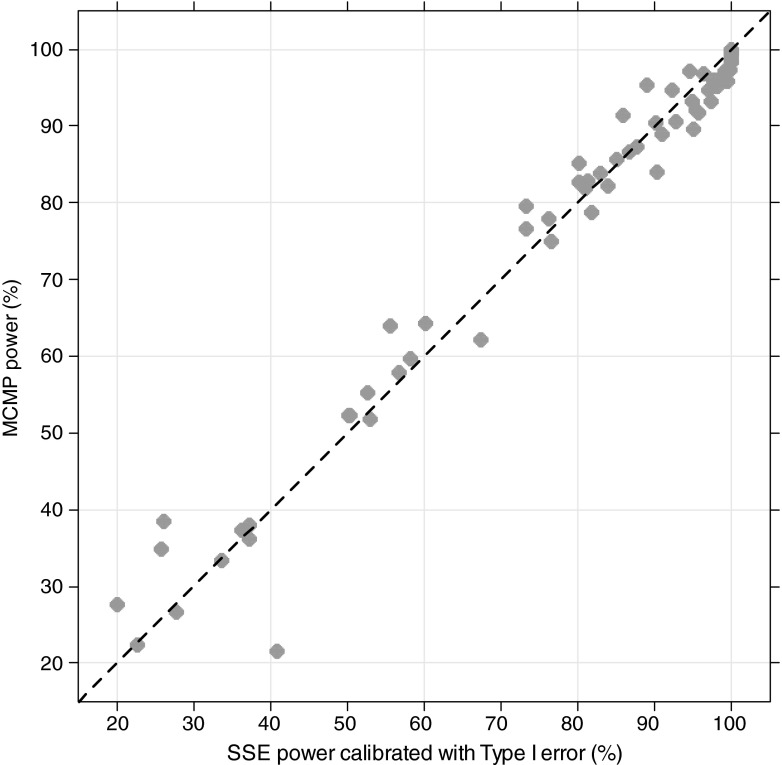
In all explored examples, the MCMP power and the calibrated simulation and estimation based power resulted in an overall good agreement between the two methods as shown in Figs. 2 and 3. For power higher than 40%, the power estimate obtained with the MCMP method was never off by more than 15% compared to the calibrated SSE. As expected for SSE, actual type I error rates for small sample sizes were found to be above the nominal 5% cut-off value as reported in Table II, resulting in up to ~30% power difference between SSEs and calibrated SSEs.

Fig. 2.

Outcome of predicted power study in six nonlinear mixed-effects models at varying sample size per study arm from stochastic simulation and estimation method (grey squares), stochastic simulation and estimation method (black triangles) calibrated with type I error rate (dark red diamond) and MCMP method (grey circle)

Fig. 3.

Concordance plot for all models-pooled calibrated stochastic simulation and estimation with type I error calibration-based power versus MCMP-based power. Plain line represents the identity reference line

Table II.

Actual Significance Levels of False Covariate Inclusion or Drug Effect Detection Corresponding to a Nominal Level of 0.05, versus the Number of Patients Per Arm

Models	Number of patients per arm	Type I error rate (%)
One-compartment, IV bolus model	5	8.8
	7.5	7
	12.5	6.8
	25	7.2
	37.5	5.9
	50	6.2
	125	4.6
One-compartment, zero-order input model	2	8.87
	6	6.54
	10	6.23
	20	6.03
	24	6.16
	30	5.46
	36	5.72
	40	5.36
	46	5.66
	52	5.71
	60	4.86
	66	5.24
	80	5
Linear disease, slope effect model	10	8.53
	20	5.42
	30	5.76
	44	5.44
	60	5.16
	80	5.02
	120	4.8
Indirect transit compartment model (FPG-HbA1c)	2	6.5
	5	5.4
	10	4.9
	15	4.3
	20	6.01
	25	6.1
	30	5.7
	35	5.8
	40	5.3
HIV viral load, bi-exponential model	25	5.2
	45	4.9
	65	5
	82	4.9
	100	4.9
	115	4.9
Digoxin two-compartment, linear effect model	4	20.44
	8	15.58
	14	13.34
	20	13.09
	30	13.67
	50	12.66

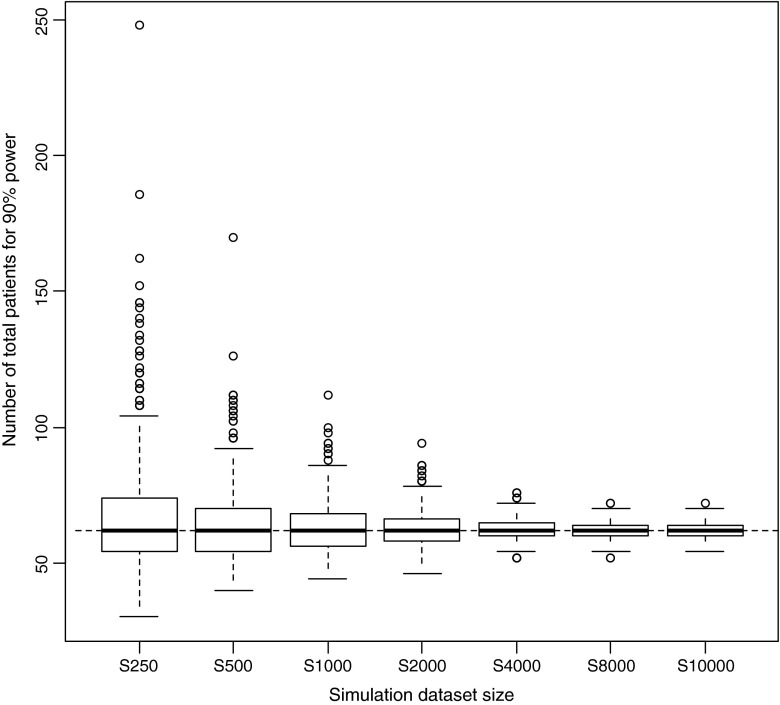
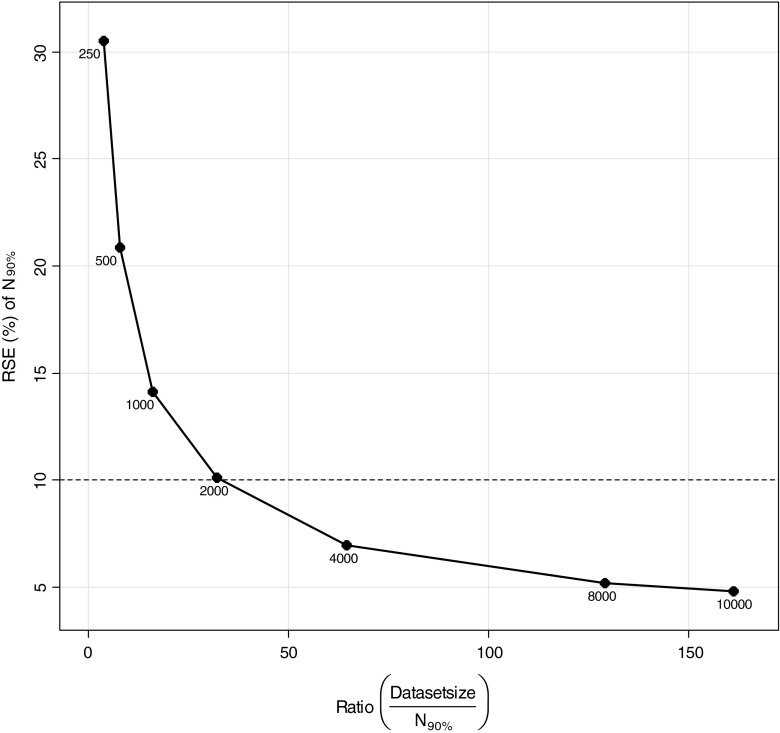
In the estimation of the relations between MCMP dataset size and precision of sample size estimates, a “true” number of patients to be included for 90% power was estimated to be 62 patients with a precision in this number related to the MCMP dataset size as illustrated in Fig. 4. Dataset sizes above 2000 and at 10,000 individuals were found necessary to obtain a variation of this number of patients less than 10% and 5%, respectively, as shown in Fig. 5.

Fig. 4.

Box-plots of number of patients distributions required for 90% power from 1000 power curves simulated from seven dataset sizes using the one-compartment infusion model with an effect size set to 35%. The solid bold line corresponds to the median, the top and bottom of the box the 25th and 75th percentiles and the whiskers to the maximum and minimum of the number of patients to be included. The dashed line corresponds to the "true" number of patients needed to reach the power level in this example

Fig. 5.

Relationship between relative standard error (RSE) of the estimate for number of patients needed to achieve 90% power (N _90%) versus the ratio of dataset size (N = 250, 500, 1,000, 2,000, 4000, 8000 and 10,000 total patients) and N _90%

In Table III, 95% confidence intervals for increasing MCMP dataset sizes show decreasing relative standard errors in 90% power prediction. Dataset sizes of 250, 500, 1,000, 2,000, 4,000, 8,000 and 10,000 individuals show a relative standard error in 90% power prediction of 6.3%, 4.2%, 2.7%, 2.1%, 1.4%, 1.1% and 1.0%, respectively.

Table III.

Number of SSEs for Equivalent Precision in 90% Power Prediction with the MCMP Method

MCMP dataset size	Ratio MCMP dataset size over N 90%	Median	95th confidence Interval (CI)	Relative standard error (RSE%)	Number of SSE for equivalent RSE
250	4	90.5	[73–97.5]	6.3	22
500	8.1	90.6	[80.0–96.3]	4.2	49.2
1000	16.1	90.3	[83.3–93.7]	2.7	124.6
2000	32.3	90.4	[85.2–93.3]	2.1	203.3
4000	64.5	90.4	[87.3–92.8]	1.4	440.8
8000	129	90.5	[88.2–92.3]	1.1	785
10,000	161.3	90.4	[88.5–92.3]	1	922.3

Reduction of samples per subject and increase in residual error for the IV bolus model resulted in shrinkage of 52% for the CL parameter. From the MCMP method, at a sample size of 210 individuals, power prediction from a calibrated SSE was found to be 90.5% versus the power prediction of 90.1% from the MCMP method.

Figure 2 shows comparisons between 3 different methods; MCMP, SSE and calibrated SSE. The computer run-time for generation of the results shown in the panel for the Type 2 Diabetes Mellitus model, an example where the estimation step dominated overall run-time, was shortest for the MCMP. The run-times for the SSE and calibrated SSE results in the same figure were 168 and 1,773 times longer.

DISCUSSION

The MCMP method presented here is a simple and efficient model-based method for power/sample size calculation. Tested on several types of data and for several simple and real-life pharmacokinetic–pharmacodynamic models such as the diabetic and the HIV viral load model, the methodology has demonstrated a good agreement in power prediction compared to the one obtained from the traditional simulation-based power calculations. This new methodology also offers an alternative to the SSE which is time-consuming and often subject to numerical computation issues from multiple simulations and estimations. The MCMP requires only one simulation and estimation step, hence leading to an important reduction in time and computation load (for example ca. 167 times compared to an SSE without calibration). This substitution is explained mainly by the fact that the overall objective function value specific to a given model, design and dataset can be described by the sum of individual objective values, allowing iOFV values to be sampled instead of OFV values from simulated studies.

One design aspect consists in allowing enough number of random samples in order to have acceptable precision in the study size estimates for a given power of interest. In all explored examples, a number of 10,000 stochastic samples results in less than 1% of relative standard error in the number of subjects’ value to reach 90% power. Increasing this number further did not reduce significantly the relative standard error for reasonable MCMP dataset sizes (results not presented). The size of the MCMP dataset must also be considered in order to provide enough samples for the stochastic sampling process, but also include enough individuals at the estimation step to avoid an over fitted model to be developed with biased values of the parameters estimated (i.e. different from simulation parameter values). We found that including 33 and 160 times the number of subjects needed to reach the desired power is sufficient if relative standard errors of 10% and 5% are acceptable for the study size prediction’s precision. Naturally this size is not known before the first MCMP dataset size is chosen, so if a too small study size was chosen, a repeat evaluation with a higher MCMP study size may be necessary to reach desired precision. We also expect this ratio to be effect size- and model-dependent, but from all explored examples, we found a 50-fold of the number of subjects needed in the study for a 90% power assessment to provide acceptable relative standard error values.

In terms of statistical inference, the newly developed method is based on the likelihood ratio test, available in all nonlinear mixed-effects software and recognized as standard for test hypothesis analysis in pharmacokinetic–pharmacodynamic modelling and simulation. This feature allows making stronger inference based on the log-likelihood change in each parameter of the model and in their respective correlations, unlike power calculation methods derived from optimal design coupled to the Wald test. The latter method is usually based on power computation derived from the expected log-likelihood change from a change in one parameter (i.e. the hypothesis-testing parameter), assumes symmetric confidence intervals and that the parameters estimates are unbiased. The MCMP method, unlike the Wald test, allows the use of estimation models that are different from the simulation model. In addition, because changes in several design parameters range and distribution are reflected in the final iOFV values used to make inference in the likelihood ratio test, the prediction in power derived from the MCMP method is dependent on the assigned design and on the different levels of randomness of the parameters (i.e. variability in population, uncertainty on parameters), hence providing a flexible tool for rapid sensitivity analysis. More importantly, the possibility to include different possible sources of bias in the model jointly with a random sampling implemented in the MCMP method could result in a more tempered and realistic prediction in power calculation, often correcting the “optimistic” power calculation derived from an optimal design approach. Another advantage with the MCMP method is that it is straightforward to change estimation method (as long as the estimation method includes evaluations of the individual contribution to the log-likelihood). This is not trivial for the methods based on the Fisher information matrix (FIM) (32–35) because an analytic solution, i.e. FIM calculated without simulations, is only available for the FIM based on the first order approximation (36). It is possible to derive an asymptotic FIM with other estimation methods (37,38) as well but these methods include simulations and the advantage in speed with the FIM-based methods over the MCMP method will be lost.

From the investigations on several models, the MCMP method was found to be a good approximation of the outcome of a calibrated SSE for power in the main region of interest (i.e. 80–90%). Also as illustrated in the result section, it may be less precise in other regions, in particular for powers lower than 20%. A possible explanation of discrepancies at these low powers is suggested by the omission of the estimation step for each sample size of the MCMP power curve. A nonlinear mixed-effects maximum likelihood estimator, like NONMEM, is asymptotically normal in its estimates with respect to the number of individuals. However, the MCMP method does not acknowledge the asymptotic differences between different sample sizes since the parameter estimates, hence the iOFV values, are not re-estimated, but used such as from a big dataset down to a smaller dataset. This is nothing that is unique for the MCMP method; indeed every method that uses this type of scaling without estimation, e.g. Fisher Information methods, will suffer from this unwanted property.

Furthermore, scaling sample size without estimation will assume the same bias (size and direction) as the bias from estimation with the big data set (which will be asymptotic, when n → ∞, towards the pure bias from the estimation method used, given the model, parameter values and the design). The effect on the power due to this assumption is much harder to predict because the bias might change sign and/or size differently between sample sizes and parameters. However, a reasonable rule of thumb could be that the size of the bias, especially for small n, will be under predicted and the major power effect from this assumption will be at small n, which will not be as likely to occur for most studies and their target power. However, as it can be seen from Fig. 2, the agreement between the MCMP and a calibrated SSE is good even when the samples sizes for 80–90% power are ca. 10–50 subjects per arm. Even smaller sample sizes are often fast to estimate and therefore more applicable for a full LRT inspection of the power. Finally, the reduction of number of samples per individual and the increase of residual error, hence the impact of higher shrinkage, did not result in a different power prediction from a calibrated SSE-based one for power assessment in the 80–90% range.

Regarding the need for type I error assessment, the dataset sizes at which the MCMP is run in estimation are in the region where the calibration indicates a close to nominal type I error magnitude. This is the reason why no type I error calibration was necessary with the MCMP. However, the MCMP method only claims to remove the dependence on sample size of the type I error and does not acknowledge other reasons for why a type I error rate can deviate from the nominal such as model misspecification. This was however not the case for most examples investigated in this manuscript since the simulation and the full estimation model were identical.

A limitation to the usefulness of MCMP as a substitute for SSE is for studies where the test is not based on a stratified covariate. The power of a test for differences between groups, where the relative group sizes are not known beforehand, cannot be reliably calculated by MCMP. Further, the MCMP method does not inform on any design flaw that will make a model numerically unidentifiable. Performing a few simulations and re-estimations with the decided sample size from the MCMP method could be used as a confirmation of numerical identifiability.

In terms of clinical application, recent comparisons made between the pharmacometric model-based power assessment approach versus traditional statistical tests (6,39–41) show that the power computation using pharmacometric models results in a significant reduction in sample sizes compared to the traditional trial approach. One of the primary reasons is that model-based power calculation methods relate closely to the longitudinal data upon which the model has been developed. Consequently, integration of all available measures collected successively during the clinical trial increases the information content upon which the inference is made. This approach, contrary to traditional statistical methods which discard all information between the starting and final measurement times, hence making difficult to interpolate, does not restrictively treat the inference as a punctual but rather as a continuous outcome. As a result, power considerations with model-based approach present the possibility to detect a specific predictor (i.e. covariate or a drug effect) and to provide valuable insights of the predictor behaviours (e.g. estimation with all dose levels of a dose–response relationship). These two advantages along with the possibility to simultaneously analyse multiple endpoints interpreted as mechanistically connected (e.g. simultaneous analysis of FPG and HbA1c in the diabetic example) substantiate the learning and confirming properties of model-based approach as suggested by Sheiner (1) in his drug development paradigm. The immediate consequences of such an approach are a reduction in costs and a reduction in risks to expose patients unnecessarily to experimental procedures. Finally, faster time computation of the MCMP method can be used to highlight more often the prognostic value of these power calculation methods in future clinical trials planning and is believed to increase the opportunity for rapid evaluation of alternative study designs and to facilitate more sensitivity analysis in clinical drug development. The development of more effective methodology for power calculations applied to nonlinear mixed-effects models are hence believed to lead to more informative and efficient clinical trials.

CONCLUSION

A new rapid and easily implemented method for power calculations with respect to the likelihood ratio test in nonlinear mixed-effects models was outlined and tested. The proposed MCMP method allowed to obtain a complete power curve with no further calibration of Type I error and was found to considerably shorten the time for sample size calculations compared to the traditional approach based on multiple simulations and re-estimations.