How noise in force fields can affect the structural refinement of protein models

Abstract

Structural refinement of predicted models of biological macromolecules using atomistic or coarse-grained molecular force fields having various degree of error are investigated. The goal of this analysis is to estimate what is the probability for designing an effective structural refinement based on computations of conformational energies using force field, and starting from a structure predicted from the sequence (using template-based, or template-free modeling), and refining it to bring the structure into closer proximity to the native state. It is widely believed that it should be possible to develop such a successful structure refinement algorithm by applying an iterative procedure with stochastic sampling and appropriate energy function, which assesses the quality (correctness) of protein decoys. Here an analysis of noise in an artificially introduced scoring function is investigated for a model of an ideal sampling scheme, where the underlying distribution of RMSDs is assumed to be Gaussian. Sampling of the conformational space is performed by random generation of RMSD values. We demonstrate that whenever the random noise in a force field exceeds some level, it is impossible to obtain reliable structural refinement. The magnitude of the noise, above which a structural refinement, on average is impossible, depends strongly on the quality of sampling scheme and a size of the protein. Finally, possible strategies to overcome the intrinsic limitations in the force fields for impacting the development of successful refinement algorithms are discussed.

Introduction

Three-dimensional structure prediction of proteins, from their sequences is one of the most challenging, and longstanding tasks in structural biology and biophysics¹. Information about three dimensional structures of biomolecules is essential for many biological studies, such as protein function prediction^2–4, computer aided drug design^2–4 and can be important in systems biology⁵. So far the most powerful and popular method developed to solve the structure prediction problem is homology modeling^6,7 based on having a known structure of a good template(s) – proteins having similarity in their overall sequence or at least in parts. In the case of new folds we use less reliable template-free (ab initio) structure prediction methodology^8,9. Homology modeling is based on the fact, that homologous proteins, which are assumed to be related by evolution, share common fold. There is also a growing conviction that existing structural databases are rich enough to cover almost completely the structural universe of proteins, measured by the number of distinct folds. Template(s)-based modeling, in general, can bring the predicted structure into proximity near 6Å (or less) from the native state, if homologous structures are present in the structural database. Homology modeling approaches have been recently enhanced by the rapid increase in the number of experimentally solved structures deposited in the Protein Data Bank (PDB)^‡. However often even the most sophisticated and successful structure prediction methods (I-TASSER^4,7, CABS⁶, Rosetta¹⁰), cannot predict the target structure with accuracy high enough for practical applications such as the drug design. Therefore future progress in computational biology critically depends on successful refinement of models generated using standard template(s)-based (or template-free) modeling techniques. So far, the major progress has been obtained in protein structure predictions, because of the strong interests of the scientific community and pharmaceutical companies in proteins specifically. Three dimensional structure predictions of RNA are less developed than protein modeling. Here we are going to consider protein modeling only, but our results are easily applicable to modeling of other biomacromolecules (including RNA) as well.

Protein structure refinement has emerged as one of the most important steps in protein structure prediction. Progress in the field of protein structure prediction has been observed and measured since 1994 by a biannual experiment, so called: Critical Assessment of Techniques for Protein Structure Prediction (CASP^†), where hundreds research groups from around the world compete to predict from the sequence structures of newly experimentally solved, yet unpublished proteins. The importance of refinement has been recently emphasized and since the 8^th edition of CASP event (CASP8) a new category of refinement of protein models was established. Assessment of this new prediction category was done recently by Ken Dill and his co-workers¹¹. Up to CASP8, protein structure refinement was often understood to be either improvement in the structural templates used in homology modeling, or improvements in the structures of loops and better side chains packing¹². Now the main task is to achieve an overall improvement. If the problem is defined in that way, it is expected to be very hard to solve. The conclusion from Dill’s analysis is that on average, there is no improvement in protein structure refinement among CASP competitors, except for some structural improvements. These conclusions have been recently confirmed by results of refinement category in CASP9, where only two groups were able to effectively improve protein models supplied by structure prediction servers, all other participants only worsened these initial structures. This shows that protein refinement is one of the most difficult problem in protein structure prediction.

Recently some new approaches for solving this essential problem have been proposed by Feig¹³, and tested successfully by his group in the refinement category in CASP9. Feig’s group¹³ has shown that having the ideal scoring function (which was considered as the RMSD from the native structure), combined with efficient large-scale generation of decoys enabled the refinement of protein structural models to high accuracy. They utilized the Normal Mode Analysis (NMA), among other methods like Monte Carlo (MC) sampling with side-chain-only (SICHO)¹⁶ force field, or molecular dynamics (MD) simulations at different temperatures. They showed that NMA is the most efficient sampling scheme, so the model in our work follows in the same spirit. The procedure used by Feig’s group was an iterative one. First they performed molecular mechanics energy minimization and then employed NMA computations around the local energy minimum. After that they generated and evalueated an ensemble of possible new conformations, along the lowest frequency normal modes. The conclusion was that there is still room for future improvement both in sampling and in scoring. But no matter which sampling scheme was used, when RMSD was used as a scoring function, protein structure refinement was possible. When some errors were introduced artificially, then refinement was possible only up to some, small extent, which can be interpreted to mean that impovements in scoring functions can have a significant impact on structure refinement.

Methods

In general, protein structure refinement is possible if a protein native-like structure sampling algorithm is reliable and can efficiently generate better structures (in terms of some specific metrics). This depends however on the proximity to the native structure and close to it refinement becomes more difficult. Sampling must be accompanied by a good scoring function to assess the quality of the generated structural models (decoys). Scoring should follow the rule, that if the score is better, then model is better. To assess the quality of protein models, it is commonly accepted to use the root mean square distance (RMSD) between the predicted model and the native state - although this is arbitrary measure and other can be applied i.e. TM-score, GDT, fraction of native contacts etc. RMSD has a disadvantage, because it is impossible to calculate RMSD without native structure. Therefore usually this metric is used to assess the ability of other scoring schemes. To calculate RMSD both structures need to be superimposed. To do that a rotation with respect to the center of their masses is performed, to minimize the positional deviations:

$$\mathit{RMSD}=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(r_i^{\mathit{decoy}}-r_i^{\mathit{native}}\right)}^2}$$ (1)

Here N is the number of points compared (usually the number of amino acids in the sequence), and r_i^decoy and r_i^native are the positions (given by the Cartesian x, y, z coordinates) of the i^th point in both structures. In cases where each amino acid is represented by a single point, we commonly identify them with the positions of the C^α atoms in the protein¹⁴.

Choosing sampling algorithm of structural models is challenging. It has been shown that the probability of generating a random structure for a protein composed of N amino acids such, that RMSD_decoy < RMSD_lim is given by the following formula¹⁵:

$$P({\mathit{RMSD}}_{\text{decoy}}<{\mathit{RMSD}}_{lim})=\frac{1}{\sigma \sqrt{2\pi }}\underset{0}{\overset{{\mathit{RMSD}}_{lim}}{\int }}{e}^{\frac{-{(x-<{\mathit{RMSD}}_{lim}>)}^2}{2{\sigma }^2}}dx$$ (2)

The values of <RMSD> and σ vary between proteins, but usually σ is assumed to be around σ = 2 Å, and <RMSD> depends on the protein size. Angular brackets denote the mean value that is the same for all proteins of the same size. We assume that <RMSD> follows the power law¹⁵: 3.333 N^1/3. The assignment of the lower integration limit to 0 differs from the one proposed by Feig¹³, who assumed that the integration in eq. 2 goes from −∞ to RMSD_lim, however it does not significantly change the probability (equation 2) and using 0 it is formally more correct.

Nevertheless, it is much harder to develop a good scoring function than to develop an efficient sampling scheme. Moreover the scoring function should be able to assign better scores to decoys that are closer to native state and lower scores to decoys that are further from the native state (in terms of a metric, such as RMSD).

In the further part of our paper we address the question of using non-ideal scoring functions for the protein structure refinement problem. To deal with this task, we designed an ideal sampling scheme based on the decoy distribution found by Feig’s group. Then we applied it to assess the efficiency of using a non-ideal scoring function, which appears to perform better in recognizing best decoys than usual atomic force fields. In this case better means correlation between RMSD of the decoy and energy for this model. We found that even small errors in the scoring function can prevent the refinement algorithm from finding a good solution, if the Feig’s procedure is applied.

The non-ideal scoring function, to assess the quality of the decoys, is designed as follows:

$$f_{\mathit{RMSD}}={\mathit{RMSD}}^0+N(0,{\sigma }_N)\times \sqrt{{\mathit{RMSD}}^0}$$ (3)

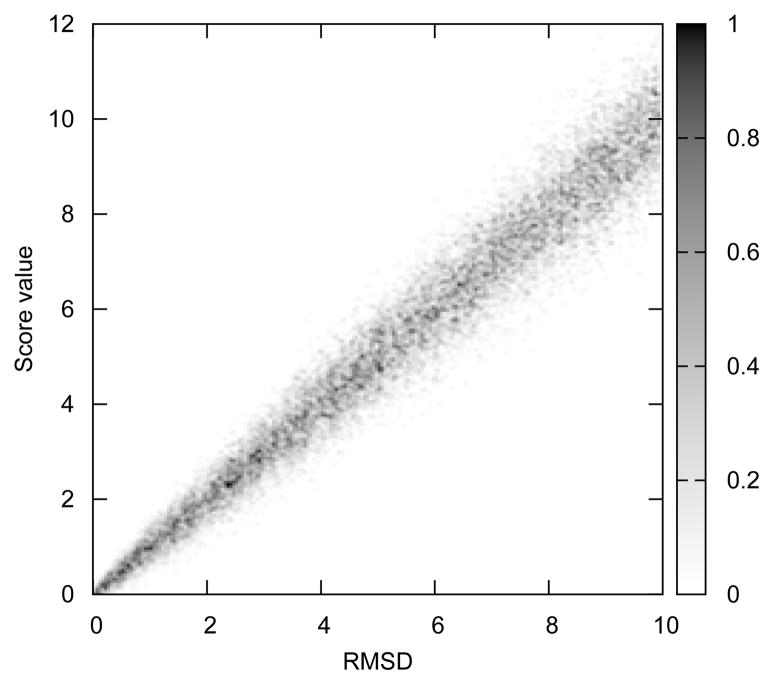
where RMSD⁰ denotes the real (true) value of RMSD of the decoy from the native structure, and σ_N is a standard deviation of Gaussian noise applied to the scoring function. Gaussian noise used in our computations is justified by the Central Limit Theorem. It means that the errors in the force field are not caused only by a single factor but instead are a superposition of many of factors, mainly because of the model coarse-graining. Here N(μ, σ) is a number generated from the Gaussian distribution function with mean value μ and standard deviation σ. Figure 1 shows an example of such distribution for a scoring function. The scoring function was designed in such a way, that the errors in assessment of quality of decoys increase, as the number of non-native interactions in the decoy increases. We suppose that the number of non-native interactions increases as decoys’ conformations gradually depart from the native state. In this way, we attempt to design a funnel-shaped energy landscape. We define non-native interaction as those, which do not exist in the native structure, when a certain cut-off distance is applied to identify interacting pairs of atoms. We notice that the shape of our scoring function in Figure 1 may be suitable protein structure prediction and is no worse than most of the existing coarse-grained force fields²² (in terms of noise in scoring function).

Figure 1.

Scoring function to assess the quality of generated decoys, computed from Eq. 3 (see text). Noise parameter σ_N is set to 0.25. The plot was computed from the distribution of energy vs. RMSD, at intervals of 0.05. For each bin, the distribution has been normalized to lie between 0 and 1.

Our ideal sampling scheme is designed as follows. In each iteration, starting from the decoy with RMSD equal to RMSD_old 250 new decoys with new RMSD_decoy value are generated according to:

$${\mathit{RMSD}}_{\mathit{decoy}}={\mathit{RMSD}}_{\mathit{old}}+N(0,{\sigma }_C)+C(<\mathit{RMSD}>-{\mathit{RMSD}}_{\mathit{old}})$$ (4)

where <RMSD> is defined similarly as in equation 2. The first term in Equation 4 corresponds to the RMSD value of the initial structure in each iteration of the refinement procedure. The second term is responsible for generation of new decoys RMSD value with the normal distribution around the starting conformation RMSD. The form of this function in Equation 4 is similar to that proposed by Feig et. al. σ_C corresponds to the magnitude of the structure deformation during a single refinement iteration (trial). It can be easily understood, if we keep in mind, that they generated decoys by applying NMA to structural fluctuations around non-native structure. The size of these deformations can be set to an arbitrarily value or taken to have some correspondence to thermodynamic parameters, such as temperature. The third term in Equation 4 is introduced by us based on results obtained by Feig’s group, and by Ken Dill’s assessment of CASP refinement results. There are additional theoretical reasons to introduce this term that are suggested by Wolynes’ energy landscape theory of protein folding^17,18; a funnel-like conformational space near the native structure is less populated than far from it. Interpretation of this fact results from the conformational entropy, since there is only one native structure, corresponding to the global minimum, and many non-native local minima. This leads to a simple shift of N(0, σ_C) distribution, that could be expressed by changing the mean value of this distribution. That is presented in Equation 4 in such a factorized form, with C being the shift parameter, to accent the separation of decoy generation in a random fashion, and the shift caused by bringing decoys to the vicinity of the native state. The parameter C strongly depends on the quality of the decoy generation algorithm, i.e., the type of deformations applied to the molecule, and the structure of the target. For each refinement run, we performed 1000 iterations. After decoys RMSDs generation in each iteration, all decoys are assessed by Equation 3, and the decoy with the best score is chosen (lowest RMSD_decoy), as a starting point for the next iteration. Then the results of over 250 experiments for each set of parameters were averaged. Because of the stochastic nature of sampling, it is important to use the average estimation of the refinement algorithm instead of considering a specific single run. It is important to remember; that we did not generate conformations of the decoys explicitly, but only considered their RMSD values from the native structure. In this way, we were able to avoid all possible inaccuracies and errors due to the sampling scheme.

Results and Discussion

It was examined how random errors in the force field (σ_N) can affect the refinement procedure. The results are shown in Figure 2. The calculations were performed for the shift parameter C = 0.005, and the length of the protein L=100 amino acids. Small values of C assure us that the shift term is not dominant in our model. From the plot (Fig. 2) we can conclude, that in the case when the white noise is applied to a nearly ideal scoring functions (where the noise is small with σ_N < 0.2) then it is possible to obtain on average convergence of the refinement algorithm usually in less than 1000 iterations. On the other hand, if σ_N is equal to or larger than 0.25 the performance of the refinement algorithm is corrupted by noise, and divergence of iteratively refined structures from the native state is observed. Of course, it is still hypothetically possible to refine the model in a very long simulation, because there is always a non-zero probability of bringing the decoy back to the proximity of the native structure. From Figure 1 we can see, that in proximity to the native structure the noise is even smaller (because of the additional scaling by the RMSD⁰ factor – see eq. 3) so that if the structure can be brought to this point, the convergence of structure refinement is more easily achieved. However, it is important to mention, that such a long refinement process is highly impractical, because it would require computing enormous numbers of decoys.

Figure 2.

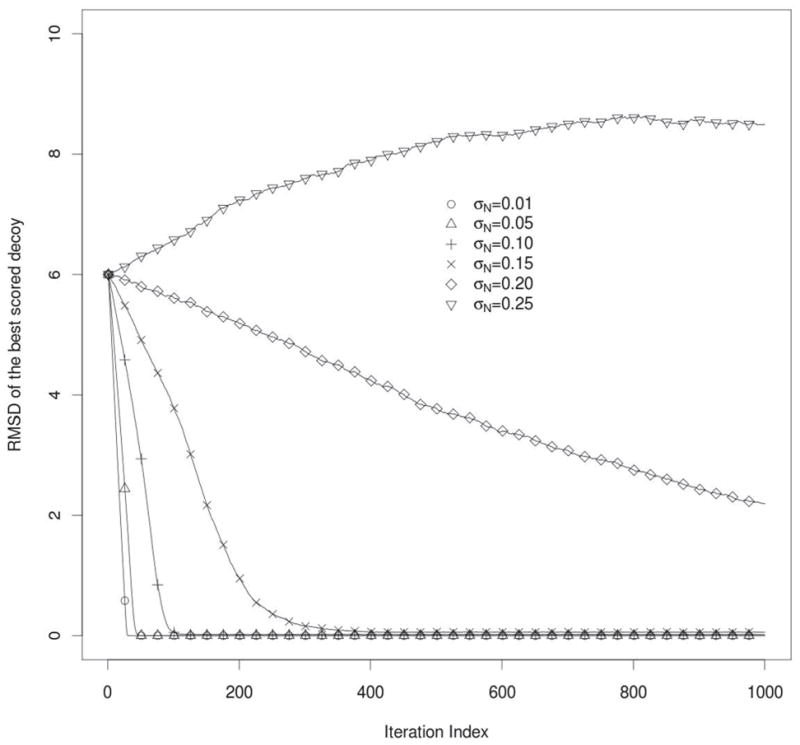
RMSD of the best scored decoys from the native structure during refinement iterations. Curves are for different values of σ_N parameter. Length of the protein is equal to L=100, σ_C=0.10, and initial RMSD = 6.0Å. Averaging was performed over 250 simulations.

The number of evaluations needed to refine the structure is determined by several factors. First is the distance (RMSD) of the starting model from the native structure. Another factor is how large are the modifications applied to the model. If we make small changes then the refinement process is slow. Because for σ_N = 0.20 we obtain quite rapid convergence of the refinement algorithm this value of σ_N has been used by us to study how the decoy generation algorithm (parameter σ_C in equation 4) behaves in the presence of the noise with this magnitude. (See Figure S1 in Supplementary Materials). In cases when we apply very small deformation to the initial decoy in the sampling procedure, the refinement leads to structural divergence, however for larger values of σ_C we obtain the structural convergence. This convergence is, of course, driven by Equation 3, but only in cases when the decoy is brought into the vicinity of the native state early in the refinement process. Otherwise, the decoy diffuses in the energy-RMSD space. It is caused by the fact that the energy function leads to the accumulation of errors in a direction away from the native structure. Therefore if the sampling scheme can generate broad range of new decoys, even if one picks a decoy that is not the best one, because of errors in quality assessment, refinement still converges. Equation 4 also suggests dependence of the sampling efficiency on the parameter C. In the case when C = 0.0, the algorithm will generate a half of the decoys that are closer to the native state than the decoy from which they were generated. The dependence of the effectiveness of the structure refinement algorithm is shown in Figure S2 in Supplementary Materials. It is notable that the effect of increasing the parameter C is opposite to the effect of changing the parameter σ_C. Therefore the effect of making bigger structural changes in generated decoys is opposite to shifting their distribution.

An important issue is the dependence between the size of protein (the length of amino acids chain: L) and the performance of the structural refinement. This problem was pointed out by Dill and co-workers, who noticed, that the refinement of larger structures in CASP is on average worse than for smaller ones¹¹. The reason for this is that the sampling scheme and its efficiency depend on the protein size. It is caused by significantly higher dimensionality of the conformational space for large proteins. To study this issue, parameters for which good convergence was observed, were chosen ( σ_C = 0.1 σ_N = 0.20). The results are presented in Figure S3 in Supplementary Materials. We see that the possibility of structural refinement of protein models is strongly dependent on protein size. For larger proteins we need a better and longer sampling scheme, and a more accurate scoring function to prevent the divergence of the refinement algorithm. It seems that for a given accuracy of the force field, and the specific sampling scheme, we can establish an upper bound for the size of protein to achieve structural refinement. Therefore even if we have an efficient refinement algorithm for refining small proteins, it can fail (diverge) in refining larger proteins. Additionally, because of entropic reasons, the probability of generating better structures decreases when the quality of decoys increases (see Fig. S4 in Supplementary Materials).

So far, we have analyzed only the possibility of structural refinement starting from the model with RMDS = 6.0Å. Normally we would have initial models with various resolutions. Therefore interesting insights can be gained from the analysis of the refinement of models with different quality (measured by RMSD) as the initial structural models. Models with resolution from 6Å to 9Å away from the native state usually come from template-free (de novo aka ab initio) protein structure prediction, while those with resolution below 6Å usually result from template-based homology modeling¹⁹. In Figure 3 we can see the results for different qualities of initial models. In case of models with resolution ranging from 6Å to 9Å, we observe that iterative refinement produces decoys with RMSD value within this range, so it seems to be impossible to move out of this range of resolution during refinement. A different situation is observed in the case of homology modeled structures. If the initial structure is predicted with a resolution of 4Å, then there is divergence. In cases with good initial models (with resolution 2–3Å)²⁰, further structural refinement is achieved. This result is consistent with Dill’s findings, who reported that for some good starting models, several research groups were able to obtain structural refinements. It means that if we can bring the model structure close enough to the native state, significantly confined conformational space facilitates a further structural refinement.

Figure 3.

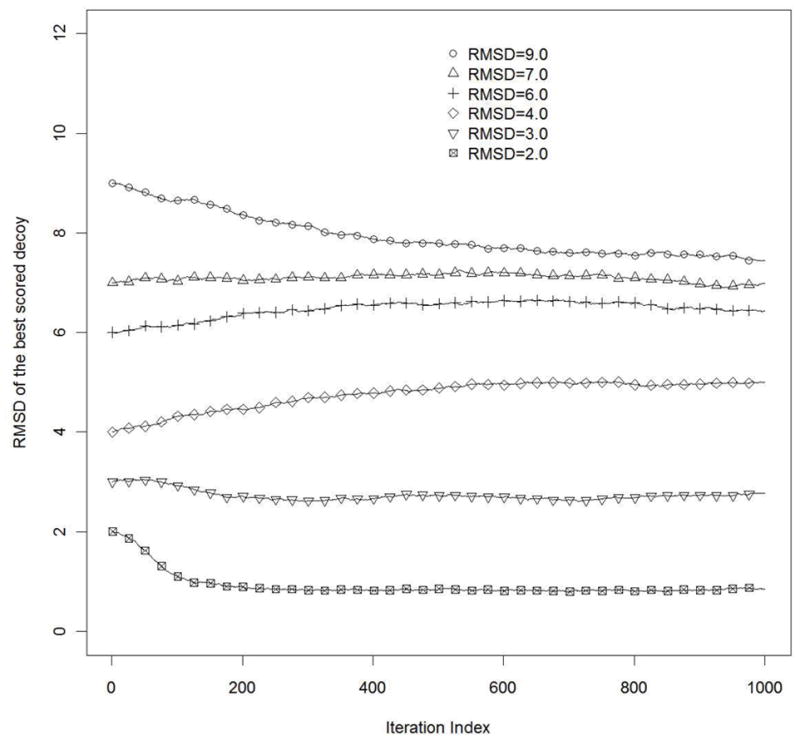
RMSD of the best scored decoys from the native structure during refinement iterations. Curves are computed for different values of the initial models quality (RMSD) with L=125, σ_N = 0.20 and σ_C = 0.10. Averaging was performed over 250 simulations.

Performance of the refinement algorithm shown in Figures 2 and S1–S3 was averaged over different setups, corresponding to different distributions used during the simulations. Therefore, the results for specific setups have been additionally investigated. The results are shown in Figure 4. The simulations were performed 5000 times, starting from RMSD = 2.0Å, and for the parameters set up: L=125, σ_C = 0.10, σ_N = 0.20. Despite of the convergence on average we can clearly observe a bimodal distribution. In some cases, the structural refinement towards the native state is possible and in some it is not. We can see a sharp distribution centered around 0Å and then quite long, smooth tail from 2Å to 8Å. The sharp peak comes from the fact, that if refinement algorithm brings structure close to native, where the amount of noise is smaller, the native structure can be iteratively achieved. Figure 4 suggests that in further refinement benchmarks (like CASP), attention needs to be paid to averaging results over many refinement trials to properly assess these methods.

Figure 4.

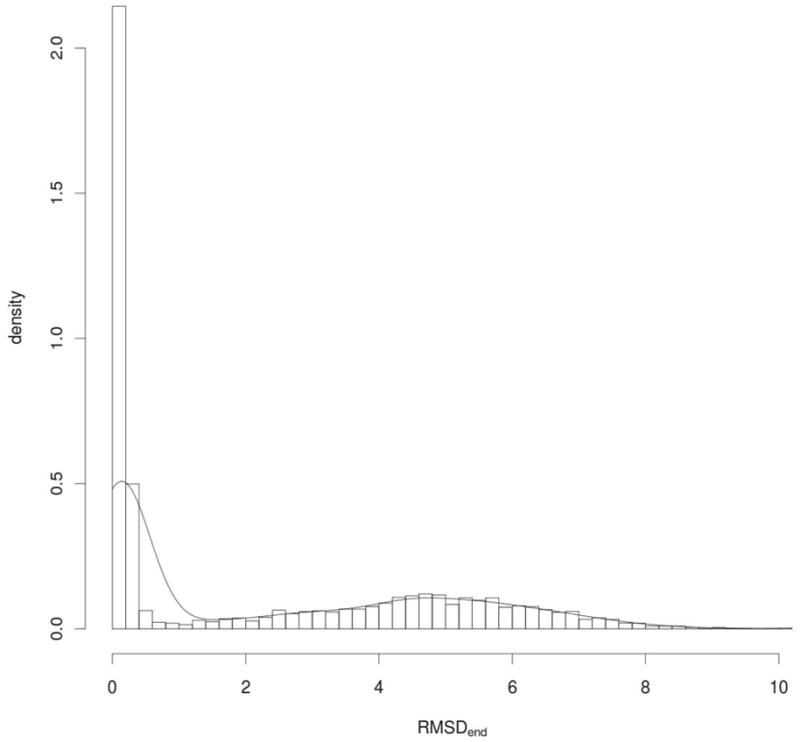
Distribution of refinement results obtained from 5000 refinement trials for L=100, σ_C = 0.10, σ_N = 0.20, and initial RMSD=6.0Å. Black line shows density of probability of obtaining given results after 1000 iterations. The average RMSD value is 2.2Å. To visualize the results, the Gaussian kernel was applied to estimate density.

Conclusions

We studied simple, stochastic model of refinement of biomolecular structures. The model is qualitative in nature so the values presented here should not be related to any particular case. Our results show that even for highly efficient sampling scheme of native-like decoys, small errors in decoy scoring function can prevent the algorithm from the possibility of refining modeled protein structures. The reason for this lies in the stochastic nature of sampling scheme and errors in force fields. An iterative refinement process can mimic diffusion of decoys on the energy funnel-like landscape, with additionally applied noise. The shape of the landscape can push the decoys away from the native structure in the presence of noise. When the magnitude of the noise exceeds a certain specific value, then decoys diffuse in such a space, and refinement cannot converge to better structure. It does not only mean that the native structure cannot be found, but also a refinement of more flawed structures is less likely possible, The parameters values are dependent on the shape of the energy function and the size of the protein. It is also important to emphasize, that the values of parameters σ_C and σ_N, for which the convergence of the refinement algorithm is obtained, are smaller than similar parameters estimated for real scoring functions used in the protein folding problem²². It seems that future advances in structural refinement of protein models depend mostly on significant progress in developing better force fields having less uncertainty²¹, which can be specifically designed for structure refinement. Another possibility of advancement in this field might be a design of a novel sampling scheme that possesses the ability of generating more likely native-like decoys.