Simple models of human brain functional networks

Abstract

Human brain functional networks are embedded in anatomical space and have topological properties—small-worldness, modularity, fat-tailed degree distributions—that are comparable to many other complex networks. Although a sophisticated set of measures is available to describe the topology of brain networks, the selection pressures that drive their formation remain largely unknown. Here we consider generative models for the probability of a functional connection (an edge) between two cortical regions (nodes) separated by some Euclidean distance in anatomical space. In particular, we propose a model in which the embedded topology of brain networks emerges from two competing factors: a distance penalty based on the cost of maintaining long-range connections; and a topological term that favors links between regions sharing similar input. We show that, together, these two biologically plausible factors are sufficient to capture an impressive range of topological properties of functional brain networks. Model parameters estimated in one set of functional MRI (fMRI) data on normal volunteers provided a good fit to networks estimated in a second independent sample of fMRI data. Furthermore, slightly detuned model parameters also generated a reasonable simulation of the abnormal properties of brain functional networks in people with schizophrenia. We therefore anticipate that many aspects of brain network organization, in health and disease, may be parsimoniously explained by an economical clustering rule for the probability of functional connectivity between different brain areas.

The human brain is a large and complex network, operating over several decades of scale in space and time (1, 2). Its organization defies complete description at a cellular scale (3); but neuroimaging techniques for whole-brain scanning have been used to describe network organization, or connectomics, at anatomical scales on the order of millimeters and centimeters (2). In the language of graph theory, these large-scale human brain networks have already been shown consistently to demonstrate a number of key topological properties in common with other complex networks. For example, human brain networks have the small-world property of high clustering and high efficiency (or short path length) (4); they are also modular (5) and comprise a number of highly connected hub nodes in a fat-tailed degree distribution (6).

It is well known that the brain overall is expensive, in the sense of having high metabolic cost relative to its mass (7), and that cost control or cost minimization is likely to have been an important selection criterion for the evolution of the nervous system (8–11). One measure of cost in a spatially embedded network like the brain is the physical distance of connections between nodes: generally, connection costs will increase with distance (8, 12). In the nervous system of the nematode worm Caenorhabditis elegans, which has been mapped completely at the cellular level of synaptic connections between neurons (13), most axonal projections are shorter than the average distance between neurons, as expected in response to an economical selection pressure (14, 15). Likewise, in sparsely connected human brain functional networks, short distance connections predominate and are typically associated with greater strength of functional connectivity between regional nodes (16).

Given these observations on the topologically complex and anatomically economical aspects of brain networks, we asked this question: what set of generative factors could explain the topology of anatomically embedded brain networks? To address this question, we consider simple models for the probability of functional connection (an edge) between two cortical areas (nodes) separated by some Euclidean distance in anatomical space (≈cm). The simplest (one-parameter) models specify that connection probability is a function only of distance between nodes (17, 18), but we show that cost penalization alone cannot account for the small-worldness, modularity, and degree distribution of normal human brain functional networks. Two-parameter models specify that connectivity is a function of distance and the topological properties of the connected nodes (19). We show that a two-parameter model, for example including a “clustering” function of nodal topology as well as a power law function of connection distance, is required to emulate many of the key topological and anatomical statistics of normal brain functional networks.

We used resting-state functional MRI (fMRI) to measure low-frequency neurophysiological oscillations at each of 140 cortical brain regions in the right hemisphere in two groups of 20 healthy volunteers and 19 participants with childhood-onset schizophrenia (COS). We estimated functional connectivity by the correlation between each pair of regional time series; and we thresholded the resulting connectivity matrices to generate sparse, fully connected graphs (Materials and Methods).

Results

For each graph, we measured global efficiency [a measure of network integration inversely related to path length (20)]; average clustering coefficient (a measure of cliquish interconnections between topologically neighboring nodes); modularity [a measure of how nearly the network can be decomposed into a set of sparsely interconnected modules, each comprising several densely intraconnected nodes (21)]; the degree distribution (the probability distribution of degree, or number of edges per node); and the distance distribution (the probability distribution of Euclidean distance between connected pairs of regions) (Fig. 1). These data confirmed prior reports of economical small-worldness, modularity, and hub nodes in human brain networks (2).

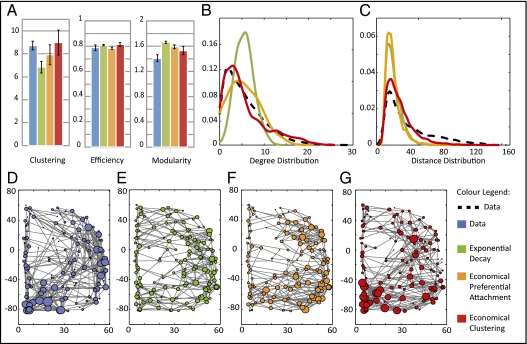
Fig. 1.

Comparison of networks simulated by three generative models vs. brain functional networks derived from experimental fMRI data on a group of 20 healthy volunteers (blue). Both the simple one-parameter model based on an exponential distance penalty (green) and the two-parameter economical preferential attachment model (orange) fail to simultaneously capture several topological characteristics of functional brain networks. In contrast, the economical clustering model (red) yields significantly more realistic networks by all of the following measures. (A) Normalized clustering coefficient, global efficiency, and modularity of brain functional networks are all well matched by the economical clustering model. All values are averaged over 20 instantiations of each network, and error bars represent the 95% confidence interval for the mean. Degree (B) and distance (C) distributions are shown in solid colored and dashed black lines for the models and data, respectively. Both distributions are better captured by the economical clustering model (red) than by the exponential decay (green) or economical preferential attachment (orange) models. (D–G) Schematic representation of the right hemisphere of the fMRI brain network for one participant (blue) and of a representative network generated by a single instantiation of each model. To ensure that these networks are representative, the single participant and the specific model instantiations displayed were each chosen to have the median value of skew in their degree distributions. The size of each node represents the degree of the corresponding brain region within the network. All networks have an overall connection density of 4% and comprise 140 nodes.

Exponential Decay with Distance.

To investigate the extent to which the topological profile of the brain networks could be attributable solely to cost minimization, we adopted a simple model for the probability of connection 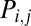between any pair of regions as a function of the distance between them (17, 18):

where 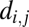is the anatomical distance between regions i and j, and η is the only parameter of the model. Using this exponential decay model with a range of different values of η, we could generate networks with variable degrees of cost penalization dictating the probability of connection between nodes.

We found, for example, that at a certain value of the model parameter, η ≈ 0.09, the simulated networks had an average modularity that matched exactly the modularity of the brain networks. However, these simulated data failed to match the empirical networks well in terms of global efficiency, clustering, or degree distribution. Indeed, it can be shown that there is no single value of η that will generate networks that are well matched to brain networks in terms of both modularity and efficiency (SI Text 1, Fig. S1). When η is large and distance penalization is high, the networks are not as efficient as brain networks, owing to the lack of long-distance connections; whereas when η is small the modeled networks are not as modular as the empirical ones. To find the compromise value of η that overall best fits the data, we used simulated annealing (SA) on an energy function based on the P values for the difference in clustering, efficiency, modularity, and degree distribution between a set of model networks and the data (Materials and Methods and SI Text 2, 3, and 4). As expected, however, the model-generated networks were not able to match simultaneously all key network characteristics observed in the data (Fig. 1). Similar results were obtained using other models of decay in connection probability as a function of distance [e.g., the power law model 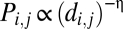]. In general, it seems that penalizing connection probability by a function of distance alone will be insufficient to simulate the topological statistics of brain functional networks (Table S1).

Economical Preferential Attachment.

Growth models for the formation of other real-life complex systems have previously been more successful by including an additional topological term in the connection probability function (19, 22), for example:

Here, 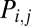is the probability of connecting nodes i and j, of degree k_i and k_j, respectively, that are a distance 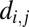apart; η is the parameter of distance penalization, as before; γ is the parameter of preferential attachment (the exponent of a power law in the product of the degrees of the connected nodes). Intuitively, this model trades off the cost-minimizing drive to shorter connection distance against the tendency to form highly connected hubs. The best-fitting parameters (estimated by SA) generated better approximations of brain networks than those simulated by cost penalization alone: the degree distribution was more realistically fat-tailed; and global efficiency, clustering, and modularity were all closer to their experimental benchmarks (Fig. 1 and Table S1).

These results support the general principle that cost minimization is likely to be a necessary but not a sufficient criterion for formation of brain networks. To more fully account for the observed characteristics of brain networks, we need to assume some complementary or countervailing generative factors that promote the emergence of complex topological features, such as the existence of hubs.

Economical Clustering Model.

We explored other possible variants of Eq. 2, using various functions of the degrees of the connected nodes to weight the formation of complex topological features, and tested each model against the same set of experimental benchmark data on human fMRI networks (Table S1). The best-fitting of these connection probability models included a power law distance penalty, as before, as well as a power law function of a topological term,

where 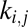is the number of nearest neighbors in common between nodes i and j; and all other notation is identical to Eq. 2. We will refer to this as an “economical clustering” model that includes a negative bias against high connection cost and a positive bias in favor of consolidating connectivity between nodes having nearest neighbors in common.

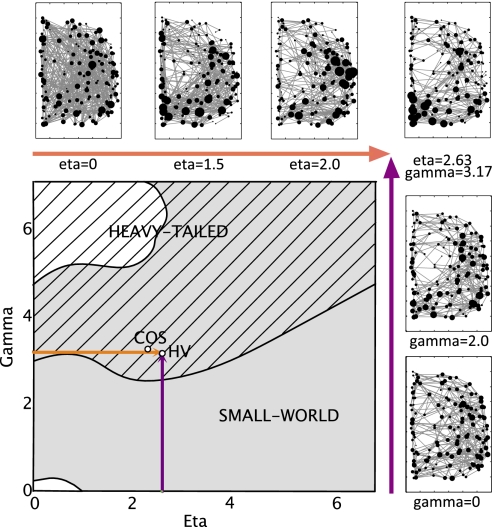
Optimizing the parameters of this economical clustering model to match the topological profile of brain networks, we found good correspondence (P > 0.05) between the simulated and fMRI networks on all of the key topological metrics of global efficiency, clustering, and modularity. Overall, the simulated networks were significantly more brain-like than either of the models previously considered (Fig. 1 and Table S1). We found these results to hold for brain networks thresholded over a range of connection densities, from 4% to 16% of all possible edges between regional nodes (SI Text 5 and Table S2). An intuitive understanding of the role of each parameter in this model can be gained by plotting a phase diagram (Fig. 2) highlighting the regions in parameter space that lead to small-world and heavy-tailed (skew S > 1) networks. We also plot schematics of the networks obtained by varying each parameter separately, from zero to their experimentally estimated values (η = 2.63, γ = 3.17). These two sections through parameter space confirm that variations in η mainly affect the distance distribution, whereas tuning γ mainly influences the degree distribution (Figs. S2 and S3).

Fig. 2.

Phase diagram of the economical clustering model. Most values of eta (η) and gamma (γ) yield small-world networks (gray area), whereas only high values of γ yield networks with heavy-tailed (skew >1) degree distribution (hashed area). The model parameters estimated to minimize mismatch between simulated and experimental fMRI datasets are shown here for both healthy volunteers (HV) and participants with childhood onset schizophrenia (COS). The orange (and purple) arrows show sections through the phase space, varying only η (or γ) respectively, whereas the other parameter is held at its optimal value estimated in healthy volunteers. Schematics of the networks obtained at various points along these sections are also shown (along zoomed-in versions of the orange and purple arrows).

However, because the model parameter estimation (by SA; SI Text 2 and Fig. S4) has minimized the mismatch between an observed dataset and simulated values of network metrics (SI Text 3 and Figs. S5–S7), one might argue that it is not so surprising that the fitted model is able to reproduce these same properties quite accurately. To address this potential issue of circularity, we did two things.

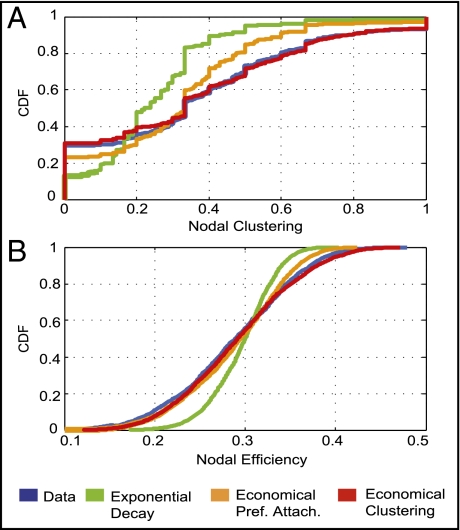
First, we explored the model's capacity to simulate brain network properties that had not been directly used as a basis for parameter estimation. For example, as shown in Fig. 1, we found that the distance distribution in the experimental fMRI networks was reasonably well matched by the economical clustering model (in comparison with the other models considered). We also found that annealing without any constraints on the degree distribution resulted in model parameters very similar to those estimated by annealing over all four network topological properties, with correspondingly good fits to all fMRI network metrics, including the degree distribution (SI Text 6.1 and Fig. S8). Additionally, as shown in Fig. 3, we found that the economical clustering model (in contrast to Eq. 1 and Eq. 2) also captured the statistical distribution of topological measures—such as the clustering and efficiency—at the local level of individual nodes in the fMRI networks, although the annealing process had been constrained only by the global average of these measures over all nodes in the networks.

Fig. 3.

Simulation of network parameters not involved in model parameter estimation. The exponential decay model (expD), economical preferential attachment model (ecoPA), and economical clustering model (ecoC) are shown in green, orange, and red, respectively. Of these, only the economical clustering model generates networks that realistically approximate the experimental (fMRI; blue) distributions of nodal topological metrics, such as clustering (A) and efficiency (B), that were not included in the process of model parameter estimation. 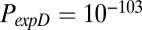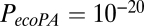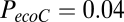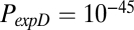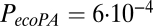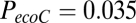The P values from a Kolmogorov-Smirnov test comparing the cumulative distributions for each parameter between the modeled and experimental networks are: , _, and for nodal clustering; and , , and for nodal efficiency.

Second, we used the generative model parameters estimated from the primary fMRI dataset (n = 20 healthy volunteers) to predict the network properties of a second independent fMRI dataset (n = 12 healthy volunteers). Thus, we tested the goodness of fit of the model on a set of experimental data that had not been used for model estimation. The economical clustering model provided a good account (compared with Eq. 1 and Eq. 2) of the statistical distributions of efficiency, clustering, modularity, degree, and connection distance in this independent test dataset (SI Text 6.2 and Fig. S9).

Modeling Network Changes in Schizophrenia.

We measured fMRI network properties experimentally in 19 people with COS and estimated economical clustering model parameters from these clinical data. Consistent with prior studies of functional connectivity and functional network organization in schizophrenia, we found that topological properties of clustering and modularity were somewhat reduced in COS patients (23–26). The abnormal profile of brain network topology in the patient group could be reasonably well matched by the economical clustering model (SI Text 7 and Fig. S10) but with rather different model parameters (η = 2.3, γ = 3.33) compared with those estimated in the group of healthy volunteers (η = 2.63, γ = 3.17). This shift in optimal parameter settings shows that the abnormal organization of brain functional networks in schizophrenia can be modeled as the outcome of an abnormally biased tradeoff between the generative factors of distance penalization and topological clustering.

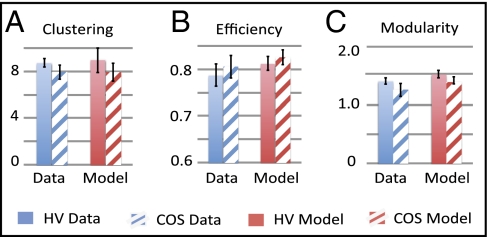
Fig. 4.

The economical clustering model is adaptive to fMRI network abnormalities in children with childhood onset schizophrenia (COS). COS (hashed bars) is associated with shifts in clustering, efficiency, and modularity (A–C) of fMRI networks, compared with the same metrics in fMRI networks of healthy volunteers (HV; solid bars). The bar charts on the right-hand side of each panel show the corresponding metrics simulated by the economical clustering model for both groups. See also SI Text 7 and Table S3.

Discussion

We have explored a number of generative models to parsimoniously simulate the complex topological and anatomical properties of human brain functional networks. We have shown that the simplest models considered, which penalize the probability of a functional connection between brain network regions as a function of the anatomical distance between them, cannot satisfactorily account for the complex topological properties of real brain networks. This result argues against the position that brain organization can be explained entirely by the principle of cost minimization (Table S4). However, we found that the addition of a topological term to the model, favoring additional formation of connections between nodes that already share nearest neighbors in common, could markedly improve the simulation of realistic brain network properties. This economical clustering model provided a good account of several network properties that were not included in the process of model parameter estimation, and when estimated in one normal sample, provided a good fit to the network properties of a second, independent normal sample.

Prior models for formation of brain anatomical networks have emphasized the importance of controlling or penalizing connection distance (17, 18). This is consistent with a large body of work, dating back to the seminal studies of Ramón y Cajal in the 19th century, indicating that the material and metabolic costs of the brain are large in proportion to its mass and that cost control is an important principle of brain organization (14). Because the metabolic cost of a connection between brain regions increases with increasing anatomical distance, cost minimization would be expected to drive the formation of connections between anatomically neighboring nodes. There are aspects of adult brain organization that are consistent with this expectation. For example, the probability distribution of connection distances in human brain networks is skewed toward shorter distances (27). The modules of brain networks also typically comprise brain regions that are anatomical as well as topological neighbors (28); so intramodular connections, which predominate in highly modular brain networks, are generally short distance.

However, it is also clear that brain networks have a high global efficiency (or short characteristic path length) that is largely attributable to the existence of long distance connections between anatomically localized modules (27). The efficiency of brain networks is a measure of their capacity for integrated processing, and several studies have shown that greater efficiency of network topology is associated with higher intelligence quotient (29, 30), greater accuracy of working memory task performance (31), or successful performance of more difficult versions of a working memory task (32). Thus, the topological attribute of high efficiency seems empirically to be important for cognitive functions of human brain networks, as also anticipated hypothetically by global workspace theory (33, 34). This is clearly difficult to reconcile with the unchallenged primacy of a cost conservation principle. Indeed, it has been shown by computational “rewiring” of the anatomical networks of C. elegans and the macaque monkey cortex that total connection distance of both these networks is not strictly minimized in nature; and when it is strictly minimized in silico there is a complementary increase in path length (or decrease in global efficiency) of the minimally rewired networks (35).

The idea that emerges from these and other prior studies is that brain network formation cannot plausibly be modeled by cost minimization alone but must rather depend on some “tradeoff,” between distance penalization and one or more other factors, which allows the emergence of realistically complex network topology (10, 36, 37). The results presented here provide some specific examples of how such a tradeoff might be rigorously defined and the considerable improvements in accuracy of brain network modeling that ensue as a result.

We investigated several possible models of competition or tradeoff between a distance penalization term and a second term weighting formation of particular topological features. The first model (Eq. 2) has been previously used to simulate the organization of the Internet (19). This economical preferential attachment model increases the probability of a connection between nodes in proportion to their degrees. Thus, high-degree nodes or hubs are more likely to form additional connections, even if separated by considerable distances. Although addition of a preferential attachment term improved the capacity of the model to capture a range of brain network properties (compared with the simpler models of distance penalization), we found empirically that alternative two-parameter models simulated experimental data even more accurately. In total, we evaluated 12 possible generative models (Table S1), varying both the cost penalization and topological terms, and found that the most accurate model overall (Eq. 3) traded-off connection distance against a topological term favoring the formation of connections between nodes that already shared nearest neighbors. Besides these empirical results indicating superior goodness of fit for one model in comparison with others, how else can we justify a preference for this economical clustering model?

First, we note that both terms of the model have some degree of face validity as biological mechanisms for brain network formation. Distance penalization, as has previously been noted (17), could be mediated mechanistically by the distance-related fall-off in concentration gradients of growth factors directing axonal projections toward target neurons. Enhanced probability of connection between neurons that already share nearest neighbors was recently observed in the rat somatosensory cortex (38). This is also compatible with Hebb's law, in the sense that neuronal groups that share common inputs from the same topologically neighboring group are more likely to be simultaneously activated and therefore to consolidate direct connections. We note that such biologically mechanistic interpretations of model parameters are no more than heuristics, and require more rigorous testing experimentally; nevertheless it is conceptually easier to imagine how local clustering might be favored (by Hebbian mechanisms) than to imagine how a preferential attachment rule might operate biologically. Indeed, unlike in engineered systems, it is unclear how any component of a brain network would have information on the degrees of all of the other nodes in the system.

Second, we note that the economical clustering model, as well as providing the most accurate simulation of global and nodal network parameters in fMRI data acquired from healthy volunteers, was also adaptive to the rather different network properties of data from people with COS. Previous studies have quite consistently demonstrated a topological profile of “subtle randomization” in schizophrenia (39), which was confirmed in these data by somewhat reduced clustering and modularity and increased global efficiency. This topological shift toward a more random configuration was simulated by a generative model with an abnormally reduced distance penalization parameter, allowing a greater probability of long distance connections. This result echoes some prior neuroimaging results, suggesting that brain networks in schizophrenia may have a greater than normal proportion of long-distance connections (27, 40) and encourages future efforts to use the modeled parameters of network formation to summarize and understand the patterns of abnormal network topology seen in people with a neurodevelopmental disorder such as schizophrenia (41, 42), as well as the processes of topological and spatial reconfiguration of human brain networks that may occur in the course of normal maturation to adulthood (43, 44).

This study also raises a number of methodological and conceptual questions (further discussion is provided in SI Text 2–4 and 8). The brain networks were constructed from fMRI time series, which have good anatomical resolution but insufficiently refined time resolution to allow estimation of high frequency dynamics or conduction delays, although these are likely to be important parameters of brain network performance. Moreover, the functional connectivity between a pair of nodes (e.g., as measured by the correlation between time series) cannot be assumed certainly to indicate that there is direct anatomical connectivity between them (45). Thus, there are empirical limits on what we can infer from these data about the mechanistic or domain-specific details of human brain network function and structure. In this context, we have adopted a modeling strategy that has been widely explored in the context of other complex networks, but not before so thoroughly developed in a neuroscientific application. We formulated some relatively simple generative models and tested their capacity to emulate the topological properties observed in brain networks. The existence of a good fit for some of these models, although statistically robust, does not prove that the brain networks were naturally selected to optimize the model parameters. The function(s) (if any) optimized by natural selection of brain networks are not yet known. So modeling brain networks cannot certainly begin from an optimality function, as one might begin to analyze or design an artificial network for which the desired function was known (46). However, a stochastic approach to brain network modeling is both tractable and arguably reasonable, given the stochastic contribution to selection of brain networks in real life. Our results show that brain network statistics can be generated quite accurately by simple (but not the simplest) probabilistic models.

Conclusion

Human brain functional networks have a complex topology, embedded in anatomical space, which can be modeled as the outcome of a tradeoff between two factors: a constraint on connection distance and a tendency for clustered connections. This is consistent with the general principle that cost minimization alone is insufficient to explain brain network organization and suggests that diverse brain network phenomena, in health and disease, may be explicable in terms of tradeoffs between a small number of biologically plausible generative factors.

Materials and Methods

Sample, Image Acquisition, and Analysis.

The fMRI data were acquired from two groups of healthy volunteers: a primary group (evaluable data on n = 20; mean age 19.7 y; 11 male) and a secondary group (n = 12; mean age 17.5 y; 6 male). The primary group of 20 healthy volunteers matched 19 participants meeting the DSM-IV criteria for COS (mean age 18.7; 9 male), recruited as part of an National Institutes of Health (NIH) study of COS and normal brain development. This study was ethically approved by the local institutional review board, and consent was acquired from all participants as well as their legal guardians. Excessive head motion during fMRI was an exclusion criterion. There were no significant differences between the groups in terms of age, sex, or maximum displacement due to head motion (details in SI Text). Participants were scanned using a General Electric Signa MRI scanner operating at 1.5 T, at the NIH Clinical Center in Bethesda, MD. One anatomical T1-weighted fast spoiled gradient echo MRI volume was acquired: echo time (TE) 5 ms; relaxation time (TR) 24 ms; flip angle 45°; matrix 256 × 256 × 124; field of view (FOV) 24 cm. Two sequential 3-min echo-planar imaging (EPI) scans were acquired while the participants were lying quietly in the scanner with eyes closed: TR 2.3 s; TE 40 ms; voxel 3.75 × 3.75 × 5 mm; matrix size 64 × 64; FOV 240 × 240 mm; 27 interleaved slices.

The images were preprocessed on the high-performance NIH Biowulf Linux cluster (http://biowulf.nih.gov), using AFNI (47) and FSL (48, 49) software. The first four EPI images were discarded to account for T1 equilibration effects. The data were then despiked, motion-corrected, skull-stripped, and registered to each participant's structural scan. Structural scans were registered to the standard stereotactic space of the Montreal Neurological Institute (MNI), using the MNI adult brain template (50, 51). Cerebrospinal fluid (CSF) and white matter were segmented with a probability threshold of 0.8. The time series for each voxel was regressed against the average CSF and white matter signals as well as the six parameters from motion correction, with all further analysis based on the residuals. Gray matter areas were defined using FSL's cortical Harvard-Oxford probabilistic atlas thresholded at 25%, excluding voxels that did not provide fMRI coverage in every participant. Voxels were then downsampled to ≈300 approximately uniform regions (52), maximizing compactness, and under the constraints that no brain regions spanned hemispheres or cortical lobes or extended over more than twice the size of the smallest region. We focused on regions in the right hemisphere to facilitate the approximation of the wiring length by the Euclidean distance between brain regions (44). This resulted in 140 regions whose average time series were used to construct brain functional networks. The maximal overlap discrete wavelet transform with a Daubechies 4 wavelet was used to band-pass filter these time series to the frequency interval: 0.05–0.111 Hz (scale 2). These preprocessed data can be downloaded for the primary group of healthy volunteers via http://intramural.nimh.nih.gov/chp/articles/matlab.html. The link also provides access to the graphs constructed for both the primary healthy volunteer and COS groups.

Graph Construction.

Binary graphs were constructed by thresholding the wavelet correlation matrix estimated for each participant. To ensure that no nodes were disconnected from the rest of the network, we used the minimum spanning tree as a backbone, then added further edges in order of decreasing correlation strength to produce binary graphs over a range of connection densities (26), from 4% to 16% of the maximum possible number of connections between N nodes. Networks simulated by generative models were likewise fully connected and controlled for connection density. All topological measures were normalized by dividing by the equivalent measures estimated from random graphs with the same number of nodes and edges.

Network Measures.

The graphs thus constructed were topologically analyzed using some of the most widely used graph theoretical network metrics (efficiency, clustering modularity, and degree); we note that these metrics are also directly related or very similar to some other well-known graph metrics (such as local efficiency, path length, or the small-world ratio of clustering to path length).

The degree, k_i, of a node i represents the number of edges connecting it to the rest of the network. The degrees of all of the nodes of a graph G form the degree distribution. The clustering coefficient C_i is defined as the ratio of the number of triangular connections between the ith node's nearest neighbors to the maximal possible number of such triangular motifs. The overall clustering coefficient 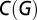is defined as the average clustering coefficient of all nodes. The path length 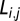between a pair of nodes i and j is defined as the minimum number of edges that need to be traversed to get from i to j. More commonly (20), one measures the average inverse path length, or global efficiency, 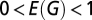. Many complex networks have a modular community structure, whereby they contain subsets of highly interconnected nodes called modules. The modularity, 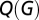, of a graph quantifies the quality of a suggested partition of the network into modules by measuring the fraction of the network's edges that fall inside modules compared with the expected value of this fraction if edges were distributed at random (21). The maximum value, 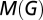, of the modularity found for any partition of a given graph into modules yields a measure of the degree of modularity of the network, compared with random networks.

Model Parameter Estimation.

The optimal parameters η and γ used for each model were estimated by SA on an energy function defined as

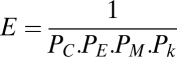where P_C is the P value associated with the t test for a difference in the mean clustering coefficients of a set of 20 simulated model networks vs. a set of 20 experimental fMRI datasets (more details are provided in SI Text 2–4). Similarly, P_E and P_M are P values of t tests for the difference between efficiency and modularity in modeled vs. experimental data, whereas P_k is the P value of the Kolmogorov-Smirnoff test between the degree distributions estimated from the simulated and experimental networks. SA aims to find the minimum of the energy function in parameter space, and thus finds the η and γ parameters that generate model networks that most closely approximate the experimental data in terms of clustering, efficiency, modularity, and degree distribution.