Scaling Properties of Glycine-Rich Sequences in Guanidine Hydrochloride Solutions

Abstract

The intrinsic polymer properties of glycine-rich sequences are evaluated with a set of iso-1-cytochrome c variants with N-terminal inserts of the sequence (GGGGGK)_n for n = 1–5. The thermodynamics and kinetics of His-heme loop formation are measured as a function of guanidine hydrochloride (GdnHCl) concentration for loop sizes ranging from 22 to 46 residues. The scaling exponent for loop formation, ν₃, evaluated using the Jacobson-Stockmayer equation is near 1.8, at 1.5 and 3.0 M GdnHCl, but it increases to 2.2 in 6.0 M GdnHCl. Previous work on a set of iso-1-cytochrome c variants with (AAAAAK)_n inserts gave ν₃ = 2.2 for alanine-rich sequences in both 3.0 and 6.0 M GdnHCl. Chain stiffness was evaluated from the relative magnitude of Flory's characteristic ratio, C_n, for alanine-rich versus glycine-rich sequences. In 3.0 M GdnHCl, C_n(Ala)/C_n(Gly) is 1.6, decreasing to 1.3 in 6.0 M GdnHCl. The data suggest that solvent-backbone interactions dominate polypeptide conformational properties under good solvent conditions whereas side-chain-dependent properties are more important under poor solvent conditions. The results provide a direct experimental assessment in terms of polymer properties of the distinct roles of Gly versus Ala in the folding code.

Introduction

Ever since Anfinsen (1) demonstrated that the amino-acid sequence of a protein is sufficient to define the structure of a protein, there has been considerable interest in cracking the folding code that translates the primary structure of a protein into its tertiary structure. Much progress has been made in predicting protein structure from amino-acid sequence. However, when a structure for a protein with a similar amino-acid sequence does not exist, the results of structure prediction methods remain unsatisfactory (2). Thus, further understanding of the intrinsic properties of amino acids when incorporated into polypeptides is essential to provide a basis for predicting sequence-dependent structural biases.

Measurements of the diffusion-limited rate constant for first contact, k_c, between monomers at the ends of a polypeptide chain suggest that sequence effects on k_c are minor, except for proline and glycine (3–7). However, the results indicated that glycine content may impact the scaling properties of loop formation in a polypeptide as given by the Jacobson-Stockmayer equation (8,9),

$$\Delta S_{loop}=-{\upsilon }_{3}R\text{ln}\left(n\right)+R\text{ln}\left({\left(\frac{3}{2\pi C_n{\ell }^2}\right)}^{{\nu }_3}{V}_i\right),$$ (1)

where ν₃ is the scaling exponent for loop formation, R is the gas constant, n is the number of monomers in the loop (loop size), C_n is Flory's characteristic ratio for a loop containing n monomers, ℓ is the distance between monomers, and V_i is the approach volume of the atoms involved in loop formation. In water, a set of poly(GlySer) polypeptides yielded ν₃ = 1.72 ± 0.08, whereas poly(Ser) polypeptides gave ν₃ = 2.1 ± 0.3 (3,5). Both these values are in the range expected for a freely joint random coil, ν₃ = 1.5 (9,10), or a random coil with excluded volume, ν₃ = 1.8–2.4 (10–12). Unfortunately, the length of the poly(Ser) polypeptides was limited to 12 residues or less, thus the large error in ν₃ for the poly(Ser) data.

Simulations of polyalanine and polyglycine conformational ensembles have been carried out using a hard-sphere potential (13). The dependence of the radius of gyration, R_g, on chain length, n, for chains from 50 to 500 residues long was evaluated from these ensembles (R_g = R_on^ν). The scaling exponents, ν, for polyglycine and polyalanine were identical (0.60 ± 0.01 and 0.61 ± 0.01, respectively), and consistent with the excluded volume limit of 0.6 for a random coil (10). Thus, simulations of polyalanine and polyglycine suggest that glycine does not affect the scaling properties of a polypeptide in contrast to the apparent, but uncertain, difference observed in experimental studies on the loop size dependence of k_c (3,5).

Glycine is a particularly important amino acid. Its small side chain allows greater flexibility for the main chain, providing access to ϕ,ψ dihedral angles about the α-carbon not accessible with other amino-acid side chains (14). As a result, glycine is important in chain reversals, such as β-turns, that are essential for compact globular protein structures (15,16). The role of glycine in the folding code is no doubt prominent. Thus, a detailed understanding of the effects of glycine on the properties of a polypeptide chain is essential.

To address the uncertainty in the literature over whether glycine affects the scaling properties of a polypeptide chain, we have now prepared a set of iso-1-cytochrome c (iso-1-Cytc) variants with predominately glycine inserts of variable length (Gly-rich variants, see Fig. 1) inserted into the flexible N-terminus of the protein (17). We analyze the polymer properties of these Gly-rich variants with our denatured state His-heme loop formation method (18–26), which allows measurement of both the equilibrium and kinetics of loop formation as a function of loop size. From the loop size dependence of loop formation, we are able to extract a fundamental polymer property, the scaling exponent for loop formation, ν₃. We also gain insight into chain stiffness. Comparison of ν₃ for our Gly-rich variants with our previous work on Ala-rich variants (19) shows that ν₃ is similar for the Ala-rich and Gly-rich sequences in 6.0 M guanidine hydrochloride (GdnHCl), suggesting that the conformational properties of polymers of Ala and Gly are similar in a good solvent. By contrast, ν₃ diverges for the Ala-rich and Gly-rich sequences at 3.0 M GdnHCl. Thus, the conformational differences of Gly-rich and Ala-rich sequences are more pronounced in a poorer solvent. Comparison of His-heme loop formation for the Gly-rich and Ala-rich variants at the same loop size allows evaluation of the relative magnitude of Flory's characteristic ratio, C_n, for Gly and Ala, a measure of chain stiffness. We find that the relative magnitude of C_n is more similar than expected from standard polymer theories.

Figure 1.

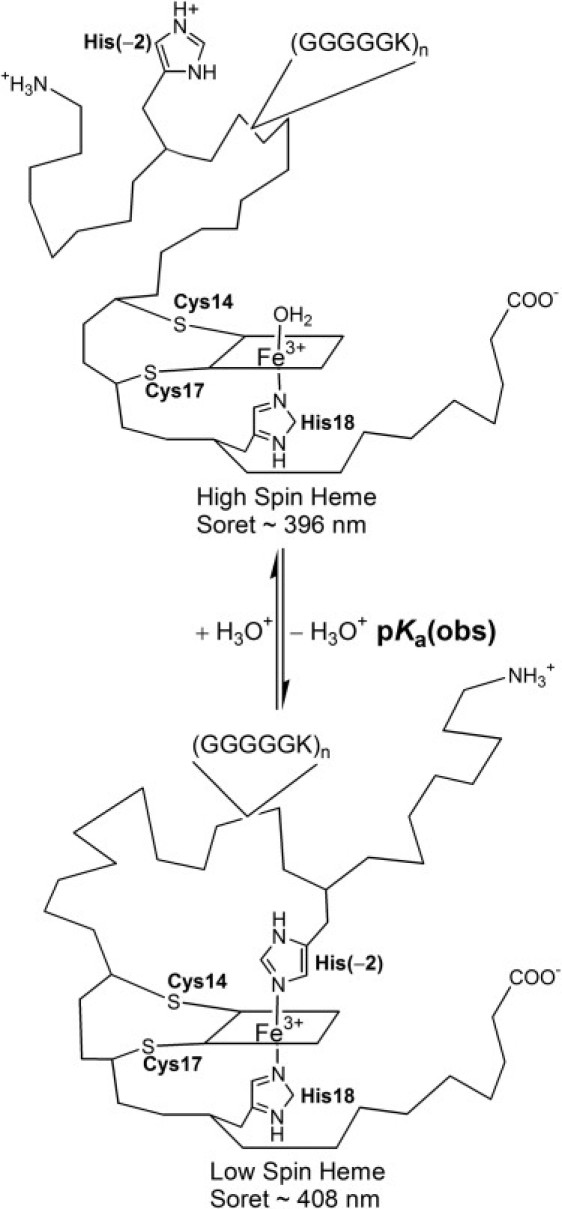
Schematic representation of histidine-heme loop formation with the NH5G-X variants under denaturing conditions.

Materials and Methods

Preparation of variants

All variants contain the following background mutations: C102S to prevent intermolecular disulfide bond formation during physical studies; H26N, H33N, and H39Q to eliminate all naturally occurring histidines in yeast iso-1-Cytc besides the heme ligand, His¹⁸; and a K(−2)H mutation to introduce the unique histidine that forms the loop in the denatured state of each of the Gly-rich variants. The NH5G-1 variant was prepared as previously described in Tzul and Bowler (21) and Tzul et al. (22). The NH5G-2 through NH5G-5 variants were prepared by sequential insertion mutagenesis (QuikChange PCR-based mutagenesis; Agilent Technologies, Santa Clara, CA) of DNA sequences into the pBTR1 vector (27) corresponding to the amino-acid sequence GGGGGK (see Table S1 in the Supporting Material for oligonucleotide sequences). The presence of each insert was confirmed by sequencing the iso-1-Cytc gene (Murdock DNA Sequencing Facility, University of Montana, Missoula, MT).

Expression and purification of variants

Escherichia coli BL21-DE3 cells (Novagen, Madison, WI) were used to express all variants from the pBTR1 vector, which coexpresses iso-1-Cytc and heme lyase allowing covalent attachment of the heme-group to iso-1-Cytc within the cytoplasm (28). Protein yields ranged from 5 to 20 mg from 2 L of 2xYT broth grown for 16–18 h at 37°C. Variants that contained fewer inserts tended to give higher yields. Yields for variants with more inserts could be increased by growing cultures for 24 h at 30°C. Isolation and purification of the Gly-rich variants were carried out as described previously (21–23). Before any of the following experiments, the protein was reduced using a small amount of sodium dithionite and purified by HPLC using a UNO S6 cation exchange column (BioRad, Hercules, CA) as described previously (22,29). The Gly-rich variants were then oxidized with a small amount of potassium ferricyanide for 1 h at +4°C. The protein was then separated from the oxidant using G-25 Sephadex beads (Sigma Chemical, St Louis, MO) equilibrated to buffer appropriate to the experiment to follow.

Protein stability measurements

GdnHCl denaturation was monitored by circular dichroism using an Chirascan spectrometer (Applied Photophysics, Leatherhead, UK) linked to a MICROLAB 500 titrator (Hamilton, Reno, NV), as described previously (21). Data at 250 nm and 222 nm were measured as a function of GdnHCl concentration in the presence of 20 mM Tris, 40 mM NaCl, and 1 mM EDTA at pH 7 and 25°C. The ellipticity at 250 nm was subtracted from the ellipticity at 222 nm at each GdnHCl concentration to correct for baseline drift during the GdnHCl titration. The free energy in the absence of GdnHCl, ΔG_u^o′(H₂O), the GdnHCl m-value, and the denaturation midpoint, C_m, were obtained by nonlinear least squares fits of the baseline-corrected ellipticity at 222 nm versus GdnHCl concentration assuming a linear free energy relationship as described previously (25). Because iso-1-Cytc with homopolymeric inserts can be susceptible to backbone cleavage (22), molecular weights of all variants were checked before and after each experiment using matrix-assisted laser desorption/ionization time-of-flight mass spectrometry. The mass spectral data showed that there was no backbone cleavage for any of the variants during experimental measurements when the proteins are handled in buffers containing EDTA (21,22).

Equilibrium measurements of His-heme loop formation in the denatured state

His-heme loop formation under denaturing conditions (1.5 M, 3.0 M, and 6.0 M GdnHCl) at 3 μM protein concentration was measured in the presence of 5 mM Na₂HPO₄, 15 mM NaCl, and 1.0 mM EDTA by pH titration monitored with the heme Soret absorbance band (using a DU 800 spectrophotometer; Beckman Coulter, Brea, CA), as described previously (24). Data at 398 nm were plotted versus pH and fit using a modified form of the Henderson-Hasselbalch equation, as described previously (24,30) giving the apparent pK_a, pK_a(obs), and the number of protons, n_p, needed to titrate off the histidine. Three trials were run for each variant at room temperature, 20 ± 2°C.

Kinetics of loop breakage in the denatured state

Loop breakage kinetics data were measured using stopped-flow mixing methods (using an SX-20 spectrometer; Applied Photophysics), monitored at 398 nm. Downward pH jumps were conducted under denaturing conditions at either 3.0 M or 6.0 M GdnHCl at 25°C. The starting buffer was 10 mM MES with 1.0 mM EDTA at pH 6.2 containing 6 μM protein. This buffer was mixed 1:1 with 100 mM citrate containing 1.0 mM EDTA at either pH 3.5 or pH 3.0. The ending pH was measured from the effluent. The ending pH for the pH 3.5 experiments was 3.57 ± 0.01 in 3.0 M GdnHCl and 3.5 ± 0.1 in 6.0 M GdnHCl. The ending pH for the pH 3.0 experiments was 3.24 ± 0.06 in 3.0 M GdnHCl and 3.22 ± 0.05 in 6.0 M GdnHCl. Data were fit to a single-exponential rise to maximum equation and the rate constant for loop breakage, k_b,His, extracted from the fit. Double-exponential fits were attempted and residuals indicated a better fit. However, the standard deviation of the magnitude of the faster rate constant was large. The seemingly better fit of the double-exponential is probably due to fitting a pressure or flow artifact. Thus, we consider the single-exponential fit to be adequate.

Results

Design of variants

To produce a set of Gly-rich variants complementary to our previously reported Ala-rich variants (19), we have inserted (GGGGGK)_n segments for n = 1–5 between an engineered histidine at sequence position −2 (i.e., K(−2)H mutation; we use the sequence numbering convention for horse cytochrome c, therefore, the first five residues of iso-1-Cytc are numbered −5 to −1) and Ala(−1) (Fig. 1). Using this set of variants, we can probe the conformational properties of Gly-rich sequences from 6 to 30 residues in length (loop sizes of 22–46 residues). A lysine is included at the end of each six-residue segment to maintain aqueous solubility. The effect of charge on loop stability is potentially a concern. However, it has long been known that GdnHCl neutralizes electrostatic effects on protein stability (31) and it has also been shown that 750 mM NaCl is sufficient to disrupt electrostatic residual structure in the denatured state (32). Thus, electrostatics should have minimal effect on His-heme loop formation with the Gly-rich variants.

The variants are named NH5G-X, where X is an integer, which denotes the number of (GGGGGK) segments following His(−2). The NH5G-X variants have had His²⁶, His³³, and His³⁹, in wild-type iso-1-Cytc mutated to Asn, Asn, and Gln, respectively (26). Thus, His(−2) forms the His-heme loop in the denatured state of the NH5G-X variants.

For both the Gly-rich and the Ala-rich variants, the 15 amino acids at the C-terminal end of the loop (closest to the CXXCH motif that attaches the heme to the iso-1-Cytc polypeptide) come from the natural sequence of iso-1-Cytc. This sequence contains no prolines but does contain two glycines (12.5% glycine). The N-terminal helix of iso-1-Cytc is essential for stability, so this segment is necessary for expression of these variants. Thus, the equilibria and kinetics of His-heme loop formation for variants with fewer inserts might experience some perturbation due to this 15-residue segment. We discuss this issue further in the context of the data presented below.

His-heme loop formation in the denatured state

The heme group of iso-1-Cytc is covalently attached through Cys¹⁴, Cys¹⁷, and His¹⁸ (Fig. 1). When deprotonated, His(−2) binds to the heme under denaturing conditions to form a loop. Because His-heme binding is linked to deprotonation of His(−2), a simple pH titration monitored at the heme Soret band near 400 nm is used to monitor denatured state loop formation. An apparent pK_a, pK_a(obs), is obtained from the data. pK_a(obs) can be broken down into two steps,

$$p{K}_{\text{a}}\left(\mathrm{obs}\right)=p{K}_{\text{a}}\left(\mathrm{His}{\mathrm{H}}^{+}\right)+p{K}_{\mathrm{loop}}\left(\mathrm{His}\right),$$ (2)

where pK_a(HisH⁺) is the intrinsic pK_a of the histidine and pK_loop(His) is the pK (= −logK) of His-heme loop formation for a fully deprotonated histidine under denaturing conditions. We have shown that pK_a(HisH⁺) = 6.6 ± 0.1 for histidine, irrespective of sequence position or GdnHCl concentration (24). Thus, we treat pK_a(HisH⁺) as a physical constant and obtain pK_loop(His) by subtracting pK_a(HisH⁺) from pK_a(obs).

Assuming random coil behavior, we can evaluate the loop size dependence of pK_loop(His) in terms of the expression for ΔS_loop in Eq. 1, yielding

$$p{K}_{\mathrm{loop}}\left(\mathrm{His}\right)=p{K}_{\mathrm{loop}}{\left(\mathrm{His}\right)}_{\mathrm{ref}}+v_3\mathrm{Log}\left(n\right),$$ (3)

where pK_loop(His)_ref is the pK_loop(His) for a loop size of n = 1. Thus, for a random coil, pK_loop(His) should depend linearly on Log(n) with a slope equal to the scaling exponent, ν₃. Equation 3 assumes that the His-heme bond enthalpy is the same for all loop sizes. This enthalpic term is incorporated into pK_loop(His)_ref. Thus, the variation in pK_loop(His) with loop size is assumed to result entirely from the unfavorable entropy of constraining a histidine that is n monomers distant from the heme to be near enough to the heme to form a bond.

Stability of variants

To determine the GdnHCl concentration needed to achieve the denatured state, we measured the global stability of all variants using circular-dichroism-monitored GdnHCl denaturation methods (see Fig. S1 in the Supporting Material). We find that all NH5G-X variants are marginally stable with free energies of unfolding in the absence of denaturant, ΔG^o′(H₂O), ranging from 1.7 kcal mol⁻¹ to 2.1 kcal mol⁻¹ (Table 1). The stabilities of the Gly-rich variants are similar to those of our previously reported Ala-rich variants (19).

Table 1.

Thermodynamic parameters for GdnHCl unfolding at 25°C and pH 7 for iso-1-cytochrome c variants

Variant	ΔGo′(H2O)∗ (kcal mol−1)	m-value∗ (kcal mol−1 M−1)	Cm∗ (M)
NH5G-1†	1.7 ± 0.4	4.3 ± 1.0	0.40 ± 0.06
NH5G-2	2.2 ± 0.1	4.5 ± 0.1	0.48 ± 0.03
NH5G-3	2.1 ± 0.2	3.5 ± 0.2	0.60 ± 0.01
NH5G-4	1.7 ± 0.1	2.6 ± 0.2	0.67 ± 0.04
NH5G-5	2.1 ± 0.1	3.3 ± 0.1	0.65 ± 0.02

^∗All parameters are the average and standard deviation of three trials.

^†Thermodynamic parameters are taken from Tzul et al. (22), in which this variant was referred to as Gly5.

The His-heme loop stabilizes the denatured state. Because the stability of the loop is expected to decrease as loop size increases, a progressive increase in global stability is expected as the length of the Gly-rich insert increases. The unfolding midpoints, C_m, show the expected trend (Table 1). However, ΔG^o′(H₂O) does not mirror this trend likely due to the short native baseline, which limits our ability to confidently evaluate this parameter. Most importantly, the data in Table 1 (and see Fig. S1) show that all NH5G-X variants are fully unfolded at 1.5, 3.0, and 6.0 M GdnHCl, the conditions used here for denatured state loop formation.

Equilibrium loop formation in the denatured state

His-heme loop formation was measured by pH titration under denaturing conditions (Fig. 2). Spectra as a function of pH show a single isosbestic point at 404 nm (Fig. 2, inset) consistent with the two-state process outlined in Fig. 1. Equilibrium parameters for pH titrations at 1.5, 3.0, and 6.0 M GdnHCl are reported in Table S2 and Fig. 3. The number of protons, n_p, needed to break the His-heme loop is near one for all variants (Table S2), as expected for the 1 H⁺ process in Fig. 1.

Figure 2.

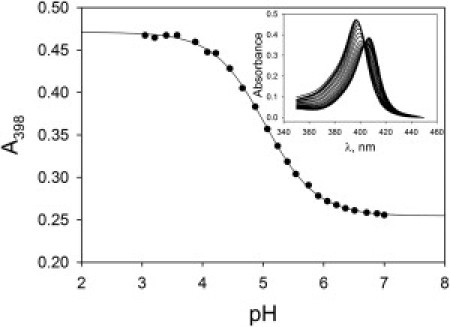
Plot of absorbance at 398 nm, A₃₉₈, versus pH for the NH5G-4 variant in 3.0 M GdnHCl at 20 ± 2°C. (Solid line) Fit of the data to a modified version of the Henderson-Hasselbalch equation as described in the Materials and Methods. (Inset) Absorbance spectra from 350 nm to 450 nm for pH values from 7 to 3 in ∼0.2 pH increments. To the left of the isosbestic point at 404 nm, absorbance increases as pH decreases.

Figure 3.

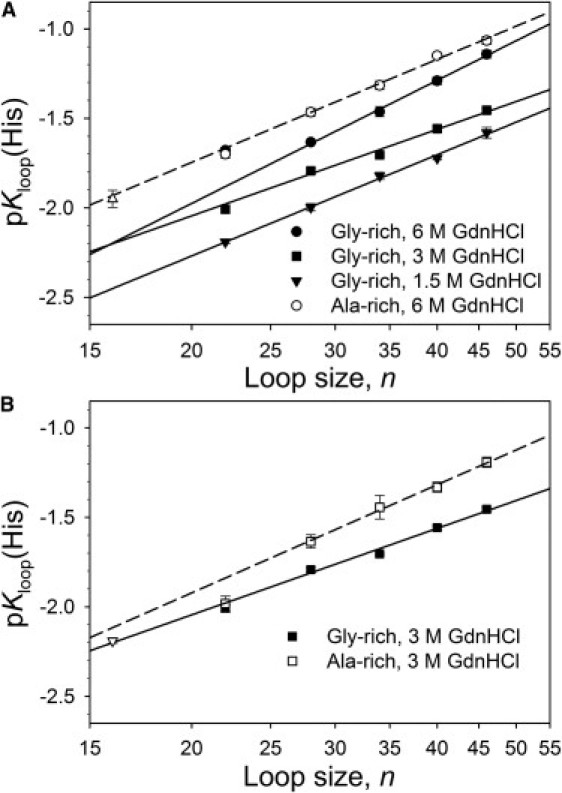
(A) Plots of pK_loop(His) versus loop size, n (scale is logarithmic), for the Gly-rich variants at 1.5 M (▾), 3.0 M (■), and 6.0 M (●) GdnHCl and the Ala-rich variants at 6.0 M GndHCl (○). Data point for the variant with no insert (n = 16) at 6.0 M GdnHCl (Δ). (B) Comparison of pK_loop(His) versus loop size, n (scale is logarithmic), for the Gly-rich (■) versus the Ala-rich (□) variants at 3.0 M GdnHCl. Data point for the variant with no insert (n = 16) at 3.0 M GdnHCl (∇). In both panels, the Gly-rich variants (solid lines) and Ala-rich variants (dashed lines) are fits of Eq. 3 to the data for n ≥ 28. The values of ν₃ obtained from these fits are reported in Table 2. pK_loop(His) was calculated using Eq. 2 and data from Table S2 in the Supporting Material using pK_a(HisH⁺) = 6.6. Data for the Ala-rich and no-insert variants are taken from Tzul and Bowler (19).

The pK_loop(His) becomes less negative (less favorable loop) as loop size, n, increases for the Gly-rich variants at 1.5, 3.0, and 6.0 M GdnHCl (Fig. 3), consistent with the less favorable entropy of forming larger loops. Data from our previously published work on Ala-rich variants at 3.0 and 6.0 M GdnHCl are shown in Fig. 3 for comparison (19). We have previously observed that pK_loop(His) at 3.0 M GdnHCl is the same for variants with either a single (GGGGGK) insert or a single (AAAAAK) insert between His(−2) and Ala(−1) (22). The same is true at 6.0 M GdnHCl (Fig. 3). Thus, for a single insert the 15 residues of native sequence nearest the heme dominate the properties of the 22-residue loop formed. With two or more inserts, the data for Ala-rich and Gly-rich variants are clearly differentiated, with equilibrium loop formation uniformly more favorable for the Gly-rich variants than for the Ala-rich variants. Thus, in evaluating ν₃ with Eq. 3, we use only data for variants with two or more (GGGGGK) or (AAAAAK) inserts (Fig. 3). Scaling exponents collected in Table 2 for both Gly-rich and Ala-rich variants are in the range expected for a random coil with excluded volume (ν₃ = 1.8–2.4) (10–12). We note that at 3.0 M GdnHCl, pK_loop(His) for iso-1-Cytc with no insert (n = 16) and for a single (AAAAAK) or (GGGGGK) insert is consistent with the line obtained from fitting the data for the Gly-rich variants with two or more inserts to Eq. 3 (Fig. 3 B). By contrast, at 6.0 M GdnHCl, pK_loop(His) for no insert (n = 16) and for a single (AAAAAK) or (GGGGGK) insert is consistent with the line obtained from fitting the data for the Ala-rich variants with two or more inserts to Eq. 3 (Fig. 3 A).

Table 2.

Scaling exponents, ν₃, as a function of GdnHCl concentration for Gly-rich versus Ala-rich variants

GdnHCl concentration	Scaling exponent, ν3∗
	Gly-rich	Ala-rich
	Equilibrium data
1.5	1.88 ± 0.11	—
3.0	1.61 ± 0.16	2.01 ± 0.10
6.0	2.28 ± 0.08	1.91 ± 0.11
	Kinetic data
3.0	1.67 ± 0.18	2.17 ± 0.16
6.0	2.24 ± 0.08	2.18 ± 0.14

^∗Reported errors are standard errors of the fits to data in Figs. 3 and 4.

Kinetics of His-heme loop formation in the denatured state

The kinetics of His-heme loop formation and breakage in the denatured state is consistent with a process involving rapid deprotonation of histidine followed by His-heme loop formation (23). This mechanism yields

$$k_{\text{obs}}=k_{\text{b},\text{His}}+k_{\text{f},\text{His}}\left(\frac{K_{\text{a}}\left({\text{HisH}}^{+}\right)}{\left(K_{\text{a}}\left({\text{HisH}}^{+}\right)+\left[{\text{H}}^{+}\right]\right)}\right),$$ (4)

for the observed rate constant, k_obs, for His-heme loop formation (33), where k_b,His is the rate constant for His-heme loop breakage, k_f,His is the rate constant for His-heme loop formation with a fully deprotonated histidine, and K_a(HisH⁺) is the acid dissociation constant of the histidine that forms the loop. Note that k_b,His can be obtained when [H⁺] >> K_a(HisH⁺) because Eq. 4 reduces to k_obs = k_b,His. Thus, downward pH jump experiments were used to obtain k_b,His (see Fig. S2 and Table S3).

In our previous work, we have observed that k_b,His decreases at higher GdnHCl concentrations (18,19). The decrease in k_b,His correlated well with the increase in solution viscosity as GdnHCl concentration increases (18,19). Thus, we have corrected k_b,His at 6.0 M GdnHCl for viscosity (k_b^6M_corr, see Table S4). The plots of k_b,His versus loop size in Fig. 4 A show that after correction for solution viscosity, k_b,His is insensitive to GdnHCl concentration for the Gly-rich variants. Our previously reported k_b,His data for the Ala-rich variants are shown for comparison in Fig. 4 A. Two differences are evident. For the Gly-rich variants, k_b,His is uniformly larger than for the Ala-rich variants at all loop sizes and k_b,His for the Gly-rich variants is relatively insensitive to loop size, whereas k_b,His for the Ala-rich variants decreases with increasing loop size before leveling out for n ≥ 34.

Figure 4.

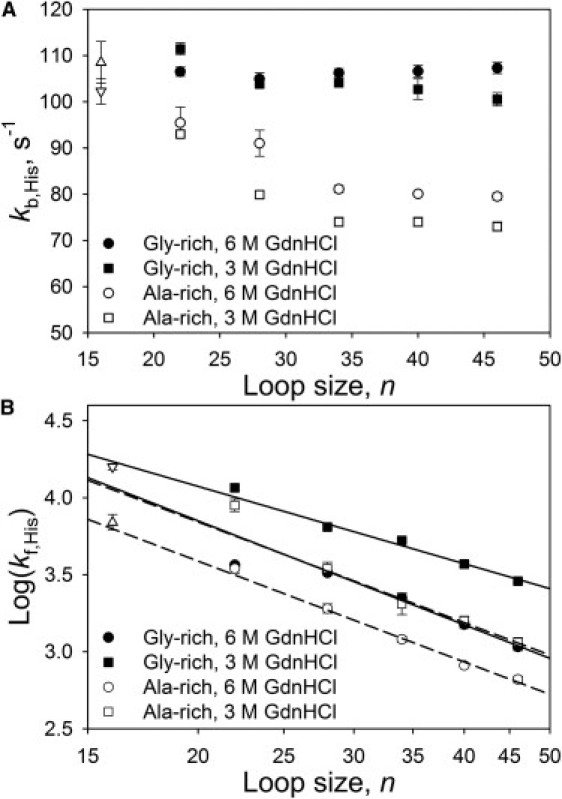
Kinetics of His-heme loop breakage and formation. (A) Plots of k_b,His versus loop size, n, for the Gly-rich variants at 3.0 M (■) and 6.0 M (●) GdnHCl and for the Ala-rich variants at 3.0 M (□) and 6.0 M (○) GdnHCl. All 6.0 M GdnHCl data points are viscosity-corrected (see Table S4). Data points for the variant with no insert (n = 16) at 3.0 M (∇) and 6.0 M (Δ) GdnHCl. (B) Plot of Log(k_f,His) versus the loop size, n (plotted logarithmically), for the Gly-rich variants at 3.0 M (■) and 6.0 M (●) GdnHCl and for the Ala-rich variants at 3.0 M (□) and 6.0 M (○) GdnHCl. Data points for the variant with no insert (n = 16) at 3.0 M (∇) and 6.0 M (Δ) GdnHCl. The Gly-rich variants (solid lines) and Ala-rich variants (dashed lines) are fits to Eq. 5 in the text for n ≥ 28. The values of ν₃ obtained from these fits are reported in Table 2. In both panels, Ala-rich and no-insert data are taken from Tzul and Bowler (19).

Because loop formation is two-state, we obtain the rate constant for His-heme loop formation, k_f,His, from K_loop(His) and k_b,His (Fig. 4 B and see Table S5). The k_f,His data for the Gly-rich variants are compared with our previously reported k_f,His data for the Ala-rich variants in Fig. 4 B (19). It is important to note that we (23) and others (34,35) have shown that His-heme loop formation is reaction-controlled, not diffusion-controlled. Thus, k_f,His for the Gly-rich variants in Fig. 4 B is ∼3 orders-of-magnitude smaller than rate constants for diffusion-controlled loop formation, k_c, obtained with poly(GlySer) peptides of comparable length at similar GdnHCl concentrations (3,36). Because formation of the His-heme bond is reaction-limited, not diffusion-limited, k_f,His is not expected to be affected by viscosity (23,34,35). Thus, the decrease in k_f,His in 6.0 M vs. 3.0 M GdnHCl is attributable to an increase in the root-mean-square end-to-end distance of the Gly-rich sequences in 6.0 M vs. 3.0 M GdnHCl. At both 3.0 M and 6.0 M GdnHCl, k_f,His is smaller at all loop sizes for the Ala-rich variants than for the Gly-rich variants, consistent with Gly-rich sequences being more compact than Ala-rich sequences under the same solvent conditions.

Even though His-heme loop formation is not diffusion-controlled, k_f,His still reflects the end-to-end distance distribution of a random coil polypeptide chain. Thus, the Jacobson-Stockmayer equation for loop entropy (Eq. 1) applies, and a plot of Log(k_f,His) versus Log(n) should be linear with a slope equal to the scaling exponent, ν₃,

$$\mathrm{Log}\left(k_{\mathrm{f},\mathrm{His}}\right)=\mathrm{Log}\left(k_{\mathrm{f},\mathrm{His}\_\mathrm{ref}}\right)-v_3\mathrm{Log}\left(n\right)$$ (5)

(see derivation in the Supporting Material). In Eq. 5, k_{f,His_ref} corresponds to k_f,His for a loop size of n = 1. As with our equilibrium data, we use only the k_f,His data for Gly-rich and Ala-rich variants with two or more (GGGGGK) and (AAAAAK) inserts, respectively, in the fits to Eq. 5 shown in Fig. 4 B. Table 2 shows that ν₃ obtained from kinetic and equilibrium data is the same for the Gly-rich variants. However, for the Ala-rich variants, ν₃ obtained from kinetic data is somewhat larger than when it is obtained from equilibrium data. The difference results from the increase in k_b,His due to steric strain at shorter loop sizes for the Ala-rich variants that perturbs pK_loop(His) for smaller loop sizes introducing an enthalpy of steric strain not present for pK_loop(His) at larger loop sizes. Thus, the ν₃ values from the kinetic data should be better estimates of ν₃ for Ala-rich sequences. Hence, our data indicate that ν₃ is similar for Ala-rich and Gly-rich sequences in 6.0 M GdnHCl. However, under poorer solvent conditions (3.0 M GdnHCl), ν₃ decreases for Gly-rich sequences, but not for Ala-rich sequences.

As with our equilibrium results, we note that at 3.0 M GdnHCl, the data for iso-1-Cytc with no inserts (n = 16) and for a single (AAAAAK) or (GGGGGK) insert are consistent with the line obtained from fitting the data for the Gly-rich variants (two or more inserts) to Eq. 5 (Fig. 4 B). By contrast, at 6.0 M GdnHCl, data for iso-1-Cytc with no inserts (n = 16) and for a single (AAAAAK) or (GGGGGK) insert are consistent with the line obtained from fitting the data for the Ala-rich variants (two or more inserts) to Eq. 5 (Fig. 4 B).

Discussion

Scaling properties

As discussed in the Results, the k_b,His data in Fig. 4 A indicate that steric strain perturbs pK_loop(His) at loop sizes <34 for the Ala-rich variants. Steric strain likely remains in the transition state for His-heme loop formation with the Ala-rich variants for loop sizes <34. However, the increase in k_b,His at small loop sizes in Fig. 4 A indicates that steric strain is partially relieved in the transition state relative to the closed-loop form. Thus, we will use ν₃ obtained from the k_f,His data in Fig. 4 B (Table 2) to compare the Gly-rich to the Ala-rich variants. At 1.5 and 3.0 M GdnHCl concentration, ν₃ is 1.7–1.9 for our Gly-rich variants. At 6.0 GdnHCl, ν₃ increases to 2.2. By contrast for the Ala-rich variants, ν₃ is invariant with GdnHCl concentration; it is near 2.2 at both 3.0 and 6.0 M GdnHCl. Thus, ν₃ for Ala-rich and Gly-rich sequences are identical in a good solvent like 6.0 M GdnHCl. The magnitude of ν₃ in a good solvent is also in the upper part of the range predicted for the excluded volume limit, ν₃ = 1.8–2.4 (10–12). Monte Carlo simulations of polyglycine and polyalanine ranging from 50 to 500 monomers in length using a hard sphere model, which should model a good solvent, also yielded identical scaling exponents for these two polymers (13).

More interestingly, ν₃ decreases to 1.7–1.9 under poorer solvent conditions for the Gly-rich variants, whereas ν₃ stays near 2.2 for the Ala-rich variants. Our results provide additional support for the difference in ν₃ observed from the loop size dependence of k_c for Gly-rich poly(GlySer) (ν₃ ∼ 1.7) versus poly(Ser) (ν₃ ∼ 2.1) in water (3). Interestingly, ν₃ is insensitive to solvent quality for poly(GlySer) (3). The insensitivity of ν₃ for poly(GlySer) to solvent conditions compared to our Gly-rich variants may reflect the high content of serine with its ability to hydrogen-bond to the main chain.

The decrease in ν₃ at lower GdnHCl concentrations for the Gly-rich variants is consistent with simple polymer theories that predict that the scaling exponent for a polymer should decrease as solvent conditions become poorer, reaching ν₃ = 1.5 in a θ-solvent where solvent-polymer and polymer-polymer interactions are of equal magnitude (10), and decreasing further as polymer-polymer interactions become progressively more dominant as solvent conditions becomes progressively poorer (11,37). In the limit of maximally compact polymers, the cubic lattice work of Chan and Dill (11) predicts that the probability of loop formation becomes essentially independent of the distance separating monomers in the chain. The observation that ν₃ obtained from our experiments on the Gly-rich and Ala-rich variants remains in the range expected for a θ-solvent or good solvent suggests that these polypeptide chains have not undergone a coil-to-globule transition (38,39) even in 1.5 M GdnHCl. Thus, whereas the decrease in ν₃ for the Gly-rich sequences indicates that some compaction of the Gly-rich polypeptide occurs in 1.5 and 3.0 M GdnHCl relative to 6.0 GdnHCl, the collapse is not so much as to preclude analysis with simple polymer theories.

Chain stiffness

Polyglycine sequences are expected to be more flexible than polyalanine sequences. Fig. 4 A shows that k_b,His is nearly independent of loop size for the Gly-rich variants. By contrast, k_b,His drops by ∼20% as loop size increases for the Ala-rich variants. These data indicate that there is little steric strain in the loops formed by the Gly-rich variants whereas steric strain is evident in the loops formed by Ala-rich sequences out to loop sizes of 34. We note that k_b,His is 30–40% larger at the longest loop sizes for the Gly-rich variants, also consistent with the greater flexibility of Gly-rich versus Ala-rich sequences. The more favorable equilibrium loop formation (more negative pK_loop(His), Fig. 3) and the larger magnitude of k_f,His (Fig. 4 B) under the same solvent conditions for the Gly-rich versus the Ala-rich variants of the same loop size are also consistent with the denatured states of the Gly-rich variants being more compact than those of the Ala-rich variants, due to the greater flexibility of Gly-rich sequences.

For a more quantitative estimate of relative chain stiffness, we can use the Jacobson-Stockmayer equation to calculate the relative chain stiffness of the Gly-rich versus the Ala-rich variants. Inspection of the Jacobson-Stockmayer equation (Eq. 1) shows that for loops of the same size but different sequence composition, differences in ΔS_loop depend only on Flory's characteristic ratio, C_n, which is a measure of chain stiffness. As with scaling properties, our k_f,His data should provide a better estimate than our pK_loop(His) data for the chain stiffness of the Gly-rich versus the Ala-rich sequences. In Eq. 5, the terms from the Jacobson-Stockmayer equation not dependent on loop size are contained within the Log(k_{f,His_ref}) term. All terms except Flory's characteristic ratio for the Ala-rich variants, C_n(Ala), and Gly-rich variants, C_n(Gly), cancel out, allowing the ratio between these two quantities to be determined from k_f,His data with

$$\frac{C_{\text{n}}\left(\text{Ala}\right)}{C_{\text{n}}\left(\text{Gly}\right)}={10}^{\left(\left(\text{Log}{k}_{\text{f},\text{His}}\left(\text{Gly}\right)-\text{Log}{k}_{\text{f},\text{His}}\left(\text{Ala}\right)\right)/{\overline{\nu }}_3\right)}$$ (6)

(see derivation in the Supporting Material), where k_f,His(Gly) and k_f,His(Ala) are k_f,His for Gly-rich and Ala-rich variants, respectively, with the same loop size and ${\overline{\nu }}_3=({\nu }_{3,\text{Gly}}+{\nu }_{3,\text{Ala}})/2$ is the average value for the scaling exponent for the Gly-rich and Ala-rich variants at the GdnHCl concentration used to measure k_f,His.

Table 3 shows that C_n(Ala)/C_n(Gly) initially increases as a function of loop size and then levels out for the longest loop sizes. Simple polymer theory predicts that C_n increases with polymer length reaching a limiting value for long polymers (9). Because Gly-rich sequences reach a limiting value of C_n faster than Ala-rich sequences (9,40) the ratio C_n(Ala)/C_n(Gly) is expected to grow with loop size leveling out for longer loop sizes as observed in Table 3. The observation that C_n(Ala)/C_n(Gly) is near 1 for a loop size of 22 also reflects the fact that the variants with one insert are most similar because the 15 amino acids of the loop closest to the heme are from the native sequence of iso-1-Cytc. We observe limiting values for C_n(Ala)/C_n(Gly) of ∼1.6 in 3.0 M GdnHCl and ∼1.3 in 6.0 M GdnHCl. Thus, the chain stiffness of the Ala-rich and Gly-rich sequences become more similar at high GdnHCl concentration.

Table 3.

Calculated relative magnitude of Flory's characteristic ratio, C_n, for the Gly-rich versus the Ala-rich variants

Loop size	%Gly		Cn(Ala)/Cn(Gly)∗
	Ala-rich	Gly-rich	3.0 M GdnHCl	6.0 M GdnHCl
22	9.1	31.8	1.15 ± 0.07	1.02 ± 0.04
28	7.1	42.9	1.38 ± 0.11	1.27 ± 0.04
34	5.8	50.0	1.64 ± 0.20	1.32 ± 0.05
40	5.0	55.0	1.56 ± 0.14	1.32 ± 0.04
46	4.3	58.7	1.61 ± 0.16	1.25 ± 0.04

^∗Average value of ν₃ for the Ala-rich and Gly-rich variants, ${\overline{\nu }}_3$ in Table 2 (kinetic data) at each GdnHCl concentration was used in Eq. 6. At 3.0 M GdnHCl, we used ${\overline{\nu }}_3=1.92\pm 0.35$. At 6.0 M GdnHCl, we used ῡ₃ = 2.21 ± 0.04. The reported error is the standard propagation of error due to the standard deviation in k_f,His and in ${\overline{\nu }}_3$ for the Ala-rich and Gly-rich variants. The data for the Ala-rich variants used in these calculations are from Tzul and Bowler (19).

The C_n(Ala)/C_n(Gly) ratios in Table 3 are surprisingly modest. Simple polymer theories predict C_n ∼ 9.27 for pure polyalanine and C_n ∼ 2.16 for pure polyglycine (9), yielding C_n(Ala)/C_n(Gly) of ∼4.3. However, every sixth amino acid in our constructs is a lysine. Also, our Gly-rich and Ala-rich variants contain 16 amino acids (two of which are Gly) derived from the natural sequence of iso-1-Cytc. Thus, our loops are not pure polyalanine or polyglycine sequences. For loop sizes of 34–46, the % glycine content approaches a constant value for each set of variants (Table 3). The Gly-rich variants with loop sizes of 34–46 range from 50–59% glycine. For these same loop sizes, the Ala-rich variants range from 4 to 6% glycine. Based on the work of Miller et al. (41), C_n(Ala)/C_n(Gly) should be 2.3–2.6 for loop sizes of 34–46 in our system. Thus, even after correcting for the actual sequence composition of the Ala-rich versus the Gly-rich variants, C_n(Ala)/C_n(Gly) is much smaller than predicted.

Consistent with our results, Krieger et al. (3) observed that the difference in k_c for poly(Ser) versus poly(GlySer) polypeptides in water was smaller than anticipated based on the expected differences in chain stiffness. They also observed that chain stiffness for the poly(GlySer) polypeptides decreased in 8.0 M GdnHCl relative to water as a result of decreased intrachain interactions—van der Waals or hydrogen bonding—due to better solvation of the polypeptide at higher GdnHCl concentration (3,42). If good solvation of polypeptides is the dominant contribution to chain stiffness at high GdnHCl concentration, solvation effects may explain the greater similarity we observe for C_n(Ala) and C_n(Gly) in 6.0 M GdnHCl (Table 3).

Physical basis for the differences between polyglycine and polyalanine

Our loop formation data clearly show that the Gly-rich and Ala-rich variants are more similar at higher GdnHCl concentrations both with regard to scaling properties and chain stiffness, whereas their polymer properties diverge at lower denaturant concentration. To begin, we consider the possible basis for the similar behavior of these polymers at high denaturant concentrations. Recent theoretical (37) and experimental (43) studies on a homopolymer of glycine show that intrachain hydrogen bonding interactions are decreased in higher concentrations of denaturant and are replaced by hydrogen bonds to the denaturant. Experiment and theory (44–46), with some exceptions (13), indicate that both alanine and glycine have a relatively high preference for the polyproline II structure. Because high denaturant concentration is known to stabilize polyproline II structure (47,48), the conformational properties of Gly-rich and Ala-rich sequences would be expected to be more similar in 6.0 M GdnHCl. Thus, the distribution of conformations should become more similar in 6.0 M GdnHCl, leading to more similar ν₃ and C_n values for Gly-rich and Ala-rich variants. In other words, solvent-backbone interactions partially neutralize the effects of side-chain sterics on polypeptide conformational properties in a good solvent.

As solvent conditions become poorer, intrachain interactions are expected to become progressively more dominant. In the extreme, a coil-to-globule transition is expected to occur (37–39,49,50). The observation that the scaling exponent remains in the range expected for a random coil at lower GdnHCl concentrations suggests that the collapse to a globule has not occurred for either the Ala-rich or Gly-rich variants at 1.5–3.0 M GdnHCl. However, the divergence of ν₃ for Gly-rich versus Ala-rich sequences and the increase in C_n(Ala)/C_n(Gly) at 3.0 M GdnHCl indicates that the peculiarities of the Gly-rich versus the Ala-rich sequences are beginning to affect chain properties. Polyalanine sequences similar to the inserts used here are known to form stable helices in water (51). Simulations of a seven-residue alanine peptide show that the γ-turn basin is preferentially populated as solvent conditions become poorer (52). By contrast, simulation (37) and experiment (43) indicate that polyglycine forms a collapsed disordered structure with nonspecific hydrogen bonds under poor solvent conditions. The ordered helical structure favored by polyalanine might be expected to stiffen the polypeptide chain relative to polyglycine at lower GdnHCl concentration under poorer solvent conditions as we observe for C_n(Ala)/C_n(Gly) (Table 3). The tendency of polyglycine to undergo nonspecific compaction in a poorer solvent (37,43) would be expected to decrease ν₃. It is interesting to note, for loop sizes of 16 and 22 where the residues within the loop are completely or predominately from the natural sequence of iso-1-Cytc, that the polymer properties are more similar to the Ala-rich variants in 6.0 M GdnHCl and more similar to the Gly-rich variants in 1.5 and 3.0 M GdnHCl despite the relatively low 12.5% Gly content of the natural sequence (Fig. 3 and Fig. 4 B). C_n decreases rapidly as glycine content is increased from 0% to 50%, decreasing more slowly at >50% glycine content (41). However, even with this steep initial decrease in C_n, the Ala-rich sequences would be expected to have backbone sterics more similar to the natural sequence of iso-1-Cytc than the Gly-rich sequences. Thus, even though all amino acids except Pro and Gly have backbone sterics similar to Ala, the chemical properties of the side chains of non-Gly/Pro amino acids appear to mediate collapse in a manner more similar to Gly than Ala under poorer solvent conditions.

Conclusions

Comparison of these data for Gly-rich variants of iso-1-Cytc with our previous work on Ala-rich variants shows that glycine does not increase the flexibility of a polypeptide chain as much as expected from simple polymer theories. However, relative to alanine it still promotes compact conformers more effectively. At high denaturant concentration, the scaling exponent and chain stiffness are more similar for Gly-rich and Ala-rich sequences, indicating that denaturant-polymer interactions and not side-chain sterics are the dominant factor in polypeptide conformational properties under good solvent conditions. At lower denaturant concentration, the polymer properties of the Gly-rich and Ala-rich variants diverge, presumably due to the increasing influence of the side chain under poorer solvent conditions, with polyglycine and polyalanine favoring nonspecific and ordered helical intrachain interactions, respectively. Clearly, a fuller understanding of the divergent effects of different side chains on polypeptide polymer properties will be important for discerning how these biases can be manipulated to define the fold of a protein.