Force-Field Dependence of Chignolin Folding and Misfolding: Comparison with Experiment and Redesign

Abstract

We study the folding of the designed hairpin chignolin, using simulations with four different force fields. Interestingly, we find a misfolded, out-of-register, structure comprising 20–50% of the ordered structures with three force fields, but not with a fourth. A defining feature of the misfold is that Gly-7 adopts a β_PR conformation rather than α_L. By reweighting, we show that differences between the force fields can mostly be attributed to differences in glycine properties. Benchmarking against NMR data suggests that the preference for β_PR is not a force-field artifact. For chignolin, we show that including the misfold in the ensemble results in back-recalculated NMR observables in slightly better agreement with experiment than parameters calculated from a folded ensemble only. For comparison, we show by NMR and circular dichroism spectroscopy that the G7K mutant of chignolin, in which formation of this misfold is impossible, is well folded with stability similar to the wild-type and does not populate the misfolded state in simulation. Our results highlight the complexity of interpreting NMR data for small, weakly structured, peptides in solution, as well as the importance of accurate glycine parameters in force fields, for a correct description of turn structures.

Introduction

The study of small autonomously folding peptides has proved a very useful ground for comparison of molecular simulations with experiment. Due to their small size and generally short folding times, the folding of these peptides can be studied with quantitative accuracy using current computational resources (1–3). Such peptides have frequently been chosen to form common protein secondary structure motifs: for example, alanine-based peptides have served as a paradigm for helix formation (4,5) and carefully selected hairpins are models for the formation of turns and sheets (6), whereas other peptides have been used to study the kinetics of loop formation (7,8). Although secondary structure elements excised from larger proteins are generally not stable in isolation, the finding that several of these systems were remarkably stable led to efforts to improve them by design. A template for β-hairpins, which has been used in several design studies, has been the C-terminal hairpin of the B1 domain of streptococcal protein G, commonly known as the GB1 hairpin (6,9). Examples include the addition of tryptophan residues to form the Trpzip family of hairpins (10), redesign of the turn sequence to enhance stability (11), and the use of D-Pro to stabilize the turn (12).

Recently, the GB1 hairpin has been used as a basis for the design of minimal, 10-residue hairpins (13,14). The structure of the GB1 hairpin was used to search a nonredundant protein database for eight-residue fragments whose backbone torsion angles matched those of the hairpin. A frequency analysis of the amino acids occurring at each position was used to design the peptide “chignolin” with sequence GYDPETGTWG, which was found to fold into a stable hairpin with ∼60% folded population at 300 K, and a structure was determined by NMR (13). The terminal residues were later optimized to produce the peptide CLN025, with ∼90% folded population at 300 K, and a crystal structure of this system has been determined (14). The abundance of NMR data, determined at different temperatures, combined with their small size, has made these two peptides attractive targets for comparison of simulation with experiment.

Here, we study the folding thermodynamics of chignolin using replica-exchange molecular dynamics (REMD) sampling and four different force fields: 1), the AMBER ff03^∗ force field modified to match helix-coil data; 2), the AMBER ff03w force field, designed for use with the highly optimized TIP4P-2005 water model; 3), the AMBER ff99SB force field; and 4), the CHARMM22/CMAP force field. With all four force fields, the peptide folds to its native structure with a population comparable to experiment at 300 K. However, the first three force fields also result in the population of a misfolded state with a population of 20–50% (depending on force field), in which Gly-7 adopts a β_PR backbone conformation, rather than the intended α_L. With CHARMM22/CMAP, the misfolded state is not observed. We find that the misfolded population observed in each simulation is strongly correlated with the relative propensity of glycine to form β_PR rather than α_L in each force field.

We have attempted to assess which simulation results are most accurate, by comparing NMR observables calculated from the simulations against experiment. Surprisingly, we find that the agreement with experimental data for chignolin is quite similar in all cases, despite the different ordered structures that are populated. Although the misfolded structure of course is in poor agreement with experiment by itself, its inclusion in the 300 K ensemble in most cases results in slightly improved agreement compared with using the folded structure alone. It is therefore difficult to determine which simulation is more accurate based on the NMR parameters for chignolin alone. We have, however, separately evaluated the parameters for glycine, using extensive NMR data compiled on Gly₃ by Graf et al. (15). We show that the force fields that populate the misfolded state indeed have more accurate glycine parameters, particularly with respect to the ψ torsion angle, which distinguishes β_PR and α_L. This suggests that the observed misfolded state is not just a force-field artifact.

Although the likely fast timescale of interconversion of the folded and misfolded state would make its direct experimental detection challenging, we have instead redesigned the hairpin to provide a reference peptide that should be truly two-state. Because the β_PR backbone conformation can only be adopted by glycine, replacing the glycine by any other residue should eliminate this particular misfolded state. Specifically, we examine the G7K mutation, in which Gly-7 is reverted to the lysine present in the original GB1 sequence. Simulations of this mutant showed that the misfold is not populated and that the peptide is stable, with a population of ∼80% near 300 K and no evidence of other stable states with significant population. Experimental NMR measurements on the mutant show its stability is similar to the original chignolin at low temperature, and the measured chemical shifts are in excellent agreement with those back-calculated from simulations.

Our results highlight the complexity of interpreting NMR data for small, weakly structured, peptides in solution (16)—a problem currently of great interest because of the desire to characterize the intrinsic structure in disordered proteins. We have also shown that small free energy differences in glycine parameters can make a significant difference to determining which conformations are populated in glycine-containing turn motifs. This stresses the importance of careful calibration of glycine parameters in force fields (17), which will be essential if simulation is to be used as a tool for interpreting such results.

Methods

Simulation methods

Replica exchange molecular dynamics (REMD) of the chignolin and the mutant were performed using the simulation package GROMACS 4.5.3 (18) with the implementation of the AMBER force fields by Sorin and Pande (19). The starting structure of chignolin (13) was taken from the Protein Data Bank database (PDB: 1UAO) and the mutant of chignolin was prepared by changing Gly-7 to Lys using the mutagenesis tool of PyMOL (Schrödinger, Portland, OR). The explicit water models were used as follows: TIP3P (20) for simulation with ff99SB, ff03^∗, and CHARMM22/CMAP, and TIP4P-2005 (21) for the simulation with ff03w, respectively. The simulations of chignolin were carried out with four different force fields—ff99SB (22), ff03^∗ (23), ff03w (24), and CHARMM22/CMAP (25–27). The G7K mutant was simulated with the ff99SB force field.

For all chignolin simulations, a similar simulation protocol was used. To begin, the system was solvated in a truncated octahedron box with 3.5 nm between nearest faces, containing ∼1030 water molecules, five sodium ions, and three chloride ions to neutralize the charge of chignolin and four sodium ions and three chloride ions to neutralize the charge of the mutant. Termini were charged (N-terminus positively and C-terminus negatively) corresponding to the experimental situation. Each system was then equilibrated at 300 K and a constant pressure of 1 atm. Subsequently, simulations were performed at constant volume at 800 K, to generate unfolded configurations. Different and completely unfolded conformations were chosen from simulation at 800 K as starting structures for REMD simulations; all prolines were confirmed to be in trans conformations. The temperatures of the 32 replicas spanned a range 278–595 K. All REMD simulations were performed at constant volume with long-range electrostatics calculated using particle-mesh Ewald with a 1.2 Å grid spacing and 9 Å real-space cutoff. The system was propagated using Langevin dynamics with a friction of 1 ps⁻¹, and replica exchange was attempted every 10 ps. Each system was run for at least 200 ns.

Cluster analysis

Cluster analysis was carried out using the g_cluster program of the simulation package GROMACS (18). Clusters were obtained by grouping conformations from the replica at 303 K using the single linkage method with a 0.6 Å cutoff. For the misfolded cluster, an additional criterion that Gly-7 be in β_PR was used to better-define this state.

NOE calculation

We have calculated proton-proton distances for comparison with the bounds estimated from nuclear Overhauser effect (NOE) measurements by a simple averaging scheme in which the NOE-derived distance r_NOE is obtained from the instantaneous distances r(t) in the REMD simulation as r_NOE = 〈r⁻⁶(t)〉^−1/6. This approach neglects 1), spin-diffusion effects and 2), dynamical contributions to the NMR relaxation rates coming from intramolecular motions on the appropriate timescale. Because we are using REMD for sampling, it would not be straightforward to evaluate the correlation functions for item 2. However, several studies have noted that a representative sampling of conformation space is more important than the exact method used for calculating the NOE build-up rate (28,29); accurate sampling should be a strength of our REMD approach.

Scalar coupling calculation

Scalar coupling constants were calculated using the g_chi program of the simulation package GROMACS (18), which uses the Karplus equation from Vuister and Bax (30) for computing ³J_HNHα couplings and Kopple et al. (31) for ³J_HαHβ couplings.

Chemical shift calculation

Chemical shifts were calculated for every 10th frame from the appropriate replica using SPARTA+ (32) and ensemble-averaged over the trajectory.

Trajectory reweighting

Reweighting of simulation trajectories was performed to assess the effect of changes in the relative free energy of α_L and β_PR on the misfolded population. We consider an adjustment of the relative energy of α_L and β_PR of ΔΔG = ΔG₁(β_PR − α_L) − ΔG₀(β_PR − α_L), in which ΔG₀(β_PR − α_L) and ΔG₁(β_PR − α_L) are the relative free energies of the β_PR and α_L regions for Gly-7 before and after adjustment, respectively. The reweighted population of misfold was estimated from

$$P_{\text{rw}}=\frac{\langle m\left(x\right)\text{exp}\left[-\beta \theta \left(x\right)\Delta \Delta G\right]\rangle }{\langle \text{exp}\left[-\beta \theta \left(x\right)\Delta \Delta G\right]\rangle },$$ (1)

in which θ(x) is a counting function equal to 1 when Gly-7 is in β_PR and 0 otherwise, m(x) = 1 for misfolded states and 0 for all other states, and β = 1/k_BT.

Gly₃ simulations

Simulations of Gly₃ were run with the AMBER ff99SB (22), ff03^∗ (23), ff03w (24), and CHARMM22/CMAP (25–27) force fields for the peptide. The water model was TIP3P (20) for all except the ff03w simulation, where it was TIP4P/2005 (21). The peptide was protonated at both termini, corresponding to the experimental conditions of pH 2 (15). Nonbonded interactions were treated as described above for chignolin, with the net charge of +1 compensated by a neutralizing background. For each force field, a single simulation of 100 ns was run at constant temperature of 300 K and pressure of 1 atm and a Langevin thermostat with friction coefficient of 0.2 ps⁻¹.

Agreement with experiment was quantified using a χ² parameter defined as

$${\chi }^2=\frac{1}{N}\sum _i\frac{{\left(J_{\text{expt}}\left(i\right)-J_{\text{calc}}\left(i\right)\right)}^2}{{\sigma }^2\left(i\right)},$$ (2)

where the sum runs over the N scalar couplings and J_expt(i) and J_calc(i) are, respectively, the i^th scalar coupling measured in experiment and calculated from the simulation using a Karplus equation (33) and σ²(i) is the uncertainty in the prediction from the Karplus equation. Parameters for the Karplus equation (DFT2 set) and σ²(i) were taken from Best et al. (34).

NMR experiments

Unlabeled peptides were purchased at >98% purity from Peptide 2.0 (Chantilly, VA). The peptides, at a concentration of ∼2 mM, were dissolved in a 20 mM sodium phosphate buffer (pH 5.5) containing 10% (v/v) D₂O. NMR measurements were performed on a 700-MHz AVANCE spectrometer (Bruker BioSpin, Billerica, MA). Proton chemical shifts were referenced to the known shift of the water signal at the experimental temperature. A set of homonuclear two-dimensional spectra (COSY, TOCSY, and NOESY) was acquired at 277 K using mixing times of 60 ms and 300 ms for TOCSY and NOESY, respectively. We obtained ¹H chemical shifts for the chignolin peptide from the deposited assignment by Honda et al. (BMRB code: 5694) (13), with ¹³C assignments obtained from HMQC spectra (natural abundance ¹³C). To reduce the noise for resonances close to the water resonance (4.7 p.p.m.), in addition to HMQC measurements in 10% D₂O + 90% H₂O, we recorded a spectrum in 100% D₂O. The ¹³C^α and ¹³C^β crosspeaks with directly bonded aliphatic protons are shown in Fig. S5 a in the Supporting Material. Mutant resonances were assigned by manual analysis of COSY, TOCSY, and NOESY spectra in conjunction, by comparison with the wild-type resonances. The assigned NOESY resonances in the fingerprint region (H^N-H^α and H^N-side-chain protons) are shown in Fig. S5 b. The ¹³C^α and ¹³C^β resonances were assigned by means of HMQC spectra recorded in 10% D₂O + 90% H₂O or 100% D₂O (see Fig. S5 c).

CD experiments

Circular dichroism (CD) measurements were made on ∼250 μM solutions of each peptide in 20 mM sodium phosphate buffer, pH 5.5. Melting curves were recorded on a spectropolarimeter (JASCO, Great Dunmow, Essex, United Kingdom) over a range of 279–363 K, monitoring the ellipticity at 213 and 229 nm. Samples were heated at a rate of 0.5 K.min⁻¹, and melting curves were found to be reversible on cooling.

Results and Discussion

Folding of chignolin in four force fields

We have used replica exchange molecular dynamics to study the equilibrium folding of chignolin, using four different all-atom force fields and explicit water:

• 1.We chose the ff03^∗ force field (23) in which the backbone ψ-torsion angle has been adjusted to reduce the excessive helical propensity in AMBER ff03 (34,35). This force field has been used successfully to fold peptides (36) and proteins (37) from both α and β structural classes, and should therefore represent a transferable backbone potential.
• 2.We selected also the AMBER ff03w force field, which is a version of AMBER ff03 matched to the optimized TIP4P-2005 water model (21). The use of the more accurate water model results in unfolded states that are less collapsed than in simulations with the TIP3P water model, used in the other simulations here.
• 3.We chose the widely used AMBER ff99SB (22) force field for which the glycine backbone appears to be more accurate than for AMBER ff03 (17) (note that ff03^∗ and ff03w do not alter glycine): accurate glycine parameters may be important for chignolin considering its presence in the turn.
• 4.Lastly, as an example of a non-AMBER force field, we chose the CHARMM22/CMAP (25–27) energy function in which a two-dimensional cubic spline potential has been introduced for the backbone to better-capture the ϕ,ψ correlations in Ramachandran free energy surfaces.

The simulations were initiated from unfolded conformations generated from a trajectory at 800 K in each force field. All initial conditions were at least 8 Å in backbone RMSD from the folded structure and did not contain cis proline. The peptide was found to fold to the native structure in all force fields. As a measure of convergence we plotted the average population within 1.6 Å of the folded structure, block-averaged over 10 ns (36), suggesting that a stable equilibrium distribution had been reached after ∼100 ns; the first 100 ns was excluded from all further analysis. Because an analysis focused on finding structures close to the published experimental structure is inevitably biased, we chose instead to use a cluster analysis using configurations from the 300 K replica to identify the predominantly populated conformations in our simulations. The clustering revealed an unexpected result: for all of the AMBER force fields, we obtained two major clusters (population >10%), in addition to a large number of clusters with smaller population (<1%). This result is in contrast to what is expected for a two-state system: for example, for the GB1 hairpin, a single predominant folded cluster was identified in simulations, with other clusters having a population of, at most, a few percent (36). With the CHARMM22/CMAP force field, however, the population of all nonnative states was negligible (∼1% or less).

In two of the force fields used, AMBER ff03^∗ and ff03w, the more populated of the two clusters corresponds to the experimentally determined fold, whereas in AMBER ff99SB the native cluster is approximately equal in population to the second major cluster at 300 K (Fig. 1). The other substantially populated cluster in each case corresponds to a misfolded state in which one of the strands is flipped such that the hydrophobic side chains are on opposite sides of the hairpin, rather than the same side as intended (see Fig. 1, g and h. Although misfolded states have been observed in simulations of other hairpins including GB1 (36,38), they generally have a very small population in the equilibrium ensemble. In this case, the misfolded population is 17%, 23%, 48%, and 1% in each of ff03^∗, ff03w, ff99SB, and CHARMM22/CMAP simulations. The remaining clusters all have a population smaller than 3%. The key to formation of the misfolded species is evidently a change in the backbone state of Gly-7, which adopts an α_L conformation in the native fold and a β_PR conformation in the misfolded state (Ramachandran distributions of this residue are shown for the folded and misfolded clusters of ff99SB in Fig. 1, e and f). We note that other simulation studies have observed a similar misfolded state for chignolin (39,40) and the related peptide CLN025 (41). Note, however, that the misfolded state was not observed in the recent study (42) of CLN025 with the CHARMM22^∗ (43) force field (Kresten Lindorff-Larsen, University of Copenhagen, personal communication, 2011)—in agreement with our finding with CHARMM22/CMAP, which has the same glycine parameters as CHARMM22^∗. This residue also appears to be key for turn formation, similar to the analogous Lys-10 in the GB1 hairpin (36,44). For the convenience of subsequent analysis, we have defined three ensembles of structures for each force field, at each temperature in the REMD simulations:), folded structures within 0.6 Å of the center structure of the folded cluster; 2), misfolded structures within 0.7 Å of the center structure of the misfolded cluster and having Gly-7 in β_PR (ϕ > 0° and ψ < −80° or ψ > 150°); and 3), full ensemble, including all configurations sampled. In Fig. 2, we show the temperature-dependent populations of each of these ensembles for the four force fields, together with the populations estimated from NMR (13). In all cases, the folded population is in reasonable agreement with experiment near 300 K (considering the small free energy difference that would account for these differences in population). The temperature-dependence of the folded population is too weak, but this low cooperativity is a well-known feature of the current generation of additive force fields (23,36,45,46).

Figure 1.

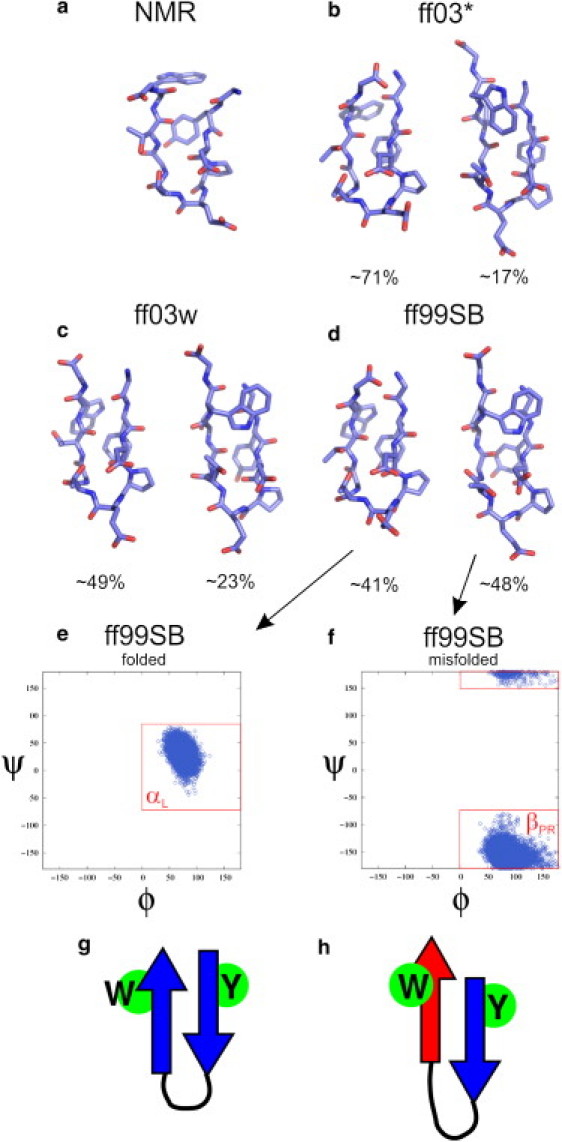
Chignolin folded structure and cluster analysis. (a) NMR structure of chignolin is shown together with the largest clusters from simulations with AMBER (b) ff03^∗, (c) ff03w, and (d) ff99SB, taken from the 303 K replica. We show the distribution of backbone (ϕ,ψ) torsion angles for Gly-7 for (e) folded and (f) misfolded conformations, obtained with ff99SB. Those for other force fields are available in the Supporting Material. (g and h) Cartoon representation of the folded and misfolded conformations, indicating the position of Trp-9 and Tyr-2 above/below the hairpin; the red strand in the misfold has been rotated 180° about its long axis relative to native.

Figure 2.

Folded populations. We show the total population of folded chignolin (blue), misfolded (red), and total folded+misfolded (black) for (a) ff03^∗, (b) ff03w, (c) ff99SB, and (d) CHARMM22/CMAP as a function of temperature. (Green) Experimental data (13). For ff03^∗ and ff99SB, the expected fraction misfold was obtained by reweighting to CHARMM-like relative free energies of α_L and β_PR for Gly-7 (maroon).

Comparison with NMR data

The only way to determine whether any of the force fields gives a reasonable description of the peptide, or whether one is more reasonable than another, is by comparison with experimental data. Fortunately, there is a large body of equilibrium NMR data for this peptide, against which the equilibrium ensembles from simulation can be compared: NOE distance restraints, backbone and side-chain scalar couplings, and chemical shifts.

Although the final comparison with experiment requires equilibrium averages of each observable be calculated over the full ensemble, to obtain more insight into the contribution of the folded and misfolded subensembles, we have calculated averages separately for these also. In Fig. 3, we show the average interproton distances from the 278 K replica, compared with the bounds defined from the NOE data for the NMR structure calculation. Fig. 3 a shows that the folded ensemble is in reasonable agreement with the NMR bounds, with only a handful of small violations. In contrast, for the misfolded state, Fig. 3 b violates a large number of the distance bounds, as expected. Remarkably, however, we find that distances computed from the full ensemble, including the misfolded state (and all remaining states outside folded/misfolded), are in better agreement with the restraint bounds than those computed from either the folded or misfolded states alone (Table 1) for the AMBER force fields. The reason this is possible is that the averaging of the distances measured by NOE build-up rates is highly nonlinear. As a result, the interproton distances may only lie within the defined bounds in a fraction of the full ensemble, and yet still satisfy the distance restraint when ensemble-averaged (16). The reason the inclusion of misfolded states can possibly improve agreement is that some of the distance restraints that are broken in the folded cluster are satisfied in the unfolded state. Examples of these are given in Fig. S2 and Fig. S3. The agreement with the NOEs does not improve upon including nonfolded structures for the CHARMM22/CMAP simulations, because the misfolded state population is too small to contribute significantly to the averages (most of the nonnative contribution comes from other unfolded structures).

Figure 3.

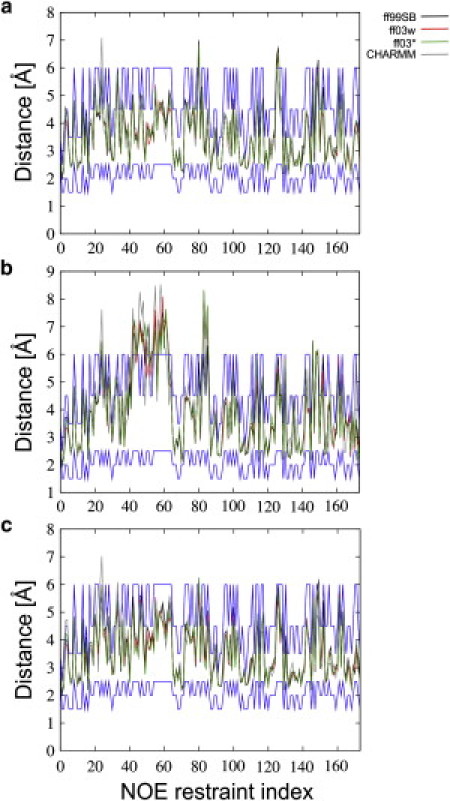
Comparison to NOE-derived distances at 278 K. We compare distances calculated (a) from the folded ensemble, (b) from the misfolded ensemble, and (c) from the full ensemble with the distance bounds estimated from the NMR data. (Green, red, black, and gray curves) Data for ff03^∗, ff03w, ff99SB, and CHARMM22/CMAP, respectively; (blue lines) the distance bounds.

Table 1.

Comparison between experimental and calculated data

Force field	Criterion	Folded	Misfolded	All
ff03∗	Sum of NOE violations (Å)	1.92	30.93	1.20
ff03w	Sum of NOE violations (Å)	1.76	39.70	1.16
ff99SB	Sum of NOE violations (Å)	3.07	31.69	1.58
C22/CMAP	Sum of NOE violations (Å)	2.97	33.31	4.19
NMR	Sum of NOE violations (Å)			0.77
ff03∗	RMS Hα c.s.d. (ppm)	0.31	0.34	0.21
ff03w	RMS Hα c.s.d. (ppm)	0.30	0.34	0.28
ff99SB	RMS Hα c.s.d. (ppm)	0.38	0.38	0.35
C22/CMAP	RMS Hα c.s.d. (ppm)	0.33	0.32	0.28
NMR	RMS Hα c.s.d. (ppm)			0.21
ff03∗	RMS 3JHNHα dev. (Hz)	0.91	1.13	0.89
ff03w	RMS 3JHNHα dev. (Hz)	0.92	1.25	0.91
ff99SB	RMS 3JHNHα dev. (Hz)	1.32	1.80	1.41
C22/CMAP	RMS 3JHNHα dev. (Hz)	1.22	1.65	1.24
NMR	RMS 3JHNHα dev. (Hz)			0.96
ff03∗	RMS 3JHαHβ dev. (Hz)	2.38	2.06	2.18
ff03w	RMS 3JHαHβ dev. (Hz)	2.35	2.04	2.08
ff99SB	RMS 3JHαHβ dev. (Hz)	2.36	2.09	2.09
C22/CMAP	RMS 3JHαHβ dev. (Hz)	2.56	2.97	2.13
NMR	RMS 3JHαHβ dev. (Hz)			2.02

Match of back-calculated data is estimated from the sum of the NOE violations (Å), and the RMS deviations of H^α chemical shifts at 293 K. Column 2: c.s.d., chemical shift deviation; dev., deviation.

We have computed ensemble-average chemical shifts over our trajectories, using the empirical shift prediction code SPARTA+ (32). The root mean-square (RMS) deviation of the computed chemical shifts from experiment improves in all cases for the full ensemble (Table 1), and in the case of ff03^∗ is equal to the deviation computed from the NMR ensemble. In the case of backbone ³J_HNHα couplings, the deviations from experiment for the simulations with ff03^∗ and ff03w force fields are smaller than the deviations from the NMR ensemble, despite these couplings being used to derive restraints for the structure calculation. The deviation from experiment for the ³J_HαHβ in simulations is similar to that for the NMR ensemble (Table 1).

Finally, we show the temperature-dependence of the H^α chemical shifts in Fig. 4, because this was also reported in the original experimental study (13). Here we have separated the shifts for Asp-3, Pro-4, Glu-5, Thr-6, and Thr-8 from Tyr-2 and Trp-9 (Gly-7 is omitted because SPARTA+ does not produce stereospecific chemical shift predictions for Gly). The prediction of shifts for Tyr-2 and Trp-9 is likely to be adversely affected by both ring-current effects, and by being close to the termini, both of which are poorly modeled by current shift prediction algorithms. However, for the remaining shifts, we obtain excellent agreement with experiment, reproducing both the data at low temperatures and the qualitatively correct temperature dependence.

Figure 4.

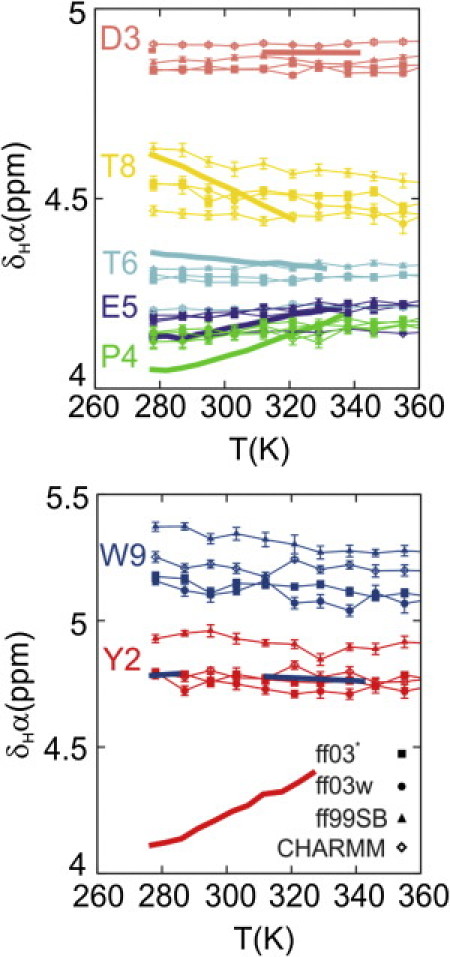
Temperature-dependence of H^α chemical shift deviations. Chemical shifts back-calculated by SPARTA+ (32) from the full simulation ensemble at each temperature are plotted together with experimental data, for ff03^∗, ff03w, ff99SB^∗, and CHARMM22/CMAP.

Thus, we find that the experimental data are satisfied well by all of the force fields, with the exception of the NOEs in the simulation with CHARMM22/CMAP. The main reason for the poor agreement of the CHARMM simulations with NOE data is the large remaining unfolded state population in CHARMM at 278 K. Population of a misfold, or a larger folded population, would improve the agreement. Thus, the experimental data do not conclusively distinguish the results, although the results with the AMBER-derived force fields are overall in better agreement with experiment.

We consider whether it might be possible to resolve the misfolded structure in experiment, if it exists. It may be assumed that like other hairpins, chignolin folds on a microsecond timescale; for comparison, the folding time of the GB1 hairpin is ∼6 μs. This means that for NMR experiments it is in the fast exchange limit (47), so that most signals will be an average over folded, unfolded, and misfolded conformations if populated; this is in contrast to the exchange of β-sheet register for larger proteins that may occur on a much slower timescale (48). Relaxation-dispersion experiments would be one potential method to probe microsecond-timescale dynamics. However, the sensitivity of this method depends on the chemical shift difference of the interconverting species, and the chemical shifts predicted by SPARTA+ for the folded and misfolded states are very similar, compared with the unfolded state. It is therefore likely that relaxation-dispersion measurements would be dominated by conversion between folded (or misfolded) and unfolded states. An alternative method to identify the misfold may be to trap it so that it can be resolved from the folded state, for example by including the peptide in a room temperature trehalose glass. However, whether or not the misfold is found in such a context will not definitively demonstrate its presence or absence in solution. In conclusion, therefore, it would not be straightforward to either confirm or disprove the existence of the misfolded state, other than possibly through accumulating even more data in solution on the original chignolin sequence.

Differences between force fields

The most noteworthy difference between force fields is in the population of the misfolded state, which is populated with all of the AMBER-based force fields (the misfolded population is comparable to that of the folded state in AMBER ff99SB) but not with CHARMM22/CMAP. Given the importance of Gly-7 in the misfolding events, this most likely relates to the backbone parameters for glycine, which are quite different in ff03^∗/ff03w, ff99SB, and CHARMM22/CMAP: the relative free energy of the β_PR backbone state is lower in ff99SB than in the ff03-derived force fields (17). Recent results in which NMR data for a short peptide were compared with simulation, suggesting that ff99SB provides the most accurate glycine representation (17). Based on the data from Aliev et al. (17) for GPGG with AMBER ff99SB, ff03 (identical to ff03^∗ for Gly and Pro), and CHARMM22/CMAP, we have estimated the free energy difference between β_PR and α_L between different force fields, i.e., ΔΔG(β_PR − α_L) = ΔG₁(β_PR − α_L) − ΔG₀(β_PR − α_L), in which ΔG₀(β_PR − α_L) and ΔG₁(β_PR − α_L) are the relative free energies of the β_PR and α_L regions of the Ramachandran map with energy functions 0 and 1. Between ff99SB and CHARMM22/CMAP ΔΔG(β_PR − α_L) ≈ 2.4 k_BT, whereas between ff03/ff03^∗ and CHARMM22/CMAP ΔΔG(β_PR − α_L) ≈ 1.4 k_BT. We use these energy differences to estimate how such a free energy difference would affect the misfolded population, by reweighting the simulation data for ff99SB and ff03^∗. As we show in Fig. 2, this reweighting results in a marked reduction of the misfolded population. Although other factors must also be important (the remaining population is still larger than obtained with CHARMM22/CMAP), the local bias of glycine toward adopting the β_PR conformation clearly plays a major role in stabilizing the misfolded state. Therefore, accurate parameterization of glycine is critical for obtaining the correct properties of turns and hairpins in simulation.

The fact that glycine parameters play a large role in determining the stability of the misfolded state of course raises the question of which set of parameters is more accurate—a particularly relevant question in this study, as the NMR data for chignolin itself do not provide a clear answer. A recent study by Aliev et al. (17) addressed this issue in the context of the peptide GPGG. When terminal residues are excluded (the CHARMM CMAP only applies to internal residues), the agreement with experiment for ff99SB, ff03, and CHARMM22/CMAP is quite similar (17). However, the scalar couplings measured in that study only probe the ϕ-torsion angle, which is clearly not the most relevant for distinguishing β_PR and α_L. We have therefore used a second data set to assess glycine parameters, namely a large set of scalar couplings measured for Gly₃ (15). For each force field, we have run long equilibrium simulations of Gly₃ under similar conditions of pH and temperature to those in the experiment. Table 2 compares the scalar couplings calculated from the long simulations of Gly₃ with experiment, for those couplings probing ϕ,ψ of the central glycine residue. We have also quantified the global agreement with experiment using a χ² parameter defined in a similar fashion to that used in previous work (23,34). The data show that overall, the force fields with the lowest χ² are those that favor β_PR: AMBER ff99SB, ff03^∗, and ff03w. More tellingly, the largest deviations from experiment for CHARMM22/CMAP are those for J-couplings probing the ψ-torsion angle of Gly-2. The Ramachandran free energy surfaces for Gly-2, shown in Fig. S4, confirm the lower free energy of α_L in CHARMM22/CMAP relative to the other force fields.

Table 2.

Comparison of experimental and calculated scalar couplings for the central residue of Gly₃

J-coupling	Torsion	Expt.	ff99SB	ff03∗	ff03w	C22/CMAP
3JHαC, res. 2	ϕ(2)	4.01	3.32	3.55	3.60	3.98
3JHNC, res. 2	ϕ(2)	1.10	1.17	0.68	0.71	0.78
3JHNHα, res. 2	ϕ(2)	5.89	5.60	6.09	6.04	6.16
3JNCα, res. 3	ψ(2)	9.05	8.23	8.24	8.38	7.50
1JNCα, res. 2	ψ(2)	12.17	11.44	11.40	11.52	11.12
χ2			1.51	1.27	0.92	2.63

Redesign to eliminate misfolding

Although direct evidence for or against the misfolded state by NMR would be quite challenging to obtain, we can redesign the hairpin to make this particular type of misfolding impossible. Because the misfolded state involves the adoption of a β_PR backbone conformation by Gly-7, an obvious question is whether this could be prevented by changing the sequence. In fact, glycine is the only residue for which this conformation is stable—which is particularly interesting because it occurs with the highest frequency at this position in the turn in the original sequence analysis (13). We chose to replace the glycine with the lysine present in the original GB1 hairpin at this position. Note that lysine also was frequently found in this position in the statistical analysis. Because the ff99SB force field showed the highest misfolded population in our simulations, we have used this to test the redesigned hairpin, running a further set of REMD folding simulations starting from the unfolded peptide.

Cluster analysis of the mutant simulations revealed that the redesign was successful, with no misfolded cluster present; this, however, was expected because the Lys-7 is not stable in the β_PR conformation. More importantly, we find that the most populated, folded cluster of the mutant is still very stable in the simulations (population ∼80% in the 300 K replica) as shown in Fig. 5 a. This can be at least partially explained by the formation of an additional salt-bridge between Asp-3 and Lys-7 (thereby stabilizing the turn) and the lack of a competing stable misfolded state.

Figure 5.

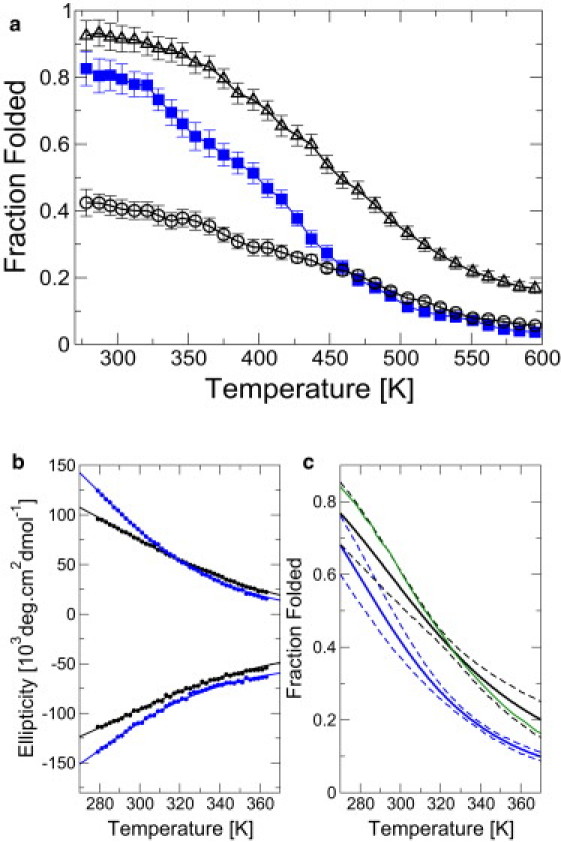
Melting curves for chignolin and G7K mutant. (a) Fraction folded from simulation for mutant (blue squares) and fraction folded (black circles) and folded+misfolded (black triangles) for original chignolin. (b) Melting curves from CD signal at 213 nm (negative values) and 229 nm (positive values), together with global fits to a two-state thermodynamic model. (c) Fraction folded as a function of temperature from fits in panel b; solid are maximum likelihood fraction, and broken lines give the 95% confidence bounds. (Green line) Published melting curve (13).

Experimental tests of redesigned hairpin

To confirm the finding that the alternative hairpin sequence was well folded and stable, we have performed NMR and CD spectroscopy measurements on the mutant. The NMR spectra of the mutant were well resolved, with chemical shift dispersion indicative of a folded structure (see Fig. S5). We have assigned H^α, C^α,C^β chemical shifts, and compared these with the shifts back-calculated from the 280 K replica using SPARTA+ in Fig. 6. We find excellent agreement with experiment, confirming that the structure is correctly folded: RMS deviations from the experimental H^α, C^α, and C^β chemical shifts are 0.28, 0.44, and 0.68 ppm, respectively.

Figure 6.

Chemical shifts for G7K mutant. (a) H^α and (b) C^α,C^β chemical shifts; (black lines and symbols) experimental data and (red symbols) data calculated from the 280 K replica of the above simulation, using SPARTA+ (32).

We have also measured the stability of both the original and mutant chignolin by following the CD signals at 213 and 229 nm as a function of temperature. Both show similar sigmoidal melting curves (Fig. 5); we have globally fitted the data at both wavelengths to a two-state thermodynamic model, obtaining thermodynamic parameters of ΔH_unfold = 20.6 (3.0) kJ/mol, ΔS_unfold = 66.9 (9.4) J/mol/K for chignolin and ΔH_unfold = 24.9 (2.1) kJ/mol, ΔS_unfold = 85.8 (6.2) J/mol/K for the mutant. (ΔC_p,unfold was fixed to zero as its inclusion in the fit did not result in a statistically significant improvement (13).) The published melting curve of chignolin obtained under similar solution conditions differs slightly from our data, but still lies within the error bounds (Fig. 5).

The results show that the experimentally inferred fraction of folded mutant or original chignolin is very similar at low temperature (see Fig. 5 c), confirming that the redesigned peptide is stable, although apparently slightly less so the original one. By contrast, our simulations with ff99SB suggest that the folded structure would be more stable with the G7K mutation; the discrepancy may be reconciled if the misfold makes a contribution to the observed CD signal that is similar to that from the native structure, in which case it would be counted as part of the folded population in experiment. Consistent with this hypothesis, the sum of the folded and misfolded populations in the original chignolin is somewhat higher than the folded population in the mutant (Fig. 5 a). Unfortunately, accurate estimation of CD signals from simulation is not feasible with the methods available at the time of writing, making a direct comparison difficult.

Concluding Remarks

We have observed in REMD simulations of chignolin that a misfolded state is populated in which Gly-7 is in a β_PR backbone conformation; the same species is formed with three different force fields, but not in a fourth force field. The existence of this species is consistent with the NMR data and, if anything, results in improved agreement with experiment, relative to the folded state populated in our simulations. This naturally raises the question of whether these two species could be directly distinguished experimentally, rather than inferred by comparison with ensemble averages. Most likely, this would be very challenging, because their interconversion likely occurs on the timescale of a few microseconds, much shorter than that on which the NMR signals are averaged. Probably the most promising avenue would be the use of infrared or optical spectroscopy, which are better able to resolve rapidly interconverting subpopulations. The observation of multiple relaxation times in temperature-jump experiments, for example, would provide at least indirect support for the misfolding hypothesis.

We have shown that the key residue controlling formation of the misfolded state is Gly-7, and indeed the relative bias of this residue for α_L and β_PR conformations plays a major role in determining the misfolded population. By assessing the parameters for glycine against an extensive set of J-coupling data for Gly₃, we have shown that those force fields that best reproduce the data are those favoring the β_PR over the α_L conformation. These results emphasize the importance of obtaining accurate glycine parameters for simulations of turns and hairpins, and suggest that the experimental data set for Gly₃ should be very useful for assessing and optimizing parameters.