Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Apr 23;2:376. doi: 10.1038/srep00376

Pressure-induced amorphous-to-amorphous configuration change in Ca-Al metallic glasses

H B Lou 1, Y K Fang 1, Q S Zeng 1, Y H Lu 1, X D Wang 1, Q P Cao 1, K Yang 2, X H Yu 2, L Zheng 3, Y D Zhao 3, W S Chu 3,4, T D Hu 3, Z Y Wu 3,4, R Ahuja 1,5,6, J Z Jiang 1,a
PMCID: PMC3332524  PMID: 22530094

Abstract

Pressure-induced amorphous-to-amorphous configuration changes in Ca-Al metallic glasses (MGs) were studied by performing in-situ room-temperature high-pressure x-ray diffraction up to about 40 GPa. Changes in compressibility at about 18 GPa, 15.5 GPa and 7.5 GPa during compression are detected in Ca80Al20, Ca72.7Al27.3, and Ca66.4Al33.6 MGs, respectively, whereas no clear change has been detected in the Ca50Al50 MG. The transfer of s electrons into d orbitals under pressure, reported for the pressure-induced phase transformations in pure polycrystalline Ca, is suggested to explain the observation of an amorphous-to-amorphous configuration change in this Ca-Al MG system. Results presented here show that the pressure induced amorphous-to-amorphous configuration is not limited to f electron-containing MGs.

The amorphous-to-amorphous configuration change (AACC) induced by pressure has been a topic of considerable research activities in several substances, e.g., ice, silicon, silica, and carbon1,2,3,4,5,6,7,8,9,10. Structural polyamorphic transitions from a low-density amorphous state to high-density amorphous state often result in an increase in atomic coordination. Such coordination increase, and thus polyamorphism, was thought to be impossible in non-directional, densely-packed metallic glasses (MGs), characterized by high coordination numbers, e.g., even up to 12–14 random nearest neighbors. Very recently, AACCs were surprisingly observed in Ce-containing MG systems11,12,13,14,15,16,17, in which the nature of AACCs is revealed due to 4f electron delocalization in Ce under high pressure14. Up to now no experimental evidence for AACCs has only been reported in non-f-electron-containing MGs. An interesting question has been raised: is AACC universal feature in metallic glasses or only in systems having f electrons? i.e., Can AACC occur in non-f-electron-containing MGs? Here we report pressure-induced amorphous-to-amorphous configuration changes in Ca-Al MGs detected by in-situ room-temperature high-pressure x-ray diffraction (XRD) measurements up to about 40 GPa. Changes in compressibility at about 18 GPa, 15.5 GPa and 7.5 GPa during compression have been detected in Ca80Al20, Ca72.7Al27.3, and Ca66.4Al33.6 MGs, respectively, whereas no clear change is detected in the Ca50Al50 MG. Possible mechanism for the AACC is presented and discussed. These results obtained here point out that the amorphous-to-amorphous configuration changes induced by pressure are not limited to f electron-containing MGs.

Results

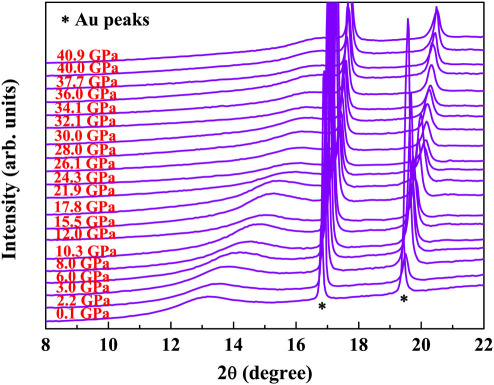
In-situ high-pressure XRD patterns for all samples studied were recorded at room temperature up to about 40 GPa. No crystallization reaction was detected in these samples in the studied pressure range whereas it was recently reported in the Ce-Al system18,19. Figure 1 shows selected high pressure x-ray diffraction patterns during compression for the Ca80Al20 MG alloy at room temperature. With increasing pressure, the main amorphous diffraction peak together with sharp Au peaks shift to high 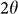Inline graphic, as expected for the densification effect of pressure. The sample retains fully amorphous structure up to about 40 GPa by judging from the smooth broad patterns. 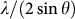The reverse main amorphous diffraction peak position, Inline graphic, correlates with the volume of glass having a power law function20,21,22, which can be conveniently used to reflect the relative volume (density) change as a function of pressure. 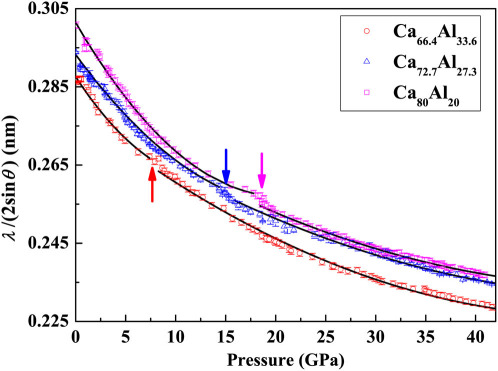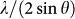Figure 2 shows the inverse main amorphous diffraction peak position, Inline graphic, of the Ca100−xAlx (x = 20, 27.3, and 33.6 at.%) MGs as a function of pressure during compression, which were estimated from the diffraction peak fitting using a Voigt line profile after subtracting baseline. It is found that at about 18 GPa, 15.5 GPa and 7.5 GPa, clear changes were detected for Ca80Al20, Ca72.7Al27.3, and Ca66.4Al33.6 MGs, respectively, whereas no clear change was detected for the Ca50Al50 MG. Amorphous-to-amorphous configuration changes occur in Ca80Al20, Ca72.7Al27.3, and Ca66.4Al33.6 MGs during compression. During pressure releases, it is found that the transformation is reversible with hysteresis. To further support this scenario, we carried out the following considerations.

Figure 1. In-situ high pressure x-ray diffraction patterns of the Ca80Al20 MG during compression at room temperature from 0.1 to 40.9 GPa.

Figure 1

Open in a new tab

The position of the broad amorphous peak shifts to higher angles with increasing pressure. Au peaks as pressure calibrant are marked.

Figure 2. The parameter, 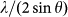Inline graphic, of the main amorphous peak, which is related to the reduced volume of the sample V(P)/V(0), as a function of pressure for Ca100−xAlx (x = 20, 27.3, and 33.6 at.%) MGs.

Figure 2

Open in a new tab

Transitions are marked by arrows. Error bars for experimental data are given and some are smaller than the symbol size. The solid lines are guides to the eye.

Discussion

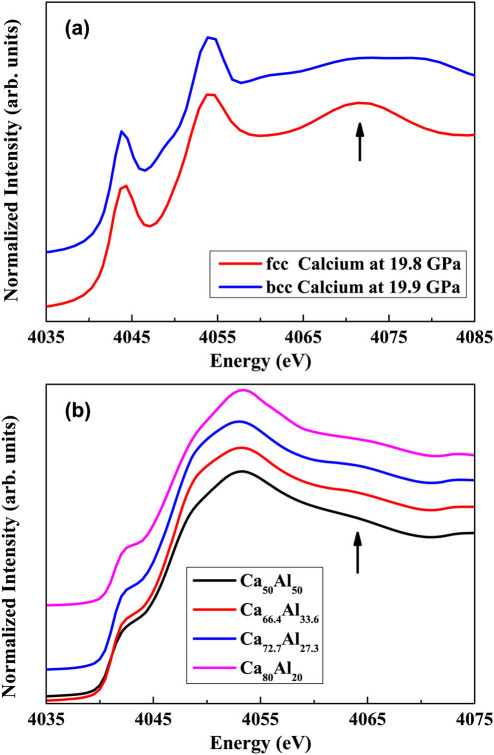
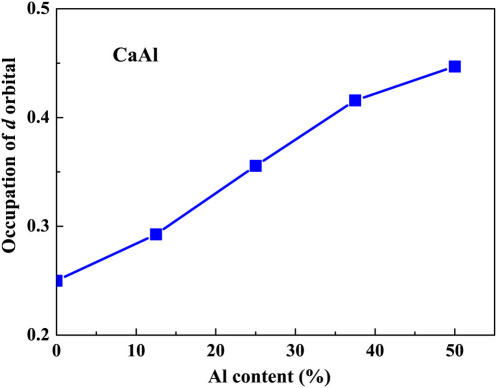
To uncover the change detected in Fig. 2, it might be useful to revisit the pure polycrystalline Ca. It was reported that for a pure polycrystalline Ca at ambient temperature, a face center cubic (fcc)-to-body center cubic (bcc) phase transition was detected at 19.8 GPa during compression accompanied by a volume change of about 2–3%23,24,25,26,27,28,29,30, which is much smaller than about 15% for pure Ce14. This transition was strongly linked with the transfer of s electrons into d orbitals of Ca under pressure26,28. We further performed both fcc- and bcc-Ca K-edge x-ray absorption near edge structure (XANES) calculations at 19.8 GPa and 19.9 GPa, respectively, as shown in Fig. 3a. By comparing XANES curves of fcc-Ca with bcc-Ca, the striking feature detected is the intensity change of the peak (4.07 keV) at around 15 eV above the main peak during the transition. We attempted to record XANES data for both Ca and Al edges for our Ca-Al MGs under pressures. However, due to extreme experimental difficulties, e.g., high absorption of low edge-energy of both Ca and Al, experimental XANES data for all studied Ca-Al MGs under pressure were not obtained. On the other hand, we do obtain good Ca K-edge XANES data for our studied Ca100−xAlx (x = 20, 27.3, 33.6 and 50 at.%) MGs at ambient pressure, as shown in Fig. 3b. Although the Ca K-edge XANES curves for Ca100−xAlx (x = 20, 27.3, 33.6 and 50 at.%) MGs differ from that for pure polycrystalline Ca, one similar feature observed is that about 15 eV above main peak a hump is detected for all studied Ca-Al MGs. For the Ca50Al50 MG, relatively speaking, the intensity of this hump is obvious low as compared with the other samples. This is also confirmed by further calculated Ca K-edge XANES data using FEFF code for the Ca13Al14 and Ca8Al3 alloys at ambient pressure (see Supplementary Fig. S1 online). To shed light on the Al effect on the charge transfer from s and/or p orbitals to d orbitals of Ca, we performed first-principles calculations based on density functional theory (DFT) for electronic structures of Ca-Al alloy. We found that Ca d orbitals dominate around the Fermi level even at high Al concentration up to 50%, although the character of d orbitals is reduced when Al concentration increases. Al atoms provide more electrons occupying d orbitals of Ca in the dilute model as showed in Fig. 4. In the pure fcc-Ca system, the occupation of d orbitals is only 0.25 and it increases to 0.29, 0.36 and 0.45 when the concentration of Al is 12.5 at.%, 25 at.% and 50 at.%, respectively.

Figure 3. Calculated and experimental data of Ca K-edge XANES for pure Calcium and CaAl metallic glasses respectively.

Figure 3

Open in a new tab

(a) K-edge XANES spectra for pure polycrystalline fcc-Ca (at 19.8 GPa) and bcc-Ca (at 19.9 GPa) as obtained by calculations in the framework of the multiple-scattering (MS) theory using the FEFF 8.2 code. Lattice parameters for both fcc- and bcc-Ca phases are from Ref.23 (b) Ca K-edge x-ray absorption near edge structure experimental curves for Ca100−xAlx (x = 20, 27.3, 33.6 and 50 at.%) MGs at ambient pressure.

Figure 4. Electrons occupying d orbitals of Ca in the dilute mode for the Ca-Al binary system as a function of Al content obtained from first-principles calculations.

Figure 4

Open in a new tab

The occupation of d orbitals of Ca increases from 0.25 in pure fcc-Ca to 0.45 when Al concentration is 50%.

Based on all considerations mentioned above, we suggest that the role of Al in binary Ca-Al alloys could be treated as “chemical pressure” to Ca, which promotes the transfer from s and p orbitals to d orbitals of Ca, explaining the experimental fact of lowering the AACC transition pressure from 19.8 GPa, 18 GPa, 15.5 GPa to 7.5 GPa as Al content increases from 0 at.%, 20 at.%, 27.3 at.% to 33.6 at.%, respectively. A similar role of “chemical pressure” was also reported in the literatures31,32,33,34,35. For the Ca50Al50 MG, following the “chemical pressure” effect, AACC already occurs at ambient pressure because of high occupation of Ca d orbitals, in agreement with the experimental observation: no change during compression in the studied pressure range.

In conclusions, we reported amorphous-to-amorphous configuration changes induced by pressure in non-f-electron-containing Ca100−xAlx (x = 20, 27.3 and 33.6 at.%) metallic glasses, which were confirmed by in-situ room-temperature high-pressure x-ray diffraction up to about 40 GPa. By comparing with pure polycrystalline Ca, together with XANES data obtained from both experiments and theoretical calculations, one mechanism, i.e., the charge transfer of s and p orbitals to d orbitals of Ca under pressure, is suggested for the origin of the amorphous-to-amorphous configuration changes induced by pressure in these non-f-electron-containing Ca100−xAlx (x = 20, 27.3 and 33.6 at.%) metallic glasses. These results obtained clearly point out that the amorphous-to-amorphous configuration changes induced by pressure are not limited to f electron-containing metallic glasses. This will open a new vista which will trigger more theoretical and experimental investigations in this and many other MG systems.

Methods

Ca100−xAlx (x = 20, 27.3, 33.6 and 50 at.%) MG ribbons with a thickness of about 35 μm and a width of about 3 mm were prepared with the single-roller melt-spinning method. In-situ high-pressure angle-dispersive XRD experiments with a wavelength of 0.6884 Å and a focused beam size of about 5×5 μm2 were performed at the beamline 15U, Shanghai Synchrotron Radiation Facility (SSRF) in China. The Ca100−xAlx (x = 20, 27.3, 33.6 and 50 at.%) MGs were cut into about 40×40×35 μm3 chips, and then loaded into a Mao-type symmetric diamond anvil cell. The sample chamber was about 150 μm in diameter drilled in a T301 stainless steel gasket. Silicone oil was used as pressure-transmitting medium while for pressure calibration Au powders were dispersed inside. The pressure applied to the sample was calculated from the lattice constant of Au using the equation of state of Au36. The silicone oil as a pressure medium used in this work could remain hydrostatic up to about 15 GPa. The pressures when the anomalous changes detected in this work for Ca80Al20, Ca72.7Al27.3, and Ca66.4Al33.6 MGs were at about 18 GPa, 15.5 GPa and 7.5 GPa, respectively. The changes detected below and above 15 GPa indicate that these anomalous changes detected here are not strongly affected by the non-hydrostatic pressure caused by the pressure medium. Each XRD pattern was collected for about 5 seconds at a given pressure using a Mar-165 CCD detector and then integrated with the FIT2D program37. Ca K-edge XANES measurements for Ca100−xAlx (x = 20, 27.3, 33.6 and 50 at.%) MGs were carried out in vacuum at the beamline 4B7A, Beijing Synchrotron Radiation Facility in China.

Theoretical Ca K-edge XANES for fcc-Ca at 19.8 GPa, for bcc-Ca at 19.9 GPa, and for Ca13Al14 and Ca8Al3 alloys at ambient pressure were carried out in the framework of the multiple-scattering (MS) theory38,39 using the FEFF 8.2 code40. The cluster for the simulations was generated by the ATOMS package41 using their respective lattice parameters23,24. In calculations, the Hedin-Lundqvist exchange-correlation potential was chosen42. A cluster of 43 atoms (for fcc-Ca) and 27 atoms (for bcc-Ca) were used in all MS calculations to obtain accurate self-consistent field (SCF), and the full MS calculation converges using a cluster up to 6 Å. It should be mentioned that Ca atoms in Ca13Al14 and Ca8Al3 alloys occupy more than one site, i.e. 5 sites for Ca8Al3 and 16 sites for Ca13Al14. A XANES spectrum contains all local structural information of different sites of the absorbed atomic species. Therefore, in the calculation for both Ca13Al14 and Ca8Al3 alloys we calculated the XANES spectrum of each individual site and then did a weighted superposition of all occupied sites. First-principles calculations based on density functional theory (DFT) in generalized gradient approximation (GGA) with the Perdew-Burke-Ernzerhof (PBE) functional43 were used to optimize crystal structures and obtain ground-state properties. Self-consistent calculations were performed using a plane-wave basis set limited by a cutoff energy of 400 eV implemented in the Vienna ab initio simulation package (VASP). The projector augmented wave potentials44 and Monkhorst-Pack k-points sampling45 were employed. The convergence for the number of k points was tested to ensure that the total energy was converged within at least 0.01 eV/atom.

Author Contributions

JZJ designed research; HBL, YKF, QSZ, KY, XHY, LZ, YDZ, XDW, QPC performed experiments; HBL, LYH, WSC, ZYW, TDH, RA, JZJ analyzed data; JZJ wrote the paper.

Supplementary Material

Supplementary Information

Supplementary Information

srep00376-s1.pdf (104.2KB, pdf)

Acknowledgments

The authors would like to thank Shanghai Synchrotron Radiation Source, Hefei and Beijing Synchrotron Radiation facility for use of the synchrotron radiation facilities. Financial support from the National Key Basic Research Program of China (2012CB825700), the National Natural Science Foundation of China (Grants Nos. 50920105101, 51050110136, 51071141, 10979002 and 10904127), the Knowledge Innovation Program of the Chinese Academy of Sciences (KJCX2-YW-N42), the Ministry of Education of China, Zhejiang University-Helmholtz cooperation fund and the Department of Science and Technology of Zhejiang province is gratefully acknowledged. The magic supercomputer in Shanghai Supercomputer Center (SSC) is also acknowledged for supporting calculations.

References

  1. Mishima O., Calvert L. D. & Whalley E. ‘Melting Ice’ I at 77 K and 10 kbar: a new method of making amorphous solids. Nature 310, 393–395 (1984). [Google Scholar]
  2. Mishima O. Reversible first-order transition between two H2O amorphs at ~0.2 GPa and ~135 K. J Chem Phys 100, 5910–5912 (1994). [Google Scholar]
  3. Stanley H. E. & Mishima O. The relationship between liquid, supercooled and glassy water. Nature 396, 329–335 (1998). [Google Scholar]
  4. Mishima O. Liquid-liquid critical point in heavy water. Phys Rev Lett 85, 334–336 (2000). [DOI] [PubMed] [Google Scholar]
  5. Poole P. H., Sciortino F., Essmann U. & Stanley H. E. Phase-Behavior of Metastable Water. Nature 360, 324–328 (1992). [Google Scholar]
  6. Kingma K. J., Meade C., Hemley R. J., Mao H. K. & Veblen D. R. Microstructural Observations of Alpha-Quartz Amorphization. Science 259, 666–669 (1993). [Google Scholar]
  7. Lacks D. J. First-order amorphous-amorphous transformation in silica. Phys Rev Lett 84, 4629–4632 (2000). [DOI] [PubMed] [Google Scholar]
  8. Sastry S. & Angell C. A. Liquid-liquid phase transition in supercooled silicon. Nat Mater 2, 739–743 (2003). [DOI] [PubMed] [Google Scholar]
  9. Vanthiel M. & Ree F. H. High-Pressure Liquid-Liquid Phase-Change in Carbon. Phys Rev B 48, 3591–3599 (1993). [DOI] [PubMed] [Google Scholar]
  10. Loerting T., Brazhkin V. V. & Morishita T. in Advances in Chemical Physics, Vol 143 (ed Rice, S. A.) 29–82 (Wiley-Blackwell, 2009). [Google Scholar]
  11. Zeng Q. S. et al. Anomalous compression behavior in lanthanum/cerium-based metallic glass under high pressure. P Natl Acad Sci USA 104, 13565–13568 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Sheng H. W. et al. Polyamorphism in a metallic glass. Nat Mater 6, 192–197 (2007). [DOI] [PubMed] [Google Scholar]
  13. Yavari A. R. The changing faces of disorder. Nat Mater 6, 181–182 (2007). [DOI] [PubMed] [Google Scholar]
  14. Zeng Q. S. et al. Origin of Pressure-Induced Polyamorphism in Ce75Al25 Metallic Glass. Phys Rev Lett 104, 105702 (2010). [DOI] [PubMed] [Google Scholar]
  15. Zeng Q. S. et al. Properties of polyamorphous Ce75Al25 metallic glasses. Phys Rev B 82, 054111 (2010). [Google Scholar]
  16. Zeng Q. S. et al. Low-density to high-density transition in Ce75Al23Si2 metallic glass. J Phys-Condens Mat 22, 375404 (2010). [DOI] [PubMed] [Google Scholar]
  17. Zeng Q. S. et al. Low temperature transport properties of Ce-Al metallic glasses. J Appl Phys 109, 113716 (2011). [Google Scholar]
  18. Zeng Q. S. et al. Substitutional alloy of Ce and Al. P Natl Acad Sci USA 106, 2515–2518 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Zeng Q. S. et al. Long-Range Topological Order in Metallic Glass. Science 332, 1404–1406 (2011). [DOI] [PubMed] [Google Scholar]
  20. Jiang J. Z., Roseker W., Sikorski M., Cao Q. P. & Xu F. Pressure effect of glass transition temperature in Zr46.8Ti8.2Cu7.5Ni10Be27.5 bulk metallic glass. Appl Phys Lett 84, 1871–1873 (2004). [Google Scholar]
  21. Yavari A. R. et al. Excess free volume in metallic glasses measured by X-ray diffraction. Acta Mater 53, 1611–1619 (2005). [Google Scholar]
  22. Ma D., Stoica A. D. & Wang X. L. Power-law scaling and fractal nature of medium-range order in metallic glasses. Nat Mater 8, 30–34 (2009). [DOI] [PubMed] [Google Scholar]
  23. Gu Q. F., Krauss G., Grin Y. & Steurer W. Experimental confirmation of the stability and chemical bonding analysis of the high-pressure phases Ca-I, II, and III at pressures up to 52 GPa. Phys Rev B 79, 134121 (2009). [Google Scholar]
  24. Huang B. Q. & Corbett J. D. Two new binary calcium-aluminum compounds: Ca13Al14, with a novel two-dimensional aluminum network, and Ca8Al3, an Fe3Al-type analogue. Inorg. Chem. 37, 5827–5833 (1998). [Google Scholar]
  25. Olijnyk H. & Holzapfel W. B. Phase-Transitions in Alkaline-Earth Metals under Pressure. Phys Lett A 100, 191–194 (1984). [Google Scholar]
  26. Ahuja R., Eriksson O., Wills J. M. & Johansson B. Theoretical Confirmation of the High-Pressure Simple Cubic Phase in Calcium. Phys Rev Lett 75, 3473–3476 (1995). [DOI] [PubMed] [Google Scholar]
  27. Yabuuchi T., Nakamoto Y., Shimizu K. & Kikegawa T. New high-pressure phase of calcium. J Phys Soc Jpn 74, 2391–2392 (2005). [Google Scholar]
  28. Maksimov E. G., Magnitskaya M. V. & Fortov V. E. Non-simple behavior of simple metals at high pressure. Phys. Usp. 48, 761–780 (2005). [Google Scholar]
  29. Oganov A. et al. Exotic behavior and crystal structures of calcium under pressure. P Natl Acad Sci USA 107, 7646–7651 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Teweldeberhan A. M. Dobois J. L. & Bonev S. A. High-Pressure Phases of Calcium: Density- Functional Theory and Diffusion Quantum Monte Carlo Approach. Phys Rev Lett 105, 235503 (2010). [DOI] [PubMed] [Google Scholar]
  31. Maroni B. et al. Pressure Effects in the Isoelectronic REFe0.85Ir0.15AsO System. J Am Chem Soc 133, 3252–3255 (2011). [DOI] [PubMed] [Google Scholar]
  32. Sergeenkov S. Influence of chemical pressure effects on nonlinear thermal conductivity of intrinsically granular superconductors. J Appl Phys 102, 066104 (2007). [Google Scholar]
  33. Lue C. S., Liu R. F., Song M. Y., Wu K. K. & Kuo Y. K. Chemical pressure effect on the transport and electronic band structure of Fe2V1−xNbxAl. Phys Rev B 78, 165117 (2008). [Google Scholar]
  34. Ru N. et al. Effect of chemical pressure on the charge density wave transition in rare-earth tritellurides RTe3. Phys Rev B 77, 035114 (2008). [Google Scholar]
  35. Horii T. et al. Chemical pressure effect in the heavy fermion compound Ce1−yLay(Ru0.85Rh0.15)2Si2. J Magn Magn Mater 310, 313–315 (2007). [Google Scholar]
  36. Anderson O. L., Isaak D. G. & Yamamoto S. Anharmonicity and the Equation of State for Gold. J Appl Phys 65, 1534–1543 (1989). [Google Scholar]
  37. Hammersley A. P., Svensson S. O., Hanfland M., Fitch A. N. & Hausermann D. Two-dimensional detector software: From real detector to idealised image or two-theta scan. High Pressure Res 14, 235–248 (1996). [Google Scholar]
  38. Lee P. A. & Pendry J. B. Theory of Extended X-Ray Absorption Fine-Structure. Phys Rev B 11, 2795–2811 (1975). [Google Scholar]
  39. Natoli C. R., Benfatto M., Brouder C., Lopez M. F. R. & Foulis D. L. Multichannel Multiple-Scattering Theory with General Potentials. Phys Rev B 42, 1944–1968 (1990). [DOI] [PubMed] [Google Scholar]
  40. Ankudinov A. L., Ravel B., Rehr J. J. & Conradson S. D. Real-space multiple-scattering calculation and interpretation of x-ray-absorption near-edge structure. Phys Rev B 58, 7565–7576 (1998). [Google Scholar]
  41. Ravel B. ATOMS: crystallography for the X-ray absorption spectroscopist. J Synchrotron Radiat 8, 314–316 (2001). [DOI] [PubMed] [Google Scholar]
  42. Tyson T. A., Hodgson K. O., Natoli C. R. & Benfatto M. General Multiple-Scattering Scheme for the Computation and Interpretation of X-Ray-Absorption Fine-Structure in Atomic Clusters with Applications to SF6, GeCl4, and Br2 Molecules. Phys Rev B 46, 5997–6019 (1992). [DOI] [PubMed] [Google Scholar]
  43. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  44. Blochl P. E. Projector Augmented-Wave Method. Phys Rev B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
  45. Monkhorst H. J. & Pack J. D. Special Points for Brillouin-Zone Integrations. Phys Rev B 13, 5188–5192 (1976). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep00376-s1.pdf (104.2KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES