Computing an organism

The “social amoebae” of species Dictyostelium discoideum roam individually through the soil as long as their bacterial food is present. The social phase for these cellular slime molds begins when the food supply is exhausted. After some hours, the assemblage of amoebae aggregate into several large groups, each of which forms a worm-like slug that propels itself toward heat and light. This brings the slug to the surface of the soil, where it executes a sophisticated internal ballet that eventually results in a fruiting body, an elegant stalk, formed by dead cellulose-walled cells, atop of which perches a bag of spores. The whole structure is about a millimeter high. Now in this issue of PNAS Marée and Hogeweg (1) have provided a computer simulation of the frog-prince transformation of slug into fruiting body.

Scientists have been intensively studying D. discoideum for decades, as a model system in developmental biology. (Dictyostelium turned up 47,500 entries in a Google search.) A tremendous boost to these studies occurred when it was discovered that the initial aggregation is induced by the pulsatile secretion of a chemoattractant that turned out to be none other than cAMP, one of a few major second messengers in mammalian physiology (2). Dictyostelium has become a “hydrogen atom” paradigm in development, for instead of hundreds of cell types as in humans, the slime mold has only two (principal) types, stalk and spore, in a ratio that is controlled over a wide range of sizes. What causes aggregation and then slug formation and motion? How are the proportions of differentiated cells controlled? And how is the morphogenetic movement organized so that it provides the appropriate geometric structure of spore-on-stalk?

Marée and Hogeweg have provided a computer simulation of the frog-prince transformation of slug into fruiting body.

Evelyn Keller and I used to think that we wrote the first theoretical paper on Dictyostelium in 1970 (3) when we formulated and analyzed equations to show how aggregation might be regarded as an instability in a uniform layer of cAMP-secreting chemotactic cells. It turns out that more than 20 years earlier a paper by the celebrated mathematician Marston Morse (4) mentioned slime molds as an example of “equilibria in nature” (the title of the paper) that could be qualitatively described by what is now known as Morse theory.

Many theoretical papers have been written on various aspects of slime mold behavior in the last three decades. Examples are major recent studies of aggregation (5) and the regulation of stalk-spore proportions (6). Earlier simulation studies by the authors and their collaborators treated slug formation and migration (7–9). The work of Marée and Hogeweg (1) is a culmination of all this effort in two senses. It deals with the so-called “culmination phase” of Dictyostelium morphogenesis and it caps years of intensive effort, for the first time offering a theoretical model that can reproduce all of the major features of the structure formation.

A simulation of a developing organism must represent the motion of a large number of interacting cells. Like other materials, cells respect the laws of physics. Each cell is not only driven by external forces but also generates internal forces by assembling and disassembling an ephemeral cytoskeleton under the direction of various controlling chemicals. A further complication is that although cell shape depends on the resultant of all of the forces, the forces themselves depend on the shape. Impressive progress has been made in coping with much of this complexity. An example is afforded by Alt and Dembo's (10) two-phase model of cytoplasmic dynamics even a simple version of which reproduces such features of cell motility as periodic ruffle formation, protrusion-retraction cycles, and centripetal flow.

Marée and Hogeweg (1) wisely avoided detailed force calculation in their broad-brush dynamic portrait of D. discoideum culmination. One major step was replacing force balancing by an alternative approximate description wherein a type of potential energy was minimized. To see what this involves, recall that one way to describe how and why a ball rolls down a mountain into a valley is to account for the gravitational forces that cause the descent. Often preferable is the alternative explanation that the ball moves to minimize its height and hence its potential energy.

Here, too, an energy can be defined, one that limns in broad strokes the influences that induce cell motion. Two such influences are differential cell adhesion and chemotaxis toward relatively high cAMP concentrations. Promotion of relatively strong cell-cell contacts (which minimize the relevant energy function) tends to yield clumps of like cells. This tendency can be overridden by the propensity of cells to move toward higher cAMP concentrations. (Motion resulting from this propensity is not simple, because it turns out that the cells are exposed to traveling waves of cAMP, with their moving maxima and minima.)

The Marée-Hogeweg simulations save computer time by considering only a two-dimensional cross section of the fruiting body. An individual amoeboid cell is represented by a blob formed of about 30 squares. [Early simulations represented a cell by a point, but this appears to be an oversimplification. The connected blob representation is a grandchild of the Potts generalization of the Ising model, fathered by the physicists Glazier and Graner (11).] Each simulated cell has a target volume; deviation from this volume is penalized by an increase in energy. Cells continually check whether a shift of their boundaries will decrease the overall energy. If the decrease is large enough then the new position is accepted. A smaller decrease makes the motion likely but not certain (the simulations are stochastic). Cells thus move in such a way as to increase cAMP concentration in their environment while adhering with different strengths to the various cell types. As it moves, cell A “pushes” cell B when the boundary of A fluctuates to invade what was previously the territory of cell B (see Fig. 1).

Figure 1.

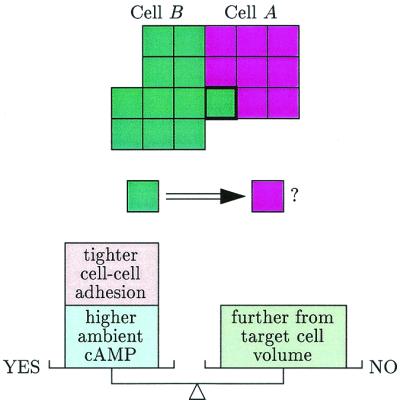
Representation of simulated cell movement. The heavily outlined square of cell A is more likely to switch to be part of cell B (corresponding to a “pushing” of B by A) if the square's “energy” is decreased by a combination of factors.

As mentioned, simulating energy-diminishing boundary fluctuations permits side-stepping the more accurate but dauntingly complex approach via differential equations. But differential equations enter the simulations when the diffusion and reaction of secreted cAMP is accounted for. Here, too, a simplification is made—the “true” cAMP dynamics is replaced by the FitzHugh-Nagumo caricature of excitability borrowed from neurobiology (14, 15).

Can one trust simulations that ignore much biological detail? Certainly the omission of known phenomenology is no a priori reason to scorn a model or simulation. For example, classical Newtonian models, bare of relativistic or quantum effects, are universally accepted to offer the right approach to problems ranging from bacterial swimming to hurricane prediction. The art is to fulfill the dictum attributed to Einstein, “simplify as much as possible but no further.”

The robustness peculiar to biology plays an interesting dual role in the evaluation of relatively simple models. On the one hand, robustness implies that variations in detail are without major significance. Such variations are unlikely to alter the essence of phenomena that are essential for survival—such as fruiting body construction in slime molds. On the other hand, this very robustness implies that a model that flawlessly reconstructs much phenomenology might well be seriously wrong in the underlying detail that it assumes.

Concerning this second point, however, new developments have indicated that the picture is more subtle and more interesting than has been thought. In their study of developing segment polarity networks, von Dassow et al. (12) found that their 50-parameter model gene networks were indeed remarkably robust when and only when their original mathematical translation of known interactions between relevant genes was supplemented by two crucial additions. E. Shochat, S. Stemmer, and I (unpublished work) found a similar phenomenon in an unpublished large-scale model of hematopoeietic cell kinetics. In essence, replacing a parameter by a small model (compare ref. 13) very considerably enlarged the range of other parameter choices that could lead to a fit with a number of kinetic results. It appears that a biological model enjoys robustness only if it is “correct” in certain essential features.

Years ago the slime mold biologist Maurice Sussman said to me that the goal of theoretical biologists should be to “compute an organism.” This has now been done by Marée and Hogeweg (1). The necessity of refining and generalizing the calculations and the importance of linking changing gene expression with cell movement means that this achievement is not the beginning of the end but rather the end of the beginning.