Biomolecular processes in the fast lane

Most processes in biology occur relatively slowly; even molecular level ones such as isomerization or ligand binding or enzyme turnovers generally occur on time scales between microseconds and seconds. There are a few well-characterized ultrafast events in nature—these include rhodopsin isomerization, light harvesting in the antenna complex of photosynthetic structures, electron transfer in photosynthetic reaction centers, and certain interprotein electron transfers. These ultrafast behaviors occur in the picosecond and subpicosecond range and have become featured problems for understanding ultrafast biological processes.

The functional environment of most molecular biological structures is highly anisotropic; metal centers in metalloproteins, binding sites in nucleic acid grooves, “hot spots” on the outer surface of proteins, and entrance vestibules to biological channels all exist in states of constrained equilibrium. Effects such as membrane binding, directed solvation, cofactor requirements, steric direction, or weak noncovalent interactions including hydrogen bonding or hydrophobic interactions can modify the effective local potential from that experienced by the free molecule. These environmental directors can entirely modify molecular processes (both ground state and photoexcited) and can do so dynamically. Reorganization and relaxation dynamics can probe this external control modality and thereby lead to better visualization and understanding of molecular biodynamical processes and structural control.

Two articles in a recent issue of PNAS address picosecond dynamics in bioconjugate molecular structures. The first involves the dynamics of excited-state small molecule ligands interacting with a protein, and the second is devoted to charge transfer between bases in DNA stacks. In both, femtosecond spectroscopic techniques are used to deduce the picosecond scale evolution of the photoexcited state.

The paper by Zhong et al. (1) is devoted to the dynamics of a bound fluorescent bicyclic molecule, 2-(2′-hydroxyphenyl)-4-methyloxazole (HMPO). Pump/probe two-photon experiments are used to follow the excited dynamics of HMPO in four different external situations: homogeneous dioxane solution, the binding cleft of a cyclodextrin, within a micelle, and complexed to a binding region of human serum albumin. After photoexcitation, the decay kinetics are monitored by observation of the fluorescence and by fluorescence up-conversion. Polarization anisotropy is measured to deduce both the overall dynamics and the rotational decay of the photoexcited state.

There are striking observations in the paper by Zhong et al.: the overall decay lifetime for fluorescence changes from roughly 45 ps in dioxane to 97 ps bound to the micelle, to 154 ps bound within the cyclodextrin, to nanoseconds bound within the human serum albumin (HSA). Similarly, rotational relaxation is almost entirely absent for the HSA-bound ligand, for up to 500 ps. The interpretation offered by the authors is straightforward: the “locking in” of the ligand by the protein is strong enough to stop molecular reorientation. Fast intramolecular stretching vibrations mediate proton transfer from the photoexcited initial state to the final state, which proceeds downhill along the potential energy surface. This stretching occurs on roughly a 200-fs time scale, unimpeded by the environment. On the other hand, the twisting motion of the ligand species drastically slows within the hydrophobic pocket of the protein.

These observations are consistent with extensive previous work in related systems. The notion that photoexcited dynamics occurs not along one single reaction coordinate, but on a potential energy surface consisting of at least two important modes, one high frequency and one low frequency, was put forward by Hopfield and Agmon (2) to explain the rebinding of carbon monoxide photodissociated from myoglobin, whose observation by Frauenfelder et al. (3) was a signal step forward in enzyme dynamics and ligand binding. Analysis of similar two-dimensional problems, involving generalization of the Kramers approach (4) and study of short-time transients, has produced an extensive theory literature on two-dimensional dynamics in glasses and protein systems (3, 5, 6).

Glassy and protein dynamics often show progress along two degrees of freedom, one far more sensitive to the environment than the other. In the 2-(2′-hydroxyphenyl)-4-methyloxazole, for example, Fig. 1 shows the planar ground state structure as well as the structure twisted around the interring C—C bond. Intramolecular twists and reorientations, which generally occur at low frequencies and involve large-scale excursions of substantial parts of the molecule, are expected to be more sensitive to the solvent environment than fast stretching modes. Even in the quite different process of intramolecular electron transfer large-scale, low-frequency motions like twisting will modify the electron transfer mixing matrix element, whereas high-frequency intramolecular stretch vibrations (whose displacements are smaller) generally do not lead to substantial changes in the mixing—this effectively modifies the Condon approximation.

Figure 1.

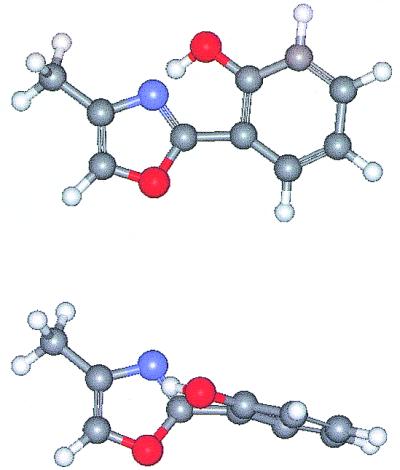
The structures of the 2-(2′-hydroxyphenyl)-4-methyloxazole ligand in the planar (Upper) and twisted (Lower) geometries. The red atoms are oxygens, the black carbon, the blue nitrogen. A photoexcited proton transfer occurs from the OH to the heterocyclic N. The twisting degree of freedom is strongly impeded by the protein environment, whereas the stretching that facilitates proton transfer is not.

Curtailed low-frequency twisting motion on the excited state, and its control by the environment, are consistent with extensive previous work; nevertheless, the direct demonstration by the difference between binding in the human serum albumin cavities and in the micelles and cyclodextrins demonstrates the effectiveness of hydrophobic interactions within protein crevices for “freezing in” molecular motions. This binding has important implications for molecular transformations in enzymatic systems: by controlling the potential energy surface evolution, protein binding can direct energy flow into productive, as opposed to useless, motions.

 By controlling the potential energy surface evolution, protein binding can direct energy flow into productive, as opposed to useless, motions.

DNA electron transfer is of interest because of possible repair and damage caused by radicals in the DNA strand. The paper by Wan et al. (7) discusses ultrafast fluorescence quenching mechanisms of photo-excited pi-bases within the DNA stack and interprets the results in terms of mechanistic models.

DNA, in addition to being the fundamental information carrier of nature, is a remarkable structural template (8). The capability to replace the individual base pairs with the other combination (AT for GC) or with different pi-bases has led to extensive investigations into modifications of both structural and biological properties. These substitutions become quite relevant when investigating the possibility of electron transport through DNA stacks; this has been of interest in the scientific community for nearly 40 years (9). The pi-interactions between the stacked based pairs, separated by a distance of roughly 3.4 Å, suggest that electron transport among the base pairs might be facile.

Such transport would hardly be unanticipated and has been long known in artificial structures. Very similar transport behavior has been seen in such molecular crystals as stacked phthalocyanines. There (10) electron transfer occurs among stacked planar pi-structures, separated by roughly 3.3 Å. The thermal charge transport in phthalocyanines is caused by localized charges undergoing polaronic hopping. With DNA, effects such as dehydration that causes deviation from the B-form structure (11), motion of the cations causing gating-type effects (U. Landman, personal communication), or major structural disruption caused by the spacial demand of unnatural base insertion can introduce complications. In experiments carefully designed to circumvent such perturbations, one would expect (12) at least two mechanisms for long-range electron transfer, a coherent mechanism corresponding to superexchange, and an injection mechanism corresponding to inelastic transport through the bridges between donor and acceptor sites.

Precisely such mechanisms were observed for exciton transport in organic crystals nearly 30 years ago (13).

Experimentally, evidence has been found for the two different mechanisms, both in charge transport in thermalized charge systems and in photoinduced electron transfer from a photoexcited initial state (14). Wan et al. (7) suggest three schemes for electrons to leave the photoexcited donor (in this case, both donor and acceptor are pi-base pairs): schemes 1a and 1b in their paper involve charge (hole or electron) injection into the bridge, whereas scheme 2 is coherent hole tunneling from photoexcited donor base to acceptor. There is no extensive published evidence for the electron transfer mechanism. Both the hole transfer mechanism and the superexchange scheme have been previously demonstrated in measurements of hole hopping in thermalized, charged DNA structures (15–17). These have shown that superexchange type transfer will occur when the gap between the energy of the initial photoexcited state D* and the charged bridge intermediate is large.

Theoretical models at various levels of sophistication have shown the transition from superexchange (coherent) electron transfer to hole injection (incoherent) electron transport between donor and acceptor species (18, 19). Indeed, direct comparison between experimental data and computational results has shown (20, 21) that for long-range charge transfer in truly aperiodic DNA structures, both injection schemes and superexchange type steps are required.

Superexchange itself is inadequate for sufficiently long-range transfer, simply because one expects the rate constant for transfer, k, to vary with distance as k = k₀ exp(−βR), with β a characteristic inverse decay length and R the centroid distance between donor and acceptor. This behavior follows from simple models, has been broadly observed in molecular structures, and will dominate for short distances and large energy gaps. For very long bridges, however, this (coherent, rapid) transfer process will be inefficient. Under those conditions, one expects injection mechanisms, whose decay length will generally (22) scale as 1/(a₁ + a₂R), to dominate.

The measurements of Wan et al. (7), done on duplex DNA structures that are expected to be minimally perturbed, strongly support previous work showing the two mechanisms (coherent superexchange and incoherent injection). It seems quite clear that two dominant mechanisms for D* decay have indeed been observed and that their characteristic time and length dependence agree with simple theoretical models.

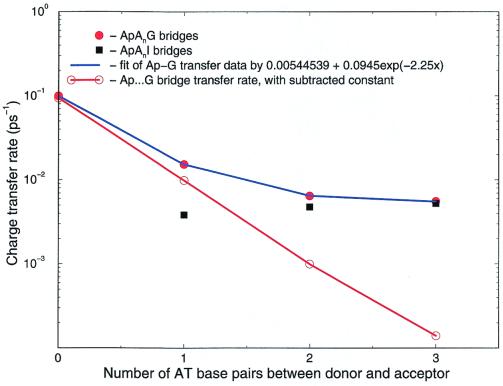
Fig. 2 shows the current data obtained from the decay of D*. The blue line shows the raw data for fluorescence decay. When the incoherent contribution is subtracted, the red line is obtained, showing (coherent) superexchange, decaying as exp{−βR}. The black dots show the injection behavior—that rate increases as short bridges are lengthened, because the energy levels for charge injection drop. For long bridges, the coherent “molecular wire” behavior will be absent in DNA, because of its characteristic exponential decay; only the hopping injection behavior will remain.

Figure 2.

Data observed from fluorescence decay of the photoexcited Ap base. The raw data are the black and red dots, the data corrected for incoherent hopping lie along the red line. The black dots show injection (incoherent) loss of the initial population, whereas the red line demonstrates coherent superexchange transfer.

One attractive way to understand the interchange between the two mechanisms is in terms of the tunnel time concept originally suggested by Landauer and Buttiker. Simple analysis suggests (23) that for long-range transfer mediated by several intermediate sites, the characteristic tunneling time for coherent transfer will be

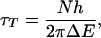where N, h, and ΔE are, respectively, the number of sites in the chain, Planck's constant, and the energy gap between the initial (photoexcited) donor and a charged localized bridge state. When this time scale is much shorter than a vibration period, one expects coherent behavior; conversely, incoherent hopping will occur when the two time scales become comparable. Both behaviors have now been observed in DNA.