Universal conditions for exact path integration in neural systems

Abstract

Animals are capable of navigation even in the absence of prominent landmark cues. This behavioral demonstration of path integration is supported by the discovery of place cells and other neurons that show path-invariant response properties even in the dark. That is, under suitable conditions, the activity of these neurons depends primarily on the spatial location of the animal regardless of which trajectory it followed to reach that position. Although many models of path integration have been proposed, no known single theoretical framework can formally accommodate their diverse computational mechanisms. Here we derive a set of necessary and sufficient conditions for a general class of systems that performs exact path integration. These conditions include multiplicative modulation by velocity inputs and a path-invariance condition that limits the structure of connections in the underlying neural network. In particular, for a linear system to satisfy the path-invariance condition, the effective synaptic weight matrices under different velocities must commute. Our theory subsumes several existing exact path integration models as special cases. We use entorhinal grid cells as an example to demonstrate that our framework can provide useful guidance for finding unexpected solutions to the path integration problem. This framework may help constrain future experimental and modeling studies pertaining to a broad class of neural integration systems.

Even without allothetic or environmental cues, animals are capable of finding their way home (1, 2), a process known as path integration or dead reckoning. This “integrative process” (3), whereby an internal representation of position is updated by incoming inertial or self-motion cues, was hypothesized over a century ago by Darwin (4) and Murphy (3). More recently, potential neural correlates of path integration have been discovered. For example, cells in brain regions associated with the Papez circuit can signal the heading direction of an animal (5, 6); grid cells in the entorhinal cortex presumably integrate this information and other self-motion cues to form a periodic spatial code (7–9); and, downstream in the hippocampus, place cells exhibit a sparser location code (10, 11).

Many computational models of path integration have been proposed. For instance, two leading classes of models of grid cells are continuous attractor networks (12–14) and oscillatory interference models (15–20). These diverse models seemingly describe a diverse class of systems; however, deeper computational principles may exist that unify the different cases of neural integration. Here we attempt to identify a general principle of path integration by starting with the exact requirement of invariance to movement trajectory in an arbitrary number of dimensions. This general approach allows us to derive a set of necessary and sufficient conditions for path integration and, for linear systems, to find explicit solutions. This framework can help unify existing models of path integration and also guide the search for unexplored solutions. We demonstrate this utility by modeling various path integration systems such as grid cells, and we show that several existing path integration models adhere to our framework.

Model

General System.

We start with the most general case by considering movement in a D-dimensional space with location coordinates described by 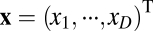and movement velocity given by 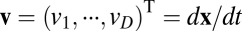, where T indicates transpose. For example, we have 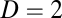for location of a rat on the floor of a room. We use an N-dimensional column vector 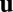to describe the state or activity of a network with N neurons. We assume that the network obeys a generic dynamical equation of the form 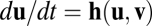, where the function 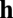does not depend explicitly on location because here we focus only on velocity input and ignore any landmark-based cues. As the location changes in time, the activity 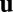can be solved as a function of time from the dynamical equation. We say that the system performs exact path integration if, starting from fixed initial conditions, the activity 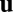at a final location depends only on that location, irrespective of the movement trajectory leading to that position (Fig. 1A). In other words, now the activity 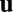is path invariant and can be regarded as an implicit function of location . The path invariance implies that 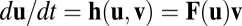for some function 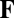. That is, the dynamical equation can be written as

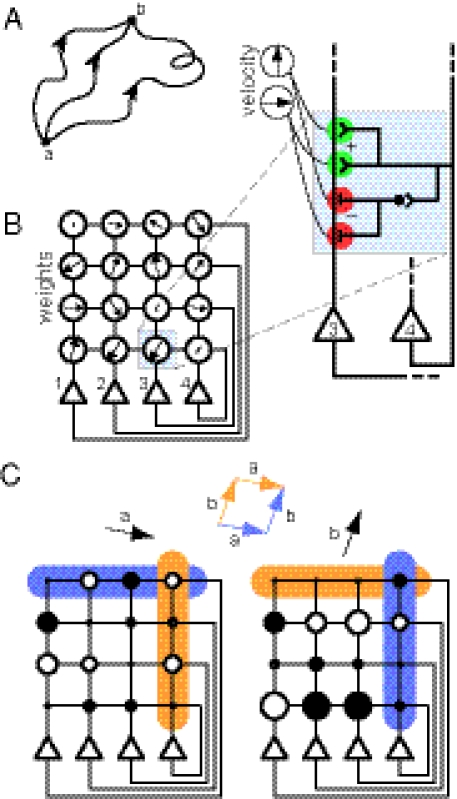
Fig. 1.

Constraints on a path integration network. (A) For the system to perform exact path integration, the network state at location b should be the same regardless of which path it took to get there from location a. (B) A four-unit network with each recurrent connection node characterized by a weight vector (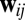 in Eq. 4), shown as an arrow that represents the preferred direction and the magnitude of velocity modulation. The effective weight of each connection is the dot product between this weight vector 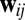and the movement velocity 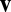. The connection from neuron 4 to neuron 3 (Left, shaded box) is expanded (Right), showing that each weight vector can be implemented by summing excitatory synapses (green) and inhibitory synapses (red, via interneurons) if these synapses are multiplicatively modulated by the component velocity inputs. (C) Illustration of commutativity condition (Eq. 5) for a linear network when one of two paths is followed: (blue) or 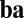(orange). For movement in a straight line ( 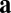or 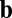), the effective weights are represented by the size of the dots and whether they are open (positive value) or closed (negative value). For the commutativity condition to hold, the dot product of the blue vectors should equal the dot product of the orange vectors. The blue vector (shaded) on the left represents the outputs from neuron 1 for direction 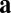, whereas the blue vector on the right represents the inputs to neuron 4 for direction 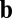(and vice versa for the orange vectors).

where matrix 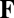depends on the network state 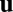but not on the velocity 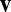. To see this, consider the derivative chain rule, 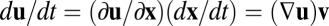, where the Jacobian matrix 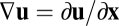depends implicitly on because 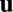is an implicit function of . Assuming this implicit function is locally invertible, we may write 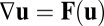and obtain Eq. 1.

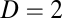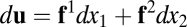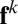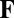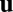Exact path integration by Eq. 1 requires an additional condition. For simplicity we show the argument for here (for generalization to higher dimensions, see SI Text 1). Consider the differential form of Eq. 1, where is the kth column of , which depends implicitly on . If activity is path invariant, its cumulative increment over any closed movement trajectory 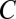must vanish: 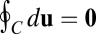. By Green’s theorem, this means that 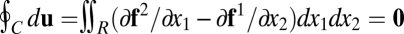for any region 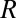bounded by 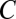. Hence 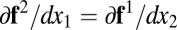. For arbitrary dimension 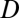, this condition becomes

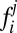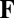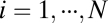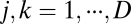where is the entry in the ith row and jth column of matrix ( and for 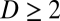). Eq. 2 specifies a necessary and sufficient condition that guarantees that the differential form 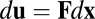is integrable with respect to the spatial variable , which in turn means that activity depends on location only and not on the movement trajectory. For 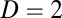or 3, Eq. 2 is equivalent to the curl-free condition for a gradient vector field (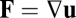). In arbitrary dimensions, the general case of Eq. 2 follows from the Poincaré lemma (SI Text 1).

Eq. 1 implies that the rate of state change should be modulated linearly by the velocity . As shown in Fig. 1B, one way to implement this general requirement is a model system where recurrent synapses are multiplicatively modulated by velocity inputs (see Discussion for other possibilities). Finally, note that Eq. 1 (as well as Eq. 3 below) does not contain a decay term such as 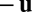commonly seen in neural models. We explain how this may be justified in SI Text 6.

Linear System.

To gain a better understanding of the dynamical equation (Eq. 1) and the path-invariance condition (Eq. 2), we simplify the system by assuming that matrix 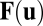is a linear function of state 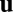. That is, for 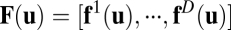, we assume each column is a vector given by 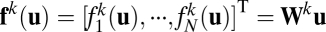, with 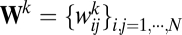being a weight matrix for each spatial dimension 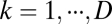. Here 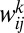is the weight of the connection from unit j to unit i, and the superscript k indicates the spatial dimension of velocity modulation. Now we can reformulate Eq. 1 as

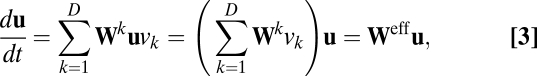where 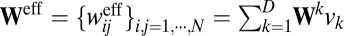is defined as the effective weight matrix. The effective weight from unit j to unit i can be rewritten as:

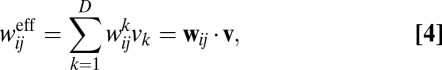which is a dot product between the instantaneous velocity 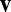and a fixed weight vector 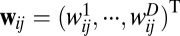. Thus, the effective weight is largest when velocity is aligned with the direction of the weight vector, zero when the two vectors are orthogonal, and negative when the angle between the two vectors is >90°. As shown in Fig. 1B, the velocity-modulated connection between a pair of units can be characterized by a single vector with the appropriate orientation and magnitude.

Working with a linear system allows us to simplify the condition from Eq. 2 to the following:

for all 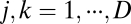(SI Text 1). In other words, the weight matrices for different spatial dimensions must commute.

Results

Eigensolutions.

We examine how the linear dynamical system in Eq. 3 generates activity 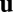as a function of location . For all of the examples considered in this paper, with the exception of the linear tuning function (see Fig. 4A), we assume that the weight matrices 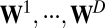have distinct eigenvalues and are thus diagonalizable (general solutions without this assumption are shown in SI Text 2). Because diagonalizable matrices share the same eigenvectors if and only if they commute, the commutative condition in Eq. 5 implies that these matrices have an identical set of eigenvectors, although their eigenvalues may differ.

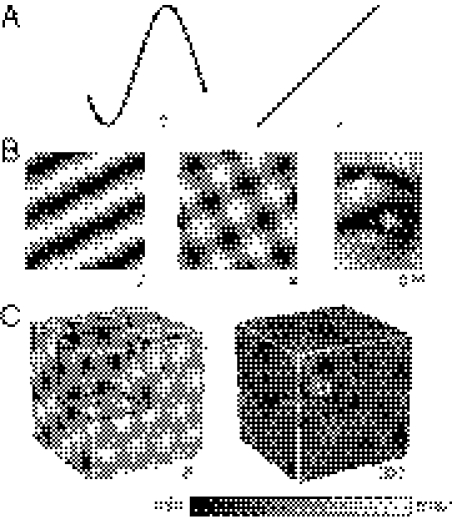
Fig. 4.

Diverse activity patterns can be generated by a linear network performing exact path integration in multiple dimensions. (A) In one dimension, the solution set includes sinusoids (Left, periodic as seen in head direction cells) and first-order polynomials (Right, nonperiodic as seen in the eye position integrator of the oculomotor system). (B) In two dimensions, the solutions are superpositions of one-dimensional patterns. These patterns can be a single sinusoidal grating (Left), two gratings at 90° to form a square grid (Center; this pattern is generated by the four-unit network of Fig. 1B), or a large number of sinusoids to form a representation of an image of a human eye (Right). (C) These solutions generalize to higher dimensions. In three dimensions, a grid based on the hexagonal close-packed lattice (Left) or a place cell based on a large number of random-frequency zero-phase sinusoids (Right) can be formed. The numbers below indicate the number of units used to generate that spatial pattern.

Whereas the solution to Eq. 3 specifies the activity 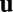as a function of time, we can replace time 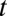with the position for any trajectory because of path invariance. For simplicity we choose our trajectory to start at the origin and move toward at a constant velocity. Now Eq. 3 becomes a homogenous linear differential equation with constant coefficients and its solution is a linear combination of basis functions,

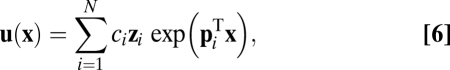where 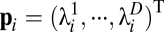, 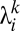is the 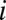th eigenvalue of matrix 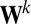, 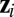is the associated eigenvector, and coefficient 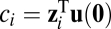. With properly chosen eigenvectors and eigenvalues, this basis function set 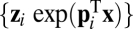can, in principle, approximate any smooth function to arbitrary precision because it can at least provide Fourier components when the eigenvalues are imaginary (SI Text 2). Weights for the linear system can be learned by a local supervised learning rule (SI Text 4 and Fig. S1).

Illustrating the Commutative Condition.

At first glance, the commutative condition (Eq. 5) is not intuitive in a biological context. For a more concrete illustration, we restate the condition as a discrete version for arbitrary movement directions. First, we choose two displacement vectors a and b (Fig. 1C). Using the matrix exponential to solve Eq. 3, we have 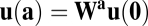, where 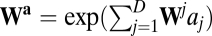with 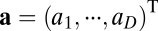. It is easy to see that path invariance requires commutativity of 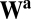with 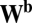because the final activity along path 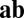is 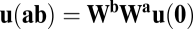, which should equal 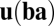, implying 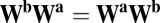for all 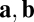, including movements in cardinal directions (as in Eq. 5).

Now we look at any pair of units and define the net influence of unit i on unit j along path 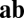as the dot product of two sets of connections for two movement segments: those from unit i to all units for movement a (ith row of 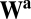and blue row in Fig. 1C) and those from all units to unit j for movement b (jth row of 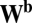and blue column in Fig. 1C). By Eq. 5, this net influence must stay the same along path 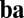. Thus, for a pair of units, path invariance puts restriction on connections involving all units in the network and not just on direct connections.

Grid Cell Simulation.

Grid cells in the rat medial entorhinal cortex fire in a hexagonal pattern. Nearby cells have the same orientation and spatial frequency but differing spatial phases, and their firing patterns are maintained in the dark (7). Here we simulate the spatial pattern of grid cell firing with a linear system governed by Eqs. 3 and 5. We show that this method can guide us to find diverse solutions that generate the same hexagonal activity pattern.

All of the examples in this section are based on sinusoidal basis functions, which are special cases of the exponential functions in Eq. 6 with purely imaginary eigenvalues (SI Text 2). We first consider a minimal network. Because a hexagonal grid can be generated by combining three sinusoids, the smallest network possible has six neurons. The connection scheme (Fig. 2A) does not show any obvious hexagonal symmetry and may even look quite random, yet the weight matrices commute and can generate a hexagonal activity pattern by integrating velocity inputs (Fig. 2 B and C). Each cell has the same activity pattern but spatially shifted according to their relative spatial phases.

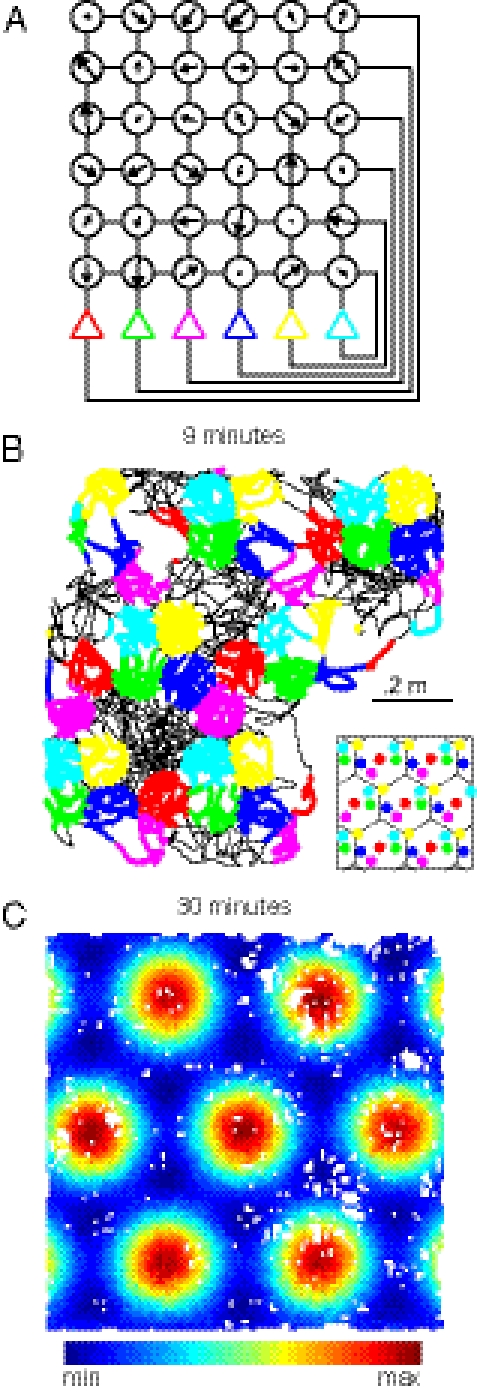
Fig. 2.

A six-unit grid cell network. (A) Weights were found for a network with randomly chosen spatial phases. This network is shown using the same convention as in Fig. 1B. (B) Simulated trajectory over 9 min is shown (black line). To display activity, spikes are plotted as colored dots whenever a unit’s activity crosses 75% of its maximum. If multiple units simultaneously cross the threshold, only the unit with highest activity is displayed. Color scheme is same as in A. Inset shows the spatial phases for each unit on top of the underlying hexagonal tiles. (C) For a full 30-min session, the average unit activity at each position (100 × 100 bins) for the first neuron (previously in red) is shown. White indicates positions not visited in the simulation. See SI Text 7 for further details.

As another example, we choose a regular arrangement of spatial phases and a regular connection pattern where each neuron receives symmetric inputs from its six nearest neighbors (Fig. 3 and Fig. S2A). In this example, the hexagonal activity pattern arises due to the inherent hexagonal symmetry of the connections. Each neuron connects to a uniformly spaced ring of other neurons and each weight vector is proportional to the relative spatial positions of the connected neurons, ensuring that the weight matrices commute (Fig. S2 and SI Text 3).

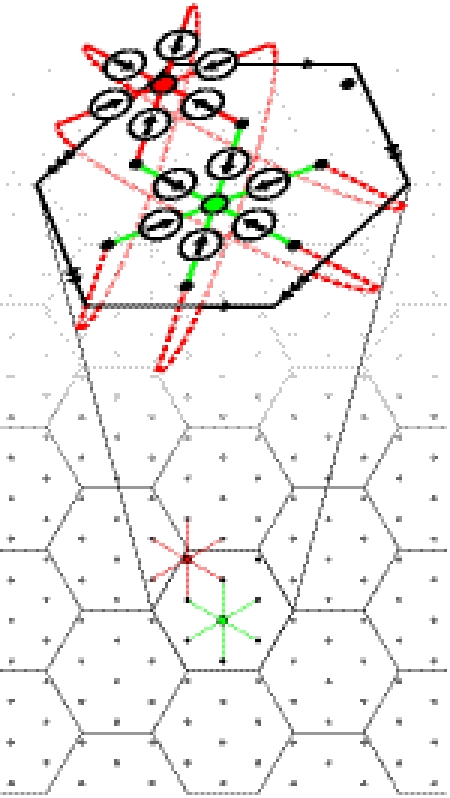
Fig. 3.

A nine-unit grid cell network with spatial symmetry. Each unit connects to its six nearest neighbors. These connections are illustrated for two of the units (green and red dots). Arrows indicate preferred directions for each weight. For the red unit, the connections wrap around the tile to the opposite edge (identified by the arrowheads). A tessellation of the hexagonal tile is also shown, illustrating that these units are evenly spaced.

We also studied a large network with many neurons with random spatial phases and found that, on average, there was a weak preference for preferred velocities out of phase with the grid orientation (Fig. S3 B–D). By contrast, for the case of evenly spaced spatial phases as in Fig. 3, the preferred weight directions all lined up exactly with the grid (Fig. S3A), an observation that is more consistent with grid cell studies (21), hinting that such biological systems may favor a radially symmetric connection scheme.

Example Solutions from the Linear System.

Any linear path integration system can be built using the eigensolutions described above after identifying the dimensionality of the system and the basis functions of the desired spatial activity pattern. A broad class of path integration systems can be simulated in this way, covering various dimensionalities and types of space, either periodic or nonperiodic. Several examples of these linear systems are shown in Fig. 4. In the one-dimensional examples, a sinusoid solution (Fig. 4A, Left) is generated by using a weight matrix with a pair of imaginary eigenvalues, whereas a linear activity pattern (Fig. 4A, Right) is generated by using a weight matrix with repeated eigenvalues of zero. In higher dimensions, arbitrarily complex patterns can be generated, ranging from an image of a human eye to a hypothetical 3D grid cell (Fig. 4 B and C). Because the solution set scales with the number of neurons and not dimensionality, a minimal model of 3D grid cells requires only two additional neurons beyond the six-unit minimal model of 2D grid cells.

Existing Exact Path Integration Models.

We chose four disparate models of exact path integrators and asked whether they adhere to our conditions. These four models are a linear eye position integrator, nonlinear bump attractor networks, oscillatory interference models, and a 3D head orientation model. Although the actual computational mechanisms in these examples are radically different, we find that these models all obey the same mathematical conditions of Eqs. 1 and 2 to achieve exact path integration (see SI Text 5 for details and proofs). Briefly, a linear eye position integrator model that produces firing rates proportional to position (22, 23) is consistent with our theory in one-dimensional space. The continuous attractor network (24–26) supports a stable activity pattern that can be moved by velocity inputs. We must first let the system settle to a stable activity pattern, after which it performs exact path integration. The oscillatory interference models (15, 16, 20, 27) of grid cells and place cells perform path integration by modulating the oscillator frequencies. Although the activity of the interfering oscillators is not spatially invariant, the envelope is. Finally, in a recent vestibular model (28), angular velocity, an inexact differential quantity, is integrated to calculate head orientation. We must first convert to a coordinate system where velocity is an exact differential quantity. With respect to the new coordinates, the system is an exact integrator.

Discussion

Path integration is a general mechanism used in various neural models. Insight into the fundamental computational principles behind accurate path integration can both unify existing models and provide guidance for future investigations into unexplored mechanisms. Here we have derived necessary and sufficient conditions for exact path integration under very general assumptions. These two conditions, multiplicative modulation and equivalence of mixed partial derivatives, arise from the chain rule and the Poincaré lemma, respectively. Each of these results bears theoretical and experimental implications for path integration.

The first condition, multiplicative modulation of inputs by velocity, is intuitively sound because doubling the speed should double the drive to move the system along the manifold of position. Various neural systems have been shown to use multiplication, including gain fields of parietal area 7a neurons (29), looming-sensitive neurons of the locust visual system (30), and conjunctive cells of the entorhinal cortex (31). Various models exist to explain how this multiplication could be implemented in a biologically plausible manner. Exponentiation by active membrane conductances of summed logarithmic synaptic inputs gives rise to an effective multiplication of inputs (32, 33). Another dendritic mechanism is that of nonlinear interaction of nearby inputs on a dendritic tree to yield multiplication followed by summation at the soma of more distal inputs (34). Alternatively, multiplication can be achieved through network effects via a properly tuned recurrent network (35). Finally, there are hints that synchrony of inputs and interplay with the theta rhythm could allow for one input to modulate other inputs (36, 37). Multiplication in a real biological system may require additional mechanisms to deal with negative weights and the degenerate case of zero net input at zero velocity.

The second condition constrains the connectivity of a path-invariant network. Computationally, equality of mixed partial derivatives provides a robust condition for identifying whether a model is path invariant. Experimentally, verifying path invariance and linking connectivity to activity patterns are more difficult. One way to test the equality of mixed partial derivatives is by in vivo patch clamp of a neuron to measure synaptic currents over a variety of paths (38). Whereas these data could provide support for path invariance, a complete network needs to be identified to have a full characterization of the dynamics of the system. For example, in our small grid cell network in Fig. 2, even if it could be measured experimentally, the connection matrix exhibits no clear symmetry, yet it produces hexagonal symmetry in its activity. Thus, one needs an explicit, quantitative model for such cases. Recent technological advancements would allow a model to be tested against simultaneously measured connectivity and activity. By combining focal optogenetic control of neurons (39), two-photon calcium imaging of a large number of neurons (40), recordings from freely moving animals via virtual reality (41) or miniaturization of optics (42), and reconstruction of neural connectivity via serial EM (43) or postmortem in vitro path clamping (44), one could both record and manipulate the functional and anatomical properties of path-invariant neurons on a large scale. Even then, accurate measurement of all network parameters would be difficult but simplifications, such as a linear approximation studied here, could make the problem more tractable.

Finally, although we have focused on spatial invariance in this paper, our results are not just limited to systems that are involved in navigation. The many other neural systems that use integration (45, 46) conform to our results as well, provided that they can be cast under our mathematical framework.