Shift-driven modulations of spin-echo signals

Abstract

Since the pioneering works of Carr-Purcell and Meiboom-Gill [Carr HY, Purcell EM (1954) Phys Rev 94:630; Meiboom S, Gill D (1985) Rev Sci Instrum 29:688], trains of π-pulses have featured amongst the main tools of quantum control. Echo trains find widespread use in nuclear magnetic resonance spectroscopy (NMR) and imaging (MRI), thanks to their ability to free the evolution of a spin-1/2 from several sources of decoherence. Spin echoes have also been researched in dynamic decoupling scenarios, for prolonging the lifetimes of quantum states or coherences. Inspired by this search we introduce a family of spin-echo sequences, which can still detect site-specific interactions like the chemical shift. This is achieved thanks to the presence of weak environmental fluctuations of common occurrence in high-field NMR—such as homonuclear spin-spin couplings or chemical/biochemical exchanges. Both intuitive and rigorous derivations of the resulting “selective dynamical recoupling” sequences are provided. Applications of these novel experiments are given for a variety of NMR scenarios including determinations of shift effects under inhomogeneities overwhelming individual chemical identities, and model-free characterizations of chemically exchanging partners.

The unprecedented scope of applications achieved by contemporary magnetic resonance reflects the degree of control that can be imparted on the spins’ evolution. Using judicious combinations of multiple-pulse sequences one can tailor Hamiltonians that highlight a variety of interactions. When coupled to the long-lived coherences typical of spin-1/2 nuclei, this enables probing matter over a broad range of conditions and scenarios—from nanomaterials to rocks under the oceans; from proteins to human metabolism and disease (1–4). Besides its wide scope of applications, NMR awakes constant interest as a benchmark for other fields of physics; in particular, the quantum information community has adopted a number of NMR paradigms as tools of its own (5–16). The most prominent example among these is the spin-echo sequence, proposed over half a century ago for removing inhomogeneous broadenings (17–19). When extrapolated to trains of π-pulses spaced by a constant delay (Fig. 1A), the resulting CPMG sequences eventually became associated to a long list of landmark measurements including T₂ determinations, structural-oriented experiments, diffusion measurements, ex situ investigations in inhomogeneous fields, kinetic chemical and biophysical determinations, spin decoupling, and single scan MRI (1–4). Overall, the extremely wide range of useful measurements that this single sequence enabled is truly remarkable.

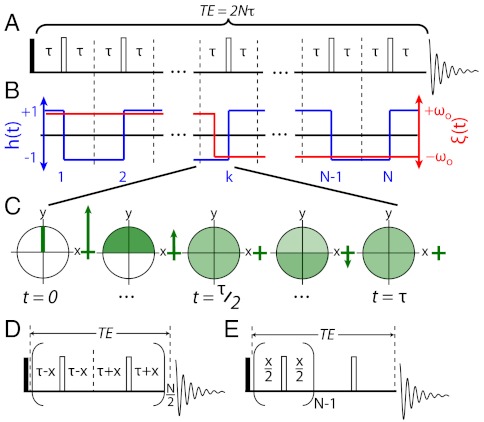
Fig. 1.

(A) Schematic diagram and timing of a CPMG sequence: solid line, π/2 pulse; hollow lines, π pulses. (B) Effective sign alternation imposed by CPMG on a qubit’s precession frequency -h(t), blue—and potential interference effects that can be incurred by a stochastic ξ(t) dynamics (red) triggering once during an arbitrary kth cycle. (C) Graphical description of how a sinc-like contribution gets imparted on the observable signal—associated in an NMR case by a distribution of spin magnetizations spreading throughout the transverse xy-plane- by the effects of this “boxcar integration” of a two-site dynamics. (D, E) Constant-time spin-echo trains capable of exploiting the observable’s oscillation in (C), for the sake of imparting on a signal a time dependence whose sole coherent, x-dependent modulation reflects ω₀.

Further CPMG generalizations have been proposed in recent years, aimed at improving the dynamical decoupling (DD) between a spin and its surroundings (5–9). In cases where environmental fluctuations are dominated by low-frequency components having a sharp cutoff, minimal decoherence was shown to arise when the modulation h(t) imposed by the pulsing on the spin-bath interactions (Fig. 1B) departs from a single, constant value (10–16). Motivated by these findings, this work seeks the design of sequences that can highlight desirable site-specific molecular features, given certain a priori known features about the fluctuations. We find that variations in the canonical CPMG timing enable interactions proportional to σ_z, such as chemical shifts, to impart a temporal modulation that one would assume beyond the reach of sequences fulfilling 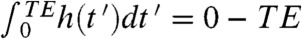being the total echo time. This is a highly unusual effect, since a common aim of all these sequences is to cancel out evolutions proportional to the σ_z terms. Still, as shown below, the presence of infrequent fluctuations in a spin’s environment can reintroduce a net Hamiltonian proportional to σ_z, whose effects can be detected with the aid of suitably designed sequences. Although we illustrate this fluctuation-driven recoupling for an NMR scenario where the interactions sought are given by chemical shifts, the application of these new sequences extends to a wider range of phenomena including spin-diffusion in coherently manipulated solid-state spin devices, motion-related phenomena in MRI, hyperfine couplings in solid-state assemblies, barrier fluctuations in Josephson junctions, or optical intermittency in photoluminescence experiments.

Theoretical Description of Selective Dynamic Recoupling

Despite the 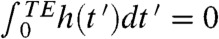refocusing condition associated with DD, oscillations in the signals can still arise from these sequences if the targeted spin is subject to infrequent jumps in its evolution frequency. In quantum control parlance this would amount to allowing for a strong fluctuation of the qubit while under the action of dynamical decoupling. In NMR one would describe this as the reintroduction of chemical shifts even under the action of CPMG, owing to environment-driven offset changes. To visualize how this can lead to periodic σ_z-driven modulations consider a spin-echo train composed of N segments, each of duration 2τ_i with a π-pulse in its center. Assume also that, to first order, the targeted spin executes on average a single spectral jump during the spin-echo train—from -ω_o to +ω_o. Since each control π-pulse imposes a sign change of the evolution phase, the train’s overall effect amounts to a square-wave modulation of the spin’s dynamic phase; this is thus refocused for all segments, except for the one where the spectral jump has occurred (Fig. 1B). The net dispersion accumulated by the ensemble due to the ξ(t) stochastic jump function, can then be computed by integrating the dynamic evolution phasor 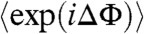over a single 2τ_i oscillation, and integrating this over all N segments comprising the π-pulse train. The signal contribution arising due to the fluctuations over TE will be

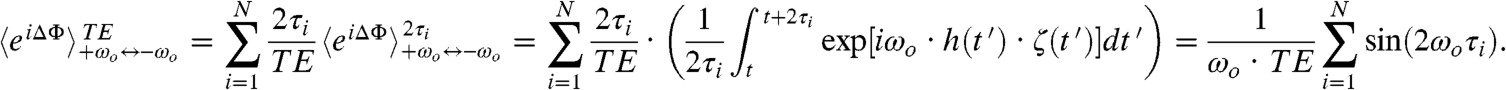[1]

The sinusoidal dependence in each term of this sum may either add or detract from the main observable signal, a nonmonotonic behavior that reflects the discrete frequency spectrum involved in the fluctuation—rather than the nature of the fluctuation or of its detailed dynamics (Fig. 1C). This dependence can be expected for any echo train experiment performed while a spin’s precession frequency changes stochastically. In magnetic resonance these frequency jumps could be driven by chemical exchange, homonuclear J-couplings, diffusion in the presence of a field gradient, or cross-relaxation (20–23). In more general instances, Eq. 1 is valid for any qubit ensemble subject to the action of DD, in the presence of telegraph noise (24) or other kinds of spectral “blinkings” (25, 26).

Although possessing a considerable potential for facilitating experimental measurements, translating Eq. 1 into a periodic signal modulation would be impractical in a CPMG scenario. Indeed, to evaluate Eq. 1’s predictions as a function of a single {τ_i = τ}_∀i, one would have to change concurrently the total time TE and/or the number of pulses N. The effect being sought would then be masked by stronger changes incurred by spin relaxation, diffusion, or pulsing nonidealities. By contrast, simple variants like those shown in Figs. 1 D and E encompassing a full refocusing, a fixed overall evolution time 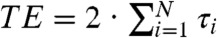, and a constant number N of π-pulses but still allowing variations in the time intervals τ_i, render the signal modulations stemming from Eq. 1 easily observable. Fig. 1D for instance separates the original spin-echo segment times τ_i into two equal groups, one of duration τ_i = τ - x and the other of duration τ_i = τ + x, with x < τ and τ = TE/2N representing the average segment time. Eq. 1 then becomes

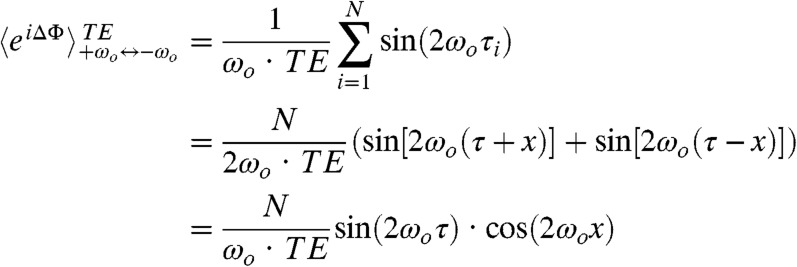[2]

For a suitably chosen sin(2ω_oτ), this yields a simple x-dependence for extracting the difference 2ω_o between the frequencies coupled by the fluctuation. Notice that varying x neither changes the total time TE nor the number of echo pulses N, allowing a reliable measurement of this coherent oscillation. A downside of this scheme is that, for some certain values of ω_o or τ, the weighting coefficient of this modulation can be small and the effect’s visibility reduced. Fig. 1E alleviates this problem with a variant whereby all segments i except one are set to an arbitrary value 2τ_i = x < TE/(N - 1), while the remaining echo segment is positioned anywhere within the π-train and given a complementary duration TE - (N - 1)x (Fig. 1E places it at the conclusion of TE as an illustration). For such a scheme, Eq. 1 becomes

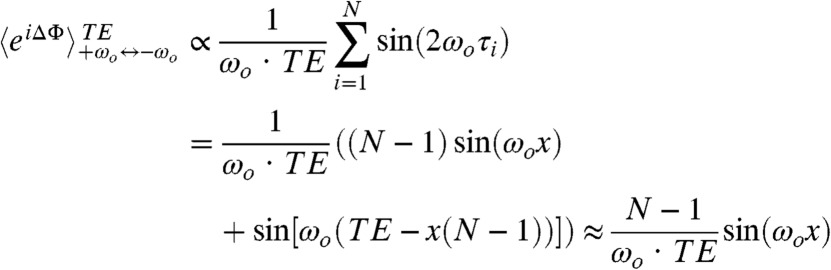[3]

This expression predicts a sinusoid which does not need a priori knowledge of sin(2ω_oτ), at the expense of a noise-like term of order N^-1 that can often be disregarded. By virtue of this, such scheme gives a simple way of extracting ω_o from the oscillations that the signals exhibit as a function of the x delay—accompanied if need be by Fourier analyses that are usually robust vis-à-vis experimental fluctuations and noise sources.

As the main aim of these spin-echoes is to exploit environment-driven dynamics to monitor solely the ω_o-dependencies that DD usually averages away, we consider them as variants of a new kind of “selective dynamical recoupling” (SDR) sequences. Although SDR schemes might seem similar to DD, especially to variable-interval sequences (5), they operate on the basis of strong, infrequent fluctuations—a regime where most DD assumptions break down. Indeed, a basic tenet of DD is that the strength of the effect one wishes to suppress is linear in the strength of the coupling to the bath spectrum (5–9). By contrast, the family of sequences here discussed uses the bath’s fluctuations nonlinearly, increasing the dephasing for some values of ω_o while decreasing these effects for others. In fact, the sequence’s aim is to make the effects of infrequent noises ω_o-dependent and hence achieve a selective reintroduction of certain targeted interactions, rather than canceling all decoherence effects.

Results and Discussion

SDR sequences—and the variant of Fig. 1E in particular—were tested in a number of experiments. The first case explored involved measuring chemical shift differences among homonuclear J-coupled spins. As we operate in the usual high-field NMR scenario, the coupling Hamiltonian H_J will be truncated to its Ising-like 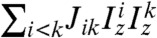components, incapable of transferring coherences or magnetizations between sites. The execution of a spin-echo train, however, can reactivate such transfers; in the slow-pulsing regime (ω_i - ω_k)τ≫1 this will only happen with a low efficiency on the order of 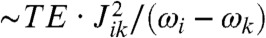, consistent with the demands involved in the derivation of Eqs. 1–3. Relying on average Hamiltonian theory (27) to compute the final modulation expected from the sequence in Fig. 1E (SI Text, Supplement A), one reaches a first-order expression for the normalized amplitude that SDR will yield for an i-spin that is J-coupled to a k-spin:

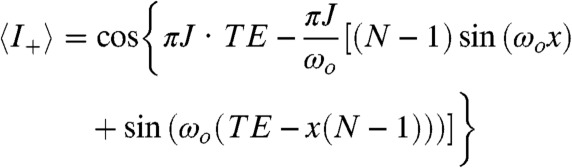[4]

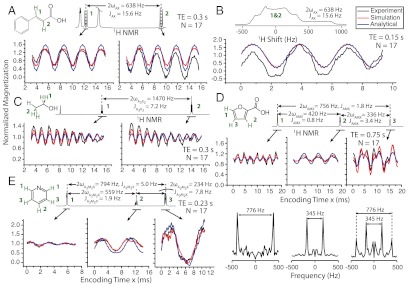
Besides an overall J-modulation that is constant for a fixed TE value, this expression is similar to that given in Eq. 3—with ω_o = (ω_i - ω_k)/2 now denoting the frequency separation between sites. Notice that given the weak, exchange-like effects driven by the J-couplings, the addition of a third qubit leads to an analogous term modulated with a different ω_o-value. Fig. 2 summarizes the resulting modulations for a number of typical J-coupled scenarios including two isolated spins, the same system under the effect of sizable field inhomogeneities that preclude the measurement of individual resonance offsets, and a number of multispin systems. Shown together with the experiments are predictions arising from Eq. 4, as well as the results of numerical simulations where the full pulse sequence was propagated on the basis of input parameters. Notice that, given the a priori known values of shifts and J-couplings, no fittings are actually involved in these comparisons. The main feature common to all these results is a clear modulation of the signals, defined solely by chemical shift differences that can be read out by Fourier transforms of the ensuing amplitude modulations. Notice that these modulations reveal spectral offsets among the coupled neighbors with high resolution even under gross inhomogeneous broadenings, and that the complexity of these patterns simply grows linearly with the number of distinct sites. Also worth stressing are the differences between these modulations and the evolution of zero-quantum states [which would also evolve as a function of frequency differences (29, 30)], or between them and experiments dominated by effective isotropic J Hamiltonians arising when applying windowless trains of π-pulses (31, 32).

Fig. 2.

Behavior observed for the illustrated compounds upon implementing the SDR sequence in Fig. 1E, as mediated by homonuclear ¹H-¹H couplings, for the indicated parameters. Experiments (black traces) are compared against simulations (red) resulting from SpinEvolution (28) computations using the indicated parameters, and analytical curves (blue) arise from the two-site modulation predicted by Eq. 4. (A) x-dependence observed for the isolated olefinic proton pair of Cynnamic acid at high-resolution. (B) Idem but for the Cynnamic acid placed in a grossly inhomogeneous magnetic field (shimming coils off), illustrating SDR’s ability to retrieve high resolution shift modulations even though it relies on fully refocused π-pulse trains. (C) Idem as (A) but for the two chemically distinct sites of ethanol/D₂O—a five-proton system. (D) Behavior displayed by the three chemically distinct protons of Furoic acid in D₂O—an AMX spin system at this field—highlighting the dual modulations at ω₀ = (ω_A - ω_M)/2 and ω₀ = (ω_M - ω_X)/2 frequencies shown by site 3 arising upon Fourier transforming its baseline-corrected modulation curve. (E) SDR modulations for Pyridine, a site that like (D) possesses three chemically distinct proton sites but by contrast to it is characterized by five magnetically inequivalent spins. All x-dependent curves are shown normalized to a value of one.

Another mechanism capable of introducing the fluctuations required by SDR, is chemical exchange. In NMR this could involve tautomerisms, binding dynamics, or spin-diffusion. For the simplest scenario, involving a chemical exchange taking place at a rate κ that is slow in the NMR timescale between equally populated states, the formalism presented in SI Text, Supplement B predicts that the sequence in Fig. 1E will modulate the normalized resonance amplitudes as

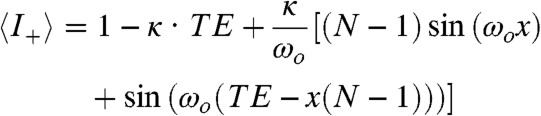[5]

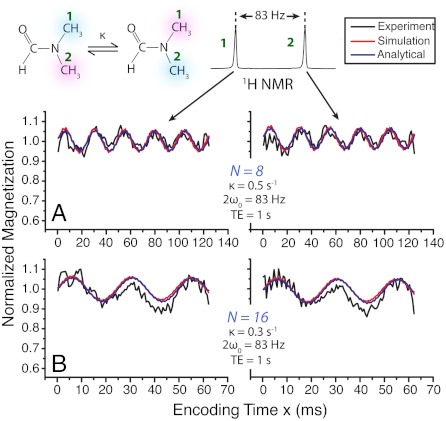
where ω_o = (ω_i - ω_j)/2 is now the half-difference between the sites interconverted by the dynamics. As illustrated in Fig. 3, these differences are again clearly visible in the modulations displayed by each of the exchanging partners. Also shown are the effects that changing the number N of π-pulses will have in the apparent modulation imparted by for a fixed overall TE. There is once again a remarkable agreement between the experimental results and these parameter-free fits. SI Text, Supplement B extends this two-site exchange to more complex networks and to unequally populated situations; these results reveal once again a desirable superposition of single-frequency modulations such as those noted in Fig. 2.

Fig. 3.

Idem as illustrated in Fig. 2, but for a case where the indicated two-site chemical exchange process drives the fluctuation ξ(t). Data were collected on 10% dimethylformamide (shown) in CCl₄ at 67 ± 0.25 (A) and 64 ± 0.25 °C (B) for a total TE of 1 sec. Simulations were done with SpinEvolution (28), and the analytical curves correspond to Eq. 5 for the indicated parameters.

The oscillatory modulations in Fig. 2 and 3 only evidence some of the instances where these recoupling sequences could be exploited. SDR can open a number of valuable NMR applications, including determinations of chemical shifts among J-coupled partners under challenging in vivo or ex situ conditions, or the definition of the precession frequencies of exchanging partners even when one of them is not clearly visible. Additional instances where these phenomena could be exploited include cross-relaxation transfers, and monitoring molecular diffusion in the presence of field gradients. In some of these instances the information being sought could also become amenable by modeling the signal’s decay (2, 3). Still, the analysis of periodic, parameter-free modulations like those introduced in this work, make the measurement process much more robust. It is also evident that cross-fertilizations are possible between spin manipulations like those hereby introduced, and other state-of-the-art control strategies within the quantum information field. Examples of these to NMR, MRI, and other spectroscopic applications, will be presented in upcoming studies.

Materials and Methods

All experiments in this study were collected at 600 MHz using a Varian VNMRS® spectrometer and a 5 mm HCN inverse probe. Sequences based on the schemes shown in Figs. 1 A, D, and E were written; in all cases ¹H π/2 pulses were 8 μs and an XY-4 (33) supercycle was used over the course of the π-pulse train. Data were processed and analyzed offline; typical acquisition conditions included two phase-alternated scans, 20 sec recycle delays, and 2 sec acquisition times.