Molecular crowding creates traffic jams of kinesin motors on microtubules

Abstract

Despite the crowdedness of the interior of cells, microtubule-based motor proteins are able to deliver cargoes rapidly and reliably throughout the cytoplasm. We hypothesize that motor proteins may be adapted to operate in crowded environments by having molecular properties that prevent them from forming traffic jams. To test this hypothesis, we reconstituted high-density traffic of purified kinesin-8 motor protein, a highly processive motor with long end-residency time, along microtubules in a total internal-reflection fluorescence microscopy assay. We found that traffic jams, characterized by an abrupt increase in the density of motors with an associated abrupt decrease in motor speed, form even in the absence of other obstructing proteins. To determine the molecular properties that lead to jamming, we altered the concentration of motors, their processivity, and their rate of dissociation from microtubule ends. Traffic jams occurred when the motor density exceeded a critical value (density-induced jams) or when motor dissociation from the microtubule ends was so slow that it resulted in a pileup (bottleneck-induced jams). Through comparison of our experimental results with theoretical models and stochastic simulations, we characterized in detail under which conditions density- and bottleneck-induced traffic jams form or do not form. Our results indicate that transport kinesins, such as kinesin-1, may be evolutionarily adapted to avoid the formation of traffic jams by moving only with moderate processivity and dissociating rapidly from microtubule ends.

Cells are crowded with macromolecules, polymers, and membranes. This crowding diminishes the diffusion of small molecules and proteins (1), increases the oligomerization and aggregation of proteins (2), and strongly restricts the mobility of larger particles and organelles (3). Despite this “congestion” in the cytoplasm, it is remarkable how efficiently transport systems deliver cargoes inside cells. In healthy cells, transport of cargoes at net rates exceeding 1 μm/s can be maintained over distances up to tens of microns in cilia and flagella (4, 5), and up to several millimeters (or more) in the axons and dendrites of neurons (6, 7). Do healthy cells have special mechanisms to avoid transport obstructions seen under pathological conditions (8, 9)?

There are several ways in which the molecular properties of motor proteins could be adapted to prevent traffic jams. For example, the robustness of intracellular transport may be due to the high forces generated by motor proteins, which may clear obstructions (8). Or the affinity of motors for their tracks may be low enough to prevent a sufficient buildup in density. Alternatively, motors may have mechanisms to sense molecular crowding and to alter their behavior in order to prevent traffic jams. So far, however, little is understood about how motor proteins behave in crowded environments, and what physical mechanisms may cause motor proteins to form traffic jams in the first place.

On highways, traffic jams form if an increase in vehicle density leads to a sufficiently large decrease in the vehicle velocity (10, 11). In this case, increasing the density beyond a critical value leads to a decrease in the vehicle flux (the velocity times the density), which reinforces the density buildup, leading to an abrupt increase in density and an associated abrupt decrease in velocity: a traffic jam. Do similar principles operate at the molecular level? Traffic jams of motor proteins on cytoskeletal filaments have been predicted theoretically (12–16), and experiments with purified proteins indicate that motor proteins have properties that may predispose them to form traffic jams: In principle, almost all the motor-binding sites on a microtubule can be occupied if the kinesin-1 (17, 18), kinesin-3 (15), or kinesin-8 (19) concentration is high enough. Moreover, abrupt local increases in kinesin-1 density on a microtubule have been reported (15), but whether these were associated with an abrupt decrease in speed was not investigated in these experiments. Finally, a decrease in average kinesin-1 speed has been observed to occur as the motor concentration is increased (20), though no abrupt speed or density changes were detected. In this work, we have used two-color total internal-reflection fluorescence microscopy (19) to simultaneously measure the speed of individual kinesin motors moving on microtubules while monitoring the local motor density. Using this strategy, we study whether motor proteins have the predisposition to form traffic jams on their own, and, if so, what are the key motor properties responsible for jams.

Results

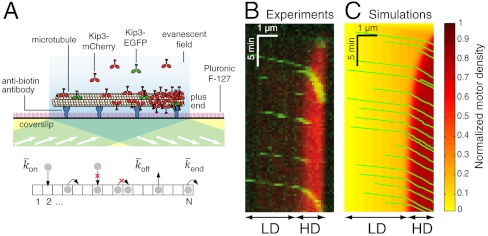
To understand how individual motors behave in crowded environments, we used the motor protein Kip3 (in the kinesin-8 family) as a model system to reconstitute high-density traffic on microtubules. Kip3 is an ideal motor for these studies. First, like other members of the kinesin-8 family (21), it is highly processive, walking tens of microns along a microtubule toward its plus end before dissociating (22). Second, it pauses at the plus end before dissociating. And third, its motor properties (e.g., processivity, end dissociation) can be tuned by altering the salt concentration in solution (19) (SI Appendix, Fig. S1). One potential disadvantage of Kip3 for these studies is that it depolymerizes microtubules (22, 23); however, we circumvented this problem by using microtubules that were grown in the presence of the slowly hydrolyzing GTP analog, guanylyl-(α, β)-methylene-diphosphonate (GMPCPP), and additionally stabilized the microtubules with taxol. Kip3 cannot depolymerize such “doubly stabilized” microtubules (19). To simultaneously measure individual motor speed and the overall motor density, we added a low concentration of EGFP-labeled Kip3 (< 0.05 nM) to variable amounts of mCherry-labeled Kip3 (0–15 nM). Both fluorophores were excited with a 488-nm laser and imaged by total internal-reflection fluorescence (TIRF) microscopy (Fig. 1A and SI Appendix, SI Methods).

Fig. 1.

Experimental and simulation results of motor-protein traffic jams on microtubules. (A, Upper) Schematic of the dual-color in vitro assay. (Lower) Schematic of the simulation with lattice-association (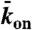), lattice-dissociation (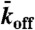), and end-dissociation () probabilities. N is the number of sites on the lattice. (B) Dual-color kymograph showing the motor density in red (Kip3-mCherry, 3.2 nM) and the trajectories of individual motors in green (Kip3-EGFP, < 0.05 nM) in the presence of 30 mM KCl. The top of the kymograph corresponds to the time when the motors were added to the microtubule. (C) Simulated kymograph using the following parameters (see text): 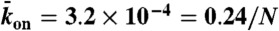with N = 750, corresponding to an association rate with 3.2 nM Kip3-mCherry in solution, 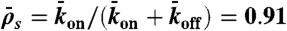, and .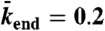

Using this assay, we found that for sufficiently high total concentrations of Kip3 (> 1 nM), an abrupt increase in motor density formed close to the microtubule plus end (red signal in Fig. 1B). This high-density (HD) region expanded toward the minus end until a steady state was reached. The density in the HD region was similar for all the microtubules present in a field of view (SI Appendix, Fig. S2). When a motor reached the HD region, it slowed down (green signal in Fig. 1B). The coexistence of a HD/low-speed region with a low-density (LD)/high-speed region was taken as the signature of a traffic jam (see Movie S1).

Our experimental observations could be simulated by the model of Parmeggiani et al. (13). In this model, the microtubule is represented as a one-dimensional lattice with N sites, each corresponding to a tubulin dimer (see Fig. 1A, Lower). The lattice corresponds to a single protofilament of the microtubule; the model therefore does not consider protofilament switching. The motors are represented as particles, at most one occupying each site. At discrete time steps (Δt) the occupancy of the sites is updated according to the following rules. (i) If the site is empty, then with probability 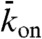the site becomes filled (proportional to the concentration of motors in solution). (ii) If the site is occupied, the particle leaves the lattice with probability 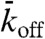; if it has not left, then it moves to the right (if the adjacent site to the right is empty) or stays (if the next site is full). A special update rule applies at the right-hand end (the end toward which the motors walk); if this site is occupied, there is a probability (not necessarily equal to 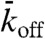) that it becomes empty. In the stochastic simulations, the sites are updated using a random-sequential update; i.e., at each time step, N sites are chosen at random (with no restriction on how many times a site is chosen) and the sites are updated one after the other. This update protocol mimics motor stepping as a random (Poisson) process (13). To relate the simulation to the experimental results, the distance between sites was set to d = 8 nm and the discrete time step to Δt = d/v₀ = 0.16 s where v₀ = 50 nm/s is the motor speed at low density. Within this time step, each motor advances on average one tubulin dimer per time step at low density, giving the correct average speed. The probabilities relate to the corresponding association and dissociation rates by 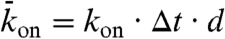, , 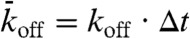and 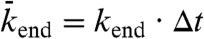where k_on is the association rate per tubulin dimer, k_off is the lattice-dissociation rate, and k_end is the end-dissociation rate. The choice of time step ensures that the probabilities are < 1.

The stochastic simulations reproduced many of the features of the experimental data (Fig. 1C). Using realistic parameters, there was a sharp transition in motor density between LD and HD regions, the motors abruptly slowed down when they crossed from the LD into the HD region, and the motor density distribution approached a steady state with similar kinetics to the experimental data.

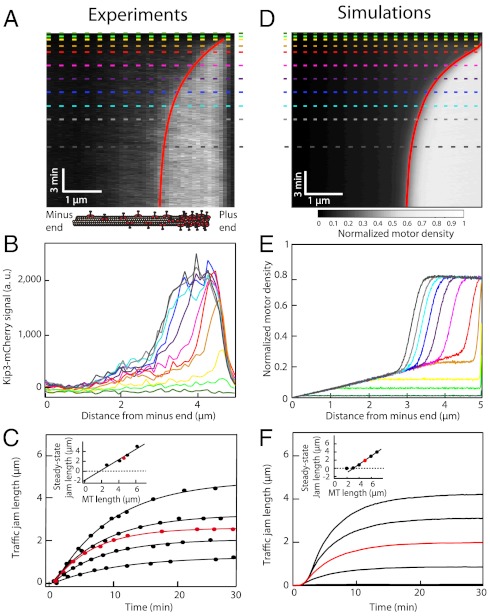
In order to better understand the mechanism of traffic jam formation, we measured the kinetics of jam growth. We made the following observations. (i) The lengths of the traffic jams increased over time and approached steady state approximately exponentially (Fig. 2 A–C). (ii) The steady-state jam length increased linearly with the microtubule length with a slope equal to one (Fig. 2C, Inset). (iii) There was a critical microtubule length necessary for jam formation (Fig. 2C, Inset). (iv) For a given Kip3 concentration, the characteristic time associated with the exponential approach to steady state was similar for all microtubule lengths (SI Appendix, Fig. S3). (v) When the motor concentration was increased, the jam length approached its steady-state value more quickly and the critical length depended on the Kip3 concentration (SI Appendix, Fig. S4). All these properties can be accounted for by an analytic model based on the assumption that the flux of motors is conserved at the boundary between LD and HD regions; the continuous curves in Fig. 2 A and C are predictions based on the model (see SI Appendix). One way to understand these results is that a certain “antenna” length (19) or “capture” length of microtubule is required to raise the density sufficiently for jam formation. According to this picture, when the flux of motors to the microtubule plus end exceeds the flux off the end, the motors start to pile up, creating an HD region at the end and a boundary between LD and HD regions. The traffic jam then grows toward the minus end. As the LD region shrinks, the number of motors that enter the jam decreases, due to the decrease in antenna length, until a steady state is reached (SI Appendix, Fig. S2); we call this a bottleneck-induced mechanism (14). The kinetics of traffic jam growth accorded with the stochastic simulations, including the slope of the steady-state jam length vs. microtubule length (Fig. 2 D–F), which shows that the Parmeggiani-Franosh-Frey model recapitulates many of the kinetic features of jam formation.

Fig. 2.

Kinetics of traffic jam growth. (A) Kymograph showing the distribution of Kip3-mCherry (3.2 nM) motors along the microtubule lattice in the presence of 30 mM KCl. The dynamics of the nonlinear growth of traffic jams were well fit (red line) using our analytic model (SI Text, Eq. S11). (B) Motor density profiles for different times corresponding to the dashed lines in A. (C) Traffic jam length as a function of time for five microtubules of different lengths at 3.2 nM Kip3-mCherry. All the data were well fit (solid lines) by our analytic model (SI Text, Eq. S11). The red line corresponds to the data in A. (Inset) Steady-state jam lengths vs. microtubule (MT) lengths. (D) Simulated kymograph of traffic jam with 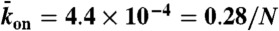, N = 625, 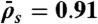, and 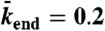. (E) Motor density profiles taken from the simulations in D at the time points indicated by dashed lines. (F) Simulations of the traffic jam growth for different microtubule lengths. The red line corresponds to the simulation in D. (Inset) Steady-state jam lengths vs. microtubule lengths.

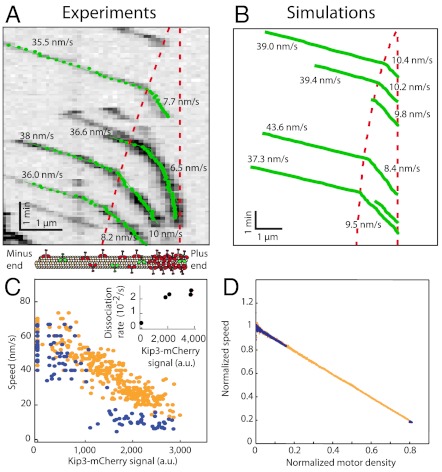
A molecular property crucial for understanding how traffic jams form is the relationship between motor speed and motor density. To determine the dependence of speed on density, single Kip3-EGFP molecules, observed in the green channel (Fig. 3A), were tracked with subpixel resolution (24). The speed in the LD region was similar to the speed in the absence of any other motors (v₀ = 56 ± 10 nm/s, SD, n = 15) (22). When the motors entered the HD region, the speed abruptly decreased. The simulations recapitulated this behavior (Fig. 3B). Results from several experiments showed that the observed motor densities and speeds clustered into two groups—LD/high speed and HD/low speed—with little overlap (Fig. 3C, blue points). To map out the full speed-density curve, we increased the salt concentration from 30 to 110 mM KCl (SI Appendix, Fig. S5); the speed decreased approximately linearly as the density increased (Fig. 3C, orange points). The slowing provides direct evidence for motor–motor interactions on the microtubule lattice. Further evidence for motor–motor interactions comes from the observed decrease in processivity with density. The run length decreased from 17 ± 5 μm (mean ± SE) in single-molecule conditions to 1.1 ± 0.4 μm in high-density assays (6.4 nM Kip3-mCherry). The run time, equal to the run length divided by the speed, also decreased with density; accordingly, the lattice-dissociation rate, k_off, the reciprocal of the run time, increased with density (Fig. 3C, Inset). Because the lattice-dissociation rate saturated over a wide range of densities where jams form (Fig. 3C Inset), 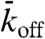was kept constant in the simulations.

Fig. 3.

Dependence of motor speed on motor density. (A) Kymograph (inverted contrast) showing the movement of individual Kip3-EGFP molecules in the presence of Kip3-mCherry (3.2 nM, not shown). Tracked data points (green) were used to calculate the indicated velocities. Red dashed lines represent the traffic jam boundary (Left) and the end of the microtubule (Right). (B) Simulated trajectories from Fig. 1C. (C) Experimental relationship between motor speed and motor density in the presence of 30 mM KCl (blue points, 0 and 3.2 nM Kip3-mCherry) and 110 mM KCl (orange points, 0 to 6.4 nM Kip3-mCherry). (Inset) Lattice-dissociation rate (s^-1) vs. motor density at 110 mM salt. (D) Simulated relationship between the normalized motor speed and density using the parameters: 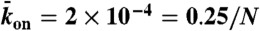with N = 1,250, 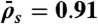, and 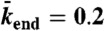(equivalent to 2 nM Kip3) (blue points); 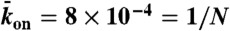with N = 1,250, 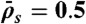, and 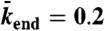(equivalent to 8 nM Kip3) (orange points).

The stochastic simulations provide insight into the nature of the motor–motor interactions on the lattice. The simulations predict a linear speed-density curve, both under conditions where distinct LD-HD regions formed (Fig. 3D, blue points) and under conditions exhibiting the full range of speeds and densities (Fig. 3D, orange points). This linear slowdown in the simulations is due to steric interference: A particle cannot step forward if the space in front is already occupied by another particle. The agreement between experiment and simulation suggests that Kip3 slows down due to simple steric interference; this is unlike car traffic, where a nonlinear dependence of velocity on density reflects the complex interactions between the cars on highways (25). The slowdown also demonstrates that the motors do not fully synchronize in a train-like motion in which the speed is independent of density (SI Appendix, Fig. S6).

To investigate experimentally how the end-dissociation rate (k_end) and the lattice-dissociation rate (k_off) affect traffic jam formation, we varied the salt concentration in our assays; both rates increased when the KCl concentration was increased. However, interpreting these results was confounded by the large number of experimental parameters (four), which also included the motor concentration (which influenced k_on) and the microtubule length. We therefore used stochastic simulations and theory to facilitate the interpretation of these data. We found that only three of the four parameters are independent: There is a trade-off between the association rate and the microtubule length in the sense that a lower association rate can be compensated for by a longer microtubule length. This trade-off is a consequence of the antenna mechanism mentioned above. In our simulations, we therefore chose three independent parameters to vary systematically and asked what ranges of values led to traffic jams and what were the properties of the jams. The parameters we used were (i) the end-dissociation probability, , (ii) the Langmuir density 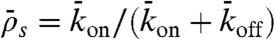, which corresponds to the steady-state, fractional occupancy of the lattice in the absence of motility (also known as the Langmuir isotherm or equilibrium density, ref. 13), and (iii) 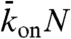, which is proportional to the rate of motor binding to the entire lattice. The propensity to form jams increased as the first parameter was decreased and the latter two parameters 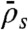and 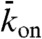were increased. To display our results in two-dimensional (as opposed to 3D) phase diagrams, we considered two values for the third parameter: 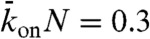, corresponding to a low total binding rate (Fig. 4, Center), and 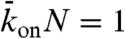, corresponding to a high total binding rate (Fig. 5, Center). In the simulations we took N = 1,250, corresponding to a 10-μm-long microtubule.

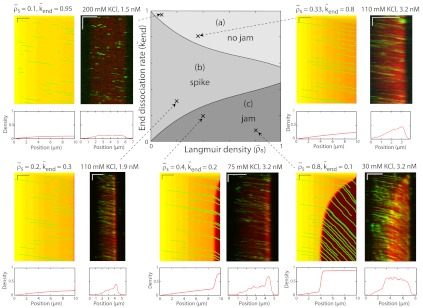
Fig. 4.

Simulated phase diagram for bottleneck-induced traffic jams at low motor concentration or for short microtubules. The central panel shows three distinct behaviors that depend on the Langmuir density (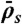, x axis) and the end-dissociation rate (, y axis). The association rate is fixed at 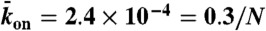, with N = 1,250. (Domain a) Only the LD region is present—i.e., no jams occur. (Domain b) A density spike forms at the microtubule end. (Domain c) LD and HD regions coexist and traffic jams are present. The surrounding panels depict examples of simulations (Right) and experimental data (Left) in the different domains of the phase diagram. Below each kymograph, a motor density profile at steady state is shown. The intensity scale bar of the simulations is the same as in Fig. 1C. The experimental density varies from 0 to 3,000 arbitrary units (a.u.) [Scale bars: 2 μm (horizontal) and 2 min (vertical).]

Fig. 5.

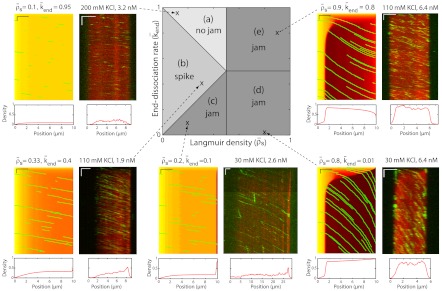
Simulated phase diagram for traffic jams at high motor concentration or for long microtubules. Central panel shows five distinct behaviors that depend on the Langmuir density (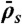, x axis) and the end-dissociation rate (, y axis). The association rate is fixed at 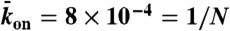, with N = 1,250. (Domain a) Only LD region is present—i.e. no jams form. (Domain b) There is only an LD region with a density spike at the microtubule end. (Domains c, d, and e) LD and HD regions coexist and traffic jams are present. (Domain c) Jams are only bottleneck-induced (due to 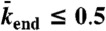) and not density-induced (due to 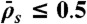). The motor-density profile reaches a plateau at the level 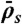in the LD region. (Domain d) Jams are both bottleneck- and density-induced due to 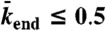and 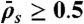. The motor density in the HD region increases toward the microtubule plus end when 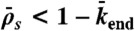, and decreases when 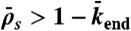. (Domain e) Jams are density-induced due to 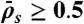but not bottleneck-induced due to 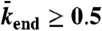. The surrounding panels depict examples of simulations and experimental data in the different domains of the phase diagram. The intensity scale bar of the simulations is identical to the one in Fig. 1C. Below each kymograph, a motor density profile at steady state is shown. The experimental density varies from 0 to 2,500 arbitrary units (a.u.) [Scale bars: 2 μm (horizontal), 2 min (vertical).]

When the binding rate is low (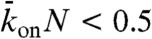), there are three steady-state behaviors that the motor-filament system can display. These behaviors are represented by different domains in the phase diagram (Fig. 4, Center). At high end-dissociation rates, no jams occur (Fig. 4, domain a). At intermediate end-dissociation rates, there is a spike in motor density (with width below the optical resolution) restricted to the very end of the microtubule, which corresponds to motors pausing and being replaced by incoming motors (Fig. 4, domain b). At low end-dissociation rates, there is a pileup of motors at the microtubule end because the flux to the end exceeds the flux from the end. An HD region is initiated at the end and propagates to form a traffic jam of finite length, a bottleneck-induced jam (Fig. 4, domain c). The boundary between domains b and c occurs when the flux to the microtubule end (by motor walking) can be just balanced by the flux off the end (due to detachment from the last subunit). We observed all three behaviors experimentally by changing the KCl concentration in solution (Fig. 4 kymographs and density scans). When the KCl concentration was increased, both the lattice-dissociation rate, k_off, and the end-dissociation rate, k_end, increased (SI Appendix, Fig. S1); this is equivalent to moving diagonally from the bottom right (30 mM KCl) to the top left (200 mM KCl) in the phase diagram. When the motor concentration was increased (at a fixed salt concentration, e.g., 110 mM KCl), the lattice association rate, k_on, increased; this is equivalent to moving horizontally from left (low motor concentration) to right (high motor concentration) in the phase diagram. There was good qualitative agreement between the experimental kymographs and the simulations (the locations of the simulations are marked by x on the phase diagram).

When the binding rate is high (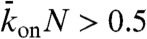), two additional behaviors are observed (Fig. 5). They occur when the critical density for jams is reached on the lattice, and not only at the microtubule end. We call these jams density-induced jams. Density-induced jams occur when the Langmuir density, 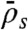, exceeds 0.5 (corresponding to the density at which the flux is a maximum, in the case of a linear speed-density curve in Fig. 3 C and D; see SI Appendix, Fig. S7). Density-induced jams occur in domains d and e of Fig. 5, Center. If the end-dissociation probability is low (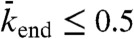), jams are both bottleneck- and density-induced; they are formed both from the end and along the lattice (Fig. 5, domain d and SI Appendix, Fig. S8). If the end-dissociation probability is high (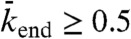), jams are only density-induced and form only along the lattice (Fig. 5, domain e). In the latter case, the density decreases all along the HD region of the microtubule, whereas in the former case, and when 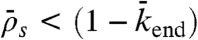, there is a higher density at the end (compare simulations in domains d and e in Fig. 5), which is responsible for a decrease in motor speed. Below the critical Langmuir density (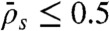), the domains of the phase diagram are similar to those in Fig. 4: no jams at high end-dissociation probabilities (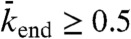, Fig. 5, domain a), and either a spike at the microtubule end for intermediate end dissociations (Fig. 5, domain b) or bottleneck-induced jams (Fig. 5, domain c) at low end-dissociation probabilities (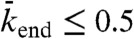). The boundary between domains b and c is given by the equality of fluxes at the plus end: 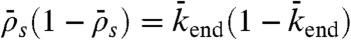and therefore 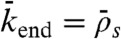, when 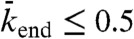and 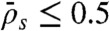. As in the case of low binding rates, there was good qualitative agreement between the experimental kymographs and the simulations as the experimental parameters were varied by changing the KCl and motor concentrations. Again, the locations of the simulations are marked by x on the phase diagram.

Discussion

We defined a traffic jam on a microtubule as the coexistence of a high-density/low-speed region (the jam) and a low-density/high-speed region, with an abrupt change in the transition region. We found that the motor protein Kip3 can form traffic jams on its own, in the absence of cargo or other microtubule-associated proteins (MAPs). This report shows that molecular motors can form a congested phase that slows transport. This behavior is a dramatic example of macromolecular crowding (2), demonstrating jamming by active, energy-dissipating molecular interactions.

By varying the motor concentration in solution, the length of the microtubules, and the lattice- and end-dissociation rates, we observed several qualitatively different behaviors: (i) no density discontinuity (no jam), (ii) a density discontinuity that was localized to the very end of the microtubule (a spike), (iii) a density discontinuity that propagated from the microtubule end (bottleneck-induced jam), and (iv) a density discontinuity that initiated on the microtubule lattice (density-induced jam). These behaviors are in good qualitative agreement with simulations based on the Parmeggiani-Franosch-Frey model (13), indicating that this model captures many of the main principles underlying the formation of molecular traffic jams. We could not test the model quantitatively, in the sense that all experimental parameters could be globally constrained, due, in part, to uncertainties in measuring the protein concentrations. Whether quantitative agreement would be possible is not certain because experiments show that two of the assumptions behind the Parmeggiani-Franosch-Frey model—the independence of the lattice-dissociation rate and end-dissociation rate on motor density—do not hold (see Fig. 3 and ref. 19, respectively).

Although all our experiments were performed using Kip3, which is in the kinesin-8 family, the mechanisms that we have uncovered allow us to extrapolate to other kinesins. For example, based on our analysis, we predict that the transport motor kinesin-1, under physiological buffer conditions, does not form jams. This prediction, which accords with the experimental results cited in the Introduction (17, 20), is based on the relatively low processivity of kinesin-1 (< 1 μm) (26) and its high end-dissociation rate (> 3 s^-1), which place it in the “no jam” region of the phase diagram. Thus we could describe these properties of kinesin-1 (and other transport motors such as kinesin-2, ref. 27, and kinesin-3, refs. 28 and 29, which also have comparatively low processivities compared to the kinesin-8s such as Kip3 studied here or Kif18A, ref. 21) as adaptations to avoid traffic jams.

Our experiments may give insight into another puzzling feature of intracellular transport. The microtubule-based transport of cellular cargoes is often saltatory (30, 31), characterized by periods of directed transport along microtubules and diffusion in the cytoplasm. To understand the logic behind this behavior, consider the following argument. If the cargo velocity decreases with density, as in Fig. 3, a cargo traffic jam will form above a critical cargo density (SI Appendix, Fig. S7). Then, a further increase in the flux cannot be achieved by increasing the density, but paradoxically, the flux is rather increased by decreasing the density—a striking example of the principle “less is more.” Saltatory motion may therefore be an adaptation to maximize cargo flux.

Why are kinesin-8s so processive? The answer is that kinesin-8s function to control microtubule length, and this control mechanism only works provided the run length is longer than the microtubule length (19). Do kinesin-8s form traffic jams in cells? First, it is possible that some kinesin-8s, such as Kif18A, do indeed form traffic jams, based on the high motor density seen adjacent to the kinetochore during mitosis (32, 33). Second, operating in cells on “nonstabilized” microtubules, Kip3, is a depolymerase which dissociates rapidly as it removes tubulin dimers from the end; thus Kip3 clears its own jams by preventing a bottleneck from forming at the end.

Cellular cargoes are expected to have a higher propensity for forming jams than the individual motor proteins studied here because cargoes may be transported by several motors and in vitro experiments show that transport by multiple motors is more processive than transport by a single motor (34). An elegant way to reduce cargo jams would be for the motors to sense the steric forces associated with crowding of their cargoes and, in response, to reduce their processivity, just as Kip3 motors increase their dissociation rate as the density increases (Fig. 3C, Inset). Thus force-dependent dissociation, thought to be responsible for motor coordination in mitosis and axonemal motility (35–37), may also be important for maximizing cargo flux, not just in regulating cargoes containing oppositely directed motors (38).

In pathological situations—mutations in motors or interference by MAPs such as tau—abnormal aggregations of cargoes with associated decreases in speed are observed (6–9). Whether these aggregations are traffic jams, as defined here, is not clear. Furthermore, the circumstances in vivo that lead, for example, to neurodegeneration (39) are much more complex than our simplified in vitro model. Nevertheless, our simplified motor-microtubule model provides insight into the logistics of intracellular transport and makes testable predictions, for example, that interfering with motor dissociation, by MAPs or by opposing motors present on the same cargo (20, 40–43), will increase the propensity for jamming.

Materials and Methods

The 6xHis-Kip3-mCherry construct was created by exchanging the coding region of EGFP in 6xHis-Kip3-EGFP by that of mCherry. Kip3 motors were expressed and purified as described previously for 6xHis-Kip3-EGFP (22). Microtubules (ratio of biotinylated to nonbiotinylated tubulin 1∶30) were polymerized in GMPCPP, further stabilized by 10 μM taxol (19), and bound to the surface of a flow chamber with antibiotin antibodies. Flow chambers were constructed and assays were performed as described previously (19). Both mCherry and EGFP fluorophores were excited with a 488-nm laser (Argon; Coherent) using TIRF microscopy. Images were recorded on an EM-CCD (iXon-DV 897; Andor) camera with image acquisition every 1–20 s. Kymographs were generated and analyzed using Metamorph software (Molecular Devices Corporation). Single-molecules were tracked by FIESTA software (24) written in MATLAB.