Correlated neural variability in persistent state networks

Abstract

Neural activity that persists long after stimulus presentation is a biological correlate of short-term memory. Variability in spiking activity causes persistent states to drift over time, ultimately degrading memory. Models of short-term memory often assume that the input fluctuations to neural populations are independent across cells, a feature that attenuates population-level variability and stabilizes persistent activity. However, this assumption is at odds with experimental recordings from pairs of cortical neurons showing that both the input currents and output spike trains are correlated. It remains unclear how correlated variability affects the stability of persistent activity and the performance of cognitive tasks that it supports. We consider the stochastic long-timescale attractor dynamics of pairs of mutually inhibitory populations of spiking neurons. In these networks, persistent activity was less variable when correlated variability was globally distributed across both populations compared with the case when correlations were locally distributed only within each population. Using a reduced firing rate model with a continuum of persistent states, we show that, when input fluctuations are correlated across both populations, they drive firing rate fluctuations orthogonal to the persistent state attractor, thereby causing minimal stochastic drift. Using these insights, we establish that distributing correlated fluctuations globally as opposed to locally improves network's performance on a two-interval, delayed response discrimination task. Our work shows that the correlation structure of input fluctuations to a network is an important factor when determining long-timescale, persistent population spiking activity.

The dynamics of the nervous system are inherently stochastic at all levels from ion channel (1) to single cell (2), neural population (3, 4), and whole-brain activity (5). A central challenge in neuroscience is to relate the neural variability expressed at the cellular and circuit levels to the variability of cognitive behavior. Short-term memory (6–8) and decision-making (9, 10) are tasks where this link can be established, because there is trial to trial variability of both subject response and associated neural correlates. Furthermore, neural representations based on probabilistic codes (11) as opposed to trial averaged responses have been successful at capturing key aspects of these behaviors (12), and spiking variability is inherent in these cognitive theories. However, relating the statistical structure of the inputs that cause spiking variability to the variability of population-wide neural activity is often difficult (13–16).

Spiking activity with timescales much longer than the timescales of typical synapses and cellular membrane potentials is an established neural correlate of working memory and decision-making. Most famously, persistent activity lasting for many seconds has been reported in prefrontal cortices of primates (6, 17, 18) and rodents (19) during delayed response tasks and premotor areas driving oculomotor gaze fixation (20, 21). In these cases, an initial transient stimulus recruits persistent firing activity, providing a neural basis for short-term working memory. These observations have led to models, both of large-scale networks of spiking neurons (22–26) and reduced attractor-based frameworks (25–34), aimed at reproducing a continuum of persistent states. A prevailing assumption in all spiking network models of persistent activity (to our knowledge) is that neurons receive statistically independent input fluctuations from sources external to the network. This assumption results in population activity with limited dynamic variability because of population averaging (16, 35), a distinct advantage when building networks with the primary task of maintaining fixed firing rates over long timescales. However, the dense architecture of cortex often provides pairs of neurons common inputs from overlapping presynaptic targets (36–38). External sensory input or intrinsic cortical dynamics may provide correlated input fluctuations to pairs of cortical cells through this presynaptic overlap (39–42), leading to trial to trial covariability of output spike trains (3). Although reported correlations are sometimes small (3, 15), even a minuscule pairwise correlation can lead to very large population variability when responses are pooled over large groups of neurons (16, 35). Hence, neuronal circuits that promote robust persistent activity despite such correlated fluctuations are critical for proper cortical function.

In a two-interval, delayed response discrimination task, the work by Romo et al. (18) combined short-term memory and decision tasks and identified populations of neurons in primate prefrontal cortex that participate in both these computations. Machens et al. (26) presented a model with mutual inhibition between two distinct populations of neurons that captured both the persistent activity and competitive decision dynamics seen in experiment. The model used independent fluctuations to all neurons; however, simultaneous recordings from neuron pairs in the same (43) and related (44) experiments show positive trial-to-trial covariability, even for neurons with opposite stimulus tuning. It is well known that mutually inhibitory networks with deterministic dynamics suppress the influence of input similarities, while amplifying input differences (27, 45). We build on these results and show that the stability of the persistent state in a trial variable stochastic network is enhanced when weakly correlated input fluctuations are distributed globally across neurons in both model populations compared with the case when correlations are only local within each population. A reduced random walk attractor model shows that the increased stability is caused by an opposing interaction between the anticorrelating mutual inhibitory circuitry and the globally correlating fluctuations. Finally, this enhanced stability of the memory state in the presence of global correlations improves task performance by a large degree. Thus, although past studies have identified constructive roles for correlations in static population coding frameworks (43, 46, 47), we analyze how correlated variability affects the dynamic stability of persistent neural activity.

Results

Persistent State Spiking Model.

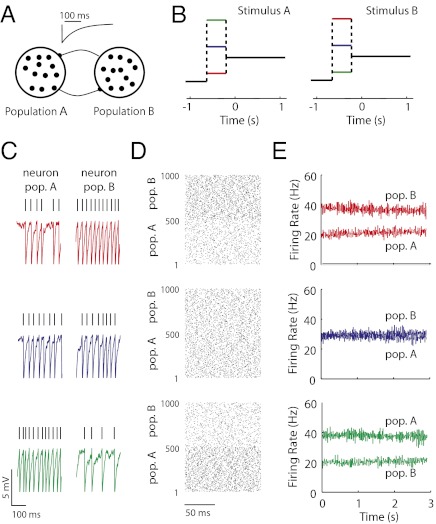
Recurrent inhibition between populations of neurons produces a competitive, winner take all dynamic, and it is a common architecture in decision-making (9, 28, 29) and persistent activity circuits (21, 26, 27). We considered the spiking responses of a network of leaky integrate and fire model neurons grouped into two functional populations (labeled A and B) having strong and symmetric interpopulation inhibition (Fig. 1A and SI Materials and Methods). The populations were presented with a static excitatory stimulus for an initial period of 500 ms, after which the stimulus was removed; the resulting long-timescale population dynamics were analyzed (Fig. 1B). The population response (ensemble-averaged firing rate) (Materials and Methods) was persistent, with rates remaining at near constant levels for seconds after stimulus removal. Furthermore, there was a continuum of such persistent states, each determined by different initial stimulus configurations (three example cases are shown in Fig. 1 C–E). In this way, the poststimulus activity was an accurate reflection of the initial stimulus, providing a model of short-term memory (26).

Fig. 1.

Recurrent inhibition produces a continuum of persistent states in a spiking network model. (A) Schematic of two populations (A and B) each having 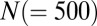leaky integrate and fire neuron models. Neurons between populations inhibited one another; the time course of a single spike-induced inhibitory current is shown (Inset). (B) Stimulation protocol showing an initial stimulus period (<0 s) when populations A and B received distinct stimuli followed by a long period (>0 s) when the populations received an equal bias. The colors indicate three example stimulation sequences. (C) Representative membrane potential traces from a neuron in either population. (D) Spike time rasters for the entire network. Population membership is indicated on the vertical axis. (E) The evolution of populations A and B firing rates (Materials and Methods). Colors in C–E match the stimulation protocols in B.

The network retained memory through a balance of competitive forces. The population with a higher stimulus-evoked firing rate suppressed the other population, effectively disinhibiting itself; therefore, it maintained high firing rates after the stimulus was removed. This balance was dynamically maintained and hence, sensitive to firing rate fluctuations. In our spiking model, the membrane potential fluctuations were substantial, consistent with in vivo neural activity (Fig. 1C). However, the fluctuations were also independently distributed to all of the neurons, producing a relatively asynchronous population dynamic (Fig. 1D). In this case, population rate variability scaled roughly inversely to population size. For reasonably sized networks, the population activity had little variability, allowing rates to remain stable for long periods of time (Fig. 1E). Thus, despite the significant single neuron variability, population averaging produced a stable persistent network state. In the next section, we relax the assumption of independent variability and consider the consequences for the stability of persistent network states.

Global Correlated Variability Preserves Persistent Network States.

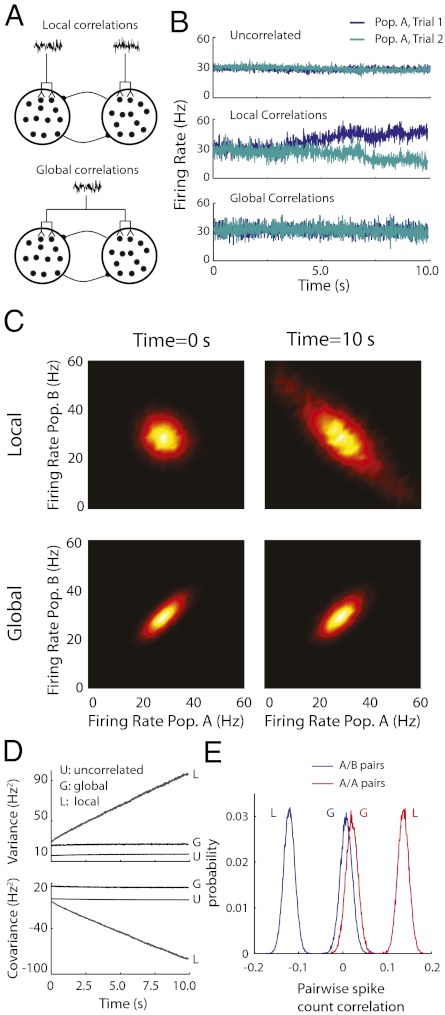
The connectivity within cortical networks is dense, with groups of neurons receiving a significant amount of common synaptic input (36–38). This overlap of synaptic architecture correlates the membrane potential fluctuations of distinct neurons, and in several cortical areas, the magnitude of correlation can be significant (39–42). In complex cortical circuits, it is difficult to determine the precise structure of the joint fluctuations to different neuron populations. This structure may depend on, for example, physical proximity (48) or functional similarity (49) between populations. We studied two simple schemes in which correlated stochastic inputs were incorporated into our two-population persistent activity model. The first scheme was a local framework, in which only neurons within the same population received correlated inputs (Fig. 2A, Upper). The second scheme was a global framework, in which all neurons, both within and between populations, received a common source of input fluctuations (Fig. 2A, Lower). The local model assumes that shared input fluctuations respect the network's functional segregation (population A vs. B), whereas the global model considers correlated fluctuations that ignore any network divisions. In both cases, the magnitude of input correlation was small (0.05), meaning that individual neurons still received a significant amount of independent variability. Despite this small degree of pairwise input correlation, its impact was dramatic at the population level (16, 35), because common fluctuations could not be attenuated through population averaging. In our model, integrated population variance increased by a factor of 25 compared with the uncorrelated case.

Fig. 2.

Influence of local vs. global correlated input variability on the stability of persistent activity. (A) Schematic of the distribution of common fluctuations in the local (Upper) and global (Lower) correlation frameworks. (B) Example pair of trials showing the temporal evolution of population firing rates with uncorrelated (Top), locally correlated (Middle), or globally correlated (Bottom) inputs. (C) The probability density of population rates 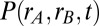for 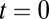s (Left) and 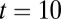s (Right) estimated from repeated trials of the spiking network model. This estimation was done for both the local (Upper) and global (Lower) correlation schemes. The 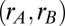grid was sampled at 1 Hz, and 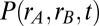was smoothed for presentation. (D) Population rate variance and covariance as a function of time for the uncorrelated (U), local (L), and global (G) correlation schemes. (E) Pairwise spike count correlation ( 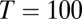ms) for all neuron pairs both within and between populations during the local and global correlation schemes.

Although both local and global correlation models received significant population-wide input variability, they nevertheless supported a continuum of persistent states during the initial poststimulus period (Fig. S1). To ease presentation, we hereafter study the symmetric case, where the persistent state has equal rates for both populations (Fig. 1 C–E, blue); however, our results are by no means limited to the case. For uncorrelated inputs, the persistent state remained stable for long periods (>10 s) after stimulus removal (example trials are in Fig. 2B, Top). In contrast, local correlations yielded a persistent state that was stable for a short period directly after stimulus removal, but the trial-to-trial population firing rates began to drift after a few seconds (example trials are in Fig. 2B, Middle). Finally, the population rates for the globally correlated model were stable long after (∼10 s) stimulus removal (example trials are in Fig. 2B, Bottom). Although the stability for the global model persistent state was similar to the uncorrelated model, the overall variability of firing rates was significantly larger, which is expected from simple pooling arguments (16, 35).

To better quantify the drift in the population rates, we performed a large number of trials (10⁴) and estimated the probability density of the joint population rates as it evolved over time. When fluctuations were local, there was a significant drift of the trial-to-trial population activity along the antidiagonal firing rate axis (Fig. 2C, Upper and Movie S1). This drift was much reduced when fluctuations were global (Fig. 2C, Lower and Movie S1). The trial-to-trial population rate variance and covariance between populations A and B computed over trials mirrored these differences (Fig. 2D). Furthermore, although the globally correlated model showed time stationary variability, its overall variability was nevertheless larger than the uncorrelated model (Fig. 2D), again because of population-wide pooling of activity. Thus, when the correlations of input fluctuations were global to the entire network rather than local to subpopulations within the network, the stability of persistent neural activity was increased.

The correlations between the spike trains of individual neuron pairs were substantially different for networks with local or global input correlation. Local input correlations produced a significant positive spike count correlation for neuron pairs that were within the same population but an equally strong negative correlation for neurons that were members of distinct populations (Fig. 2E). In contrast, global input correlations produced weak pairwise correlations (Fig. 2E). This attenuation was caused by cancelation mechanisms similar to those operative in balanced cortical circuits (15). Furthermore, for the model with global input correlations, neuron pairs that were in different populations had a mean correlation that was positive (0.01), albeit smaller than the correlation for neurons within the same population (0.02) (compare blue G with red G curves in Fig. 2E). This finding was in contrast to the large negative correlation (−0.13) observed for neurons in different populations when input correlations were local (compare blue L with blue G curves in Fig. 2E). Paired recordings in prefrontal cortex of primates (43) participating in a delayed response task showed a net positive correlation for all neuron pairings (within-population pairs had a mean correlation coefficient of 0.15, and across-population pairs had a mean correlation coefficient of 0.05) (table 1 in ref. 43). Although we do not expect a quantitative match between our model and the data, the qualitative match that all correlations were positive gives strong experimental justification for the global input model.

In total, although globally correlated fluctuations represent a larger source of overall input covariability, they do not destroy long-term persistent activity and result in weaker pairwise correlations than a model with only local correlations. We next study a reduced framework to uncover the core mechanism for these findings.

Random Walk Firing Rate Model.

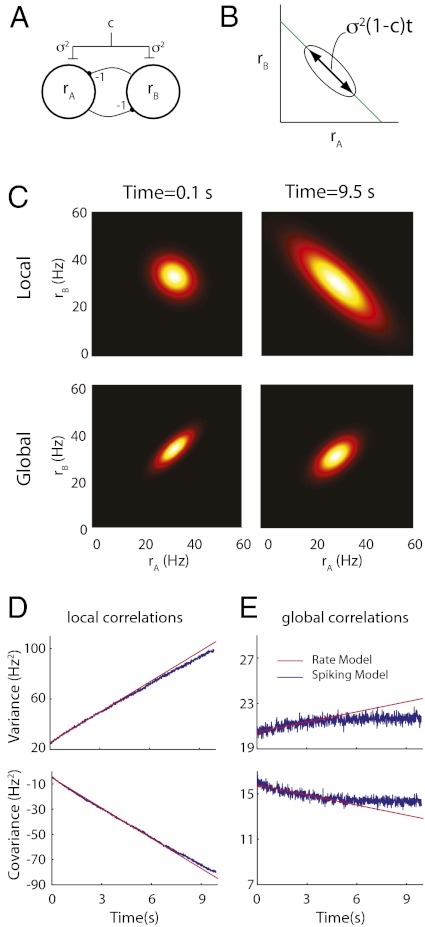
Phenomenological models often consider the aggregated firing rate of a population of cells rather than individual spiking activity (50). In particular, firing rate models of mutually inhibitory populations have captured key aspects of decision-making (28, 29) and short-term memory (26) circuits. We considered a firing rate model of our persistent state network (Fig. 3A) where the population firing rates 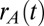and 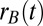obeyed the stochastic differential equations (Eq. 1)

Fig. 3.

Phenomenological random walk firing rate model of persistent activity. (A) Schematic showing the rate model framework with 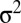(the total input variance to a population) and 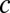(the input correlation given to the two models). (B) Schematic showing the line attractor (green line) and trial variable spread along the attractor (circle). (C) The probability density 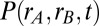shown for 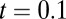s (Left) and 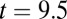s (Right) for the model with local (Upper) and global (Lower) correlations. The density is Gaussian, with mean and variance calculated from the associated Fokker–Planck equation (SI Materials and Methods). (D) Comparison between the population rate variance (Upper) and covariance (Lower) computed from the spiking network simulations and the analytic solutions from the firing rate model. Both networks had local correlated fluctuations ( 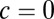for firing rate model). E is the same as D but for the models with global fluctuations ( 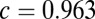for firing rate model).

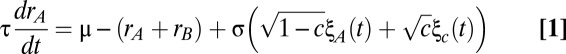and (Eq. 2)

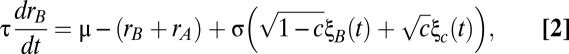where 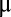is a symmetric mean input and 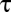is the population timescale. The coupling between the populations caused degeneracy in the dynamics, with a continuum of neutrally stable states (i.e., a line attractor) along the antidiagonal 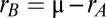(Fig. 3B, green line). The population activity and coupling was linear to facilitate analysis; for a general class of nonlinear models, our model is an appropriate limiting case (SI Materials and Methods and Fig. S2).

Population-wide input fluctuations were modeled by the combination of three Gaussian white noise processes: 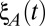and 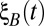were private fluctuations to populations A and B, respectively, and 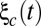was a global fluctuation to the two populations. The total fluctuations to a population had intensity 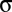, with the input correlations between populations set by 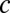(Fig. 3A). In our reduced model, 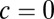corresponds to the local correlation spiking network, whereas 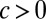corresponds to a globally correlated network. The model is a 2D Ornstein–Uhlenbeck process (51), and the associated Fokker–Planck equation gave an analytic solution for the time-dependent probability density 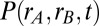(SI Materials and Methods shows a full derivation).

The density 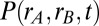is Gaussian, with a mean 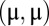and a time-dependent variance and covariance. Importantly, the degeneracy of the model makes the stochastic motion along line attractor akin to a Brownian walk, having a time-dependent spread (covariance) proportional to (Eq. 3)

For the local model (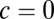), the spread is maximal and covers a large range of the linear attractor as time elapses (Fig. 3C, Upper and Movie S2). Fitting the reduced model parameters (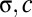) to the spiking simulations (SI Materials and Methods) yielded 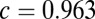for the global network. The large 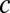value resulted from population averaging that amplified the weak pairwise correlations (Fig. 2E). This finding caused a much reduced spread along the line attractor for the global model (Fig. 3C, Lower and Movie S2). The variance and covariance of the spiking simulation population activity for both local (Fig. 3D) and global (Fig. 3E) correlations were well-matched to the analytic results from the firing rate models. Thus, despite the complexity of the spiking network, the population activity behaves like a Brownian walk for moderate timescales, justifying our simplified rate model approach. However, our theoretical expressions must break down for sufficiently long timescales, because firing rates in the linear model were unbounded, whereas the firing rates from the spiking simulations must remain positive.

In total, the structure of mutual inhibition created a line attractor persistent state that was organized along the antidiagonal in firing rate coordinates (26). Globally correlated fluctuations were orthogonal to the direction of instability and thus, best mitigated drift of the persistent state caused by input fluctuations.

Global Correlations Improve Discrimination in Delayed Response Task.

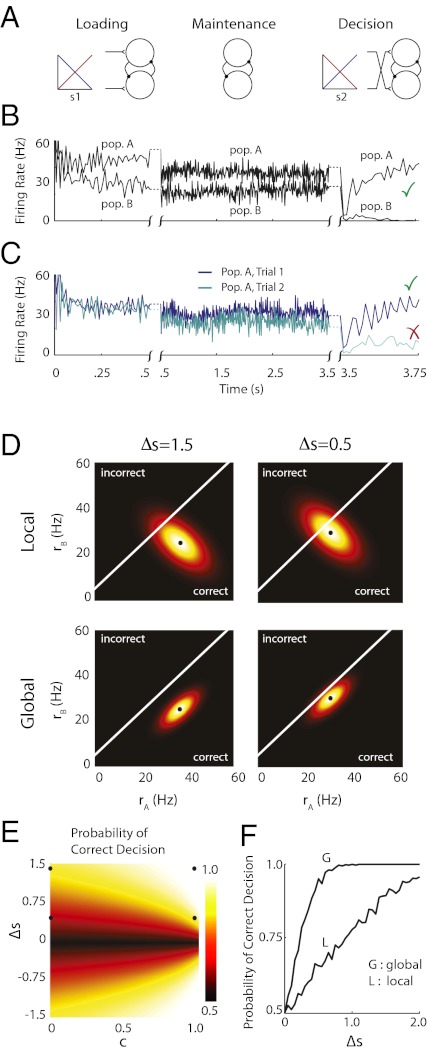
The motivating experiments for the mutual inhibition model of persistent activity were from primate prefrontal cortex recordings during a delayed response, two-interval discrimination task (18, 26, 43). Briefly, a vibrating input with a fixed frequency was presented to the fingertips, and neurons sensitive to this stimulus could be grouped into two classes (our populations A and B) based on their response: neurons either increased or decreased their firing rate to increasing input frequency (Fig. 4A, Left). This initial stimulus loaded the network in a specific location on the line attractor (Fig. 4B, Left). The stimulus was removed (Fig. 4A, Center), and the loaded state was maintained in working memory during a delay period (Fig. 4B, Center). Finally, a second stimulus was presented, and the monkey was directed to indicate if the first stimulus vibrated at a frequency that was faster than the second stimulus (Fig. 4A, Right). This decision task had the neural correlate that one population's firing rate reached a high value, whereas the other decreased its firing rate, with the specific choice depending on which stimulus had the higher frequency. The initial model by Machens et al. (26) replicated this memory and decision task. However, when input fluctuations were correlated in our model, the sizable trial to trial variability sometimes caused a misclassification error by the spiking network (Fig. 4C). We investigated the effects of local and global correlations on the performance of network discrimination in the delayed, two-interval discrimination task.

Fig. 4.

Global correlations improve task performance in a two-interval, delayed response discrimination task. (A) Schematic showing the stimulation during the loading, maintenance, and decision stages of the task. (B) Spiking network population firing rates (populations A and B) during one trial of the task (local correlations). At the decision stage, the model performed the correct decision (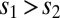). (C) Population A firing rates for two separate but otherwise identical trials of the task. The fluctuations cause one trial to produce the incorrect decision. (D) Analytic densities 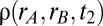for the rate model with 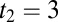s for local (Upper) and global (Lower) correlations for tasks where 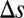is large (Left) or small (Right). (E) Probability of correct decision for the firing rate model in (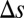, 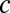) parameter space computed from integrals of 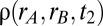. The dots correspond to the four cases shown in C. (F) Probability of correct decision computed from the spiking model (5,000 trials) as a function of 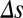for local and global correlations.

Without loss of generality, we assumed that the first stimulus (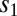) loaded the network to the symmetric 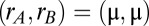state. We computed the density 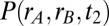from the firing rate model, where 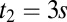was the presentation time of the second stimulus. The value of the second stimulus (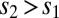) defined a line in 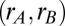space, and a reasonable approximation to the decision process is that realizations with joint rates that were below (above) the line led to correct (incorrect) discriminations (Fig. 4D). For discriminations between first and second stimuli with large differences 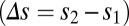, the distance between the loaded firing rate 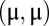and the decision line was large. In this case, the decision task was robust to moderate variability, and both local and global models performed adequately (Fig. 4D, Left). However, for finer discriminations, the reduction of spread along the line attractor for global correlations greatly enhanced the probability of correct decision compared with the model with local fluctuations (Fig. 4D, Right). To explore this result, we integrated 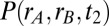below the decision line to find the probability of correct decision over a large range of 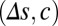parameter space (Fig. 4E and SI Materials and Methods). When |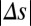| was small, the probability of correct decision was dramatically improved with increasing 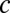, whereas for large |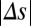|, the decision process was less affected by 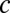. Finally, we verified this prediction with simulations of the spiking network during the decision process for both local and global input correlations (Fig. 4F). For small 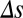, the presence of global fluctuations increased task performance from near 65% correct decision for local to almost 95% for global input correlations.

In summary, global as opposed to local input correlations greatly enhanced performance for fine discriminations in a delayed response task. This enhancement was because of the increased stability of the persistent state for global correlations, enhancing the fidelity of the final stimulus comparison.

Discussion

Inhibitory interaction between distinct populations of neurons is an often proposed mechanism for persistent neural activity. It is known that mutual inhibition between populations amplifies input differences to populations while suppressing input similarities (27, 45). However, how these principles operate in a persistent activity model that exhibits trial to trial variability has not been addressed. Previous spiking models of persistent activity have assumed that external input fluctuations are independent for all neurons (22–26, 33), and thus, population pooling attenuates the variability at the network level (16). Heuristic firing rate models with stochastic inputs are not limited to small variability, and past work with them has given insight about how fluctuations promote stochastic drift along a continuum attractor (33, 34). However, these studies have also assumed that the fluctuations to distinct populations are uncorrelated, being equivalent to the local correlation model in our study. Our primary finding was that robust stability of the persistent state required common fluctuating inputs to be globally distributed over the network as opposed to only locally within each population. In our spiking model, the recurrent inhibition and global correlations balance to give overall weak positive pairwise spike correlations, consistent with the experimental recordings that motivated the model (43). Finally, this enhanced stability with global fluctuations improved network performance in a two-interval, delayed response discrimination task.

Our network modeled functionally segregated populations that were distinguished by their stimulus preference. Global correlations to such a network require trial-variable inputs that are not related to this segregation and rather indiscriminately correlate the activity of all neurons. Although this assumption is unreasonable for populations with a clear spatial lateralization (21, 52), it is appropriate for persistent activity networks in prefrontal cortex that are involved in working memory (18, 43, 44). In these areas, simultaneous recordings from neuron pairs show fast-timescale cross-correlagrams of spiking activity peaked at a zero lag (43, 44), consistent with a source of common input. The magnitude of output spike train correlation is larger for neuron pairs that have similar tuning than those pairs with dissimilar tuning, and therefore, output correlations are related to population segregation. However, this finding does not necessarily imply that external input correlations are local, because it is also consistent with neurons in the same population receiving common inhibition from within the network (this finding is the case for our network) (Fig. 2E). Recently, mean field techniques have been developed that can combine internal and external sources of correlation (15, 53–55). Using these techniques to analyze the dynamic behavior in our network is an interesting potential avenue of study.

It is known that the combination of an anticorrelated stimulus tuning and positive trial to trial correlations improve population-based codes compared with codes in which neurons have independent variable activity (46, 47). Furthermore, when decisions involve a comparison between two population rates, a subtractive computation can benefit from correlated variability (43). In both of these cases, there is an anticorrelating deterministic structure (trial averaged), and thus, positive correlations in stochastic activity (trial variable) best mitigate the impact of fluctuations on computation. Our model extends this general principle of improving network function by matching the structure of network dynamics with the joint structure of stochastic inputs, to the case of persistent state networks. Other models of persistent activity involve either recurrent excitation (22, 23) or feedforward architectures (30). Correlated activity in these networks will no doubt also affect persistent neural activity, but how the structure of input fluctuations will interact with circuit-based dynamics is unclear and open to future investigation.

Materials and Methods

A detailed description of the spiking network model can be found in SI Materials and Methods. We let the spike train from neuron 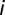of population 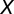be 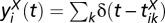, where 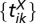is a set of spike times (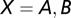). The firing rate of population 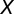over time window 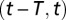is the random variable 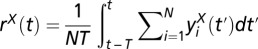. Population rate variance was measured as 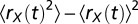, and covariance was measured as 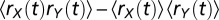; here, 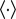is an expectation over trials. We take 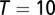ms, and we use 10⁴ trials to compute population statistics. The reduced firing rate model and associated analysis are presented in SI Materials and Methods.