The Infinitely Many Genes Model for the Distributed Genome of Bacteria

Abstract

The distributed genome hypothesis states that the gene pool of a bacterial taxon is much more complex than that found in a single individual genome. However, the possible fitness advantage, why such genomic diversity is maintained, whether this variation is largely adaptive or neutral, and why these distinct individuals can coexist, remains poorly understood. Here, we present the infinitely many genes (IMG) model, which is a quantitative, evolutionary model for the distributed genome. It is based on a genealogy of individual genomes and the possibility of gene gain (from an unbounded reservoir of novel genes, e.g., by horizontal gene transfer from distant taxa) and gene loss, for example, by pseudogenization and deletion of genes, during reproduction. By implementing these mechanisms, the IMG model differs from existing concepts for the distributed genome, which cannot differentiate between neutral evolution and adaptation as drivers of the observed genomic diversity. Using the IMG model, we tested whether the distributed genome of 22 full genomes of picocyanobacteria (Prochlorococcus and Synechococcus) shows signs of adaptation or neutrality. We calculated the effective population size of Prochlorococcus at 1.01 × 10¹¹ and predicted 18 distinct clades for this population, only six of which have been isolated and cultured thus far. We predicted that the Prochlorococcus pangenome contains 57,792 genes and found that the evolution of the distributed genome of Prochlorococcus was possibly neutral, whereas that of Synechococcus and the combined sample shows a clear deviation from neutrality.

Introduction

The concept of a biological species is difficult to apply to bacteria (Cohan 2002). Traditional species are ecologically distinct, their divergence is irreversible, and their diversity is limited by outcrossing. For demarcating bacterial species, a cutoff of 3% divergence in 16S ribosomal RNA sequence was previously recommended as a conservative and practical criterion (Goebel and Stackebrandt 1994). However, even phenotypically identical bacteria coexisting in the same environment that follows this criterion frequently have significantly different gene content (Akopyants et al. 1998; Lawrence and Hendrickson 2005). Indeed, experimental data indicate that new genes will be discovered even after sequencing hundreds of genomes (Koonin and Wolf 2008; Lapierre and Gogarten 2009). Accordingly, the concept of the pangenome was introduced to describe the global gene repertoire of a bacterial taxon (Medini et al. 2005; Tettelin et al. 2005). It consists of the core genome, the genes shared by all members of this taxon, and the dispensable (or accessory) genome, the genes present in some but not all the isolates that belong to this taxon (Medini et al. 2008; Kittichotirat et al. 2011).

An important prediction of the distributed genome hypothesis is that individual cells maintain compact genomes, whereas, at the population level, a huge number of dispensable genes exist. This pattern can be explained by assuming that new genes are brought into the population, for example, by horizontal gene transfer (HGT) from other populations or taxa, and may subsequently be lost (Dagan and Martin 2007).

The evolutionary advantage of a distributed genome is that new variants of the compact genomes can be generated by HGT events between strains within the population (Coleman and Chisholm 2010). Although the distributed genome hypothesis was first validated in pathogenic bacteria (Ehrlich et al. 2008), a wealth of data, both from the genomes of closely related bacteria and from metagenomes, have shown that this hypothesis appears to be universally true (Koonin and Wolf 2008; Lapierre and Gogarten 2009).

We have chosen data from two genera of model organisms, the marine picocyanobacteria Prochlorococcus and Synechococcus, to study a distributed genome. These genera are model organisms for biodiversity in the ocean (Bragg et al. 2010; Coleman and Chisholm 2010). Marine picocyanobacteria are major determinants of primary marine productivity and biogeochemical mineral cycles (Partensky et al. 1999) and exhibit a high degree of genomic diversity (Kettler et al. 2007; Scanlan et al. 2009). Their genes have contributed significantly to metagenomic analyses (Venter et al. 2004). Homologs of picocyanobacterial genes have also been found in the genomes of cyanophages, which may be important players in maintaining diversity in picocyanobacteria (Avrani et al. 2011). Marine picocyanobacteria can be divided into several genetically and physiologically distinct populations. In case of Prochlorococcus, two so-called ecotypes that are specifically adapted to low-light (LL) or high-light (HL) conditions were recognized early on (Moore et al. 1998). Based on the extensive genome analyses of cultivated isolates (Dufresne et al. 2003; Rocap et al. 2003; Kettler et al. 2007; Scanlan et al. 2009) and fieldwork (Johnson et al. 2006; Martiny et al. 2009; Rusch et al. 2010; West et al. 2010), the existence of several more distinct clades was suggested. However, it is at present not known how many of such separate, genetically and physiologically distinct, clades can be expected to exist, nor has the Prochlorococcus effective population size or an upper bound for the genetic diversity among them ever been estimated.

Theoretical and evolutionary concepts provide a crucial framework for understanding the underlying reasons for genomic diversity, the number and distribution of genes among closely related but different cells in a bacterial taxon, and the evolution of bacterial genomes in general. From a well-supported model, predictions can be derived about shared genomic variation, the total number of genes available in a population, and the percentage of genes that have thus far been identified.

The main goal of the present paper is to present the infinitely many genes (IMG) model for the bacterial pangenome. It is based on first principles of bacterial genome evolution and incorporates gene gain, gene loss, and genetic drift. Here, gene gain means that a new gene is added to the genome of an individual, for example, through uptake of genetic material from the environment, by HGT from another taxon or by mutation of existing genes, which leads to a totally new gene. Gene loss denotes the event that a single gene present is mutated, loses its function, and subsequently is not carried over to later generations. Such gene gains and losses are mapped onto the genealogy of a population sample, leading to a precise description of its pangenome. By taking a genealogical perspective, this model is in contrast to existing approaches for a quantitative prediction of the pangenome (Medini et al. 2005; Tettelin et al. 2005; Hiller et al. 2007; Hogg et al. 2007).

Using gene frequency data, the IMG model returns quantitative predictions for various statistics such as the average genome size, the pangenome size, and the gene frequencies in the dispensable genome. Moreover, the IMG model provides a framework to determine whether a distributed genome has been shaped as a consequence of neutral evolution or by adaptation. In particular, we provide a statistical test of neutrality using the IMG model. In contrast to other population genetic tests of neutral evolution for single nucleotide polymorphism (SNP) data (e.g., Tajima 1989; Fu and Li 1993), the test takes into account independent information about the underlying genealogy, such as that provided by phylogenetic analyses of ribosomal DNA (rDNA) or the concatenated sequences of core genes. We take this phylogeny as a proxy for the underlying true organismal tree. In addition, we provide a simulation tool for the IMG model that can be applied to any group of bacteria. This framework is rich enough to account for extensions like horizontal gene flow within the bacterial population, effects of selective events, and point mutations within genes. Resulting statistical methods for parameter estimation and inference leading to a deeper understanding of genome evolution in bacteria will be the subject of future research. (See Box 1 for the most important notions and Box 2 for a brief description of the IMG model.)

Box 1. Glossary.

Gene gain	The first occurrence of a new gene in a population is a gene gain event. One way to gain a new gene is via HGT from other populations or uptake of genetic material from the environment. Another mechanism is mutation of duplicated genes followed by subfunctionalization. The IMG model does not distinguish the mechanism by which a gene is gained but assumes that there is a single origin of each gene in a population.
Gene loss	Mutations resulting in pseudogenization followed by deletion of genes will lead to gene loss events.
HGT between populations	If a specific gene is absent in the focal population, but present in a different population, a HGT to the focal population results in a gene gain. The IMG model assumes that each gained gene in the focal population is different from previously gained genes. In other words, the reservoir of genes to be gained is infinitely large.
HGT within populations	If genes present in some individuals of the focal population are horizontally transferred to other individuals of the same population, we speak about HGT within populations. This mechanism is not implemented in the IMG model presented here.
Population	Here, we mean any group of bacteria under consideration, which may contain closely as well as distantly related individuals.
True organismal tree	In a clonal population of prokaryotes, the genealogy given by the clonal lineages gives the true organismal tree. This tree is ultrametric. If HGT within the population is weak, the phylogeny of most genes is in accordance with the organismal tree. Moreover, phylogenies based on highly conserved regions or gene content may serve as a proxy for the organismal tree. In the IMG model, the organismal tree is given by the coalescent, a standard model from population genetics. See also Box 2.

Box 2. The IMG Model.

In the IMG model, the relationship between individuals is based on an underlying “true” genealogy, by which we mean the organismal ultrametric tree. Assuming neutral evolution, we model the true genealogy by a random tree called the coalescent: For a population of size N_e and a sample of size n, the coalescent is a random ultrametric tree arising from the following stochastic process: Starting in the present with a sample of size n, two randomly chosen ancestral lines are merged roughly after an exponentially distributed time with rate $\left(\begin{array}{c}n\\ 2\end{array}\right)$. Restarting with the remaining n − 1 lines, another exponential time with rate $\left(\begin{array}{c}n-1\\ 2\end{array}\right)$ given the next coalescent event, etc. The process is stopped when reaching the most recent common ancestor. On this tree, a branch of length of 1 corresponds to N_e generations.

Along the lineages of this “true clonal” tree, gain of any new gene occurs at rate θ/2, and each gene present is lost at rate ρ/2. Each gene gain event gives, for example, by HGT from another population, the single origin of a new gene in the population, which is taken from an unbounded (infinite) reservoir of genes. HGT within the population is neglected. In particular, the case that a gene lost in a lineage will be regained is not considered in this model. Under the above assumptions, several statistics can be predicted, for example, the average number of genes per genome, the average number of genes differing in two individuals, or the gene frequency spectrum. These predictions can be used for estimation of gene gain and loss rates and for statistical tests.

Materials and Methods

IMG Model

Consider a single prokaryotic individual. We assume that its genome consists of two parts: genes that are necessary for survival (these comprise the core genome) and genes that can be present or absent without any fitness advantage or disadvantage to the individual (these comprise the dispensable genome). The number of genes in the core genome is denoted by c. For the evolution of the dispensable genome, we assume that new genes are gained (by mutation or from an external source) with probability u and existing genes are lost with probability v per generation. Because the pool of genes that can potentially be gained by HGT or mutation is unlimited, we refer to this mutation model as the IMG model. Rescaling u and v by a large, constant effective population size, N_e, we set θ = 2N_eu and ρ = 2N_ev. In these terms, θ corresponds to the average number of genes gained in 2N_e generations along a single line of descent and ρ corresponds to the rate of losing a single gene (when time is measured in units of 2N_e generations). Precisely, if a line carries x genes, it gains θ new genes and loses x·ρ genes in 2N_e generations on average. Hence, the equilibrium size of the dispensable genome is x = θ/ρ genes. More precisely, Huson and Steel (2004) show that the size of the dispensable genome of a single prokaryotic individual is Poisson distributed with parameter θ/ρ at equilibrium. In particular, given that the dispensable genome usually comprises several hundred genes, θ will be orders of magnitudes larger than ρ in our applications.

For the evolution of a population of prokaryotes, we take the standard neutral model from population genetics, in which the genealogy of a sample of n individuals is approximately given by the coalescent (for review, see Box 2 and Wakeley 2008). Neutrality here means that all individuals have the same chance to produce viable offspring, that is, gene content neither confers a fitness advantage nor a fitness disadvantage. The genealogy is meant to represent the true organismal or clonal genealogy of the sample and therefore must be ultrametric.

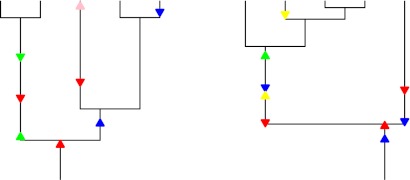
The evolution of the dispensable genome along the coalescent is modeled as follows: The number of genes in the dispensable genome of the most recent common ancestor of the sample is Poisson distributed with parameter θ/ρ. Gene gain and loss events occur along the coalescent from the most recent common ancestor (MRCA) until the time of sampling. New genes are gained, for example, by taking up genetic material from the environment at rate θ every 2N_e generations. In addition, genes present are lost at rate ρ every 2N_e generations. (See fig. 1 for an illustration.)

FIG. 1.—

Two realizations of the IMG model. The underlying genealogy is given by the coalescent, and gene gain (triangle up) and loss events (triangle down) are superimposed on the coalescent. Gene gain and loss events of the same genes are marked in the same color.

The IMG model comes with various sources of randomness: 1) the clonal genealogy of the population sample is random and is given by the coalescent, 2) genes are gained by random uptake, and 3) genes present are lost randomly. Previously, Baumdicker et al. (2010) investigated genomic patterns arising from the IMG model based on a sample of n individuals taken at random from the population, when averaging over all sources of randomness. In our notation, we use 𝔼_θ,ρ,c[.] when averaging over all three sources of randomness, whereas we write 𝔼_θ,ρ,c[.|τ] when we fix the genealogical tree τ and only average over random events of gene gain and loss along τ.

We review here some important features of this model. See the Supplementary Material online for a brief derivation of each of these quantities. We denote by Gⁿ the number of different genes found in n individuals and by G_iⁿ the number of genes found in exactly i of n individuals. (Note that Gⁿ = G₁ⁿ + ⋯ + G_nⁿ.)

• The expected number of genes in the genome of one individual and the expected number of differences between the genomes of two individuals are given by

  (1)

  respectively.
• The expected number of different genes in the whole sample is

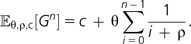
  (2)
• We refer to G₁ⁿ,…,G_nⁿ as the gene frequency spectrum, and for k = 1, …, n − 1,

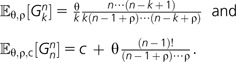
  (3)
• The number of new genes expected in the nth individual, denoted as S_n, is

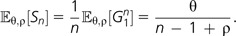
  (4)

Estimating θ and ρ

Given a set of n complete genomes of prokaryotes, we use algorithms described in the Data Source (below) to determine which genes (or gene clusters) appear jointly in subsamples of individuals. This analysis yields the observed gene frequency spectrum, denoted (g₁ⁿ,…,g_nⁿ). For example, g₁ⁿ is the number of genes present in a single individual in the sample.

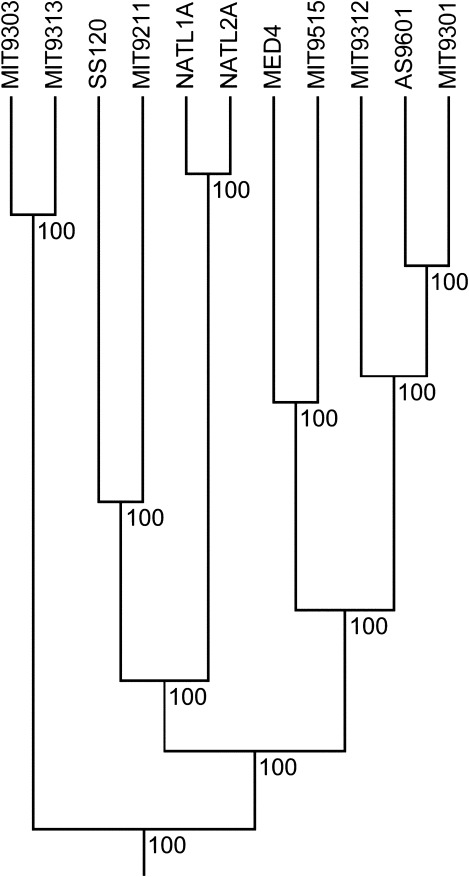
Our goal is to estimate θ and ρ based on the gene frequency spectrum and independent information on the genealogy of the sample, obtained from divergence data. Because this tree must be a proxy for the true organismal tree, we require that it is ultrametric, implying a clock-like behavior of evolution. We use an ultrametric tree obtained by the software ClonalFrame (Didelot and Falush 2007) based on the sequences of all core genes present in one copy per genome here; see figure 3 for Prochlorococcus.

FIG. 3.—

The phylogeny of Prochlorococcus based on 913 core genes. Sequences were aligned using muscle, and the tree was inferred by the software ClonalFrame using the parameters -x 17500 -y 2500 -z 50 -G -H. Numbers indicate the probability that the respective branch appears in a random draw from the posterior distribution as given by ClonalFrame.

For these estimators, we use 1) a calibration of the tree, which uses coalescent theory, and 2) a feature of the IMG model from Proposition 5.5 in Baumdicker et al. (2010). 1) Consider an ultrametric genealogical tree τ of the sample (e.g., based on the ClonalFrame output or 23S rDNA divergence). From τ, we read off the intercoalescent times T₂ = t₂,…,T_n = t_n. Here, because the coalescent predicts that the random times T₂,…,T_n are independent and T_i has rate $\left(\begin{array}{c}i\\ 2\end{array}\right)$, we use a timescale on the tree such that

(5)

2) Recall that the number of genes present in a single individual is Poisson distributed with parameter $\frac{\text{θ}}{\text{ρ}}$. Similarly, consider a sample of n = 2 individuals and their time of the most recent common ancestor t from τ. For the average number of genes present in only one of the two individuals, we have to distinguish several classes of genes: genes that were present in the most recent common ancestor of both individuals and were lost exactly in one of the two ancestral lines and genes that were not present in the most recent common ancestor of both individuals and were gained along any of the two ancestral lines up to the most recent common ancestor. Adding up these two cases, the average number of genes present only in one individual is

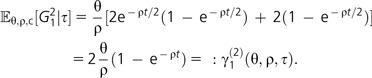(6)

(Note that the result from equation [3] arises when averaging the last expression over the exponentially distributed coalescence time t.) More precisely, arguing as in Huson and Steel (2004), given τ, the random number G₁² is Poisson distributed with parameter γ₁⁽²⁾(θ,ρ,τ).

In general, we have to extend the last calculations to a sample of size n ≥ 2. Here, we obtain numbers γ_i⁽ⁿ⁾(θ,ρ,τ), i = 1,…,n, such that, given τ, the random number G_iⁿ is Poisson distributed with parameter γ_i⁽ⁿ⁾(θ,ρ,τ). Using these parameters, it is straight forward to obtain maximum likelihood estimators of θ and ρ: Observe that for the likelihood function L(.), the phylogeny τ, and the observed gene frequency spectrum g₁ⁿ,…,g_{n − 1}ⁿ,

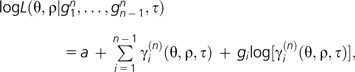where a does not depend on θ and ρ. Maximizing this log likelihood for θ, ρ, we obtain the estimates $\widehat{\mathrm{\theta }},\widehat{\mathrm{\rho }}$. Additionally, an estimator for c is obtained by

In order to obtain reasonable starting values in the maximizing procedure, we fit the observed average number of genes g¹ and the observed average number of differences g₁² to the predictions from equation (1).

Test of Neutrality

Once the estimators $\widehat{\mathrm{\theta }}$ and $\widehat{\mathrm{\rho }}$ are given, the neutrality test works as follows:

Based on $\widehat{\mathrm{\theta }}$ and $\widehat{\mathrm{\rho }}$, gene frequency spectra (G₁ⁿ,…,G_nⁿ) are simulated using a random genealogy, the coalescent. This gives an approximation of the distribution of

(7)

where G_iⁿ is the number of genes present in i individuals. (Note that ${\mathrm{𝔼}}_{\widehat{\mathrm{\theta }},\widehat{\mathrm{\rho }}}\left[G_i^n\right]$ does not depend on τ here.) The weight of the distribution of χ² above $x_{\widehat{\mathrm{\theta }},\widehat{\mathrm{\rho }}}^{\text{2}}(g_1^n,\dots ,g_n^n)$ gives the P value.

For the simulation of frequency spectra, we use the software IMaGe (see http://omnibus.uni-freiburg.de/∼fb6/). In each iteration, we obtain realizations of the random variables G₁ⁿ,…,G_{n − 1}ⁿ, and we can compute χ² from equation (7), where the expectations are based on the estimators $\widehat{\mathrm{\theta }}$ and $\widehat{\mathrm{\rho }}$ used as input for the simulations. Having thus simulated the distribution of χ², we can now decide whether we are able to reject neutral evolution based on the observed gene frequency spectrum.

False-Positive Rate of the Neutrality Test

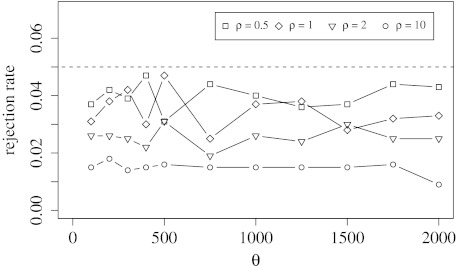
In order to obtain the false-positive rate of the neutrality test, we simulated 1,000 data sets for different values of θ and ρ under neutrality and computed the P value for each with the IMaGe Software. If the P value was below 0.05, we rejected the hypothesis of neutrality. The rejection rate in this setting equals thus the false-positive rate and should be at most 0.05; see figure 2.

FIG. 2.—

The false-positive rates of the neutrality test are shown for different values of θ. The gene loss rate was set to ρ = 0.5, 1, 2, 10. For each parameter combination, we simulated 1,000 independent data sets, each of size n = 7.

Sampling Bias

Note that it is possible to correct the test of neutrality for sampling bias (see Supplementary Material online). We assume here that the n individuals are sampled from the source population so as to be as distantly related as possible. This option allows us to assess whether a small P value is simply due to nonrandom sampling of individuals from the population.

Estimating the Effective Population Size

We have estimated the combined parameters θ = 2N_eu and ρ = 2N_ev. If branch lengths on the tree τ can be given in terms of numbers of generations, both the effective population size and gene gain and loss probabilities per generation can be obtained. Here, we take a 23S rDNA distance of 1% to represent about 50 Myr divergence, as suggested in Dufresne et al. (2005). (The maximal divergence between strains is taken in order to obtain an upper bound for the estimate of the time to the latest common ancestor.) For translating numbers of years to numbers of generations, we need an estimate for the generation time. We take one generation per day, which might be a slight overestimation as compared with table 2 in Jacquet et al. (2001).

Table 2.

Observations and Predictions for Various Statistics and Models for Prochlorococcus

	Observation	IMG Model, Fixed Tree	IMG Model, Random Tree	Extrapolation	Supragenome
Model parameters	—	Tree, θ,ρ,c	θ,ρ,c	a,b,c,d,α	G1, … , G7
Genes per individual, G11	2,019	2,033	2,033	—	2,032
Pangenome size, G2	2,562	2,308	2,641	—	2,581
Pangenome size, G11	5,025	5,025	5,245	5,041	5,023
Pangenome size, G1000	?	—	15,225	28,051	9,421
Pangenome size, GNe	?	—	57,792	15,337,650	9,421
Genes in frequency at least 1%	?	—	8,549	—	9,421
New genes in 12th individual, S12	?	—	167	177	159

NOTE.—For example (second line), we compare the average number of genes per individual for observed and predicted values. Question marks indicate that the relevant numbers are to dates unknown.

Using the calibration of the tree and the generation time, we obtain an ultrametric tree τ where all branch lengths are assigned a number of generations. Our procedure to obtain the effective population size is based on the assumption that τ is in fact a realization of a coalescent tree. We use the intercoalescent times T_i, that is, the number of generations where the ultrametric tree τ has i lineages. From τ, we read off the intercoalescent times T₂ = t₂, …, T_n = t_n, measured in generations. Because the random times T₂, …, T_n are independent, we obtain the unbiased estimate:

(8)

k-Clades

The bacteria within a taxon can be categorized into ecotypes. For a given phylogeny and estimators $\widehat{\mathrm{\theta }}$ and $\widehat{\mathrm{\rho }}$, we define a k-clade to be any set of individuals that are expected to differ by at most k genes. Note the following for the IMG model: given two individuals separated by a genealogical distance of 2tN_e generations, the expected number of genes differing between the two is 2θ(1 − e^−ρt)/ρ; see equation (6). Thus, the expected number of differences is smaller than k for 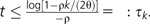. In the coalescent, the duration for which i lines are present is expected to be $\frac{2}{i(i-1)}{N}_{\text{e}}$ generations, so 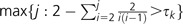k-clades are expected to be present. Conversely, it has been shown empirically that ecotypes differ by k genes on average (for some number k). Therefore, using $\widehat{\mathrm{\theta }}$ and $\widehat{\mathrm{\rho }}$, it is possible to estimate the number of ecotypes, that is, the number of clades that differ by k genes or more.

Extrapolation Model

We compare the IMG model to other models of the bacterial pangenome. To estimate the number of core genes for the total population, the approach taken by Medini et al. (2005) and Tettelin et al. (2005) is relevant: when sequencing n genomes, there is a number G_nⁿ genes common to all genomes whose discovery rate is assumed to decay exponentially, that is, G_nⁿ≈a·bⁿ + c for parameters a > 0, 0 < b <1, and c > 0. In a similar way, it is possible to look at the number of genes an additional individual would add to the known gene pool, S_n. In Tettelin et al. (2008), it is recognized that a power-law decay based on Heaps' law (a rule from linguistics for counting new words in long texts; see Section 7.5 in Heaps 1978) can be used, that is, S_n ≈ d · n^−α. We fitted d and α to our observed values of S_n for random orders of the individuals; see the Supplementary Material online for more details.

Supragenome Model

The supragenome model from Hogg et al. (2007) posits that genes occur in d different classes. It assumes the existence of G_i genes, which occur at frequencies of μ_i for i = 1, …, d. Note that G = G₁ + ⋯ + G_n is the total number of genes in the pangenome. Just as in the original paper, we fixed d = 7 and the frequencies μ₁ = 0.01, μ₂ = 0.1, μ₃ = 0.3, μ₄ = 0.5, μ₅ = 0.7, μ₆ = 0.9, and μ₇ = 1.0. Therefore, G₇ represents the number of genes that occur at a frequency of 1.0 or the core genome. The genome of an individual can then be generated by adding any gene of class i with probability μ_i for i = 1, …, 7. The parameters G₁, …, G₇ are estimated by maximum likelihood, which maximizes the probability of generating 11 genomes with identical gene frequency distribution to that observed in the data set; see the Supplementary Material online for more details.

Data Source

Genome sequences of 11 marine Synechococcus isolates and 11 Prochlorococcus isolates were downloaded in Fall 2007 from GenBank (for accession numbers, see supplementary table S1a, Supplementary Material online). All 22 cyanobacterial genome sequences have been published (see Dufresne et al. 2003; Rocap et al. 2003; Kettler et al. 2007; Dufresne et al. 2008), and, except for Synechococcus WH5701, all sequence information belongs to a single scaffold (Dufresne et al. 2008). In addition, we used a random sample of 11 genomes from aquatic bacteria as a control for the test of neutrality (supplementary table S1b, Supplementary Material online).

Gene Modeling

Because we noted discrepancies in the way the cyanobacterial genomes were annotated (see supplementary table S2, Supplementary Material online, for the cyanobacterial genomes), the analyses were performed by omitting all existing annotation and remodeling genes. Therefore, genes in all 22 of the genomes were modeled by GeneMark (Borodovsky and McIninch 1993) with the default parameters, and databases of all open reading frames were generated for each genome sequence. Note that the gene length is set to a minimum of 45 nt in GeneMark. For the 11 aquatic strains, we relied on the genes as given by the National Center for Biotechnology Information database.

Clustering

The databases resulting from the gene modeling were compared with each other by BlastP (BLOSUM62) within the cyanobacteria and the aquatic bacteria, respectively. Clusters of homologous genes were generated by the MCL algorithm (Enright et al. 2002) using BlastP scores as input. Genes i and k from two different individuals are said to be homologous if 1) the BlastP e value is below 10⁻⁸, 2) the percentage of identity given by β(i, k) satisfies β(i, k) ≥ max{max_{j ≠ 1} β(i, j) − 10,10} (where j is taken from the same individual as k), 3) a similar requirement for the length of i and k, and 4) MCL puts i and k in the same gene cluster.

From these data, we calculated the number of gene clusters common to all genomes (core genes) or present in a subset of genomes (dispensable genes). We did not annotate gene functions because we were exclusively interested in the number of orthologs between genomes. An overview of the accession numbers, genome sizes, modeled numbers of genes, and gene clusters per genome is provided in supplementary table S1a, Supplementary Material online. These calculations yielded 1,100 ortholog gene clusters in the core genome.

Shared Gene Content Tree

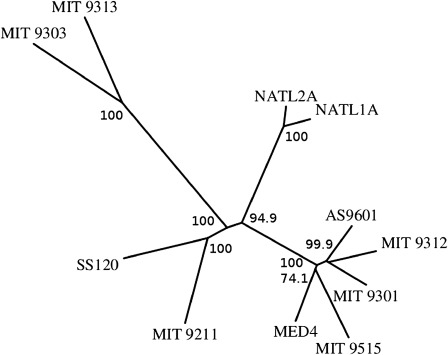
Phylogenetic relationships between genomes based on shared gene content can be visualized as trees. Phylogenetic trees were inferred using PHYLIP version 3.66 (Felsenstein 1997) (Fitsch–Margoliash option). The trees were built with the individual distances between genome A and genome B set to the percentage of noncommon genes in these two individuals (fig. 4).

FIG. 4.—

The gene content tree for Prochlorococcus. The bootstrap values have been computed using random samples of the generated gene clusters.

Estimating the True Organismal Tree

In order to reconstruct the true organismal tree, we used the software ClonalFrame (Didelot and Falush 2007), which can handle a large set of genes as input to infer the most probable organismal tree. Here we used the set of core genes present in each of the sampled individuals, excluding those core genes with multiple copies per individual. For the combined sample of Prochlorococcus and Synechococcus, 913 genes fulfilled this criterion, whereas only 130 such core genes were found in the 11 aquatic bacteria. For each of these genes, a muscle alignment (Edgar 2004) was constructed. The software ClonalFrame was used to estimate the true organismal tree using the parameters -x 17500 -y 2500 -z 50 -G -H. ClonalFrame simulates the posterior distribution of trees given the muscle alignments. From this posterior distribution, ClonalFrame computes an ultrametric consensus tree, which was used for the presented analysis using IMaGe.

Results

The IMG Model and the Test of Neutrality

Before we started to analyze the data set of 22 cyanobacterial genomes, we ran two control studies. First, we used simulations to check whether the test has approximately the correct rejection rate. This procedure was necessary because we used an estimation of the gene gain and loss rate within the test. As seen in figure 2, the rejection rate never exceeds 0.05 and thus the test is conservative. Second, we wanted to see if the test can reject neutrality at all for a data set from natural populations. Here, we used 11 randomly sampled genomes from aquatic bacteria. We estimate $\widehat{\mathrm{\theta }}=30.301$, $\widehat{\mathrm{\rho }}=10.8$, and $\widehat{c}=302$, and the P value for our statistical test on this data set is 0.00004 and 0.00002 when correcting for sampling bias. Because evolution of all aquatic bacteria can hardly be assumed to have been neutral, these results are reasonable.

The cyanobacterial data set was analyzed in two ways: 1) as a combined sample of all 22 genomes and 2) as two samples of 11 genomes each, considering the genomes of Prochlorococcus and of Synechococcus separately. We estimated the model parameters θ, ρ, and c using genealogical information from a phylogeny based on 913 core genes (fig. 3 and table 1).

Table 1.

Estimators for the IMG Model and the P Value for the Test of Neutrality

	Ne	$\widehat{\mathrm{\theta }}$	$\widehat{\mathrm{\rho }}$	$\widehat{\mathbf{c}}$	P Value
Prochlorococcus	1.01 × 1011	2,309.17	2.80	1,208	0.630
Synechococcus	1.42 × 1011	4,422.04	3.38	1,430	0.0105
Combined	2.79 × 1011	6,631.75	5.25	1,099	<0.0001

The test of neutrality for the IMG model yielded significant results for Synechococcus and the combined data set of Synechococcus and Prochlorococcus. A nonsignificant result was found for Prochlorococcus (table 1). In addition, when the correction for sampling bias was used, the P value was P = 0.057 for the Synechococcus data set and <10⁻⁴ for the combined sample. Thus, sampling bias can explain some of the deviation from the null model; however, these results still suggest nonneutral evolution, at least for Synechococcus.

Model Comparison

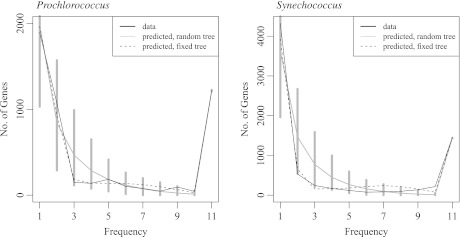
The observed gene frequency spectrum g₁ⁿ,…,g_nⁿ, the basis of the neutrality test, and the spectrum predicted by the IMG model are shown in figure 5. Note that the predicted spectrum can be computed either on a fixed tree (again we used the tree inferred by ClonalFrame) or on a random tree, the latter being the usual approach in population genetics.

FIG. 5.—

The gene frequency spectrum for our data set of 11 individuals of Prochlorococcus and Synechococcus, respectively. The x axis gives the number of individuals a gene can be present in, and the y axis gives how many genes are present in that frequency. Predictions are obtained using estimates from table 1 either on a fixed tree or on the average over a random tree.

Because Prochlorococcus showed the least deviation from neutrality in our neutrality test, we used this data set for comparing the IMG model with previous approaches. For the extrapolation model (see Materials and Methods), we estimated S_k ≈ 878.01 · k^−0.64 (recall that S_k is the number of new genes in the kth sequenced individual) and G_k^k≈467.94·0.68^k + 1214.34 (where G_k^k is the number of genes present in all k sampled individuals). For the supragenome model, estimators were obtained for d = 7 frequency classes (which come with frequencies μ₁ = 0.01, μ₂ = 0.1, μ₃ = 0.3, μ₄ = 0.5, μ₅ = 0.7, μ₆ = 0.9, and μ₇ = 1.0, respectively), as in the original paper (Hogg et al. 2007). This resulted in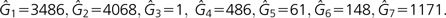

Using these three approaches, we computed predictions for various statistics for comparison with the data set. We calculated the average number of genes per individual and the pangenome sizes in a sample of n = 2, n = 11 and in a sample of n = 1,000 individuals, as well as the number of genes in frequency at least 1% and the number of new genes added by sequencing the 12th Prochlorococcus individual; see table 2. For the IMG model, these numbers are derived from equations (1), (2), (3), and (4) using estimators from table 1. The extrapolation model was not used to predict G₁¹, as the extrapolation will only give reasonable results for n ≥ 3. For such n, the extrapolation model implies

where K is the average number of genes per individual in the sample. In the supragenome model, the expected number of genes per individual is given by $G^1={\displaystyle {\sum }_{i=1}^7{G}_i{\text{μ}}_i}$. More generally, we obtain

The number of new genes in the 12th individual is given by G¹² − G¹¹.

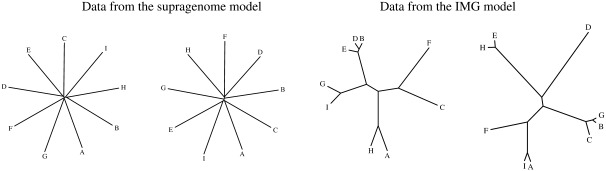
For both the supragenome model and the IMG model, it is possible to simulate data on the presence and absence of genes in a sample. Using the shared gene content in simulated data, we inferred the underlying genealogy for both models. Because the supragenome only takes presence and absence of genes into account, these genealogies are almost star like; see figure 6.

FIG. 6.—

Data (i.e., a sample of 11 complete genomes) are generated according to the supragenome model and the IMG model, respectively. This means that the data consist of information about presence and absence of genes. Then, the gene content tree, inferred from pairwise distances of individuals, is drawn.

k-Clades

Prochlorococcus and other marine picocyanobacteria can be divided into several clades or genetically and physiologically distinct populations. These clades separate Prochlorococcus into sublineages such as LL–adapted and HL–adapted ecotypes that partition themselves vertically along the light gradient in the water column. The 11 available Prochlorococcus genomes are divided into the five clades HLI, HLII, LLI, LLII/LLIII, and LLIV (Moore et al. 1998; Johnson et al. 2006). The lowest average difference between these clades is k = 433.6 different genes between HLI and HLII. In Rusch et al. (2010), the existence of two thus far uncultivated clades occurring in the high-nutrient, low-chlorophyll, iron-depleted waters of the Pacific and Indian Oceans was documented. Another novel Prochlorococcus clade has recently been discovered in high-nutrient, low-chlorophyll waters in the South Pacific Ocean (West et al. 2010). Based on our estimators $\widehat{\mathrm{\theta }}$ and $\widehat{\mathrm{\rho }}$ for Prochlorococcus, setting k = 433.6, we expect at least 18 such k-clades.

Discussion

The IMG Model

Although the amount of genomic data for various bacterial taxa increases at a rapid pace, our understanding of the relative importance of the evolutionary forces, which shape these genomes, is still far from complete. It is evident that classical evolutionary factors, such as mutation, selection, recombination/HGT, and genetic drift, are underlying genome evolution in bacteria. However, bacteria differ from eukaryotes because their genome is much more variable in gene content. We present here the IMG model, which is the first mechanistic model which applies a population genetic approach to genome evolution of bacteria. In addition, we present here the first test of hypotheses about neutral evolution of the distributed bacterial genome. The IMG model is based on the genealogy of the sampled individuals and the mechanisms of gene gain—for example, by HGT from a different taxon or simple uptake of genetic material from the environment—and gene loss. This approach is in line with traditional models from population genetics such as the infinitely many alleles model (Kimura and Crow 1964) and the infinite sites model (Kimura 1969). The equivalent of the two alleles of an SNP in the infinite sites model are presence and absence of a gene in the IMG model. The greatest difference between the IMG model and traditional population genetic analysis is that the IMG model can use independent phylogenetic information from 16S and 23S rDNA, sequences of core genes, or other conserved genomic regions.

Recently, Collins and Higgs (2012) have extended the IMG model by assuming that the dispensable genome may fall in several classes, each of which comes with its own rate of gene gain and loss. In particular, they show that a model with two different classes of dispensable genes, but without assuming that any of the genes is essential for survival, gives a reasonable fit of the gene frequency spectrum for 172 complete genomes of Bacilli.

Test of Neutrality and Adaptive Forces

The IMG model comes with only three model parameters, and it can be used to estimate the gene gain and loss rates. In addition, it can be tested and is able to accurately explain various statistics. Once a significant result of this test is found (as e.g., for the combined sample of Prochlorococcus and Synechococcus), the source of the deviation from neutrality must be found, such as 1) HGT, 2) varying population size, 3) positive selection, and 4) negative selection.

The sample of 11 aquatic bacteria shows a clear deviation from neutrality. This is not surprising because these individuals occupy different ecological niches and are hence exposed to different selection pressures. For example, among the marine bacteria, we chose Persephonella marina, a chemolithotrophic, thermophilic hydrogen-oxidizing bacterium isolated from a deep sea hydrothermal vent, colonizers of sediment (Hyphomicrobium denitrificans), and phytodetrital macroaggregates (Rhodopirellula baltica), an obligate microaerophilic magnetotactic cocci (Magnetococcus), and Shewanella baltica isolated from a deep anoxic basin in the Baltic Sea. Among the nonmarine strains is a cyanobacterial isolate from a rice field (Cyanothece), a freshwater fish pathogen (Flavobacterium psychrophilum), and Geobacter metallireducens, an organism able to gain energy through the dissimilatory reduction of iron, manganese, uranium, and other metals. In particular, these bacteria belong to widely different taxa (three very different alpha 2 gamma-, one delta-proteobacteria, two Bacteroidetes/Chlorobi, one each from the Aquificae, Planctomycetacia, and Cyanobacteria), which diverged a long time ago. Although neutral evolution can be rejected for the random sample of aquatic bacteria, the P value of 0.00004 could still be improved. To do so, information other than the gene frequency spectrum must be included in the test. Additionally, power could be gained from the presence or absence of pairs of genes, which is equivalent to the analysis of linkage disequilibrium of SNPs in the infinitely many sites model.

The IMG model takes an extreme view of bacterial genome evolution because it assumes that genes in the core genome are absolutely necessary for survival, whereas genes in the dispensable genome behave neutrally. In particular, the presence or absence of dispensable genes are assumed not to lead to any change in fitness, whereas in nature, several dispensable genes are known to affect fitness (e.g., the nitrite and nitrate assimilation genes in uncultured Prochlorococcus cells from marine surface waters; Martiny et al. 2009). Moreover, the loss of some genes in marine picocyanobacteria is probably not neutral. Prochlorococcus cells are extremely small at only 0.5–0.8 long and 0.4–0.6 μm wide (Morel et al. 1993), and this small size is thought to facilitate the uptake of rare nutrients due to the high surface-to-volume ratio of these cells (Chisholm 1992). Because cell size and genome size are correlated, the loss of genes and the resulting reduction of genome size should be advantageous in the nutrient-poor marine environment. The frequencies of genes related to phosphorus acquisition are ecosystem specific (Coleman and Chisholm 2010). In Prochlorococcus, genes related to phosphorus acquisition, metabolism, and uptake (which are upregulated during P-starvation) are more abundant in populations from phosphorus-poor habitats, such as the Atlantic near the Bermuda, compared with the Oceans close to Hawaii. Using a comparative genomics approach, Coleman and Chisholm (2010) argue that these genes were recently transferred and spread through the Atlantic population by HGT and positive selection. However, only 29 out of 2,854 genes in Prochlorococcus show significantly different frequencies between Bermuda and Hawaii, suggesting that much of the variation in gene content is in fact neutral.

The Underlying Genealogy in the IMG Model

In our analysis, we use the coalescent as a model for the true organismal tree of the sample under consideration and a core gene–based phylogeny τ as a proxy for this true tree. For both trees, there are alternative possibilities. Although the approximation of the true tree by the sequences of many genes should be a reliable method, in principle, τ can be inferred by any algorithm generating an ultrametric tree, like UPGMA or ClonalFrame. As well as the algorithm, the particular genes used to construct the tree τ will effect the estimates of θ and ρ. However, because the IMG model is based on the coalescent, methods taking coalescent theory into account should be preferred to construct τ.

The choice of the coalescent in the IMG model is inspired from population genetic theory because it arises as the equilibrium tree for a constant size population. However, it has not been shown yet that the standard neutral model is a good null model for prokaryotic evolution. Because the notion of species remains unclear for prokaryotes, models for macroevolution could be used as well, for example, birth and death trees (Nee 2001) or the tree arising in a critical branching process (Aldous and Popovic 2005). Moreover, Cohan (2002) suggests the stable ecotype models, where ecotypes are purged by periodic selection and may as well inhabit new ecological niches. However, the resulting genealogical tree has not been studied yet. Another choice is suggested in Collins and Higgs (2012) who use gene gain and loss along a star-like phylogeny. However, they conclude that the coalescent gives superior results.

The Role of HGT Within Populations

As a general pattern, it has been shown that HGT can be a strong force in shaping bacterial genomes (Ochman et al. 2000), in particular in early evolution (Vogan and Higgs 2011). Whereas the IMG model as presented above takes into account HGT between distant taxa, leading to gene gain in the sequenced population, HGT within the population is not taken into account. One objective of future research will be to extend the IMG model to include the possibility of horizontal gene flow within a population, which was started in Baumdicker and Pfaffelhuber (2011). Such a model-based analysis may lead to statistics, which can disentangle the effects of these evolutionary forces on gene content variation.

HGT has long been known to be an important player in prokaryotic evolution (Doolittle et al. 2003). A quantitative analysis is today given by using phylogenetic networks (Huson and Bryant 2006) rather than trees and findings of specific HGT events along a given phylogeny. Halary et al. (2010) suggested that horizontally transferred genes may belong to different worlds that relate to different mechanisms and pools of shared genes. Dagan and Martin (2007) have analyzed different models for HGT along given phylogenies. In particular, they compared the loss-only model, with single-origin and multiple-origin models. In the loss-only model, all genes are assumed to be present in the MRCA, whereas the single-origin model assumes—as the IMG model—that every gene present was gained or horizontally transferred exactly once along the phylogeny. Multiple-origin models then allow for multiple such gain events of single genes, which is not taken into account in the IMG model due to the assumption that all gained genes are new. Dagan and Martin (2007) concluded that loss-only and single gain models frequently imply ancestral genomes, which are much larger than present ones. However, their analysis is based on data through distant groups, from Archaea to Proteobacteria. In contrast, having a population genetic basis, the IMG model should only be applied to more closely related taxa. At least for cyanobacteria that we study here, their figure 3 suggests that the single-origin model is realistic in the sense that ancestral genomes can well be of the same size as present ones.

For future applications of the IMG model, the ratio of HGT between taxa to HGT within taxa will be of importance. If the sampled sequences are only distantly related, HGT events between ancestral lines of the sampled sequences must be taken into account, leading to a low ratio, rendering the assumption of single origins of genes made in the IMG model false. In contrast, if the sampled sequences are closely related, the potential number of genes that are imported from distant taxa is vast, leading to a high ratio. Here, the assumptions made by the IMG model as presented in the present paper seem realistic.

Comparison to Other Models

Among the models presented here, the IMG model is the only one that incorporates evolutionary forces such as gain and loss of genes. It can be extended to include other forces such as HGT within the population and selection, leading to different patterns of genomic diversity. Both the extrapolation model (Medini et al. 2005; Tettelin et al. 2005, 2008) and the supragenome model (Hogg et al. 2007; Snipen et al. 2009) are purely descriptive, and statistical inference for bacterial evolution has so far not been developed based on these models.

Our numerical comparison of the IMG model (three parameters) with the extrapolation model (five parameters) and supragenome model (seven parameters) revealed that all three models are capable of predicting particular quantities, such as the total number of genes in a bacterial population; see table 2. The IMG model yields reasonable estimates in comparison with the other two models despite being based on only three parameters. The extrapolation model falls short when predicting important statistics, as it gives only a fit to the pangenome and a fit to the new genes in the next individual for large sample sizes n.

The supragenome model gives better approximations to the gene frequency spectrum than the IMG model (table 2). However, the gene frequency spectrum consists of only 11 summary statistics for our Prochlorococcus data set, and the IMG model can explain these numbers using only three parameters instead of the seven parameters required by the supragenome model (not counting the additional seven different frequencies of the frequency classes).

The supragenome model leads to unrealistic conclusions in at least two respects. First, it does not predict the number of genes that occur at small frequencies (below 1% in our analysis). However, such genes may comprise the largest part of the distributed genome in many populations (fig. 5). Second, regarding the separation of clades, the estimation for the number of k-clades from the IMG model seems reasonable. In the supragenome model, the inferred genealogies using gene content trees is almost star like (see fig. 6). This implies that the number of k-clades coincides with the sample size for small k and equals 1 for larger k. In particular, the supragenome model fails to estimate the correct number of k-clades in almost all cases.

The difference between predictions from the extrapolation, supragenome, and IMG model is most apparent when comparing the predicted size of the pangenome of a bacterial taxon depending on the sample size. Whereas the extrapolation model predicts a power law for the growth of the pangenome with the sample size, the supragenome model assumes a closed (bounded) pangenome, although the IMG model predicts a logarithmic increase of the number of genes; see equation (2). Interestingly, Donati et al. (2011) find a logarithmic increase in the size of the pangenome in a sample of Streptococcus pneumoniae.

Prochlorococcus and Synechococcus

Using independent phylogenetic information, we obtained estimators for the gene gain and loss rates, θ and ρ. These also result in estimators for the probability of a single gain or loss during one round of replication (gain: 1.14 × 10⁻⁸ and loss: 1.38 × 10⁻¹¹ for Prochlorococcus).

The combined gene frequency spectrum for Prochlorococcus and Synechococcus shows a deviation from the expectation under the IMG model. The data set from Synechococcus itself gives a significant result, suggesting that other forces, such as population expansion, HGT within the population, or selection, act at least on Synechococcus.

A closer look at the data reveals the most severe deviation between observed and expected gene frequency spectra. We find a reduced number of genes present in two (out of 11 Synechococcus strains) and an elevated number of genes present in 10 of the 11 strains. The reason for the discrepancy between the observed and predicted number of genes present in 2 out of 11 is that the estimator tries to adapt to an excess of singleton genes in the data and thus overestimates the number of genes in 2 of 11 strains. Possible reasons for this discrepancy are sampling bias, population growth, population structure, and selection. However, sampling bias does not lead to an increased number of high-frequency variants. Accordingly, the neutrality test rises to 0.057, which suggests that sampling bias is not the only source of deviation from the neutral model.

It is reasonable to assume that most of the genes in the dispensable genome are deleterious because selection acts to minimize the genome due to energetic considerations (Lane and Martin 2010). As a result, we expect that most of the ancient genes in the dispensable genome have been filtered out while more recently gained genes are still present. This form of selection can also lead to an excess of singleton genes. It is important to note, however, that the same selective forces cannot explain an increased number of high-frequency genes, which might instead be due to epistasis in the dispensable genome.

HGT can lead to the rejection of the neutrality test as well. However, HGT cannot explain the excess of singletons because this mechanism would instead result in a higher number of genes at intermediate frequency (Baumdicker and Pfaffelhuber 2011). This result is in agreement with the main conclusion of Luo et al. (2011), who suggest that HGT is not the primary reason for the genome size difference between Prochlorococcus and Synechococcus. In assessing the effect of population structure on the gene frequency spectrum, it should be kept in mind that Synechococcus is found in more diverse habitats, including coastal and open ocean waters in tropical, temperate, and polar regions (for review, see Scanlan et al. 2009), whereas Prochlorococcus is restricted to the ultraligotrophic open ocean waters of tropical and subtropical regions. These observations suggest a stronger population structure for Synechococcus and thus a more severe deviation from the IMG model.

Effective Population Sizes

Effective population sizes for bacteria are difficult to estimate (Fraser et al. 2009). Assuming that the inferred phylogenies are in fact realizations of coalescent trees, such estimates can be obtained. The effective population size determined here for Prochlorococcus (1.01 × 10¹¹) is relatively large as compared, for example, to that previously reported for Escherichia coli (2.5 × 10⁷, Charlesworth and Eyre-Walker 2006).

The large population size of Prochlorococcus reported here is in line with previous observations by Hu and Blanchard (2009), who rejected the hypothesis of a small effective population size based on an analysis of substitution rates and inefficient purifying selection. Moreover, from the effective population size of Prochlorococcus and equation (2), we obtained an estimate of 57,792 genes for the Prochlorococcus total gene pool using the IMG model. This number depends on the estimates of the generation time and the time to the most recent common ancestor of Prochlorococcus. Although more data would lead to better estimates for these two parameters, the dependence is weak: we would predict 32,072 genes if the latest common ancestor lived 2,000 years ago and the prediction increases only to 65,267 genes if the latest common ancestor lived when life on earth began. In any case, most of these genes are present only in a very few individuals. Nevertheless, several thousand genes in picocyanobacteria, which are present at significant frequencies in the pangenome, remain yet to be sequenced.

Supplementary Material

Supplementary materials are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).