A domain-based model for predicting large and complex pseudoknotted structures

Abstract

Pseudoknotted structures play important structural and functional roles in RNA cellular functions at the level of transcription, splicing and translation. However, the problem of computational prediction for large pseudoknotted folds remains. Here we develop a domain-based method for predicting complex and large pseudoknotted structures from RNA sequences. The model is based on the observation that large RNAs can be separated into different structural domains. The basic idea is to first identify the domains and then predict the structures for each domain. Assembly of the domain structures gives the full structure. The use of the domain-based approach leads to a reduction of computational time by a factor of about ~N² for an N-nt sequence. As applications of the model, we predict structures for a variety of RNA systems, such as regions in human telomerase RNA (hTR), internal ribosome entry site (IRES) and HIV genome. The lengths of these sequences range from 200-nt to 400-nt. The results show good agreements with the experiments.

Introduction

Pseudoknot is an important RNA motif that frequently occurs in many biologically significant RNAs, including viral RNAs, such as influenza virus,¹ hepatitis delta virus (HDV),^2-5 turnip yellow mosaic virus (TYMV),⁶ tobacco mosaic virus (TMV),⁷ beet western yellow virus (BWYV),^8,9 and the intergenic region (IGR) of cricket paralysis virus-like (CrPV-like) internal ribosome entry site (IRES).¹⁰ Moreover, pseudoknots are found in most large RNAs, such as rRNAs (rRNA).^11,12 These pseudoknots often involve long-range tertiary interactions between distant domains of RNA. Pseudoknots play a variety of structural and functional roles that are essential in biological processes.^13,14 For example, a pseudoknot is found to be a vital component for promoting efficient frameshifting.^14-17 Disruption of the pseudoknot structure is found to decrease the frameshifting efficiency. Other examples include the essential functional roles of pseudoknotted structures in CR1/CR2/CR3 domain in telomerase activity¹⁸ and IRES. In the ribosome-binding domain of IRES from a Dicistroviridae intergenic region,¹⁹ biochemical studies revealed a well-conserved pseudoknot structure which is functionally important.

Several computational methods, including the heuristic methods,^20-22 the dynamic programming algorithms,^23-25 the simulational methods^26-28 and the integer programming method,²⁹ have led to many useful predictions for RNA secondary structures including pseudoknots. However, the currently available dynamic programming algorithms based on the physical conformational entropy parameters^30-32 can only treat pseudoknots of limited chain length, primarily due to the rapidly increasing computational time for the conformational enumeration/sampling. Heuristic methods are computationally efficient. However, they do not guarantee that the predicted structure has the lowest free energy. Moreover, the heuristic method is often based on simplified approximations for the loop entropies in a pseudoknot,²² which may cause inaccuracy.

Many of the current pseudoknot folding algorithms are focused on simple H-type pseudoknots.⁴⁶ A canonical H-type pseudoknot consists of two stems and two loops, where each loop spans across a helix stem. With the extensive computational studies in recent years,^30-38 prediction of simple H-type pseudoknot is becoming more and more reliable. For example, a recently developed virtual bond-based RNA folding model (called “Vfold” model) allows direct calculation of pseudoknot loop entropy parameters and can predict H-type pseudoknots with an accuracy around 90%.³² Inclusion of the entropy parameters in the Vfold model distinguishes it from the other existing computational models.^27,31,39-45 For large pseudoknotted RNAs that go beyond the H-type pseudoknots, however, the structure prediction remains a challenge. One of the bottleneck is lacking loop entropy parameters for large and complex pseudoknots.^34,35

In order to predict the large and complex pseudoknot structure, in this study, we employ the virtual bond model (Vfold) to calculate and tabulate loop entropy parameters with the different structural contexts. To treat long RNA chains, we develop a domain-based method to decompose the large RNA structure into weakly coupled structural domains. Compared with the other domain-based algorithms for the secondary structures,^47,48 the algorithm reported here has the advantage of being able to treat pseudoknot structures. For each domain, which has a shorter chain length, we can apply our Vfold model to predict the stable structures. The use of the domain-based method causes a reduction of the computational time by a factor of about N² for an N-mer chain. As an application of the domain-based model, we predict the stable structures for the 210-nt catalytic domain of human telomerase RNA, the 192-nt IGR of CrPV-like IRES and several functional regions of the HIV genome. The results show a good theory-experiment agreement. We aim to predict all the stable as well as the alternative structures. For example, as we will show, for the hTR domain, we found that a long hairpin-like structure has the comparable thermodynamic stability as the hTR pseudoknot. In the predicted hairpin-like structure, we find nucleotides in single-stranded region that are used by telomerase reverse transcriptase (TERT) to synthesize telomere. We note that a previous experiment⁴⁹ suggested a hairpin structure that coexists with the pseudoknot structure. Our results echo the experimental finding.

Results

Domain-based approach to structure prediction

Our entropy parameters give the free energy for a given structure. However, the calculation of a partition function involves a vast ensemble of graphs, and, for an N-nt chain, the structural calculation from the base pairing probability distribution requires the computation for N (N-1)/2 partition functions Q_ij (see Eq. 1 in Materials and Methods). The Vfold model can predict the structure for the pseudoknotted structure with sequence length ~100 nts. For longer sequence, the method becomes computationally limited. In the following, we develop a domain-based partition function theory in order to efficiently tackle larger and more complex RNA structures. Our basic strategy is to factorize the large complex structures into domains that are computationally more tractable. To illustrate the method, we use a graph to represent a structure where the horizontal straight line in the graph represents the backbone chain and a curved link is added between two pairing nucleotides; see Figure 1. According to the presence/absence of cross-linked base pairs (curved links) in the graph, we classify two types of structural domains: pseudoknotted (C_PK in Fig. 1) and non-pseudoknot (C_S in Fig. 1) domains. The partition function for the non-pseudoknot domains can be calculated using the computationally efficient dynamic programming algorithm while the calculation for the pseudoknotted domains is computationally demanding. The essence of our approach is to recursively reduce a structure into domains until irreducible domains, namely, pseudoknotted domains, are reached.

Figure 1.

An RNA pseudoknot structure contains several smaller domains such as C_PK(a₁,b₁) and C_S(a₂,b₂), where C_S represents a structure in which boundary nucleotides a₂ and b₂ form base pair with each other and C_PK(a₁,b₁) is an H-type pseudoknot structure, in which a₁ and b₁ form base pairs with other nucleotides.

First, we use partition functions to identify the domain boundaries such as (a₁, b₁), (a₂, b₂) and (a₃, b₃) in Figure 1.

(1) We first identify the 5′ boundary of each domain. For each nucleotide a_i (1 ≤ a_i ≤ N), we consider the ensemble ( = the macrostate z in Eq. 1) of all the structures with a_i as the 5′ boundary of a domain. For each nucleotide a_i, we use Eq. One to calculate the probability for a_i to be the 5′ boundary nucleotide of a domain. The a_i 's of the large probabilities are identified as the 5′ boundary nucleotides.

(2) Similarly, for each 5′ boundary nucleotide found above, we can identify the 3′ boundary nucleotide. Specifically, for each 5′ boundary nucleotide a_i identified above, we consider the ensemble (= the macrostate z in Eq. 1) of all the structures that contain a domain “i” bound by the nucleotides a_i and b_i (> a_i). For each nucleotide b_i, we use Eq. One to calculate the probability for the formation of a domain bound by (a_i, b_i). The (a_i, b_i) pairs with large probabilities are identified as the domain boundaries.

Applying the above method to hTR (Fig. 2), we found G17 and G209 as the 5′ and 3′ boundaries, respectively (see Fig. 2A). In the above computation, we distinguish the pseudoknotted and the non-pseudoknot domains. Using the recursive algorithm,³⁰ we can identify all the 5′ boundaries in the efficient (one-time) partition function calculation for the chain. We include the pseudoknot structures in the calculation of the partition function. For M identified 5′ boundaries, we need to perform M times partition function calculations to find all the 3′ boundaries. Usually M is much smaller than the sequence length N. Therefore, this approach can effectively reduce the original N(N-1)/2 partition function calculations into a much smaller number (~M) of calculations.

Figure 2.

A schematic figure for the domain-reduction method to predict the stable structure of an 210-nt hTR domain. (A) In the first step, using the partition algorithm we find the boundary nucleotides for the domains; see (a₁,b₁),(a_2,b₂) and (a₃,b₃) in Figure 1. Through this step, we find a domain closed by the base pair (G17, G209). (B) In the second step, we find the continuous helix from base pair G17-G209 to U32-U194 and we truncate the sequence by deleting the the helix from G17-G209 to U32-U194. We repeat the domain-reduction process to identify the pseudoknot or closed secondary structure domain for the truncated sequence. We identify a domain closed by base pair (G33, C191). We also find another continuous helix from G33-C191 to U38-C186. (C) We truncated the sequence by deleting this helix. (D) We continue the process until we reach a pseudoknotted domain or a domain of less then 130 nts. For example, we find the short pseudoknot domain with 122 nts from G63 to U184. In the last step, we use our free energy/partition function model to predict the detailed structure for the final minimum domain. Assembly of the structure domains gives the stable structure for the 210-nt hTR domain.

Second, we recursively reduce the domains. If the sequence gives a continuous train of Waston-Crick base pairs (= a helix) that starts from the boundary base pair (see the continuous helix from base pair G17-G209 to U32-U194 in Fig. 2), we identify the helix and remove it. This would result in a shorter chain which goes from nucleotides 33 to 193 (Fig. 2B). We further apply the above domain-reduction procedure to this shorter chain. Continuous iteration of the above procedure will lead to shorter and shorter chains (Fig. 2C). The domain reduction process stops when we reach a pseudoknotted domain, which is irreducible, or the domain size is small enough (less than 130 nt) for an efficient calculation using the Vfold model. For hTR in Figure 2, the irreducible domain is bound by nucleotides 63 and 184 (see Fig. 2D).

Next, for the irreducible domains, using the entropy parameters and partition function theory (see Eq. 1), we predict the structures from the base pairing probability; see Figure 2D for the predicted structure of the pseudoknotted domain.

The domain-based methodology developed here has three advantages over other pseudoknot models.^20,22-25 First, for a long sequence, the model can explicitly account for the entropy parameters for the formation of the pseudoknots. Second, the model is based on the complete conformation ensemble. Third, based on base pairing probabilities, the model enables prediction for all the stable and metastable states. This is important for large RNAs which can fold into multiple alternative structures.

Figure S1 shows the workflowchart for predicting the structure from the sequence. For a given sequence, if the length is <100 nt, we run the Vfold model directly, otherwise, we run the domain-based algorithm reported in this article. In the domain-based method, for each irreducible pseudoknot domain, we run the Vfold model to predict the structure.

Comparison with other models

To measure the accuracy of the predicted structures, we introduce the sensitivity (SE) and the positive predictive value (PPV) parameters, which are defined as following:

(SE, PPV) = (1, 1) and (0, 0) correspond to the perfectly accurate and the completely failed predictions, respectively. A low SE and/or PPV parameter indicates a high rate of false negative (positive) in the prediction. In Table 1, we tested the model accuracy on nine different pseudoknot structures, such as VMV,⁵⁰ SARS-CoV,⁵¹ HDV,⁵² HDV-anti,⁵³ TMV.L,⁵⁴ TYMV,⁵⁵ IGR IRES,¹⁰ Tetrahymena telomerase⁵⁶ and Human telomerase RNAs,⁵⁷ and compared the results with six of the existing state of the art models, i.e., HotKnots,²² ProbKnot,³⁷ pknotsRE,²³ STAR,²⁶ pknots-RG²⁵ and NUPACK.²⁴ Our model shows significant improvements with (SE, PPV) = (0.92, 0.88). We note that the present model also gives good predictions for non-pseudoknotted structures. For example, Table S1 of reference 58 gives a (SE, PPV) value close to (1.0, 1.0) for 12 hairpin structures.

Table 1. The sensitivity SE (upper) and positive predictive value PPV (lower) values for seven different pseudoknot models. We used nine complex pseudoknot structures such as VMV, SARs-CoV, HDV, anti-HDV, TMV-L and TYMV, IGR IRES, Tetrahymena telomerase and Human telomerase as the test sequences. Overall the Vfold model gives better predictions for the structures of these sequences.

Sequence ID	length	Vfold	HotKnots	ProbKnot	pknotsRE	STAR	pknots-RG	NUPACK
VMV	67	1.0	0.5	0.5	1.0	0.5	0.5	1.0
SARS-CoV	71	0.96	0.92	0.69	1.0	0.73	0.92	0.85
HDV	87	0.9	0.4	0.43	0.46	0.6	0.96	0.63
HDV-anti	91	1	0.16	0.29	0.41	0.62	0.16	0.41
TMV.L	84	0.96	0.52	0.56	0.52	0.64	0.8	0.52
TYMV	86	0.96	0.72	0.88	0.72	0.88	0.76	0.44
IGR IRES	192	0.81	0.74	0.66	0.50	0.47	0.59	failed to run
Tetrahymena telomerase	159	0.68	0.61	0.66	0.45	0.39	0.66	failed to run
Human telomerase	210	0.98	0.70	0.76	0.48	0.48	0.54	failed to run
Average		0.92	0.58	0.60	0.62	0.59	0.65
VMV	67	1.0	0.41	0.41	0.61	0.41	0.41	0.64
SARS-CoV	71	1.0	0.86	0.78	1.0	0.9	0.92	0.96
HDV	87	0.93	0.44	0.42	0.46	0.7	0.93	0.61
HDV-anti	91	0.78	0.14	0.21	0.31	0.6	0.14	0.32
TMV.L	84	0.96	0.61	0.78	0.59	0.69	0.83	0.61
TYMV	86	1	0.78	0.88	0.78	0.88	0.79	0.5
IGR IRES	192	0.76	0.73	0.63	0.67	0.51	0.71	failed to run
Tetrahymena telomerase	159	0.60	0.53	0.50	0.37	0.45	0.57	failed to run
Human telomerase	210	0.87	0.55	0.60	0.32	0.38	0.42	failed to run
Average		0.88	0.56	0.58	0.57	0.61	0.64

Genomic and anti-genomic HDV pseudoknot

Both genomic and antigenomic RNAs of HDV contain a self-cleavage domain with sequence length about 90 nt. Biochemical and structural studies^2-5 indicate that the domain folds into a pseudoknotted structure. We apply the above free energy model and the domain-based method to predict the native structure for HDV pseudoknot. The theory gives satisfactory predictions with (SE, PPV) = (0.9, 0.93) for genomic HDV and (SE, PPV) = (1.0, 0.78) for the anti-genomic HDV. The predicted structure (Fig. 3) is nearly identical to the experimentally determined structure³ except that the P2 stem is slightly longer in the predicted structure. In the calculation, we have used our calculated parameters for the loop entropy⁵⁹ and the empirical free energy parameters for base stacking (in the helices) and the coaxially stacking.^60,61 The model gives improved predictions as compared with other models (see Table 1). Since the different models are based on the same free energy parameters (for the helices), we attribute the improvement in the structure prediction to the use of more accurate entropies (for the loops).

Figure 3.

The predicted structure at t = 37°C for antigenomic HDV ribozymes. Our Vfold model gives a much more accurate prediction with (SE, PPV) equal to (1.00, 0.78) than other models.

TYMV and TMV pseudoknot

The 3′ end of Turnip yellow mosaic virus (TYMV) RNA forms a tRNA-like structure. The pseudoknotted structure in the 3′ end is vital for viral transcription.⁶ For a 86-nt truncated TYMV sequence,²² our model predicts the native structure with (SE, PPV) equal to (0.96, 1.0). Here we allow coaxial stacking between domain I and domain II (as shown in the NMR measurement).⁶² The predicted structure (Fig. S2) nearly exactly agrees with the experimentally measured structure.⁶ Similarly, the model predicts the native structure for tobacco mosaic virus-tomato strain (TMV-L) RNA (see Table 1)⁷ with (SE, PPV) is equal to (0.96, 0.92).

CR1/CR2/CR3 domain of the wild-type hTR

According to the experimental result,⁵⁷ there exists a pseudoknot structure in the CR1/CR2/CR3 domain, which has a >20-bp long stem. The large end-end distance of the stem requires a long loop to connect the two ends of the stems. Conformational enumeration for loop entropy calculation is only viable for stem length less than 12 bps.³⁰ Thus, we develop a method to estimate the loop entropy across a long helix stem (see the Supplementary Material).

Previous studies on the functional role of hTR suggest the possible presence of a functionally important molecular switch between a hairpin-like structure and the hTR pseudoknot.^63,64 These experiments are based on pseudoknot-forming small portion of the whole domain. The whole 210-nt pseudoknot domain of hTR is much more complex than a simple H-type pseudoknot.⁶⁵ The free energy model developed in the present study allows us to predict the structures for the whole domain.

NMR and thermodynamic experiments show the presence of multiple loop-stem tertiary interactions in hTR pseudoknot.⁵⁶ To treat loop-stem interactions, we previously developed a model to fit the empirical loop-stem base triples from thermodynamic data.⁵⁸ The parameters were derived from simple H-type pseudoknots. It is not clear whether the parameters would be applicable to more complex structures such as the whole hTR pseudoknot domain. For the present large domain structure, to simplify the calculation, we assume a total of 4 kcal/mol free energy contribution from the tertiary interactions. The NMR study shows three A·(A-U) base triples between loop 1 and stem 2 in hTR pseudoknot.¹⁸ Our previous calculation⁵⁸ shows that a single U•(A-U) base triple contributes about 1.3 kcal/mol to the free energy at room temperature. Thus, the estimated 4 kcal/mol is close to the energy contribution from three A·(A-U) base triples. Our theory predicts four stable structures I, II, III and IV (see Fig. 4). The structures have similar thermodynamic stabilities. In the following, using structure I as an illustrative example, we show how the structures are predicted.

Figure 4.

The predicted structures for I, II, III and IV (in Figure 5) at room temperature. The free energy differences between the different structures are less than 0.5 kcal/mol.

In the first step, using the domain-reduction method (see Materials and Methods), we predict a structural domain from G17 to G209, as denoted by the closing base pair [17, 209] (see Figs. 2, 4 and 5). Our calculation shows that the probability for the formation of the [17, 209] domain is 0.94. We then remove the continuous helix from base pair G17-G209 to G31-U195 (see Fig. 4A). For the resultant truncated sequence from nucleotides 32 to 194, the domain-reduction procedure leads to four alternative domain structures (see Fig. 5 and I, II, III and IV in Fig. 4). Structures III and IV each contains two sub-domains closed by base pairs [33, 180] and [181, 191] for III and by [35, 179] and [181, 191] for IV. Structures II, III and IV (see Fig. 4) all contain a stable domain [56, 151] (see Fig. S3b for the detailed structural information for the domain). The high similarity between structures II, III and IV suggests that we may classify them into one (stem-loop) structure. Structure I contains a pseudoknotted domain (denoted as PK in Fig. 5) bound by nucleotides 63 and 184 (see Fig. S3a). The predicted structure I agrees exactly with the structure derived from phylogenetic analysis.^56,57,65

Figure 5.

The predicted stable domain of hTR. There are four stable structures (I, II, III and IV) at room temperature. The non-PK and PK represent the non-pseudoknot and pseudoknot domains, respectively. The corresponding value is the probability for finding each domain.

Our predicted structural distribution (Figs. 4 and 5) for the whole pseudoknot domain of hTR shows coexisting pseudoknot (Fig. 4-I) and stem-loop structure (Fig. 4-II, III and IV). We note that the long stem-loop structure has been detected in a previous biochemical analysis.⁴⁹ It is important to note that the (highly conserved) template sequence (see Fig. 4) in the predicted pseudoknotted and stem-loop structures is single-stranded and thus is directly accessible for the synthesis of telomere with telomerase reverse transcriptase (TERT).

Our previous kinetic study⁶⁶ for the folding kinetics of the small truncated pseudoknot showed that the hairpin structure is kinetically accessible. Our present study on the whole domain further shows the presence of a (thermodynamically stable) stem-loop structure. The result would facilitate our understanding of the functional relevance of the conformational switch⁶³ between stem-loop structure and pseudoknot in telomerase activity.

Structure of IGR IRES

An internal ribosome entry site (IRES) is a sequence domain inside a mRNA, which can recruit the ribosomes for the protein synthesis.^67,68 Computational prediction of the IRES tertiary structure is limited by the inability to treat the pseudoknotted structure.^69,70 With the domain-based method, we can now predict the stable structure for IGR IRES. We applied the domain-reduction method and found three domains bound by nucleotides [1, 70], [72, 143] and [147, 190], respectively (see Fig. 6A). Further domain-reduction calculations for the [72, 143] give two sub-domains [81, 94] and [97, 137] (see Fig. 6B). The theoretical predictions show good agreement with the experiments with (SE, SP) values equal to (0.84 and 0.77).¹⁰ We correctly predict the domains I and III. However, the current form of our theory does not treat the long range kissing interaction between residues C139-G143 and C36-G40.¹⁰

Figure 6.

(A) The predicted stable structural domain of IGR IRES at room temperature. Also shown in the figure are the probabilities for forming each domain. (B) The predicted structure for the domains. We correctly predict domain I and domain III. Domain III is a pseudoknot structure. For domain II, the model cannot treat the long-range tertiary interaction between residues C139-G143 and C36-G40. The SE and SP values for the predicted structure are 0.84 and 0.77, respectively. In (a), the non-PK and PK represent the non-pseudoknot and pseudoknot domains, respectively.

Structure of HIV-1 5′UTR

The structure of the HIV-1 5′ untranslated region (UTR) is still not fully studied. Until now, there is no consistent structural model for the 5′ UTR. Previous computational and experimental studies confirmed the different hairpin domain such as the trans-activation region (TAR) and the polyadenylation signal hairpin [poly(A)] in the 5′ UTR.

However, recent studies based on both the experimental and computational analysis^71,72 identified a long-range base pairings between nucleotides G108-C114 and G335-U341 in the native structure of HIV-1 NL4–3 RNA genome, which questions the existing structural model for HIV-1 5′ UTR.^73,74 We note that the long-range interaction can be identified by the MPGAfold program, but it may not exist in the native structure.²⁷

We use the domain-based method to predict the native structure for a truncated HIV-1 HXB2 sequence.⁷⁴Figure 7 shows the native structure of the truncated sequence. The predicted structure is similar to the branched multiple hairpin (BMH) conformation, which contains a long-ranging interaction (called the U5-AUG interaction).⁷⁵ The U5-AUG interaction is confirmed by recent SHAPE analysis in HIV-1 NL4–3 sequence.⁷¹ Our prediction supports the BMH structure. Our model, which is based on the thermodynamic calculation, does not predict the stable (long-distance interaction) LDI conformation. This is consistent with the experimental observation.^71,76 The LDI conformation could be formed as a kinetic intermediate.⁷⁷

Figure 7.

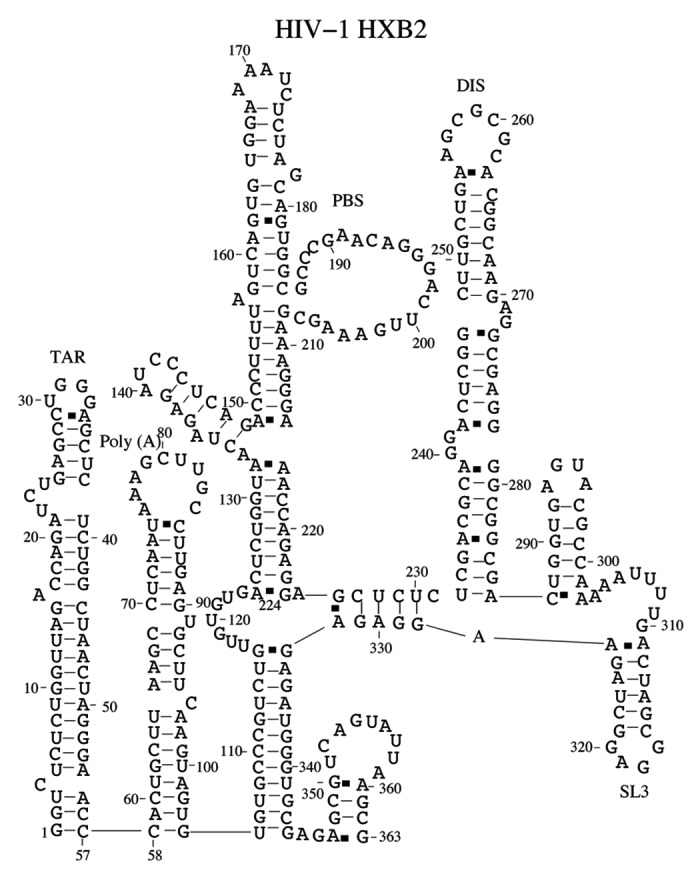
The predicted native structure for HIV-1 HXB2 sequence at room temperature. We correctly predict the TAR, Poly(A), PBS, DIS and SL3 domains. In addition, we find that nucleotides 105–116 form base pairings with nucleotides 333–344. The long-range interaction has been found in HIV-1 NL4–3 sequence.⁷¹

Discussion

In summary, we have developed a domain-based model to predict the stable structures for large RNAs with pseudoknotted structure. Tests of the model for a series of the complex pseudoknotted structures (HDV, anti-HDV, TYMV and TMV) yield high accuracy with average (SE, PPV) equal to (0.96, 0.92). The sequence lengths for HDV, anti-HDV, TYMV and TMV pseudoknots are all <100 nt. Thus, we run the Vfold model directly for these sequences. Furthermore, applications of the domain-based method for the prediction of the stable structures for hTR, IGR IRES and HIV give structures that are consistent with experimental findings. For the IGR IRES sequence, the model predicts a pseudoknot-like structure in the 3′ end, which is consistent with the experiment. For HIV 5′ UTR, the model does not predict pseudoknotted domains for the 363-nt truncated sequence. The structure predicted by the model is in accordance with the recent experimental results.⁷¹

For the hTR sequence, our model predicts a long stem-loop that coexists with a pseudoknotted structure. Based on the predicted structures, we propose that the telomerase activity may be connected to the metastability of the structure and the conformational switch between the pseudoknotted structure and the stem-loop structure. The result is consistent with earlier experimental reports on the hTR pseudoknot.^49,63,64 It was proposed in these experimental studies that the conformational switch between the hairpin and the pseudoknot may be important for the hTR activity. Our theoretical predictions here support the experimental findings. We note that our results here are based on the calculations for the large hTR domains instead of the truncated short sequence of the model system studied in the experiments.¹⁸ The theoretical prediction here may be useful to facilitate understanding of the structure-function relationship for hTR.

Although this newly developed model can predict the large and complex pseudoknotted structure based on a physical model for RNA folding free energy, the model cannot treat loop-stem tertiary interaction between a large loop and a long stem. The previous work for estimating the loop-stem tertiary interaction is restricted to a short loop and a short stem.⁵⁸ For a long loop, we need to develop an ab initio model to evaluate the energetics for loop-stem tertiary interactions. Moreover, the current form of the model cannot give the free energies for structures involving long-range tertiary interactions such as the pseudoknots found in large rRNAs. As a result, the model cannot predict pseudoknots formed by inter-domain long-range contacts in large RNAs.^11,12 Furthermore, we can extend our algorithm to include the pseudoknot motif in the prediction of sRNA and their targets in bacteria. The pseudoknot motif is usually neglected in the existing algorithms.⁷⁸

Materials and Methods

The free energy of folding for a structure s is calculated from ΔG_s = ΔG_helix – TΔS_loop, where T is the temperature, ΔG_helix and ΔS_loop are the free energy and the entropy for the helix stems and the loops, respectively. In order to account for the intraloop base stacks, we define an irreducible loop as a loop that contains no stable base stacks, including canonical and mismatched base stacks. Here a mismatched base stack is formed by a Watson-Crick (WC) base pair stacking on a non-WC base pair. The purpose of using irreducible loops is 2-fold. First, for a given (regular, non-irreducible) loop, it allows us to enumerate the conformations through the different assignments of the (intraloop) mismatches.⁷⁹ The model gives (nonzero) loop enthalpy as the ensemble (Boltzmann) averaged sum of the enthalpies of the intraloop mismatches. Second, for a given irreducible loop, the simplicity of the conformations (without stable base stacks) makes the conformational count possible. We note that the conformational entropy for an irreducible loop can only come from the theoretical calculation. We predict the structures from the probability distribution for the formation of the different base pairs. Consider a macrostate z defined as the ensemble of all the structures, the folding free energy ΔG_z for the state can be computed from the partition function

(1)

where k_B is the Boltzmann constant and the sum is over all the conformations “s” accessible to the macrostate z. The ratio between Q_z and the total partition function gives the probability p_z for the formation of the macrostate z. If macrostate z is the ensemble of structures that contain a specific base pair (i,j), p_z would be the probability of forming base pair (i,j). From the base pairing probability distribution for the different base pairs (i,j), we deduce the structure.

The key step in the above procedure is the evaluation of the free energy ΔG_s for a given structure s. While the free energy for the helix stems ΔG_helix can be approximately evaluated from the nearest neighbor model,⁶⁰ the evaluation of the conformational entropy ΔS_loop for the loops/junctions requires a model. With the virtual bond-based RNA folding model (Vfold model), we develop a method to compute the entropy parameters.

We evaluate the entropy as k_B lnΩ, where Ω is the number of accessible conformations. We compute Ω through direct enumeration of chain (loop) conformations within the given structural context. Based on the rotameric properties of RNA backbone, we enumerate RNA conformations using a 3-vector virtual bond conformational representation for each nucleotide (Vfold model).³² We model a helix stem as an A-form helix using the experimentally measured atomic coordinates.⁸⁰ The (r, θ, z) coordinates (in a cylindrical coordinate system) for the P, C₄, and N₁ (or N₉) atoms are (8.71 Å, 70.5 + i32.7, -3.75 + i2.81), (9.68 Å, 46.9 + i32.7, -3.10 + i2.81), and (7.12 Å, 37.2 + i32.7, -1.39 + i2.81) (i = 0,1,2,…),⁸⁰ respectively. For the other strand, we need to negate θ and z to obtain the coordinates in cylindrical coordinate system. For a loop/junction, we generate the conformations of the loop through self-avoiding walks in the diamond lattice by using the Vfold model.⁵⁹ By counting the number of viable conformations of the loop, we calculate the entropy parameter of the loop.

In the present theory, we neglect the loop-stem tertiary interaction in order to keep the computational efficiency for the prediction of large (pseudoknotted) structures. Loop-stem tertiary contacts can contribute a non-zero enthalpy to the loop free energy. Our previous studies show that the loop-stem tertiary interactions do not change the native folded secondary structures for many H-type pseudoknots and only affect the stability of these pseudoknots.^30,58 The benchmark test (see Table 1) shows that the current pseudoknot model based on explicit entropy calculation can indeed give good predictions for large pseudoknotted secondary structures.

Energetics parameters for the complex pseudoknot structure

We use hTR pseudoknot¹⁸ (see Fig. 8A) to illustrate the strategy. The structure contains three stems S₁, S₂ and S₃ and four loops L₁, L₂, and . We aim to evaluate and tabulate the entropy parameters for general structures with the different helix and loop lengths. Exhaustive computer enumeration of all the possible conformations for all the possible helix and loop lengths is not viable. To circumvent the problem, we first reduce the original structure so the entropy calculation becomes tractable.

Figure 8.

(A) A schematic diagram for a complex pseudoknot structure. (B) The simplified pseudoknot with stem S₃ replaced by a phantom nucleotide. (C) We divide the pseudoknot structure in (B) into two separate simple structures: a structure with stem S₁₂ and loop L₃ and an H-type pseudoknot with stems S₁ and S₂ and loops L₁ and L₂.

1. The effect of stem S₃ on the conformations of loop L₃ ( = + ) is mainly through the base pair (a, b). Therefore, to evaluate the number of viable conformation for loop L₃, we can replace stem S₃ with the base pair (a, b). Furthermore, we replace the (rigid) base pair (a, b) with a single nucleotide (see Fig. 8B) and accordingly, the length of loop L₃ is equal to ++1.

2. Neglecting the excluded volume interaction between loop L₃ and loops L₁ and L₂, we calculate the entropy parameter for loop L₃ and loops L₁ and L₂ separately. In the calculation, we account for the presence of the helices by considering the volume exclusion from the helix stems (see Fig. 8C). The entropy parameters are functions of the helix and loop lengths. The entropy parameters for loops L₁ and L₂ are dependent on the stem lengths S₁ and S₂ and can be adopted from Table 2 of reference 30. For the entropy parameter of loop L₃, we use a long stem S₁₂ to represent stems S₁ and S₂. The length of stem S₁₂ is equal to the sum of the length of S₁ and the length of S₂. The approximation is based on the fact that stems S₁ and S₂ tend to coaxially stack and form a quasi-continuous helix.⁶⁴

Table 2. The entropy parameters (ΔS/k_B) for the formation of loop L₃ in the pseudoknot motif of Figure 8B, where L is the length of loop L₃ and S₁₂ is the length sum of stem S₁ and stem S₂.

S12/L	1	2	3	4	5	6	7	8	9	10	11	12	13	14
4	–	–	–	–	–	–	-12.8	-12.4	-12.5	-12.5	-12.7	-12.7	-12.9	-12.9
5	–	–	–	–	–	–	–	-12.8	-12.8	-12.7	-12.8	-12.8	-12.9	-12.9
6	–	–	–	–	–	–	–	-15.5	-14.0	-13.8	-13.7	-13.6	-13.6	-13.5
7	–	–	–	–	–	–	–	-14.2	-14.2	-14.0	-14.0	-13.9	-13.9	-13.9
8	–	–	–	–	–	–	–	-14.5	-13.8	-13.4	-13.3	-13.2	-13.2	-13.3
9	–	–	–	–	–	–	–	–	-14.8	-13.8	-13.5	-13.4	-13.4	-13.4
10	–	–	–	–	–	–	–	–	-14.9	-13.8	-13.5	-13.4	-13.4	-13.4
11	–	–	–	–	–	–	–	–	-14.8	-14.2	-14.1	-14.0	-14.0	-14.0
12	–	–	–	–	–	–	–	–	-16.6	-15.4	-14.9	-14.6	-14.5	-14.4
13	–	–	–	–	–	–	–	–	–	-17.0	-16.1	-15.5	-15.3	-15.0
14	–	–	–	–	–	–	–	–	–	–	-18.3	-17.1	-16.5	-16.0
15	–	–	–	–	–	–	–	–	–	–	–	-22.8	-21.1	-19.9

The entropy parameters for loop L₃ depend on the length of stem S₁₂. Figure 9A shows the distribution of the end-end distance, which is defined as the distance between the P atom in the 5′ starting nucleotide of the loop L₃ and the P atom in the 3′ end of the loop L₃. The end-end distance increases as the sum (S₁₂) of the length of stem S₁ and the length of stem S₂ increases. Table 2 shows the entropy parameters for loop L₃. In the calculation, the maximum loop length for a computationally viable calculation is 14 nts. larger loops, we extrapolate the entropy parameters using following formula:

Figure 9.

(A) The end-to-end distance for a loop (see L₃ in Fig. 8) with the different stem lengths (S₁₂). The length of stem S₁₂ is the sum of the stem S₁ length and the S₂ length. The end-to-end distance of a loop is defined as the distance between the P atom at the 5′ end of loop L₃ and the P atom at the 3′ end of loop L₃. (B) The comparison of the computational time between the original Vfold model (square) for predicting pseudoknot structure and the new domain-based algorithm for the calculation of the probability for a specific nucleotide to be the 5′ boundary of a domain (circle). The computer resource that we use is Dell EM64T cluster with the Intel (R) Xeon(R) 5150 (2.66 GHz) processor.

ΔS = aln(l – l_min + 1) + bl + c 2

where l_min is the minimal loop length L₃ in Table 2. We fit the parameters a, b and c based on the entropy values for shorter loops listed in Table 2. Table 3 shows the fitted parameters a, b and c.

Table 3. The fitted parameters for the loop entropies in Equation 1.

stem length	4	5	6	7	8	9	10	11	12	13	14	15
a	0.66	0.20	2.27	0.14	1.49	1.96	2.13	1.09	2.19	1.51	1.77	2.73
b	-0.23	-0.08	-0.44	0.013	-0.28	-0.43	-0.48	-0.24	-0.35	-0.11	-0.06	-0.06
c	-11.1	-12.2	-11.8	-14.3	-12.3	-10.9	-10.6	-12.6	-13.4	-15.9	-17.7	-22.1

The total loop entropy of hTR pseudoknot () is given by the following formula:

(3)

where ΔS(S₁₂,L₃) is the entropy for loop L₃ and ΔS(S₁,S₂,L₁,L₂) is the loop entropy for the reduced H-type pseudoknot (see Fig. 8C). The loop entropy parameter for the H-type pseudoknot can be read out from the entropy table reported in the previous studies.³⁰

Our previous models^30,32 only treat simple H-type pseudoknot structures. In the current study, we extend the Vfold model to deal with more complex pseudoknot motif, such as a pseudoknot embeded in a hairpin loop (a → b in Fig. 8). The current model allows us to calculate and tabulate the entropy parameters for such complex pseudoknotted motifs. Furthermore, we develop a domain-based approach to treat pseudoknot-forming long sequences. With this new method, we can easily treat the sequence length with 400 nts. However, in the original Vfold model,^30,32 it is difficult to predict the pseudoknot structure even for a 100-nt sequence (see Fig. 9B).

Computational time

The recursive process of domain-reduction quickly converges to the irreducible domain, thus, the procedure is computationally efficient. The computational time is limited only by the size of the pseudoknotted domain. For each irreducible pseudoknotted domain, the computer time for calculating the partition function scales as O(N¹¹).³⁰ For the RNA secondary structure, the computer time scales as O(N⁴).⁵⁹ Therefore, the total computational efficiency is limited by the calculations for the pseudoknotted domains.

The computer time t(L) for searching for the 5′ domain boundary nucleotides (using Eq. 1) grows algebraically with the sequence length L (see Fig. 9B). For a sequence of 400 nt, it takes less than 4 h. The required computer time for the present approach is significantly shorter than the original Vfold model, which can only treat sequences less than 100 nt (see Fig. 9B). It takes about the same computational time to find the 3′ boundary nucleotides for the domains. For a large RNA with M domains, the total computer time is approximately 2M t(L). For a system with M = 5 domains, it takes about 40 h to predict the full structure for a 400-nt sequence. The domain-based method is computationally feasible for large RNAs. In addition, we compared the computational times for our model and other existing models. We found that our model is slower than HotKnots, ProbKnot, STAR and pknots-RG and faster than pknotsRE and NUPACK.

Supplementary Material

Additional material

Supplementary PDF file supplied by authors.

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed