Prediction System for Rapid Identification of Salmonella Serotypes Based on Pulsed-Field Gel Electrophoresis Fingerprints

Abstract

A classification model is presented for rapid identification of Salmonella serotypes based on pulsed-field gel electrophoresis (PFGE) fingerprints. The classification model was developed using random forest and support vector machine algorithms and was then applied to a database of 45,923 PFGE patterns, randomly selected from all submissions to CDC PulseNet from 2005 to 2010. The patterns selected included the top 20 most frequent serotypes and 12 less frequent serotypes from various sources. The prediction accuracies for the 32 serotypes ranged from 68.8% to 99.9%, with an overall accuracy of 96.0% for the random forest classification, and ranged from 67.8% to 100.0%, with an overall accuracy of 96.1% for the support vector machine classification. The prediction system improves reliability and accuracy and provides a new tool for early and fast screening and source tracking of outbreak isolates. It is especially useful to get serotype information before the conventional methods are done. Additionally, this system also works well for isolates that are serotyped as “unknown” by conventional methods, and it is useful for a laboratory where standard serotyping is not available.

INTRODUCTION

According to the most recent report from the Centers for Disease Control and Prevention (CDC) (20), Salmonella was the second most common pathogen among all food-borne pathogen outbreaks, accounting for 23% of the outbreaks, 31% of the illnesses, and 62% of the hospitalizations reported. Detailed strain identification, including serotype identification, is critical for efficient epidemiological investigation of Salmonella outbreaks (18) and is helpful in determining the relatedness of individual cases for outbreak source tracking (21).

The standard serotyping method, which relies on the detection of somatic (O) and flagellar (H) antigens present on the cell surface of Salmonella, requires specialized skills and reagents; in addition, it is expensive and may take a couple of days to complete (11, 12, 14). Numerous molecular techniques have been used to serologically type Salmonella isolates based on microarrays (5), real-time PCR (16), repetitive sequence-based PCR (25), multiplex primer extension (2), multilocus sequence typing (15), and bead-based arrays (6). Each of these methods has advantages and drawbacks in terms of cost, speed, robustness, and sensitivity (24). Although these methods are improvements over the historical method in various aspects, none has been evaluated as the ideal method to be conducted on a massive scale for the routine microbiological laboratory (24).

Pulsed-field gel electrophoresis (PFGE) was adapted to Salmonella in the 1990s and is now still the most widely used method to identify and characterize Salmonella strains in outbreaks (8). It has been reported that PFGE excels in tracking the source of Salmonella infection for different serovars (22). Although it is also labor-intensive and time-consuming, PFGE fingerprinting with conventional serotyping is considered the gold standard for Salmonella subtyping (7). The PulseNet network (http://www.cdc.gov/pulsenet), coordinated by the CDC, uses PFGE as the preferred subtyping method (10). By the end of 2010, around 350,000 profiles of about 500 Salmonella serotypes had been submitted to PulseNet. These data are valuable for Salmonella outbreak source tracking until PFGE fingerprinting is replaced by new, simpler sequence-based methods. Considering the significant value of the PFGE patterns, an ability to deduce the serotype of a Salmonella isolate based on its PFGE profile would be highly attractive in that it would limit the need for both PFGE and traditional serotyping for rapid strain identification and source tracking (27). Liebana et al. (18) compared several methods for discriminating Salmonella isolates of five serovars and concluded that certain serotypes could be deduced solely by their PFGE patterns. Gaul et al. (9) further described the correlation of serotypes to PFGE subtypes based on an analysis of 674 isolates from 12 Salmonella serotypes and concluded that PFGE fingerprints could potentially provide an alternative method for screening and identifying Salmonella serotypes. Both results were based on hierarchical cluster analysis performed by GelCompar II software (version 1.01; Applied Maths, Kortrijk, Belgium) and BioNumerics software (Applied Maths, Inc., Austin, TX), respectively (9, 18). Hierarchical cluster analysis is an unsupervised algorithm in which the clusters are determined only based on the pairwise similarities of the samples, and no training set data are required. In BioNumerics, for example, hierarchical cluster analysis groups bacterial isolates with similar PFGE patterns in the same cluster to understand their similarities and differences and to find or characterize the relationships among isolates (27). No serotype information is utilized in the analysis; therefore, it is ineffective for use in prediction or identification of serotypes. We recently introduced a classification approach (27) to identify Salmonella serotypes of isolates based on PFGE patterns. The classification model was applied to a data set of 866 PFGE patterns consisting of eight serotypes; the overall accuracy of correct identification of the eight serotypes was 96.3%. Although the approach reached high prediction accuracy, the number of isolates and the number of serotypes analyzed in the study were small; four of the eight serotypes in this study had fewer than 50 isolates.

Classification has received new attention in identifying disease presence (1) and predicting which cancer patients would benefit from chemotherapy and which would experience unnecessary toxic side effects based on profiling of patterns of gene expression (1). Development of a classification model involves two steps: (i) model building and (ii) performance assessment. Typically, the data are divided into a training set and a test set; the classification model (rule) is developed on the training set and then applied to the samples in the test set to assess its performance. Classification performance depends greatly on the classification algorithms and characteristics of the data to be classified. The random forest (RF) and support vector machine (SVM) classification algorithms are most widely used in classification of high-dimensional molecular data (1, 19); both algorithms have been shown to consistently perform better than other classical classification algorithms, such as κ-nearest neighbor method, classification tree, and linear discriminant analysis (17).

Classification accuracy is estimated by applying the developed model to the future samples that presumably emulate the population of the current samples. If the current samples do not adequately represent the future samples, then the estimates of prediction accuracy can be biased. For example, if the sample size in the present study is inadequate to represent the population that might be seen for future samples, then the estimated accuracy (e.g., the estimated 96.3% accuracy in our previous work) is likely too optimistic. In this study, a classification model was developed by learning the PFGE patterns of the isolates of known serotypes from the training samples; the model was subsequently used to classify the serotype of a future sample based on its PFGE pattern. When PFGE patterns from various isolates are compared by performing band matching through BioNumerics software, the compositions of band classes depend on the compositions of the isolate groups. The same isolate may have slightly different sizes of bands compared with different isolates. In other words, the PFGE band sizes generated from different combinations of samples are not comparable and need to be normalized (standardized) before data analysis.

In this study, we expanded our previous work using RF and SVM classification algorithms to develop classification models for epidemic investigation of food-borne pathogen outbreaks. The classification model was applied to a large database of 45,923 PFGE patterns randomly selected from all submissions to the CDC PulseNet from 2005 to 2010 and covering 32 commonly encountered serotypes. The goal of the study was to develop a new tool for early and fast screening and source tracking of outbreak isolates. The tool allows the fast and accurate prediction of serotypes of Salmonella isolates from outbreaks before the conventional methods are used. It will also be useful either to distinguish an isolate that is serotyped as “unknown” by conventional methods or to apply in a laboratory where standard serotyping is not available. A new method to normalize band sizes was also developed.

MATERIALS AND METHODS

PFGE fingerprint data set.

A total of 45,923 XbaI-PFGE patterns of Salmonella enterica isolates from PulseNet were considered in this study. These patterns were randomly selected from each of 32 serotypes from all the submissions in the PulseNet national Salmonella database from 2005 to 2010. More than 99% of the isolates were collected from stool, blood, urine, or unknown sites of patients from the United States. Less than 1% of the isolates came from various foreign countries. The PFGE fingerprinting was performed by PulseNet-participating laboratories at their state/local laboratories. The results were uploaded to PulseNet electronically and directly by the state and local health departments. The serotype information of the patterns was obtained by the traditional serotyping method (4, 11, 12, 14) from the state laboratories and CDC serotyping lab.

Because of the limitation of the BioNumerics software for processing more than 20,000 PFGE patterns, the data were divided into three groups (Table 1). Group 1 (G1) was randomly selected from the constructed database from PulseNet, followed by the random selection of group 2 (G2). G1 and G2 had approximately equal numbers of isolates for all 32 serotypes. These two groups were used alternatively as the training and test groups to develop the classification algorithm. The remaining 6093 patterns in group 3 (G3) were used as additional external validation, and their serotype information was coded to prevent potential bias.

Table 1.

Selected Salmonella serotypes and numbers of patterns in three groups used in this study

S. enterica serotype group and name	No. of patterns in the present study				Isolates from human sources, 1996-2006a
	Group 1	Group 2	Group 3	Total	Rank	Total no. for the period	% of total
Most frequent serotypes (n = 20)
Agona	980	973	0	1,953	14	5,820	1.5
Braenderup	923	927	158	2,008	13	5,833	1.5
Enteritidis	929	914	495	2,338	2	69,547	17.8
Hadar	905	929	147	1,981	16	4,392	1.1
Heidelberg	915	1,008	191	2,114	4	20,473	5.2
I 4,[5],12:i:−	922	927	431	2,280	15	4,698	1.2
Infantis	917	926	235	2,078	11	6,031	1.5
Javiana	910	890	302	2,102	5	13,513	3.5
Mississippi	904	908	187	1,999	17	4,063	1.0
Montevideo	954	923	164	2,041	7	9,459	2.4
Muenchen	915	961	94	1,970	8	7,960	2.0
Newport	914	911	180	2,005	3	32,955	8.4
Oranienburg	963	988	0	1,951	9	6,783	1.7
Paratyphi B var. L(+) tartrate+	908	916	187	2,011	19	3,987	1.0
Poona	906	949	101	1,956	20	3,100	0.8
Saintpaul	954	940	358	2,252	10	6,322	1.6
Thompson	907	934	204	2,045	12	5,903	1.5
Typhi	935	1,006	0	1,941	18	3,990	1.0
Typhimurium	918	923	223	2,064	1	75,058	19.2
Typhimurium var. 5−	908	925	313	2,146	6	9,523	2.4
Less frequent serotypes (n = 12)
Anatum	106	116	256	478	23	2,218	0.6
Bareilly	100	101	225	426	24	2,051	0.5
Berta	109	100	293	502	21	2,488	0.6
Derby	105	107	181	393	29	1,642	0.4
Hartford	105	113	313	531	27	1,836	0.5
Litchfield	134	103	164	401	30	1,567	0.4
Mbandaka	159	111	162	432	25	2,048	0.5
Panama	124	104	288	516	28	1,698	0.4
Paratyphi A	115	20	0	135	35	1,163	0.3
Schwarzengrund	119	106	0	225	31	1,538	0.4
Senftenberg	97	92	0	189	32	1,457	0.4
Stanley	117	102	241	460	22	2,273	0.6
Total	19,877	19,953	6,093	45,923		390,767	100.0

^aData were derived and calculated from the CDC's Salmonella annual summary of 2006 (4). Rank indicates the frequency of isolation, with lower numbers indicating greater frequency. During this period, the 20 most frequent serotypes were represented by 299,410 isolates, or 76.6% of the total of 390,767 isolates for the period, and both groups together were represented by 321,389 isolates, or 82.2% of the total number of isolates.

The gel images were processed and analyzed by BioNumerics software according to the PulseNet protocol developed by CDC (26). BioNumerics software was used to perform band matching of PFGE patterns of various isolates in groups 1, 2, and 3. The presence or absence at each band position was coded 1 or 0, respectively.

Standardization of band classes across groups.

Since the band classes for the three groups were created separately, they were not comparable across groups. The classification model developed from the training data set cannot be directly applied to the test data or to future data. To make serotype prediction consistent and comparable, the band classes of all PFGE patterns must be standardized for the algorithms. Two methods were developed to standardize the band classes for cross-group analysis. In both methods the band classes created from the training data were used as the standard. The first standardization method normalized band sizes of test data via BioNumerics software. The band class for the training data was created and saved as the standard; the test data had band matching performed by loading the saved standard through BioNumerics software. This method was named the BioNumerics fixed-band method. In the second method, the bands of each sample in the test data were normalized according to the corresponding means of the band sizes of two adjacent bands of the training data. For example, suppose the training data consisted of band sizes of a1, b1, c1, d1, etc., and test data consisted of a2, b2, c2, d2, etc. For each PFGE pattern in the test group, if a2 ≤ (a1+ b1)/2, a2 was normalized to a1, and if a2 > (a1 + b1)/2, it was adjusted to b1. This new method is referred to as the NCTR fixed-band method.

Classification.

Two classification algorithms, the RF (3) and SVM (23), were used to build the classification model. RF was developed by Breiman to improve performance over the decision tree algorithm (3) and is available as the package RandomForest in R. SVM was introduced by Vapnik (23), and the SVM program in R in the e1071 package was used. This method finds a linear boundary in the input feature space or may be expanded to allow the boundary to be found in a higher dimensional space by projecting the input space into a large, potentially infinite, space.

Two-fold cross validation was used to assess the performance of the classification model. In 2-fold cross validation, the model is trained on G1 and tested on G2, followed by training on G2 and testing on G1. Thus, the entire data are classified once. The classification accuracy of each serotype was calculated as the proportion of correct classification. The overall accuracy was the average of the 2-fold partition repeated 100 times. The classification model was further validated using a separate data set, G3, of 6,093 patterns with their serotype information blinded to minimize potential bias.

Distance matrix development.

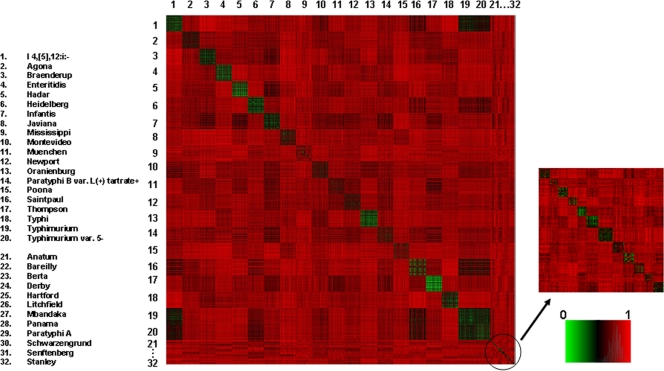
To interpret the differences in prediction accuracies for various serotypes, the distance matrix of 32 serotypes was developed. Group 1 and group 2, normalized by the group 1 standard band class, were combined, resulting in 39,830 patterns of 32 serotypes. The distance matrix presents the dissimilarities of any two patterns in the whole group. The dissimilarity was measured by Jaccard distance (13), and the values ranged from 0 to 1 (see Fig. 1).

Fig 1.

Distance matrix of 32 serotypes.

RESULTS

PFGE fingerprint data set.

Group data are presented in Table 1. Group 1 (n = 19,877), which was randomly selected first, included all 32 serotypes and all the sources where the Salmonella isolates were extracted. Group 2 (n = 19,953) was randomly selected to have approximately equal numbers of patterns in each of 32 serotypes, except for S. enterica serotype Paratyphi A, which had only 20 patterns. The band classes for group 1 and group 2 were created separately by BioNumerics software. Group 1 consisted of 60 bands ranging from 20 kb to 1,100 kb, while group 2 consisted of 61 bands in the same range (Table 2). Some of the bands from the two groups were the same size, but most of them differed slightly.

Table 2.

Band sizes generated from G1 and G2 patterns

Banda	Band size (kbp) by group
	G1	G2
1	1,101	1,101
2	1,037	1,038
3	979	994
4	890.8	893.2
5	850.7	850.4
6	790.7	791.6
7	746.6	746.9
8	710.9	711.4
9	666.1	666.5
10	645.6	645.5
11	603.7	603.4
12	582.1	581.9
13	560.1	560.5
14	538.3	541.2
15	513.4	522.4
16	497.2	506.4
17	481.2	482.5
18	459.9	459.9
19	438.7	438.9
20	411.8	412
21	392.1	392.1
22	373.9	373.9
23	357.5	357.8
24	342.8	342.9
25	334.4	334.5
26	322.4	322.4
27	308.9	308.9
28	290.8	290.8
29	275.6	275.6
30	256.7	256.7
31	247.2	247.4
32	237.5	237.7
33	223.2	222.6
34	211.9	210.4
35	194.6	194.7
36	183.4	183.4
37	175	175
38	168.3	168.2
39	160.1	160.4
40	145.8	148.2
41	136.1	137
42	127.2	127.8
43	118.8	118.9
44	110.4	110.4
45	103.8	103.7
46	97.28	97.48
47	84.87	86.87
48	75.75	83.71
49	70.79	75.74
50	66.11	70.78
51	61.22	66.1
52	53.56	61.27
53	47.45	53.3
54	42.79	46.43
55	37.2	42.69
56	32.79	37.12
57	30.88	32.77
58	28.82	30.88
59	25.36	28.88
60	21.33	25.32
61		21.34

^aThere are 60 bands in G1 and 61 bands in G2.

Comparison of two standardization methods.

RF and SVM classification algorithms were applied to the PFGE patterns normalized by the two standardization methods using the band class of either group 1 or group 2 as the standard. The accuracies of all predictions are listed in Table 3. First the RF model was trained on the band class of group 1 patterns as the standard and was tested on the band class of group 2 normalized by the BioNumerics fixed-band method. The accuracies are shown in the second column from the left. The third column shows the accuracies of the following prediction of RF by training on standard group 2 and testing on standardized group 1. Thus, all of the data were classified once, and the average accuracies are listed in the fourth column. The remaining three columns show the accuracies from the same RF classification model applied on PFGE bands but normalized by the NCTR fixed-band method. The accuracies of SVM algorithms applied to PFGE patterns standardized by the two methods are also shown in Table 3. Except for the S. enterica serotype I 4,[5],12:i:− (accuracies of approximately 90% to 93%) and S. enterica serotypes Typhimurium and Typhimurium var. 5− (accuracies if approximately 64 to 72%), the other 20 most common serotypes had prediction accuracies above 98% (most higher than 99%) when the NCTR method was used to standardize band classes but above only 96% when the BioNumerics method was used in both RF and SVM classifications. When the RF algorithm was applied (Table 3), the total average accuracy from the NCTR method was 95.9%, which was higher than that of 95.1% using the BioNumerics method. The same result was obtained when the SVM algorithm was used (96.1% for the NCTR method and 95.1% for the BioNumerics method) (Table 3).

Table 3.

The prediction accuracies of RF and SVM algorithms on PFGE patterns standardized by the BioNumerics fixed-band method and NCTR fixed-band method using either the group 1 or group 2 band class as the standard

Algorithm and S. enterica serotype group and name	% Accuracy by method and groupa
	BioNumerics fixed-band method			NCTR fixed-band method
	G1 as the standard	G2 as the standard	Avg of the serotypes	G1 as the standard	G2 as the standard	Avg of the serotypes
RF algorithm
Most frequent serotypes (n = 20)
I 4,[5],12:i:−	90.1	90.5	90.3	91.7	91.0	91.3
Agona	99.9	99.7	99.8	99.9	99.7	99.8
Braenderup	98.9	98.7	98.8	99.7	99.8	99.7
Enteritidis	99.6	99.5	99.5	99.7	99.8	99.7
Hadar	99.4	99.0	99.2	99.0	98.5	98.7
Heidelberg	99.5	99.8	99.6	99.9	99.7	99.8
Infantis	98.5	98.7	98.6	99.8	99.9	99.8
Javiana	99.7	99.5	99.6	99.9	99.0	99.4
Mississippi	99.4	99.1	99.3	99.4	99.4	99.4
Montevideo	96.2	97.2	96.7	99.8	99.6	99.7
Muenchen	98.3	98.7	98.5	98.9	99.3	99.1
Newport	98.0	98.1	98.1	99.3	99.5	99.4
Oranienburg	98.5	98.3	98.4	99.4	99.2	99.3
Paratyphi B var. L(+) tartrate+	98.3	97.6	97.9	99.7	99.6	99.6
Poona	98.9	98.7	98.8	97.8	98.1	98.0
Saintpaul	99.7	99.6	99.6	99.6	99.2	99.4
Thompson	98.2	98.0	98.1	100.0	99.4	99.7
Typhi	99.9	99.8	99.8	99.6	99.7	99.6
Typhimurium	66.6	64.8	65.7	70.9	68.5	69.7
Typhimurium var. 5−	70.9	72.1	71.5	72.8	72.0	72.4
Less frequent serotypes (n = 12)
Anatum	75.9	78.3	77.0	96.6	96.2	96.4
Bareilly	82.2	72.0	77.1	75.2	52.0	63.6
Berta	95.0	97.2	96.2	94.0	99.1	96.7
Derby	91.6	91.4	91.5	88.8	88.6	88.7
Hartford	97.3	97.1	97.2	98.2	95.2	96.8
Litchfield	98.1	94.8	96.2	97.1	97.0	97.0
Mbandaka	99.1	96.2	97.4	100.0	99.4	99.6
Panama	90.4	90.3	90.4	91.3	81.5	86.0
Paratyphi A	100.0	96.5	97.0	100.0	88.7	90.4
Schwarzengrund	93.4	95.8	94.7	97.2	95.0	96.0
Senftenberg	81.5	74.2	77.8	92.4	86.6	89.4
Stanley	93.1	91.5	92.2	92.2	91.5	91.8
Total for the group			95.1			95.9
SVM algorithm
Most frequent serotypes (n = 20)
I 4,[5],12:i:−	91.5	91.2	91.3	93.0	92.3	92.6
Agona	99.5	99.7	99.6	100.0	100.0	100.0
Braenderup	98.6	98.5	98.5	99.8	99.7	99.7
Enteritidis	99.3	98.9	99.1	99.8	99.8	99.8
Hadar	99.1	99.1	99.1	99.1	98.5	98.8
Heidelberg	99.5	99.7	99.6	99.8	99.9	99.8
Infantis	98.4	98.0	98.2	99.8	99.8	99.8
Javiana	99.8	99.5	99.6	99.9	99.6	99.7
Mississippi	99.6	99.6	99.6	99.6	99.2	99.4
Montevideo	97.3	97.9	97.6	100.0	99.6	99.8
Muenchen	99.5	99.0	99.3	99.6	99.6	99.6
Newport	98.4	98.6	98.5	99.6	99.6	99.6
Oranienburg	97.2	98.1	97.6	99.4	99.6	99.5
Paratyphi B var. L(+) tartrate+	98.1	97.9	98.0	99.5	99.4	99.5
Poona	99.5	99.7	99.6	99.3	99.3	99.3
Saintpaul	99.1	99.6	99.4	99.5	99.2	99.3
Thompson	98.0	98.2	98.1	99.8	99.1	99.5
Typhi	100.0	100.0	100.0	99.8	99.9	99.8
Typhimurium	65.5	64.8	65.2	67.9	66.0	67.0
Typhimurium var. 5−	72.1	70.3	71.2	72.8	71.3	72.0
Less frequent serotypes (n = 12)
Anatum	50.9	68.9	59.5	98.3	95.3	96.8
Bareilly	93.1	85.0	89.0	91.1	66.0	78.5
Berta	94.0	96.3	95.2	95.0	96.3	95.7
Derby	88.8	91.4	90.1	86.0	89.5	87.7
Hartford	96.5	95.2	95.9	95.6	95.2	95.4
Litchfield	92.2	90.3	91.1	94.2	94.8	94.5
Mbandaka	97.3	95.6	96.3	99.1	98.7	98.9
Panama	92.3	96.0	94.3	90.4	88.7	89.5
Paratyphi A	100.0	92.2	93.3	100.0	90.4	91.9
Schwarzengrund	92.5	93.3	92.9	99.1	95.0	96.9
Senftenberg	91.3	85.6	88.4	91.3	89.7	90.5
Stanley	94.1	94.0	94.1	95.1	95.7	95.4
Total for the group			95.1			96.1

Comparison of two classification algorithms.

In Table 3, both the RF and SVM classification algorithms predicted the 20 most common serotypes with higher accuracies than those of 12 minority serotypes in all prediction groups. A comparison of the data for RF and SVM in Table 3 shows varied but slight differences in prediction accuracies, except for several of the 12 less common serotypes (S. enterica serotypes Anatum, Bareilly, and Senftenberg using the BioNumerics method and S. enterica serotype Bareilly using the NCTR method). The total average accuracies of the SVM algorithm (95.1% using the BioNumerics method and 96.1% using the NCTR method) were higher than those of the RF algorithm (95.1% for both standardization methods). In addition, the combination of the SVM algorithm with the NCTR standardization method produced the highest accuracies.

To test the reliability of the results above, we selected the G1 band class as the standard and combined G1 and G2, normalized by the NCTR method, into one group for both RF and SVM classifications. The average accuracies were calculated after the 2-fold cross-validation was repeated 100 times (Table 4). Seventeen out of the 20 most common serotypes had average prediction accuracies above 97.5% using the RF prediction model and above 98.9% using the SVM prediction model. The total average accuracies were 96.0% for RF and 96.1% for SVM, values which are close to or the same as the results presented in Table 3 (95.9% for RF and 96.1% for SVM).

Table 4.

Average accuracies of RF and SVM classification analyses on 39,829 PFGE patterns (including both G1 and G2) normalized by the NCTR fixed-band method using G1 as the standard set of band class^a

S. enterica serotype group and name	RF avg accuracya (% [SD])	SVM avg accuracya (% [SD])
Most frequent serotypes (n = 20)
I 4,[5],12:i:−	92.5 (5.99)	92.5 (5.00)
Agona	99.9 (1.15)	100.0 (0.98)
Braenderup	99.8 (1.34)	99.6 (1.10)
Enteritidis	99.7 (1.47)	99.7 (1.87)
Hadar	99.0 (1.81)	98.9 (1.97)
Heidelberg	99.8 (1.05)	99.7 (1.97)
Infantis	99.8 (1.21)	99.8 (1.10)
Javiana	99.5 (2.32)	99.6 (1.89)
Mississippi	99.3 (2.00)	99.4 (1.86)
Montevideo	99.6 (0.65)	99.7 (1.29)
Muenchen	99.0 (3.01)	99.5 (2.28)
Newport	99.5 (1.97)	99.4 (2.40)
Oranienburg	99.4 (1.52)	99.5 (1.66)
Paratyphi B var. L(+) tartrate+	99.5 (1.98)	99.4 (2.45)
Poona	97.5 (3.99)	98.9 (2.80)
Saintpaul	99.3 (3.01)	99.4 (2.69)
Thompson	99.6 (3.04)	99.5 (2.58)
Typhi	99.7 (1.46)	99.9 (1.11)
Typhimurium	68.8 (8.79)	67.8 (10.29)
Typhimurium var. 5−	71.8 (12.01)	71.8 (12.13)
Less frequent serotypes (n = 12)
Anatum	96.8 (1.39)	97.4 (1.50)
Bareilly	80.6 (4.24)	88.7 (3.54)
Berta	97.8 (1.24)	95.9 (0.94)
Derby	87.7 (2.34)	88.1 (1.87)
Hartford	97.0 (1.33)	96.2 (1.28)
Litchfield	96.6 (1.19)	94.5 (2.01)
Mbandaka	99.6 (0.66)	98.5 (0.67)
Panama	89.7 (2.05)	91.8 (2.35)
Paratyphi A	98.3 (1.41)	98.1 (1.21)
Schwarzengrund	96.8 (1.38)	96.8 (1.80)
Senftenberg	92.4 (2.68)	91.9 (2.57)
Stanley	92.3 (1.89)	95.7 (2.04)
Total	96.0	96.1

^aTwo-fold cross validation was used with 100 repetitions.

Misclassifications.

Tables S1A and B in the supplemental material exhibit detailed aspects of the classifications shown in Table 4. The numbers on the diagonal show the correct classifications for each of 32 serotypes, and the off-diagonal numbers indicate the mispredicted patterns. For example, 1,710 out of 1,849 patterns were correctly classified as S. enterica serotype I 4,[5],12:i:−, while 139 patterns were misclassified: one pattern was mispredicted as S. enterica serotype Hadar, one was mispredicted as S. enterica serotype Montevideo, one was mispredicted as S. enterica serotype Poona, 95 were mispredicted as S. enterica serotype Typhimurium, and 40 were mispredicted as S. enterica serotype Typhimurium var. 5−. The average accuracy was 92.5% after 100 repetitions. For S. enterica serotype Agona, the average prediction accuracy was 99.9%, with only 2 out of 1,953 patterns misclassified as S. enterica serotype Infantis and S. enterica serotype Montevideo (see Table S1A in the supplemental material). Most misclassification patterns were in the S. enterica serotypes Typhimurium, Typhimurium var. 5−, and I 4,[5],12:i:− using both RF and SVM algorithms. Around one-third of the patterns of S. Typhimurium and S. Typhimurium var. 5− overlapped with each other.

Further validation.

The classification models of RF and SVM, which were trained and tested by 39,830 PFGE patterns (including both group 1 and group 2), were further validated by an additional 6,093 PFGE patterns (group 3) with their serotypes coded to avoid possible bias. The patterns of group 1 were combined with the normalized patterns of group 2 and used as the training set, the normalized band class of group 3 was used as the test set, and the prediction accuracies by RF and SVM were calculated (Table 5). The SVM classification exhibited overall better prediction as expected, with accuracies higher than 97.2% for the top 20 serotypes, except for three serotypes (S. Typhimurium, S. Typhimurium var. 5−, and S. enterica serotype I 4,[5],12:i:−), and higher than 91.2% for the 12 less common serotypes. Most of the PFGE patterns (5,761 out of 6,093 patterns for RF and 5,798 out of 6,093 patterns for SVM) were correctly predicted to serotype; the overall accuracies were 94.5% for the RF classification and 95.1% for the SVM classification. Details are given in Tables S2A and B in the supplemental material.

Table 5.

Further validation of RF and SVM prediction models on an additional 6,093 PFGE patterns (group 3)

S. enterica serotype group and name	% Accuracy (no. of correct predictions/no. of PFGE patterns)
	RF model	SVM model
Most frequent serotypes (n = 20)
I 4,[5],12:i:-	93.5 (403/431)	94.0 (405/431)
Braenderup	100 (158/158)	100 (158/158)
Enteritidis	99.8 (494/495)	99.8 (494/495)
Hadar	98.6 (145/147)	98.6 (145/147)
Heidelberg	100 (191/191)	100 (191/191)
Infantis	100 (235/235)	99.6 (234/235)
Javiana	98.7 (298/302)	99.3 (300/302)
Mississippi	98.4 (184/187)	98.9 (185/187)
Montevideo	99.4 (163/164)	99.4 (163/164)
Muenchen	98.9 (93/94)	98.9 (93/94)
Newport	95.6 (172/180)	97.2 (175/180)
Paratyphi B var. L(+) tartrate+	100 (187/187)	99.5 (186/187)
Poona	98.0 (99/101)	100 (101/101)
Saintpaul	99.4 (355/358)	99.4 (356/358)
Thompson	100 (204/204)	99.0 (202/204)
Typhimurium	62.3 (139/223)	63.2 (141/223)
Typhimurium var. 5−	72.5 (227/313)	70.0 (219/313)
Less frequent serotypes (n = 12)
Anatum	97.3 (250/256)	98.4 (253/256)
Bareilly	88.9 (201/225)	93.8 (212/225)
Berta	95.2 (279/293)	97.6 (286/293)
Derby	90.1 (63/81)	91.2 (65/81)
Hartford	98.1 (307/313)	99.0 (310/313)
Litchfield	98.8 (162/164)	99.4 (163/164)
Mbandaka	99.4 (161/162)	99.4 (161/162)
Panama	92.7 (267/288)	94.1 (271/288)
Stanley	92.9 (224/241)	95.0 (229/241)
Overall	94.5 (5,761/6,093)	95.1 (5,798/6,093)

Distance matrix of the 32 serotypes.

Fig. 1 shows the heat map of 39,830 PFGE patterns of 32 serotypes, including those of group 1 and group 2. The large squares represent the patterns of the 20 most common serotypes, consisting of approximately 1,900 PFGE patterns for each serotype; the small squares represent 12 less common serotypes with approximately 200 PFGE patterns each. The squares on the diagonal show the distances of the patterns within the same serotype, while the other squares exhibit the distances between the patterns of the corresponding horizontal and vertical serotypes. It is difficult to discern the relationships of the 12 less common serotypes because of limited data size. For the top 20 serotypes, the squares on the diagonal (mostly green) are distinguishable from other squares in the heat map, except for S. enterica serotypes Typhimurium and Typhimurium var. 5−. The patterns of S. enterica serotype I 4,[5],12:i:− were very close to those of S. Typhimurium and S. Typhimurium var. 5−.

DISCUSSION

It is a challenge to develop new analytical tools to make full use of the valuable data in PulseNet and maximize the application by combining concepts and techniques from various research disciplines. Although a good correlation between PFGE patterns and Salmonella serotypes has been reported (9, 18), it is not efficient enough, and typically, the cutting of the dendrogram to form clusters is based on subjective visual analysis. Additionally, it is difficult to apply hierarchical cluster analysis to large data sets (27). Our previous work (27) applied statistical classification to PFGE patterns and provided a more efficient alternative method for determining Salmonella serotypes than the conventional hierarchical cluster analysis. Since only 866 PFGE patterns of eight serotypes were included in the analytical database, however, our previous algorithm had limitations.

The prediction accuracy is estimated by applying the prediction model based on the current samples to presumably emulate the population of the future samples. If the samples in the present study do not adequately represent the future samples, then the estimates of prediction accuracy can be biased (1). The 32 serotypes selected in this study comprised 82.2% of all the isolates reported during 11 years nationwide (Table 1), and there were not many differences between the percentages of each year (75.5% to 86.4%) (4). The patterns from other serotypes were limited. The database constructed in this study, which consisted of Salmonella isolates from 2005 to 2010 in PulseNet, was assumed to represent similar coverage. Therefore, the algorithm trained on this data set should be applicable to predict all possible Salmonella candidates, with a limited misprediction rate even with rare serotypes. To keep high prediction accuracies in the future, the training data set in the algorithm should be kept updated by the addition of PFGE entries of new types and of new commonly occurring serotypes.

Since the top 20 serotypes covered 76.6% and the 12 less common serotypes covered 5.6% of total Salmonella isolates in 11 years, both groups 1 and 2 had around 900 to 1,000 PFGE patterns for each of the top 20 serotypes and approximately 100 for each of the 12 less common serotypes (except for the S. enterica serotype Paratyphi A because of the data limitation). Inclusion of various patterns for the most common serotypes was maximized in order to increase the prediction sensitivity of the algorithms.

When a prediction system is put into practical use, standardization is necessary to keep prediction results comparable and consistent. The NCTR fixed-band method, created in this study was shown to normalize the band class of the testing set to that of the training set better than the conventional BioNumerics fixed-band method (Table 3). In addition to the higher accuracies, the NCTR method made the prediction process easier and more applicable than the conventional BioNumerics method. The NCTR method was able to transfer the standard band class into certain parameters in the model and normalize the band class of future candidates to that of the standard with no need to load and save the standard band class in BioNumerics and run the band-matching function every time through the software. This is especially useful for a large data set because BioNumerics was designed to treat fewer than 20,000 patterns. In this study, the band class of group 1 was a better standard since group 1 patterns were selected first from the database; it included all available variants of PFGE patterns in the database, such as sources, extraction locations, and time. When G1 band class was used as the standard and training set, the prediction accuracies were higher because the models were already trained by as much as possible before being applied to the prediction of the testing group (Table 3).

Statistically, hierarchical cluster analysis is generally considered to be unsupervised in the sense that the isolates are grouped based only on the pairwise similarities among their PFGE profiles without using serotype information. This type of analysis only arranges the isolates into subsets with similar PFGE profiles to distinguish their underlying phylogenetic structures or to discover new subtypes (27). In contrast, the supervised classification approach focuses on studying the correlations between PFGE patterns and serotypes and applies the information learned from the training set as the rules for prediction in the test set, improving the Salmonella serotype prediction (27). In this study, we introduced another classification method, SVM, and compared the functionality of both the RF and SVM classification models on prediction using large data sets.

It is worth mentioning that some of the misclassification could be due to the incorrect serotyping results or to mistakes in inputting the serotype information into the PulseNet database. Further analysis may confirm this possibility. For the 20 most common serotypes, Tables 3, 4, and 5 show that under all conditions the lowest prediction accuracies were consistently for S. enterica serotypes Typhimurium and Typhimurium var. 5− and S. serotype I 4,[5],12:i:−. The supplemental data (see Tables S1A and B and S2A and B) give more details regarding the false predictions. The mispredictions of each of these three serotypes were found mostly in the other two serotypes, especially between S. Typhimurium and S. Typhimurium var. 5−. In Table S1B in the supplemental material, for example, 594 out of 1,841 S. Typhimurium isolates were mispredicted: 435 as S. Typhimurium var. 5− and 156 as S. enterica serotype I 4,[5],12:i:−. For the S. Typhimurium var. 5−, 517 out of 1,833 patterns were mispredicted: 454 as S. Typhimurium and 52 as S. enterica serotype I 4,[5],12:i:−. Correspondingly, most of the mispredictions of S. enterica serotype I 4,[5],12:i:− were in S. Typhimurium and S. Typhimurium var. 5−, and only 2.2% were other serotypes. These results were correlated with the fact that these three serotypes are closely related and their PFGE patterns were very similar. Actually, S. enterica serotype I 4,[5],12:i:− lacks the second-phase H antigen 1,2 and is the monophasic variant of S. Typhimurium, whose formula is I 4,5,12:i:1,2. The S. Typhimurium var. 5−, whose obsolete name is S. Typhimurium var. Copenhagen, was considered an O:5-negative variant of S. Typhimurium a few years ago, and its formula is I 4,12:i:1,2. In many reports, S. Typhimurium var. 5− was even included in S. Typhimurium (4), and no genetic differences were detected between these two variants (11). The similarities of the PFGE patterns among the three serotypes, especially S. Typhimurium and S. Typhimurium var. 5−, resulted in their low prediction accuracies. If S. Typhimurium var. 5− is included in the S. Typhimurium serotype, the prediction accuracy increases to 94.0%.

The serotype prediction accuracies and the relationships between the 32 serotypes, especially the top 20 serotypes, could be visually described from the distance matrix of the serotypes (Fig. 1). The distinguishable squares on the diagonal, except for the squares of S. Typhimurium and S. Typhimurium var. 5−, indicate the interserotype differences of the PFGE patterns, which allow the prediction of these serotypes with high accuracies. The indistinguishable squares of S. Typhimurium and S. Typhimurium var. 5− reveal that the patterns of these two serotypes are very similar, which resulted in their low prediction accuracies. These two serotypes accounted for most of the misclassified patterns, in agreement with the heat map image. To achieve high prediction accuracies, the patterns of isolates within one serotype need to be not only similar to each other but also far away from the patterns of other serotypes. Figure 1 also shows the small distances between patterns of S. enterica serotype I 4,[5],12:i:− and those of S. Typhimurium and S. Typhimurium var. 5−., which is in agreement with the prediction accuracy and misclassified patterns of S. enterica serotype I 4,[5],12:i:−.

In summary, RF and SVM classifications were applied to a data set of 45,923 PFGE patterns covering 32 Salmonella serotypes from CDC PulseNet. The SVM algorithm showed consistently overall higher accuracies than the RF algorithm. The NCTR fixed-band method was developed to standardize PFGE band classes for prediction. The application of the classification algorithms can satisfy the need for fast and early identification and source tracking of outbreak isolates. It is especially useful to predict and get the serotype information of outbreak isolates before the conventional methods are used in a laboratory where serotyping is available. The results of this study, together with our previously published results (27), suggest that new analysis methods developed from the concepts of mathematics, statistics, and computer science could optimize current technologies and make the data more useful.