Cerebral energetics and the glycogen shunt: Neurochemical basis of functional imaging

Abstract

Positron-emission tomography and functional MRS imaging signals can be analyzed to derive neurophysiological values of cerebral blood flow or volume and cerebral metabolic consumption rates of glucose (CMR_Glc) or oxygen (CMR_O2). Under basal physiological conditions in the adult mammalian brain, glucose oxidation is nearly complete so that the oxygen-to-glucose index (OGI), given by the ratio of CMR_O2/CMR_Glc, is close to the stoichiometric value of 6. However, a survey of functional imaging data suggests that the OGI is activity dependent, moving further below the oxidative value of 6 as activity is increased. Brain lactate concentrations also increase with stimulation. These results had led to the concept that brain activation is supported by anaerobic glucose metabolism, which was inconsistent with basal glucose oxidation. These differences are resolved here by a proposed model of glucose energetics, in which a fraction of glucose is cycled through the cerebral glycogen pool, a fraction that increases with degree of brain activation. The “glycogen shunt,” although energetically less efficient than glycolysis, is followed because of its ability to supply glial energy in milliseconds for rapid neurotransmitter clearance, as a consequence of which OGI is lowered and lactate is increased. The value of OGI observed is consistent with passive lactate efflux, driven by the observed lactate concentration, for the few experiments with complete data. Although the OGI changes during activation, the energies required per neurotransmitter release (neuronal) and clearance (glial) are constant over a wide range of brain activity.

To a first approximation, cerebral energy consumption under normal conditions is supplied by the oxidation of glucose (1, 2). The reaction stoichiometries

1

require that the cerebral metabolic rate of oxygen (CMR_O2) consumption equals six times the cerebral metabolic rate of glucose (CMR_Glc) consumption. The experimental values are described by the oxygen-to-glucose index (OGI), where

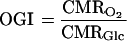2

Under awake resting conditions, global measurements from arterial-venous differences, and local measurements from positron-emission tomography studies of humans have consistently yielded OGI ≈ 5.5 (1, 3). Given the closeness of this ratio to that expected from complete glucose oxidation, this mechanism has been accepted as describing the energy source. However, the ≈10% discrepancy in the OGI at rest remains unexplained. Furthermore, this departure from the theoretical OGI was shown to become larger under stimulated conditions, some 10 years ago, in the positron-emission tomography experiments of Fox and Raichle (4, 5). Three different positron-emission tomography techniques were used in those studies to separately measure the change in cerebral metabolic consumption rates of oxygen (ΔCMR_O2), the change in cerebral metabolic consumption rates of glucose (ΔCMR_Glc), and the increment in cerebral blood flow (ΔCBF) in subjects undergoing either somatosensory or visual stimulation. During visual stimulation, ΔCBF ≈ ΔCMR_Glc ≈ 50%, whereas ΔCMR_O2 ≈ 5%. Similar values were obtained in the somatosensory study. On the basis of their results, Fox and Raichle proposed that stimulations of brain activity were fueled by glycolysis (i.e., non-oxidative glucose metabolism). Subsequent imaging experiments, obtaining values of ΔCMR_O2 and ΔCMR_Glc during similar stimulations, while not demonstrating the extreme departures of those first experiments (6, 7), have qualitatively agreed with a further reduction of the OGI during sensory stimulation. Additional support for a reduction in OGI during sensory stimulation came from findings of lactate accumulation. In the human brain, lactate was measured by ¹H NMR during a visual stimulation (8, 9). The increased production of lactate occurred in the human brain under steady state conditions where blood oxygenation level-dependent (BOLD) functional MRI experiments showed that the available supply of oxygen actually increased during the same stimulation, ruling out the possibility that the increase in lactate (and decrease in OGI) were caused by an inadequate blood oxygen supply (10, 11).

The observation that %ΔCMR_Glc > %ΔCMR_O2 during sensory stimulation led to the proposal that cerebral functional activity (e.g., neurotransmission, action potentials) requires little energy relative to the basal needs of the brain (4–6). However this conclusion is at odds with the evidence that in the resting nonstimulated state the majority of energy consumption in the cerebral cortex is used to support functional processes (12). ¹³C magnetic resonance spectroscopy (MRS) showed that cerebral glucose oxidation is coupled to glutamate neurotransmitter release and glutamate/glutamine cycling (12, 13, 14), in both resting and anesthetized states. This evidence is supported and extended by studies which have found extensive electrical activity in the resting brain (15), whereas the large decreases in glucose and oxygen consumption associated with deep anesthesia (12) are paralleled by decreases in electrical activity (16). Another unexplained aspect of brain energy substrates centers on the function of glycogen in the brain. Glycogen is the single largest energy reserve of the brain (17). Brain glycogen has been proposed to be exclusively an emergency fuel source during extreme stress, such as severe hypoglycemia and cerebral ischemia. Given the rarity of these conditions this hypothesis lacks conviction as being the sole purpose of this glycogen store, particularly because the relatively low glycogen concentration in the brain (18) could only support brain energy consumption for a short time (19) under ischemic conditions. Two results point to a role for the glycogen pool in normal metabolism: (i) a decrease in brain activity, as induced with barbiturate anesthesia (20), results in an increase in brain glycogen content showing a response of this pool to functional conditions; and (ii) many of the activators of glycogenolysis, such as monoamines (noradrenaline, serotonin, histamine) and vasoactive intestinal peptide, are located within discrete populations of neurons and are increased on activation of specific neuronal circuits and only within spatially defined domains (21). Both observations argue against the hypothesis that glycogen serves solely as a global energy reserve for periods of physiological/pathological stress and a coupling between neuronal activity and glycogen is indicated. However, despite considerable research into many aspects of brain glycogen (21), its function remains unclear.

In this paper we develop a novel metabolic model, which proposes that a primary function of the cerebral glycogen pool is to help provide energy rapidly in support of glutamate neurotransmitter clearance by astrocytes. This consumption and subsequent resynthesis of glycogen explains the reduction of OGI during stimulation and relates it to the observed concentration of lactate, whereas maintaining neuronal and astrocytic energy consumption per neurotransmitter cycle constant across the wide range of brain activity.

Metabolic Model of the Coupling Between Glutamate Neurotransmitter Cycling and Neuroenergetics

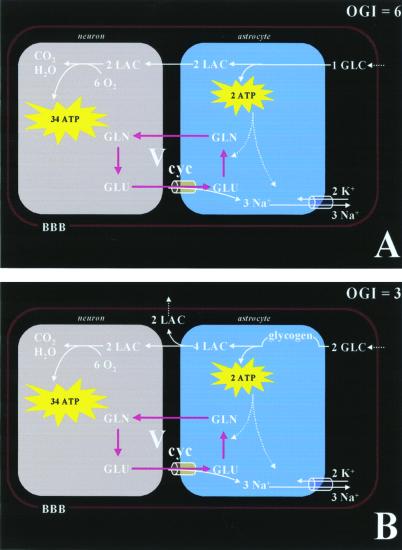
Our ¹³C NMR spectroscopy studies of metabolic fluxes in the brain (12, 14, 22, 23), combined with studies in isolated astrocytes by Pellerin and Magistretti (24) have provided the metabolic model shown in Fig. 1A. The model relates the stoichiometry of cortical glucose metabolism to a specific aspect of neuronal activity, i.e., cycling of neurotransmitter glutamate between neurons and astrocytes. In this model, astrocytes in the cerebral cortex remove glutamate [and γ-aminobutyric acid (GABA)] from the synaptic cleft to terminate synaptic transmission. Glutamate is taken up by astrocytes via a Na⁺-dependent, electrogenic transporter and converted therein to glutamine by the astrocytic enzyme glutamate synthetase [GABA undergoes a similar uptake by astrocytes followed by conversion to glutamate and, subsequently, to glutamine. The flux between GABA and glutamine has recently been determined to be 10–20% of the glutamate neurotransmitter flux in the awake human cerebral cortex (14)]. Glutamine cycles back to the neuron, where the enzyme glutaminase converts it back to glutamate for repackaging into vesicles and for further exocytotic release.

Figure 1.

Proposed pathways of energy metabolism and glutamate–glutamine neurotransmitter cycling between neurons and glia. Action potentials reaching the presynaptic neuron cause release of vesicular glutamate into the synaptic cleft, where it is recognized by glutamate receptors postsynaptically and cleared by Na⁺-coupled transport into glia, where it is enzymatically converted to glutamine, which passively diffuses back to the neuron and, after reconversion to glutamate, is repackaged into vesicles. A direct consequence of the metabolic model (12, 13) is that neuronal firing is quantitatively linked to clearance of extracellular glutamate by the astrocyte, which requires 2 moles of ATP per mole of glutamate cycled between neurons and astrocytes (see text for details). (A) Ideally, 1 mole of glucose produces 2 moles of ATP in the astrocyte via glycolysis. The two equivalents of lactate generated in the astrocyte are completely oxidized in the neuron to generate ≈34 ATP molecules. This creates a scenario where the stoichiometry between oxygen and glucose (i.e., OGI) is 6. Under normal rates of neuronal firing, the rate of energy production via glycolysis is sufficient to restore Na⁺ gradient and glutamine synthesis in the astrocyte, and matches the glutamate release by the neuron. (B) Alternatively, to generate 2 moles of ATP in the astrocyte via the glycogen shunt, 2 moles of glucose have to be used and 4 moles of lactate to be produced. Some of the extra lactate is effluxed into the blood, whereas the rest is oxidized in the neuron to generate ≈34 ATP molecules. However, in this case, the stoichiometry between oxygen and glucose consumption (i.e., OGI) is 3. Under high neuronal firing rates, because the rate of glial energy production via glycolysis is not rapid enough, the glycogen shunt is activated to restore Na⁺ gradient and glutamine synthesis in the astrocyte such that the glutamate release by the neuron is matched. The main difference between A and B is that the latter produces 1 ATP/glucose less, which is energetically less efficient for glutamate clearance. Thus, more lactate is produced in the latter case where some is effluxed into the blood circulation. BBB, blood brain barrier; GLC, glucose; GLN, glutamine; GLU, glutamate; LAC, lactate.

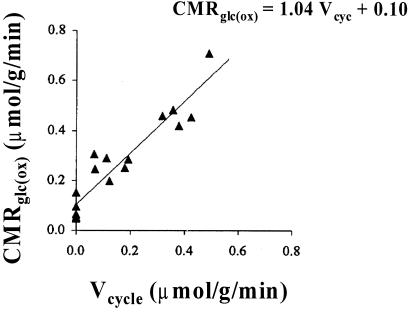
By using ¹³C NMR spectroscopy we have measured the in vivo flux of ¹³C label cycling between glutamate and glutamine (V_cycle) in the rat cerebral cortex (12, 22). In the same ¹³C NMR experiment, the flux of ¹³C label from the [1-¹³C]glucose into glutamate yields a measurement of the tri-carboxylic acid cycle rate (V_TCA). The neuronal component of the cerebral metabolic rate of glucose oxidation (CMR_Glc(ox)) may be obtained from this measurement because V_TCA is tightly coupled to oxidative phosphorylation (25, 26). In the anesthetized rat, the experimental data showed that, during graded anesthesia, the relationship between neuronal oxidative glucose consumption (which accounts for ≈80% of CMR_Glc in cortical gray matter) and glutamate neurotransmitter cycling is (12)

3

in units of μmol⋅g⁻¹⋅min⁻¹. These results revealed an ≈1:1 coupling between incremental energy production (CMR_Glc(ox)) and the energetic needs of glutamate neurotransmitter cycling (V_cycle), with a small (≈15%) basal nonsignaling energetic component (Fig. 2).

Figure 2.

¹³C MRS measurements of glutamate neurotransmitter cycling, V_cycle, and the rate of glucose oxidation, CMR_Glc(ox), with graded anesthesia in rat brain (12). The best linear fit (solid line) to the data (filled symbols) produces CMR_Glc(ox) = 1.04 V_cycle + 0.10, which indicates that each mole of neurotransmitter glutamate cycling requires oxidation of one mole of glucose. Because the resting awake state value for CMR_Glc(ox) in rat cortex is ≈0.8 μmol⋅g⁻¹⋅min⁻¹, ≈85% of the cortical energy consumption is dedicated to V_cycle. Thus, in the resting, awake state, a very small component of energy production via glucose oxidation (see small intercept) is dedicated to nonsignaling functions of glutamatergic neurons, and the rest is dedicated to neurotransmitter function. (Adapted from figure 4 of ref. 12.)

In the quantitative energetics of the model (Fig. 1A), glucose transported across the blood brain barrier enters astrocytes, where it is converted into lactate, which is then released into the extracellular space leading to neuronal uptake and oxidation. Glycolysis of glucose in astrocytes is coupled to neuronal activity by providing the two ATP equivalents required for astrocytic clearance of neurotransmitter glutamate. The restoration of astrocytic ion gradients requires one ATP equivalent per glutamate equivalent released and cleared. A second ATP is required in astrocytes for the glutamine synthetase reaction converting glutamate to glutamine. Because glycolysis produces 2 ATP for each mole of glucose converted to two moles of lactate, each mole of glutamate cycled by this mechanism requires glycolysis of one mole of glucose in the astrocyte. The ¹³C NMR measurements of the relation between fluxes V_cycle and CMR_Glc(ox) as in Eq. 3. have demonstrated that the model quantitatively fits the in vivo measurements of these two fluxes (12, 13, 22).

The astrocytic energy requirements are accounted for by glycolytic production of 2 ATP/glucose or 1 ATP/lactate (Fig. 1A). In this model, the large majority of ATP from the oxidation of glucose is produced in neurons by oxidation of lactate to meet neuronal energetic needs, which include restoration of ionic membrane potentials, vesicularization of glutamate, docking and exocytosis of vesicles. The complementary and coupled roles of astrocytes (for glutamate clearance) and neurons (for glutamate release) establishes a stoichiometry between the astrocytic production of 2 ATP and the CMR_O2 needed to completely oxidize two lactate equivalents in the neuron. Although glucose uptake and oxidation occur in different compartments, the stoichiometry described above would yield the theoretical OGI of 6 (Fig. 1A).

If, however, astrocytic metabolism of glucose follows an inefficient pathway so that glial production yields less than 2 ATP/glucose (or less than 1 ATP/lactate), the OGI will decrease because more glucose must be converted to lactate to provide the two ATP equivalents needed to clear the release of one glutamate neurotransmitter (Fig. 1B). This scenario would reduce the OGI and also generate more lactate than is needed to support neuronal functional energetics. We propose that the glycogen shunt is the inefficient pathway followed.

Cycling of Glycogen by Neuronal Firing and Subsequent Resynthesis

Glycogen is primarily localized in astrocytes (21), although ependymal and choroid plexus cells, as well as some large neurons in the brainstem, contain small amounts of glycogen. The enzymes for the synthesis and degradation of glycogen (glycogen synthase and glycogen phosphorylase, respectively) have been extensively characterized, and, at least in the case of glycogen phosphorylase, immunocytochemical evidence suggests its localization is very similar to that of glycogen itself (21). During glycogenolysis ≈90% of the residues are phosphorolytically cleaved to glucose-1-phosphate, which is converted isoenergetically to glucose-6-phosphate. This “glycogen shunt” is a less efficient route for conversion of glucose to lactate than the “glycolytic” pathway, yielding only 1 rather than 2 ATP/glucose (Fig. 1B). If all of the glucose flux through glycolysis proceeded via the glycogen shunt, the ratio of CMR_Glc(ox)/V_cycle would be 2:1 instead of 1:1, as shown in Fig. 1B. Under these conditions the OGI would be 3 instead of the theoretical value of 6, and there would be an extensive overproduction of lactate, which, at steady state, must efflux into the circulating blood.

Control of the activity of glycogen phosphorylase, and thereby of glycogenolysis, is exercised rapidly by hormonal messengers and calcium (27). This mechanism allows glycogenolysis to be controlled by the rapid Ca²⁺ glial uptake that accompanies changes in the Na⁺ gradient triggered by glutamate uptake. The rapid response has led to glycogen phosphorylase being described as the fight-or-flight enzyme.

The cellular distribution of glycogen synthase is more diverse, occurring in most cell types but with higher staining in neurons (28, 29). The activities of both enzymes (i.e., synthase and phosphorylase) are regulated by phosphorylation via cAMP cascades and by Ca²⁺ stimulation of phosphorylase kinase. Glycogen is synthesized by a pathway that utilizes uridine 5′-diphosphate glucose (UDP-glucose) as the activated glucose donor. The net reaction for glycogen synthesis from glucose-6-phosphate consumes one ATP equivalent.

To understand why the energetically inefficient “glycogen shunt” might exist in vivo, it is necessary to consider the time course of neuronal activity in the glial/neuronal model coupling energy to neurotransmitter flux (Fig. 1). In general, cerebral cortex glutamatergic neurons respond to synaptic inputs by adjusting their firing rate. As a consequence, the energy requirements of both the neuron itself and of the astrocytes surrounding it will vary temporally and in synchrony with the firing patterns of the neuron. After neuronal firing, there will be an immediate demand for astrocytes to remove glutamate from the synaptic cleft. As noted above, this situation is accomplished by coupling glutamate uptake with two astrocytic ATP equivalents: one is used to repump the Na⁺ and the other to support glutamine synthetase. Glutamate must be sequestered very rapidly—within 10 ms (30) to maintain proper synaptic function. In the absence of intense activation, the average rate of ATP production in astrocytes from glycolysis is sufficient to maintain adequate glutamate clearance, as evidenced by the OGI approaching 6 at rest. During intense activation, unless the rate of ATP production rapidly increases, the astrocytic membrane potential will drop, resulting in inefficient clearance of glutamate. We propose that glycogen provides a fast supplementary source for astrocytic energy production, with slower replenishment of the glycogen between spikes (Fig. 3). This modification allows astrocytic clearance to accommodate the increased neuronal release during intense bursts of neuronal firing. Because the glycogen consumed is subsequently replaced by glycogenesis to maintain steady state (Fig. 3), this increased flux through the glycogen shunt results in a less efficient conversion of glucose to lactate (Fig. 1B). The result is a cycle of glycogen degradation and synthesis (Fig. 3), coupled temporally to the bursts of neuronal firing, with a consequential decrease of OGI and increase in lactate generation.

Figure 3.

Glycogen provides a rapid ancillary source for astrocytic energy production, with slower replenishment of the glycogen in between spikes. This process allows astrocytic clearance of glutamate to accommodate the increased neuronal release during heightened rates of neuronal firing. The glycogen consumed is subsequently replenished by glycogen synthesis to maintain a steady state concentration, as shown in cases of low (A) and fast (B) firing rates. Under rapid firing bursts, the glycogen synthesis may not completely replenish glycogen breakdown, and hence a new steady state concentration of glycogen would be reached (not shown). The increased flux through the glycogen shunt, i.e., a cycle of glycogen degradation and synthesis, results in an energetically less efficient conversion of glucose to lactate (Fig. 1B). In brief, the proposed model suggests that, during increased firing rates, timely degradation and synthesis of glycogen provide astrocytic energy for neurotransmitter clearance, and as a consequence of which, OGI is decreased and lactate is elevated—a process that is energetically less efficient.

The Glycogen Shunt Model

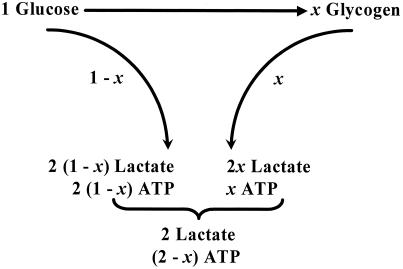
Our hypothesis is that glial glucose flux is partitioned between glycolysis and glycogenolysis such that the fraction following the glycogenolytic pathway increases with neuronal activity (Fig. 4). For any state of activation, a value of this partitioning relates observed departures of the OGI from the 6:1 ratio to the observed lactate concentrations. The model (of glial/neuronal cooperation) requires that 2 ATP equivalents, produced by non-oxidative glycolysis in the astrocyte, are needed to clear the one equivalent of released neuronal glutamate. However, when a fraction x of CMR_Glc proceeds through the glycogen shunt, the ATP to glucose ratio drops to (2 − x), CMR_O2 decreases to (6 − 3x)CMR_Glc, and excess lactate is produced.

Figure 4.

The proposed pathways of energy metabolism in brain, which includes both glycolysis and the glycogen shunt. If a small fraction of glucose (x) is diverted through the shunt, then the total amount of ATP produced per mole of glucose is (2 − x), which is the net of the following reactions:

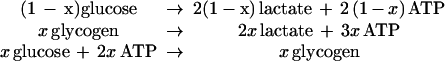The consequences of a fraction x of CMR_Glc flowing through the shunt are evaluated in Fig. 4. The value of OGI expected from the fraction x through the glycogen shunt is

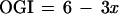4

For every glucose going through the shunt (2 − x) mole of lactate are oxidized and x moles of lactate are transported to blood; hence, the excess lactate efflux (V_out) is given by

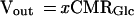5

At steady state, the excess lactate must efflux across the blood-brain barrier, which is facilitated by monocarboxylic acid transporters. The passive transport of lactate is driven by its concentration so that a Michaelis-Menten kinetic relation should exist between lactate concentration and its efflux. Thus, the glycogen shunt provides a relationship between measured lactate concentrations and the OGI. To date, data sets in which both OGI and lactate have been measured are scarce, consisting of only three conditions (see Fig. 5). Based on the experimental conditions, the lactate transporter parameters can be explored.

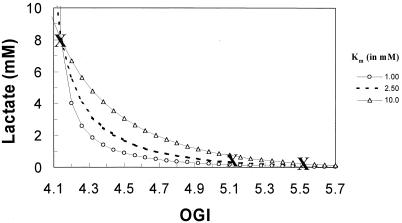
Figure 5.

The OGI vs. lactate dependence (lines) in the mammalian brain can be determined from experimental data (cross symbol): resting human/rat brain with OGI = 5.52 (1); active human brain with OGI = 5.16 (6); and seizure activity in rat brain with OCI = 4.14 (1). The total amount of lactate produced in rat brain during biccuculine-induced seizure is 8 mM whereas the resting lactate level in human brain is 0.6 m M. Using the Michaelis-Menten transport kinetics for lactate (Eq. 6) and the OGI relationship (Eq. 2), a relationship can be derived that is independent of T_max. Therefore, changes in lactate (from the seizure point) can be reflected into changes in OGI for a range of K_m values for lactate transport across the blood-brain barrier. The best fit of the model to the scarce data is with K_m of 2.5 mM, which corresponds to T_max of about 0.75 μmol⋅g⁻¹⋅min⁻¹.

Assuming Michaelis-Menten transport kinetics for lactate we have

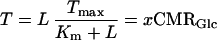6

where L is lactate concentration, and T and T_max are measured V_out and maximum rate of efflux, respectively, and K_m is the lactate concentration at half T_max. The two kinetic parameters have been evaluated by several experiments with values of 1 mM < K_m < 5 mM (31–33). Although the three data sets provide more than enough information to evaluate these two parameters, we feel that only the seizure data are accurate enough to determine the values of L and x quantitatively. In Fig. 5, the reliable value of L = 8 mM during seizure is plotted vs. the experimental OGI = 4.1. Three calculated curves show the expected experimental values of OGI vs. L where K_m has been assumed to have three different values of 1.0, 2.5, and 10.0 mM, and T_max is calculated to fit the seizure data. The set of K_m = 2.5 mM and T_max = 0.75 μmol⋅g⁻¹⋅min⁻¹ agrees very well with measurements and provides a realistic fit to the existing data (31–33) and a framework for future studies. Qualitatively, Fig. 5 illustrates the expected linkage between the decrease in OGI and the increase in lactate.

Discussion

The reason for a disproportionate increase in CMR_Glc relative to CMR_O2 during activation has remained unexplained since the initial reports by Fox and Raichle (4, 5). It was proposed (5) that brain energy metabolism during sensory stimulation is fundamentally different from during rest and requires only the small amount of energy available from glycolysis, reflecting a low energy cost of neuronal function. This explanation is inconsistent with electrical recordings (15) and ¹³C NMR studies (12) that have shown high levels of electrical firing and neurotransmitter release under resting conditions of normal sensory stimulation where OGI is 5.5. Both measurements of brain activity have also shown that energy consumption is mainly devoted to firing even under mild anesthesia. It also is contradicted by several types of brain activation (e.g., complex visual stimuli and motor and cognitive tasks) that increase both glucose and oxygen consumption with a much lower degree of uncoupling (6).

The Glycogen Shunt Hypothesis Addresses the Question of Why Neuronal Activity Has Different Energetic Requirements Depending on the Nature of the Stimulus.

The shunt explains this apparent departure from oxidative glycolysis by introducing a stimulation-dependent inefficient pathway for the production of glial ATP from glucose non-oxidatively. This inefficient glycogenolytic flux increases with activity, allowing glial clearance of glutamate neurotransmitters to proceed rapidly enough to match neurotransmitter release during bursts of increased neuronal firing. The excess lactate formed increases efflux from the brain, passively carried by monocarboxylic acid transporters. The energetic inefficiency of the glycogen shunt is offset by its serving to deliver the high power required for neurotransmitter clearance during activation by supplementing the glycolytic pathway. Lactate formation does not necessarily indicate inefficient use of glucose by the body (as opposed to the brain) because, as Brooks (34) has shown, lactate can be shuttled to an oxidative site.

We have recently shown how a glycogen shunt can satisfy similar power requirements in the muscle (35). That proposal was supported by ¹³C NMR experiments of muscle glycogen during long-term aerobic exercise, which showed that, whereas the glycogen levels remained constant, there was continuous synthesis and degradation as measured by the incorporation of ¹³C-labeled glucose (36). Support for the rapid energy consumption and restoration in muscle had been demonstrated by ³¹P NMR of phosphocreatine levels with 1 ms time resolution showing a 3-mM drop in phosphocreatine concentration during contraction and a subsequent restoration to basal levels, all within ≈30 ms (37). Evidence from these and other muscle experiments suggested that a large fraction of the contraction energy flowed through the glycogen shunt.

Based on the Results in Muscle a Test of the Model Could Be Obtained by Measuring the Turnover of the Glycogen Pool Under Stimulated Conditions.

If plasma glucose is enriched by ¹³C during stimulation, then the flux into glycogen could be measured by ¹³C NMR. In the brain, the only measurements of this turnover by Choi et al. (38) were done in the resting anesthetized rat, and the very small value of x observed, not unexpected under these conditions of deep anesthesia, neither supports nor refutes the model. These results show that, if the shunt is followed under these conditions, only a small percentage of the glycogen pool is exchanging.

The most important consequence of this proposal is the unification of the energetic basis of brain activity. In the model, the coupling between neuronal energy consumption and activity remains the same, independent of the stimulus for neuronal activity. A constant energetic coupling greatly simplifies the interpretation of functional imaging studies. Provided that a measure of CMR_O2 is obtained from the functional imaging experiment, the amount of neuronal activity can be derived from Eq. 3. Recent calibrations (39) of the contributions of alterations in blood flow and volume to BOLD measurements have allowed Δ CMR_O2 to be derived from the experiments. Hence, CMR_O2 and CBF can be imaged quantitatively in humans in the near future and converted into maps of neuronal activity. Some implications of deriving quantitative neuronal activity from functional imaging studies for psychology and the study of mind have been addressed previously (39–41).

Abbreviations

OGI

oxygen-to-glucose index

CBF

cerebral blood flow

CMR_Glc(ox)

cerebral metabolic rate of glucose oxidation

BOLD

blood oxygenation level dependent

CMR_glc

cerebral metabolic rate of glucose consumption

CMR_O2

cerebral metabolic rate of oxygen consumption

V_cycle

glutamate-glutamine neurotransmitter cycling rate

MRS

magnetic resonance spectroscopy