Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born

Abstract

We present an implementation of generalized Born implicit solvent all-atom classical molecular dynamics (MD) within the AMBER program package that runs entirely on CUDA enabled NVIDIA graphics processing units (GPUs). We discuss the algorithms that are used to exploit the processing power of the GPUs and show the performance that can be achieved in comparison to simulations on conventional CPU clusters. The implementation supports three different precision models in which the contributions to the forces are calculated in single precision floating point arithmetic but accumulated in double precision (SPDP), or everything is computed in single precision (SPSP) or double precision (DPDP). In addition to performance, we have focused on understanding the implications of the different precision models on the outcome of implicit solvent MD simulations. We show results for a range of tests including the accuracy of single point force evaluations and energy conservation as well as structural properties pertainining to protein dynamics. The numerical noise due to rounding errors within the SPSP precision model is sufficiently large to lead to an accumulation of errors which can result in unphysical trajectories for long time scale simulations. We recommend the use of the mixed-precision SPDP model since the numerical results obtained are comparable with those of the full double precision DPDP model and the reference double precision CPU implementation but at significantly reduced computational cost. Our implementation provides performance for GB simulations on a single desktop that is on par with, and in some cases exceeds, that of traditional supercomputers.

1. Introduction

Since the first simulation of an enzyme using molecular dynamics (MD) was reported by McCammon et al.¹ in 1977, MD simulations have evolved to become important tools in rationalizing the behavior of biomolecules. The field has grown from that first 10-ps-long simulation of a mere 500 atoms to the point where small enzymes can be simulated on the microsecond time scale²⁻⁴ and simulations containing millions of atoms can be considered routine.^5,6 However, such simulations are numerically very intensive, and using traditional CPU-centric hardware requires access to large-scale supercomputers or well-designed clusters with expensive interconnects that are beyond the reach of many research groups.

Numerous attempts have been made over the years to accelerate classical MD simulations by exploiting alternative hardware technologies. Some notable examples include ATOMS by AT&T Bell Laboratories,⁷ FASTRUN by Columbia University and Brookhaven National Laboratory,⁸ MDGRAPE by RIKEN,⁹ and most recently Anton by DE Shaw Research LLC.¹⁰ All of these approaches have, however, failed to make an impact on mainstream research because of their excessive cost. Additionally, these technologies have been based on custom hardware and do not form part of what would be considered a standard workstation specification. This has made it difficult to experiment with such technologies, leading to a lack of sustained development or innovation and ultimately their failure to mature into ubiquitous community-maintained research tools.

Graphics processing units (GPUs), on the other hand, have been an integral part of personal computers for decades, and a strong demand from the consumer electronics industry has resulted in significant sustained industrial investment in the stable, long-term development of GPU technology. In addition to low prices for GPUs, this has led to a continuous increase in the computational power and memory bandwidth of GPUs, significantly outstripping the improvements in CPUs. As a consequence, high-end GPUs can be considered standard equipment in scientific workstations, which means that they either already exist in many research laboratories or can be purchased easily with new equipment. This makes them readily available to researchers and thus attractive targets for acceleration of many scientific applications including MD simulations.

The nature of GPU hardware, however, has until recently made their use in general purpose computing challenging to all but those with extensive three-dimensional (3D) graphics programming experience. However, the development of application programming interfaces (APIs) targeted at general purpose scientific computing has reduced this complexity substantially such thatGPUs are now accepted as serious tools for the economically efficient acceleration of an extensive range of scientific problems.^11,12

The computational complexity and fine grained parallelism of MD simulations of macromolecules makes them an ideal candidate for implementation on GPUs. Indeed, as we illustrate here for implicit solvent and in a subsequent paper¹³ for explicit solvent, the careful implementation of modern MD algorithms on GPUs can provide capability, in terms of performance, that exceeds that achieveable with any current CPU-based supercomputer. Several previous studies have investigated the use of GPUs to accelerate MD simulations.¹⁴⁻²⁰ For a detailed review of the use of GPUs for acceleration of condensed phase biomolecular MD simulations, we refer the reader to our recent review.¹²

In this manuscript, we present our high-performance GPU implementation of implicit solvent generalized Born (GB) MD for the AMBER²¹ and CHARMM²² pairwise additive force fields on CUDA-enabled NVIDIA GPUs. We have implemented this within the AMBER^23,24 PMEMD dynamics engine in a manner that is designed to be as transparent to the user as possible, and we give an overview of what the code currently supports, as well as our plans for future developments. We discuss the specifics by which we exploit the processing power of GPUs, both in serial and using multiple GPUs, and show the performance that can be achieved in comparison to conventional CPU clusters. We also discuss our implementation and validation of three specific precision models that we developed and their impact on the numerical results of implicit solvent MD simulations.

2. GPU Programming Complexities

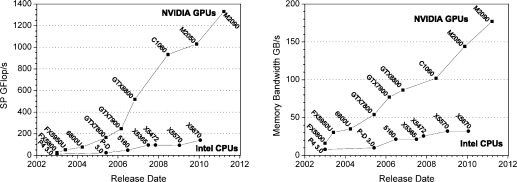
As illustrated by Figure 1, GPUs offer a tremendous amount of computing power in a compact package. This, however, comes at the cost of reduced flexibility and increased programming complexity as compared to CPUs. In order to develop software that runs efficiently on GPUs, it is necessary to have a thorough understanding of the characteristics of the GPU hardware architecture. A number of manuscripts have already discussed this in detail in the context of MD.^{11,12,15,17,25} For this reason, we provide simply a brief overview of the complexities involved in programming GPUs as they relate to our implementation, focusing on NVIDIA hardware. For a more detailed description, the reader is referred to the publications cited above.

Figure 1.

Peak floating-point operations per second (Flop/s; left) and memory bandwidth (right) for Intel CPUs²⁶ and NVIDIA GPUs.²⁷

2.1. Vectorization

A GPU is an example of a massively parallel stream-processing architecture which uses the single-instruction multiple data (SIMD) vector processing model. Unlike a regular CPU, which typically operates on one to four threads in parallel, GPUs typically process threads in blocks (termed warps within the CUDA programming language²⁸) containing between 16 and 64 threads. These thread blocks logically map to the underlying hardware, which consists of streaming multiprocessors. At the time of writing, high-end GPUs typically have between 16 and 32 multiprocessors. For example, an NVIDIA M2090 GPU consists of 16 multiprocessors, each containing 32 cores for a total of 512 cores. All threads in a single block must execute the same instruction on the same clock cycle. This necessarily implies that, for optimum performance, codes must be vectorized to match the size of a thread block. Branching must therefore be used with extreme care since if any two threads in the same warp have to follow different code paths of the branch, then threads in the warp will stall while each side of the branch is executed sequentially.

2.2. Memory Model

The memory hierarchy of GPUs has its origins in their graphics lineage, and the high density of arithmetic units comes at the expense of cache memory and control units. All of the cores making up a multiprocessor have a small number of registers that they can access, a few kilobytes (64 kB on an M2090) of shared memory [this can be split into directly accessible memory and L1 cache; in the case of an M2090, it can be split 48/16 kB or 16/48 kB; in the case of AMBER, the configuration is switched at runtime for optimal performance of a given kernel] which is private to each multiprocessor and a small amount (typically 48 kB) of high-speed but read-only texture memory. The majority of the memory (6 GB on an M2090), termed global device memory, is available to all multiprocessors. While being fast compared to the main memory accessible by CPUs, access to the device memory by GPUs is still relatively slow compared to the local cache memory. The nature by which the multiprocessors are connected to this memory also means that there is a significant performance penalty for nonstride-1 access. Finally, it should be noted that currently the CPU and GPU memories are in different address spaces and this requires careful consideration. The unique nature of this memory model leads to several considerations for optimizing GPU performance, including optimizing device memory access for contiguous data, utilizing the multiprocessor shared memory to store intermediate results or to reorganize data that would otherwise require nonstride-1 memory accesses, and using the texture memory to store read-only information, such as various force field parameters, in a fashion that allows very rapid access.

2.3. GPU to CPU Communication

As mentioned above, the CPU and GPU memories are, at the time of writing, in different address spaces. This means it is up to the programmer to ensure that the memories are synchronized as necessary to avoid race conditions. However, there is a big performance penalty for such synchronizations which have to occur via the Peripheral Component Interconnect Express (PCIe) bus, and thus they should be avoided unless absolutely necessary.

2.4. GPU to GPU Communication

The traditional method for programming scientific algorithms in paralleluses the message passing interface (MPI)²⁹ in which each thread runs in a separate address space. When running GPUs in parallel under an MPI paradigm, additional complexity is introduced since sending data between two GPUs involves copying the data from the memory of the sending GPU to the CPU memory of the corresponding MPI thread over the PCIe bus, an MPIsend by this CPU thread, and corresponding MPIreceive by the receiving CPU thread, which copies the data between the memories of the CPUs, and finally copying the data to the memory of the receiving GPU. Clearly, this introduces additional considerations for maximizing parallel performance as compared to traditional CPU programming.

At the time of writing, there are efforts to streamline GPU to GPU communication, particularly within a single node but also for Infiniband connections between nodes. One such approach under development by NVIDIA and Mellanox is termed GPUDirect,³⁰ which ultimately seeks to unify address spaces between multiple CPUs and GPUs. Currently, the degree to which this can be utilized is heavily dependent on the underlying hardware design. Therefore, at present, the added complexity of using the advanced features of GPUDirect, beyond the pinned memory MPI optimizations offered by GPUDirect version 1, on the large number of possible different hardware combinations is not worth the effort for a widely used production code.

2.5. Mathematical Precision

Early versions of GPUs in NVIDIA’s lineup (prior to the GT200 model) only supported single precision (SP) floating point arithmetic. This was due to the fact that graphics rendering did not require double precision (DP). Scientific algorithms, however, typically require DP arithmetic (for a discussion in the context of quantum chemistry, see for example the work by Kniziaet al.³¹). The generation of GPUs at the time of our initial implementation (2008) supported DP in hardware, but only at 1/8 the performance of SP. In the latest generation of cards, at the time of writing, termed the Fermi lineup by NVIDIA, the DP to SP performance ratio is 1/2 and thus equivalent to that in CPUs. This, however, only holds for the professional (termed Tesla) series of cards. The significantly cheaper gaming cards (termed GeForce) still only support DP at a fraction of the speed of SP. It is therefore important to optimize the use of DP such that it is only used when necessary to maintain numerical accuracy.

2.6. Programming Model

Early use of GPUs for scientific computing was hampered by the lack of an application programming interface (API) for general purpose calculations. The problems to be solved had to be described in terms of a graphics pipeline employing either OpenGL or DirectX, which made the software development time-consuming and hardware-specific. The barrier to utilizing GPU hardware for general purpose computation has since been reduced by the introduction of GPU programming models such as the Brook stream programming language,³² OpenCL,³³ and NVIDIA’s Compute Unified Device Architecture (CUDA)²⁸ and the availability of corresponding software development toolkits (SDKs). The AMBER implementation uses CUDA, which is a relatively simple extension of the standard C programming language that allows one to code in an inherently parallel fashion and perform all necessary operations to access and manipulate data on a GPU device. Realizing the full potential of GPUs, however, still requires considerable effort as indicated above and outlined below to take advantage of the particular GPU architecture, and not all algorithms are suitable to achieve good performance on these massively parallel processors.

3. Overview of the AMBER Implicit Solvent GPU Implementation

The nature of MD simulations requires what in computer science is referred to as strong scaling, that is, reduction of the solution time with an increasing number of processors for a fixed total problem size. This enables access to simulations at longer time scales, which is required for a proper convergence of results. This becomes more important as one moves to larger system sizes since the number of degrees of freedom increases. Weak scaling, that is, the solution time with the number of processors for a fixed problem size per processor, is only of secondary importance, since this merely enables simulating larger molecules at currently attainable time scales. Our implementation therefore has focused on accelerating problem sizes that correspond to those typically studied by AMBER users. In the case of GB simulations, this is in the range of 300 to 30 000 atoms.

The initial driving force in accelerating AMBER implicit solvent GB calculations with GPUs was to provide the scientific community with a computational tool that would allow an individual researcher to obtain performance on a simple desktop workstation equivalent to that of a small CPU cluster. Such a tool alleviates the costs, both capital and recurring, involved in purchasing, maintaining, and using individual research compute clusters. To this end, our goal was that a single state-of-the-art GPU should provide a performance equivalent to that of four to six high-end CPU cluster nodes. Such an approach also removes the need to purchase and maintain expensive interconnects that are required to achieve scaling even on a modest number of nodes.

Beyond this initial serial development, which was first released as an update to AMBER 10³⁴ in August 2009, we have also developed a parallel implementation based on the MPI-2²⁹ message passing protocol, released as an update to AMBER 11²³ in October 2010, that allows a single job to span multiple GPUs. These can be within a single node or across multiple nodes. As shown below, it is possible with this implementation to achieve a performance improvement that goes beyond simply making a desktop workstation faster, ultimately providing a performance capability that surpasses what is achievable on all current conventional supercomputers. Achieving this level of performance required implementing the entire implicit solvent MD algorithm including energy and force evaluations, restraints, constraints, thermostats, and time step integration on the GPU. As described in section 3.2, CPU to GPU communication only occurs during I/O or to some extent when data is sent between GPUs during parallel runs.

While we have designed our GPU implementation to achieve substantial acceleration of implicit solvent MD simulations over that achievable with AMBER’s CPU implementation, our overriding goal has always been to maintain the precision of the calculations. To this end, we have focused on ensuring that GPU simulations will match CPU simulations. All approximations made in order to achieve performance on GPU hardware have been rigorously tested as highlighted in the following sections.

An additional design goal has been to attempt to preserve forward compatibility of our implementation. Using the CUDA programming language provides this by abstracting the program from the underlying hardware. The GPU accelerated version of AMBER can be used on all NVIDIA cards that support double precision in hardware, that is, those with hardware revision 1.3 or 2.0 or higher. Our choice of CUDA and NVIDIA graphics cards was largely guided by the fact that, at the time we began this work, OpenCL was not mature enough to offer the same performance and stability benefits that CUDA did. A port to OpenCL is certainly possible, and this would support AMD hardware. However, with the public release of the CUDA API³⁵ by NVIDIA and the release of CUDA compilers for x86 platforms by PGI,³⁶ it is possible that an AMBER implementation will soon be available on a variety of accelerator hardware.

3.1. Features of the Implementation

We have attempted to make our GPU implementation all-inclusive of the features available in the PMEMD program. At the time of writing, the majority of features applicable to implicit solvent simulations are available as described below.

Supported Methods

Support is provided for all GB models currently implemented within AMBER³⁷⁻⁴¹ as well as the analytical linearized Poisson–Boltzmann (ALPB)⁴² model. In addition to constant energy simulations, thermostats have been implemented to perform constant temperature simulations. This includes all three thermostats available in PMEMD, that is, the Berendsen weak coupling algorithm,⁴³ the Andersen temperature coupling scheme,⁴⁴ and the Langevin dynamics thermostat.⁴⁵ Constraints for hydrogen bond distances use a GPU version of the standard SHAKE algorithm^46,47 employed in PMEMD, and harmonic restraints to a reference structure are supported.

To the best of our knowledge, no GB formalism currently exists that corrects for the errors introduced by the use of cutoffs for long-range nonbonded interactions. The use of cutoffs in GB simulations as implemented in PMEMD does not conserve energy, and their use involves an approximation with an unknown effect on accuracy. For this reason, we chose not to implement van der Waals (vdW) and electrostatic cutoffs in the GPU version of this code. [Cutoffs for the nonbonded interactions are implemented for explicit solvent simulations with periodic boundary conditions using the particle mesh Ewald (PME) method, as described in a later paper.] However, cutoffs in calculating the effective Born radii are supported.

Reproducibility

A design feature of the GPU code that goes beyond the CPU implementation is the deterministic nature of the implementation on a given hardware configuration. Serial CPU calculations for a given set of input parameters on identical hardware are perfectly reproducible. This does not hold for the parallel CPU implementation since the need to load balance aggressively to achieve good parallel scaling means that the order of numerical operations is not defined, and therefore two simulations started from identical conditions will always diverge due to rounding differences. This poses a problem when transitioning to microsecond or greater simulation time scales since it can be of advantage to store trajectory information less frequently than what is optimal in order to conserve available storage space and produce data files of manageable size. It is thus not possible to go back to a given point of the simulation and analyze the trajectory in finer detail by restarting and sampling more frequently unless the implementation is deterministic. The deterministic nature of the GPU code coupled with machine precision binary restart files (currently under development) makes this mode of simulation possible. This also makes debugging and validation easier.

Transparency

Another key feature and a primary design goal of our GPU acccelerated implementation is that its use is completely transparent to the user. As far as the user is concerned, our GPU implementation is indistinguishable from the CPU implementation, and using the GPU version of the code is simply a case of switching the executable name from pmemd to pmemd.cuda or from pmemd.MPI to pmemd.cuda.MPI for the MPI parallelized implementation. All other items such as input and output files and regression tests within the code remain identical. The only difference to be noticed by the user is an increase of performance. This guarantees effective uptake of our GPU implementation by the scientific commmunity because there is no learning curve for the use of the code, and all tools and scripts that have been developed for the CPU version of PMEMD can be utilized without modifications.

System Size

The maximum system size that can be treated with the GPU implementation is a function of both the GPU hardware and the MD simulation parameters. In particular, Langevin temperature regulation and the use of larger cutoffs for the effective Born radii calculations increase the memory requirements. The physical GPU hardware also affects memory usage since the optimizations used are nonidentical for different GPU types. Table 1 gives an overview of the approximate maximum atom counts that can be treated with the present version of the code. The dominant sources of GPU memory usage are the output buffers used for the nonbonded interactions as described in section 3.2. The memory used by those buffers is proportional to the square of the number of atoms. Currently, the atom count limitations imposed by GPU memory usage are roughly identical in serial and parallel.

Table 1. Approximate Maximum Atom Counts That Can Be Treated with the GPU Implementation of GB Implicit Solvent Simulations in AMBER 11 Using the SPDP Precision Model^a.

GPU card	GPU memory	simulation type	max atoms
GTX-295	895 MB	constant E	20 500
		constant T	19 200
Tesla C1060	4.0 GB	constant E	46 350
		constant T	45 200
Tesla C2050	3.0 GB	constant E	39 250
		constant T	38 100
Tesla C2070	6.0 GB	constant E	54 000
		constant T	53 050

^aTest systems are droplets of TIP3P water molecules. All simulations use SHAKE (AMBER input ntf=2, ntc=2); a time step of 2 fs; the Hawkins, Cramer, Truhlar GB model³⁷ (AMBER input igb=1); the default cutoff value of 25 Å for GB radii (AMBER input rgbmax=25); and temperature control with the Langevin thermostat (AMBER input ntt=3), if applicable. Error-correction code (ECC) was switched off on the Tesla cards.

3.2. Technical Details of the Implementation

In classical MD, the majority of the computational effort is spent evaluating the potential energy and gradients, which has to be repeated each time step. In the case of the AMBER pairwise additive force fields,²¹ the potential takes the form

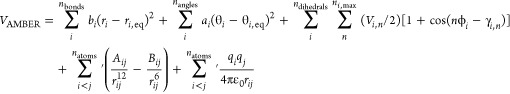1

where the bond and angle terms are represented by a simple harmonic expression with force constants b_i and a_i and equilibrium bond distances/angles r_i,eq and θ_i,eq, respectively. Torsional potentials for the dihedral angles are represented using a truncated Fourier expansion in which the individual terms have a potential V_i,n with periodicity n and phase shift γ_i,n. The last two terms are the vdW interaction represented by a Lennard-Jones potential with diatomic parameters A_ij and B_ij and the electrostatic interaction between atom-centered point charges q_i and q_j separated by the distance r_ij. The prime on the summation of the nonbonded interactions indicates that vdW and electrostatic interactions are only calculated for atoms in different molecules or for atoms in the same molecule separated by at least three bonds. Those nonbonded interactions separated by exactly three bonds (1–4 interactions) are reduced by the application of independent vdW and electrostatic scale factors, termed SCNB and SCEE in AMBER, which are dependent on the specific version of the force field (2.0 and 1.2, respectively, for the ff99SB⁴⁸ version of the AMBER force field).

The CHARMM force field²² takes a similar form but includes three additional bonded terms:

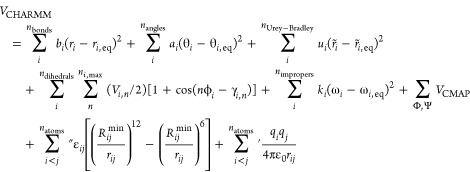2

The two-body Urey–Bradley terms account for angle bending between atoms that are separated by two bonds using a harmonic potential with force constant u_i and equilibrium distance r̃_i,eq. The improper dihedrals with force constant k_i describe out-of-plane bending and are used to maintain planarity and prevent undesired chiral inversions. Within the AMBER force field, improper dihedrals are treated in the same way as proper dihedrals. The third additional term is a cross term between two sequential protein backbone dihedral angles ϕ,ψ termed CMAP.⁴⁹ Additionally, the CHARMM and AMBER force fields handle 1–4 nonbonded interactions in a different manner. The single prime on the electrostatic summation has the same meaning as described above for the AMBER force field with the exception that 1–4 interactions are not scaled. The double prime on the vdW summation implies the same exclusions as the single prime but the use of different values R_ij^min and ε_ij for 1–4 interactions.

In the GB implicit solvent model, the effect of a surrounding solvent is described via a continuum electrostatics model that uses a pairwise descreening approximation and in general also includes a Debye–Hückel term to account for salt effects at low salt concentrations. The general form of the correction to the energy of the solute is given as

3

where q_i and q_j are the atomic partial charges, ε_r is the relative permittivity of the solvent, and κ is the Debye–Hückel screening parameter.³⁸ The function f_ij^GB interpolates between an effective Born radius R_i when the distance r_ij between atoms is short and r_ij at large distances according to

4

The effective Born radius R_i reflects how deeply buried a charge is in the low-dielectric medium (solute), and it depends on the intrinsic radius ρ_i of an atom and the relative positions and intrinsic radii of all other atoms in the solute. The models implemented in PMEMD differ in the intrinsic radii and the function that is used to determine the effective Born radii.

The remainder of this section discusses key aspects of the GPU implementation of these equations. This includes design features to maximize performance while preserving accuracy as well as addressing issues of reproducibility which are critical when moving to longer time scale simulations.

Integration with the Existing Code Base

One of the initial ideas we considered when implementing GPU acceleration for AMBER was to write an entirely new code from scratch in a combination of C++ and CUDA. However, this was quickly dismissed for a number of reasons. In particular, we wanted to

• 1.keep the maintenance of the AMBER code base simple
• 2.minimize the amount of coding required
• 3.simplify the way in which features are ported to the GPU
• 4.maintain backward compatibility with existing input files and regression tests.

The approach we ultimately chose was to utilize the existing Fortran code base in PMEMD and extend it with calls to specific CUDA kernels for the GPU acceleration with the CUDA code protected with #IFDEF CUDA preprocessor directives. Building and testing is automated within the existing installation procedure.

A series of GPU synchronization routines provide an abstract way to copy relevant data to and from the GPU memory, for example, gpu_upload_vel() and gpu_download_vel() for atomic velocities. A complete list of synchronization routines is provided in the Supporting Information. For performance, we have implemented the entire MD algorithm on the GPU, which means uploads (to GPU memory) are only needed at the beginning of a run and downloads (to CPU memory) are only needed when I/O is required, for example, downloading the coordinates to write to the trajectory file. It remains nevertheless simple to add new features to the code in a way that will work for both the CPU and GPU (see the Supporting Information for an example). While this limits the performance for the new feature due to repeated up- and downloads, it does provide a mechanism by which new features can be easily added and tested with the GPU code before writing an additional GPU kernel.

Reproducibility

In order to achieve performance in parallel on CPUs, it has always been necessary to include complex dynamic load balancing algorithms and extensive use of asynchronous communication within the implementation. This arises from the fact that the CPUs are expected to perform a number of tasks above and beyond running the underlying simulation. For example, the operating systems run multiple daemons controlling I/O and various other OS related tasks. In addition, the latency between any two CPUs in a large parallel run can span an order of magnitude or more. As a result, the various MPI threads become desynchronized. Load balancing and asynchronous communication is used to minimize the resulting effect. A downside of this is that the order of operations is not well-defined in the CPU implementation. This results in rounding differences between otherwise identical runs. Due to the chaotic nature of numerically integrating Newton’s equations of motion, this means that two initially identical simulations will always decorrelate on time scales of a few nanoseconds or less. There is nothing inherently wrong with this; the two simulations are just exploring two different regions of phase space. As mentioned previously, this does, however, pose a problem when one starts to routinely run simulations on the microsecond time scale since it can be necessary to return to a given point in a simulation and repeat it exactly while saving the output more frequently. This is something that Shaw et al. attempted to address with a bit-wise reversible integrator⁵⁰ based on scaled integers. However, this did not solve the issue when using the SHAKE algorithm. The architectural design of the GPU with many floating point units controlled by a single instruction unit, and the fact that the GPU is not required to time slice with OS related tasks, means that work can be divided between GPU threads and indeed entire GPUs in a predetermined fashion without detrimentally impacting performance. This can be exploited by careful programming and bookkeeping to ensure that the order of floating point operations is always predefined at each given time step. The GPU implementation of PMEMD has been designed such that any two simulations with identical starting conditions run on the same GPU model will always be bit-wise identical. This is extremely useful for debugging purposes, for example, for detecting shared memory race conditions, and has also been used to determine that the use of ECC on GPUs has little to no impact on the reliability of AMBER simulations.⁵¹

For Anderson and Langevin thermostatted simulations, it is necessary for the random number generator (RNG) to also be perfectly deterministic in order for any two initially identical simulations to be reproducible. To this end, we use the parallelized RNG that is implemented in the CURAND library and available with the CUDA Toolkits.

Precision Model

In AMBER, all of the traditional CPU codes are written entirely using double precision (DP) floating point arithmetic. This is in contrast to developments by early adopters of GPU technology. For example, the OpenMM library of Pande et al.¹⁵ uses single precision (SP) floating point numbers throughout the calculations with the exception of a single double-precision accumulator in the reduction phase of the force accumulation. Use of SP in all places within the code, however, can cause substantial instabilities in the MD simulations. For example, energy conservation in the NVE ensemble can become problematic. While this error can be hidden using tightly coupled thermostats, the true effects of such approximations have not been well characterized.

We distinguish three different precision models in our GPU implementation in which the contributions to the nonbonded forces are calculated in single precision arithmetic, but bonded terms and force accumulation are in double precision (SPDP), or everything is computed and accumulated in single precision (SPSP) or double precision (DPDP). The exception to this is the SHAKE algorithm (see below), which is implemented in DP for all precision models since it involves calculating relative differences in distance on the order of 10^–6 Å. Attempting to use SP for the SHAKE algorithm as implemented leads to numerically unstable simulations. The aim in developing our SPDP precision model for the GPU implementation of PMEMD was to achieve numerical stability during MD simulations equivalent to that of traditional DP implementations but with performance as close to the SPSP model as possible. As highlighted in the subsequent sections, the SPDP model achieves these aims and for this reason is the default precision model used in the GPU implementation of PMEMD, although the other precision models can be chosen if desired.

Nonbonded Interactions

Our approach to the calculation of nonbonded interactions is similar to that described in Friedrichs et al.¹⁵ having been developed at the same time and with overlapping authors but with several differences and additional optimizations, including the way in which accumulations are handled.

The algorithm used for the calculation of the nonbond forces is identical for all three precision models. The pairwise interactions between atoms i and j, which can schematically be represented by a matrix as in Figure 2, are grouped together into tiles of dimension W × W. The evaluation of the nonbond forces for each tile is dynamically assigned to independent warps across all of the Streaming Multiprocessors (SMs) of a given GPU, which are each running a sufficient number of threads to bury operational latency. The reason for doing this is that the GPU schedules work in terms of warps which effectively perform the same mathematical operation on W values at once. In the case of NVIDIA, all current GPUs process warps as 32-threads-wide; in this case, optimum performance is achieved by making W = 32. Since the interaction between two atoms i and j is symmetric, only the blue diagonal tiles and the green off-diagonal tiles need to be considered for the calculation as described below. Unlike the CPU code, which can just simply loop over atoms i and j, it is crucial to divide up the calculation on the GPU into as many warp size blocks as possible. However, this presents a problem when it comes to accumulating the forces for each atom since the warps can be scheduled for computation in any order. A naïve accumulation of the resulting forces on each atom can thus lead to race conditions and incorrect results. The use of atomic operations within the nonbond routine to avoid this problem, however, represents a serial bottleneck that would be unacceptable in terms of performance. The approach we use is thus to allocate (N/W) + 1 output buffers per atom where N is the total number of atoms and W is the warp size. In the case of the nonbond force calculation, each output buffer is three double-precision-values-wide for the SPDP and DPDP precision models and three single-precision-values-wide for the SPSP precision model corresponding to the force in the x, y, and z directions of Cartesian coordinate space. Forces calculated within a tile can then be summed for each atom without fear of overwriting memory effectively providing a separation in space between tiles. At the conclusion of the force calculation, we assign one thread per atom in linear order and cycle through the output buffers, summing them to obtain the total force on each atom.

Figure 2.

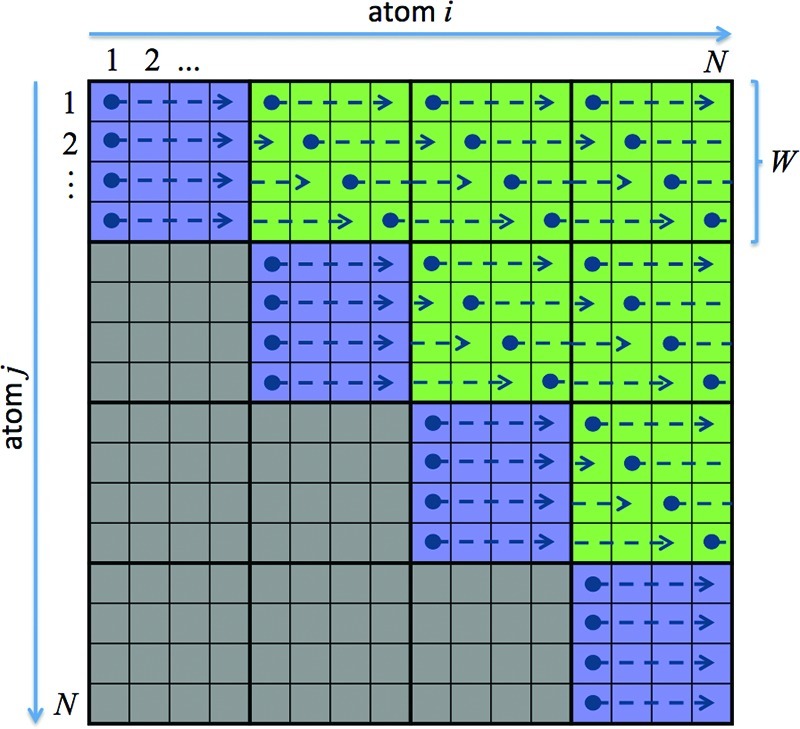
Schematic representation of the work-load distribution for the calculation of nonbond forces with N atoms. Each square represents the interactions between two atoms i and j for which the resulting forces need to be evaluated. These are grouped together in tiles of size W × W that are each assigned to an independent warp. Due to symmetry, only the blue diagonal tiles and the green off-diagonal tiles need to be considered for the calculation. For details, see the text.

While this approach provides a separation in space between tiles, it is still necessary to deal with race conditions within a tile. We have to distinguish on-diagonal tiles (blue) and off-diagonal tiles (green), see Figure 2. The on-diagonal tiles include the interaction of atoms i to i + W – 1 with themselves and thus include the self-interaction from the GB term. In contrast, off-diagonal tiles include the interaction of atoms i to i + W – 1 with j to j + W – 1, where i ≠ j. To avoid race conditions, it is necessary to handle these two types of tile in different ways.

On-diagonal tiles store two copies of the coordinates and associated parameters for each atom, one set in shared memory (index atom i in Figure 2) and the second set in the registers (index atom j in Figure 2). Each thread in the warp then runs linearly through shared memory (atom j), accumulating only the force acting on the register atoms i in the corresponding force output buffer. As illustrated in Figure 2, on the first iteration, the force on atom i resulting from interacting with itself is obtained and stored in the corresponding register for i, while simultaneously the force on atom i + 1 resulting from interacting with atom i is obtained and stored in the register for atom i + 1. Similarly the forces on atoms i + 2 to i + W – 1 resulting from interacting with atom i are obtained and stored in the corresponding output buffer. All threads then step to the next column to obtain the forces on atoms i to i + W – 1 due to interactions with atom i + 1 etc. This approach does some excessive computational work since, for any given atom pair ij, the force on atom j is just the negative of the force on atom i, and thus only the upper or lower triangle of the tile would have to be considered. However, this is far outweighed by the advantage of avoiding race conditions that would result from several threads updating their force contribution to the same atom.

In the case of off-diagonal tiles, a different approach is taken such that the symmetry in the interactions is exploited while avoiding race conditions. Again, the coordinates and associated parameters of atoms labeled j to j + W – 1 are placed in the registers, while the coordinates and associated parameters of atoms i to i + W – 1 are placed in shared memory. If the off-diagonal tiles were handled in the same fashion as the on-diagonal tiles, on the first iteration, the force on atom j due to interacting with atom i would be calculated and from this the corresponding force on atom i obtained by negation. At the same time, the force on atom j + 1 due to interacting with atom i would be calculated and from this the corresponding force on atom i obtained by negation. Thus, the forces on atom i due to all atoms j of the tile would be calculated at the same time, which would require atomic operations to accumulate correctly. The solution to this problem that is implemented in AMBER is to partition the off-diagonal tiles in time as illustrated in Figure 2. By starting each thread offset by its thread ID, we avoid race conditions in the accumulation and eliminate the need for performance destroying atomic operations.

Generalized Born Terms

The GB terms are calculated in an identical fashion to the nonbond terms described above. The Born radii are first calculated within their own kernel and reduced to per atom radii in an analogous fashion to how the nonbond forces are handled. The remainder of the nonbond calculation is then split over two additional kernels.

Bonded and 1–4 Interactions

The bonded and 1–4 terms represent a very small fraction of the computational workload (typically <1% of an iteration), and thus optimization of their calculation is not critical for performance compared with, for example, the nonbond interactions. However, efficient calculation on a GPU still requires some consideration in how these terms are calculated in order to exploit the massive parallelism within the GPU while avoiding race conditions and memory overwrites. Our implementation simply creates a list of the interactions, sorted by type, and then divides up the bonded and 1–4 terms across SMs on a per interaction basis. Since the resulting forces need to be summed for each atom, there is the potential for a race condition to occur during this reduction if two or more GPU threads attempt to accumulate forces for the same atom at the same time in global memory. Our initial attempts to avoid this used atomic operations for reduction of the resulting forces to individual atoms but showed very poor performance. Our solution to this is to make use of the tile reduction buffers from the nonbond calculation as described above and then sum these forces in the reduction step used in the nonbond calculation.

Harmonic Restraints

At the time of writing, the AMBER GPU implementation supports harmonic restraints to a reference structure. These are handled in an identical fashion to the bonded interactions being calculated as a bond between an atom and a fixed virtual particle representing the reference structure.

SHAKE Algorithm

The SHAKE implementation is currently restricted to hydrogen atoms since this represents >99% of the types of simulation AMBER users run. This restriction has the benefit that each heavy atom and its attached hydrogen atoms can thus be handled independently. Our approach is to simply spawn a thread for each heavy atom during the SHAKE calculation. This provides sufficient parallelization to keep the GPU busy. The use of double precision entirely within the SHAKE routine provides sufficient precision to handle shake tolerances on the order of 10^–7 Å and thus avoids complexities involved in attempting to implement SHAKE constraints in an internal coordinate representation as would be required if SHAKE was to be carried out in single precision.

Coordinate Update

Integration is carried out on the GPU in a manner analogous to that on the CPU since it is intrinsically parallel given that each atom can be handled independently. The updated coordinates are stored in global memory on the GPU. The integration is done on the GPU rather than on the CPU to negate the need for expensive copy operations of the coordinates back and forth between CPU and GPU.

Thermostats

As mentioned above, three different thermostats are supported. The Berendsen and Langevin thermostats are applied in the same way during the coordinate update step, while the Anderson thermostat is implemented as a separate kernel that randomizes the velocities at regular intervals. The reason for including the Berendsen and Langevin thermostats within the integration kernel is that they operate on every time step, while the Anderson thermostat is typically called every few hundred time steps. In the case of the Langevin thermostat, a total of 3N random numbers are required on each step, which are extracted from a pool of GPU generated random numbers, stored in global memory, which is refilled as needed using the parallel random number generator implemented within the CURAND library from the CUDA toolkit. The same pool is used for the Anderson thermostat as needed.

Additional Optimizations

In the interest of performance and conserving limited GPU resources, the energy is only calculated alongside the forces when needed. Calculation of the energies causes a small degree of register spillage to global memory as well as additional code execution, and since one only periodically needs these values, typically only every 1 to 2 ps when writing to the output file, it is not necessary to calculate these on every iteration. Additionally, this is one aspect of the algorithm that is allowed to be nondeterministic at the level of double-precision round-off error. We allow this because the energy values have no effect on the trajectory of the simulation. However, it was disturbing to observe this in action in the SPSP mode where nondeterminism was initially allowed at the level of single-precision round-off error. This was harmless as the forces remained consistent, but in the interest of avoiding confusion among end-users, with regression tests showing differences for repeat runs in SPSP mode, all energy summation was promoted to double-precision where differences in round-off of the energies are seen only once in approximately 10⁶ printed interactions.

Parallelization

The parallel GPU implementation is currently written exclusively using MPI. The reasons for this were to maximize portability of the code and avoid hardware-induced complexities such as the fact that inter-GPU communication as implemented in CUDA 4.0 requires all GPUs to be on the same PCIe controller. Support for GPU to GPU copies in different nodes is also not yet sufficiently mature to be exploited in a widely used software package. For these reasons, the current parallel GPU scaling should be considered as a lower bound on performance that will likely improve considerably in subsequent versions of AMBER running on next generation hardware.

Unlike the CPU MPI implementation, the GPU MPI implementation is fully deterministic for a given number of nodes and GPUs. At present, our GPU implementation performs significant load-balancing between the SMs within each GPU rather than between GPUs, which makes it possible to produce a deterministic implementation. Achieving good parallel scaling on CPU clusters has always required the use of extensive load-balancing due to the noise introduced from the operating system sharing the CPU resources on a node. GPUs on the other hand provide significantly more stable performance, and thus load balancing between GPUs is not as critical.

In the current version of the software (AMBER v11), the GPU parallel support for GB calculations is implemented by dividing the force calculation evenly and linearly across all GPUs. For M GPUs running a simulation consisting of N atoms, GPU i calculates all forces for atoms (i – 1) × N/M + 1 to i × N/M. Since GB is a full O(N²) calculation, this introduces a small degree of redundancy at the GPU level with a worst-case outcome of doing twice the overall calculation, but usually much less than this as long as N ≫ M. As currently implemented, there are three stages to the calculation in parallel, each in need of synchronizing force data across all GPUs. The procedure used consists of three sequential MPI_allGather operations per iteration to merge Born radii, Born force, and general force data. As the hardware evolves and GPUs can reliably communicate directly with each other within a node, we intend to scrap the internode MPI communication and instead replace it with direct peer to peer copies between GPUs.

4. Performance

To assess both the serial and parallel performance that can be achieved with GPU accelerated AMBER, we ran a series of MD simulations representative of typical research scenarios using the GPU and CPU implementations on a variety of hardware. The systems used consisted of partially folded TRPCage⁵² (304 atoms), ubiquitin^53,54 (1231 atoms, PDB code 1UBQ), apo-myoglobin (2492 atoms), and nucleosome (25 095 atoms, PDB code 1KX5).

In all three simulations, the ff99SB⁴⁸ version of the AMBER force field was used with a time step of 2 fs and bonds to hydrogen atoms constrained using the SHAKE algorithm. The Hawkins, Cramer, and Truhlar GB model³⁷ (AMBER input igb=1) was used with no cutoff applied to the nonbonded interactions and a cutoff of 15 Å for the calculation of the effective GB radii. The output and trajectory files were written to every 1000 steps (2 ps). Input files for these simulations are provided in the Supporting Information.

The software base used for all simulations was AMBER version 11, including patches 1–15 for AmberTools and patches 1–17 for AMBER, which were released on August 18, 2011.⁵⁵ The executables were built under the RedHat Enterprise Linux 5 operating system with Intel compiler version 11.1.069, the Intel MKL library version 10.1.1.019, and the NVIDIA CUDA compiler version 4.0. MVAPICH2 version 1.5 was used for the parallel runs for both the CPU and GPU versions of the code. The default SPDP precision model was used in the GPU code. While the Fortran compiler and use of MKL has little impact on the GPU code performance, this compiler/library combination gives the best performance for the CPU code and thus forms a fair basis when assessing the capabilities of the GPU implementation. Both the CPU and GPU simulations were run on machines equipped with a SuperMicro X8DTG-DF motherboard with dual hex-core Intel X5670 processors clocked at 2.93 GHz and Mellanox quadruple data rate (QDR) Infiniband interconnects. Each compute node was equipped with one GPU and one Infiniband card, which were each connected to a PCIe x16 slot. Error-correction code (ECC) was switched off on the Tesla cards, and the 64-bit NVIDIA Linux Driver version 275.21 was used. Additionally, CPU simulations were run on the XSEDE Trestles supercomputer at the San Diego Supercomputer Center, whose nodes are equipped with four oct-core AMD Opteron 6136 processors clocked at 2.4 GHz and also interconnected with QDR Infiniband.

Serial GPU Performance

The results of the simulation timings for single GPU runs are summarized in Table 2. For small simulations such as TRPCage with 304 atoms where the GPU’s arithmetic hardware cannot be fully utilized, the serial GPU implementation is approximately twice as fast as a current state of the art CPU node. The real advantage of the AMBER GPU implementation, however, becomes apparent for implicit solvent GB simulations of medium to large systems with 2500 to 25 000 atoms. For apo-myoglobin (2492 atoms), the serial GPU version of the code is significantly faster on a single GPU than a state of the art CPU node. For nucleosome, this performance gap increases dramatically such that a simulation that takes two weeks on a single desktop machine with one GPU would take nine months using the same desktop machine without GPU acceleration.

Table 2. Single GPU Throughput Timings (ns/day) for AMBER GB Simulations with a Time Step of 2 fs Using the Parallel CPU Version on One Node (12 Intel X5670 Cores or 32 AMD Opteron 6136 Cores) and the Serial GPU Version with the SPDP Precision Model on One Node (One Intel X5670 Core and One GPU)^a.

CPU/GPU	TRPCage (304 atoms)	ubiquitin (1231 atoms)	apo-myoglobin (2492 atoms)	nucleosome (25 095 atoms)
GPU version
M2090 (6 GB)	399.9	184.2	78.1	1.42
C2070 (6 GB)	364.1	157.2	64.3	1.09
C1060 (4 GB)	234.6	78.3	31.5	0.40
GTX580 (1.5 GB, PNY XLR8)	471.1	215.9	88.7	–
CPU version
32 × Opteron 6136	225.0b	29.9	10.3	0.08
12 × X5670	247.1	19.8	6.6	0.07

^aFor details on the hardware and software stack, see text. A dash indicates insufficient GPU memory for the simulation.

^bThe CPU code requires >10 atoms per core, and thus the TRPCage simulation was run on 24 CPU cores.

Parallel GPU Performance

The parallel performance of the GPU and CPU implementations is compared in Table 3. A throughput of up to 135.1 ns/day for apo-myoglobin and up to 3.95 ns/day for nucleosome can be achieved with eight NVIDIA M2090 GPUs, which is a factor of 4 to 5 faster than the maximum throughput that can be achieved on a typical supercomputer given that the CPU scaling plateaus long before it reaches the performance achieved by the GPU implementation. Even a single GPU is a factor of 2 to 3 faster than the CPU scaling limit.

Table 3. Multi-GPU Throughput Timings (ns/day) for AMBER GB Simulations with a Time Step of 2 fs Using the Parallel CPU Version (12 Intel X5670 Cores or 32 AMD Opteron 3136 Cores on Each Node) and the Parallel GPU Version with the SPDP Precision Model (One Intel X5670 Core and One GPU Per Node)^a.

CPU/GPU	apo-myoglobin (2,492 atoms)	nucleosome (25,095 atoms)
GPU version
8 × M2090	135.1	3.95
4 × M2090	115.0	2.71
2 × M2090	93.1	1.80
1 × M2090	78.1	1.42
CPU version
2048 × Opteron 3136	–	0.53
1024 × Opteron 3136	–	0.78
512 × Opteron 3136	–	0.65
256 × Opteron 3136	–	0.55
128 × Opteron 3136	29.8	0.31
64 × Opteron 3136	18.3	0.17
32 × Opteron 3136	10.3	0.08
12 × X5670	6.6	0.07

^aFor details on the hardware and software stack, see the text. A dash indicates lower speed than with less nodes.

Precision Model Performance

As mentioned above, the AMBER GPU implementation supports three different precision models. The DPDP model is logically equivalent to the traditional DP approach used on the CPU. However, the use of DP on GPUs can be more detrimental to performance than its use on CPUs. Therefore, the desire to achieve high performance prompts for use of SP where possible. It is critical though to use SP carefully in order not to detrimentally affect the accuracy of the MD. For this reason, we designed our hybrid precision SPDP model to achieve performance very close to that achievable with SP but in a manner that does not impact accuracy. While we recommend using the SPDP precision model, it is instructive to compare the performance of the different precision models available in the AMBER GPU implementation. As shown in Table 4, the single precision (SPSP) model achieves the highest performance as expected but, as highlighted in section 5, at the cost of accuracy. Our hybrid SPDP precision model, however, achieves a performance of greater than 75% of the SPSP precision model with accuracy comparable to that of the full double precision (DPDP) model, which is between 4 to 7 times slower.

Table 4. Throughput Timings (ns/day) for AMBER GB Simulations of Apo-Myoglobin (2,492 atoms) with a Time Step of 2 fs Using the Serial GPU Version with Different Precision Models^a.

precision model	SPSP	SPDP	DPDP
M2090 (6 GB)	92.7	78.1	25.8
C2070 (6 GB)	73.7	64.3	20.5
C1060 (4 GB)	41.2	31.5	5.4
GTX580 (1.5 GB, PNY XLR8)	111.4	88.7	16.0

^aFor details on the hardware and software stack, see the text.

5. Validation

A critical and often overlooked aspect of any major change to a widely used scientific software package is a detailed validation of any and all new approximations made. In the case of the AMBER GPU implementation the validation falls into two distinct categories. The first is a detailed testing of the code itself to ensure that it correctly simulates the existing systems and does not introduce any new bugs or contain critical logic errors. This is the key reason why we implemented a full double precision (DPDP) model within the GPU code. This precision model matches the CPU code to machine precision and thus can be used to check that the GPU code is indeed giving the correct answers. This allowed us to take the CPU-based regression tests that we have used for many years to validate an AMBER installation and run them using the GPU code and obtain answers to the limits of machine precision. More complex, however, is the second category for validation which is the careful testing of our hybrid (SPDP) precision model. This is significantly more complex since it requires a careful evaluation of any subtle differences in the dynamics as well as ensemble properties from converged simulations run in DPDP and SPDP precision. In this section, we attempt to extensively validate our SPDP model comparing a number of key observables across all three, DPDP, SPDP, and SPSP, precision models.

5.1. Single Point Forces

The first metric tested was the effect of the numerical precision model on the force calculations as compared to a reference precision model, in this case, the result from the CPU implementation. We are using the starting structures of the test systems described in section 4 above. The deviations in the forces are summarized in Table 5. The DPDP model matches the reference forces very closely with maximum deviations not exceeding 10^–7 kcal/(mol Å) and RMS deviations not exceeding 10^–8 kcal/(mol Å), even for systems as large as nucleosome. These deviations are entirely due to the different order of execution of the floating point operations in the CPU and GPU implementation. The DPDP GPU implementation of PMEMD will thus generate trajectories of precision equivalent to the CPU implementation. The forces obtained from the SPSP model, however, show very large deviations from the reference values on the order of up to 10^–2 kcal/(mol Å) for the largest system studied. Such large deviations introduce significant numerical noise into the simulations, and it is reasonable to expect that this may render the results of MD simulations questionable. Calculating the force contributions in SP and accumulating them in DP, however, leads to an improvement of more than 1 order of magnitude in all cases for the SPDP model as compared to the SPSP model. In the following section, we will indeed show that the forces obtained from the SPSP model are not precise enough to conserve energy in biomolecular MD simulations and can lead to instabilities in long time scale MD simulations, while the SPDP model is sufficient for this purpose.

Table 5. Deviations of Forces (in kcal/(mol Å)) of the AMBER PMEMD GPU Implementation Using Different Precision Models As Compared to Reference Values Obtained with the CPU Implementation.

precision model	TRPCage (304 atoms)	ubiquitin (1231 atoms)	apo-myoglobin (2492 atoms)	nucleosome (25 095 atoms)
max deviation
SPSP	3.0 × 10–3	4.8 × 10–3	4.2 × 10–3	2.7 × 10–2
SPDP	5.6 × 10–5	3.7 × 10–4	1.6 × 10–4	1.1 × 10–3
DPDP	1.1 × 10–8	7.3 × 10–8	3.4 × 10–8	8.0 × 10–8
RMS deviation
SPSP	5.0 × 10–4	6.1 × 10–4	4.1 × 10–4	1.5 × 10–3
SPDP	7.0 × 10–6	1.5 × 10–5	8.1 × 10–6	3.0 × 10–5
DPDP	1.5 × 10–9	3.6 × 10–9	2.6 × 10–9	3.2 × 10–9

5.2. Energy Conservation

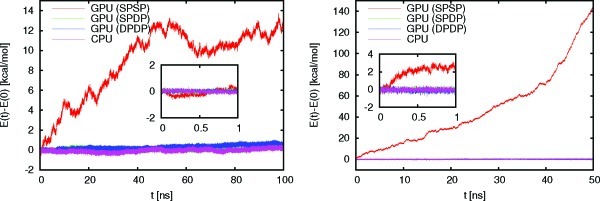
One of the most important gauges for judging the precision of MD software is its numerical stability, which is reflected in its ability to conserve the constants of motion, in particular the energy. To this end, we have performed constant energy MD simulations of the first three test systems described in section 4 above. We collected data for 100 ns (TRPCage), 50 ns (ubiquitin), and 20 ns (apo-myoglobin) after an initial equilibration for 1 ns at 300 K using Langevin dynamics. Center of mass motion was removed before starting the constant energy runs. In addition to simulations using a time step of 2 fs with bonds to hydrogen atoms constrained using the SHAKE algorithm with a relative geometrical tolerance of 10^–6, we have run simulations using time steps of 0.5 and 1.0 fs without constraints.

The energy drifts along the trajectories are summarized in Table 6, while Figure 3 shows a plot of the total energy for the trajectories of TRPCage and ubiquitin for the different precision models at a time step of 0.5 fs. The corresponding plot for apo-myoglobin is very similar to that for ubiquitin and can be found in the Supporting Information along with plots for the larger time steps. The plots underline that it is important to validate the precision models for trajectories that are long enough to uncover numerical instabilities. While the SPSP model seems to perform reasonably well for a trajectory of 1 ns length, in particular for smaller systems like TRPCage, it becomes apparent that the errors introduced lead to unacceptably large energy drifts in the long term. Apart from the magnitude in the energy drift, the plots for the other time steps show a similar behavior (See Supporting Information). Table 6 shows that the SPDP model is able to conserve energy to the same degree as the full double precision model (DPDP) and the reference CPU implementation. The SPSP model, on the other hand, shows energy drifts that are 1 to 2 orders of magnitude larger and, on the time scales investigated, leads to completely unphysical results. While the CPU implementation and the GPU implementations with the full double precision model (DPDP) and mixed precision model (SPDP) achieve excellent energy conservation on the order of 10^–6 kT/ns/dof, where dof means degree of freedom, for simulations with a time step of 0.5 fs, the energy drift for the SPSP model remains as large as with a time step of 1.0 fs. In addition, the energy drift for the SPSP model is not constant and in general increases significantly along the trajectory as the temperature increases, which eventually leads to unstable simulations.

Table 6. Energy Drifts Per Degree of Freedom (kT/ns/dof) from Simulations of 100 ns (TRPCage), 50 ns (Ubiquitin), and 20 ns (Apo-Myoglobin)^a.

time step	0.5 fs	1.0 fs	2.0 fs
TRPCage (304 atoms)
CPU	0.000006	0.000066	0.000355
GPU (DPDP)	0.000012	0.000082	0.000382
GPU (SPDP)	0.000003	0.000070	0.000222
GPU (SPSP)	0.000184	0.000252	–
ubiquitin (1231 atoms)
CPU	0.000004	0.000011	–0.000216
GPU (DPDP)	0.000001	0.000006	–0.000247
GPU (SPDP)	0.000003	0.000030	–0.000165
GPU (SPSP)	0.001065	0.000305	–
apo-myoglobin (2492 atoms)
CPU	0.000012	0.000094	0.000416
GPU (DPDP)	–0.000004	0.000117	0.000290
GPU (SPDP)	0.000019	0.000185	0.000139
GPU (SPSP)	0.002230	0.000442*	–

^aThe SHAKE algorithm to constrain bond lengths to hydrogen atoms was used for a time step of 2.0 fs; no constraints were used for smaller time steps. A dash indicates that the system heated up extremely during the simulation to the point that it is meaningless to report an energy drift. An asterisk indicates that the energy drift increases dramatically for longer time scales.

Figure 3.

Total energy (kcal/mol) along constant energy trajectories using a time step of 0.5 fs without constraints. Shown are results for TRPCage (left) and ubiquitin (right) for different precision models. The insets show the first nanosecond of each trajectory.

By way of comparison to other GPU implementations of MD, the closest published constant energy GB simulation is that of the λ repressor (1254 atoms) using OpenMM.¹⁵ Simulations of this system at a time step of 1.0 fs over 1 ns of simulation time without constraints using the GPU implementation of OpenMM gave energy drifts of 0.0054 kT/ns/dof (NVIDIA hardware) and 0.0178 kT/ns/dof (ATI hardware) (Table 3 of Friedrichs et al.¹⁵) compared with our values of 0.000006 kT/ns/dof (DPDP), 0.000030 kT/ns/dof (SPDP), and 0.000305 kT/ns/dof (SPSP) for the similarly sized ubiquitin system (1231 atoms). It is also interesting to compare the energy conservation achieved with the AMBER GPU implementation using the typical simulation settings that one would use in a production MD simulation with those published for the OpenMM implementation. Most AMBER simulations would use SHAKE constraints and a 2 fs time step with the SPDP precision model, which for ubiquitin gives an absolute energy drift of −0.000165 kT/ns/dof. This compares extremely favorably with the drift of 0.0060 (NVIDIA hardware) and 0.0558 (ATI hardware) for OpenMM. The energy conservation of the AMBER GPU implementation looks even better when one considers that the OpenMM constraint numbers were obtained with a smaller time step of 1 fs.

5.3. Structural Properties

On the molecular level, protein dynamics are at the heart of biological function.⁵⁶ MD simulations that are able to accurately describe protein motions aid in understanding the multitude of functions that proteins carry out and can be used to interpret and predict experimental results that are related to its structural and dynamic properties, for example, NMR spectroscopic parameters such as spin relaxation^57,58 or residual dipolar couplings.^59,60 In order to scrutinize the reliability of our implementation for protein dynamics, we present results of MD simulations of ubiquitin with the different accuracy models of our GPU implementation and compare these to trajectories obtained with the CPU implementation which serves as a reference. We focus on root-mean-square deviations (RMSDs) and root-mean-square fluctuations (RMSFs) of the C_α backbone carbon atoms with respect to the crystal structure (PDB code 1UBQ(53,54)). The highly flexible end tail of ubiquitin (residues 71 to 76) was excluded from our analysis. Results for the radius of gyration R_g of ubiquitin can be found in the Supporting Information.

Although the use of a thermostat will to some extent cover up numerical noise introduced by numerical inaccuracies in the implementation, we are analyzing constant temperature simulations here since typical biomolecular AMBER simulations are generally run with some form of temperature control. In order to obtain statistically meaningful results, 50 independent MD trajectories each of 100 ns length were generated at 300 K both for the CPU implementation and for each of the precision models of the GPU implementation. The ff99SB⁴⁸ force field was used for all simulations with a time step of 2 fs and bonds to hydrogen atoms constrained using the SHAKE algorithm with a relative geometrical tolerance of 10^–6. The GB model developed by Onufriev et al.⁴⁰ (AMBER input igb=5) was used with no cutoff applied to the nonbonded interactions and a cutoff of 15 Å for the calculation of the effective GB radii. The output and trajectory files were written to every 1000 steps (2 ps). Temperature control during production runs was achieved with the Berendsen weak coupling algorithm⁴³ using a time constant of τ_T = 10.0 ps for the heat bath coupling. The initial coordinates and velocities that form the starting point of the 50 trajectories were generated using the CPU implementation as follows. After energy minimization for 2000 steps followed by heating and an initial equilibration for 1 ns at 300 K using Langevin dynamics with a collision frequency of γ = 1.0 ps^–1, snapshots were extracted at time intervals of 4 ns from a constant temperature MD simulation at 300 K. Each of these snapshots was then assigned random velocities corresponding to a temperature of 10 K followed by heating and equilibration to 300 K using Langevin dynamics for 50 ps and removal of any center of mass motion that may have been introduced. Using the CPU generated restart files in all cases guarantees that any numerical differences observed between the various implementations can be traced back to the numerical precision of the implementation and is not an artifact of different initial conditions. Input files for these simulations are provided in the Supporting Information.

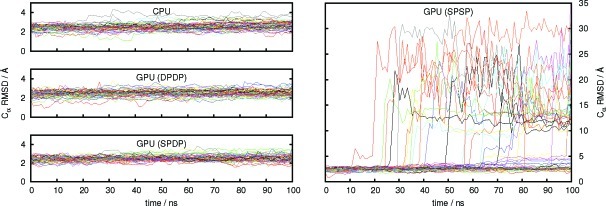
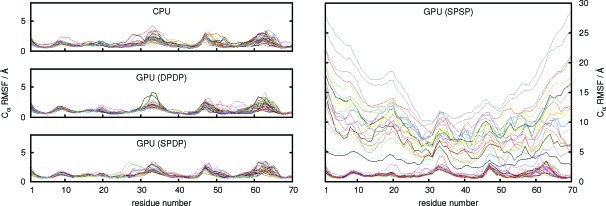
The plot of the RMSD values vs time (Figure 4) clearly shows the stability of the MD simulations using the CPU implementation and the GPU implementation with the full double precision model (DPDP) and the mixed single/double precision model (SPDP). The value of R_g also remains constant throughout all simulations of ubiquitin using the CPU and GPU DPDP and SPDP versions of the code (see Supporting Information), indicating that the relative compactness of the protein is maintained. The R_g value stays around 11 to 12 Å, typical for proteins of this size, assuming a spherical conformation,⁶¹ and are in good agreement with the R_g reported for other native-state simulations of ubiquitin.⁶² The RMSF values for each residue for the 50 native-state simulations are shown in Figure 5. The data show an excellent agreement among the CPU implementation and the GPU implementation using both the DPDP and the SPDP precision model with the majority of the residues remaining within 2 to 3 Å of their positions in the experimental structure and somewhat larger fluctuations around residue numbers 33, 48, and 63. On the time scale investigated, no major structural change is taking place during the simulation, confirming that the protein remains within a native-state ensemble.

Figure 4.

Root-mean-square deviations (RMSDs) of the C_α backbone carbon atoms of ubiquitin (excluding the flexible tail, residues 71–76) with respect to the crystal structure for 50 independent trajectories as obtained with the CPU implementation and the GPU implementation of PMEMD using different precision models.

Figure 5.

Root-mean-square fluctuations (RMSFs) of the C_α backbone carbon atoms of ubiquitin residues 71–76 with respect to the crystal structure for 50 independent trajectories of 100 ns length as obtained with the CPU implementation and the GPU implementation of PMEMD using different precision models.

The situation is very different for the SPSP precision model of the GPU implementation. While approximately half of the trajectories show a similar behavior and stability as the trajectories obtained with the other precision models and the reference CPU implementation of PMEMD, the remaining trajectories experience a very large increase in the RMSD values (Figure 4) and a corresponding increase in the RMSF values (Figure 5). The reason for this behavior is that the numerical noise introduced in the simulations due to rounding errors can lead to an accumulation of errors such that ubiquitin starts to unfold. This is accompanied by an increase in R_g (see Supporting Information) and is also reflected in the large RMSF values of the residues close to the termini of the protein. Since it cannot be predicted whether a simulation using the SPSP precision model will be stable or not, no judgment can be made whether the results obtained are meaningful. The GPU implementation of PMEMD should thus only be used with the DPDP and the SPDP precision models. On the basis of the results shown here, we recommend the use of the mixed-precison SPDP model since the numerical results obtained are comparable with those obtained with the full double precision DPDP model but at significantly reduced computational cost.

6. Conclusions and outlook

We presented a framework for the acceleration of classical molecular dynamics simulations on graphical processing units within the PMEMD program of the software package AMBER. In this contribution, we described the efficient and highly precise implementation of implicit solvent generalized Born molecular dynamics simulations realizing performance that exceeds that achievable on any current conventional supercomputer. The implementation supports serial runs on a single NVIDIA GPU or parallel runs across multiple GPUs using MPI. Performance for moderately sized systems can exceed 100 ns per day, making microsecond or longer simulations routine on deskside workstations. For large systems, the performance differential between our GPU code and the CPU implementation increases significantly. A GB simulation of the nucleosome running on just one NVIDIA M2090 GPU completes in two weeks what a current high-end workstation would take nine months to run using CPUs. This massive performance increase for minimal investment in hardware will transform the traditional molecular dynamics workflow, providing a platform for sustained innovation.

The implementation is transparent to the end user and does not require any specialized knowledge beyond that required to run the traditional CPU code. Our GPU implementation supports the majority of the features provided by the CPU implementation including the AMBER and CHARMM families of biomolecular force fields. It reads traditional AMBER input and writes standard AMBER output. We have developed a hybrid precision model for floating point arithmetic termed SPDP that provides performance close to full single-precision calculations but retains energy drifts in constant energy MD simulations and structural properties of proteins for long time scale MD simulations equivalent to what is achievable with full double precision. Energy conservation with our hybrid SPDP model is approximately 1 to 2 orders of magnitude better than what has been published for other similar GPU implementations of molecular dynamics. Simulation size is limited by the memory available on GPU cards, which at the time of writing is at maximum 6 GB corresponding to approximately 54 000 atoms.

The current cost benefits of GPUs are enticing, and this is driving both soft- and hardware development at a rapid pace. In a few short years, GPU-based MD codes have evolved from proof-of-concept prototypes to the production level AMBER GPU implementation we described here. With GPUs becoming ubiquitous in workstations and also as accelerators in high-performance computing (HPC) platforms, the impact of our implementation on the field of molecular dynamics is broad and transformative. A GPU accelerated implementation of the particle mesh Ewald (PME) algorithm for explicit solvent calculations is also available in AMBER 11 as described in another publication.¹³ This, along with future support for advanced features including accelerated MD (aMD), umbrella sampling, replica exchange MD (REMD), thermodynamic integration (TI), polarizable force fields, and constant pH simulations means the use of GPUs is a viable alternative to traditional supercomputers for classical molecular dynamics simulations.

Supporting Information Available

A list of GPU synchronization routines and AMBER input files used for the performance tests of section 4, for the validation of the accuracy of single point forces of section 5.1, for the validation of energy conservation of section 5.2, and for the validation of the numerical accuracy of structural properties of section 5.3. Plots showing the energy conservation for the trajectories of TRPCage, ubiquitin, and apo-myoglobin for the different precision models and time steps of 0.5, 1.0, and 2.0 fs. Plots showing the radius of gyration R_g for the ubiquitin simulations of section 5.3. This material is available free of charge via the Internet at http://pubs.acs.org/.

The authors declare no competing financial interest.

Author Present Address

^∥ Unilever Centre for Molecular Science Informatics, Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, United Kingdom

Author Present Address

^⊥ Department of Chemistry and Biochemistry, Boise State University, 1910 University Drive, Boise, Idaho 83725−1520, United States