Abstract
The acoustic startle reflex (ASR), a defensive response, is a contraction of the skeletal and facial muscles in response to an abrupt, intense (>80 db) auditory stimulus, which has been extensively studied in rats and humans. Prepulse inhibition (PPI) of ASR is the normal suppression of the startle reflex when an intense stimulus is preceded by a weak non-starting pre-stimulus. PPI, a measure of sensory motor gating, is impaired in various neuropsychiatric disorders, including schizophrenia, and is modulated by cognitive and emotional contexts such as fear and attention. We have modeled the fear modulation of PPI of ASR based on its anatomical substrates and taking into account data from behaving rats and humans. The model replicates the principal features of both phenomena and predicts underlying neural mechanisms. In addition, the model yields testable predictions.
Keywords: Acoustic startle reflex, Prepulse inhibition, Fear modulation, PPI computational model
1 Introduction
The startle reflex occurs in response to intense and abrupt auditory, visual or tactile stimuli. The focus of our model is on the acoustic startle reflex (ASR). The startle reflex is suppressed when an intense stimulus is preceded by a weak non-starting prestimulus. In rats, PPI is severely reduced after manipulations of limbic cortex, striatum, pallidum or pontine tegmentum (Fendt et al. 2001).
PPI of the ASR has been extensively studied; in particular, there exists an extensive neuropharmacological literature associated with the disruption, inhibition, and facilitation of PPI (Bast et al. 2001; Braff et al. 2001; Depoortere et al. 1997; Geyer et al. 2001), and computational modeling (Leumann et al. 2001; Schmajuk et al. 2006).
Physical, emotional, or cognitive states can modify PPI through the activity in cortical and subcortical structures. There is evidence for the modulation of PPI of ASR due to emotional contexts (Li et al. 2009; Winslow et al. 2002). Processing structures for fear (Grillon 1998; Grillon et al. 1997) and attention (Heekeren et al. 2004; Lang et al. 1990) and their influence on the activity of the nuclei related or connected to PPI pathway have been extensively studied.
This study will focus on a continuum of states that span from extreme emotional fear to extreme security. These two extreme states are incompatible, but between these extremes, intermediate states occur with varying degrees of fear and security.
We will postulate that separate groups of neurons in amygdala are active in the extreme states and develop a model of the fear regulation of PPI, which itself modulates ASR. The model will display the major characteristics observed in these phenomena and will predict general features of the biological network responsible for this behavior.
2 Models
2.1 Model neural network for acoustic startle reflex and prepulse inhibition
The models for ASR and PPI presented in this study are based on neuroanatomical studies of the biological substrates. ASR pathway in the bottom line of Fig. 1 starts from the cochlea (C), through the cochlear root nucleus (CRN) (Lee et al. 1996; Koch et al. 1997) to the nucleus reticularis pontine caudalis (NRPC) (Koch et al. 1992), and to the motor neurons (MN) at the spinal level. These connections are excitatory. PPI pathway begins at the projection from the CRN and dorsal cochlear nucleus to the inferior colliculus (IC) (Leitner et al. 1985; Li et al. 1998), continues to the superior colliculus (SC) (Swerdlow 1992; Swerdlow et al. 2001) to the pontine tegmental nucleus (PTN) (Swerdlow and Geyer 1993), and ends at the NRPC (Fendt et al. 2001). This last connection is inhibitory, and the others are excitatory. The central issue is the slower flow of prepulse information through the PPI pathway, such that the faster flow of the startle pulse signal through its pathway, just two synapses between the cochlea and the motoneurons, converges at the same time at the nucleus NRPC (Koch et al. 1992), responsible for the output of ASR response. Besides, the model meets the goal of reproducing accurately ASR response and PPI effect as determined by the intensities of the acoustic stimuli and the time interval durations.
Fig. 1.
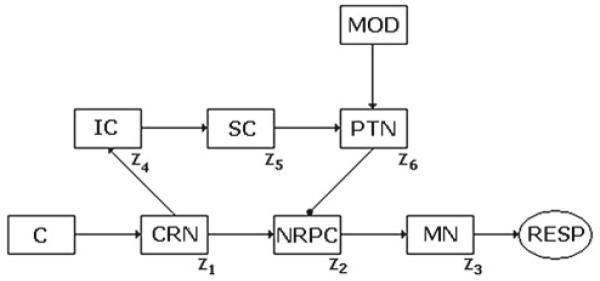
Network for ASR and PPI: C cochlea, CRN cochlear root nucleus, NRPC nucleus reticularis pontine caudalis, IC inferior colliculus, SC superior colliculus, PTN pontine tegmental nucleus, MN motor neurons, RESP motor response, MOD modulatory network
An outline of the model network is shown in Fig. 1, where every neuronal nucleus is represented by a unique neuron, the activity, state, or dynamics of which is taken close enough to a representative state of the whole assembly of neurons in that nucleus. It is usual in computational neuroscience to develop models in which it is not necessary to simulate a neural nucleus or an entire natural neural population through a much smaller model neural assembly. For some purposes, for instance, particular simple information processes, not complex processing, there are not compelling reasons to consider the internal dynamics of these subsystems since the essentials can be captured using a very simple model, with an appropriate dimensionality and accurate results, as can be seen from this study and other studies too.
The modulatory network proposed projects onto PTN from amygdala. This pathway provides an output related with the emotional context emerging from cortical structures within the brain. A model of the modulatory structure (MOD) in Fig. 1 is developed later in this article.
At the level of CRN, acoustic stimuli that exceed a threshold corresponding to 80–85 dB (Koch 1999) are transmitted as a startle signal for triggering ASR in NRPC. Weaker stimuli (<85 dB) are sent to IC for a more complex processing. The prepulse, non-triggering ASR by itself, temporarily inhibits ASR pathway by means of a loop through IC, SC, and PTN. Stronger stimuli (>85 dB) are prevented from propagating through the loop.
There is a critical time interval, called the lead time interval T or the interstimulus interval, between 20 and 800 ms in rodents (Hoffman and Ison 1980; Yeomans et al. 2006; Plappert et al. 2004) or between 45 and 2,020 ms in monkeys (Winslow et al. 2002), between the prepulse onset and the pulse onset, relation (8), which comes from the transmission time difference between PPI pathway and ASR pathway, converging at the NRPC. The strongest inhibition of ASR occurs when the prepulse, with 10–30-ms duration, precedes the startle stimulus by the lead interval (Swerdlow 1992). The modulatory signal, named F, coming from amygdala in the emotional regulatory network projecting onto PTN, will be examined after establishing the dynamics of ASR and PPI.
The mathematical model developed in this study employs mean firing rates as variables describing the neuronal nuclei states, which are thought to be representative states among those corresponding to the neuronal assemblies forming every nucleus. The dynamics of the model for PPI of ASR based on mean firing rates z j is summarized in Eqs. (1)–(6). These equations arise from the basic integrate-and-fire model, Lapicque (1907): written here in terms of mean firing rates. Equation (1) describes nucleus 1 (CRN) activity and the dependence of nucleus 1 activity on the stimulus x through a fraction term, sigmoidal in shape, and resembling the Naka–Rushton response–stimulus functions. Equation (2) shows nucleus 2 (NRPC) activity and the excitatory action of nucleus 1 if nucleus 1 activity stays above the threshold a, and the inhibitory action of nucleus 6 on nucleus 2. Equation (3) depicts nucleus 3 (MN) as well as the afferent excitatory projection from nucleus 2. Equation (4) determines nucleus 4 (IC) activity and the excitatory action of nucleus 1 on nucleus 4, if nucleus 1 activity stays below the threshold a. Equation (5) defines nucleus 5 (SC) activity and the excitatory action of nucleus 4 on nucleus 5. Equation (6) explains nucleus 6 (PTN) activity and the excitatory action of nucleus 5 on nucleus 6, along with the modulatory factor F, describing the emotional neural circuit modulatory influence to be considered later.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where z1 is associated to the CRN, z2 to the NRPC, z3 to MN, z4 to IC, z5 to SC, and z6 to PTN. Notations P1 and P2 correspond to the prepulse and pulse intensities, with durations, (T2 – T1) and (T4 – T3), being 30 ms in our particular simulations. Relation (7) represents the successive occurrence of the prepulse and pulse at T1 and T3, respectively, one after another. Constants A, B, C, and D are the semisaturation values for the fractions where they are, which are similar in shape to the Naka–Rushton sigmoidal functions (Naka and Rushton 1966). Constant b determines the maximum slope for the term where it is in. Constant a acts as a threshold for the terms where it appears in, taking into consideration the definition given for the suffix + in the relation (9). We added noise as a background signal in z1 using a uniform distribution with a mean value reaching a tenth of the maximum value.
The parameters values are as follows: Semisaturation constants:
For some neurons/units in this model, not directly connected to the stimuli source but located as internal units (see Eqs. (3) and (5)), it is possible to simplify the transfer function to the linear identity function because it can be considered that these neurons/units responses fall in the first quasi-linear segment of a sigmoid function, and besides, there is no concern on an unbounded growing external stimulus.
Prepulse and pulse intensities:
Threshold a, slope b, and time constants:
The ASR pathway supports a reflex answer to possible aversive or dangerous stimuli, and therefore it has to be a fast pathway, ensuring the shortest latency motor response observed in the startle reflex. That is the reason for having τ1 = 10 ms in this 3-synapses circuit. On the other hand, the prepulse inhibition (PPI) pathway is participating in protecting a mild prepulse processing from disrupting by second pulses, and consequently, it has to provide an appropriate time-window delay for coinciding and inhibiting the second signal at the NRPC level in the ASR pathway. That is the reason for having τ2 = 15 ms in two synapses out of four in the PPI circuit.
The CRN unit has a sigmoid transfer function. For x = A, the transfer function reaches half of its maximum value, i.e., 0.5. Stimulus x runs over the interval [10–120] dB . Then, for the transfer function to easily reach values around 1 for stimulus values in the superior half of the interval, i.e., [60–120] dB, the semi-saturation constant A has to have a value much smaller than 60.
This is expected from the CRN sensibility for acoustic stimuli intensities inside the interval [0,120] dB.
The semisaturation constant B value determines that nucleus 2, NRPC, responds with short attenuation and high sensibility to the afferent projection from nucleus 1, as long as this one surpasses threshold a. Semisaturation constant C value, along with slope b, allows the inhibition signal from nucleus 6, PTN, onto nucleus 2, NRPC—studying as a modulatory factor in reducing nucleus 2 activity, as seen from the experimental data (Fendt et al. 2001) about PPI of ASR. The unit representing the IC, equation (4) is receiving an excitatory projection from the CRN, and is the gate for the PPI pathway. As with other units not connected with the acoustic source signal, its semi-saturation constant C has a value smaller than 0.5, since its afferent is the CRN activity value constrained to be smaller than 1.0. The same applies for NRPC and PTN. Semisaturation constant D value provides nucleus 6, PTN, with a high sensitivity to the afferent signal coming from nucleus 5, SC.
Factor F in Eq. (6) establishes the modulation on PPI due to emotional contexts, processed by the cortex or by subcortical nuclei associated or connected to the limbic cortex, such as the amygdala complex. Nucleus 3, representing MN in the brain stem and the spinal cord, MN, finally projects the motor behavior’s signal onto the face and body skeletal muscles, expressing the startle reflex.
As mentioned before, ASR pathway engages just two nuclei between cochlea and MN in the spinal cord: the CRN and the nucleus reticularis pontine caudalis, NRPC. This small number of synapses is expected from a neural circuit involved into a reflex response.
The pathway carrying out the prepulse responsible for PPI involves IC, SC, and PTN. These nuclei are represented in the model by units 4, 5, and 6. In this model, we propose that IC does not process stimuli triggering ASR. This hypothesis appears in Eq. (4) with the presence of the threshold a. Nuclei 5 and 6 play the role not only of relaying units but also processing units for the signals coming from the modulatory network, as it will be seen later.
2.2 Model neural network for modulation of PPI
PPI is affected by emotional states, and specifically in different ways by fear conditioning and by innate fear stimuli (Ishii et al. 2010; Grillon 1998; Grillon et al. 1997). Fear conditioning has been studied as a source of enhancement of PPI (Ishii et al. 2010) while innate fear appears to be related with the potentiation of ASR and the attenuation of PPI (Davis 2006). PPI is considered a sensorimotor gating mechanism protecting the processing of the first weaker signal (prepulse) from disruptive interruptions produced by the stronger signal (pulse). PPI is enhanced under fear conditioning probably because the subjects become more attentive to detect, recognize, and process a fear source in weak stimuli, once the subjects have established context memories associated to aversive situations. On the other hand, innate fear seems to trigger a potentiation of the reflex defensive responses. In this model, innate fear is represented as a continuous variable taking values over some range which might correspond in human subjects to recordings of blood pressure elevation, perspiration, piloerection, skin electrical conductance, and other objective measures correlated with fear. Keeping this constraint in mind, we developed a simple model of modulation of the PPI. Attenuation of PPI due to an emotional context of fear takes place when amygdala’s activity influences the neural pathway for ASR via projections from amygdala to NRPC or via connections between amygdala and PTN, through nucleus accumbens (Iversen et al. 2000; Wilson 2004). This model considers the last pathway for the amygdala modulation over PPI. There are two ways for affecting PPI of the ASR: modulating the ASR pathway or modulating the PPI pathway. Our unique objective was to consider and model the emotional modulation of PPI via the projection from amygdala to PTN through nucleus accumbens, which is considered here as a relay stage in this process. It was interesting for us to focus on the modulatory network action directly onto the PPI pathway rather than exploring the other way. The PPI pathway is protecting, in some way, the prepulse processing from being disturbed by a disrupting second pulse. That is the importance of this circuit.
A biologically inspired network model for the modulation of PPI is shown in Fig. 2. There is an input unit that provides the emotional context in a very first processing stage, there are two excitatory pools of neurons (EN1 and EN2), two inhibitory pools of units (IN1 and IN2), two additional nuclei, named FIN and FEN, and finally, there is an output unit (O) signal or mean firing rate, which produces the modulatory factor F into the PPI network.
Fig. 2.
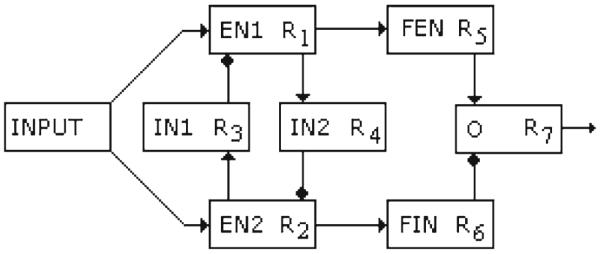
The model neural network for the emotional modulation of the PPI by fear. EN1 and EN2 are excitatory neurons, IN1 and IN2 are the inhibitory interneurons, FIN is an inhibitory unit, and FEN is an excitatory one. O is the output unit
The output firing rates of each unit in the network are denoted by R j . An input nucleus or contextual condition source provides an emotional context, variable y in Eq. (10), which can be thought of as a product of the interactions between cortices or nuclei involved in the first stage of the processing of the emotional charge of the external environment and internal states, and projected to units EN1 and EN2. In this model, the variable y runs over the interval [1,10] where y → 1 describes conditions of the security and the absence of fear and y → 10 describes extreme fear. The output of EN1, R1, is quite sensitive to mild fear conditions and secure states, but the output of EN2, R2, responds strongly to extreme fear conditions. This is represented mathematically by the dynamics in Eqs. (10) and (11), where for y → 1, and θ1 = 5.0, EN1 is more activated than EN2, but for y → 10 and θ1 = 5.0, EN2 is more activated. The units IN1 and IN2 have inhibitory outputs R3 and R4, and receive excitatory inputs from EN2 and EN1, respectively. Thus, EN1 and EN2 reciprocally inhibit each other through IN1 and IN2 inhibitory projections as seen in Fig. 2.
The outputs of units EN1 and EN2, R1 and R2, respectively, have feedforward excitatory inputs to FEN and FIN, and the output neuron O receives excitatory input R5 from FEN and an inhibitory input R6 from FIN. The output O neuron modulates the PPI network.
We propose that EN1 and EN2 correspond to neuronal assemblies in the cingulate cortex, taking into account data from Vogt (2005), and that IN1 and IN2 correspond to local GABAergic interneurons there. FIN and FEN as well as O correspond to nuclei inside the amygdala.
The network’s dynamics is described by the Eqs. (10)–(16):
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
The values chosen for the unitless parameters are: α = 10, θ =0.5, θ1 = 5.0, β = 0.91, and τ = 5.0.
Equation (10) describes the dynamics of nucleus EN1, which responds largely to values of the variable y corresponding to absence of fear or security conditions, and receives an incoming inhibitory signal R3 from nucleus IN1. It also shows a significant recurrence weighed by parameter β. Equation (11) shows the response of nucleus EN2, increasing for values of y corresponding to fear-generating conditions and decreasing for the inhibitory signal R4 from nucleus IN2. As before, there is also an important recurrence in EN2 mediated by parameter β. Values for θ1 and θ are heuristically tuned such that nuclei EN1 and EN2 responses in the interval [0,1], are centered for centered values of the afferent signal y, R3, and R4 through their respective intervals of variation.
Equations (12) and (13) show the activation states R3 and R4 dynamics of the inhibitory nuclei IN1 and IN2 respectively, under their excitatory inputs coming from EN2 and EN1. Equations (14) and (15) represent the dynamics for the relay nuclei FEN and FIN, with excitatory input signals from EN1 and EN2, respectively. Finally, Eq. (16) describes the dynamics of nucleus O, taking into account the excitatory signal from nucleus FEN and the inhibitory one from nucleus FIN. At every equation in the model, we have considered the same heuristics for the role of parameters θ1 and θ. Parameter α value allows a more expanded response interval for nucleus O, needed for the modulatory dynamics on nucleus PTN into PPI network.
3 Results
3.1 Experiments and results from the model for ASR and PPI
We first proved that for prepulse intensities below the threshold of 85 dB, the network model responded with PPI as long as the pulse intensity is above this threshold. Next, we observed how PPI is affected by the lead time interval T (Figs. 3, 4). Finally, we explored how PPI varied with the prepulse intensity (Fig. 5). When the prepulse intensity was 85 dB, the prepulse itself triggered ASR, but for prepulse intensities smaller than the threshold and with the pulse intensity at 85 dB, the PPI as quantified in Eq. (17) followed the expected behavior shown in Fig. 3.
| (17) |
where P is the percent PPI, RPP is the response to an intense pulse after a mild prepulse, and RP is the response to the pulse alone. RP is defined as the maximum activity value in the stimulus interval.
Fig. 3.
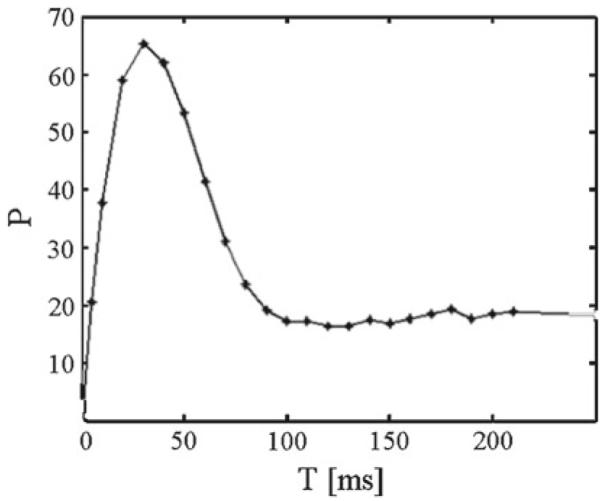
Percent prepulse inhibition P as function of the lead time interval T for pulse intensity set to 85 dB and prepulse intensity to 80 dB
Fig. 4.
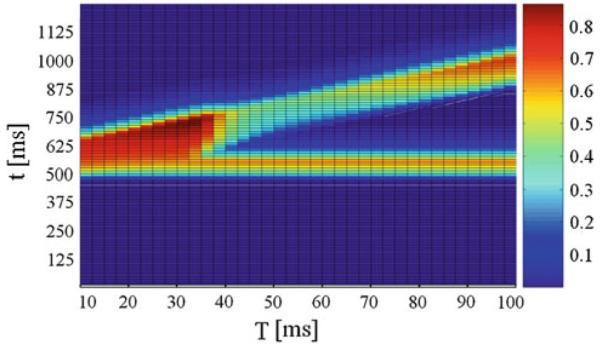
Normalized activity on unit NRPC depending on the lead time interval T and time t. The pulse intensity was set to 85 dB and the prepulse intensity to 80 dB. On the x axis T is the lead time interval. On the y axis t is time
Fig. 5.
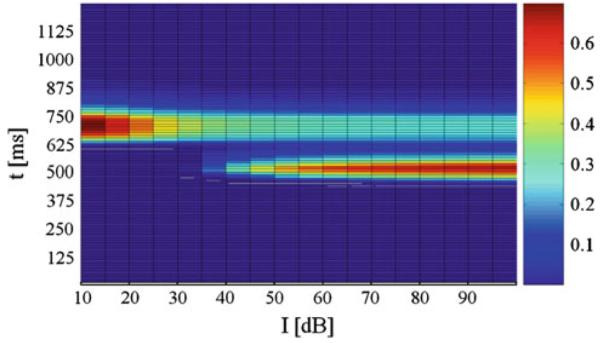
Normalized activity on unit NRPC depending on the prepulse intensity I and time t. The pulse intensity was set to 85 dB and the lead time interval to 40 ms dB. On the x axis, I is the prepulse intensity. On the y axis, t is time
When the lead time interval T or interstimulus interval, was varied, P was maximal in our model at 40 ms, as in Figs. 3 and 4. This replicates the essential features of the PPI of the ASR in rats and humans (Braff et al. 2001; Geyer et al. 2001). As it can be seen from Figs. 3 and 4, there was a decrease in P for lead intervals lower than 35 ms and higher than 100 ms and, consequently, an increasing activity level on NRPC was observed as P decreased. Besides, this model shows a decreasing response on NRPC to the pulse with increasing prepulse intensities (Fig. 5), i.e., a greater value in P for increasing prepulse intensities, consistent with experimental results (Hoffman and Searle 1965).
3.2 Experiments and results from the model modulatory network
The input to the modulatory network varied from 1 to 10, corresponding to emotional conditions ranging from security to fear. For each value of y, the output neuron O produced a mean firing rate R7 that determined the modulatory factor F into the PTN nucleus, given by the Eq. (18). The curve correlating the y values and the F modulatory factor values is shown in Fig. 6.
| (18) |
Equation (18) describes the modulatory factor F onto the PTN nucleus (Fig. 1), which is the bridge between PPI network and ASR network.
Fig. 6.
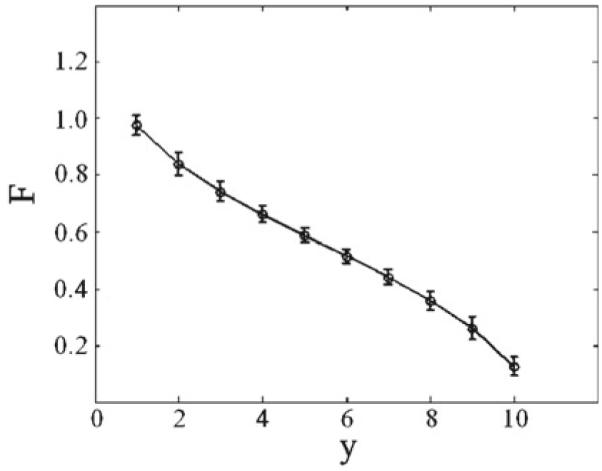
Response from the output neuron O in the modulatory neural network depending on the arbitrary fear scale parameter
The modulatory neural network proposed complies with the previously established criteria, type of connectivity, and interactivity seen in the brain, and the same can be experimentally tested.
The network performed correctly because of the reciprocal inhibitory interaction between EN1 and EN2. The output unit received the inhibitory input from FIN and excitatory input from FEN, which produced the expected output. The effect of the signal R7 on PTN is given through parameter F in Eq. (6). Figure 7 shows the results provided by our models for small values of F approaching 0.
Fig. 7.
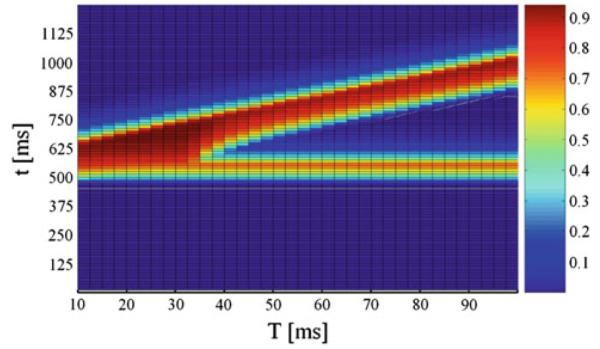
Normalized activity on unit NRPC depending on the lead time interval T and time t under modulatory factor F = 0.1. The pulse intensity was set to 85 dB and the prepulse intensity to 80 dB. On the x axis, T is the lead time interval. On the y axis, t is time
For F = 1.0, PPI of ASR takes place without attenuation as seen before in Figs. 4 and 5. For this value of F, security conditions are in place, corresponding to bottom values (y → 1) of y, as shown in Fig. 6, and according with experimental data showing normal PPI under emotional states relating with security or tranquility (Swerdlow 1992). Our model network keeps the dependence form of PPI on the lead temporal interval, showing the greatest inhibition of ASR for a lead interval of 40 ms, as mentioned before in Swerdlow (1992). The model network shows a decreasing response to the pulse with increasing prepulse intensities, as seen above. For F = 0.1, PPI of ASR shows sharp attenuation or disruption as shown in Fig. 7. For this value of F, fear-related stimuli are acting, corresponding to top values (y → 10) of y, as shown in Fig. 6. These results agree with observations and experimental data, showing strong attenuation of PPI under fear-related emotional states (Winslow et al. 2002; Lang et al. 2000).
4 Conclusions and discussion
The attenuation of PPI of the startle reflex due to innate fear occurs when some activity in the amygdala influences indirectly on the neural circuit involved in the startle reflex via the projection from the amygdala to the Caudal Pontine Reticular nucleus (NRPC). There are also anatomical connections between the amygdala and the pedunculo PTN via the nucleus accumbens involved in the PPI (Iversen et al. 2000; Wilson 2004).
At the core of our model is the exclusion between emotional neural representations associated to opposed emotions or feelings, like extreme fear and absolute security, and the coexistence of intermediate emotional states between those extremes, along an arbitrary scale, proposed for quantifying a continuous variation in the intensity of superpositions of those emotions.
The dynamic model defined by Eqs. (10)–(16) describes the processing in time of physiological conditions [variable y in (10)] associated with triggering an innate emotional state of fear or security. The deployment or display of any innate emotional state is not instantaneous; it requires the engagement of the particular neural substrates necessary for processing those activating conditions for this emotional state. The relevance of this detailed dynamic model lies in applying a well-known canonical circuit of competitive structures (Shepherd 2004) encoding different parts of the full range of the variable y with different degrees of sensitivity and obtaining a suitable modulatory parameter F.
The emotional modulation of PPI coming from amygdala and cingulate cortex via PTN as shown in Fig. 1 first requires the processing of the emotional context in which ASR and PPI would take place. Consequently, the modulatory factor F in Eq. (6) does not appear instantaneously since it exists or comes into existence from the above mentioned dynamics depicted by Eqs. (10)–(16). Therefore, the relationship between y and F shown in Fig. 6 should not be considered as an instantaneous functional relationship but as a causal relationship in time between them. Taking into consideration what is mentioned here, this implies as a necessary assumption that in absence of a particular innate fear emotional condition, the subject experiences an emotional state of security as a background emotional condition or pre-existing emotional condition which, can be altered at any moment by emotional processes responding to particular stimuli.
The goal was met in the modulatory network by introducing two nuclei EN1 and EN2 with mutual inhibition, each one sensitive to a different extreme of the fear-security scale. This type of interaction between nuclei is common when there are two incompatible neural state representations. Describing the regulation of the PPI process as a gain modulation at the level of the Pedunculo PTN reproduces the natural behavior observed in rats and humans. The functional achievement of the proposed two models based on simple but plausible assumptions over the interactions between the neural substrates, described by dynamic equations, allows for a broader theoretical approach for research on sensorimotor gating of the startle reflex and its emotional modulation. Although the mathematical models in this study do not constitute the ultimate approximation, their resemblance to neurobiology is closer than other models seen in the specialized literature (Schmajuk et al. 2006; Leumann et al. 2001). Besides, different possible theoretically driven speculations about the neurophysiology implied can be experimentally tested; furthermore, neuropharmacology facts and results could be connected with parameters in our models. Future study can be devoted to model the well-known modulations of PPI and ASR by different drugs considering detailed dynamics into the parameters of this model.
Acknowledgments
We thank the three anonymous reviewers for their comments. Their acute review of our manuscript helped us improve the same significantly.
Abbreviations
- ASR
Acoustic startle reflex
- PPI
Prepulse inhibition
- C
Cochlea
- CRN
Cochlear root nucleus
- NRPC
Nucleus reticularis pontine caudalis
- MN
Motor neuron
- IC
Inferior colliculus
- SC
Superior colliculus
- PTN
Pontine tegmental nucleus
- AM
Amygdala
- MOD
Modulatory structure
Contributor Information
David Fernando Ramirez-Moreno, Departamento de Física, Universidad Autonoma de Occidente, Cali, Colombia.
Terrence Joseph Sejnowski, Computational Neurobiology Laboratory, Howard Hughes Medical Institute, Salk Institute, La Jolla, CA 92037, USA; Division of Biological Sciences, University of California San Diego, La Jolla, CA 92093, USA.
References
- Bast T, et al. Hyperactivity, decreased startle reactivity, and disrupted prepulse inhibition following disinhibition of the rat ventral hippocampus by the GABAA receptor antagonist picrotoxin. Psychopharmacology. 2001;156(2–3):225–233. doi: 10.1007/s002130100775. [DOI] [PubMed] [Google Scholar]
- Braff DL, et al. Human studies of prepulse inhibition of startle: normal subjects, patient groups, and pharmacological studies. Psychopharmacology (Berl) 2001;156:234–258. doi: 10.1007/s002130100810. [DOI] [PubMed] [Google Scholar]
- Davis M. Neural systems involved in fear and anxiety measured with fear—potentiated startle. Am Psychol. 2006;61:741–756. doi: 10.1037/0003-066X.61.8.741. [DOI] [PubMed] [Google Scholar]
- Depoortere R, et al. Potentiation of prepulse inhibition of the startle reflex in rats: pharmacological evaluation of the procedure as a model for detecting antipsychotic activity. Psycopharmacology (Berl) 1997;132(4):366–374. doi: 10.1007/s002130050357. [DOI] [PubMed] [Google Scholar]
- Fendt M, et al. Brain stem circuits mediating prepulse inhibition of the startle reflex. Psychopharmacology. 2001;156:216–224. doi: 10.1007/s002130100794. [DOI] [PubMed] [Google Scholar]
- Geyer MA, et al. Pharmacological studies of prepulse inhibition models of sensorimotor-gating deficits in schizophrenia: a decade in review. Psychopharmacology. 2001;156:117–154. doi: 10.1007/s002130100811. [DOI] [PubMed] [Google Scholar]
- Grillon C. Effect of darkness on acoustic startle in Vietnam veterans with PTSD. Am J Psychiatry. 1998;155:812–817. doi: 10.1176/ajp.155.6.812. [DOI] [PubMed] [Google Scholar]
- Grillon C, et al. Darkness facilitates the acoustic startle reflex in humans. Biol Psychiatry. 1997;42(6):453–460. doi: 10.1016/S0006-3223(96)00466-0. [DOI] [PubMed] [Google Scholar]
- Heekeren K, et al. Attentional modulation of prepulse inhibition: a new startle paradigm. Neuropsychobiology. 2004;49:88–93. doi: 10.1159/000076416. [DOI] [PubMed] [Google Scholar]
- Hoffman HS, Ison JR. Reflex modification in the domain of startle: I. Some empirical findings and their implications for how the nervous system processes sensory input. Psychol Rev. 1980;87:175–189. [PubMed] [Google Scholar]
- Hoffman HS, Searle JL. Acoustic variables in the modification of startle reaction in the rat. J Comp Physiol Psychol. 1965;60(1):53–58. doi: 10.1037/h0022325. [DOI] [PubMed] [Google Scholar]
- Ishii D, et al. Enhancement of acoustic prepulse inhibition by contextual fear conditioning in mice is maintained even after contextual fear extinction. Prog Neuropsychopharmacol Biol Psychiatry. 2010;34:183–188. doi: 10.1016/j.pnpbp.2009.10.023. [DOI] [PubMed] [Google Scholar]
- Iversen S, et al. Emotional states and feelings. In: Kandel E, Schwartz JH, Jessell TM, editors. Principles of neuroscience. 4th edn McGraw-Hill; New York: 2000. pp. 982–998. [Google Scholar]
- Koch M. The neurobiology of startle. Prog Neurobiol. 1999;59:107–128. doi: 10.1016/s0301-0082(98)00098-7. [DOI] [PubMed] [Google Scholar]
- Koch M, et al. Loss of the acoustic startle response following neurotoxic lesions of the caudal pontine reticular formation: possible role of giant neurons. Neuroscience. 1992;49:617–625. doi: 10.1016/0306-4522(92)90231-p. [DOI] [PubMed] [Google Scholar]
- Koch M, et al. The acoustic startle response in rats—circuits mediating evocation, inhibition and potentiation. Behav Brain Res. 1997;89:35–49. doi: 10.1016/s0166-4328(97)02296-1. [DOI] [PubMed] [Google Scholar]
- Lang PJ, et al. Emotion, attention, and the startle reflex. Psychol Rev. 1990;97:377–395. [PubMed] [Google Scholar]
- Lang PJ, Davis M, Ohman A. Fear and anxiety: animal models and human cognitive psychophysiology. J Affect Disord. 2000;61:137–159. doi: 10.1016/s0165-0327(00)00343-8. [DOI] [PubMed] [Google Scholar]
- Lapicque L. Recherches quantitatives sur l’excitation électrique des nerfs traitée comme une polarisation. J Physiol Pathol Gen. 1907;9:620–635. [Google Scholar]
- Lee Y, et al. A primary acoustic startle reflex pathway: obligatory role of cochlear root neurons and the nucleus reticularis pontis caudalis. J Neurosci. 1996;16(11):3775–3789. doi: 10.1523/JNEUROSCI.16-11-03775.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leitner DS, et al. Role of the inferior colliculus in the inhibition of acoustic startle in the rat. Physiol Behav. 1985;34:65–70. doi: 10.1016/0031-9384(85)90079-4. [DOI] [PubMed] [Google Scholar]
- Leumann L, et al. A neural network approach to the acoustic startle reflex and prepulse inhibition. Brain Res Bull. 2001;56(2):101–110. doi: 10.1016/s0361-9230(01)00607-4. [DOI] [PubMed] [Google Scholar]
- Li L, et al. Prepulse inhibition following lesions of the inferior colliculus: prepulse intensity functions. Physiol Behav. 1998;65:133–139. doi: 10.1016/s0031-9384(98)00143-7. [DOI] [PubMed] [Google Scholar]
- Li L, et al. Top-down modulations of prepulse inhibition of the startle reflex in humans and rats. Neurosci Behav Rev. 2009;33:1157–1167. doi: 10.1016/j.neubiorev.2009.02.001. [DOI] [PubMed] [Google Scholar]
- Naka KI, Rushton WAH. S-potentials from luminosity units in the retina of fish (Cyprinidae) J Physiol. 1966;185:587–599. doi: 10.1113/jphysiol.1966.sp008003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plappert C, Pilz P, Schnitzler H. Factors governing prepulse inhibition and prepulse facilitation of the acoustic startle response in mice. Behav Brain Res. 2004;152:403–412. doi: 10.1016/j.bbr.2003.10.025. [DOI] [PubMed] [Google Scholar]
- Schmajuk NA, et al. Startle and prepulse inhibition as a function of background noise: a computational and experimental analysis. Behav Brain Res. 2006;170:182–196. doi: 10.1016/j.bbr.2006.02.021. [DOI] [PubMed] [Google Scholar]
- Shepherd GM. Introduction to synaptic circuits. In: Shepherd GM, editor. The synaptic organization of the brain. 5th edn Oxford University Press; Oxford: 2004. [Google Scholar]
- Swerdlow NR, Geyer MA. Prepulse inhibition of acoustic startle in rats after lesions of the pedunculopontine tegmental nucleus. Behav Neurosci. 1993;107:104–117. doi: 10.1037//0735-7044.107.1.104. [DOI] [PubMed] [Google Scholar]
- Swerdlow NR, Caine SB, Braff DL, Geyer MA. The neural substrates of sensorimotor gating of the startle reflex: a review of recent findings and their implications. Psychopharmacology. 1992;6:176–190. doi: 10.1177/026988119200600210. [DOI] [PubMed] [Google Scholar]
- Swerdlow NR, et al. Neural circuit regulation of prepulse inhibition of startle in the rat: current knowledge and future challenges. Psychopharmacology. 2001;156:194–215. doi: 10.1007/s002130100799. [DOI] [PubMed] [Google Scholar]
- Vogt BA. Pain and emotion interactions in subregions of the cingulated gyrus. Nat Rev Neurosci. 2005;6:533–544. doi: 10.1038/nrn1704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson C. Basal ganglia. In: Shepherd G, editor. The synaptic organization of the brain. 5th edn Oxford Press; Oxford: 2004. pp. 361–415. [Google Scholar]
- Winslow JT, Parr LA, Davis M. Acoustic startle, prepulse inhibition, and fear-potentiated startle measured in rhesus monkeys. Biol Psychiatry. 2002;51:859–866. doi: 10.1016/s0006-3223(02)01345-8. [DOI] [PubMed] [Google Scholar]
- Yeomans JS, et al. Midbrain pathways for prepulse inhibition and startle activation in rats. Neuroscience. 2006;142:921–929. doi: 10.1016/j.neuroscience.2006.06.025. [DOI] [PubMed] [Google Scholar]


