Analysis of gene expression levels in individual bacterial cells without image segmentation

Abstract

Studies of stochasticity in gene expression typically make use of fluorescent protein reporters, which permit the measurement of expression levels within individual cells by fluorescence microscopy. Analysis of such microscopy images is almost invariably based on a segmentation algorithm, where the image of a cell or cluster is analyzed mathematically to delineate individual cell boundaries. However segmentation can be ineffective for studying bacterial cells or clusters, especially at lower magnification, where outlines of individual cells are poorly resolved. Here we demonstrate an alternative method for analysing such images without segmentation. The method employs a comparison between the pixel brightness in phase contrast vs. fluorescence microscopy images. By fitting the correlation between phase contrast and fluorescence intensity to a physical model, we obtain well-defined estimates for the different expression levels of gene expression that are present in the cell or cluster. The method reveals the boundaries of the individual cells, even if the source images lack the resolution to show these boundaries clearly.

Introduction

The measurement of gene expression activity in individual cells provides information that is unavailable from measurements of population-averaged expression [1]. One very important example is the study of noise and heterogeneity in gene expression, where even clonal cells in identical chemical and physical environments can express significantly different phenotypes. Heterogeneous gene expression in a population of cells can play an important role in cellular development and decision making, information processing, and pathogenicity [2,3]. The use of fluorescent reporter proteins allows experimenters to observe and record these different levels of gene activation present in a population of cells. By analyzing and fitting the resulting population-wide distributions, researchers can gain insight into how individual regulatory networks manage or even exploit noise in gene expression, and how global factors such as ribosome abundance affect expression across the genome [4].

Extracting expression information from microscopy images of single cells requires appropriate algorithms for image analysis. Analysis starts with correct recognition of the set of image pixels that is associated with an individual cell. In two-dimensional images that contain closely proximal or clustered cells, accurate location of boundaries or edges among the clustered cells is a technical challenge. This process is known as segmentation [5]. A number of different segmentation methods have been described in the literature and old methods are continually being improved. Classical methods of segmentation that remain in wide use include the Otsu method for threshold selection [6] as well as watershed methods [7,8]. Numerical methods such as level set functions can also be applied by evolving active contours to the cell boundaries [9,10]. Such methods are implemented in widely used image analysis software such as CellProfiler [11], and CellID [12].

Bacterial cells, which are typically smaller than eukaryotic cells, can pose particular challenges for single cell analysis. They are often clustered and variable in size or shape, so that boundaries between cells are often poorly resolved except at high magnification. Despite these difficulties, methods have been proposed for distinguishing bacterial shapes such as rods and spheres, and segmentation methods for bacterial images have been described. Sieracki et al. compared a number of different threshold selection methods and concluded that the second derivative of the intensity profile gave accurate estimates for edge positions and brightnesses for several bacterial cell types [13]. Massana et al. presented useful methods for measuring bacterial size and volume from two-dimensional images [14]. CMEIAS software, invented for the classification and analysis of bacterial morphotypes, uses this calculation to identify up to eleven bacterial shapes and to measure roundness, compactness, and Fourier descriptors [15,16]. Another example of a bacterial segmentation is the active contour, which was used for cocci cell classification [17]. Wang et al. performed image segmentation using hybrid filters and masking [18].

Some image analysis algorithms employ sub-pixel resolution to distinguish the boundaries of cell clusters. This was initially accomplished by forming an interpolated contour along the cell and defining internal coordinates to differentiate between cells [19]. The use of fluorescence intensity profiles enhances this sub-pixel analysis [20,21]. MicrobeTracker software combines a number of cell segmentation methods as well as cell shape and time-dependent data to resolve individual bacteria within clusters at subpixel resolution [22]. The Schnitzcells package also combines segmentation with temporal tracking [23].

However, these subpixel analysis methods typically require images at 100× magnification. If many cells are to be characterized, this high magnification may necessitate use of motorized stages and focusing equipment. Cell tracking methods have been devised for use at lower magnification, but these have not resolved the cell boundaries within clusters [24]. This raises the question of whether it is possible to extract single-cell expression data from images of bacterial clusters collected at lower resolution. Here we present a simple method for extracting expression levels from cell cluster images without use of a cell segmentation algorithm. The method is based on a combined analysis of phase contrast and fluorescence images of the same bacterial cluster at low magnification. It makes no use of the spatial relationships (proximity, neighbors, contours, etc.) between image pixels. Instead it makes use of the fact that an expressed fluorescent protein (e.g. GFP) tends to diffuse throughout the bacterial cell, so that the concentration of the fluorescent protein at a given pixel has a simple mathematical relationship to the phase contrast intensity of the same pixel. The result is that the method can identify the groups of pixels that are associated with different expression levels (i.e. different cells). We demonstrate this approach by analyzing phase contrast and fluorescence images of bacteria (Streptococcus mutans at 20× magnification) that are expressing green fluorescent protein upon activation of an inducible promoter.

Methods

Principle of the method

The Zernike phase contrast microscope allows an experimenter to use transmitted light to observe objects that do not absorb light but do generate a phase shift in the light that they transmit [25]. Because such “phase objects” affect only the phase, and not the intensity, of the light arriving at the image plane, they create little contrast in a conventional bright field image and are not readily visible unless a stain or dye is applied. The phase contrast microscope makes use of the phase object’s tendency to diffract the plane wave that is incident from the condenser. The phase contrast objective introduces a phase shift (α = ±π/2) into the diffracted light before recombining it with the undiffracted plane wave. Interference between the phase shifted light and the undiffracted plane wave converts the phase variation in the image plane into an intensity variation. The result is drastically improved image contrast that renders the phase object visible.

For measurement of gene expression activity, a reporter such as gfp that encodes a fluorescent protein is often placed under the control of the promoter of interest. The reporter protein generates fluorescence that can be observed in an epiillumination microscope. The experimenter can collect both phase contrast (in transmitted white light) and fluorescence images of the same cell or cluster of cells, and then attempt to count the total reporter protein (i.e. total fluorescence count) within each cell contour that is detected in the corresponding phase contrast image.

Therefore we consider a pair of phase and fluorescence images showing the same N bacterial cells that are expressing a fluorescent reporter protein, where i denotes an individual cell (i = 1 → N). We assume that the fluorescent protein produced within each cell diffuses and spreads uniformly throughout that cell. Then, if a cell i is located at position (x,y) in the image, then the concentration of fluorescent protein at (x,y) is proportional to the total concentration of other cytoplasmic protein and macromolecules at that location. This total concentration is responsible for the optical phase shift ϕ(x,y) (relative to the image background) at that location. Therefore we anticipate that the reporter fluorescence FL(x,y) observed at location (x,y) obeys

$$FL(x,y)=r_i\varphi (x,y)$$ (1)

Here r_i is a coefficient that describes the average concentration of fluorescent reporter in cell i. It measures the activity of the reporter in that cell, and r_i is presumably the same for all the pixels that belong to one cell i. Generally however r_i will take different values for different cells. Equation (1) suggests that, if an image shows several different cells located across a range of (x,y) values, a scatter plot of FL(x,y) vs ϕ(x,y) will consist of several straight lines, where the slope of each line equals one of the expression levels r_i that are present in the imaged cells. Since the intensity of the phase contrast image I(x,y) is a function of _ϕ(x,y), we can also find the different r_i values by analyzing a scatterplot of FL(x,y) vs I(x,y). The following section describes this analysis.

Relation between phase contrast and fluorescence images

Following Born and Wolf [25] we describe the disturbed wave produced by a phase object in the specimen plane, described by the coordinates (x,y), as:

$$\mathrm{F}(x,y)={\mathrm{e}}^{\mathrm{i}\phi (x,y)}$$ (2)

The undisturbed light collected by the microscope objective is passed through a phase plate whose transmission function has an absorption parameter a and a phase shift α:

$$\mathrm{A}=a{\mathrm{e}}^{\mathrm{i}\alpha }$$ (3)

The absorption parameter a < 1 is a fixed parameter of the phase contrast objective (typically a = 0.7-0.8) and provides improved contrast in the image. The sign of the phase shift α determines the appearance of the phase contrast image: In the usual case of positive phase contrast (α = −π/2), phase objects with higher refractive index (relative to background) appear dark against a light background.

The disturbed waves are recombined with the undisturbed (but phase shifted) waves at the image plane to give the phase contrast image, whose intensity is

$$\mathrm{I}(x,y)={\mid \mathrm{C}\mid }^2(a^2+2\{1-a\cos \alpha -\cos \phi (x,y)+a\cos [\alpha -\phi (x,y)]\})$$ (4)

Here C is a constant that depends on the illumination, aperture, and other instrument parameters. For positive phase contrast this reduces to

$$I(x,y)={\mid \mathrm{C}\mid }^2(a^2+2\{1-\cos \phi (x,y)-a\sin \phi (x,y)\})$$ (5)

Inserting Eqn. (1) then gives

$$I(x,y)={\mid \mathrm{C}\mid }^2\left(a^2+2\left\{1-\cos \frac{FL(x,y)}{r_i}-a\sin \frac{FL(x,y)}{r_i}\right\}\right)$$ (6)

Equation (6) shows the relationship between the phase contrast I and fluorescence FL intensities for the image pixels (x,y) of cell i. If the phase shifts ϕ(x,y) are small then a scatter plot of I versus FL for one cell – where each pixel contributes one point to the scatter plot – will be nearly linear. However the presence of the cosine function in Eqn. (5) and (6) can generate significant nonlinearity and curvature in the scatter plot. Figures 1 and 2 below show that when several cells with different expression levels r are present in one image, then Eqn. (6) leads to an I versus FL scatter plot that consists of several distinct curves, where each curve corresponds to one of the r values that are present.

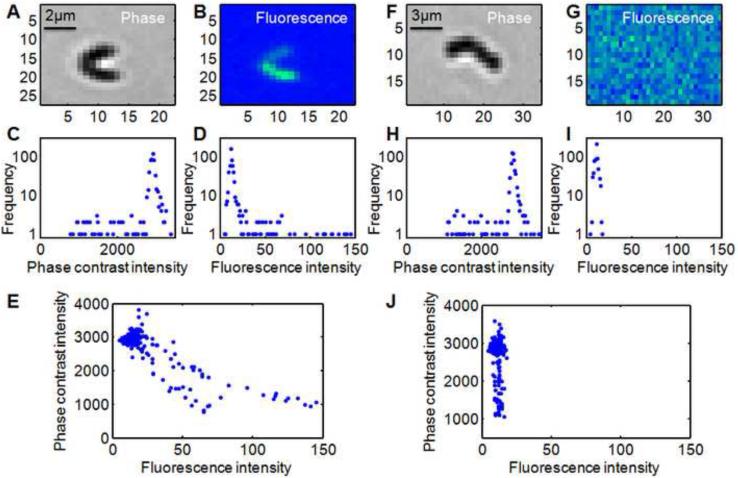
Figure 1.

Analysis of (A-E) reporter “on” and (F-J) reporter “off” clusters of a PcomX::gfp reporter strain of S.mutans at 20× magnification ([XIP]=36 nM). Panels C,H and D,I show the intensity histograms for the phase contrast and fluorescence images respectively. The sharp peak in each histogram results from the uniform background region that surrounds the cell cluster. Panels E and J show the phase-fluorescence scatter plots. Each point in the scatter plot shows the brightness of one pixel as it appears in the phase contrast and fluorescence images.

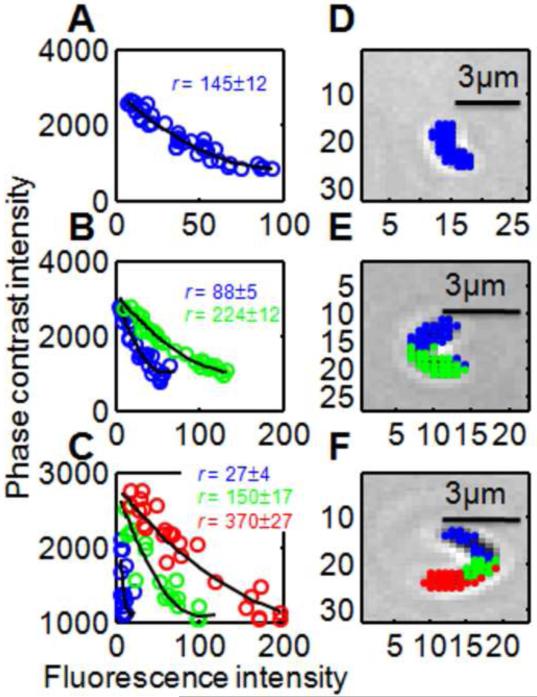
Figure 2.

Data analysis for three subimages showing S.mutans in [XIP] = 36 nM. In the phase-fluorescence scatter plots (panels A,B,C) each point represents a subimage pixel. (Pixels from the image background have been removed by cutoff.) The indicated expression levels r generate the black solid curves, via Eqn. (7). The points in the scatter plots have been color coded according to the curve (ie the r-value) they lie closest to. Panels D,E,F show the original phase contrast images, with the pixels from the scatterplot highlighted according to the same color code as in the scatter plots.

Below we demonstrate this approach by analyzing phase and fluorescence images of Streptococcus mutans cells that express a gfp reporter. Streptococcus mutans is a Gram-positive bacterium that colonizes the surface of the tooth in humans and is of interest as a primary cause of dental caries. The studied strain harbors a plasmid containing PcomX::gfp, so that it expresses the green fluorescent protein GFP upon activation of PcomX. PcomX is the promoter for comX, which controls a set of proteins that are required for the cell to enter the state of genetic competence. The PcomX::gfp reporter can be activated by the addition of exogenous peptide signals, such as the CSP and XIP peptides, that trigger genetic competence in S.mutans [26]. By analyzing images of small clusters of S.mutans adhered to a glass coverslip we can determine the parameters r_i that characterize the heterogeneous PcomX activity in response to XIP.

Preparation of S.mutans

An overnight culture of Streptococcus mutans harboring the PcomX::gfp plasmid was diluted 30× into fresh medium (BHI) and then incubated for 3 hrs, reaching OD = 0.3. Cells were then supplied with a continuous flow of exogenous XIP peptide in defined (FMC) medium while they adhered to the glass coverslip window of a perfusion chamber. The exogenous XIP activates the PcomX::gfp reporter and leads to GFP fluorescence in the cells.

The perfusion chamber was placed on a microscope stage at 33 °C and imaged at low magnification using a Nikon CFI Plan Fluor 20× NA 0.50 phase objective and a TE2000U inverted microscope. Phase and green fluorescence images were collected hourly through the same objective, with a Nikon 96362 zero-shift GFP filter cube used for the fluorescence. Fluorescence exposures were 3 seconds with an Intensilight mercury lamp. Images were collected on a Photometrix CoolSnap HQ2 cooled CCD camera and analyzed in Matlab (The Mathworks, Inc.). A flat field correction is applied to the fluorescence images before analysis.

Data Analysis

Figure 1 shows representative phase contrast and fluorescence images of small clusters of S.mutans cells adhered to glass. Figures 1A (phase) and 1B (fluorescence) appear to show two cells in which PcomX is switched on to different levels. However, as each cell is only ~2 μm (six pixels) in length, the individual cells are poorly resolved in the phase contrast image (Figure 1A). Nevertheless a comparison of the phase (I) and fluorescence (FL) intensities for these clusters shows the behavior anticipated by Eqn. (6): The scatter plot in Figure 1E reveals two distinct curves, corresponding to two values of r_i present in the image. That is, the image shows two cells in which PcomX is activated to different levels. Figures 1F and 1G shows a different cluster with a weak GFP fluorescence that does not rise above the background level. The corresponding scatter plot (Figure 1J) shows a much steeper curve than in Figure 1E, signifying (via Eqn. (6)) a much smaller value of r_i. This is consistent with PcomX being switched off for this cell.

The extraction of r_i values from the S.mutans images was performed as follows:

1. We collected a pair of phase and fluorescence images at 20× showing the same large field of view containing a large number (> 100) of small clusters of cells. This is most easily accomplished using a epifluorescence phase contrast microscope with a zero-shift fluorescence filter cube.

2. The two images were subdivided into a set of phase and fluorescence subimages, each containing one cluster of (typically) 1-3 cells. Each subimage, roughly 25×25 pixels, contains both the cell cluster and some of its surrounding background. Figures 1 and 2 show typical subimages.

3. For Each Subimage, We Generate The Histogram Of Pixel Intensities In Both The Phase And Fluorescence Subimages. The Background Pixels In The Image Contribute A Dominant, Near-Gaussian Peak In Both The Phase I And Fluorescence Fl Histograms (Panels C,D,H,I Of Figure 1). From These Gaussian Peaks We Find The Mean And Standard Deviation Of The Phase I And Fluorescence Fl Background Intensities. This Allows Us To Define A Cutoff That Distinguishes Cell-Associated Pixels From The Surrounding Background.

4. We first offset the fluorescence subimage intensity values by subtracting the mean fluorescence background from all pixels. This produces a subimage in which the fluorescence background has zero average intensity.

   In the phase subimage a cell appears darker than its background. Therefore for each phase subimage we define a cutoff phase intensity I_max at 1.5-2.5 standard deviations below the mean phase contrast background.

   For each subimage we then select those pixels whose phase intensity is below the cutoff phase intensity and whose (offset) fluorescence intensity is above zero. These “thresholded” pixels are presumed to include all pixels that are potentially part of a cell or cluster, as opposed to background.

5. For each subimage we generate the scatterplot of the phase I versus fluorescence FL values for the thresholded pixels. Figure 2 shows that the number of different expression levels r_i present in the subimage is readily determined from these scatterplots.

6. Given the number of expression levels N in the subimage, we then fit the scatterplot to a variant of equation (6)

   $$I(x,y)=A\left(a^2+2\left\{1-\cos \frac{FL(x,y)}{r_i}-a\sin \frac{FL(x,y)}{r_i}\right\}\right)+B$$ (7)

The fit parameters are A and B, which describe the intensity scale and background brightness of the phase images, and the set of expression levels {r_i} (i = 1 → N). (The parameter a = 0.7-0.8 is not a fit parameter but rather an instrument constant. Within its narrow range of values it has little effect on the fits or the relative magnitudes of the r_i obtained from the analysis.) Fitting the scatter plot from each subimage to Eqn. (7) leads to a set of values {r_i}.

Results and Discussion

Our software for fitting Eqn. (7) to the scatter plots can obtain values for as many different expression levels r_i as the subimage contains. Given a fluorescence and phase contrast subimage and initial guesses for N different expression levels r_i, the routine determines which of the subimage pixels are most consistent with each of the expression levels. That is, it assigns each pixel to one of the initial guess expression levels such as to give the best agreement with Eqn. (7). For example in Figure 2A, all pixels in the scatter plot were assigned the same r_i. In Figure 2B the pixels in the scatter plot have been assigned to two different groups (shown as green and blue) according to which of two r_i values better fits them. Having made this assignment the software calculates the total sum of squares error in the fit to Eqn. (7). It then refines the initial guesses for the r_i until the sum of squares (for that subimage scatter plot) is minimized.

One outcome of the fit is an assignment of an expression level to each of the pixels in the subimage. Figure 2 (panels D,E,F) shows that assignment for three representative subimages. A remarkable feature of the data analysis is that pixels assigned the same expression level are almost invariably contiguous (or nearly so) in the actual images, forming well-defined, cell-shaped regions in the image. In this sense the data analysis finds contiguous regions that have uniform expression levels r_i, even though the analysis makes no use of any spatial or proximity information about the pixels. The correlation between phase and fluorescence intensities is sufficient to identify discrete bacterial cell boundaries in a low resolution microscopy image.

The method does require a clear fluorescence signal to succeed. The subimages in Figure 1 show one case in which the imaged cells are fluorescing above background (PcomX switched on, Figure 1A,1B), and one case in which the cell(s) are fluorescing below background (PcomX switched off, Figure 1F,1G). Our method does not allow any determination of r_i for a cell that does not fluoresce brighter than the background, because in this case (switched off) the points in the scatter plot (Figure 1J) align vertically and a fit to Eqn. (7) cannot be obtained. Therefore, prior to fitting to Eqn. (7), we applied a cutoff criterion to the fluorescence in order to determine whether the cell or cluster in a given subimage was on or off. We first found the mean fluorescence of the thresholded (see Step 4 in Methods) pixels in the subimage. If this mean fluorescence was greater than one standard deviation above the fluorescence background, then the subimage was presumed to contain an on cell, allowing it to be fit to Eqn. (7). If not, then cells in the subimage were presumed to be off and the r value for the subimage was recorded as zero.

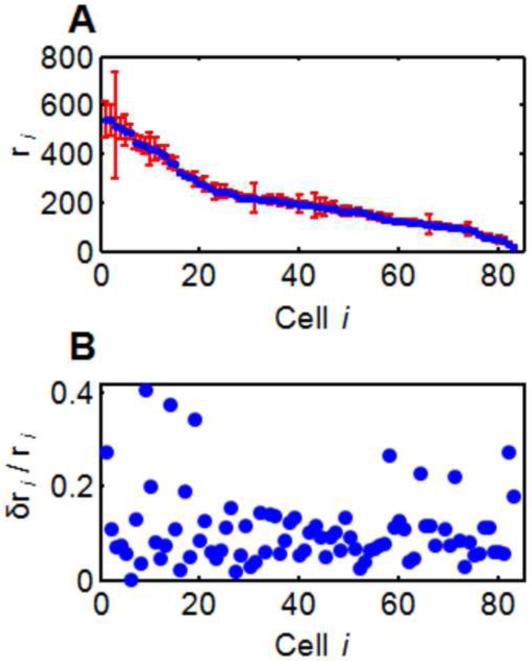
Figure 3 shows the set of r-values obtained by fitting the subimages for 83 cells, along with a bootstrap estimate of the errors, δr_i. The bootstrap indicates that the uncertainty δr_i/r_i is typically 5-15%, independent of r_i. Given the wide range of the r_i we consider this uncertainty to be very reasonable.

Figure 3.

(A) PcomX::gfp expression levels r_i identified in an S.mutans experiment ([XIP] = 157 nM). The indicated uncertainties are calculated from a bootstrap fit to Eqn. (7). (B) The relative uncertainty δr_i / r_i is typically 5-15%, independent of r_i.

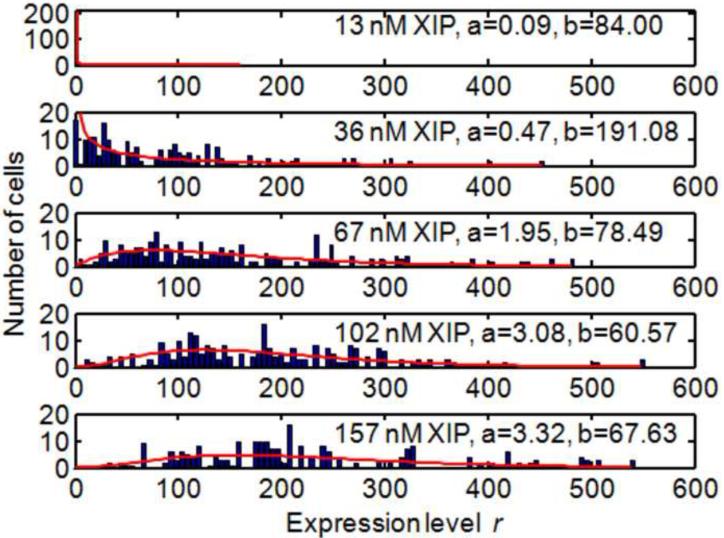
Finally, Figure 4 shows the results of applying this data analysis to a set of Streptococcus mutans cell images, each of which was collected at a different XIP concentration. Each image was subdivided into subimages showing clusters of (typically) 1-3 cells, and these subimages were analyzed by the methods described to yield 60-100 individual r-values. Cells for which an expression level r could not be determined were assigned r = 0 as explained above. Each histogram can be fit to a gamma distribution to yield the parameters a and b which characterize the rates of transcription and translation respectively [4,27].

Figure 4.

Histograms of expression levels obtained for S.mutans PcomX::gfp for different [XIP]. Solid curves show the fit to the gamma distribution that gives the parameters a and b describing transcription and translation rates.

Most approaches for analyzing images of cell clusters are based on cell segmentation. However, if matched fluorescence and phase contrast images are collected, then individual gene expression levels can be extracted from images without use of segmentation. This allows expression levels to be determined at low magnification. We demonstrated this method by analyzing noisy expression of a PcomX::gfp reporter in S.mutans. Our method is physically-based and highly automated. It could be completely automated by introducing a χ² criterion to determine the optimal number of expression levels present in any cell cluster.

Highlights.

• We present a method for extracting gene expression data from images of bacterial cells

• The method does not employ cell segmentation and does not require high magnification

• Fluorescence and phase contrast images of the cells are correlated through the physics of phase contrast

• We demonstrate the method by characterizing noisy expression of comX in Streptococcus mutans

Abbreviations

GFP

green fluorescent protein

XIP

comX-inducing peptide,