Concatenation and Concordance in the Reconstruction of Mouse Lemur Phylogeny: An Empirical Demonstration of the Effect of Allele Sampling in Phylogenetics

Abstract

The systematics and speciation literature is rich with discussion relating to the potential for gene tree/species tree discordance. Numerous mechanisms have been proposed to generate discordance, including differential selection, long-branch attraction, gene duplication, genetic introgression, and/or incomplete lineage sorting. For speciose clades in which divergence has occurred recently and rapidly, recovering the true species tree can be particularly problematic due to incomplete lineage sorting. Unfortunately, the availability of multilocus or “phylogenomic” data sets does not simply solve the problem, particularly when the data are analyzed with standard concatenation techniques. In our study, we conduct a phylogenetic study for a nearly complete species sample of the dwarf and mouse lemur clade, Cheirogaleidae. Mouse lemurs (genus, Microcebus) have been intensively studied over the past decade for reasons relating to their high level of cryptic species diversity, and although there has been emerging consensus regarding the evolutionary diversity contained within the genus, there is no agreement as to the inter-specific relationships within the group. We attempt to resolve cheirogaleid phylogeny, focusing especially on the mouse lemurs, by employing a large multilocus data set. We compare the results of Bayesian concordance methods with those of standard gene concatenation, finding that though concatenation yields the strongest results as measured by statistical support, these results are found to be highly misleading. By employing an approach where individual alleles are treated as operational taxonomic units, we show that phylogenetic results are substantially influenced by the selection of alleles in the concatenation process.

Phylogenetic analysis of concatenated sequence data has remained the standard in multilocus systematic studies, despite growing awareness of the processes that can lead to discordance among unlinked gene trees (Maddison 1997; Degnan and Rosenberg 2009) and the increased availability of species tree reconstruction methods that consider the overall distribution of gene trees (e.g., Ané et al. 2007; Liu et al. 2008; Kubatko et al. 2009; Heled and Drummond 2010). The continued use of concatenated phylogenetics may have its merits given the demonstration that the addition of gene sequence data into a single matrix can increase the probability of phylogenetic accuracy (Gadagkar et al. 2005; Rokas and Carroll 2005), as well as the findings of genome-level studies where the concatenated tree is similar to the tree preferred by species tree methods that consider the reconstruction of individual gene trees (e.g., Rokas et al. 2003; Cranston et al. 2009). Still, simulation work has shown that the concatenation of sequence data drawn from loci with highly conflicting gene trees can result in strongly supported, but inaccurate, trees (Kubatko and Degnan 2007), and empirical studies have questioned the high degree of certainty in concatenated phylogenetic estimates in light of largely uncertain results provided by species tree reconstruction methods (Belfiore et al. 2008).

The difference between these two perspectives may result from discrepancies in species tree branch lengths, where longer branches lead to less gene tree discordance and greater convergence between concatenated and species tree analyses, on the one hand, or to the prevalence of introgressive hybridization, which will tend to increase gene tree discordance (Leache 2009), on the other. However, in practice, empiricists will not know the actual lengths of branches in the species tree and will have trouble making judgments about the underlying source of strong branch support in concatenated trees. Coupling concatenated phylogenetic analyses with methods that quantify the degree of gene tree concordance will be useful in interpreting concatenated results.

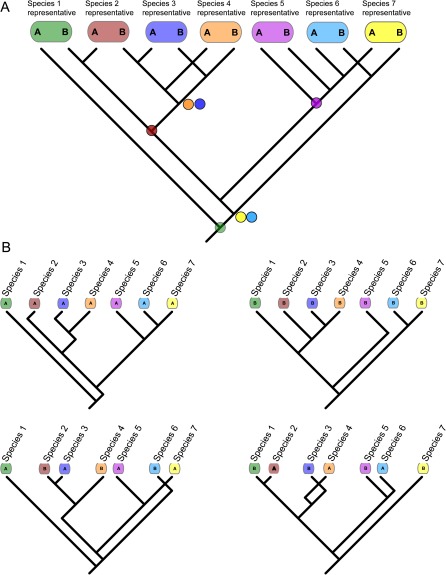
One major, but often unconsidered, challenge to the implementation of concatenated analysis of nuclear data is the choice of alleles across loci. In concatenated analyses, an individual is the operational taxonomic unit (OTU) in a tree, even if it is a representative of a lineage. If an individual OTU is heterozygous at multiple loci, the choice of alleles for building a concatenated matrix is far from obvious and simply selecting a single allele at given loci will not necessarily solve the problem. In the case of incomplete lineage sorting, heterozygous alleles can have gene tree coalescences that are deeper than their actual species divergence (e.g., fig. 1A) and the individual gene tree relationships among individuals (or species) can vary according to which allele is sampled (assuming accurate gene tree reconstruction) (fig. 1B). From a concatenated perspective, the result is that the “phylogenetic information” contained within a multilocus data matrix can vary depending on which alleles are chosen across loci. Many species tree methods of analysis circumvent this problem by making the species the focal OTU in the analysis and using the many alleles (or gene copies) within species (and individuals) to make inferences about ancestral history (e.g., Liu et al. 2008; Heled and Drummond 2010). The subsampling of alleles within OTUs in coalescent-based species tree analysis has been shown to efficiently yield accurate reconstruction (Hird et al. 2010; Ence and Carstens 2011). However, of the many studies employing concatenated analyses of multilocus data, we are unaware of any that have investigated the effect of subsampling alleles within individuals on their concatenated phylogenetic estimates.

FIG. 1.

A figurative demonstration of the effect of allele choice or sampling on the inference of the species tree from a single nuclear gene. (A) The full gene tree will contain two alleles (or gene copies) from each individual chosen to represent a species (or higher taxon). For heterozygous individuals, the two different alleles may coalesce at a point in the past (dots on nodes) that is deeper than the speciation events that gave rise to them. (B) Four possible different trees (out of many), resulting from choosing a single allele from each heterozygous individual depicted in (A). The overall figure is meant to convey the possible variation in the information content of a concatenated matrix when multiple loci are used that contain heterozygous individuals.

Mouse lemurs are one of the most diverse species-level clades among all of the primates and are a lineage within the family Cheirogaleidae, a clade of nocturnal lemurs that all feature diminutive body sizes. At least 16 species-level lineages of Microcebus have been diagnosed on the basis of mitochondrial DNA (mtDNA) and a four-gene nuclear data set using phylogenetic and population genetic criteria (Weisrock et al. 2010) though there has been little resolution of the phylogenetic relationships among lineages. Phylogenetic evidence thus far suggests that Microcebus is a recently diverged group (Yoder et al. 2000; Yang and Yoder 2003) and that incomplete lineage sorting is expected to be a dominant pattern among gene trees reconstructed for the group (Heckman et al. 2007). Furthermore, the phylogenetic placement of Microcebus within the Cheirogaleidae and the relationships among cheirogaleid lineages have never been fully explored using DNA sequence data. Relationships among the major generic lineages (Allocebus, Cheirogaleus, Microcebus, Mirza, and Phaner) have shifted in studies using morphological, immunological, and repetitive DNA data (Sarich and Cronin 1976; Crovella et al. 1995; Stanger-Hall 1997). Previous studies that used mtDNA sequence data to resolve relationships among cheirogaleid lineages either lacked the inclusion of Phaner (Pastorini et al. 2001), or poorly resolved its placement within the lemur clade (Roos et al. 2004). An 18-gene nuclear DNA study that focused on relationships among major lineages of lemurs (Horvath et al. 2008) lacked the inclusion of Phaner, despite suggestions that it may represent the sister lineage to all remaining cheirogaleids (Pastorini et al. 2001). To date, the best evidence for phylogenetic relationships among the major cheirogaleid lineages has come from presence-absence patterns of short interspersed elements (SINEs; Roos et al. 2004). Overall, however, phylogenetic relationships among species of Microcebus, and among cheirogaleid genera, have yet to be fully assessed using multi-locus sequence data and more modern methods of phylogenetic reconstruction.

Here, we aimed to estimate phylogenetic relationships among mouse lemur (Microcebus) lineages and genera of the Cheirogaleidae using mtDNA and a 12-gene nuclear DNA sequence data set. In this study, we used the most complete taxon sampling of Microcebus lineages to date and have included representatives of all four remaining cheirogaleid genera, including Phaner. We applied a range of phylogenetic approaches to meet this goal, including concatenated analyses, Bayesian concordance analyses, and coalescent-based species tree analyses. In our use of a concatenated phylogenetic analysis, we addressed the issue of allele sampling within individuals by creating replicate data sets that randomly sampled a single allele from each individual. We analyzed these replicate data sets using Bayesian phylogenetic analysis, and in addition to comparing the resulting consensus trees, we used Robinson–Foulds (RF) distances to quantify the differences between posterior distributions and visualize their distributions in ordination space. Collectively, these methods allowed us to ask the fundamental question of whether or not allele sampling within individuals significantly affected our phylogenetic results. In addition, we compare these concatenated results with the results of Bayesian concordance analysis of similarly pruned gene trees to assess how levels of support in the concatenated trees compare with quantified measures of gene tree concordance. Finally, we attempted to estimate a species tree using a coalescent-based Bayesian approach that accounts for the presence of multiple alleles sampled from within individuals and species.

Materials and Methods

Taxon and Genetic Sampling

This study used DNA sequence data collected from 16 evolutionarily distinct lineages of mouse lemurs delimited in Weisrock et al. (2010). Two individuals were sampled for most lineages (table 1). For two cryptic lineages delimited within Microcebus murinus (Microcebus sp. from Bemanasy and Microcebus sp. from Mandena), we sampled one individual (table 1). In total, we collected DNA sequence data from 29 individual mouse lemurs. DNA sequence data were collected from two representative individuals of the cheirogaleid genus Allocebus and a single representative individual of the remaining cheirogaleid genera (Cheirogaleus, Mirza coquereli, and Phaner pallescens). Sequence data were also collected from single representative individuals of Propithecus d. diadema, P. tattersalli, and P. verreauxi coquereli (family Indriidae) and from Lepilemur ruficaudatus (family Lepilemuridae). Both of these genera represent outgroup lineages to the Cheirogaleidae based on the multilocus phylogenetic results of Horvath et al. (2008).

Table 1.

Evolutionary Lineages of Microcebus and Cheirogaleid Outgroups Used in This Study.

Species Taxon	Individuala	Locality
Microcebus berthae	Jorg73	Kirindy
	JMR045	Lambokely
Microcebus griseorufus	JMR022	Mahavelo
	RMR64	Beza Mahafaly
Microcebus lehilahytsara	JMR001	Riamalandy
	RMR95	Ambohitantely
Microcebus mittermeieri	RMR187	Marojejy
	RMR191	Marojejy
Microcebus murinus	RMR46	Andranomena
Microcebus myoxinus	JMR072	Ambalimby
	RMR32	Bemaraha
Microcebus ravelobensis	RMR55	Ankaranfantsika
	RMR61	Ankaranfantsika
Microcebus rufus	RMR142	Andrambovato
	SL100F71	Ranomafana
Microcebus sambiranensis	RMR41	Manongarivo
	RMR163	Ambanja
Microcebus simmonsi	RMR102	Tampolo
	RMR115	Isle St. Marie
Microcebus tavaratra	RMR71	Ankarana
	RMR72	Ankarana
Microcebus sp.—Bemanasy	RMR217	Bemanasy
Microcebus sp.—Iv/Man	RMR207	Ivorona
	RMR209	Manantantely
Microcebus sp.—Marolambo	RMR131	Marolambo
	RMR136	Marolambo
Microcebus sp.—Mandena	00-016A-8982	Mandena
Microcebus sp.—Mt. d’Ambre	RMR154	Montagne d’Ambre
	RMR160	Montagne d’Ambre
Allocebus trichotis	DPZ05_AF5	Analamazaotra Special Reserve
	DPZ07_AM2	Analamazaotra Special Reserve
Cheirogaleus medius	n/a	n/a
Lepilemur ruficaudatus	n/a	n/a
Mirza coquereli	DLC2037	n/a
Phaner pallescens	DPZ17_LR	Kirindy
Propithecus d. diadema	DLC6564	n/a
Propithecus tattersalli	DLC6196	n/a
Propithecus verreauxi coquereli	DLC6583	n/a

Note.—Full descriptions of localities can be found in Weisrock et al. (2010). n/a, not applicable.

^aAll individual IDs represent field numbers associated with the Yoder or Kappeler labs or Duke Lemur Center accession numbers.

DNA sequence data were collected from a total of 12 nuclear loci and from the mitochondrial COX2 and COB genes (table 2). The genes used here are a combination of nuclear genes developed in a recent phylogenomic study of extant lemur diversity (Horvath et al. 2008) and of nuclear and mitochondrial genes that have proven useful in population-level studies of mouse lemurs (Yoder et al. 2000; Heckman et al. 2007). Human orthologs of each nuclear gene are encoded on a different chromosome; therefore, all genes used here are considered to be unlinked and independent of one another. The majority of sequence data was newly generated for this study. All sequence data from the genera Cheirogaleus, Lepilemur, Mirza, and Propithecus, as well as sequences from three individual mouse lemurs (M. berthae [Jorg73], M. murinus [DLC7006], and M. ravelobensis [RMR55]), were taken from GenBank (Horvath et al. 2008; Weisrock et al. 2010). For all remaining mouse lemur lineages, sequence data from four loci (ADORA3, ENO, FGA, and VWF) were taken from Weisrock et al. (2010).

Table 2.

Details for the Molecular Markers Used in This Study.

Gene	Nuclear Gene Type	Length (bp)	% Missing seq. Dataa	Variable Sitesa	Number of Distinct Site Patternsa	Number of Allelesa,b	Proportion of Heterozygous Sitesa,c	Model	lnL 95% Highest Posterior Densityc	Number of Distinct Topologies in Posterior Distributiond
ABCA1	Intron	637	0.1	40	93	45/60	0.0025	GTR + G	−2307.2 to −2344.5	1,000
ADORA3	Exon	384	0.0	20	23	16/60	0.0017	HKY + G	−1194.4 to −1223.3	1,000
AXIN1	Mostly Exon	900	3.3	36	63	29/58	0.0016	GTR + I + G	−2187.3 to −2224.6	1,000
CFTR-Pair B	Mostly Intron	638	0.2	47	75	32/60	0.0028	GTR + G	−2139.8 to −2172.9	1,000
ENO	Mostly Intron	905	0.0	114	144	49/60	0.0044	GTR + G	−3386.7 to −3422.4	1,000
ERC2	Mostly Intron	796	3.4	28	102	39/58	0.0008	HKY + G	−2286.2 to −2319.5	1,000
FGA	Mostly Intron	635	0.0	93	79	31/60	0.0036	GTR + I	−2275.1 to −2322.3	1,000
LRPPRC-Pair B	Mostly Intron	784	0.1	37	103	38/60	0.0009	GTR + G	−2219.7 to −2254.6	1,000
LUC7L	Mostly Intron	700	6.7	20	81	36/56	0.0005	GTR	−1540.8 to −1583.7	1,000
SREBF2	Mostly Intron	695	7.1	37	121	40/56	0.0024	GTR + G	−2318.3 to −2351.9	1,000
VWF	Mostly Intron	813	0.0	89	113	45/60	0.0058	HKY + I + G	−3397.5 to −3435.2	1,000
ZNF202	Exon	849	0.4	27	82	42/60	0.0011	HKY + I + G	−1920.1 to −1955.2	1,000
mtDNA-COX2	Coding	684	10.0	135	442	30/30d	n/a	HKY + I + G	−11195.7 to −11220.2	768d
mtDNA-CYTB	Coding	1,140	6.7	367	442	30/30d	n/a	HKY + I + G	−11195.7 to −11220.2	768d
Total		10,560		1,087

Note.—GTR, general time reversible; HKY, Hasegawa–Kishino–Yano; n/a, not applicable.

^aBased solely on the Microcebus sequence data.

^bThe number in the denominator indicated the total number of Microcebus gene copies in each data set.

^cThis proportion is calculated from the total number of cells in the unphased data matrix (i.e., number of individuals × length in bp).

^dBased on the sampled posterior distribution of 1,000 trees from Bayesian phylogenetic analysis performed in MrBayes.

Sequence data were collected for all individuals for the loci ABCA1, ADORA3, CFTR-Pair B, ERC2, FGA, LRPPRC-Pair B, and ZNF202. For some individuals, we were unable to generate sequence data from the nuclear loci AXIN1, ENO, LUC7L, SREBF2, VWF and from the COB and COX2 mitochondrial genes. For the most part, missing sequence data were limited to some outgroup taxa; however, a small number of Microcebus sequences also had a small amount of missing data. Polymerase chain reaction (PCR) primer information for all loci can be found in Horvath et al. (2008). Details of the PCR and sequencing methods can be found in supplementary file S1 (Supplementary Material online). Most nuclear PCR products that generated sequence exhibiting polymorphic sites or length heterogeneity were cloned using a Topo^® TA Cloning Kit (Invitrogen, Carlsbad, CA), and for each cloned PCR, eight colonies were sequenced to identify alleles. For a small number of heterozygous sequences, we identified alleles using an algorithmic approach in the program PHASE version 2.1 (Stephens et al. 2001). We used the default model in PHASE, which did not consider the potential for recombination among polymorphic sites within a sequence. For each locus, we included phased sequences generated via cloning and we ran five independent runs, each starting with a different random number seed. In each run, we used 1,000 iterations, a thinning interval of two steps and a burn-in of 100 iterations. We compared the output from the multiple PHASE runs to verify that similar results were being obtained.

A summary of all collected sequences for all individuals and genes used in this study along with their GenBank accession numbers are presented in supplementary table S1 (Supplementary Material online). In addition, all aligned sequence data sets have been deposited in the Dryad online repository (http://dx.doi.org/10.5061/dryad.3mt58823).

Intraindividual Gene Copy Sampling

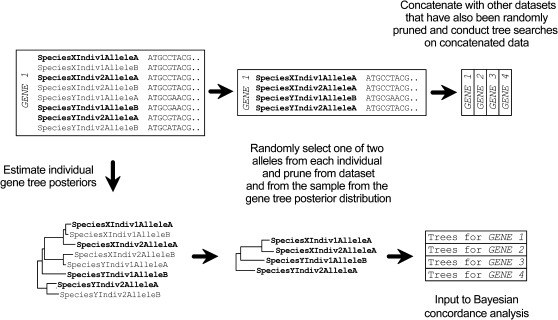
For our concatenated and concordance analyses, it was necessary for us to sample a single haploid sequence from each individual. This step was required for two main reasons. First, in concatenated and concordance analysis of nuclear sequence data, there is no clear or obvious way to pair haploid sequences from two or more heterozygous genes within an individual. For example, should allele A from gene 1 be concatenated with allele A of gene 2 or allele B of gene 2? Second, Bayesian concordance analysis implemented in the version of BUCKy used in this study (see below) is limited to gene trees with 32 tips, which is well below the total number of haploid gene sequences in our individual nuclear gene data sets. Our limitation to 32 tips in each gene tree is also expected to increase the probability of informative results from BUCKy analyses. As the number of tips in the tree increase, so does the number of possible trees, which can make it harder to provide BUCKy (which caps the input of trees for each locus at 1,000) with a representative and unbiased sample of trees from the posterior distribution for each locus.

To deal with these two issues, we developed a pruned-sampling approach to reduce individuals down to a single randomly chosen gene copy or a single tip in a gene tree. Bayesian concordance analysis uses posterior distributions of trees as input, and so for these analyses, it was necessary to prune tips in a gene tree as opposed to gene copies in a DNA alignment. We reasoned that the accuracy of gene tree reconstruction would be increased through the inclusion of all available haploid sequences. Therefore, we developed a pruning strategy to remove one of the two gene copies (i.e., alleles or tips in the tree) from each Microcebus individual in a gene tree generated from the full sample of gene copies for all individuals (fig. 2). This pruning strategy was performed on the Bayesian posterior distributions of trees generated for each nuclear gene. The same gene copies (tips) were pruned from all trees within a single-gene posterior distribution. In addition, we randomly pruned one of the two representative individuals of the species M. ravelobensis, M. simmonsi, and M. tavaratra. These three species were each found to be monophyletic in all mitochondrial and most nuclear gene trees examined in Weisrock et al. (2010). We also randomly pruned one of the two individuals of Allocebus trichotis and two of the three Propithecus taxa. We did not perform allele pruning on the non-Microcebus taxa. The majority of these sequences were taken from GenBank, and polymorphic sites were already coded as Ns. The Phaner and Allocebus sequence data collected for this study were completely homozygous and did not require the separation of alleles. The overall result of this pruning strategy was posterior distributions of trees with a total of 32 tips. To assess the variation in Bayesian concordance results based on this pruning strategy, we replicated the random pruning procedure ten times for each single-gene nuclear data set. mtDNA data only required the pruning of individuals to match those present in the 32-taxon nuclear trees.

Fig. 2.

A pipeline of the steps involved in the pruning of allelic sequences from individuals to create replicate concatenated data sets and of pruning allelic tips from individuals in gene trees to create replicate sets of trees for Bayesian concordance analysis. One allele was randomly selected and pruned from each individual from each gene alignment and the same alleles were pruned from the trees sampled from each gene tree posterior distribution. This process resulted in data sets that can be concatenated or used in concordance analyses.

For concatenated phylogenetic analysis, a single allele (gene copy) was pruned from each Microcebus individual in the single-gene nuclear DNA sequence alignments (fig. 2). As in the tree pruning, we also pruned one of the two representative individuals of the species M. ravelobensis, M. simmonsi, and M. tavaratra and we pruned one of the two individuals of A. trichotis and two of the three Propithecus taxa. Ten replicate prunings of each nuclear data set were generated to match the ten replicates of pruned posterior distributions of gene trees (i.e., we pruned the same gene copies from replicate 1 of the sequence alignments that were pruned from replicate 1 of the gene trees as described above).

All random pruning procedures of tips in gene trees and of alleles from sequence data sets were performed with an automated script in the R programming language, written by the authors. This script, along with example files for one of the nuclear loci, is available on Dryad using the above referenced link.

Gene Tree Reconstruction

Posterior distributions of gene trees were reconstructed from each of the individual nuclear data sets and from a data set of the combined mtDNA genes using a Bayesian analysis in MrBayes version 3.1.2 (Ronquist and Huelsenbeck 2003). For these analyses, the full set of sampled gene copies from all individuals was included, even when nuclear gene copies within an individual were represented by the same haplotype. Downstream application of Bayesian concordance analysis required that the same tips be present in all posterior distributions of trees. Therefore, individual gene data sets with missing data were analyzed with question marks completing the data line for an individual with missing data. The expectation is that the phylogenetic placement of these individuals will be random across the posterior distribution of trees and should therefore not affect results. Evolutionary models for each locus were assessed for the haplotype data sets using Akaike Information Criteria in MrModeltest v2.3 (Nylander 2004). The low level of genetic variation within each nuclear data set, and the fact that most are intronic, led us to forego exploring a partitioning strategy, and we analyzed each as a single partition. MtDNA data for individual mouse lemurs were concatenated and analyzed in a two-partition framework with model parameters estimated separately for the cox2 and cytb genes. As with the nuclear genes, we did not explore further partitioning within each mtDNA locus. Partitioning strategies of mtDNA loci have been shown to be important in the use of whole mtDNA genome data when using Bayesian methods to reconstruct deep phylogenetic relationships (Brandley et al. 2005); however, the majority of our phylogenetic study is focused on the resolution of relatively recent divergences, and we felt that the improvement afforded by a higher partitioning strategy would be minimal. Four Markov chains were used with the default temperature parameter of 0.2. Default priors were used in all analyses, and random trees were used to start each Markov chain. Chains were run for 25 million generations with samples drawn every 50,000 generations for a total of 500 samples. Four replicate analyses were run for each data set. In all cases, replicate analyses converged on the same posterior distribution as determined through similar distributions of −lnL values and parameter estimates visualized in the program TRACER v1.3 (Rambaut and Drummond 2007). In all replicate analyses, effective sample size (ESS) values indicated that samples drawn after the first 12.5 million generations (i.e., 250 samples) yielded independent estimates of parameter estimates (i.e., ESS values of 250). Therefore, we used the latter 250 samples from each replicate and combined them to produce a 1,000 sample representation of the posterior distribution. Consensus trees were then generated in MrBayes using the allcompat option. In addition, the 95% credible set of trees are presented based on the cumulative probabilities of trees in the sampled posterior distributions. Because the 95% credible set of trees represents an estimate and does not necessarily represent a 0.95 probability of containing the true topology, we use it as an overall measure of the certainty, or uncertainty, in tree reconstruction. High proportions of distinct trees to samples (e.g., 950/1,000) are viewed as an indicator that there is little certainty in phylogenetic reconstruction, whereas low proportions indicate strong certainty in phylogenetic reconstruction.

Concatenated Phylogenetic Analysis

Bayesian phylogenetic analysis was performed on concatenated data sets of all nuclear genes and on concatenated data sets of all nuclear and mitochondrial genes. The concatenated data sets used here were built from the 32-taxon pruned nuclear data sets described above. The nuclear data sets generated in the first round of pruning were concatenated, as were the second round, third round, etc., resulting in ten sets of nuclear concatenated data. Nuclear concatenated data were also matched with the 32-taxon mtDNA data to create ten nuclear + mtDNA concatenated data sets. All concatenated analyses were performed in MrBayes using similar settings to those described above for the gene tree analyses. We used a partitioned approach with model parameters estimated separately for all nuclear and mtDNA genes. Markov chains were run for 10 million generations with samples drawn every 10,000 generations for a total of 1,000 samples. Four replicate analyses were run for each data set. In all cases, replicate analyses converged on the same posterior distribution relatively early in the analysis (well before 1 million generations), as determined through similar distributions of −lnL values and parameter estimates visualized in Tracer. In each replicate, after discarding the first 250 samples (2.5 million generations), ESS values were at least 450, with many replicates exhibiting complete independence among samples (i.e., ESS = 750). Therefore, we combined the latter 750 samples of each replicate to form a total of 3,000 samples as a representation of the posterior distribution. Consensus trees were generated in MrBayes using the allcompat option. The 95% credible set of trees are presented for all analyses using interpretations as described above.

Comparison of Concatenated Phylogenetic Trees

To assess the consistency of phylogenetic estimation across replicate concatenated data sets, we plotted trees from the concatenated Bayesian posterior distributions in ordination space using multidimensional scaling (MDS) of tree-to-tree pairwise distances implemented in the Tree Set Viz module version 2.1 (Hillis et al. 2005) in the Mesquite software package (version 1.05) (Maddison and Maddison 2010). MDS analyses in Tree Set Viz analyses were performed separately on the nuclear concatenated analyses and on the nuclear + mtDNA analyses. In both cases, 500 trees were randomly sampled from the posterior distribution of each of the ten concatenated replicates and combined into a single nexus-format tree file (containing 5,000 trees) for analysis in Mesquite. Unweighted RF distances, which measure the dissimilarity between the topology of two trees, were calculated for all pairwise tree comparisons and used in the MDS analyses. The default step size in Tree Set Viz was used in all analyses and MDS was allowed to proceed until the stress function ceased changing out to six decimal positions. To avoid being trapped in local optima, this procedure was repeated multiple times to insure that similar results were being achieved. The final stress values for the nuclear concatenated and nuclear + mtDNA concatenated analyses were 0.249132 and 0.171799, respectively. The results of MDS analyses were plotted as 2D representations of multidimensional space.

To provide a tree-like visual comparison to the MDS ordination plots, we also used Mesquite to construct a 50% majority-rule consensus tree using the consensus trees generated from each of the ten concatenated replicates. Consensus trees were generated from both the nuclear and the nuclear + mtDNA concatenated replicates.

Finally, to provide a quantitative description of the level of similarity or dissimilarity between trees generated from the concatenated replicates, we calculated the average RF distance between trees drawn from two different posterior distributions using the treedist program in the PHYLIP software package version 3.69 (Felsenstein 2005). We used a sample of 1,000 unrooted trees from each posterior distribution and calculated the distances between the 1,000 corresponding pairs of trees in each set of comparisons (e.g., tree 1 vs. tree 1, tree 2 vs. tree 2, etc.). We also calculated RF distances for all pairs of trees within a single replicate.

Bayesian Concordance Analysis of Pruned Trees

As one alternative to concatenation, we used Bayesian concordance analysis (BCA) (Ané et al. 2007) to provide an estimate of the level of concordance in reconstructed branches among the posterior distributions of gene trees generated for each nuclear gene and the combined mtDNA genes. Using the single-gene posterior probabilities (PPs) of trees and a single-parameter prior probability (α) representing the expectation for different genes to reconstruct different trees, BCA produces a joint posterior distribution that can feature shifts in tree probabilities from the single-gene estimates. For example, a low single-gene PP for a particular tree can increase if other genes find that tree to have higher single-gene PPs. A useful description of the joint posterior distribution is the clade concordance factor (CF), which is a summary statistic describing the proportion of genes across the joint posterior distribution that contain a particular clade. These clade CFs can be a useful metric for determining the number of genes contributing phylogenetic information to a particular branch reconstruction. BCA is also a useful method for our study because of the flexibility it provides by not making assumptions about the causes of discordance (e.g., incomplete lineage sorting, horizontal gene transfer, or paralogy).

We explored a range of prior probability distributions for the number of distinct trees that should exist across all genes with analyses run with α values of 0.1, 1, 10, and 100 (an α = 0 indicates all posterior distributions are represented by the same trees; an α = ∞ indicates each gene should have a distinct set of trees). All analyses were run in BUCKy version 1.3 (Larget et al. 2010) with four Markov chain Monte Carlo (MCMC) chains for 1 million generations following a burn-in period of 100,000 generations. Two replicate analyses were run at each α value. This analytical approach was applied to each of the ten replicate sets of pruned nuclear posterior distributions of gene trees and to the ten replicate sets of pruned nuclear and mtDNA posterior distributions of gene trees. For each replicate, CFs were calculated for all possible bipartitions in the 32 tip tree. From these CFs, a primary concordance (PC) tree was constructed from the set of bipartitions with the highest overall CFs.

To provide an easy interpretation of the concordance results, we present all CFs as a product of the raw concordance factor (output from BUCKy as a proportion) multiplied by the total number of gene trees in an analysis. For example, a CF = 0.5 in the concordance results from our 12 nuclear genes would be presented as a CF = 6.

Coalescent-Based Species Tree Analysis

We performed Bayesian species trees estimations using a coalescent model that accounts for incomplete lineage sorting as a mechanism for gene tree discordance using the program BEST version 2.3 (Liu 2008). All analyses were performed using data from the 12 nuclear loci. Because these analyses do not require the linking of alleles across loci, we were able to utilize the full unpruned nuclear data sets. In our attempt to produce results that indicated convergence on the posterior distribution, we performed analyses on a series of data sets that varied in their taxonomic sampling. First, BEST analyses were conducted on a data set containing all Microcebus lineages and the remaining four cheirogaleid taxa. In this round, we initially ran BEST analyses for 50 million generations (trees sampled every 10,000 generations) and explored a range of prior distributions for the effective population size parameter θ, with inverse gamma distributions with means of 0.0015 (α = 3, β = 0.003), 0.015 (α = 3, β = 0.03), 0.15 (α = 3, β = 0.3), and 0.5 (α = 3, β = 1). These analyses suggested that the two larger prior distributions resulted in a faster (but not complete) approach to a stable posterior distribution. Therefore, we subsequently ran analyses for a total of 500 million generations (trees sampled every 100,000 generations) using prior distributions on θ with means of 0.15 and 0.5. In all analyses, the individual gene trees were estimated using substitution models as described above for the MrBayes analyses. All analyses used a uniform gene mutation prior (set at 0.5, 1.5) and a Poisson distribution for the neighborhood size around the maximum tree (set at the default value of 5). Finally, we explored a range of chain temperatures, with higher temperatures increasing the probability of heated chains moving throughout parameter space. Temperatures of 0.1, 0.125, 0.15, and 0.175 were used. For each combination of θ prior and chain temperatures, we performed four replicate analyses each using a different random starting seed. Next, we performed a similar set of analyses on two smaller data sets that limited taxon sampling within Microcebus with the hope that this would improve the potential for convergence on the posterior distribution. In one data set, we included all samples from all M. murinus lineages, M. griseorufus, and M. ravelobensis. Analyses of this first data set were performed as described above except that the BEST analyses were run for 275 million generations. In the second data set, we included all samples from the remaining Microcebus lineages, as well as M. ravelobensis. Microcebus ravelobensis was included with both data sets because of its uncertain placement as either the sister lineage to the M. murinus + M. griseorufus clade or in a clade with the remaining Microcebus lineages. Analyses of the second data set were performed as described above except that the BEST analyses were run for a total of 325 million generations.

Results

Full details regarding levels of variation among Microcebus individuals for each marker can be found in table 2. Briefly, mtDNA genes were considerably more variable than individual nuclear loci and accounted for 502 (46.2%) of the 1,087 total variable sites (table 2). Nonetheless, the nuclear genes contained a substantial amount of genetic variation. Nuclear intronic sequences contained the greatest levels of information, relative to exonic sequences, both in the number of variable sites and number of distinct site patterns (table 2).

Individual Gene Trees

The Bayesian posterior distributions of trees for individual loci contained many distinct topologies, indicating substantial uncertainty in phylogenetic reconstruction. All nuclear loci had posterior distributions with 950 trees (out of 1,000 sampled trees) in the 95% credible sets of trees (table 2), indicating relatively low certainty in the reconstruction of each gene tree. The mtDNA posterior distribution had a slightly reduced number of trees (718) in the 95% credible set.

Consensus trees for the single-locus posterior distributions are not presented here (due to space limitations) but are available on the Dryad online data repository through the link referenced above in the Materials and Methods section. However, a general description can be provided. Higher level phylogenetic relationships for the major cheirogaleid lineages exhibited general congruence across individual loci. All but three gene trees resolved the family Cheirogaleidae as monophyletic, often with high PPs. Two exceptions to this pattern, ENO and VWF, are the result of missing sequence data for some non-cheirogaleid outgroup taxa, leading to their nested placement within various Microcebus clades. In the third exception, the complete ERC2 data matrix placed the genus Phaner outside of the larger cheirogaleid clade and sister to the genus Propithecus. Of the ten gene trees that resolve a monophyletic Cheirogaleidae, seven place the genus Phaner as the sister lineage to all remaining cheirogaleids and six of these gene trees place the genus Cheirogaleus as sister to all remaining cheirogaleids, excluding Phaner. Relationships among Allocebus, Microcebus, and Mirza were considerably more variable across gene trees, ranging from the placement of Allocebus and Microcebus in a clade with PP = 0.93 in the ZNF2 gene tree to the placement Mirza and Microcebus in a clade with a PP = 0.95 in the ABCA1 gene tree.

Summarizing phylogenetic reconstruction for allelic lineages within Microcebus across the 13 gene trees by visual comparisons was less obvious, though a few notable patterns can be described. First, there was considerable variation in the degree of phylogenetic resolution within Microcebus across gene trees, as evidenced by some gene trees featuring numerous branches with very low PPs (e.g., the ERC2 gene tree contained 18 branches within Microcebus with a PP < 0.1) and gene trees featuring numerous branches with moderate to high PPs (e.g., the FIB gene tree). This was not an all-or-nothing pattern, as many gene trees were heterogeneous for these patterns, containing PPs indicative of uncertainty for some reconstructions, yet strong support for other relationships. Second, there was clear discordance across gene trees for some sets of relationships that were strongly supported within individual gene trees. For example, all gene copies sampled from the species M. griseorufus, M. murinus, and M. ravelobensis are placed in a clade with a PP = 0.99 in the LRPPRCB gene tree, whereas M. ravelobensis gene copies are placed in a clade with gene copies sampled from all other mouse lemur lineages with a PP = 0.98 in the FIB gene tree.

Phylogenetics of Concatenated Data Sets

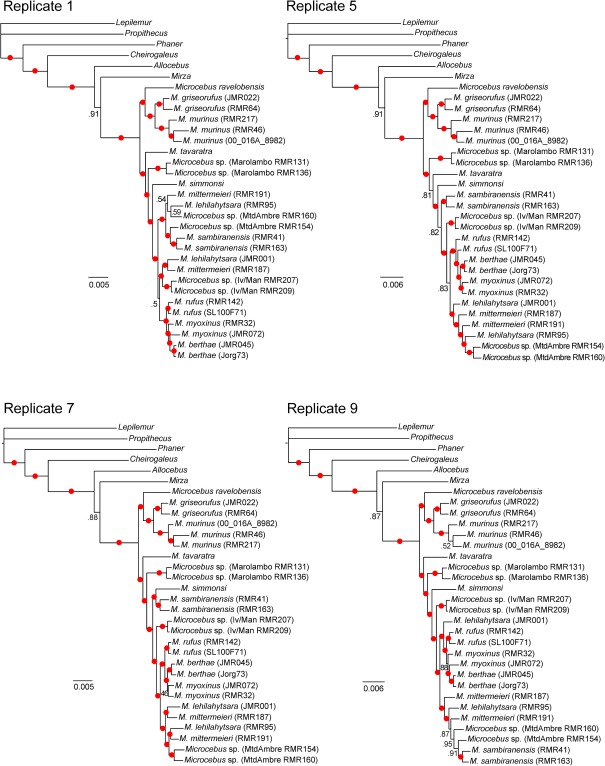
Bayesian phylogenetic analysis of concatenated data sets containing a single randomly sampled nuclear allele for each individual showed greater consistency in posterior distributions with a much smaller number of distinct topologies than those produced in analyses of individual gene trees (table 3). Across the ten replicates of concatenated nuclear data, the number of distinct trees in the Bayesian 95% credible set ranged from 3 to 62. The addition of mtDNA data to the concatenated nuclear data further reduced the number of trees in the 95% credible set in nine of ten replicates, with a range of three to nine distinct tree topologies (table 3). The level of certainty seen in the concatenated posterior distributions was also reflected in the consensus trees generated for each replicate, with the majority of branches in each tree receiving PPs > 0.95 (see fig. 3 for a subsample of four replicates and supplementary fig. S1A, Supplementary Material online for all ten replicates of the nuclear data and see supplementary fig. S1B, Supplementary Material online for all ten nuclear + mtDNA concatenated replicates).

Table 3.

Total Number of Distinct Tree Topologies Present in the 95% Credible Set of Trees in the Bayesian Posterior Distribution.

Concatenated Replicate	1	2	3	4	5	6	7	8	9	10
Nuclear
Number of distinct trees	15	10	6	27	6	3	10	62	37	30
Nuclear + mtDNA
Number of distinct trees	3	3	5	4	4	3	5	5	7	9

Note.—The posterior distribution is based on a sample of 3,000 trees.

FIG. 3.

Bayesian majority-rule consensus trees reconstructed for four of the ten replicate nuclear concatenated data sets. Trees are presented as phylograms with branch lengths representing the average number of substitutions per site. Filled circles on branches indicate PP support of 0.95 or greater. Numbers on branches represent PPs < 0.95.

Phylogenetic relationships among cheirogaleid genera were consistent and strongly supported across all concatenated nuclear (fig. 3 and supplementary fig. S1A, Supplementary Material online) and nuclear + mitochondrial (supplementary fig. S1B, Supplementary Material online) replicates. The Cheirogaleidae was resolved as monophyletic, and Phaner was placed as the sister lineage to a clade containing all remaining cheirogaleids. Within this clade, Cheirogaleus was placed as the sister lineage to a clade containing Allocebus, Microcebus, and Mirza. All three of these relationships received PPs = 1.0 in all replicate analyses. In addition, in all replicates, Microcebus and Mirza were consistently placed in a clade to the exclusion of Allocebus. This latter relationship received more varied measures of support in the nuclear concatenated trees (PPs = 0.86–0.94) but received stronger support in the nuclear + mitochondrial concatenated (PPs = 0.97–0.98).

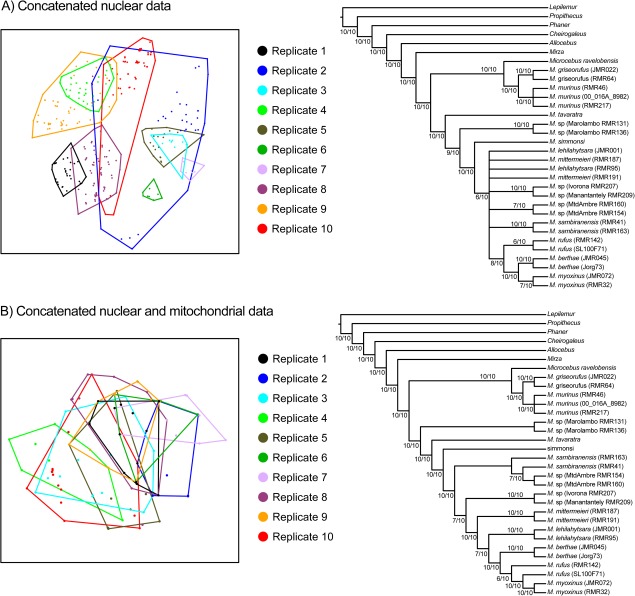
Relationships among Microcebus lineages were highly inconsistent across concatenated nuclear replicates, despite very high PPs (>0.95) for the majority of branches within each replicate (fig. 3 and supplementary fig. S1, Supplementary Material online). These differences in phylogenetic estimation across replicates were evident in the MDS plots of trees in multidimensional space, which revealed that the posterior distributions of many of the concatenated nuclear replicates occupied different regions of tree space (fig. 4A). For example, nuclear replicate 1 exhibited slight overlap with nuclear replicate 8, but otherwise occupied a completely distinct region of tree space from all other nuclear replicates. The degree to which the posterior distribution of any nuclear replicate overlapped with the posterior distributions of other nuclear replicates in tree space varied; however, all nuclear replicates formed nonoverlapping distributions with at least one other nuclear replicate. It is important to note that the MDS plots considered all trees sampled in the posterior distribution and not just the 95% credible set of trees. A focus solely on the 95% credible set would be expected to further reduce the overlap of posterior distributions in tree space.

FIG. 4.

Different representations of the variance in cheirogaleid concatenated phylogenetic reconstruction that occurred when different alleles were sampled from an individual. Two-dimensional visualization of tree space using MDS of unweighted RF distances between trees are presented for (A) trees sampled from the posterior distributions of the ten replicate nuclear concatenated data sets and (B) trees sampled from the posterior distributions of the ten replicate nuclear + mitochondrial concatenated data sets. In both plots, minimum convex polygons encompass individual posterior distribution of trees. Corresponding majority-rule consensus trees (using a 50% minimum threshold) are presented to the right of each ordination plot. These consensus trees were reconstructed from the ten replicate consensus trees of each data source. Numbers on branches represent the number of times a branch was present.

A majority-rule consensus tree constructed from the ten nuclear concatenated replicates highlighted many of Microcebus relationships that conflicted across replicates (fig. 4A). For example, relationships among eight species (M. berthae, M. lehilahytsara, M. mittermeieri, M. myoxinus, M. rufus, M. sambiranensis, and two undescribed lineages) were inconsistent enough across replicates to result in a large polytomy. Again, this result occurred despite the fact that relationships among these species (or their representative individuals) were reconstructed with very high measures of support and minimal uncertainty in many replicates.

Analysis of concatenated nuclear and mitochondrial data resulted in greater consistency in phylogenetic relationships across replicates than in the nuclear concatenated data alone; however, differences across replicates were still evident. For example, replicate 1 overlapped in tree space with all but one other replicate (replicate 4) (fig. 4B). The corresponding majority-rule consensus tree reflected this increase in consistency, with greater resolution in branches among Microcebus lineages, but also highlighted relationships that varied across replicates (fig. 4B). For example, the placement of the Microcebus sp. lineage from Ivorona and Manantantely shifted positions across replicates, with placement in a clade with M. berthae, M. lehilahytsara, M. mittermeieri, M. myoxinus, and M. rufus found in seven of ten replicates. In this example, it is important to point out that alternative relationships in the other three replicates are backed by strong measures of branch support (i.e., PPs > 0.95).

Average RF distances between replicate posterior distributions were considerably smaller for the mitochondrial + nuclear concatenated results, relative to the nuclear concatenated results (table 4).

Table 4.

Average RF Pairwise Distances between Posterior Distributions Resulting from Concatenated Bayesian Phylogenetic Analysis of the Ten Nuclear Replicate Data Sets (below diagonal) and the Ten mtDNA + Nuclear Replicate Data Sets (above diagonal).

	1	2	3	4	5	6	7	8	9	10
1	3.8/1.45	4.8	3.57	5.98	3.79	1.42	5.26	3.31	1.88	5.39
2	20.58	4.89/1.01	3.97	6.72	3.49	3.68	6.0	7.4	4.59	6.07
3	19.02	11.13	1.67/1.47	3.66	6.24	3.91	2.97	4.88	3.42	3.07
4	15.59	11.13	18.88	4.71/1.91	8.97	6.55	5.1	3.73	5.81	2.23
5	20.25	13.47	9.07	22.09	2.34/2.03	2.7	6.46	6.29	4.19	8.3
6	14.53	15.02	9.72	20.16	11.72	0.39/0.5	5.83	3.94	1.84	5.89
7	17.34	11.3	4.53	16.29	13.00	9.06	2.04/1.14	6.16	5.14	4.54
8	13.4	20.3	14.97	13.78	16.2	14.61	15.4	4.68/1.0	3.9	3.45
9	11.28	19.69	20.2	10.54	21.28	21.31	19.17	13.72	3.36/2.15	5.26
10	21.85	17.68	16.03	16.29	17.03	20.22	19.01	18.1	16.8	3.67/1.84

Note.—Values on the diagonal are average RF pairwise distances among trees within the posterior distribution of a nuclear concatenated replicate (before slash) and within the posterior distribution of a mtDNA + nuclear concatenated replicate (after slash).

Concordance Analysis of Gene Trees

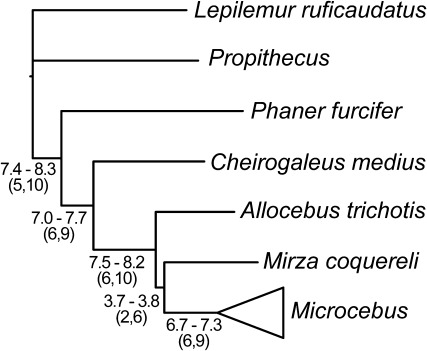
Bayesian concordance analysis of the nuclear data produced PC trees with consistent and relatively high CFs for most relationships among cheirogaleid genera across replicate sets of pruned nuclear gene trees (fig. 5). The monophyly of the Cheirogaleidae was supported by CFs of 7.4–8.3, with 95% credibility intervals ranging from a low of 5 to a high of 10. Similar values were resolved for a clade containing Cheirogaleus, Allocebus, Microcebus, and Mirza and for a clade containing these latter three genera (fig. 5). Mirza and Microcebus were placed in a clade to the exclusion of all other cheirogaleid genera in all replicates; however, this relationship received lower mean CFs (3.7–3.8) with 95% credibility intervals as low as 2. An alternative relationship placing Allocebus and Microcebus in a clade received lower CFs (2.1–2.3) with 95% credibility intervals that include a CF of 1 (results not shown). Concordance analysis of the mtDNA and nuclear gene trees produced similar results for relationships among cheirogaleid genera, with slight increases in CFs and 95% credibility intervals for relationships among cheirogaleid genera (results not shown).

FIG. 5.

Phylogenetic tree with nuclear-based clade CFs for relationships among genera of the Cheirogaleidae. CFs are presented as the number of genes (out of 12) supporting a relationship and are presented as the range calculated across all ten replicates of pruned nuclear gene trees. Numbers in parentheses represent the lowest and highest CF from the 95% credibility intervals across the ten replicates. Branch lengths are based on a concatenated tree (nuclear replicate 1) and are presented here to provide a relative comparison of lengths. Relationships in this tree match those of the PC trees across all replicates.

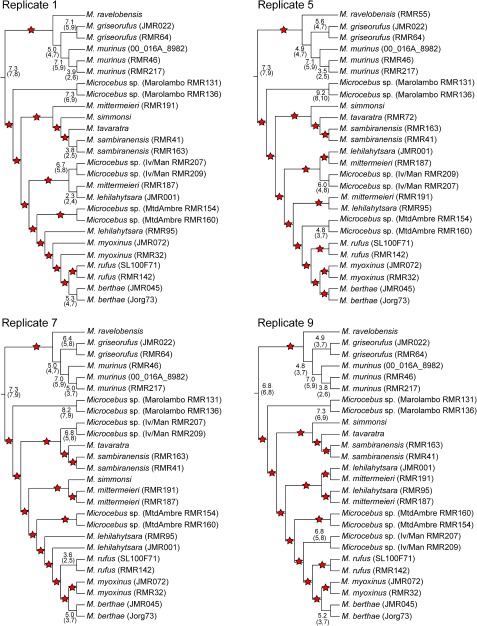
Bayesian concordance analysis of nuclear gene tree replicates resulted in PC trees with considerable variation in phylogenetic relationships among Microcebus individuals and lineages (see fig. 6 for a subsample of four replicates and supplementary fig. S2, Supplementary Material online, for all ten replicates), a result that was maintained in the analysis of both mitochondrial and nuclear gene trees (results not shown). Across all replicates, the majority of branches within the Microcebus clade received very low CFs, often with 95% credibility intervals that included 0 or 1. Few relationships involving Microcebus lineages were both consistent across replicates and received CFs indicating support from more than gene: 1) Microcebus was resolved as a monophyletic group in all nuclear replicates with CFs ranging from 6.7 to 7.3, 2) M. griseorufus and M. murinus were placed in a clade with CFs ranging from 4.8 to 5.0, and 3) the three individuals of M. murinus, each diagnosed as a separate lineage in Weisrock et al. (2010), were placed in a clade with CFs ranging from 7.0 to 7.1. All remaining clades that were consistently present in the PC trees across replicates and received 95% credibility intervals that did not include 0 or 1 involved individuals from the same Microcebus lineage.

FIG. 6.

PC trees reconstructed from four of the ten replicates of pruned nuclear gene trees. CFs are presented as the number of genes (out of 12) supporting a relationship. To simplify interpretations, stars are placed on branches with CFs that have 95% credibility intervals including 0 or 1, indicating low concordance among gene trees. The trees presented here are restricted to relationships among Microcebus individuals and species. Relationships among cheirogaleid genera were consistent across replicates and are presented in figure 5.

Coalescent-Based Species Tree Estimation

The majority of our BEST analyses resulted in patterns that indicated a lack of convergence on the posterior distribution. In our analyses of Microcebus and all other cheirogaleid genera, the initial use of prior distributions for θ with means of 0.0015 and 0.015 produced runs (50 million generations) with a wide range of lnL values and little convergence across replicates (results not shown). Our use of larger mean values for the θ prior tended to result in runs that more rapidly approached a stable distribution with what initially appeared to be greater convergence across independent replicates. However, when longer BEST analyses were run (500 million generations) using the two larger θ priors, our results still indicated a lack of convergence on a stable posterior distribution. For example, even after 250 million generations, the multiple replicates for each θ prior produced stable lnL distributions but with considerable variation (supplementary fig. S3A, Supplementary Material online). The largest lnL values were seen in a single replicate, using a mean θ prior of 0.15, which produced a stable distribution around an lnL of approximately −20,600. Similar results were achieved across the different heating values, indicating that this did not improve the ability of chains to find and converge on the same posterior distribution (results not shown).

BEST analysis of the larger Microcebus data set (excluding M. griseorufus and M. murinus lineages) resulted in similar patterns. Although replicate analyses appeared to converge on a similar sampling distribution early in the analysis, individual replicates would often make a large jump in lnL values (see supplementary fig. S3B, Supplementary Material online, for an example using a mean θ prior of 0.15). In other analyses, replicate analyses did not make large shifts in their posterior distributions but did not converge on the same posterior distribution (see supplementary fig. S3C, Supplementary Material online, for an example using a mean θ prior of 0.5). In all of our analyses of this data set, the replicate featuring a stable sampling distribution with the highest lnL values was never matched by another replicate.

Analysis of the M. griseorufus, M. murinus, and M. ravelobensis data set did produce results consistent with convergence on the posterior distribution (supplementary fig. S3D, Supplementary Material online). All analyses across different θ priors and heating schemes produced the same stable sampling distribution with a mean lnL of −13,742 (after a burn-in of 100 million generations). These results supported the M. griseorufus + M. murinus clade and the monophyly of M. murinus lineages with PPs = 1.0. Resolution within the M. murinus clade was much weaker, with the placement of M. murinus and the Bemanasy Microcebus sp. lineage in a clade with a PP = 0.43.

Discussion

Cheirogaleid Phylogeny

Our work here provides the first set of convincing DNA sequence-based results for the phylogenetic placement of the genus Phaner, the cheirogaleid genus that has received the least systematic attention. Studies of morphology (Stanger-Hall 1997), repetitive DNA (Crovella et al. 1995), and immunological distances (Sarich and Cronin 1976) have all produced conflicting phylogenetic relationships for Phaner, and previous mitochondrial-based (Pastorini et al. 2001) and nuclear-based (Horvath et al. 2008) DNA sequence studies of the Cheirogaleidae did not include Phaner in their taxonomic sampling. Our multilocus phylogenetic results are concordant with the SINE-based results of Roos et al. (2004) and provide substantial support for the placement of Phaner as the sister lineage to all remaining cheirogaleids. The resolution of this relationship is notable here because of its concordance across both concatenated trees and the Bayesian PC trees, with Bayesian CFs (7.0–7.7) indicating support from a high number of the nuclear loci. Similar patterns of phylogenetic resolution were seen for the monophyly of the Cheirogaleidae and for the placement of Cheirogaleus as the sister lineage to a clade containing Allocebus, Microcebus, and Mirza, all of which were consistent with previous DNA sequence–based phylogenetic results (Pastorini et al. 2001; Horvath et al. 2008). Collectively, these results indicate that the internal species tree branches for these relationships were long enough to produce concordant phylogenetic signal across most loci, and, therefore, the results seen in the concatenated trees are likely to represent a good estimate of the underlying phylogeny.

In contrast, the level of support for the resolution of relationships among Allocebus, Microcebus, and Mirza was less convincing. Although concatenated analyses consistently placed Microcebus and Mirza in a clade, often with moderate to high branch support (particularly when the mtDNA sequence data were included), CFs for this clade were considerably lower than for other inter-generic relationships (fig. 5), indicating substantial discordance among gene trees. Similar to the mitochondrial tree of Pastorini et al. (2001), the lengths of the internal branch leading to the clade of Microcebus and Mirza in our concatenated trees were substantially shorter than internal branches for other inter-generic relationships, suggesting a relatively short amount of time separating the divergences of Allocebus, Microcebus, and Mirza. This would explain the discordance among gene trees for the phylogenetic positions of these lineages but also indicates that caution should be used in interpreting any single-gene tree as a best estimate of their phylogeny. Continued systematic research, including the further use of coalescent-based Bayesian analyses to model gene tree discordance within a species tree framework, will likely be necessary to further elucidate the relationships among these three lineages.

Microcebus Phylogeny

Numerous studies have used gene trees to investigate lineage diversification of the mouse lemurs, primarily from the perspective of assessing cryptic species diversity (Yoder et al. 2000; Louis et al. 2006; Olivieri et al. 2007; Weisrock et al. 2010). Although analyses of multilocus sequence data have provided robust support for the delimitation of numerous independent geographic lineages (Weisrock et al. 2010), phylogenetic inferences into the spatial and temporal aspects of Microcebus diversification have been largely based on mitochondrial gene trees (Yoder et al. 2000; Yang and Yoder 2003; Louis et al. 2006). For example, the initial divergence within Microcebus has been argued to be either a split between eastern and western Madagascar populations coincident with wet and dry forest types (Louis et al. 2006) or a split between northern and southern biogeographic regions of the island (Yoder et al. 2000), both of which are supported by alternate reconstructions of the mitochondrial gene tree derived from different genic regions. Our point here is not to argue for or against particular hypotheses but to instead emphasize that the substantial gene tree discordance within Microcebus translates into an inability to make inferences about species tree evolution from any single-gene tree. Although we are limited in making specific phylogenetic hypotheses for the mouse lemurs, we do echo the conclusion of Heckman et al. (2007) that gene tree discordance concerning species-level relationships in Microcebus is most-likely driven by incomplete lineage sorting, this based on the paucity of signatures of introgression in mitochondrial gene trees and nuclear STRUCTURE plots (Weisrock et al. 2010). Furthermore, we also suggest that the substantial gene tree discordance resolved among mouse lemur lineages may be a signature of an underlying rapid radiation, a pattern similar to that seen in multilocus studies of other species radiations (e.g., Takahashi et al. 2001; Belfiore et al. 2008).

Allele Sampling in Multilocus Phylogenetics

The larger significance of this study was the demonstration that the results of phylogenetic analysis of concatenated nuclear sequence data can be substantially influenced by the choice of alleles in the concatenation process. Through phylogenetic analysis of replicate concatenated data sets in which alleles from individuals are randomly paired across genes, we uncovered three major patterns that indicate that caution is warranted when using gene concatenation. First, across replicate Bayesian consensus trees, concatenated-based relationships among Microcebus individuals and species varied substantially (fig. 3). With the exception of the placement of M. ravelobensis, M. griseorufus, and the M. murinus clade, all other Microcebus lineages had discordant phylogenetic placements in at least two replicates. Second, phylogenetic inconsistency across replicates was backed by strongly supported phylogenetic results for individual concatenated data sets and did not result from uncertainty in phylogenetic estimation. The number of distinct trees found in the 95% credible set of each concatenated posterior distribution was small (table 3) and the majority of branches in the consensus trees received strong measures of support (PPs ≥ 0.95). In other words, each concatenated replicate resulted in very strong support for different sets of relationships. Third, differences in phylogenetic reconstruction across replicates largely resulted from the sampling of trees from very different regions of tree space. This was particularly true for the nuclear concatenated data, which featured highly nonoverlapping posterior distributions for many replicates in MDS ordination space (fig. 4A) and relatively high RF distances between posterior distributions (table 4). The addition of the mtDNA data to concatenated analyses reduced the average distance between replicate posterior distributions of trees (fig. 4B and table 4) but still resulted in different, but strongly supported, trees.

The patterns revealed in our concatenated phylogenetic results have similarities to those identified in both simulation (Kubatko and Degnan 2007) and empirical (Belfiore et al. 2008) studies, where concatenation of sequence data generated from gene trees with high levels of discordance led to strongly supported but inaccurate phylogenetic reconstructions. Such conditions are likely to occur in species trees that feature short branch lengths between speciation events and high discordance among gene trees as a function of incomplete lineage sorting (Maddison 1997; Maddison and Knowles 2006; Kubatko and Degnan 2007). In these situations, concatenation of data from a single individual or OTU results in the amalgamation of alleles across loci with different underlying phylogenetic histories, and, probably not surprisingly, analysis of these data can result in an inaccurate estimate of the species tree. In our study, the lack of a known species tree for Microcebus and the Cheirogaleidae limits specific conclusions about the phylogenetic accuracy of any of our concatenated replicates. However, given the existence of a single species tree, the largely nonoverlapping posterior distributions across replicates, particularly with the nuclear data, indicated that many of the concatenated trees yield incorrect estimates of phylogeny, despite their strong measures of branch support. These phylogenetic results suggest that the Microcebus species tree may feature a series of short branch lengths and that its reconstruction presents a challenge to standard phylogenetic approaches.

The conclusions we infer here from our concatenated results are also backed by the results of our Bayesian concordance and BEST analyses. Across the BCA replicates, the PC tree varied in the set of relationships with the highest CFs, and in contrast to the concatenated results, relationships in the PC trees had substantially low CFs, indicating considerable discordance for relationships among Microcebus individuals and lineages across loci (fig. 5). Although this may be attributed, in part, to low sequence variation in some loci and limited resolution in individual gene trees, the robust resolution of many branches in the individual gene trees indicated the potential for actual gene tree discordance. Our attempt at producing a species tree using BEST produced results consistent with this gene tree discordance. Despite running our MCMC chains for as many as 500 million generations, replicate analyses failed to converge on the sampling distribution with the highest lnL values, indicating a failure to sample from the posterior distribution. This result is consistent with a species tree featuring many short branches and large ancestral population sizes, a set of conditions that will have produced substantial gene tree discordance and that could require very large numbers of genes to be resolved in a coalescent framework (Edwards et al. 2007). The patterns of gene tree discordance we see in our data are strongly suggested to limit the inferences we can make from the results of concatenated analyses.

The variation seen across the concatenated posterior distributions of trees also highlighted a challenge in the concatenation of nuclear data that is rarely addressed: Individuals and species have a direct comparison across gene trees, but their gene copies do not. When haploid sequences are collected from heterozygous genes within an individual, there is no straightforward way to concatenate the different alleles across genes: Should allele 1 from gene A be paired with allele 1 or allele 2 from gene B? Often the solutions in concatenated studies are to use a consensus sequence within a species-level OTU, to use degenerate base codings (e.g., R and Y) for polymorphic sites within individuals or to randomly sample an allele from each gene. Our approach here was to explore the effects of randomly pairing a single allele from each gene. The results of these concatenated explorations—that OTUs comprised of different combinations of alleles across genes can result in very different posterior distributions of trees—indicate that choosing which allelic sequences to use in the generation of concatenated should be an important consideration in multilocus studies. We expect results similar to ours to be seen in concatenated species tree reconstruction studies that feature both short internal branches (as found in Kubatko and Degnan 2007) and short tip branches, with both factors providing the opportunity for species or populations to maintain ancestral alleles. This can also be important for deep phylogenetic studies, anywhere in the tree where there is a short duration between speciation events (Edwards et al. 2005), but may be an especially important issue for the reconstruction of recent species radiations with short tip branch lengths and high rates of lineage formation.

Finally, we point out the difference in perspectives on the effect of sampling alleles between species tree methods that use intraspecific alleles to make inferences about the ancestral branching history of a species-level OTU (e.g., Liu et al. 2008; Kubatko et al. 2009; Heled and Drummond 2010) versus those that take a concatenated approach where the individual serves as the OTU. A number of recent studies have demonstrated that the sampling of a very small number of alleles per species in studies employing the former methods is sufficient to accurately reconstruct a tree (Hird et al. 2010; Ence and Carstens 2011). In contrast, we demonstrate here that the sampling of a single allele from an individual in concatenated studies has the potential to lead to phylogenetic inconsistency. Systematists using concatenated approaches should consider the potential for strongly supported, but inconsistent, phylogenetic results when sampling alleles within individuals and may consider performing a replicated approach similar to that used here to explore the potential for variation in their phylogenetic estimates.

Supplementary Material

Supplementary file, table S1, and figures S1–S3 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).