Abstract
An important challenge in statistical genomics concerns integrating experimental data with exogenous information about gene function. A number of statistical methods are available to address this challenge, but most do not accommodate complexities in the functional record. To infer activity of a functional category (e.g., a gene ontology term), most methods use gene-level data on that category, but do not use other functional properties of the same genes. Not doing so creates undue errors in inference. Recent developments in model-based category analysis aim to overcome this difficulty, but in attempting to do so they are faced with serious computational problems. This paper investigates statistical properties and the structure of posterior computation in one such model for the analysis of functional category data. We examine the graphical structures underlying posterior computation in the original parameterization and in a new parameterization aimed at leveraging elements of the model. We characterize identifiability of the underlying activation states, describe a new prior distribution, and introduce approximations that aim to support numerical methods for posterior inference.
Keywords: probabilistic graphical modeling, role model, gene-set analysis
1 Introduction
A common problem in statistical genomics concerns the points of contact between genomic data generated experimentally and exogenous functional information that has been accumulated by bioinformatics projects like GO and KEGG (The Gene Ontology Consortium, 2000; Kanehisa and Goto, 2000). In this rather extensive domain of data integration, functional information is used in two complementary ways. One mode is about data reduction. The experimentalist is faced with hundreds of genes that exhibit some interesting property in her experiment, and the inferential problem is to summarize the functional content of the identified genes. As a prime example, enrichment analysis seeks to identify functional categories that are over-represented in the experimentally identified gene list. Alternatively, functional categories are used to boost the signal-to-noise ratio. A weak gene-level signal differentiating two cellular states is easier to detect if it is consistent over a set of genes having some shared function. In either mode of application, the integration of experimental and functional data is a central component of the genomic data analysis.
A number of useful statistical methods and software tools have been developed to address the challenge. Fisher’s exact test and related random-set enrichment methods operate conditionally on the experimental data and aim to detect overrepresentation of a category among experimentally interesting genes (e.g., Drăghici et al., 2003; Beiβbarth and Speed, 2004; Grossman et al. 2007; Newton et al., 2007; Jiang and Gentleman, 2007; Bauer et al., 2008; Sartor et al. 2009). Other approaches test category differential expression from replicated microarray data (e.g., Barry et al., 2005; Subramanian et al., 2005; Efron et al., 2007; Liang and Nettleton, 2010), while others develop models of gene-level results using functional categories (Lu et al. 2008; Bauer, et al. 2010), or use categories as predictors in regression models (e.g., Park et al., 2007; Stingo et al., 2011). Careful comparisons among selected methods have helped to clarify their relative advantages and disadvantages (e.g., Goeman and Bühlmann 2007; Barry et al. 2008). This list of citations hardly does justice to the field, and a detailed evaluation of the state-of-the-art is beyond the present scope. Suffice it to say that all methodological contributions in this domain have made simplifying assumptions on how the functional information relates to the experimental data on test. The continued expansion of the functional record makes some of these simplifications ever-more problematic.
Variation in category size makes it difficult to infer a prioritized list of significant functional categories. Methods that test either over-representation or category differential expression suffer from a power imbalance across categories owing to this variation. Power is related to size of both effect and category; large categories may deliver a small p-value by virtue of large size and small effect, while scientific relevance is linked more to the size of the effect. Thus ranking categories by p-value tends to inflate the importance of large ones; while ranking them by an estimated effect tends to inflate the importance of small categories, since in these chance variation will more easily place them in a high ranking position.
As the functional record is complex and extensive, it necessarily encodes a substantial amount of overlapping information. GO organizes functional information in three directed acyclic graphs (biological process, molecular function, cellular component), wherein each graphical node is a functional category and directed edges convey proper-subset information. For example, the category response to hydroperoxide (GO:0033194) is a subset of response to oxidative stress (GO:0006979). It is less well appreciated that functional categories in GO overlap to a much greater extent than is suggested by any of the GO graphs. Of course overlaps among categories from different graphs are not immediately indicated, but there is also the issue that many pairs of categories share genes without one category being a proper subset of the other. A consequence of this phenomenon is that overlapping categories have positively correlated test results, often resulting in lists of significant functional categories that are unduly long (sometimes longer than an input list of significant genes!). An investigator may find that results of a statistical analysis have added relatively little insight because these results are muddied by complexities in the functional record that have been poorly accounted for.
Category overlap is related to the fact that many genes are multi-functional. The concept is called pleitropy in genetics, and it may be more the rule than the exception. For example, the PCNA1 gene (proliferating cellular nuclear antigen, 1) is involved in DNA mismatch repair; it plays another role in cell cycle regulation. At writing, 5056 human genes were annotated to 220 KEGG pathways, with over half these genes (2631) annotated to 2 or more pathways. Similarly, 14047 human genes were annotated to 13026 GO categories that contained between 1 and 500 genes, with a median number of 11 recorded functional properties per gene. (R package org.Hs.eg.db, version 2.4.6).
Category-differential-expression methods assert that a category is non-null if any of its contained genes is non-null. This basic premise is groundwork for the construction of test statistics and inference procedures, but it is at odds with the multi-functionality of genes. In the cellular state under experimentation, a gene may be non-null by virtue of one (or perhaps a subset) of its functions. A method which finds another of that genes’ functions to be non-null may have inferred a spurious association. The presence of spurious associations unduly limits and complicates inference about the functional content of gene-level data. By way of analogy, suppose that we’re watching a movie featuring an actor (e.g., Mike Meyers in The Spy Who Shagged Me) who plays more than one character (Dr. Evil, Austin Powers, & Fat Bastard). And suppose further that our movie-watching skills are so limited that rather than being able to recognize what characters are in a given scene, we only recognize the actors involved. Then of course the recognition that Mike Meyers is doing something interesting in the scene does not imply, for example, that Austin Powers is doing something interesting (maybe it is actually Dr. Evil)! In genomics we know that a gene can have different functional roles depending on the biological scene in which it plays a part. We may get closer to understanding that biology if our analytical methods are more in line with this fact.
Experimental data are measured on genes, while inference is required at the level of functional categories. Any legitimate method designed to infer something about a given functional category surely needs to use the experimental data on genes in that category. At issue is what other information ought to be used, and how that information should be incorporated into the calculations. Most category-inference methods are global: if they use any data beyond the gene-level data from the category on test, it is information from genome-wide summaries or summaries computed across the collection of categories. Basic enrichment methods, for example, use a genome-wide statistic on the proportion of genes that show some significant feature of interest. Many methods obtain category-specific p-values and then use the collection of p-values to get a false-discovery-rate correction. Global methods do not use specific information on category assignments of the genes in the category on test. We call a category-inference method local if, by contrast, it does use this functional information. Several local testing methods have been developed to utilize some overlap information (Jiang and Gentleman 2007; Grossman et al. 2007). Although useful, they suffer from inherent difficulties with sequential testing and they do not consider the full extent of category overlaps. Recently there has been a development of local category inference methods based on probability models of genetic and functional data (Lu et al. 2008; Bauer et al. 2010). These approaches are compelling because they address the overlap problem head-on and may provide an accurate representation of the the multivariate functional signal underlying observed data. They too, however, are limited by their computational complexity, by the nature of reported inferences, and by undue restrictions on gene-level data.
In the Bauer et al. (2010) model, non-null behavior starts with the functional category rather than the gene. Each gene inherits non-null behavior from non-null categories to which it is annotated. This is in contrast to the category-differential-expression methods, where a category is non-null if any of its contained genes is non-null. The apparently simple switch dramatically transforms the statistical problem. Inference on a given category relies on gene-level data on that category, but it also requires information on other functional properties of these same genes, since any non-null behavior may be attributable to a different function than the one on test. This suggests that gene-level data from genes in overlapping categories are also relevant, but again their behavior may be affected by yet other categories to which they are assigned. Continuing this regress, genes that are functionally distant from the category on test contribute to the final inference. Approximate Bayesian inference is possible via Markov chain Monte Carlo sampling (MCMC). We appreciate the transformative effect of MCMC, but we also recognize limits on the ability to assess Monte Carlo error; one cannot be confident in inferences derived from slowly mixing chains operating in high dimensions. Even if convergence is assured, there are limitations in what can be inferred using marginal posterior summaries as in Bauer et al. (2010). Aspects of functional-category inference suggest that the posterior mode would also be useful to compute, though this is beyond the reach of MCMC in high-dimensions. We discuss the point further in Section 6.
The present paper initiates the development of probabilistic graphical modeling for functional-category inference. Probabilistic graphical modeling is a highly active field at the interface of statistics and machine learning (e.g., Koller and Friedman, 2009). It considers how to organize and deploy inference computations derived from generative probability models for data using graphical structures and algorithms. Belief propagation algorithms (e.g., the junction-tree algorithm) use message-passing schemes to represent the results of inferential calculations on sub-problems. New algorithms that leverage advances in high-throughput computing enable message passing on large and complicated graphs (e.g., Mendiburu et al. 2007; Gonzalez et al. 2009). In Sections 2 and 3 of this paper, we examine the graphical structures underlying posterior computation, both in the original parameterization of Bauer et al. (2010), and in a new paramaterization that is designed to leverage simplifying elements of the model. We develop some theory to represent mappings between parameterizations; this has implications for posterior computation and it also clarifies identifiability and consistency issues. We introduce a new prior distribution designed to operate more naturally in the new parameterization. In Section 4, we investigate approximation schemes for reducing graph complexity and we present model extensions aimed at improving the performance of model-based local category inference. Finally, we deploy exact computations in two small examples to demonstrate properties of posterior inference (Section 5). Our numerical experiments use functional-category information made available through the Bioconductor project (Gentleman et al. 2004).
2 The role model and the category intersection graph
The role model has potential in a number of domains, so it is described here using generic terminology. We have a number of different parts p = 1,2, …, P, and from these are formed a number of wholes w = 1,2, …, W. The parts comprising each whole are known in advance and recorded in a P × W incidence matrix I = (Ip,w), where Ip,w = 1 if part p is in whole w, else it is 0. We’ll also say p ∈ w if Ip,w = 1. Each whole is comprised of at least one part, and each part can be present in more than one whole. (In our case, parts are genes and wholes are functional categories.) Experimental data are available on the parts, say x = {xp}. Depending on the particular application the data may take various forms; either a vector of measurements across multiple samples, or a summary statistic of some kind. The simplest case, and the one in focus in this paper, has xp the binary indicator of whether or not part p is reported on a short list of interesting parts. (The last note in Section 6 discusses more general forms of part-level data.) Observed data x are viewed as the realization of a random element X whose joint distribution depends on latent activation states Z = {Zw} of the wholes, which indicate whether each w is null (Zw = 0), or non-null (Zw = 1). We also use the language active and inactive to express Zw = 1 or Zw = 0, respectively. The simplest role model is:
| (1) |
| (2) |
where α,β, and π are unknown parameters all in (0,1), with α < β. Additionally, the model asserts conditional independence among {Xp} given {Zw}. The statement in (2) says that Xp has rate β if any of the wholes to which it contributes is activated; otherwise it has rate α. Bauer et al. (2010) described this model for genes and categories, and proposed to rank what we call the wholes by MCMC-approximated marginal posteriors P(Zw = 1|X = x).
The prior (1) requires amendment in order to cope with general collections of wholes. For example, if a whole w′ is fully contained in another w (as happens routinely in GO) then activities Zw and Zw′ ought to be related. In category inference, w′ corresponds to a property that is more specific than w. To say “property w is activated” is to say “genes with property w are activated” from which it follows that “genes with property w′ are activated”, and thus “property w′ is activated.” Notice that the implication is not symmetric. If a subset is activated it does not follow that a containing set is activated. Indeed a goal of the inference is to assess the proper level of granularity regarding the activity states of the categories as evidenced by the apparent activity states of the genes. As inference considers activity as a property both of individual parts and of sets of parts, we require a clear definition of their relationship. The following assumption is key.
Activation hypothesis
A set of parts is active if and only if all parts in the set are active.
Various implications follow. A single part p is active if p ∈ w for any w such that Zw = 1. This precisely expresses model (2) and the interpretation of an active part as one delivering a higher success probability on Bernoulli data than a non-active part. Also, if the whole w is the union of various subsets; then all those subsets being active is equivalent to Zw = 1. The activation hypothesis is equivalent to asserting that any subset of an active set is itself active. The hypothesis is related to the true path rule used in GO, to the extent that both convey logical constraints on collections of related categories. However, it seems not to have been expressed clearly in prior work. One might object to the activation hypothesis on the grounds that it is too strict, perhaps because it does not allow wholes to be activated by a subset of their parts. However, a sufficiently rich collection of wholes ought to include this relevant subset, and so if data point to activation of this subset, it is this subset that the inference procedure ought to detect (rather than the larger set). Furthermore, our language could get unduly complicated if we allow activated sets that contain no activated genes. A more important issue, however, concerns what we could ever hope to estimate about the whole-level activation states from partlevel data. We take up the issue again in the next section. For now, consider the set 𝒵 of valid activation-state vectors across the wholes
Although the i.i.d. prior on {Zw} gives positive probability to vectors outside of 𝒵, certainly we can amend the prior by conditioning to enforce the activation hypothesis.
Returning to the statistical inference problem, we aim to develop Bayesian posterior computations over activation states {Zw} in order to express concisely the functional content of our gene-level data. We could apply the MCMC approach of Bauer et al. (2010), but we are concerned about Monte Carlo error and also the restriction to marginal posterior summaries. Sometimes, limitations of MCMC can be overcome by numerical methods from probabilistic graphical modeling. From this perspective we start with a factorization of the joint posterior distribution into factors that have arguments localized on a certain undirected graph. Here we consider parameters α,β, and π in (1, 2) as fixed in order to simplify discussion. (Ultimately, we would like to estimate these from the data, and thus deploy empirical Bayesian computations, or possibly integrate them out.) The posterior distribution over whole-level activation states in the role model introduced above is:
| (3) |
where p(z) is the suitably conditioned i.i.d. Bernoulli(π) prior distribution. Although expressed as a product over parts, p(z|x) also can be expressed as a product of data-dependent factors that are local functions on the intersection graph of the wholes. (The intersection graph has nodes equal to the wholes and edges between wholes that share parts.)
Proposition 1 The role-model posterior in (3) satisfies:
| (4) |
where ψw is a data-dependent function of both zw and neighboring states znb(w) = {zw′ : w ∩ w′ ≠ ϕ}.
A proof is in Section 6. Because the joint posterior factorizes into local functions over the intersection graph, this graph can be used, in principle, to support various inference computations implied by the role model. Figure 1 gives a simple example of the category intersection graph. Ideally, one would like to utilize the entirety of GO or KEGG. However the associated intersection graphs are highly complex and prohibit exact numerical methods (e.g., Figure 2). Fortunately, inference in large-scale problems can proceed using alternative formulations or approximations, as we now discuss.
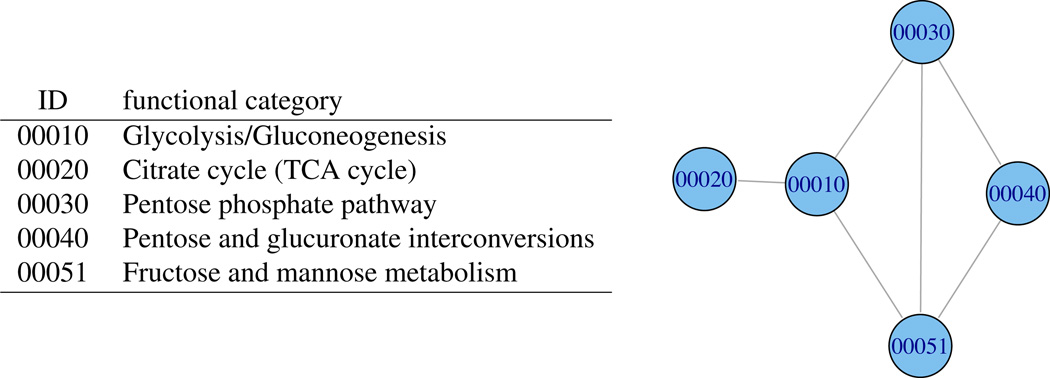
Figure 1.
Category intersection graph from 5 KEGG pathways (the first 5 by ID order). Sets are of size 62, 32, 26, 25, and 33 genes, respectively. Edges in the graph indicate set overlap.
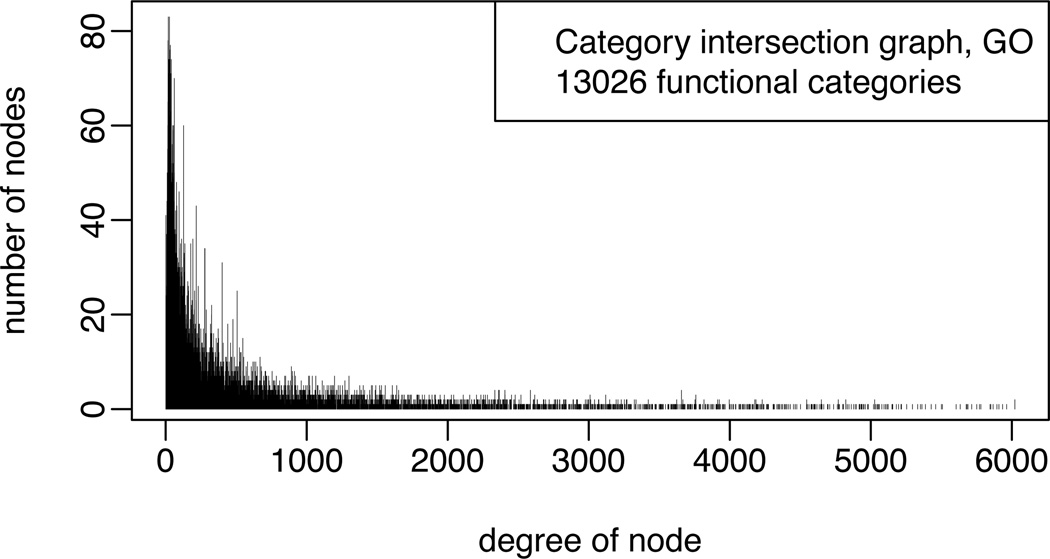
Figure 2.
Degree distribution of intersection graph of GO (categories holding between 1 and 500 human genes). It is somewhat remarkable that so many overlaps are possible. The most extreme case is the category cell motility (GO:0048870), which annotates 495 human genes and shares genes with 6160 other categories among the 13026 GO categories that annotate between 1 and 500 human genes. These 13026 categories annotate 14047 genes. The median number of other category assignments per cell-motility gene is 64, and one gene happens to be in 631 other categories.
3 Reparameterization and the function profile graph
A reparameterization of the role model (1,2) offers another route to approximate inference. This reparameterization supports the same sampling model and it continues to rely on graphs to organize posterior computation, but in many cases it delivers simpler overall graph structure. Recall the incidence matrix I indicating which parts are in which wholes. Nothing so far disallows the possibility that different parts have the same rows in I. To proceed further it is helpful to consider the distinct rows of I, which we call atoms, following Boca et al. (2010). In category inference an atom corresponds to a particular profile of 0’s and 1’s across the functional record; it is the set of genes (parts) that have the same profile of category inclusions and exclusions. Each part p is an element of some atom. We say that a whole w is assigned to an atom ν, and express this w → ν, if and only if Ip,w = 1 for all p ∈ ν. Similarly w ↛ ν if and only if Ip,w = 0 for all p ∈ ν. Indeed, the atom ν is the intersection of wholes assigned to it and whole complements for wholes not so assigned. Thus, rather cryptically,
While wholes (categories) can overlap, atoms cannot. Furthermore, every whole is the union of atoms to which it is assigned:
and in this way the atoms form a sort of basis for the collection of wholes. Table 1 shows an example. Boca et al. (2010) introduced atoms in a decision-theoretic analysis of the same basic data-integration problem. Their aim was somewhat different from ours, in that they sought a subset of atoms (rather than functional categories) whose activation could explain gene-level data.
Table 1.
Eleven atoms from the example shown in Figure 1 where there are 5 wholes (each a KEGG pathway). The atom entry gives the unique row of the incidence matrix I associated with the involved genes. For example, there are 4 genes involved in both Glycolysis/Gluconeogenesis and Fructose and mannose metabolism (the first and last pathways) and not involved in the other three.
| atom | # genes | atom | # genes |
|---|---|---|---|
| 00011 | 1 | 10100 | 3 |
| 00110 | 1 | 01000 | 25 |
| 10101 | 8 | 00001 | 20 |
| 11000 | 7 | 00100 | 14 |
| 00010 | 23 | 10000 | 40 |
| 10001 | 4 |
While the functional record is becoming ever more complex, the number of atoms is bounded by the number of genes, and this is far smaller than the theoretical maximum 2W. In other words, the vast majority of functional profiles do not manifest themselves. This feature is one reason why considering the role model from the atom perspective has potential advantages. To pursue this, we first construct atom-specific activation Bernoulli variables from the activation states of the wholes:
| (5) |
Again, the atom is activated if any of the wholes to which its parts are assigned is activated. The range of mapping (5) is
| (6) |
where N is the number of atoms. The notation is intended to convey the set of all atom-level activation vectors a that could have been produced from whole-level activation vectors z which satisfy the activation hypothesis. Indeed this property is convenient, because, as we prove in Section 6:
Proposition 2 The mapping (5) from 𝒵 to 𝒜 is one-to-one, and has inverse
A computational strategy is supported by this finding. We perform posterior computations over atom-level activations in 𝒜, and then transform findings back to the whole-level of interest. The finding also supports the identifiability of whole-level activation states from part-level data. If part-level data were to increase, then we would consistently estimate the atom-level activation states. Thus we would consistently estimate the whole-level activation states by Proposition 2. Without the activation hypothesis, there could be states that are beyond our ability to estimate, regardless of the amount of part-level data.
Rather conveniently, the role-model posterior distribution (3) can be re-expressed on the transformed scale as:
| (7) |
where xν = Σp∈ν xp summarizes the part-level data at atom ν, and where p(a) is a prior distribution. Conditionally upon the activation states, xν is the realization of a Binomial random variable, based on nν = Σp∈ν 1 trials (i.e., the atom size). Thus (7) simplifies further
| (8) |
Just as the intersection graph of the wholes is the data structure supporting posterior inference in the original parameterization, there is another graph – we call it the function profile graph – that supports atom-level computations. Its nodes are the atoms. One might try having an edge between ν and ν’ if a common whole w is assigned to both, but this is more than we need. Instead, we create a directed edge from ν to ν’ if: (1) the assignments at ν′ are a proper subset of the assignments at ν, and also (2) there is no other atom ν* with assignments that are a subset of assignments at ν and a superset of assignments at ν’ (Figure 3). We say ν is a parent of ν’ and ν’ is a child of ν.
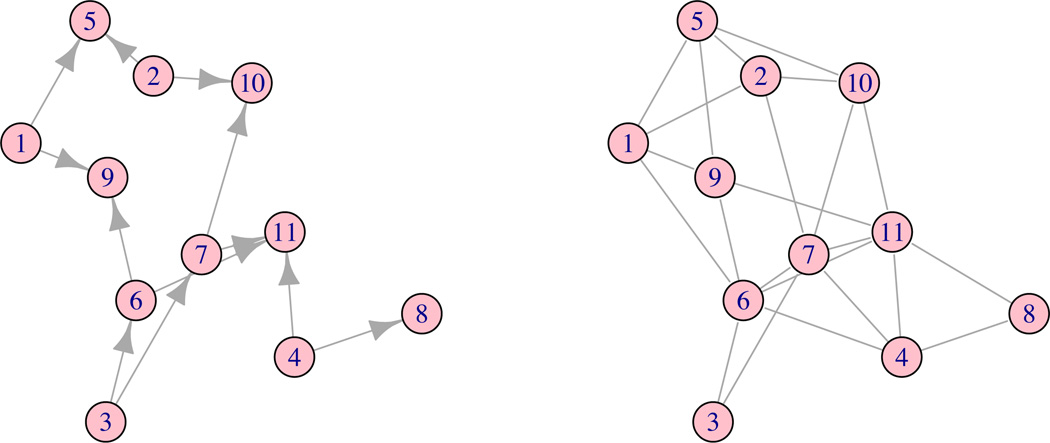
Figure 3.
Reparameterizing the role model with a function profile graph: The nodes in each panel represent 5 atoms. Each atom shows a profile of assignments (1) or not (0) to 4 wholes w. A directed edge goes from ν to ν′ if the assignments at ν include those at ν′ (except we omit redundant edges e.g., no edge from 1110 to 0100.) The middle and right panels show logical dependencies on activity variables. E.g., in the middle panel, knowing Aν = 0 implies Aν′ = 0 for all downstream atoms, and knowing Aν′ = 1 on the right panel implies Aν = 1 for all upstream atoms.
The relevance of the function profile graph becomes more apparent when we occupy the nodes with atom-level activity variables Aν. We see that the edges of the function profile graph express role-model information. For example, knowing Aν = 0 implies that for no w assigned to ν do we have Zw = 1. Naturally this forces Aν′ = 0, when ν′ is a child of ν, since assignments to ν′ are a subset of those going to ν. By the same token, knowing that Aν′ = 1 is equivalent to knowing that at least one w assigned to ν′ has Zw = 1, which forces Aν = 1 when ν is a parent of ν′. Essentially, the logic of atom-level activations is encoded by the function profile graph. Let 𝒜* denote all possible binary activation vectors a = (a1,a2, …, aN) that respect the function profile graph in the sense above; i.e.,
| (9) |
Curiously, the collection 𝒜 in (6) does not necessarily constitute all of 𝒜*, though we do have 𝒜 ⊂ 𝒜*. (See Section 6.) Importantly, the mapping from 𝒜* does map onto the original set of activity vectors 𝒵, in the mathematical sense.
Part of the computational complexity in the original parameterization stems from the fact that the category intersection graph allows an arbitrary function of Zw on neighboring nodes to affect the state at a given node (i.e., the ψw in (4)). But model (2) encodes a very specific function (through max), which is used to advantage in the proposed reparameterization. There is an effect on graph properties, which in some cases, leads to simpler posterior computations.
As we review briefly at the end of this section, the computational tools from probabilistic graphical modeling are developed from factorizations and their associated undirected graphs. To support inference we need an undirected version of the function profile graph, which we obtain by a form of moralization used in graphical models analysis. Specifically, we include an undirected edge between any two nodes ν and ν′ that are both parents of a common child. We also include an undirected edge between any two nodes ν and ν′ that are children of a common parent. (This two-way moralization comes from the fact that information flows both ways along a given directed edge.) Finally we make all remaining directed edges undirected. The resulting graph is the undirected function profile graph. An example is given in Figure 4.
Figure 4.
Function profile graphs for the small KEGG example shown in Figure 1, with 11 atoms as listed in Table 1.
Proposition 3 For a suitable prior p(a) over 𝒜*, the posterior distribution in (8) is the product of functions ψ̃ν that are local in the undirected function profile graph:
| (10) |
Coupled with Proposition 2, the above result indicates that we can perform inference computations on the function profile graph, and then transform back as needed to get inference on whole-level activation states. In GO, for example, the transformation provides a much simpler graph (Figure 5). Unfortunately this simpler graph is still too complicated for exact numerical methods. Approximation methods discussed in the next section offer several approaches to address this challenge.
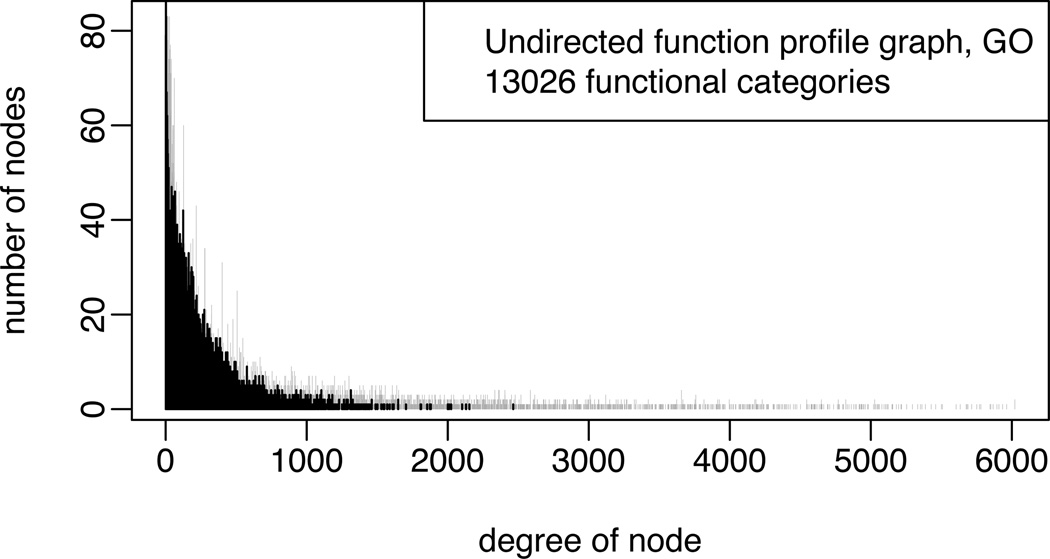
Figure 5.
Degree distribution of the undirected function profile graph of GO (categories holding between 1 and 500 human genes). The maximal degree is 2464; the graph itself has 10366 nodes (atoms). The corresponding results for the category intersection graph (from Figure 2) are repeated here in grey. Not shown are results for the directed function profile graph, which is much simpler, having maximal degree 268.
4 Approximations and graph-based computations
Filtering categories
Instead of including the entirety of GO or KEGG in a role-model computation, we could select a smaller set of categories based on an initial filter. For example, we could filter by marginal p-value from an enrichment test. We investigated this approach using three gene lists obtained by Keller et al. (2008) in a murine study of diabetes. Using microarrays, this study profiled genome-wide expression of of islet (Data A), adipose (Data B), and gastrocnemius (Data C) cells, among others not shown. Of interest were genes exhibiting co-expression within each tissue; co-expression modules holding 85, 150, and 114 genes, respectively, were identified for followup. Role-model computations address the functional content of these lists. We use the lists here simply to demonstrate how much graph simplification can be achieved by filtering.
Using a normal approximation to Fisher’s exact test, as implemented in the R package allez (Newton et al. 2007), we considered GO and KEGG categories holding no more than 500 genes, and two p-value cut-offs (p = 0.01, p = 0.001). Table 2 summarizes the complexity of the category intersection graph and the function profile graph derived from these data-dependent category collections. The maximal degree of the function profile graph is usually smaller than the maximal degree of the category intersection graph, with graph complexity substantially reduced compared to the case of no filtering. Even so, the graphs remain too complex for the deployment of exact numerical methods. One solution strategy is to approximate the functional record itself, as we discuss next.
Table 2.
Graph properties when filtering GO and KEGG according to marginal enrichment p-value. For each data set, the rows correspond to filtering at p = 0.01 and p = 0.001, respectively. The number of nodes in the intersection graph equals the number of categories that are significant by the marginal test. max D and mean D refer to the maximal and mean degree of the graph. The function profile graph has more nodes (atoms) than the intersection graph and also fewer edges per node, on the average, but similar maximal degree. Data sets are discussed in the text.
| intersection graph | function profile graph | |||||||
|---|---|---|---|---|---|---|---|---|
| undirected | directed | |||||||
| Data | # nodes | max D | mean D | # nodes | max D | mean D | max D | mean D |
| A | 465 | 394 | 149.3 | 2190 | 409 | 72.1 | 85 | 7.9 |
| 348 | 285 | 106.9 | 1553 | 284 | 55.8 | 46 | 7.4 | |
| B | 313 | 234 | 69.7 | 1190 | 195 | 32.4 | 44 | 6.1 |
| 264 | 196 | 58.9 | 922 | 132 | 29.3 | 38 | 5.9 | |
| C | 398 | 328 | 106.4 | 2015 | 355 | 55.1 | 56 | 7.1 |
| 280 | 197 | 61.1 | 1123 | 187 | 37.2 | 34 | 6.4 | |
Ablating annotations
There is a class of approximation schemes that work by modifying the incidence matrix I to have fewer non-zero entries. We describe one such ablation scheme that retains a fraction of each part’s column assignments, preferentially retaining assignments to small wholes. The rationale is that a small whole is more proximal to a part than a large one, and so its data, on the average, may be more relevant to the state of that part than the data from a larger whole. Without loss of generality, suppose that the columns of I (i.e., the wholes or categories) are organized in increasing order of size. Fix a retention parameter ρ ∈ (0,1]. Create a new incidence matrix Ĩ of the same dimension as I, initially with Ĩ = I. Working one part p (i.e., row) at a time to update Ĩ, let denote the number of wholes containing part p. If Ip,w* = 1, set Ĩp,w* = 0 if
| (11) |
with the caveat that every p be retained to at least one whole. The resulting incidence matrix is more sparse than the original, and it produces ever simpler graphs as the retention rate ρ is reduced. Table 3 shows the effects of ablation on the function profile graph of KEGG. Results for GO are similar (not shown). Knowing how this ablation affects posterior probabilities remains to be evaluated.
Table 3.
Ablating annotations in KEGG. We start with the 5052 genes annotated to 219 KEGG pathways containing no more than 500 genes. The category-defining incidence matrix is ablated as in (11), and properties of the undirected function profile graph are obtained. The right-most column shows the size of the largest clique in a triangulated version of the undirected function profile graph.
| ρ | # atoms | genes per atom | max D | mean D | max clique |
|---|---|---|---|---|---|
| 1 | 1093 | 4.6 | 214 | 34.3 | 436 |
| 1/2 | 735 | 6.9 | 110 | 20.4 | 249 |
| 1/4 | 395 | 12.8 | 41 | 7.8 | 59 |
| 1/8 | 260 | 19.4 | 24 | 2.9 | 13 |
| 1/16 | 220 | 23.0 | 8 | 1.3 | 5 |
The proposed ablation scheme increases the average size of atoms and reduces the complexity of the function profile graph. Ablation does not remove part-level data from the system, nor does it remove functional categories. Rather, heavily annotated parts are simplified and they convey their effect directly to the smallest wholes containing them. Consider, for example, two overlapping wholes w1 and a larger one w2. With ρ < 1, the atom w1 ∩ w2 is affected. The annotation of those parts to the larger whole is ablated, and the parts (and their data) are delivered to the smaller whole. In this way the ablated incidence matrix delivers posterior computations over a reduced collection of atom activations; from results of that inference, we can trace back to the real atoms and infer activations over the real functional categories.
Graph-based computations
Our premise is that numerical methods from probabilistic graphical modeling can support posterior computation for the role model. We are motivated partly by the discrete nature of functional-category inference and partly by advances in this domain of statistical computing. Our theoretical considerations suggest what graphs might be used, and our numerical experiments provide some insight into the properties of these graphs for GO and KEGG. Very little has been said so far about the actual calculations and how these need to be organized. We make a few brief remarks here.
There are several ways to organize exact belief propagation algorithms. By one route, the supporting undirected graph is the conditional independence graph associated with the joint posterior under consideration. This graph is triangulated (every cycle of 4 or more nodes has an edge between non-adjacent nodes) by adding edges if necessary, and then its cliques (maximal complete subgraphs) are found. A junction tree is formed, with nodes equal to these cliques, and with edges between these nodes that satisfy the running intersection property. That is to say, if a node from the original graph is in any two cliques (nodes in the tree), then it is in every clique-node on the unique intervening path in the tree. This property is key for subsequent algorithms to properly marginalize activation states inside the graph. A number of technical issues affect this computational sequence, but they are routinely addressed using graphical algorithms. Inference proceeds via message passing. In a simple approach to computing the marginal posterior distribution of a variable in some particular tree node, we make that node the root of the tree and we send messages towards that root from any ready nodes. A node is ready after it has received messages from all its neighbors that are distal from the root. The messages themselves are vectors holding conditional probabilities of data in the distal nodes conditional on the activation states at the node receiving the message. By the rules of probability, outgoing messages are computed by summing over certain latent activation states, and it is this component of the computation that is very sensitive to graph complexity. At some point the exact posterior computation requires manipulating 2M sums, where M is the size of the largest clique represented in the junction tree: hence our interest in the maximal clique size of the triangulated graph (Table 3). Evidently, exact computations are feasible using the atom transform in an approximate version of the problem in which we ablate weakly informative annotations.
In loopy belief propagation we give up on exact posterior computation. We do not attempt to triangulate the original graph, find cliques, or form a junction tree. One approach uses factor graphs, which are bipartite graphs having nodes for factors and other nodes for arguments of those factors (Kschischang et al. 2001). We emphasized the factor structure of posterior distributions in both Proposition 1 and Proposition 3 because it is relevant to loopy belief propagation on the factor graph. Edges go between arguments and any factors in which they participate, and so the degree structure of the factor graph is essentially the same as the degree structure of the undirected graphs we have thus far considered. Approximate posterior computation proceeds by transmitting conditional probability messages along edges of the factor graph. Without further intervention, the complexity of these computations is exponential in the maximal degree of the graph (rather than clique size). Advances such as in Mendiburu et al. (2007) and Gonzalez et al. (2009) indicate that accurate and computationally efficient algorithms may be feasible on large and complex graphs, such as those we have with model-based inference and functional categories.
5 Two small examples
As demonstration of role-model posterior inference, we consider here two artificial examples that display properties relevant to more realistic scenarios. The data sets are smaller than would occur in practice in order to facilitate exact computations and a clear view of relevent inference properties.
The first example (A) involves the 5 KEGG pathways of Table 1, covering 146 genes. Shown in Table 4 are summaries of gene-level data on the 11 atoms in this example, where each gene provides a binary indicator of its apparent activity. Table 5 shows this data at the set level, and compares the raw rate of apparent activity xc/nc with the (one-sided) Fisher p-value and with the (estimated) marginal posterior probability of activity from model (1). (Parameters α, β, and π were estimated by marginal maximum likelihood, and so the inference is empirical Bayesian.) All inference methods identify KEGG pathway 00030 as most interesting, with 11/26 of its genes indicating the active state. The example is more telling in the assessment of other pathways. Pathway 00040 is ranked second best by posterior probability but second worst by other statistics. This change in ranking has to do with the structure of pathway overlaps. Pathway 00010 has the second best raw rate (10/62), but it is not highly ranked by posterior probability because a number of these 10 active genes are discounted owing to their participation in other pathways. This phenomenon is expected to persist in more realistic examples: the marginal posterior computation automatically discounts the contribution of genes to one functional category if the activity of those genes can be explained by compensatory factors.
Table 4.
Example A: atom level data on KEGG example from Table 1
| atom ν | size nν | xν | atom ν | size nν | xν |
|---|---|---|---|---|---|
| 00011 | 1 | 0 | 10100 | 3 | 2 |
| 00110 | 1 | 1 | 01000 | 25 | 1 |
| 10101 | 8 | 4 | 00001 | 20 | 1 |
| 11000 | 7 | 1 | 00100 | 14 | 4 |
| 00010 | 23 | 2 | 10000 | 40 | 3 |
| 10001 | 4 | 0 | Totals | 146 | 19 |
Table 5.
Inference in example A: estimates use π̂ = 0.49, α̂ = 0.10, β̂ = 0.15
| KEGG ID c | size nc | xc | xc/nc | Fisher p | P̂(Zc = 1|data) |
|---|---|---|---|---|---|
| 00010 | 62 | 10 | 0.16 | 0.27 | 0.30 |
| 00020 | 32 | 2 | 0.06 | 0.94 | 0.28 |
| 00030 | 26 | 11 | 0.42 | 0.00 | 0.89 |
| 00040 | 25 | 3 | 0.12 | 0.66 | 0.40 |
| 00051 | 33 | 5 | 0.15 | 0.46 | 0.30 |
Table 6 presents basic data on a second example (B), including the atoms-to-wholes incidence matrix and some data on the 11 atoms that constitute the 7 wholes. The relatively high rate of pairwise overlap among the wholes is intended to model redundancies such as those evident in much of GO. Naturally, overlaps may make it difficult to uncover underlying signals, but the example is rigged so that all atoms contributing to whole #4 appear fully activated. Whole-level data and marginal posterior summaries (for one fixed parameter setting, not estimated) are shown in Table 7. Not unexpectedly for this highly stylized example, the marginal posterior probabilities are maximized at whole #4, and decrease through wholes that have lower empirical activity rates. More interstingly, the example suggests a certain deficiency associated with the marginal posterior inference. Specifically, three wholes {3,4,5} would be named on a short list of wholes targeting no more than 50% posterior false discovery rate. In fact, the gene-level activity data are well explained using only the activation of whole #4. This is the maximum a posteriori (MAP) estimate of the joint state. We know that the MAP estimate is the Bayes estimate under 0–1 loss, while a Hamming-loss delivers the estimate {3,4,5} (e.g., Carvalho and Lawrence, 2008). It is not a completely academic issue in this case, because redundancies in the wholes cause negative correlations in the joint posterior (Table 8). For example, the state Z4 is negatively correlated with all other Zw’s (recall they are i.i.d. and thus uncorrelated in the prior.) After calling Z4 = 1 we might subsequently discount the possibility of either Z3 = 1 or Z5 = 1, since Z4 = 1 already explains the data. The negative correlations are not large in this example, but they may be greater in practice and, in any case, they suggest greater parsimony in the MAP estimate. The general phenomenon revealed by this example is discussed further at the end of the next section. Having access to all sorts of posterior summaries surely will benefit practice, although at present realistic problems permit only MCMC computation and marginal rather than joint posterior summaries.
Table 6.
Incidence matrix and atom data in artificial example B
| whole w | data | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| atom ν | 1 | 2 | 3 | 4 | 5 | 6 | 7 | xν | nν |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| 2 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 2 |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 2 |
| 4 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 2 | 2 |
| 5 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 |
| 6 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 2 | 2 |
| 7 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 2 | 2 |
| 8 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 |
| 9 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 2 |
| 10 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 2 |
| 11 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 |
Table 7.
Marginal posterior inference, artificial example B: π = 1/2, α = 1/2, β = 3/4
| whole w | nw | xw | P(Zw = 1|data) |
|---|---|---|---|
| 1 | 10 | 7 | 0.39 |
| 2 | 10 | 8 | 0.46 |
| 3 | 10 | 9 | 0.52 |
| 4 | 10 | 10 | 0.58 |
| 5 | 10 | 9 | 0.52 |
| 6 | 10 | 8 | 0.46 |
| 7 | 10 | 7 | 0.39 |
Table 8.
Posterior correlations among {Zw}, artificial example B.
| whole w | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | 1.00 | |||||||
| 2 | 0.07 | 1.00 | ||||||
| 3 | −0.01 | −0.02 | 1.00 | |||||
| whole w | 4 | −0.06 | −0.08 | −0.10 | 1.00 | |||
| 5 | 0.00 | −0.01 | −0.03 | −0.10 | 1.00 | |||
| 6 | 0.01 | 0.00 | −0.01 | −0.08 | −0.02 | 1.00 | ||
| 7 | 0.00 | 0.01 | 0.00 | −0.06 | −0.01 | 0.07 | 1.00 | |
6 Proofs and notes
Proposition 1: The posterior is proportional to the prior p(z) times the likelihood . Taking the likelihood first, factors p(xp|z)= p(xp|maxw*:p∈w* zw*) that involve a given whole w are from all those parts p ∈ w, and thus depend on the activation states zw* for any other wholes w* that also contain those p’s; that is znb(w). There is not a unique assignment of these part-based factors to whole-based factors ψw in (4), but any such assignment must allow the possibility that at most zw and the neighboring activation states contribute to ψw.
By independence, Bauer’s i.i.d. Bernoulli(π) prior for the Zw’s factorizes over the category intersection graph. It remains to confirm that such factorization continues when we condition each realization z to satisfy the activation hypothesis 1[z ∈ 𝒵]. The activation hypothesis is equivalent to saying that any subset of an activated set is active, which is a combination of properties of sets and their neighboring subsets.
Proposition 2: Let a ∈ 𝒜 denote a vector a = (a1,a2, …, aN) of atom-level activation states. This vector results from mapping, through (5), some vector z = (z1, z2, …, zW) ∈ 𝒵 of whole-level activation states satisfying the activation hypothesis. Suppose we have another point z* ∈ 𝒵 for which z* ≠ z and z* also maps to the same vector a. If we reach a contradiction then no such z* exists, and the mapping is one-to-one.
As we are fixing the vector a, we can partition the atoms into those ν for which aν = 0 and those for which aν = 1. Call these respective index sets V0 and V1. First consider ν ∈ V0. By supposition and definition of aν,
| (12) |
Thus all sets w assigned to ν must have . That is, at all wholes w assigned to any ν for which aν = 0.
Next consider some ν ∈ V1. In contrast to (12), we have
| (13) |
Either side can be zero by virtue of any one of the factors, and so we do not immediately get . However, we can eliminate from both sides of (13) any factors corresponding to sets w already considered above that map to some other atom ν′ with aν′ = 0. Then (13) reduces to
| (14) |
Any w in this set {w : w → ν, w ↛ ν′ ∈ V0} may be comprised of multiple atoms, but all of them are in V1 and thus are activated, like ν itself (aν = 1). Since w equals a union of activated atoms, it must be activated, by the activation hypothesis. That is, for all w in (14), . By applying this argument to all ν ∈ V1, we complete the proof that for all wholes, and thus mapping (5) is one-to-one. The inversion formula encodes the rule that any subset of an activated set of parts is activated.
Proposition 3: From (8) the posterior p(a|x) is proportional to a prior p(a) times a product of atom-specific (likelihood) factors. Thus it suffices to find a prior p(a) that is local on the undirected function profile graph. We have restricted the domain to vectors a = (a1,a2, …, aN) in 𝒜*, according to (9). Note that this restriction can be presented as a local function on the function profile graph:
where B1,ν and B2,ν encode the two constraints in (9). Various priors are possible. A simple one entails i.i.d. Bernoulli(π) atom activities Aν that are then conditioned to be in 𝒜*.
There are problems in trying to use Bauer’s i.i.d. Bernoulli(π) prior on the Zw’s to induce a prior over 𝒜. For one, we needed to amend this prior so that the Zw’s satisfy the activation hypothesis. A larger issue is that the induced distribution may not be local on the function profile graph. For example, a given Zw might be assigned to two atoms that are unconnected in the function profile graph. Choice of prior has an effect on the computations.
We mentioned in Section 3 that for some collections of wholes, 𝒜* ≠ 𝒜. As an example, consider three wholes made from three parts, with incidence matrix
Every pair of wholes (columns) overlaps, so the category intersection graph is complete. But no profile of assignments is a subset of any other, so the function profile graph has no edges. The atom-level activation vector (1,0,0) is not a possible result of any whole-level activations, since activating any sets would activate two or three atoms.
Marginal posterior inference versus MAP inference
Even if MCMC convergence is assured, there is a problem in using it to drive inference about non-null functional categories. Suppose that 𝒞true holds all the truly non-null categories, and 𝒞α,marg holds a list of estimated non-null categories, estimated by marginal computations set up to target a false discovery rate of α = 5%, say. Typically, this would go by calling a category non-null if its MCMC-estimated marginal posterior probability of being null is less than α. Considering the positive association of related GO categories (in terms of gene content), and considering a potential sparsity in the true signal 𝒞true, it is quite likely that related categories will be negatively associated in the joint posterior distribution, given experimental data (as in artificial example B, Section 5). Simply put, if taking one category to be non-null explains the nonnull’ness of some gene-level data, then there is no incentive for a related category to be non-null. As a consequence of this negative posterior association, there will be a discordance between marginal findings in an FDR-controlled list and the actual state of 𝒞true. The true joint state may be much simpler (i.e., many fewer non-null categories), but measuring this state is not within the reach of MCMC for even a moderately-sized problem. Arguably, the joint state is better estimated in this case by the maximum a posteriori (MAP) estimate, which is the Bayes estimate under 0–1 loss. The MAP estimate may be associated with a high level of posterior uncertainty, as Bauer et al. (2010) argue, but its relative simplicity may be useful for providing a concise summary of functional content. Ideally the analyst is able to compute both marginal posterior summaries and MAP summaries to make the most informed inferences.
Extending the role model
Bauer’s model is limited by its restriction to binary gene-level data and by an assumed homogeneity of responses within the activated and inactivated classes. Inactivated states all deliver conditionally independent responses with a common success probability α, and activated states similarly deliver responses with success probability β > α. This constrains the atom level counts xν = Σp∈;ν xp to be Binomially distributed given the activation states. A more flexible approach within the same general framework allows each part p to have its own Beta distributed success probability; then atom counts xν are more broadly distributed as Beta-binomial counts. In place of two basic parameters α and β we need 4 parameters to encode the activated and inactivated Beta distributions; this seems to be a small price for the added flexibility. Posterior computations may also benefit from the flattening out of the posterior distribution over activation states. Yet further extensions are natural, such as to quantitative responses and exponential-family observation models.
Software
Tools in R (version 2.12.1) were used throughout. For annotation information, we used Bioconductor packages org.Hs.eg.db and org.Mm.eg.db, both versions 2.4.6. For graph computations we used igraph version 0.5.5-1 (Csardi and Nepusz, 2006), RBGL version 1.26.0 (Carey et al. 2010), and gRbase version 1.3.4 (Ren et al. 2010).
Acknowledgments
This work was funded in part by R01 grants ES017400, GM076274 and DE017315. Qiuling He was supported by a fellowship from the Morgridge Institute of Research administered by the UW program, Computation and Information in Biology and Medicine. The authors thank Michael Gould for helpful discussions and Giovanni Parmigiani, Simina Boca, and their co-authors for sharing a preprint of Boca et al. 2010.
Contributor Information
Michael A. Newton, University of Wisconsin, Madison
Qiuling He, University of Wisconsin, Madison.
Christina Kendziorski, University of Wisconsin, Madison.
References
- Barry WT, Nobel AB, Wright FA. Significance analysis of functional categories in gene expression studies: a structured permutation approach. Bioinformatics. 2005;21:1943–1949. doi: 10.1093/bioinformatics/bti260. [DOI] [PubMed] [Google Scholar]
- Barry WT, Nobel AB, Wright FA. A statistical framework for testing functional categories in microarray data. Annals of Applied Statistics. 2008;2:286–315. [Google Scholar]
- Bauer S, Grossman S, Vingron M, Robinson PN. Ontologizer 2.0– a multifunctional tool for GO term enrichment analysis and data exploration. Bioinformatics. 2008;24:1650–1651. doi: 10.1093/bioinformatics/btn250. [DOI] [PubMed] [Google Scholar]
- Bauer S, Gagneur J, Robinson PN. GOing Bayesian: model-based gene set analysis of genomic-scale data. Nucleic Acids Research. 2010;38:3523–3532. doi: 10.1093/nar/gkq045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beiβbarth T, Speed TP. GOstat: Find statistically overrepresented Gene Ontologies within a group of genes. Bioinformatics. 2004;20:1464–1465. doi: 10.1093/bioinformatics/bth088. [DOI] [PubMed] [Google Scholar]
- Boca S, Corrada Bravo H, Leek JT, Parmigiani G. A decision-theory approach to set-level inference for high-dimensional data. Johns Hopkins University Biostat Working Paper. 2010;211 [Google Scholar]
- Carey V, Long Li, Gentleman R. RBGL: An interface to the BOOST graph library, R package version 1.26.0. www.bioconductor.org.
- Carvalho LE, Lawrence CE. Centroid estimation in discrete high-dimensional spaces with applications in biology. Proceedings of the National Academy of Sciences. 2008;105:3209–3214. doi: 10.1073/pnas.0712329105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csardi G, Nepusz T. The igraph package for complex network research. InterJournal, Complex Systems. 2006:1695. igraph.sf.net. [Google Scholar]
- Drǎghici S, Khatri P, Martins RP, Ostermeier GC, Krawetz SA. Global functional profiling of gene expression. Genomics. 2003;81:98–104. doi: 10.1016/s0888-7543(02)00021-6. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani R. On testing the significance of a set of genes. Annals of Applied Statistics. 2007;1:107–129. [Google Scholar]
- Gentleman RC, Carey VJ, Bates DM, Bolstad B, Dettling M, Dudoit S, Ellis B, Gautier L, Ge Y, Gentry J, Hornik K, Hothorn T, Huber W, Iacus S, Irizarry R, Leisch F, Li C, Maechler M, Rossini AJ, Sawitzki G, Smith C, Smyth G, Tierney L, Yang JY, Zhang J. Bioconductor: open software development for computational biology and bioinformatics. Genome Biology. 2004;5(10):R80. doi: 10.1186/gb-2004-5-10-r80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Gene Ontology Consortium. Gene ontology: tool for the unification of biology. Nature Genetics. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goeman JJ, Bühlmann P. Analyzing gene expression data in terms of gene sets: methodological issues. Bioinformatics. 2007;23:980–987. doi: 10.1093/bioinformatics/btm051. [DOI] [PubMed] [Google Scholar]
- Gonzalez J, Low Y, Guestrin Residual Splash for optimally parallelizing belief propagation. Proceedings of the 12th International Conference on Artificial Intelligence and Statistics (AISTATS); Clearwater Beach Florida, USA. 2009. Volume 5 of JMLR. [Google Scholar]
- Grossman S, Bauer S, Robinson PN, Vingron M. Improved detection of overrepresentation of Gene-Ontology annotations with parent child analysis. Bioinformatics. 2007;23:3024–3031. doi: 10.1093/bioinformatics/btm440. [DOI] [PubMed] [Google Scholar]
- Jiang Z, Gentleman R. Extensions to gene set enrichment. Bioinformatics. 2007;23:306–313. doi: 10.1093/bioinformatics/btl599. [DOI] [PubMed] [Google Scholar]
- Kanehisa M, Goto S. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Research. 2000;28:27–30. doi: 10.1093/nar/28.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller MP, Choi Y, Wang P, Belt Davis D, Rabaglia ME, Oler AT, Stapleton DS, Argmann C, Schueler KL, Edwards S, Steinberg HA, Chaibub Neto E, Kleinhanz R, Turner S, Hellerstein MK, Schadt EE, Yandell BS, Kendziorski C, Attie AD. A gene expression network model of type 2 diabetes links cell cycle regulation in islets with diabetes susceptibility. Genome Research. 2008;18:706–716. doi: 10.1101/gr.074914.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koller D, Friedman N. Probabilistic graphical models. MIT Press; 2009. [Google Scholar]
- Kschischang FR, Frey BJ, Loeliger HA. Factor graphs and the sum-product algorithm. IEEE Transactions on Information Theory. 2001;47:498–519. [Google Scholar]
- Liang K, Nettleton D. A hidden Markov model approach to testing multiple hypotheses on a tree-transformed gene ontology graph. Journal of the American Statistical Association. 2010;105:1444–1454. [Google Scholar]
- Lu Y, Rosenfeld R, Simon I, Nau GJ, Bar-Joseph Z. A probabilistic generative model for GO enrichment analysis. Nucleic Acids Research. 2008;36:e109. doi: 10.1093/nar/gkn434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendiburu A, Santana R, Lozano JA, Bengoetxea E. A parallel framework for loopy belief propagation; GECCO ’07: Proceedings of the 2007 GECCO conference companion on genetic and evolutionary computation; 2007. pp. 2843–2850. [Google Scholar]
- Newton MA, Quintana FA, den Boon JA, Sengupta S, Ahlquist P. Random-set methods identify distinct aspects of the enrichment signal in gene-set analysis. Annals of Applied Statistics. 2007;1:85–106. [Google Scholar]
- Park MY, Hastie T, Tibshirani R. Averaged gene expressions for regression. Biostatistics. 2007;8:212–227. doi: 10.1093/biostatistics/kxl002. [DOI] [PubMed] [Google Scholar]
- Ren SA, Jsgaard HA, Dethlefsen C, Bowsher gRbase: A package for graphical modelling in R. R package version 1.3.4. 2010 CRAN.R-project.org/package=gRbase. [Google Scholar]
- Sartor MA, Leikauf GD, Medvedovic M. LRpath: a logistic regression approach for identifying enriched biological groups in gene expression data. Bioinformatics. 2009;25:211–217. doi: 10.1093/bioinformatics/btn592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stingo FC, Chen YA, Tadesse MG, Vannucci M. Incorporating biological information into linear models: a Bayesian approach to the selection of pathways and genes. Annals of Applied statistics. 2011 doi: 10.1214/11-AOAS463. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian A, Tamayo P, Mootha VK, Mukherjee S, Ebert BL, Gillette MA, Paulovich A, Pomeroy SL, Golub TR, Lander ES, Mesirov JP. Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proceedings of the National Academy of Sciences. 2005;102:15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]