The Influenza Fusion Peptide Adopts a Flexible Flat V Conformation in Membranes

Abstract

Knowledge about the influenza fusion peptide (FP) membrane insertion mode is crucial for understanding its fusogenic mechanism. NMR and electron paramagnetic resonance experiments showed that in micelles, the FP inserted as a fixed-angle inverted V. In membranes, however, it was shown to insert as a straight α-helix (by molecular-dynamics simulations) and to adopt multiple kinked conformations (by solid-state NMR). In this work we performed explicit-solvent molecular-dynamics simulations of the influenza FP, and its F9A and W14A mutants, in POPC membranes. The ${}^1\text{H}_{\alpha }$ chemical shifts predicted from the molecular-dynamics structures are in excellent agreement with the experimental values obtained for the three peptides. The peptide orientation and conformations observed from the simulations lead to a flexible flat-V model in which the peptide lies almost flat on the membrane surface and alternates between kinked and straight-helix conformations.

Introduction

A flu infection starts with the entry of an influenza virus into a host cell. To accomplish this, the virus binds to the host cell surface receptors, is endocytosed, and fuses its membrane with the endosomal membrane (1–3). The binding and membrane fusion steps are mediated by hemagglutinin (HA), a glycoprotein embedded in the viral membrane. HA is a homotrimer whose monomers are each composed of two disulfide-bound subunits (4). The 20 N-terminal residues of HA2, the second subunit of HA, constitute the fusion peptide (FP), the only part of HA that inserts into the endosomal membrane during the fusion process (5). It was also shown that FPs alone, without the rest of HA, catalyze membrane fusion in a pH-dependent manner (6,7). The establishment of a comprehensive model for membrane fusion catalysis by the FP is required for the development of membrane fusion inhibitors with the ability to prevent infection (8,9).

The structure of the peptide was previously resolved from NMR experiments in dodecylphosphocholine (DPC) micelles at fusogenic pH 5, and consists of two helices linked by a kink at a fixed angle (10,11). The membrane insertion was estimated from electron paramagnetic resonance (EPR) experiments, and the results indicate that the FP with this rigid structure inserts into membranes as an inverted V, with the two termini pointing toward the center of the membrane, and residue N12 at the apex of the angle structure. Membrane fusion is impaired by mutations that disturb the kink, supporting the notion that the fixed-angle kink is essential for fusogenicity (11,12). The inverted-V insertion was also observed to be stable in membranes in several short molecular-dynamics (MD) simulations (13–16). However, evidence from the literature depicts various models against this fixed-angle inverted-V model. From different NMR experiments, it was observed that the FP takes multiple kinked conformations (17,18) or has a flexible hinge (19–21). In addition, some longer MD simulations also revealed straight helical conformations (22,23) with some flexibility (23). Finally, recent NMR experiments showed that the peptide adopts a tight hairpin conformation (24) similar to the pronounced kink found in MD simulations (25).

Peptide sequences vary from one NMR study to another, but in every case they differ from the original 20-amino-acid sequence that was used in this work because it is extremely aggregative and poorly soluble in aqueous media. This problem was experimentally overcome by the addition of few amino acids at the C-terminus (10,17,18,21,24,26), or by the mutation of a few residues (19,20). The additional C-terminal sequence consists of a few conserved residues from the original HA2 sequence (21), a few apolar residues followed by four lysines (10,17,18), or both approaches combined (24,26) (in the latter references, the peptide sequence was from a different strain). Considering only experiments performed with a peptide that includes the same FP amino sequence used in this work, the FP was found in different conformations: with a fixed-angle inverted-V structure (10), with multiple kinked conformations (17,18), and in equilibrium between helical and nonhelical conformations (21). Therefore, we propose that the FP is flexible, and this flexibility allows the multiple conformations reported in the literature.

In this work. we conducted a total of 4.8 μs of explicit-solvent MD simulations of the wild-type (WT) FP and two mutants, F9A and W14A, in 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) membranes. Residues F9 and W14 are located on each side of the FP kink, and F9A mutant was found to conserve fusogenicity and a fixed-angle kink (12), whereas W14A did not (11). Straight helical and multiple kinked conformations are observed from the trajectories for the WT, with a predominance of straight helical conformations, in agreement with the spectroscopic measurements of Chang et al. (21). The WT lies almost flat on the membrane, as a flexible flat V, in contrast to the fixed-angle inverted V found in micelles (10). The length of our simulations allowed conformational transitions between straight helical and kinked conformations, supporting the hypothesis of a flexible FP in membranes. The F9A and W14A mutants adopt a flexible flat V conformation in membranes as well. However, these mutants are more flexible than the WT, with W14A being the most flexible, consistent with a broad kink angle distribution observed experimentally (11,12), and can adopt a hairpin conformation, or unfold at the C-terminus in the case of W14A. The ¹H_α chemical shifts predicted from the MD conformations are in excellent agreement with the experimental values obtained for the three peptides (11,12,27).

Methods

Peptides in POPC bilayers

The FP of type 3 HA from influenza virus strain X-31 with sequence GLFGA-IAGFI-ENGWE-GMIDG (hereafter referred to as the WT) was studied along with its F9A and W14A mutants. The starting conformations for the WT simulations were selected among the 20 NMR structures of the peptide in DPC micelles at pH 5.0 from Protein Data Bank (PDB) entry 1IBN (10). Four models (models 1, 5, 12, and 19) were chosen for the presence or absence of some hydrogen (H)-bonds that stabilize the kinked structure as described previously (16). Four starting conformations for each mutant were also used. These conformations were derived from the WT conformations, where the coordinates of mutated side chains were determined using the internal coordinates from CHARMM topology files (28). The neutral glycine (GLYN) patch was used for the first residues, and the amidated C-terminus (CT2) patch was used for the last residues. The GLYN patch was adapted from the CHARMM22 topology as described previously (16). Glutamic and aspartic acids were unprotonated according to common methods (13–16,22,23). It was previously proposed that at least E11 is protonated at pH 5 (18,20), and that protonation would influence the FP insertion depth (23,25) but not its conformations (25,29).

For each of the four initial structures, the peptide was put in place at the position and orientation in bilayers suggested by the work of Han et al. (10), i.e., the C_α of N12 at the average position of the lipid phosphate groups (∼19 Å from the bilayer center (30)), and an angle of 37° with the bilayer plane for the N-terminal helix formed by residues 2–10. Next, the initial configuration of the bilayer around the peptide was constructed from pre-equilibrated and prehydrated POPC lipids as described previously (31–33), with a cross-sectional area of 64 Å² per lipid (34). The POPC bilayer consisted of 123 lipids (64 for the lower leaflet and 59 for the upper, where the peptide stands), and ∼30 water molecules for each lipid. Finally, 10 Cl⁻ and 13 Na⁺ ions were added for a concentration of ≈150 mM NaCl via random replacement of water molecules >6 Å away from any solute or previously placed ion.

Simulations

For each of the three peptides studied (WT, F9A, and W14A), we produced eight 200-ns trajectories, for a total of 24 trajectories. First, we calculated four 200-ns trajectories for each peptide using the starting conformations selected from NMR models, as described in the previous section. We then used the final conformations obtained from this first series of WT simulations as starting conformations for a second series of four 200-ns simulations of each peptide. This yielded simulations of mutant peptides starting from both experimental structures and structures equilibrated with the WT sequence. For each trajectory, the peptide was held fixed for the first 10 ns, and the first 50 ns were considered as equilibration and discarded from analysis. This provided a total of 1.2 μs of equilibrated sampling for each peptide.

Simulations were performed with the program NAMD2 (35) using the CHARMM27r force field (36) with the CMAP correction (37), TIP3P waters (38,39), revised tryptophane parameters (40), and periodic boundary conditions. The cutoff for the short-range electrostatics and the Lennard-Jones interactions was 11 Å, with the latter smoothed via a switching function over the range of 8–11 Å. Long-range electrostatics were calculated via the particle mesh Ewald (PME) method (41), using a sixth-order interpolation and a grid spacing of ≈1 Å. NPT ensembles were generated at 30°C by Langevin dynamics with a damping coefficient of 1 ps⁻¹. Isotropic pressure was controlled by a Nosé-Hoover Langevin piston at ≈210 ± 10 bar to account for long-range Lennard-Jones terms following the long-range correction method (42). Pressure for the long-range correction method was updated every 10 ns with a long cutoff at 30 Å. All covalent bonds involving hydrogen atoms were constrained using SHAKE (43), and drifting of the center of mass due to PME was removed. The simulations used a 2-fs time step with the multiple time steps r-RESPA integrator updating bonded, van der Waals, and short-range electrostatics every step, and long-range electrostatics updated every 2 steps. Nonbonded pair lists were updated every 10 steps and coordinates were saved every 10 ps for analysis.

Results and Discussion

Position and orientation in the bilayer

Fig. 1 shows the two typical conformations (straight helix (Fig. 1 A) and kinked (Fig. 1 B)) that the WT in a POPC bilayer experienced during the simulations (a detailed analysis of the conformations is given in the next section). Starting from the inverted-V model proposed by Han et al. (10), the peptide changes conformation and reorients in all of the trajectories within 50 ns after removal of constraints on the peptide's position. It then adopts either a straight α-helical or kinked conformation and lies almost flat in the plane of the membrane. These conformations are likely the consequence of a balance between hydrophilic and hydrophobic forces, and the reorganization of the backbone H-bonds.

Figure 1.

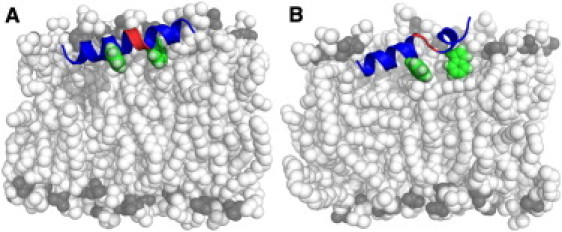
(Color online only). Side views of the (A) straight helix and (B) kinked conformations of the WT FP. The straight helix and kinked conformations account for ∼70% and ∼30% of the WT sampling, respectively. Peptide backbone in blue cartoon. Hinge region residues N12 and G13 in red cartoon. Residues mutated in this work (F9 and W14) are in spheres, heavy atoms are in green, and hydrogens are in pale green. Membrane lipids are in spheres, head and tails are in white, and phosphates are in gray. The image was built with the PyMOL molecular graphics system, version 1.2r2 (Schrödinger, LLC).

The peptide's solvent-accessible surface area (SASA) was calculated from the equilibrated part of the trajectories. Table S1 in the Supporting Material gives the values for the whole peptide and for each residue of the three peptides. For the WT, the SASA is 402.83 ± 11.90 Å² for the whole peptide. The 10 residues of the C-terminal are exposed to the solvent to a greater extent than the 10 residues of the N-terminal (313.39 ± 13.64 Å² and 89.44 ± 5.40 Å², respectively). This is not a surprising result considering that seven out of 10 of the hydrophobic residues are located in the N-terminal half of the peptide, and all of the hydrophilic residues are located in the C-terminal half. This amino-acid distribution gives rise to a hydrophobic gradient along the peptide's sequence that is not compatible with the inverted-V conformation proposed by Han et al. (10), and leads to the peptide's shallow tilt insertion angle observed in the simulations. However, the greater exposure of the second half of the peptide to the solvent was also observed experimentally from amide D-H exchanges (21). The total SASAs of F9A and W14A are significantly higher than that for the WT, with a larger exposure for F9A (442.27 ± 10.66 Å² and 426.30 ± 17.52 Å², respectively).

The average insertion depth of each residue relative to the average lipid phosphate position for the three peptides are plotted in Fig. 2 (WT insertion depths are compared with the experimental results of Han et al. (10) in Fig. S1). The three insertion profiles are similar, with the WT inserted slightly deeper than the mutants, in accord with the lowest SASA reported above. As shown in Fig. 2, the N-termini are inserted deeper than the C-termini, with residues D19 at the apex, in agreement with amide D-H exchange experiments (21) for the WT, giving rise to a shallow tilt angle from the bilayer plane uniformly over the two termini. The insertion of the WT N-terminal half is in good agreement with the experimental results of Han et al. (10) (Fig. S1). For the WT C-terminal half, N12 has an insertion depth radically different from the EPR results (≈8 Å above the lipid phosphates), but the remaining residues display a similar insertion, with a slightly shallower insertion of the C-terminus from MD simulations. The difference in C-terminal insertion depth as compared with the work of Han et al. may be due to the unprotonated state of the three ionizable residues located in this segment used in MD simulations, because it was previously observed that the protonation of these residues favors a slightly deeper insertion into the membrane (10,21,23,25). The N12 C_α average insertion depths are 2.2 ± 0.2 Å for WT, 1.2 ± 0.5 Å for F9A, and 1.4 ± 0.4 Å for W14A under the phosphate average position. Despite a different side-chain insertion depth, the C_α insertion depth of N12 of the WT is in very good agreement with the prediction of Han et al. (10), who placed this residue at the same position as the lipid phosphate groups along the bilayer normal, and is also in agreement with the membrane location of this residue observed from amide D-H exchange experiments (21). Nevertheless, these results are in contrast to the inverted-V model of Han et al. (10), where N12 is at the apex with its side chain ≈8 Å above the lipid phosphates. However, the uniform tilt for the WT was also observed from the experimental results of Macosko et al. (44) and from implicit-solvent simulations of Sammalkorpi and Lazaridis (23). Moreover, this uniform tilt angle over both termini is in accord with the hydrophobic gradient observed along the peptide's sequence.

Figure 2.

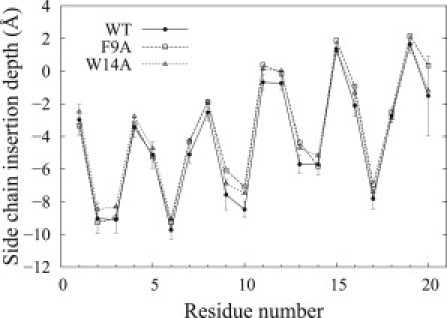
Side-chain insertion depths under the phosphates per residue. Side-chain heavy atoms were used for the calculations. The WT peptide inserts 0.6 ± 0.2 Å deeper into the membrane than the two mutants.

We calculated the orientation of the peptides relative to the membrane plane from the trajectories using the peptide order parameters S_ATR, as described in a previous work (16). The tilt angle is identical within standard errors for both termini and the three peptides, with an average value of 19 ± 2°. The experimental values for this tilt angle range from ≈20° (45) to ≈45° (46) for the whole peptide, whereas Han et al. (10) obtained an angle of 38° for the N-terminal segment using spin-label insertion depth profiles from site-specific mutations and EPR data. However, small tilt angles were reported in several previous MD studies (22,23,25).

Conformations and secondary structures

Fig. 3 shows, for each of the three peptides studied in this work, 20 conformations extracted from equally spaced snapshots taken from their respective 1.2 μs of equilibrated trajectories. These results indicate that the three peptides adopt predominantly a straight-helix conformation but can also adopt other conformations. The straight-helix conformations account for 69% of the observed conformations for the WT, and for 60% and 44% for the F9A and W14A mutants, respectively. The remaining conformations observed for the WT are the kinked conformations (31%). For F9A, the remaining conformations are kinked (35%) and hairpin (5%), whereas W14A visits kinked (30%), hairpin (13%), and unfolded C-terminal (13%) conformations.

Figure 3.

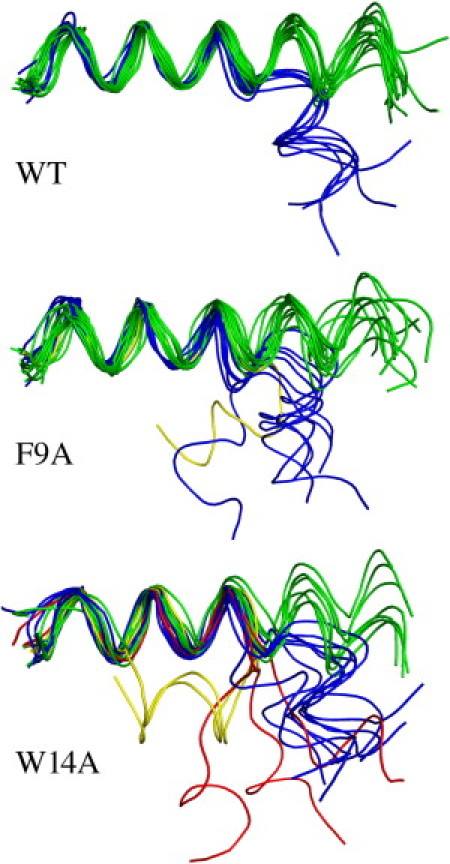
(Color online only). Top-view 20 conformations of the WT (top), F9A mutant (middle), and W14A mutant (bottom) FPs taken from equidistant frames of the 1.2-μs-long total equilibrated simulation time. Helical (green), kinked (blue), hairpins (yellow), and unfolded C-termini (red) conformations are shown.

We quantified the helicity of the peptides from the helical fraction of each residue (i.e., the fraction of time each residue spent in the helical conformation throughout the simulations) as determined using Kabsch and Sander's (47) definition of an α-helix. The helical fractions were calculated for the three peptides and from the PDB 1IBN, and the results are presented in Fig. S2. As shown in the figure, the simulated peptides display identical helicity for residues 1–11 despite the mutation of F9A in this region, whereas the helicity for the second half of the peptides differs, with some similarities between WT and F9A. The lower helicity of residues 12–20 of W14A is due to its unfolding. The helicity of WT and 1IBN is similar for residues 4–9, but it strongly differs for the kink region, where residues 11–13 of 1IBN are in a turn configuration. Finally, the second helix of 1IBN, defined by residues 15–18, has a slightly higher helicity than the WT. As for the WT MD simulations, Chang et al. (21) also observed from nuclear Overhauser effect spectroscopy a weaker helical character for the residues in the kink region, and structural fluctuations for residues located at the C-terminus.

Fig. 4 shows the backbone H-bond patterns observed in the kink region for each peptide conformation, for 1IBN and the three peptides. For 1IBN (Fig. 4 A), the kink is stabilized by i+3 bonds between G8 and E11, and F9 and N12, in addition to an i+5 bond between F9 and W14. The i+3 bonds of G13 and W14 with G16 and M17 account for the short 3₁₀ helix. It is observed from the trajectories that the peptides reorganize their conformation within 50 ns after the removal of the constraints on the positions, in the equilibration phase. The H-bond patterns adopted by the WT are presented in Fig. 4, B and D, and those adopted by F9A and W14A are presented in Fig. 4, C–E. The kinked conformation of WT is stabilized by an H-bond between I10 and G13 (Fig. 4 B), but there is no particular H-bond to stabilize the kinked conformation of F9A and W14A (Fig. 4 C). With either WT or a mutant, a straight α-helix can be formed from the kinked conformation by the formation of i+4 backbone H-bonds of I10 and E11 with W14 and E15 (Fig. 4 D). The transition between kinked and hairpin conformations of F9A and W14A is mainly driven by apolar contacts between N- and C-terminal helices. All of the peptide conformational transitions also imply rotations of backbone dihedral angles of residues N12 and G13.

Figure 4.

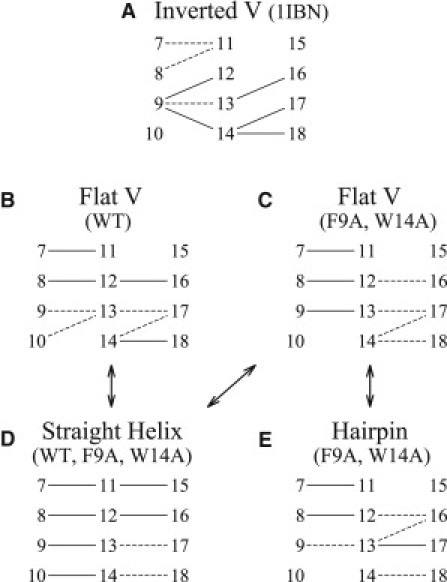
Backbone H-bond patterns found in PDB 1IBN and for the different conformations adopted by the three peptides. Each number refers to a residue. Each line represents an H-bond between the carbonyl of the residue on the left and the amine of the residue on the right. Plain lines are drawn for H-bonds that are present in 60–100% of the structures. Dashed lines are drawn for bonds that are present in 20–60% of the structures. H-bonds are defined by a distance of ≤2.4 Å between the carbonyl oxygen and the amine hydrogen. Numerical values of the occurrences of each H-bond are given in Table S2.

These results illustrate that the FP and its mutants can adopt multiple conformations when bound to membranes, with the WT having the highest helical content and W14A C-terminal unfolding. The increase in helicity was also observed from previous MD simulations (14,16,22), and it was suggested to be a consequence of a lower exposure of the peptide to water solvent in membranes than in micelles (16). From the conformations and the helical content, F9A shares more similarities with the WT than W14A. This is in agreement with the structural similarity between the F9A mutant and the FP found experimentally (12). Again, the multiple conformations observed in this work are in contrast to the fixed-angle inverted-V model described in the literature (10–16). Nevertheless, the flexibility observed for the WT in this work is in agreement with previous modeling works (23,25), the multiple conformations found from solid-state NMR (17,18), the experimental observations of Chang et al. (21) from various spectroscopic methods, and the experimental chemical shifts presented in the next section.

Chemical shifts

The ${}^1\text{H}_{\alpha }$ chemical-shift predictions for the conformations extracted from MD simulations for the three peptides (Fig. 3) as well as for their respective PDB structures (1IBN, 2JRD, and 2DCI for WT, F9A, and W14A, respectively) were calculated with the use of SPARTA+ (48). SPARTA+ predictions are based on quantitative relations between chemical shifts and protein structures derived from a neural network training of a database of hundreds of protein x-ray structures. The protein structure descriptors include backbone and side-chain conformations, H-bonding, electric fields, and ring-current effects. The chemical-shift differences from the experimental values for the WT and 1IBN are compared in Fig. 5, and the chemical-shift differences for F9A (12) and W14A (11) and their respective PDB structures are compared in Fig. S3 (similar membrane protein and membrane peptide chemical-shift comparisons are reported in Bhate et al. (49) and Ikeda et al. (50), respectively).

Figure 5.

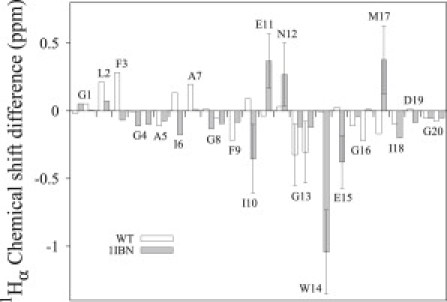
Average ${}^1\text{H}_{\alpha }$ chemical-shift differences between experimental values (27) and SPARTA+ computed values for the WT and 1IBN structures (10). The error bars are represented only for the residues with a significant difference from the experimental value.

The chemical-shift differences from the experimental values are greater on average for 1IBN, with a root mean-square deviation (RMSD) of 0.293 ppm, than for the WT, with an RMSD of 0.158 ppm (Fig. 5). The very good agreement between the WT chemical-shift predictions and the experimental values indicate that the conformations observed from the MD simulations in model membranes are representative of the peptide conformations from NMR experiments in DPC micelles. Moreover, the lower RMSDs observed for the WT than for 1IBN suggest that the WT conformations surpass the 1IBN conformers in terms of being representative of the experimental results. For the WT structures, only residue G13 displays a deviation from experimental values greater than the standard deviation of 0.25 ppm inherent to the prediction method (48), whereas there are six residues for 1IBN (I10, E11, N12, W14, E15, and M17; Fig. 5). The greatest difference is observed for W14, with 1.043 ppm. These differences are discussed further below.

Residue G13 is located in the kink region, defined by itself and residue N12. The ${}^1\text{H}_{\alpha }$ chemical-shift differences between SPARTA+ predictions from MD structures and the experimental results for the two G13 protons are −0.324 and −0.304 ppm, whereas these differences are neglectable for neighboring residues N12 and W14. According to SPARTA+, the main contribution to the chemical shifts of these protons comes from the torsion angles (−0.271 ppm for both protons) and the ring current (−0.135 and −0.110 ppm) due to the proximity of F9 side chain. However, G13 is the glycine with the lowest SASA by far (see Table S1). As a consequence, G13 has its two H_αs exposed only to the apolar lipid chains. Solvent molecules make an important contribution to the chemical shift through H-bonding, anisotropy of solvent molecules, polar effects, and van der Waals interactions (51). For example, the chemical shift of α-protons of a glycine could increase up to ≈0.7 ppm depending on the polarity of the solvent (52). However, contributions from solvent molecules are not taken into account in the predictions of SPARTA+, which was trained using a database of globular proteins. We suggest that the difference between the SPARTA+ chemical-shift prediction of G13 ${}^1\text{H}_{\alpha }$ and the experimental results of Li et al. (27) arise because of the important solvation of G13 by the bilayer.

For the case of 1IBN, residues E11, N12, and M17 have higher predicted chemical shifts compared with their respective experimental values, with respective differences of 0.369, 0.269, and 0.378 ppm, whereas their predictions from WT structures are in very good agreement. For both 1IBN and WT, E11 and N12 H_α are located far from F9 and W14 side chains, resulting in no contribution from the ring-current effect to the chemical shift. Moreover, the 1IBN E11 and N12 H_αs are inserted approximately at the lipid phosphate level (10), where the interface is composed mainly of waters and phosphate groups (53), and should be hydrated and should not experience a significant change in solvent polarity. Therefore, the main contribution to the chemical shifts comes from the secondary structure. Residues E11 and N12 have a higher helical content for WT, as reported in the previous section, that would explain the deviations observed for 1IBN. For residue M17, the ring-current contribution is moderate for both 1IBN and WT, although it is positive for 1IBN (0.167 ppm) due to the proximity of the F9 side chain, and negative for the WT (-0.110 ppm) due to the proximity of the W14 side chain. Similarly, the secondary structure contributions to the chemical shift are of the opposite sign for 1IBN and WT: the amide of residue M17 is H-bonded with the carbonyl of W14 (as in a 3₁₀ helix), whereas it is in an α-helical structure in the WT. In addition, 1IBN M17 H_α is in the vicinity of the D19 carbonyl backbone in many structures, and should be located approximately at the lipid carbonyl level in the membrane (see Han et al. (10)), with a lower exposure to polar chemical groups. Therefore, the results suggest that either proximity to D19 or lipid carbonyls, or the secondary structure and the side-chain conformation may be the origin of the 1IBN M17 chemical-shift deviations.

The predicted chemical shifts of the remaining residues from 1IBN (I10, W14, and E15) are underestimated compared with their experimental values, with respective differences of −0.354, −1.043, and −0.378 ppm, whereas their predictions from WT structures are again in very good agreement. These deviations arise mainly from large ring-effect contributions predicted by SPARTA+ (−1.379 to −0.625 ppm), due to their close proximity to W14 (for I10 and E15) and F9 (for W14) side chains. This proximity occurs in the inverted-V structure of 1IBN, and is not observed from WT conformations as shown in Fig. S4.

Hence, 1IBN structural characteristics that have been proposed to stabilize the fixed-angle inverted-V structure (10) (i.e., close proximity of the I10 H_α and W14 side chain and the W14 H_α and F9 side chain, and dihedral angles of E11 and N12) conflict with the experimental chemical shifts. Instead, the chemical shifts predicted from the MD structures observed in this work are in very good agreement with the experimental values.

In similarity to the WT, the chemical shifts predicted for F9A and W14A are in better agreement with experimental results (11,12) than those for their respective PDB structures (Fig. S3).

Flexible flat-V model

Flexibility is defined here by the ability of the peptide to explore a number of conformations; a higher degree of flexibility implies a higher number of accessible conformations. The flexibility of the FP is apparent from Fig. 3, with WT being the most rigid, followed by F9A, and W14A being the most flexible. Quantitatively, the average root mean-square fluctuations (RMSFs) of the backbone heavy atoms relative to the average structure are 1.8 Å, 2.2 Å, and 2.6 Å for WT, F9A, and W14A, respectively. The RMSFs from the NMR structures are 1.2 Å for 1IBN (WT), 0.8 Å for 2JRD (F9A mutant), and 1.8 Å for 2DCI (W14A mutant). These values are significantly lower than those obtained from the MD conformations, suggesting a higher rigidity for the experimental structures. The W14A mutant has the highest flexibility from both NMR and MD structures, but F9A is found to be less flexible from the NMR structures compared with the MD structures. However, results from both the NMR and MD approaches agree on the higher rigidity of the WT compared to W14A.

To locate the regions with higher flexibility, we calculated the standard deviations σ of the backbone Φ dihedral angles for each residue. The results are plotted in Fig. S5 for the three peptides. Excluding the termini, the largest deviations are observed for the hinge region (residues 12 and 13) for the three peptides, with a maximum for the G13. As for the RMSF, the highest deviations are observed for W14A, followed by F9A and the WT.

For all of the peptides, transitions between kinked and straight helical conformations were scarce, with a timescale of ≈100 ns between transitions, and not observable in shorter MD simulations. We tracked conformational transitions by following the kink angle θ between the N-terminal and C-terminal helices through the trajectories. Fig. 6 shows the kink angle for the WT trajectories starting with structures 5 and 19 of PDB 1IBN. The kink angles θ < 150° correspond to the kinked conformations with the H-bond pattern presented in Fig. 4 B. The time series of the kink angle for the mutants and two remaining WT simulations are plotted in Fig. S6, Fig. S7, and Fig. S8. For the WT, as expected from the higher level of helicity of this peptide, the main conformational change experienced is from kinked to straight helix. The peptide explored once the reverse change, from straight helix to kinked (Fig. 6, structure 19, first trajectory). The WT also explored different kink angles (Fig. 6, structure 5, both trajectories; structure 19, second trajectory). For F9A, the straight helical conformation is well explored but involves short-lived deviations from an ideal helix (Fig. S7, structures 1 and 12, first trajectory). F9A also experienced few more kink angles than the WT during transitions to the hairpin conformation (Fig. S7, structure 19, first trajectory). Finally, the W14A peptide explored the greatest number of kink angles and spent the least time as a straight helix.

Figure 6.

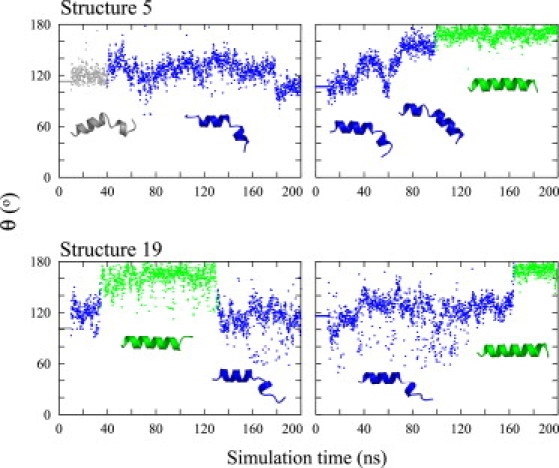
(Color online only). Time series of the kink angle θ from WT simulations starting with structures 5 and 19 from PDB 1IBN. For these two structures, as with all others used in this work, an initial 200-ns simulation (left) is performed. The final snapshot of this initial simulation is used as the starting conformation for a second 200-ns simulation (right). Helical conformations are in green, kinked flat-V conformations are in blue, and inverted-V conformations are in gray.

The kink angle distributions for the three peptides are plotted in Fig. S9. The distributions of WT and F9A display two main components, corresponding to the straight helical and kinked conformations, whereas for W14A the distribution is wider, consistent with a higher flexibility. These distributions are in qualitative agreement with the distance distributions between residues F3 and I18 observed from double electron-electron resonance spectroscopy (12). In addition, the wider distance distribution (12) and the broad kink angle distribution from the NMR structure (11) of W14A support the higher flexibility we observed for this peptide. These results underscore the importance of residue W14 in the structural integrity of the FP.

In general, the conformations observed from the simulations in this study differ from the fixed-angle kink model proposed by Han et al. (10). In the work presented here, the hydrophobic pocket present in the kinked conformations is lost for the majority of conformations observed from the trajectories. Nevertheless, the chemical shifts predicted from the MD structures agree with the experimental values, validating the conformations observed from the simulations. These results are consistent with the observation that the kinked structure is not energetically very stable (54). However, our simulations were at least 20 times longer than the previous MD simulations that revealed the inverted-V model (13–16).

The results presented in this work all point toward a flexible flat-V model for the FP in membranes. We propose that this flexible flat-V model would allow the peptide to adapt to the strong curvature found at different stages of membrane fusion. In this model, the FP lies almost flat in the plane of the membrane and samples different conformations, switching between straight helical and kinked conformations. This model is in agreement with the results of Chang et al. (21), who observed a significant helical form in equilibrium with the nonhelical form of the peptide, with higher structural fluctuation for residues located in the kink region, residues at the N-terminal being buried in the lipid medium, and residues at the C-terminal being more exposed to water.

Conclusion

In this work, we studied the WT influenza FP and two mutants, F9A and W14A, in POPC membranes from 4.8 μs of explicit-solvent MD simulations. The three peptides reside at the lipid/water interface. They take either straight α-helical or kinked conformations and lie almost flat in the plane of the membrane. The hydrophobic gradient along the peptide sequence is not compatible with the inverted-V conformation proposed by Han et al. (10) and leads to a shallow tilt insertion angle. The nonfusogenic W14A is the most flexible and differs from the other two peptides in its tendency to unfold at the C-terminal helix. These results underscore the importance of residue W14 in the structural integrity of the FP, as experimentally determined by Lai et al. (11).

To test the validity of the simulated structures, we calculated the differences among the SPARTA+ (48) ${}^1\text{H}_{\alpha }$ chemical-shift predictions, experimental values for the MD conformations, and previously published PDB structures. The WT chemical-shift predictions are in very good agreement with experimental values, whereas PDB 1IBN structural characteristics that have been proposed to stabilize the fixed-angle inverted-V structure (10–12) conflict with some of the experimental chemical shifts. Excellent agreement is also found between predicted and experimental values for both mutants.

The results presented in this work point toward a flexible flat-V model for the FP in membranes. This model differs from the fixed-angle inverted-V model found in DPC micelles (10–12). FP flexibility is in agreement with previous MD simulations (23) and different NMR results (17–21). An almost flat insertion is compatible with modeling studies (22,23,25). The flexible flat-V model would allow the peptide to adapt to the strong curvature found at different stages of membrane fusion.