CARDIAC MODELS IN DRUG DISCOVERY AND DEVELOPMENT: A REVIEW

Abstract

Cardiovascular diseases are among the leading causes of death in the developed world. Developing novel therapies for diseases like heart failure is crucial, but this is hampered by the high attrition rate in drug development. The withdrawal of drugs at the final hurdle of approval is mostly due to their unpredictable effects on normal cardiac rhythm. The advent of cardiac computational modeling in the last six decades has significantly aided the understanding of heart function. Recently, these models have been increasingly applied towards designing and understanding therapies for cardiac disease. This article will discuss how cellular models of electrophysiology, cell signaling and metabolism have been used to investigate pharmacological therapies for cardiac diseases including arrhythmia, ischemia and heart failure.

I. Introduction

Computational modeling has played an important role in understanding heart physiology and pathology since the first model of the cardiac action potential 50 years ago (1). These models have been invaluable in understanding an organ whose function is the result of a complex system of nonlinear feedback loops that span single ion channels, cardiac cells and the whole heart (2). Despite its remarkable robustness, the heart is afflicted by various diseases that are complex and multifaceted (3). Heart disease remains the leading cause of premature death in developed societies. Approximately 2300 Americans die of cardiovascular disease each day, an average of one death every 38 seconds (4). The failure of many therapies targeting cardiac arrhythmia (5), contrasted with the success of counter-intuitive therapies like beta blockers in heart failure (6), highlights the difficulty in developing therapies for cardiovascular disease. A common causes of drug withdrawal from the market is due to their propensity to cause fatal cardiac arrhythmia (7) resulting in significant financial loss (8) and complicating new drug development (9).

Computational modeling can serve as a useful tool both for developing new therapies and evaluating current treatment of cardiovascular diseases and drugs with cardiovascular consequences. This idea is beginning to gain traction with the formation of the preDICT project, a consortium of pharmaceutical companies and academic institutions charged with the mission to model, simulate and predict the impact of pharmacological compounds on heart rhythm (10). Computational modeling has also been identified as a key component of the Critical Path Initiative, a project launched by the US Food and Drug Administration to improve drug and medical device development (11). The Critical Path Initiative lists six broad areas where innovation is needed including harnessing bioinformatics. Clinical trial simulation using in silico disease models was identified as a specific scientific opportunity to aid in this endeavor (12). This represents a shift in the drug approval process from requiring only empirical evidence to an increased emphasis on mechanistic understanding of drug action (13).

Models now exist for many aspects of cellular cardiac biology including electrophysiology, metabolism and signaling networks. These processes do not function in isolation, and there are significant efforts to integrate these models to simulate heart function in increasing detail (14). This review will discuss how models at cellular and tissue scales of cardiac biology can be used to assess current therapies, test therapies in development and suggest new targets (Table 1).

Table 1.

Examples of cardiac computational models used to investigate the effect of drugs and therapies.

Target	Pathology	Drug/Treatment	Reference
INa	LQT3	mexiletine	31
INa	LQT3	ranolazine	39
IKr	acquired LQTS	E-4031	43
IKr	LQTS	sotalol (pro-arrhythmic)	48
IKr	LQTS	NS1643	50
IK-ATP	ischemia	pinacidil	65
INa-H	ischemia	blocker of Na-H exchanger	67
INa(f,L)	ischemia	blocker of late sodium channel	69
Cr,Adenine, Pi	heart failure	elevating all 3 pools	75
CaMKII	T-wave alternans	CaMKII inhibitor	83
CaMKII	myocardial infarct	CaMKII inhibitor	87
AC	heart failure	AC overexpression	92
CaMKII	heart failure	inhibition of CaMKII phosporylation of RyR	96
β-adrenergic receptor	LQT1	β-adrenergic receptor blocker	98
β-adrenergic receptor	LQT3	propranalol	101
LCC	LQT8	reduction of LCC current	104
α-adrenergic receptor	pathological hypertrophy	α-adrenergic receptor blocker	109

II. Therapies targeted against arrhythmias

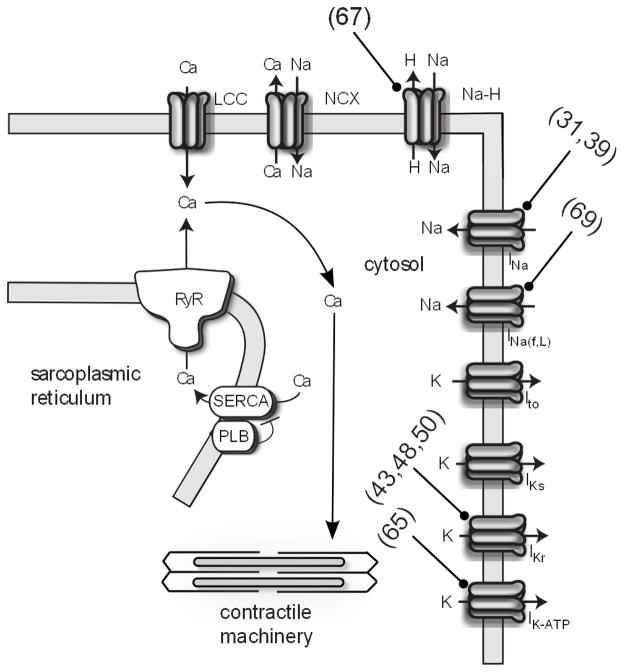
Modeling the electrical activity of the heart (cardiac electrophysiology) is perhaps the most advanced area of cardiac computational biology, and it has been the most successful in drug development (15). The role of cardiac electrophysiology is to coordinate the mechanical pumping of the heart in a process called excitation-contraction coupling (16). The key emergent property of cellular electrophysiology is the action potential, which reflects an intricate interplay between an array of ion channels (Figure 1). Fast activating sodium channels in the cell membrane are the first to open when a cardiac myocyte is slightly depolarized above a threshold. Increased sodium current (I_Na) strongly depolarizes the membrane, which activates L-type calcium channels (LCC) to increase calcium current (I_Ca). This influx of calcium induces ryanodine receptors to release an even larger amount of calcium from the sarcoplasmic reticulum, specialized calcium stores, into cytosolic space; a process called calcium-induced calcium release (CICR). It is this rise in cytosolic calcium that activates a myocyte’s contractile machinery (Figure 2). Relaxation occurs when calcium is re-sequestered into the sarcoplasmic reticulum by the sarcoplasmic reticulum calcium ATPase (SERCA) and the cell’s membrane potential is repolarized by potassium currents.

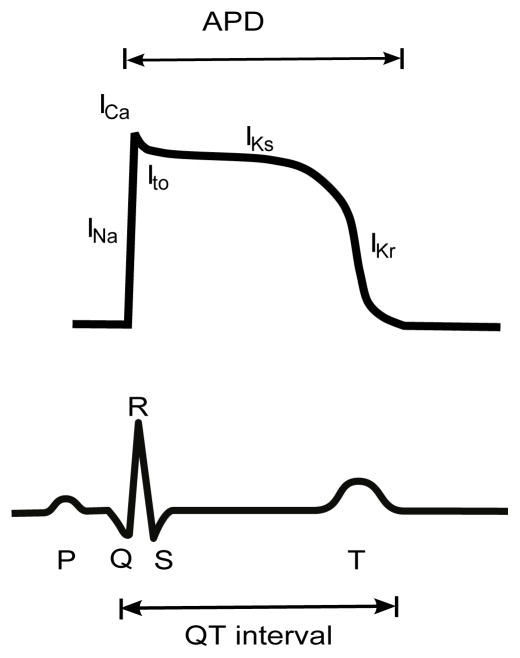
Figure 1.

Cardiac ventricular action potential and electrocardiogram. Predominant ion fluxes at different phases of the action potential are indicated. APD, action potential duration.

Figure 2.

Schematic of cardiac electrophysiology and contraction. Targets of computational models are indicated with blunt arrows (references in parenthesis). I_Na(f,l), late sodium current; I_K-ATP, ATP dependent potassium current; PLB, phospholamban; NCX, sodium-calcium exchanger.

There are multiple channels with different properties that carry the repolarizing potassium current including the transient outward potassium current (I_to), which influences the early repolarization phase, and the delayed rectifier potassium currents (i.e. I_Ks and I_Kr.) Alterations in the orchestrated changes in ion flow can cause severe pathology. One such example is Long QT syndrome (LQTS), a family of diseases (LQT1-8) characterized by prolonged action potential duration (APD), which is measured as an increased QT interval on an electrocardiogram (17). LQTS is caused predominantly by either a reduction of potassium current or an increase in sodium current. This can occur due to genetic mutations or drugs acting on channels that carry both currents. Without treatment, 13% of individuals carrying gene mutations that cause LQTS will suffer cardiac arrest or sudden death due to the development of ventricular tachycardia (18). Understanding the mechanistic bases of arrhythmias and applying such knowledge to improve therapy is a great challenge in cardiac electrophysiology (19).

The earliest computational model of cardiac electrophysiology by Noble was based on the Hodgkin-Huxley model for the neuron action potential, predating the discovery of the calcium current (1). The first ventricular cell model, developed using experimental data from a variety of mammals, was published in 1977 by Beeler and Reuter and included the effect of intracellular calcium dynamics on the action potential (20). Luo and Rudy subsequently developed biophysically detailed models of a guinea pig ventricular myocyte by taking advantage of improved measurement of ionic currents from patch clamping (21, 22). By replacing the description of the calcium current in the Luo-Rudy models with detailed models of the L-type calcium channel and ryanodine receptor, Jafri et al. (23) were able to mechanistically represent calcium-induced calcium release. A notable feature of the Jafri-Rice-Winslow model was the inclusion of Markov state models of the L-type calcium channel and ryanodine receptor. This is a departure from Hodgkin and Huxley’s approach which used phenomenological descriptions of ion channel function (24). Ion channels are composed of protein subunits whose conformational changes “gate” ionic currents, causing shifts between inactive, closed or open states (25). The probability of a channel being in a certain state often depends on the previous state (26). Experimental observations of channel gating and aspects of channel structure can be replicated by modeling this channel property as a probabilistic Markov process (27).

Markov models can simulate the molecular basis of arrhythmias caused by mutations in ion channels and the effect of pharmaceutical compounds (27). There is evidence that drug binding affinity is often determined by the conformational state of the ion channel (28). This level of drug-channel interaction is important when developing drugs for patients suffering from LQT3, the most lethal subtype of LQTS (29). LQT3 is caused by mutations in the gene SCN5A, which encodes the α-subunit for the sodium channel. One such mutation results in deletion of three amino acid residues in the channel protein (ΔKPQ mutants) which causes a small persistent current during the plateau phase of the action potential, delaying repolarization (30). Clancy et al. (31) examined the mechanisms of drug block of the sodium channel by modifying Markov models of both the wild type and the ΔKPQ mutant channels (32). The ΔKPQ channel model was able to simulate the experimentally observed faster recovery from inactivation compared to the wild-type channel. By including additional model states for drug binding, they investigated the drugs mexiletine (an open state blocker) and lidocaine (an inactivation state blocker). The model predicted that lidocaine induces a rightward shift in voltage-dependent sodium channel availability, consistent with experimental data. The Markov models for SCN5A were then integrated with the Luo-Rudy model of the ventricular action potential. Simulations suggested that low doses of mexiletine can shorten the action potential duration in LQT3 without affecting the peak sodium current, which underlies the action potential upstroke. Conversely, lidocaine was predicted to have a lesser effect on action potential duration but blocked the peak current at high doses. This study illustrated how the specific mechanisms of drug action can have a significant impact on cellular physiology.

Electrophysiology models have now been developed for a variety of animal species, allowing representation of species-specific propensity for arrhythmia and other aspects of pathophysiology (24). The scarcity of human data, due to the lack of non-invasive techniques, increases the need for computational models of the human heart to gain further insight into cardiac disease (33). Models of the human ventricular myocyte have been developed by Priebe et al. (34), ten Tusscher et al. (35), Iyer et al. (36) and Grandi et al.(37). Like most models in biology, these models are constrained by limited available experimental data and each has specific applications for which its use is appropriate. The ten Tusscher-Noble-Noble-Panfilov (TNNP) model has the advantages of being based mostly on data obtained from human ventricular myocytes and is less complex due to the use of Hodgkin-Huxley-type equations for ion channels (38). Fredj et al. (39) replaced the sodium channel equations in the TNNP model with the Clancy-Rudy SCN5A Markov model (32) to investigate the potential therapeutic effect of ranolazine, an antianginal drug, on LQT3 human patients with ΔKPQ mutant sodium channels. In vitro experiments with a cell line expressing mutant channels confirmed their hypothesis that ranolazine is a use-dependent blocker that reduces sustained sodium current without affecting peak current. Simulations with the model containing the mutant ΔKPQ sodium channel showed a decrease in ventricular cell action potential duration in the presence of ranolazine. This suggests its potential as a treatment for LQT3 arrhythmias.

The rapid delayed rectifier potassium current (I_Kr) is encoded by the Human Ether-a-go-go Related Gene (hERG) and its mutations cause LQT2 (40). Drugs that inhibit this repolarizing potassium current prolong action potential duration and the QT interval (causing acquired LQTS), which can increase the risk to develop arrhythmia (41). hERG channels can exist as heteromers consisting of hERG 1a and 1b or as homomers of hERG1a. Despite evidence that the hERG 1a/b heteromers underlie the cardiac repolarizing current (42), little is known about how hERG hetero/homomers differ and how the hERG 1b subunit influences channel properties (especially in the context of pharmaceutical channel block). In-vitro experiments by Sale et al. showed that hERG heteromers have a quicker transition to an open state than hERG homomers (43). This suggests that an open channel blocker should be more effective against hERG heteromers but paradoxically, experimental results showed that hERG homomers were more inhibited by open channel block. To explain this mechanistically, the authors turned to the TNNP model, replacing the original I_Kr model with a Markov model that represents both hERG heteromers and homomers. They discovered that the additional channel gating mode of hERG 1a homomers results in more complete block by the open channel blocker E-4031, thus increasing the risk for acquired LQTS.

One of the challenges of understanding arrhythmia and developing effective therapies is linking molecular mechanisms from single cell to tissue levels (33). A cross-section of the ventricular wall reveals at least three different cell types: epicardial, endocardial and midmyocardial (44). These cells have different electrophysiological characteristics due to the differential expression of various channel proteins (45) including the repolarizing potassium currents (46). This heterogeneity results in tissue level characteristics including delay of repolarization across the ventricular wall or transmural dispersion of repolarization (47). Drugs that delay repolarization produce a substrate for reentrant arrhythmias (44). The electrical signal measured transmurally across the wall reflects properties of the whole body electrocardiogram with respect to QT interval and T wave morphology (3). This tissue heterogeneity can be modeled in its most basic form by using a 1D cable electrophysiology model. This consists of a string of cells with changes made to channel expression in order to simulate the different ventricular cell types (3). Brennan et al.(48) used a 1D fiber model to investigate sotalol, an anti-arrhythmic drug that targets I_Kr. They developed a Markov model of human hERG to represent the binding kinetics of sotalol (49), which was then included in the TNNP human myocyte model. Single cell simulations indicated that sotalol prolongs action potential duration, similar to experimental data obtained from human ventricular tissue, and is thus pro-arrhythmic. By inserting the modified ventricular models into a fiber model, the authors showed that sotalol increased T-wave dispersion and amplitude (all pro-arrhythmia markers), linking molecular properties of sotalol with observed tissue level phenomena. A similar approach was used by Pietersen et al. to investigate NS1643, a hERG channel opener (50). NS1643 causes an increase in channel conductance (51) and a depolarizing shift in voltage dependency of inactivation (52) which is anti-arrhythmic at the cellular level. Predicting whether NS1643 can be pro-arrhythmic at the tissue level or which of its effect on channel conductance and inactivation is crucial is difficult. Using simulations of a string of 100 human ventricular cells, the authors determined that NS1643 can be pro-arrhythmic at the tissue level (by increasing the vulnerable window for reentry) with the effect on channel inactivation having a larger contribution. However, simulations suggest that at low external potassium concentrations, the effect on channel conductance is more pronounced and increases the drug’s anti-arrhythmic properties by causing a greater reduction of the action potential duration. This indicates a specific condition (hypokalemia) in which the drug would be more beneficial in preventing arrhythmia and illustrates how models can be used to explain drug effects in different experimental conditions. Electrophysiology models can also be used in screening lead compounds as demonstrated by Mirams et al. who use a variety of ventricular action potential models to predict the arrhythmic risk of 31 drugs (53). Using drug IC₅₀ values and therapeutic concentrations to calculate channel properties under drug influence, the authors were able to identify simulation of action potential duration prolongation as an improved measure of potential risk for Torsade-de-Pointes arrhythmias. The study is also a good example of the utility of collaboration between academia and industry in leveraging computational modeling for drug discovery.

III. Therapies targeted against ischemia and metabolic disorders

Computational models of cardiac metabolism have been built to investigate the changes in the metabolic state of a myocyte during pathological conditions like myocardial ischemia (54) and heart failure (55), and its effect on cardiac electrophysiology. Deficiencies in energy input and waste removal results in alterations to the cardiac action potential, contributing to failure of contraction (56). This condition is most pronounced during ischemia, the block of blood flow to the heart, and is a major trigger for arrhythmias (57). The heart consumes more energy than any other organ (58). To acquire this energy, it uses fatty acids and glucose to produce adenosine triphosphate (ATP) in the mitochondria, which is then shuttled to the contractile machinery through the utilization of creatine (59). When ischemia occurs after complete cessation of blood flow, the concentration of oxygen drops drastically (anoxia) resulting in decreased production of ATP (60). This is accompanied by elevated extracellular potassium concentration and increased blood acidity (61). Electrophysiological changes during the initial stages of ischemia are extremely rapid, making it difficult to study experimentally (54). The large number of simultaneous perturbations to the ischemic myocyte and the difficulty developing in vitro models of ischemia also emphasize the need for computational models in this area.

Expanding on the Luo-Rudy model, Shaw et al. (60) studied the ionic mechanisms underlying changes in the action potential in acute ischemia. By increasing the extracellular potassium concentration and changing the channel properties of the ATP sensitive potassium current, L-type calcium current and the sodium current, the authors were able to replicate the shortened action potential and conduction failure seen experimentally during ischemia.

The ATP-sensitive potassium channel plays a key role in the effects of ischemia on the heart (62). The effects of potassium channel openers in ischemia are controversial with conflicting views on whether they are protective or arrhythmogenic (63, 64). Trenor et al.(65) used a model of the ATP-sensitive potassium channel (66), incorporating the effect the potassium channel opener pinacidil, and integrating it with the Luo-Rudy model. The single cell model was able to replicate the experimentally observed reduction in action potential duration due to pinacidil. To study the effects of pinacidil in acute regional ischemia, the authors implemented a two-dimensional virtual heart tissue model. They noticed that the effect of pinacidil was strongly dose-dependent and had a strong anti-arrhythmic effect at high doses.

Ch’en et al. (67) opted to concentrate on the effects of acidosis and ATP depletion in ischemia. They incorporated equations describing ATP hydrolysis and intracellular pH into the DiFrancesco-Noble action potential model (68). The combined model, despite its limited scope, was able to correctly simulate ischemia-induced sodium overload (due to activation of the sodium-hydrogen exchanger, which causes calcium overload through activation of the sodium-calcium pump) seen experimentally. From their simulations, the authors suggested that cardiac arrhythmia can be attenuated by blocking the sodium-hydrogen exchanger. The cardiac action potential is also influenced by a late sodium current which is small but may contribute significantly to sodium/calcium overload during ischemia. Simulations performed by Noble et al. (69) suggest that blocking the late sodium current in conditions where the action potential is prolonged (e.g. with drugs affecting hERG) would be protective against arrhythmia.

The link between metabolism and calcium handling in a myocyte was modeled by Michailova et al.(70). Specifically, they investigated the effect of calcium and magnesium buffering by ATP and ADP and included ATP regulation of ion transporters. However, they did not explicitly simulate mitochondrial activity (71). An integrated cardiac cell model that linked electrophysiology and contraction with mitochondrial energy generation was developed by Cortassa et al. (72). This model was composed of an earlier model of cardiac mitochondrial metabolism which matched experimental data obtained from rat mitochondria (73). Another biophysically detailed model of cardiac mitochondria was developed by Beard et al.(74) and was used by Wu et al. (75) to investigate the evolution of the metabolic state in pathological hypertrophy, a precursor to heart failure. Heart failure, the inability of the heart to supply the body with enough blood (76), is characterized by a complex blend of changes to normal function including reduced mitochondrial ATP synthesis (55). The model is able to correctly predict the drop in cytoplasmic inorganic phosphate concentration seen in moderate left ventricular hypertrophy. They explored possible metabolic therapies by changing levels of creatine, adenine and exchangeable phosphate and discovered that altering levels of creatine alone was not sufficient, consistent with experimental studies (77). Their simulations suggest elevating levels of all three metabolites could be a beneficial metabolic therapy.

IV. Therapies targeted against signaling disorders

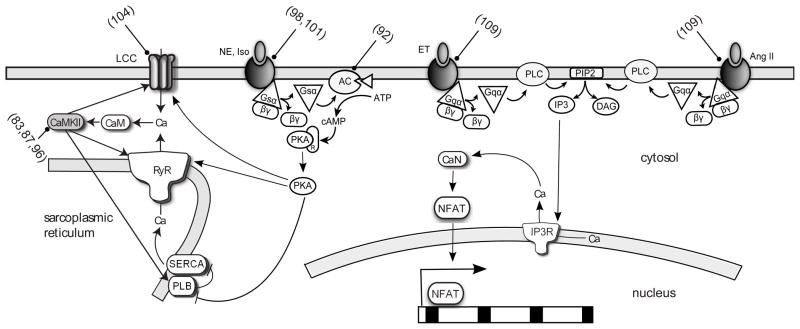
Modeling of disorders of cell signaling networks in myocytes is still in its infancy (33) despite the fact that drugs targeting cardiac signaling pathways are among the most heavily prescribed (78). Intracellular signaling pathways manage cellular processes like cell growth and contractility (79). A unifying feature of some signaling pathways in myocytes is the ubiquity of calcium as a second messenger (80). In addition to its role in contraction, calcium can also signal through Ca/calmodulin dependent protein kinase (CaMKII), a serine/threonine protein kinase, which is activated when bound by the calcium/calmodulin complex (Figure 3). CaMKII regulates cardiac gene expression through phosphorylation of transcription factors like CREB and HDAC (81) but also has an important role in calcium mobilization through phosphorylation of proteins like ion channels (82). By modeling the influence of CaMKII on calcium handling, Livshitz et al. (83) were able to show its potential effect on T wave alternans. T wave alternans are beat-to-beat variations in the amplitude of the T wave of the electrocardiogram and is associated with dispersion of repolarization, ventricular arrhythmia and sudden death (83). This is hypothesized to originate from variation in action potential duration at the cellular level coupled with variation in calcium transient amplitude. Livshitz et al. reformulated the CICR kinetics in the Hund-Rudy model (84), a canine ventricular action potential model that includes the CaMKII regulatory pathway. Their model was able to reproduce the experimentally observed frequency-dependent activation of CaMKII and the effect of CaMKII inhibition on calcium transients. Futher simulations showed that increased CaMKII activity causes increased alternans. They identify combined CaMKII inhibition and modulation of repolarizing currents as a possible intervention for suppressing T wave alternans.

Figure 3.

Schematic of β-adrenergic, α-adrenergic and Ang receptor signaling network. Targets of computational models are indicated with blunt arrows (references in parenthesis). AC, adenylate cyclase; CaM, calmodulin; CaN, calcineurin; ET; endothelin; NE, norepinepherine; IP3R, IP3 receptor; Iso, isoproterenol.

CaMKII can auto-phosphorylate in order to retain kinase activity in the absence of calcium (85). Oxidation can also cause persistent activation independent of auto-phosphorylation (86). Levels of reactive oxygen species, hydrogen peroxide and superoxide are elevated following myocardial infarction resulting in increased levels of oxidated CaMKII. In order to ascertain the impact of oxidative activation of CaMKII following a myocardial infarct, Christensen et al. (87) used the Hund-Rudy model with the inclusion of an oxidized active state for CaMKII in addition to the calcium and autophosphorylation-mediated active states. Their cardiac fiber model described two regions of the epicardium: the normal and the border zone. The border zone of a myocardial infarct is the region of the epicardium that survives a transmural infarct and is often the site of reentrant excitation, which causes ventricular tachycardia (88). Enhanced CaMKII activity was predicted to increase recovery from inactivation of the sodium channel which promotes reduced conduction velocity, a marker for increased risk of arrhythmia (89). Based on their simulations, one may anticipate that inhibition of CaMKII or upstream redox pathways in the infarct border zone could reduce re-entrant arrhythmia and ventricular tachycardia. Indeed, overexpression of a CaMKII inhibitor in mice has been shown to protect from cardiac remodeling following myocardial infarction (90).

Extracellular stimuli for essential processes reach the cell via primary messengers, including catecholamines and hormones, and activate a diverse array of cellular receptors on the plasma membrane (79). These include β-adrenergic receptors, a family of G-protein coupled receptors found predominantly in cardiac, airway smooth muscle and adipose tissue. Binding of the catecholamines epinephrine or norepinepherine results in the coupling of the receptor to the guanine nucleotide binding protein G_s, with the subsequent release of the G_sα subunit following hydrolysis of guanosine triphosphate. G_sα then activates adenylate cyclase resulting in the production of cyclic AMP. Cyclic AMP causes the dissociation of the regulatory and catalytic subunits of protein kinase A (PKA). This allows PKA’s catalytic subunit to phosphorylate various protein targets including L-type calcium channel, phospholamban (inhibitor of SERCA), ryanodine receptor (RyR) and troponin. The key result of classical β-adrenergic receptor activation in the heart is increased cardiac output (91). Saucerman et al. (92) developed a model describing the β₁-adrenergic receptor pathway, the most dominant receptor isoform, integrated with the Luo-Rudy model and modified for the rat ventricular myocyte. The model was able to reproduce the experimentally observed temporal response to β₁-adrenergic stimulation including cAMP, PKA activity and phospholamban phosphorylation. It then served as a platform for investigating possible therapeutics for heart failure where desensitization of the β-adrenergic receptor system occurs (93). Their model predicted that adenylate cyclase overexpression, which can be achieved through gene therapy, increased the generation of cyclic AMP which in turn increased the β₁-adrenergic response with minimal side effects compared with β₁-adrenergic receptor or G_s overexpression. They also suggested that a hypothetical drug that increases the affinity of G_sα and adenylyl cyclase could be effective.

CaMKII is overexpressed in heart failure (94) and its activity appears to contribute to some aspects of β-adrenergic signaling (95). Soltis et al. (96) investigated the consequences of integrated β-adrenergic and CaMKII signaling by developing a combined model of both pathways and their regulation of excitation-contraction coupling. The model was validated against key experimental readouts including CaMKII-mediated phosphorylation of the ryanodine receptor and phospholamban and effects of CaMKII on Ca dynamics such as I_Ca facilitation and acceleration of relaxation. Their model predicted that increased CaMKII expression coupled with β-adrenergic stimulation is pro-arrythmogenic due to a synergy of PKA and CaMKII effects on I_Ca, RyR, and phospholamban. CaMKII-mediated increase in RyR phosphorylation played a key role and was necessary to predict spontaneous delayed after-depolarizations during β-adrenergic signaling. Thus blocking the ability of CaMKII to phosphorylate the RyR could be a potential therapy in such conditions.

Patients with LQT1 are susceptible to sudden cardiac death during β-adrenergic stimulation due to mutations in KCNQ1, a gene that encodes the repolarizing potassium current I_Ks (17). One particular KCNQ1 mutation observed clinically is KCNQ1-G589D, which disrupts the channel’s ability to form a signaling complex with PKA and phosphatase 1, mediated by the scaffolding protein yotiao (97). Saucerman et al. (98) investigated the whole-cell and tissue-level consequences of this disruption by integrating the Saucerman-McCulloch model of β-adrenergic signaling with a model of the rabbit ventricular myocyte integrated into a heterogenous 3D ventricular wedge model. The functional consequences of β-adrenergic signaling predicted by the model agreed with literature from rabbit ventricular myocytes including kinetics and dose response to isoproterenol, enhanced current through the KCNQ1 channel, and decreased action potential duration. Single cell model simulations suggested that the KCNQ1 mutation promotes early after depolarization (triggers for arrhythmia) only in the context of β-adrenergic stimulation. This effect was amplified at the tissue level with the appearance of T-wave abnormalities in simulated ECG’s, including dispersion of repolarization and T-wave inversion. Thus these simulations helped explain the in vivo consequences of KCNQ1 mutation and why β-blockers are effective for LQT1 patients. Indeed, a subsequent clinical report illustrated remarkably similar “Himalayan” T-waves in an LQT1 patient, who was subsequently treated with a β-blocker and implantation of a cardioverter-defibrillator (99).

In another subtype of the LQT syndrome, LQT3, it is unclear whether activation of the β-adrenergic system is beneficial or deleterious (100). In order to investigate this discrepancy, Ahrens-Nicklas et al. (101) incorporated a description of the human SCN5A-ΔKPQ mutation associated with LQT3 into a modified version of the Luo-Rudy (102)and used the Saucerman-McCulloch model of β-adrenergic signaling to predict phosphorylation levels of channels for I_Ks and I_Ca. This allowed the investigation of the pharmacology of LQT3 mutant channels in the context of a human-like action potential. The tissue effect of the various pharmacological agents was observed by performing transmural fiber simulations. In order to model the effects of β-blockade, decreased phosphorylation of I_Ks and I_Ca channels were predicted based on the decreased cyclic AMP production seen with the β-blocker propranolol. In addition, the authors incorporated the separate sodium channel blocking effects of propranolol into a Markov model of the ΔKPQ sodium current. Computational modeling allowed the authors to investigate various β-blocker levels and pacing protocols that have produced apparently contradicting results in published experiments. Isoproterenol decreased action potential duration and suppressed early after depolarization for all 3 ventricular cell types (endocardial, midmyocardial and epicardial). The fiber simulations showed that transmural dispersion of repolarization was decreased in the model following isoproterenol stimulation consistent with in vivo observations (100). An important observation was that this beneficial effect of isoproterenol was pacing–pattern dependent, explaining the discrepancies observed in vivo. Low doses of propranalol increased transmural dispersion and action potential duration, worsening the LQT3 phenotype. However, the high doses of propranolol had the opposite effect on the LQT3 phenotype which suggested to the authors that this beneficial effect was due to increased late sodium current blockage.

Timothy syndrome is a form of long QT syndrome (LQT8) caused by a mutation in the CACNA1C gene that encodes for the α_1C-subunit of the L-type calcium channel (17). This mutation eliminates voltage-dependent inactivation of the channel, thus leaving it open (17). The resulting susceptibility to arrhythmia is ultimately deadly and patients rarely survive past 3 years (103). Sung et al. (104) investigated the influence of β-adrenergic stimulation on arrythmogenesis in Timothy Syndrome by making modifications to a Markov model of the L-type calcium channel in a modified version of the Luo-Rudy model (105). β-adrenergic modulation of various ion channels was simulated by changing channel parameter values to mimic saturating concentrations of a β-adrenergic agonist. The authors discovered that β-adrenergic stimulation, when combined with CACNA1C mutation, increases the occurrence of alternans, delayed after-depolarizations and early after-depolarizations (all triggers for arrhythmia). These predictions help validate the use of β-blockers as treatment for Timothy syndrome patients. Further simulations identified reduction of the L-type calcium current as the most effective target for reducing β-adrenergic-stimulated arrhythmia. The authors also identified reduction of SERCA-mediated Ca uptake as another potential target.

Several signaling pathways have been implicated in pathological hypertrophy, the abnormal growth that often leads to heart failure (106), including the inositol-4-5-biphosphate (IP₃)-calcineurin pathway (107). IP₃ is produced in response to the activation of members of the G_q family of G-protein coupled receptors including the α-adrenergic, endothelin and angiotensin receptors. Activation of these receptors results in liberation of G_qα which activates phospholipase C. Phospholipase C causes hydrolysis of phosphatidyl inositol-4-5-biphosphate to form the second messenger IP₃. IP₃ is thought to contribute to activation of the phosphatase calcineurin, which causes changes in cardiac gene expression through its effect on the transcription factor NFAT (108). In order to understand the control mechanisms underlying pathway activation, a computational model of the IP₃ pathway described above was developed by Cooling et al. (109). Model parameters were fit to match the relatively fast kinetics of IP₃ in response to endothelin-1 seen experimentally. Then, by changing only the parameters for receptor activation, the model was able to predict the experimentally-observed slower kinetics in response to angiotensin. Global sensitivity analysis suggested that the most sensitive parameter controlling the IP₃ transient was the rate constant for phosphorylation of the active receptor. Despite both agonists stimulating IP₃ production via an identical signal transduction pathway, the IP₃ responses are remarkably distinct. From their simulation results, an effective strategy at combating pathological hypertrophy influenced by IP₃ can be achieved by targeting the receptors for endothelin-1 and angiotensin II. This could be more successful than attempts at attenuating hypertrophy with calcineurin inhibitors(110), especially since G-protein coupled receptors are among the most druggable protein targets(111). Indeed, angiotensin converting enzyme (ACE) inhibitors and angiotensin receptor blockers are widely used for heart failure.

V. Future directions

The rate of attrition in drug discovery represents one of the most serious challenges to the pharmaceutical industry (9). A main reason is the difficulty in extrapolating pre-clinical data to predict clinical efficacy (9). Computational modeling can help bridge this gap at various stages in the drug discovery pipeline (112). Species-specific models of the cellular cardiac action potential allows the quantification of properties of potential drugs in various species and, with the help of human models, gain further insight into how the drugs might function in a clinical setting (33). In addition, the further integration of electrophysiology, signaling and metabolic models will allow the accurate simulation of complex diseases like heart failure with multiple etiologies.

Improvement of current signaling and metabolic models and the development of disease-specific models will require the integration of data made available by the recent emergence of cardiac specific proteomic (113) and metabolic (114) data sets. For example, data on expression levels of calcium handling proteins in heart failure myocytes (115) was used by Winslow et al. (116) to develop a heart failure ventricular cell model. By changing the expression levels of four proteins, namely SERCA, sodium-calcium exchanger, inward rectifying potassium channel and the calcium independent transient outward potassium channel, they were able to simulate the observed changes in calcium transients and action potential duration seen in failing cardiac cells (117). These approaches will need to be extended further, because for example in dilated cardiomyopathy, one of the leading causes of heart failure, over 100 proteins are differentially expressed in humans (118).

Unraveling the complexity of disease states will require development of new systems modeling approaches that leverage the breadth of available ‘omics data (15). For example, Berger et al. (119) combined protein-protein interaction and drug databases to identify a signaling network consisting of 1629 gene products that regulates ion channels involved in LQTS. Comprehensive cardiac models such as these may help predict off-target effects and unexpected connections. Simulation of multi-target treatment can also be achieved (as opposed to the identification of a single “silver bullet”), to overcome disease network properties like redundancy, crosstalk and robustness (120). This has led to the development of successful drug therapies for complex diseases affecting other organ systems including cancer and depression (121).

Cardiac phenomena like arrhythmias depend on changes at the molecular and cellular level but they are fatal because of their effect on whole organ function (122). In addition to 1D fiber, 2D sheet and 3D ventricular wedge models, whole heart models have been developed to examine the role of heart anatomy on arrhythmia (3). Multiscale electromechanical models of the heart have also been developed (123) and, if coupled with molecularly-detailed ion channel and signaling models, present a unique opportunity to explore drug intervention for conditions associated with structural remodeling such as myocardial infarction and hypertrophy. A limiting feature of multiscale models is the high computational requirements, with the simulation of one cardiac cycle in a human whole-heart model developed by Potse et al.(124) requiring approximately 2 days on 32 processors. Future advances in CPU performance and the use of alternative tools including GPU-aided simulations (125) will make multi-scale computational models more feasible, presenting an opportunity to merge tissue modeling with physiologically based pharmacokinetic models (126). Pharmacokinetics, which determines how rapidly and for how long a drug is available at a particular organ (127), is crucial for predicting clinical efficacy (128). Integrating multi-scale models with pharmacokinetic models will result in a modeling platform that is as close to clinical trials as possible. A recent example of the utility of this strategy is provided by Wu et al.(129) who use a multi-scale tissue model to investigate soluble VEGF receptor’s potential as an anti-angiogenic therapeutic.

It is important not to underestimate the challenges involved in applying computational models to drug discovery and development. A key step in every model’s development is the choice of the appropriate level of mechanistic detail. Most models are carefully optimized to address a particular set of biological questions or applications, often employing Albert Einstein’s advice to “make everything as simple as possible, but not simpler.” But when repurposing a model for drug discovery or integrating models to tackle multi-scale phenomena, one must carefully re-evaluate the underlying model assumptions and revalidate for the new experimental system. Parameter selection is particularly difficult when integrating multiple models, as most models are based on data from a range of experimental systems and animal species (10, 129). And as modeling efforts are generally data-limited, the majority of models described above were validated only under a limited set of available experimental conditions. While fully comprehensive model validation is not feasible, a key challenge is to identify the extent of validation that builds sufficient confidence in new model predictions to guide the next experimental or clinical phase. Systematic efforts to validate fundamental aspects of myocyte physiology across a range of models are likely to help in this regard (130).

Despite these challenges, cellular computational modeling has already informed the development of several drugs including ranolazine and ivabradine (10). Such modeling approaches have until recently been primarily used in academia. For the goals of FDA’s Critical Path Initiative to be realized, it will require increased collaboration between academia and industry to harness the potential of cardiac computational modeling for drug discovery and development. The rewards of this collaboration should help reduce the clinical burden of cardiovascular disease.