Using Gene Expression Noise to Understand Gene Regulation

Abstract

Phenotypic variation is ubiquitous in biology and is often traceable to underlying genetic and environmental variation. However, even genetically identical cells in identical environments display variable phenotypes. Stochastic gene expression, or gene expression ‘noise’, has been suggested as a major source of this variability, and its physiological consequences have been topics of intense research for the last decade. Several recent studies have measured variability in protein and mRNA levels, and have discovered strong connections between noise and gene regulation mechanisms. When integrated with discrete stochastic models, measurements of cell-to-cell variability provide a sensitive ‘fingerprint’ with which to explore fundamental questions on gene regulation. In this review, we highlight several studies that used gene expression variability to develop a quantitative understanding of the mechanisms and dynamics of gene regulation.

Identical genotype and environmental exposure are not sufficient to guarantee a unique phenotype. Consider a single mother cell dividing into two daughter cells of equal volume. During the division process, all the molecules in the mother cell are in Brownian motion according to the laws of statistical mechanics. The probability that each daughter cell inherits the same number of molecules is infinitesimally small. Even in the event that the two daughter cells receive exactly one copy of a particular transcription factor, each transcription factor will perform a Brownian random walk through its cellular volume before finding its target promoter and activating gene expression. Because Brownian motion is uncorrelated in the two daughter cells, it is statistically impossible for both genes to become activated at the exact same time, further amplifying the phenotypic difference between the two daughter cells. These are just two examples of the many sources of gene expression variability that arise in isogenic cells exposed to the same environment.

The origins and consequences of stochastic gene expression, or gene expression ’noise’, have been studied extensively during the last decade and have recently been reviewed in detail (1–6). Here we focus on recent works that integrate experimental and computational analyses of gene expression noise to systematically test and refine our understanding of regulation in different genes, regulatory pathways and organisms. We discuss how combining single-cell measurements and stochastic analyses can reveal qualitative and quantitative features of gene regulation that are hidden by bulk assays or deterministic analyses. In the first part of this review, we discuss how the cell-to-cell variability in gene expression of a particular transcript or protein has been used to develop a quantitative understanding of the underlying gene regulation. In the second part, we cover how statistical correlations in the fluctuations of different transcripts and/or proteins can be used to infer gene regulatory interactions.

Inferring models of gene regulation from variability in gene expression

Poisson expression statistics

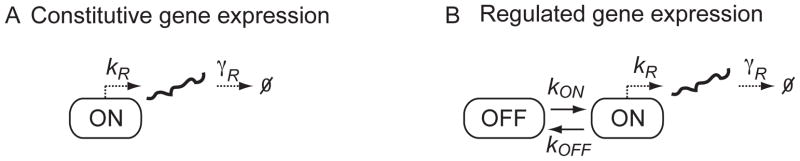
In the simplest possible model of constitutive gene expression (Fig. 1A), a transcript is produced at a constant rate k_R and destroyed in a first-order reaction with rate constant γ_R. If the total number of a particular transcript m is large, the kinetics can be approximated by the following deterministic differential equation:

$$\frac{dm}{dt}=k_R-{\gamma }_{R}m$$ [1]

Fig. 1. Constitutive versus regulated gene expression.

A) Schematic of a constitutive gene expression model with transcription rate k_R and mRNA degradation rate constant γ_R. B) Schematic of a two-state (ON, OFF) model with transition rates k_ON and k_OFF.

This approximation breaks down in cells when the copy numbers of transcripts are small. For example the average transcript copy numbers of the constitutive housekeeping genes MDN1, KAP104, and DOA1 in budding yeast are 6.1, 4.9, and 2.6, respectively (7). These low copy numbers suggest a probabilistic reformulation of Eq. [1]. In the constitutive expression model, transcript births and deaths occur as uncorrelated events, such that in any short time interval, dt, the probability of one transcript production is k_R·dt, and the probability of one transcript degradation is γ_R·m·dt. For equilibrium to be possible, the probability of having m transcripts, Prob(m), and producing another must be equal to the probability of having (m+1) transcripts, Prob(m+1) and having one degrade. In other words, k_R·Prob(m) = γ_R·(m+1)·Prob(m+1) for any m, which is only possible if the copy number distribution follows a Poisson distribution (8).

It is possible to quantify the variability in transcriptional regulation at the mRNA level using single molecule fluorescent in situ hybridization (smFISH) (9, 10). In this technique, endogenous mRNA transcripts are labeled with a large number of fluorescently modified DNA oligonucleotides. As a result, a fluorescence microscope can detect the precise location of each individual mRNA molecule as a diffraction-limited spot. Zenklusen et al. (7) used smFISH to count specific mRNA molecules in intact fixed yeast cells and found that the constitutive gene expression model offers surprisingly good quantitative matches to transcriptional behaviors for the housekeeping genes MDN1, KAP104, and DOA1 in budding yeast. The measured numbers of mRNA transcripts per cell were well described by Poisson distributions for all three genes. By measuring the number of partially formed nascent mRNA in each nucleus, Zenklusen et al. also determined that subsequent transcript production events were uncorrelated (7), again consistent with the constitutive expression model.

Two-state model of gene regulation

Although the constitutive gene expression model captures the fluctuations of several housekeeping genes in budding yeast (7), it does not perform as well when gene expression is regulated. Since deviations from Poisson behavior indicate regulation, can quantifying these deviations reveal the mechanism of regulation? A key parameter to quantify the deviation from Poisson statistics is the Fano factor, which is the ratio between the variance, σ², and the mean, m̄, of the mRNA copy number distribution, σ²/m̄ (8). For a Poisson distribution, the Fano factor equals one. Golding et al. (11) determined a Fano factor of 4.1 for a synthetic transcript driven by the P_lac/ara promoter in Escherichia coli, indicating that the transcript distribution was significantly wider than a Poisson distribution. A two-state model of gene expression (12–16) can fit this data much better. This model considers two promoter states: an OFF state, in which no transcription occurs and an ON state, which has transcription rate k_R. The constants k_ON and k_OFF define the transition rates between the two states, and γ_R is a first-order rate constant for transcript degradation (Fig. 1B). The OFF state is usually associated with a closed chromatin state in which the binding sites for transcription factors are inaccessible, whereas the ON state is associated with the open active chromatin state (14).

According to the two-state model, the average fraction of cells in the ON state is f_ON = k_ON/(k_ON + k_OFF), and the average number of mRNA molecules in each cell is m̄ = f_ONk_R/γ_R. The expression for the Fano factor in steady-state can be written as (12):

$$\frac{{\sigma }^2}{\overline{m}}=1+\frac{(1-f_{ON})k_R}{(k_{ON}+k_{\mathit{OFF}}+{\gamma }_R)}$$ [2]

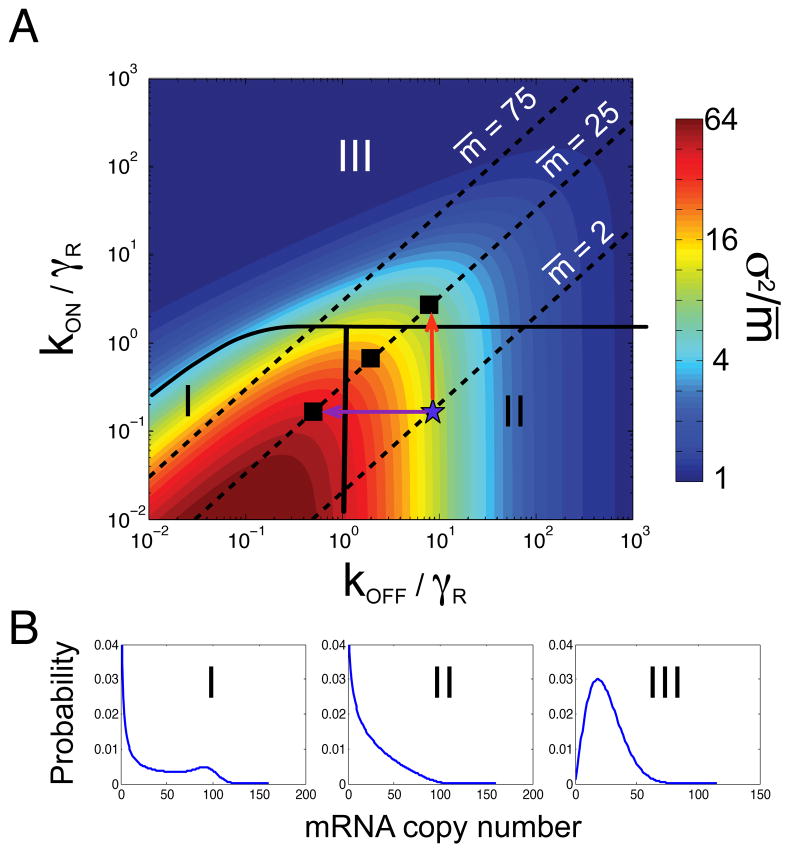
Figure 2A uses a heat map to illustrate the Fano factor’s dependence upon k_OFF and k_ON for a fixed transcription rate k_R. In order to compare the variability at equal expression levels, the three dashed lines denote parameter combinations that produce an average of 2, 25 and 75 mRNA per cell. Although the average expression level is constant along these lines, the Fano factor varies significantly, as does the qualitative shape of the mRNA distribution. For example, Fig. 2B shows the distributions corresponding to the filled squares on the m̄ = 25 line in Fig. 2A. Although each parameter set yields an average of 25 molecules per cell, they exhibit three distinctly different behaviors for the variability of m between cells. Based on differences in the mean, Fano factor, and qualitative shapes of distributions, we can dissect the parameter space into three different “phenotype” classes (14, 17). In class I, both k_ON and k_OFF are slow, and cells separate into distinct ON and OFF populations yielding a bimodal mRNA distribution (Fig. 2B, left) and resulting in a large Fano factor. In class II, k_ON is slow and k_OFF is fast, and therefore most cells are OFF. In this case, the low value of f_ON contributes to low means and Fano factors, but occasional mRNA bursts give rise to long exponential tails in the mRNA distribution (Fig. 2B, middle). Finally, in class III, k_ON is fast in comparison to either γ_R or k_OFF, and the system spends very short periods in the OFF state. The dynamics of this special case collapses down to that of the constitutive expression model, with an effective transcription rate $k_R^{\mathit{eff}}=k_R{f}_{ON}$ and a Poisson-like mRNA distribution (Fig. 2B, right).

Fig. 2. Effects of transcriptional control on mRNA distributions.

A) Heat map of the cell-to-cell variability (Fano factor, σ²/m̄), versus normalized gene activation rate k_ON/γ_R and normalized deactivation rate k_OFF/γ_R with fixed production and degradation rates (k_R = 100, γ_R = 1). Lines of equal average mRNA expression are shown for 2, 25, and 75 molecules. The parameter space is separated into three classes (I,II,III) that exhibit different types of cell-to-cell variability. B) Representative distributions from each class: Class I corresponds to systems with long OFF and ON periods, giving rise to bimodal distributions with clearly delineated ON/OFF populations. Class II corresponds to populations with short ON and long OFF periods, giving rise to occasional mRNA bursts and long distribution tails. Class III includes systems with short OFF periods, giving rise to continuous production and more graded unimodal distributions. All three distributions have the same average of 25 mRNA and correspond to the squares in (A). Distributions were computed using the Finite State Projection approach (34).

A cell can increase the average mRNA copy number m̄ from 2 (indicated by the blue star in Fig. 2A) to 25 by either decreasing k_OFF (purple arrow in Fig. 2A) or increasing k_ON (red arrow in Fig. 2A). Increasing k_ON converts a class II phenotype into a class III phenotype, resulting in more Poisson-like expression. Conversely, decreasing k_OFF shifts the system to class I, corresponding to bimodal expression. Thus, although both modulation mechanisms yield the same change in average mRNA levels, their single-cell statistics are quantitatively and qualitatively different. Below we highlight several studies that exploit these differences to learn more about the gene regulatory control mechanisms.

As in studies of constitutive expression, single-cell responses of regulated genes have been examined at the mRNA level. Raj et al. (15) used smFISH to study gene expression variability in mammalian cells. They integrated an inducible tetO promoter into the genome and quantified mRNA numbers and locations. The measured mRNA distributions had long exponential tails that closely matched those of the class II phenotype, corresponding to bursts of mRNA that were short, infrequent, and intense. Furthermore, Raj et al. observed that ON cells exhibited extra-bright clusters of nascent transcripts and elevated levels of nuclear mRNA, whereas OFF cells lacked these transcription site spots and had far fewer nuclear mRNA. In this context, spatial variability provided quantitative insight into transcriptional dynamics. More recent smFISH studies have also discovered mRNA distributions from all three classes for a myriad of other genes in several model organisms, including bimodal distributions of class I in cell-cycle and inducible genes in yeast (19); long exponential distribution tails corresponding to class II in E. coli (20), rRNA (21) and coding and long non-coding RNA (22) transcription in yeast; and unimodal Poisson-like distributions of class III in yeast (7).

Single molecule FISH has also been used to explore how transcriptional regulation changes between conditions (15, 19). Raj et al. (15) showed that an increase in the transcriptional activator tTA or the number of activator binding sites increased the transcriptional activity of the tetO promoter in mammalian cells. Quantitative comparisons of measured mRNA distributions with the two-state model revealed that activation was consistent with either k_OFF modulation (purple arrow in Fig. 2A) or k_R modulation. In a recent study, So et al. also integrated experimental and computational analyses to find that that k_OFF modulation is a common motif, which regulates mRNA expression in twenty independent E. coli genes, whose mRNA expressions span four orders magnitude (19). Using smFISH (10), they measured mRNA distributions in 150 different combinations of genes and growth conditions that modulate those genes. After correcting for different gene copy numbers and mRNA lifetimes, the mRNA mean and Fano factor were computed and plotted for every gene and experimental condition, and the resulting scatter plot was closely fit by Eq. [2], where k_ON and k_R were constant, and k_OFF was selected to match the mean expression.

While the former studies explored gene regulation at the mRNA level, similar conclusions have been reached through single-cell analyses at the protein level. Raser and O’Shea (14) used single-cell measurements of fluorescent proteins concentrations to show that induction of the PHO5 promoter in budding yeast increases the expression level while reducing the cell-to-cell variability. This trend was explained as the system starting in class II and increasing k_ON to switch toward class III (red arrow in Fig. 2A). Similarly, Octavio et. al. (22) explored the regulation of the FLO11 gene in yeast. Using inducible promoters to control the regulatory proteins Flo8, Sfl1, Tec1, Ste12, Phd1, Msn1 and Mss1, they pushed the system into each of the three phenotypes. Then, by elucidating how each transcription factor altered the variability in gene expression, they determined the mechanisms by which each factors modulated transitions between an OFF state, an intermediate ‘competent’ state, and the fully active ON state.

Inferring gene regulatory interaction from correlations between fluctuating genes

The examples above illustrate how the expression distribution of a particular transcript or fluorescent protein reporter can be used to quantify the transitions between active and inactive transcription states and to determine the mechanism by which regulators modulate this process. In many of these studies, the analysis of regulatory behavior required the application of an external input or a change in environmental conditions. It is not always easy to introduce such a perturbation, but what if they already existed in nature? As discussed above, most cellular proteins undergo stochastic fluctuations, which can activate or repress downstream processes and thereby introduce valuable perturbations. As a result, when multiple transcript or protein species are monitored in the same cell, important additional information can be extracted by analyzing how different species correlate with one another. This correlation analysis was used in experiments focused on synthetic gene networks in E. coli, where expression levels of several genes were monitored in the same cell using fluorescent reporters. By analyzing the pair-wise correlation between the different fluorescent reporters, the major fluctuation sources could be determined (23, 24).

In a recent study, Stewart-Ornstein et al. (25) used fluorescent proteins to examine the pair-wise correlations of hundreds of different yeast genes, whose expression levels varied over three orders of magnitude. Even without using exogenous perturbations, single-cell steady state measurements could reveal clear groups of genes whose stochastic fluctuations were strongly coordinated. These collections of genes, which they labeled “noise regulons,” corresponded to functional groups related to stress response, mitochondrial regulation, and amino acid biosynthesis. Furthermore, Stewart-Ornstein et al. showed that steady-state correlations were strongly predictive of the proteins’ dynamic response to heat shock.

Using a two-color RNA fluorescent in situ hybridization assay, Gandhi et al. (18) measured pair-wise correlations between RNA species regulated by the same promoter or by two different promoters. The Gal4-regulated genes GAL1, GAL7 and GAL10 were induced with 2% galactose, and their distributions were measured at steady state. As expected, single-cell correlation analyses showed strong correlations between GAL1 and GAL7 as well as between GAL1 and GAL10. mRNA correlations were also found in other regulatory genes. Transcripts of the genes SWI5 and CLB2, which are expressed in the G2/M stages of the cell cycle, were strongly correlated with each other, but weakly anti-correlated with NDD1, which dominates during the S-phase. On the other hand, constitutive genes such as MDN1 (ribosome biogenesis), PRP8 (pre-mRNA splicing) and KAP104 (nucleocytoplasmic transport) exhibited much less coordination.

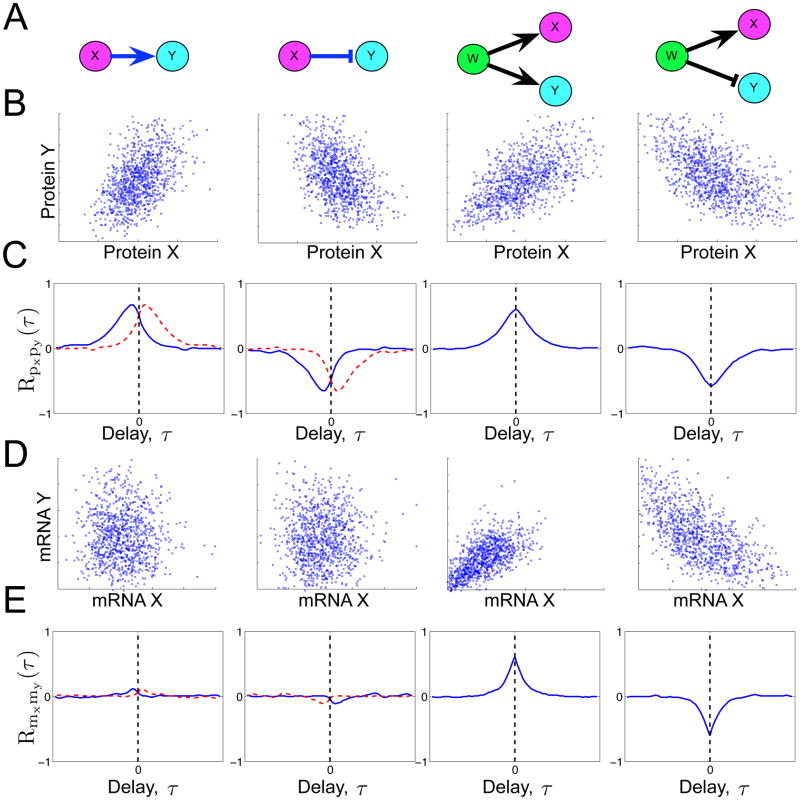
Although correlations at a single time point can reveal static relationships among different mRNA and protein species, this view lacks information about the system’s history and causal relationships. If two proteins X and Y are correlated, the questions remain: does X activate Y; does Y activate X; or does a third protein W control them both? To illustrate this, Fig. 3A shows simple motifs by which proteins W, X and Y could relate to one another, and Fig. 3B shows typical scatter plots of the single-cell expression for proteins X and Y for these motifs. When static correlations cannot discriminate between these motifs, dynamic correlations in single-cell fluctuations may help (26). Such analyses make use of the cross-correlation function (26), R_XY (τ) = 〈X(t + τ)Y(τ)〉/σ_Xσ_Y, which measures how fluctuations in Y at time t relate to those in X at time t + τ. Here, 〈…〉 denotes the covariance of two variables, and σ_X and σ_Y are the standard deviations of X and Y respectively. The magnitude of R_XY (τ) reveals positive or negative regulation, and the timing of peaks in R_XY (τ) reveals causality in this regulation. As examples, Fig. 3C plots the cross-correlation functions between proteins X and Y for each of the motifs in Fig. 3A. For the first motif, where X activates Y, the blue line in Fig. 3C (left) shows that R_XY (τ) has a maximum, and since X is upstream of Y, this peak occurs at a negative delay time. Conversely, when protein Y is a repressor of X, R_XY (τ) has a minimum at a positive τ (Fig. 3C, second column, red line). If both X and Y were both controlled by W, the maximum or minimum would occur at τ= 0, and its sign would be positive or negative depending upon whether W has the same or different effects on X and Y (Fig. 3, right columns).

Fig. 3. Different regulatory motifs yield different steady-state correlations.

A) Schematics of four possible regulator motifs: X activates Y; X represses Y; W activates both X and Y; and W activates X but represses Y. For each motif, mRNA is produced according the constitutive model; protein is translated from mRNA as a first order reaction; and both mRNA and protein degrade as a first order reaction. Regulation changes to the transcription rate are defined k_R(X) = αX⁴/(M⁴ + X⁴) for activation k_R(X) = αM⁴/(M⁴ + X⁴) for repression. B) Scatter plots of the populations of protein X and protein Y at steady state. C) Dynamic cross-correlation functions of protein X and protein Y, versus the correlation time delay. The magnitude of R_XY (τ) indicates how strongly X(t+τ) is correlated (positive) or anti-correlated (negative) with Y(t). For causal events, where X activates (or represses) Y, peaks (or dips) appear in R_XY (τ) at negative values of τ. Blue lines correspond to the motif in (A), and red lines correspond to the same motif in which X and Y have been interchanged. D) Scatter plots for mRNA X and mRNA Y populations. E) Dynamic cross-correlation for mRNA X and mRNA Y. Simulations were conducted using the stochastic simulation algorithm (35).

Dunlop et al. (26) tested this dynamic correlation approach in live cells by inserting three fluorescent protein reporters of different colors into the E. coli genome. Yellow fluorescent protein (YFP) was fused to the λ CI repressor, which controlled expression of red fluorescent protein (RFP). Cyan fluorescent protein (CFP) was placed on a separate constitutive promoter. Using fluorescence time-lapse microscopy, all three colors could be monitored simultaneously over several hours. Dynamics of the YFP-RFP pair were anti-correlated with a delay of about 120 minutes, clearly revealing that CI-YFP repressed RFP (similar to Fig. 3, second column, blue line). Conversely, the unregulated YFP-CFP pair exhibited a delay-free correlation characteristic of common upstream regulators (extrinsic noise) that affect both YFP and CFP in a similar fashion (similar to Fig. 3, third column). Thus, the causal relationships of all three reporters were uniquely determined. Extending and applying this approach to the CRP-GalS-GalE feed-forward loop in E. coli, they analyzed how the relationship between GalS and GalE varies under different fucose levels and under the influence of GalR (26).

While correlations at either mRNA or protein levels can reveal gene regulatory relationships, the two do not always perform equally well. To illustrate this, Fig. 3D–E shows scatter plots and cross-correlations between the mRNA X and mRNA Y corresponding to protein X and protein Y, respectively. Although protein X and protein Y are coordinated for all four motifs in Fig. 3, this is not the case for their mRNA levels. This can be explained by the disparate times scales of mRNA and protein. Fast degrading mRNA may exhibit fluctuations with a broad frequency bandwidth. Conversely, slow degradation of proteins filters out fast fluctuations but keeps slow fluctuations. Constitutively expressed mRNA X has both fast and slow fluctuations, but protein X only transmits the slow fluctuations downstream. The result is that the dynamics of mRNA X and mRNA Y are dominated by uncorrelated fast fluctuations, which overshadow their correlated slow fluctuations. On the other hand, protein X and protein Y only contain the better-correlated slow fluctuations. In other words, two mRNA species can be mostly uncorrelated with one another, yet produce protein in a coordinated fashion. Gandhi et al. (18) observed such a circumstance in budding yeast, when they found very little correlation between pairs of transcripts that encode for coordinated proteins of the same protein complex, including proteasome and RNA polymerase II subunits. They even found correlation lacking in two alleles of the same gene. In a related study, Taniguchi et al. (27) looked at over 1000 genes in E. coli and measured both mRNA and protein copy numbers in single cells. They found that for most genes, even the numbers of mRNA and protein molecules were uncorrelated. These studies suggest that understanding of regulatory phenomena requires one to consider regulation at both the mRNA and the protein level.

From these studies, it is now clear that variability in single-cell measurements contains a wealth of information that can reveal new insights into the regulatory phenomena of specific genes and the dynamic interplay of entire gene networks. As modern imaging techniques begin to beat the diffraction limitations of light (28) and flow cytometers become affordable for nearly any laboratory bench (29), we find ourselves in the midst of an explosion in single-cell research. With the advent of single cell sequencing (30, 31) it might be possible to determine the full transcriptome of many single cells in the near future and to determine the full expression distributions and correlations for all genes in the genome. We expect that the approaches described in this review, which have been pioneered using the model microbial systems, will be readily applied to mammalian cells and tissues (32, 33).