Direct observation of stick-slip movements of water nanodroplets induced by an electron beam

Abstract

Dynamics of the first few nanometers of water at the interface are encountered in a wide range of physical, chemical, and biological phenomena. A simple but critical question is whether interfacial forces at these nanoscale dimensions affect an externally induced movement of a water droplet on a surface. At the bulk-scale water droplets spread on a hydrophilic surface and slip on a nonwetting, hydrophobic surface. Here we report the experimental description of the electron beam-induced dynamics of nanoscale water droplets by direct imaging the translocation of 10- to 80-nm-diameter water nanodroplets by transmission electron microscopy. These nanodroplets move on a hydrophilic surface not by a smooth flow but by a series of stick-slip steps. We observe that each step is preceded by a unique characteristic deformation of the nanodroplet into a toroidal shape induced by the electron beam. We propose that this beam-induced change in shape increases the surface free energy of the nanodroplet that drives its transition from stick to slip state.

Water movement at the interface plays a crucial role in the function of biological membranes (1), flow of liquids through pores (2, 3) and over surfaces (4), hydration of biomolecules (5–7), and chemical reactions in aqueous solutions (8). Although much is known about the movement of bulk water, most of what is known about interfacial water results from modeling and computational simulations (9, 10). Nanometer-diameter water droplets, because of their high surface-to-volume ratio and small number of molecules, present an ideal system for theoretical explorations of interfacial water dynamics induced by external forces. Such studies describe how external driving forces imposed by thermal (11), chemical (12), and topographic gradients (13) can lead to motion of nanometer-diameter droplets, and local fluctuations may result in the breakup of liquid nanojets (14). These theories imply that perturbations, either from external physical forces or chemical nonuniformities are coupled to dynamics of a nanodroplet through changes in shape and thus causing translocation of nanometer size droplets. Interestingly, very recent simulations also predict that nanometer-diameter water droplets will slip on hydrophilic surfaces (15) similar to those on hydrophobic surfaces (16, 17). However, studying the structural dynamics of nanodroplets is experimentally challenging because one needs to be able to externally induce the movement and be able to image the subsequent dynamic process of nanoscale droplets. Although atomic force microscope probes have measured the interfacial forces between liquids (18) and scanning transmission electron microscopy (TEM) has imaged small numbers of static water molecules confined in carbon nanotubes (19), these approaches fail to directly relate structure and dynamics of nanoscopic liquids. The ability to externally induce the movement and directly study the motion of model nanodroplets in contact with substrate interface may provide an insight to dynamic properties of interfacial water by experimentally complementing theoretical simulations. Such studies will be critical in the design of materials tailored to the adhesion and flow of liquids at the interface (20, 21).

Hydrodynamic slip of water that results in the movement of water over the surfaces generally occurs on hydrophobic surfaces (16, 17). However, it may be possible that a hydrophilic surface with dense favorable absorption sites for water molecules can promote water slip at nanoscale as water molecules easily migrate across the closely spaced atomic absorption sites (15). The atomic spacing in hydrophilic amorphous silicon nitride (Si₃N₄) is suitably dense, 1.73 Å between Si and N atoms (22), making flat Si₃N₄ membrane a great candidate for observing the movement of interfacial water. Here, we report the dynamic TEM imaging of structural changes in 10- to 80-nm-diameter droplets of water induced by an electron beam that directly lead to deformation and translocation of these nanodroplets on flat Si₃N₄ membranes. Thus in our study, electron beam directly deforms and forces the movement of nanodroplets, which differs from general discussion of interfacial water flow focused on substrate-water interaction.

Results and Discussions

We are able to examine the dynamics of nanometer-diameter droplets of water in a microfabricated environmental liquid cell that isolates the water sample from the vacuum of a TEM (23–25). The liquid cell consists of two approximately 20-nm-thick electron translucent Si₃N₄ membrane windows that are separated and sealed by an approximately 200 nm indium spacer (see SI Text, Fig. S1). The liquid cell interior was rendered hydrophilic by glow discharge to create the adsorption sites for water molecules and to aid in the filling of the liquid cell. At the bulk scale, macroscopic water droplets (approximately 1 μL) on these glow-discharged surfaces are flat, whereas droplets on cleaned but untreated surfaces are hemispherical with varying contact angles (less than 90°), depending on the degree of hydrophilic interaction (Fig. 1A). Under continuous exposure to the 120-keV electron beam, the window-enclosed bulk water (approximately 200-nm thick) retracts, initially leaving a thin film (approximately 5–20 nm) of water on the hydrophilic Si₃N₄ membrane. We observe that subsequent dewetting of the remaining thin water layer leaves droplets with sizes in the range of 10–80 nm on the membrane (see SI Text, Fig. S2). When the electron beam is shut off, the surfaces rewet as water film moves in (low-intensity imaging of such process is shown in Movie S1). For Si₃N₄ window membranes exposed to a beam, a small uniform offset of the membrane surface potential (approximately 100–200 mV) lasting for a few hours even in the absence of the beam is measured (see SI Text, Fig. S3). However, the fact that the surface rewets after the beam is turned off and all the while the membrane remains charged suggests the dewetting of the window membrane is not caused by modification of the window surface.

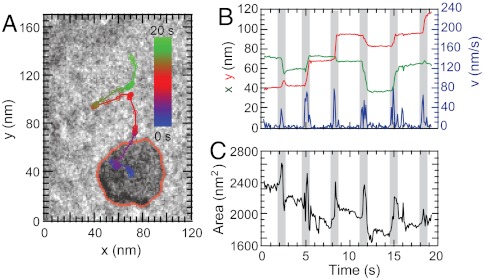
Fig. 1.

Stick-slip movement of nanodroplet. (A) 1 μL water droplet on an untreated (Left) and a glow-discharged (Right) Si₃N₄ film maintains cap-like shape with contact angles of 59° and 16°, respectively. (B) TEM micrograph series of a translocating water nanodroplet on a Si₃N₄ membrane surface. The stationary droplet elongates by extending lamella, shifts its mass to a new position, and comes to rest. (C) Intensity map of transmitted electron beam of the same droplet. The water mass fluctuating inside the droplet results in a shift of liquid mass to the rim of the droplet followed by extension of the protruding film from the rim. The thin front sheet fills from water in the droplet, which slowly advances forward. (D) The cross-sectional view of the droplet and contact angle hysteresis during the stepping process of the nanodroplet. (E) Schematic illustration of the beam-induced translocation process.

When irradiated by the same 120-keV electron beam of the TEM, a nanodroplet moves in discrete steps on the hydrophilic surface and not by a continuous flow (Fig. 1B). We visualized the internal dynamics of the water inside a nanodroplet by mapping the relative water mass from the electron absorbance (Fig. 1C). Within a stationary nanodroplet, the liquid mass exhibits small fluctuations under a uniform electron beam during which the water redistributes to the droplet rim (see Movie S2) and assumes a torus-like structure with nonuniform thickness (Fig. 1 C and D). The droplet advances at the steepest side of the torus when a thin lamella extends from the rim as schematically illustrated in Fig. 1 D and E. The mass of water then shifts into this protrusion, causing the torus shape to flatten and the rear of the nanodroplet to recede. The angles at which both the advancing (θ_adv) and receding (θ_rec) contact lines slip are set by molecular interactions at the liquid–solid interface, surface roughness, and chemical heterogeneities (26, 27). This type of motion is characteristic of a stick-slip mechanism (28, 29) in which the nanodroplet slips when the redistribution of water overcomes interfacial forces between the nanodroplet and the substrate.

The stick-slip motion is clearly seen when the dynamics of a 50-nm nanodroplet are plotted and quantified (Fig. 2 A and B) through six stick-slip cycles. Each step is characterized by a burst of movement (20–80 nm/s peak velocity) that coincides with a transient increase in area (Fig. 2C). These bursts are separated by a pause which reduces the average speed to approximately 10 nm/s (189 nm total travel distance in 19.2 s). The change in interface area during slipping is limited by the initial size of the nanodroplet.

Fig. 2.

Dynamics of a moving nanodroplet. (A) Path traced by the droplet during 19.2 s, during six steps. The droplet boundary is traced with red line (see Movie S2). (B) x (green curve), y (red curve) position and instantaneous velocity (blue curve) of the droplet’s centroid position illustrate distinct steps taken during the translocation. (C) With each step the nanodroplet elongates as illustrated by the change in area versus time. The gray-shaded regions in graphs (B) and (C) highlight the slipping events.

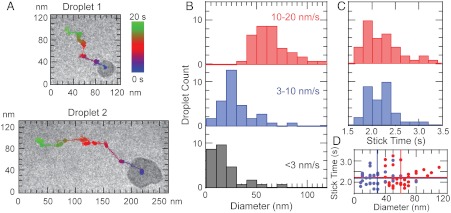
To investigate the relationship between dynamics and nanodroplet size, we compared two nanodroplets with diameter of approximately 30 nm (droplet 1) and 60 nm (droplet 2) under identical electron beam conditions as shown in Fig. 3A (see Movies S3 and S4). During a 20-s period, the 30-nm droplet traveled 276 nm while the 60-nm droplet traveled 353 nm (see SI Text, Figs. S4 and S5). Similarly, very small nanodroplets (less than 20 nm) often tend to get pinned on the surface and do not move (see Movie S5). A histogram of the nanodroplet size at different average speeds obtained with the electron flux in the range of 60–80 e/(Ų·s) (Fig. 3B) shows that larger diameter nanodroplets are on average faster than the smaller nanodroplets and that very small nanodroplets are essentially immobile. A distribution of average stick times, a time interval between two consecutive slipping attempts, indicates that these stick times are independent of nanodroplet size (Fig. 3 C and D). It has also been shown that the velocity of macroscopic droplet increases with droplet size when driving force is introduced by either physically (30) or chemically (31, 32) induced surface energy gradient (33, 34). However, contrary to smooth flow observed in macroscopic droplets driven by surface energy gradient, the induced movement of nanodroplets happens in discrete slip steps only when deformation causes sufficient change in surface free energy.

Fig. 3.

Size effects on a nanodroplet translocation. (A) TEM micrograph of 30 nm (droplet 1) and 60 nm (droplet 2) along with their corresponding paths during 20 s (see Movies S3 and S4). (B) Distribution of droplet diameters for droplets moving with an average speed of less than 3 nm/s (stuck), 3–10 nm/s (slow), and 10–20 nm/s (fast) when exposed to an electron flux of 60–80 e/(A²·s). (C) Distribution of droplet stick times for droplets moving at 3–10 nm/s (slow), and 10–20 nm/s (fast) when exposed to an electron flux of 60–80 e/(A²·s). (D) Droplet stick time versus droplet diameter for droplets moving at 3–10 nm/s (blue), and 10–20 nm/s (red) when exposed to an electron flux of 60–80 e/(A²·s). Solid lines represent average value of stick time (horizontal lines) and diameter (vertical lines).

Generally, the step size (lamella extension from the rim of the droplet) will depend on the balance between surface and adhesion energies of the droplet interfaces. To estimate the slip step size, we consider a simplified hemispherical droplet sitting on a solid surface that undergoes a shape deformation influenced by electron beam, with surface area of πR² at the solid–liquid interface and 2πR² at the liquid–air interface. The surface free energy of such droplet is G(R) = 2γπR² + πR²(γ_LS^-γ_SG), where γ = 72 mJ/m², γ_LS, and γ_SG are surface energy density at liquid–gas, liquid–solid, and solid–gas interfaces, respectively (35). The small steps of ΔR can result from a deformation-induced increase in the surface energy, ΔG = G(R + ΔR) - G(R) ≈ (dG/dR)_ΔR=0ΔR + 1/2(d²G/dR²)_ΔR=0ΔR² = π(2γ + γ_LS^-γ_SG)ΔR², where (dG/dR)_ΔR=0 = 0, as the droplet deforms because the surface energy of the unperturbed droplet is at a minimum (36). Therefore, such a change in surface energy can lead to a step of

[1]

where ΔG = ε is the energy barrier that needs to be overcome for a nanodroplet to slip by ΔR. This barrier energy for a nanodroplet with 2R = 50 nm is an adhesion energy at the interface between the water and the surface. Using macroscopic equilibrium contact angle measurement of θ_c = 16°, where contact angle can be expressed as cos θ_c = (γ_SG - γ_LS)/γ: ε = πR²γ(1 + cos θ_c), we obtain a step size of ΔR ≈ 34 nm, similar to our experimental observations (Fig. 1B).

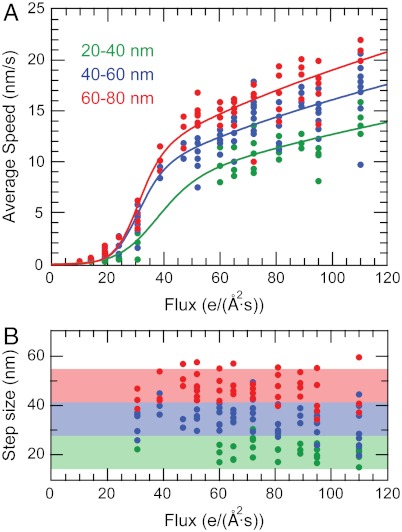
The nanodroplet deformation and the subsequent translocation are observed above a threshold electron flux. The relation between average speeds of nanodroplets and electron flux of imaging beam is plotted in Fig. 4A. The influence of a power delivered by electron flux on average speed of nanodroplets can be qualitatively described by the Kramer’s type transition-state relation (37). The nanodroplet moving with velocity v experiences an interfacial drag force at the droplet–substrate interface that is proportional to the velocity of the nanodroplet: F_d ∼ v. The driving power for such a nanodroplet can be estimated to be P = F_d·v ∼ v². Because the driving power, P, must be linearly proportional to the electron flux, Φ, we have phenomenological description of velocity as

[2]

where v₀ is a velocity factor, Φ_t is the threshold flux for droplet to move, Φ is the irradiating electron beam flux, and α is the transfer coefficient. The average translocation speeds for nanodroplets are plotted in Fig. 4A, qualitatively capturing the relation between the average velocity and the electron flux. The fit of Eq. 2 to speed data reveals that the threshold flux (Fig. 4A) required to overcome the nanodroplet’s adhesion to substrate are 37 ± 5, 32 ± 2, and 31 ± 1 e/(A²·s) for droplets 20–40, 40–60, and 60–80 nm diameter, respectively. The corresponding slip step (lamella extension) sizes for moving nanodroplets are bigger for larger nanodroplets and appear to be independent of electron flux as predicted by Eq. 1 (Fig. 4B). It is unlikely that the slight temperature change in droplet and the substrate may induce the substantial redistribution of water in a nanodroplet because temperature increase in a nanodroplet in reference to substrate is calculated to be uniform and insignificant (SI Text, Figs. S6–S8). However, the formation of toroidal nanodroplets under electron flux raises interesting issues about the possible role of electrostatic forces on water redistribution. One possible mechanism is that charging of a nanodroplet when high-energy electrons ionize a small fraction of water molecules and repulsive forces inside the nanodroplet may lead to formation of the toroidal structure (see SI Text). The exact nature of the mechanism that drives the motion of the nanodroplets remains an open question, and future theoretical explorations may elucidate the mechanism.

Fig. 4.

Nanodroplet movement as a function of the electron flux. (A) Average speed as a function of electron flux for droplets that are greater than 20 nm in diameter. (B) Step size of moving nanodroplet where the shaded regions represents the step size range set by Eq. 1 for nanodroplets with the diameter of 20–40 nm (green), 40–60 nm (blue), and 60–80 nm (red).

On a final note, there is an ongoing debate about the role of deformation in nanoscale friction (38, 39). For example, atomically thin sheets susceptible to out-of-plane deformation are observed to exhibit stick-slip movement due to enlarged contact area and therefore increased static friction between the sliding surfaces as a result of deformation (39). It is therefore very interesting to note that in the case of electron beam-induced movement of liquid nanodroplets, the deformation at liquid–air interface that does not result in increase of interfacial contact area promotes slipping and not sticking. Our real-time imaging of the electron beam-induced movements of water nanodroplets associated with the intradroplet redistribution of water mass differs from other examples of movements where the driving force is induced by introducing physical or chemical gradients on a substrate. However, our study reveals that a sufficient deformation resulting in change of surface free energy of liquid nanodroplets as a possible pathway for driving nanodroplet movement. Electron beam-induced deformation and subsequent motion of the water droplets may bear important consequences for movement of other deformable nanoscale objects residing on adherent surfaces. The direct observations of beam-induced movement of nanodroplets presented may serve as a platform for future studies of liquid dynamics at the nanoscale, which has not yet been accessible and is a highly debated topic among many disciplines. By studying the dynamics of water at these scales, it is possible to understand the energy dissipation and conversion at liquid–solid interfaces. Dynamics properties of water and other liquids at the nanoscale have potential applications in the future design of flexible liquid nanodevices and will aid in designing new lubrication techniques for nanoelectromechanical systems.

Materials and Methods

TEM Liquid Cell.

A low-stress silicon nitride (Si₃N₄) film with a thickness of approximately 20 nm was deposited by low-pressure chemical vapor deposition on both sides of 300-μm-thick, 4-in silicon (Si) wafers (Ultrasil). The fabrication details of liquid cells were described previously (25). Prior to the experiment, chips were cleaned with hydrochloric acid [with 10% (vol/vol)] to remove any metal residues. Next, the Si₃N₄ membrane surface was rinsed with acetone, isopropyl alcohol, and water followed by plasma cleaning (P = 3.3 W) for 45 s. Finally, the two pieces (bottom and top) were aligned by their windows and bonded together at 125 °C in a vacuum for 2 h to form a single liquid chamber (see SI Text). The liquid cell was filled with spectroscopic grade water (320072-2L; Sigma), and both reservoirs were sealed with a copper gasket and placed in specimen holder of an FEI T12 TEM. The images were acquired at the rate of 10 and 20 frames per second with a GATAN Orius SC200 camera. Electron flux was measured post specimen and represents transmitted electrons.

Image Processing.

We applied the segmentation algorithm in Definiens Developer-XD to find the boundaries of the droplet area, centroid position of the droplet area, border length, and mean intensity. If the change in the centroid positions of the droplet area between two consecutive frames were within the range of a few pixels (less than 10 pixels), then it was considered to be the same object. The droplet boundaries were defined in three consecutive steps. First, images were smoothened using a median filter with a 3 × 3 or 5 × 5 matrix size. Next, a rolling disk algorithm was used to reduce the intensity gradient over the whole image plane to efficiently implement an autothreshold algorithm. Finally, upon identifying the probable droplets in the image, a pixel-based shrink and grow algorithm of both probable droplet and background was used to identify the actual droplet with its original shape (see Movie S2).