Abstract
In conventional spectroscopy, transitions between electronic levels are governed by the electric dipole selection rule because electric quadrupole, magnetic dipole, and coupled electric dipole-magnetic dipole transitions are forbidden in a far field. We demonstrated that by using nanostructured electromagnetic fields, the selection rules of absorption spectroscopy could be fundamentally manipulated. We also show that forbidden transitions between discrete quantum levels in a semiconductor nanorod structure are allowed within the near-field of a noble metal nanoparticle. Atomistic simulations analyzed by an effective mass model reveal the breakdown of the dipolar selection rules where quadrupole and octupole transitions are allowed. Our demonstration could be generalized to the use of nanostructured near-fields for enhancing light-matter interactions that are typically weak or forbidden.
Keywords: absorption spectra, plasmonics, quantum dot, exciton
Light-matter interactions that govern most forms of spectroscopy, light harvesting, optical imaging, photodetection, optical communications, and data storage are conceptually founded on the laws of far-field optics (1, 2). Electronic and vibrational transitions excited by the electromagnetic (EM) field of light involve the motion of electrons and atoms on the length scale of 1 Å, the typical size of a molecule. Because the size (r) of a molecule is 103 times smaller than the wavelength (λ) of the light, it is common to approximate that a molecule subjected to light experiences a uniform electric field (1, 2). Spatial variations of this field across the molecule are neglected in the far-field limit. In this limit, the electric field can excite only those transitions that involve the induction of an electric dipole moment across the molecule, which is assumed to be a point (3). The latter is commonly postulated in the form of the electric dipole selection rule (4); however, a range of transitions that are important for spectroscopies such as circular dichroism, Raman scattering, Raman optical activity, singlet-triplet transitions, and magneto-optical phenomena are forbidden in an electric far-field. Common examples include electric quadrupole (q), magnetic dipole (m), and coupled electric dipole-magnetic dipole excitations (μ·m) (2, 5).
By the use of nanostructures (6–9), photonic crystals (10), or complex laser interference excitation schemes (11, 12), it is possible to engineer electromagnetic fields of light with spatial variations on the nanoscale approaching molecular length scales and to achieve optical phenomena beyond those allowed by conventional far-fields (13, 14). Jain et al. showed that magneto-optical Faraday rotation of a magnetic nanocrystal could be resonantly enhanced by placing it within the near-field of a plasmonic nanoshell, possibly via enhancement of the quadrupolar and μ·m transitions in the strongly graded electric field near the nanostructure (9). Tang and Cohen (11, 12) recently showed that at the nodes of a standing wave of circularly polarized light, circular dichroism cross-sections are amplified an order of magnitude compared to those in the far-field originating from a superhelical twist of the electromagnetic field at these nodes.
We focused on the most fundamental form of light-matter interaction, electronic absorption spectroscopy, and theoretically demonstrated the possibility of manipulating the fundamental selection rules of electronic absorption by using nanostructured electromagnetic fields (15). Unlike the allowed electric dipole transition, the strength of which relies only on the intensity of the electric field, an electric quadrupole transition requires an electric field gradient across the extent of the molecule (3). Such gradients approach zero in a far-field. Consequently, the strength of a quadrupole transition is smaller than that of a dipole-allowed transition by a factor of (r/λ)-2 or (k·r)-2 ∼ 106, where k is the wave vector of the excitation. Transitions of higher multipolar order (l = 3,4,…) have even lower strengths ∼(k·r)-2(l-1) relative to the dipole-allowed transition. It may be possible, however, to enhance such forbidden transitions by taking advantage of the high wave vector k of nanostructured fields, especially through localized surface plasmon resonances (16–18).
We show how forbidden transitions can become allowed in a semiconductor nanorod (e.g., CdSe or CdS). This model system offers discrete quantized narrow excitonic levels with a range of wave vectors. Our choice of a near-field source is a metal nanosphere tip (19) (see Fig. 1); however, one may use an alternative source such as the tip of a near-field scanning optical microscope (NFSOM) (20). The resonant near-field of the metal nanoparticle produced under light excitation polarized along the nanorod long-axis assumed in the z direction penetrates into the nanorod on one side then rapidly decays from the metal nanoparticle surface providing a strong field gradient in the direction of the long axis (21).
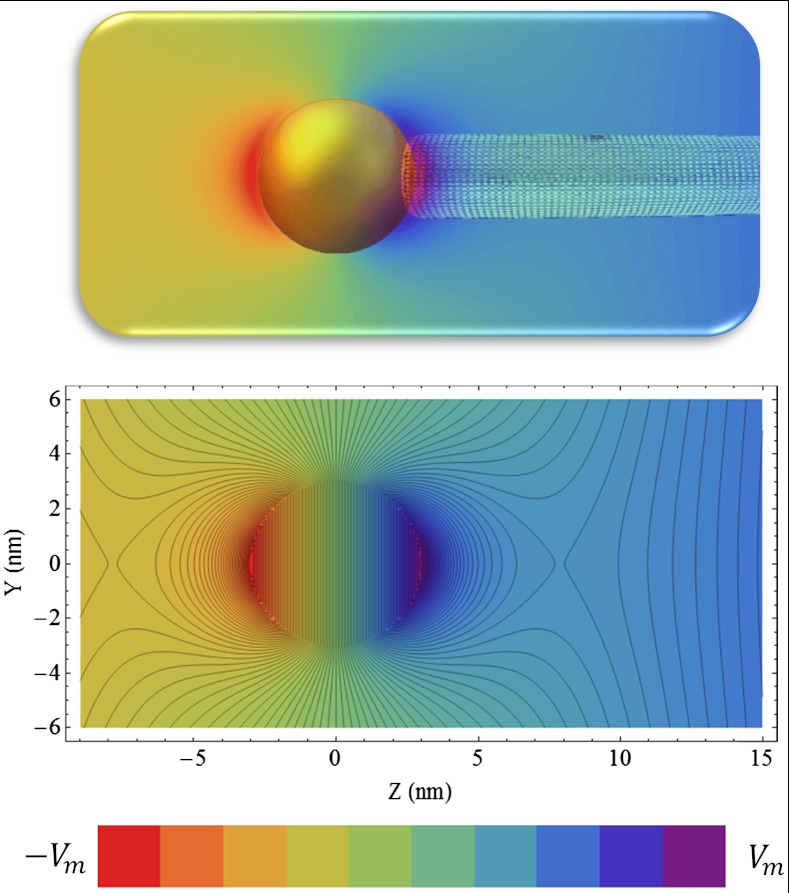
Fig. 1.
(Upper) Schematic illustration of the geometry of a metal-tipped nanorod used to model the effect of a near-field on the optical transitions of a nanoscale system. (Lower) Isopotential contour lines of the near-field potential generated by a gold nanoparticle of 6 nm diameter. Vm is the maximal potential on the surface of the gold nanoparticle (see SI Materials and Methods).
Results and Discussion
When the system composed of a nanorod and a metal tip is exposed to a homogeneous external field E(t) = E0eiωt + c oscillating at frequency ω, the nanorod is subject to an electric potential ϕ(r,ω), and it will undergo optical transitions with a rate of absorption given by the following equation:
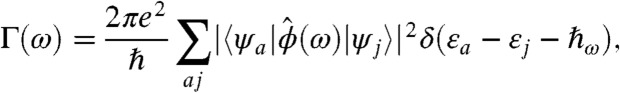 |
[1] |
where εa and εj are the electron and hole eigenenergies and ψa(r), ψj(r) are the corresponding orbitals, respectively. The above expression reduces to the well-known dipolar absorption spectrum when ϕ(r,ω) = -E0z for a uniform electric far-field (4). The conventional selection rules 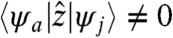 are replaced by
are replaced by 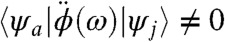 . In the calculations below, the delta function is substituted by a Lorentzian, i.e.,
. In the calculations below, the delta function is substituted by a Lorentzian, i.e.,  , where γ = 0.1 eV is the phenomenological line width.
, where γ = 0.1 eV is the phenomenological line width.
The far-field driving the system is pointing in the z direction, and its interaction with the metallic tip, modeled as a sphere of radius and dielectric function ϵ1(ω), produces the total potential 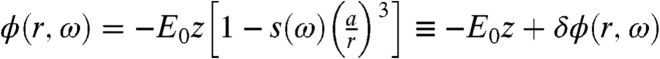 outside of the sphere (contour plotted in Fig. 1) and ϕ(r,ω) = -E0z[1 - s(ω)] inside the sphere (22). Here,
outside of the sphere (contour plotted in Fig. 1) and ϕ(r,ω) = -E0z[1 - s(ω)] inside the sphere (22). Here, 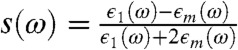 and ϵm is the dielectric constant of the surrounding medium. The potential outside of the sphere is composed of the uniform field potential (-E0z) supplemented by a dipolar term [
and ϵm is the dielectric constant of the surrounding medium. The potential outside of the sphere is composed of the uniform field potential (-E0z) supplemented by a dipolar term [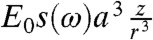 ] that is contour plotted (see Fig. 1, Lower). One can show that the electric field immediately outside of the sphere is enhanced by a factor of |1 + 2s(ω)| illustrated by the hotspots along the z direction near the sphere (see Fig. 1).
] that is contour plotted (see Fig. 1, Lower). One can show that the electric field immediately outside of the sphere is enhanced by a factor of |1 + 2s(ω)| illustrated by the hotspots along the z direction near the sphere (see Fig. 1).
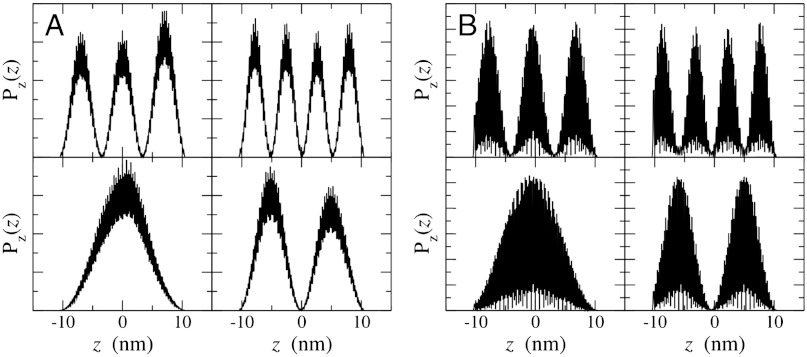
To calculate the absorption spectrum of the nanorod subject to such a field, one requires as input the orbitals and orbital energies that were obtained from a screened pseudopotential approach (23, 24). A real-space grid was used to represent the wave functions, and the filter-diagonalization method (25) was used to extract the states near the valence (conduction) band maximum (minimum). Fig. 2 shows several single particle wave functions projected on the long axis of a CdSe nanorod with an aspect ratio of 71/2. The high frequency oscillation is not noise; rather, it is a consequence of the rapidly oscillating Bloch function of the unit cell. To analyze the selection rules in the absorption spectrum of the nanorod, it is useful to assign quantum numbers to the eigenstates according to an effective mass description of a particle in a cylinder (26). Accordingly, the number of nodes along the z axis or, equivalently, the longitudinal quantum numbers ke,h allow such designation of the eigenstates participating in a given transverse band. For the nanorod without a close-by metal tip, the simple effective mass model predicts allowed optical transitions only when ke = kh. Although these rules are not strictly obeyed in the more elaborate atomistic calculations, the ke ≠ kh transitions do present themselves as allowed transitions with very small oscillator strength.
Fig. 2.
Z-axis probability density Pz(z) = ∫dxdy|ψke(x,y,z)|2 for low-energy electron (A) and hole (B) states in a CdSe nanorod of diameter D = 2.8 nm and length L = 20.6 nm.
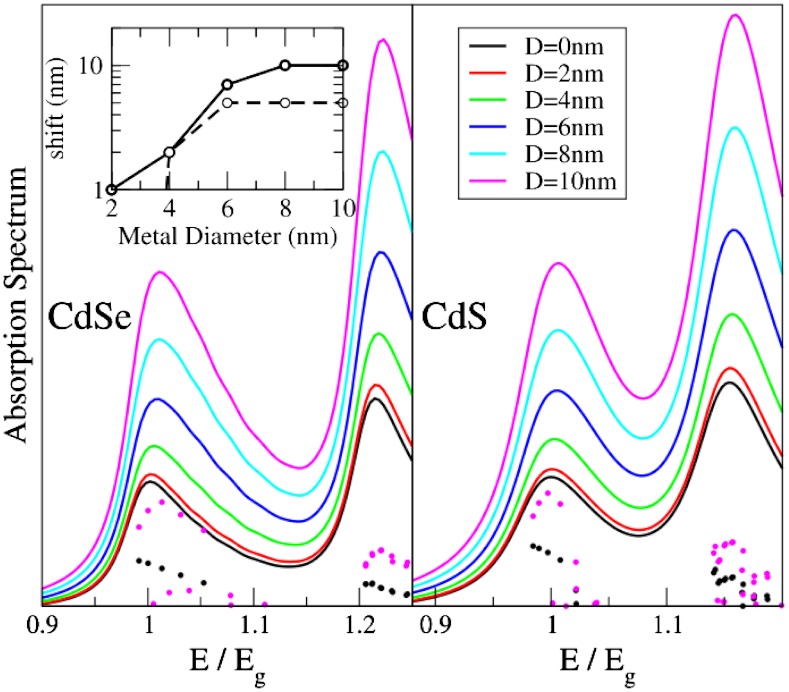
The calculated absorption rate of CdSe and CdS nanorods (of length L = 20 nm and diameter D ≈ 2.8 nm for CdSe and D ≈ 2.5 nm for CdS) as a function of the size of the metal tip are shown in Fig. 3. The spectra show two distinct peaks that can be associated with transitions to different transverse bands composed of many longitudinal transitions (26) The spectra exhibit a small blue shift as the metal tip diameter increases (see Inset), and it saturates above a metal tip diameter of approximately 6 nm. The saturation can be traced to two competing effects: (i) the spatial extent where the near-field decays into the rod, which would result in larger shifts as the diameter of the tip increases, or (ii) the shortening of the electron/hole longitudinal wave length as the energy of the transition increases. A more dramatic effect observed in the near-field absorption spectrum is the enhancement of the absorption rate as the metal tip diameter increases, which is analogous to the surface enhanced Raman scattering phenomena. In these calculations, we used 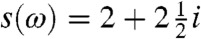 independent of the frequency [see SI Materials and Methods for details concerning s(ω) for gold and silver tips].
independent of the frequency [see SI Materials and Methods for details concerning s(ω) for gold and silver tips].
Fig. 3.
The absorption rates in CdSe (Left) and CdS (Right) 20 nm nanorods of aspect ratio 71/2 (see SI Materials and Methods). The lines represent results for different metal tip diameters ranging from zero (black) to 10 nm (magenta) in steps of 2 nm. The relative oscillator strengths for the strongest transitions are shown for individual transitions for the smallest and largest metal tip sizes. (Inset) The absorption maximum (blue) shift as a function of metal tip diameter. Solid and dashed lines correspond to CdSe and CdS, respectively.
In Fig. 3, we show oscillator strengths of individual transitions calculated from the detailed atomistic model. The dipole-allowed transitions, shown as black dots, could be associated with the electron-hole excitations of different longitudinal waves (see Fig. 2) that follow the effective mass model selection rules ke = kh (27). Transitions that violate this selection rule although strictly forbidden in the effective mass model are weakly allowed in the atomistic calculation. These transitions, however, are not plotted in Fig. 3 as their weak intensity is below the threshold used to plot significant optical transitions. The lowest transition observed is ke = kh = 1, and higher transitions involve ke = kh = 2. In the effective mass model, these transitions have identical oscillator strengths, whereas in the atomistic calculation they decay with increasing ke = kh.
The transitions in the presence of the metallic tip are shown as magenta dots in Fig. 3 for the largest tip studied. The near-field of the metal tip induces two unique phenomena:
- The strongest dipole-allowed transition is no longer at ke = kh = 1, it has a higher value depending on the size of the tip (ke = kh = 3 for the case shown), which contributes to the blue shift observed in the absorption (this effect is different from the shift discussed in ref. 28). One can show that within a single band effective mass model the matrix element determining the near-field optical selection rules can be approximated (Eq. 2):
where φe,h(r) is the electron/hole envelop wave functions, and db is the bulk dipolar transition moment. To leading order, this term increases with the radius of the metal tip (a), and it saturates at large values of a. Furthermore, for the special case where ke = kh, we found that this term increased (nearly linearly) with the longitudinal quantum number. The reduction in the dipolar terms in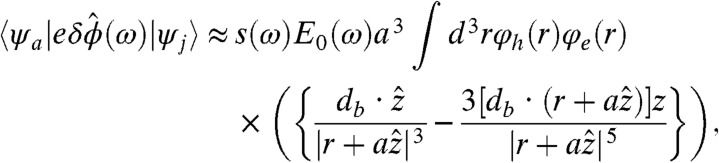
[2] 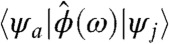 , with increasing ke = kh, is more than offset by the increase in the near-field term. The latter is manifested as the observed maximum in the oscillator strength shifting to quantum numbers above ke = kh = 1.
, with increasing ke = kh, is more than offset by the increase in the near-field term. The latter is manifested as the observed maximum in the oscillator strength shifting to quantum numbers above ke = kh = 1. More strikingly, we observed a large oscillator strength associated with transitions with selection rules ke = kh ± 1 (quadrupole-allowed), ke = kh ± 2 (octupole-allowed), etc. that are dipole-forbidden and, therefore, are negligible in intensity in a far-field. In the effective mass approximation these transitions become allowed in the presence of a near-field because
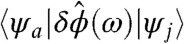 is nonzero even when ke ≠ kh. These dipole-forbidden transitions appear at higher energies, and they also contribute to the blue shift in the spectrum. In Table 1, we provide a list of transitions for a CdSe nanorod with an aspect ratio of 71/2 alongside the magnitude of enhancement resulting from the near-field. Whereas both dipole-allowed and dipole-forbidden transitions are enhanced in the near-field (attributable to increased electric field intensity in the near-field), the enhancement in the latter is much more dramatic. The latter is indeed a manifestation of the larger excitation wave vector of a near-field compared to a far-field. An increase in the excitation wave vector by n-fold would enhance a quadrupole-allowed mode transition n2-fold relative to a dipole-allowed mode.
is nonzero even when ke ≠ kh. These dipole-forbidden transitions appear at higher energies, and they also contribute to the blue shift in the spectrum. In Table 1, we provide a list of transitions for a CdSe nanorod with an aspect ratio of 71/2 alongside the magnitude of enhancement resulting from the near-field. Whereas both dipole-allowed and dipole-forbidden transitions are enhanced in the near-field (attributable to increased electric field intensity in the near-field), the enhancement in the latter is much more dramatic. The latter is indeed a manifestation of the larger excitation wave vector of a near-field compared to a far-field. An increase in the excitation wave vector by n-fold would enhance a quadrupole-allowed mode transition n2-fold relative to a dipole-allowed mode.
Table 1.
List of enhancement factors of the first absorption peak of CdSe nanorod with an aspect ratio of 71/2
| Ke | Kh | Enhancement |
| 1 | 1 | 1.6 |
| 1 | 2 | 15.7 |
| 2 | 1 | 3.5 |
| 2 | 2 | 1.9 |
| 3 | 1 | 10.6 |
| 1 | 3 | 1.0 |
| 3 | 2 | 19.5 |
| 2 | 3 | 19.8 |
| 3 |
3 |
2.2 |
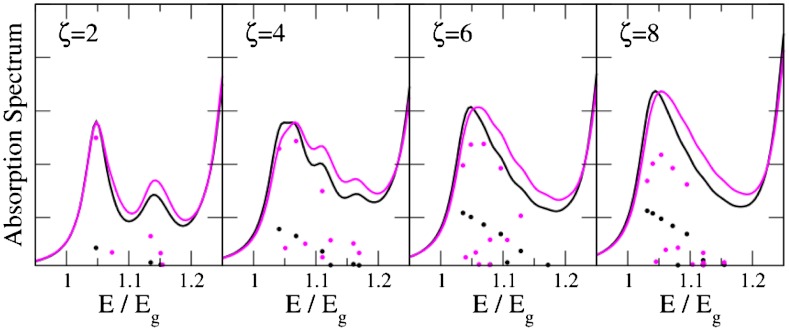
To our knowledge, such higher multipole transitions have not been directly observed or predicted to occur in any molecular or nanometer scale systems in the linear response regime, i.e., for weak fields. Near-field excitation makes higher-order transitions easily accessible. The dependence of the absorption rate and oscillator strengths on the aspect ratio of the nanorods is shown in Fig. 4. The appearance of dipole-forbidden transitions is observed irrespective of the aspect ratio. For the smallest aspect ratios, enhancements are the strongest because the near-field nearly spans the entire nanorod; however, because the longitudinal transitions are still strongly confined (note the appearance of a small peak associated with transitions of ke = kh = 2 for ξ = 2), the lowest excitation remains the strongest, resulting in negligible spectral shifts (see ξ = 2 in Fig. 4). As the aspect ratio increases for a given nanorod width, the spacing between higher longitudinal transitions decreases (the first peaks are then composed of many longitudinal transitions) resulting in a finite spectral shift where higher transitions become more enhanced.
Fig. 4.
The absorption rate of a series of CdSe nanorods of different aspect ratios for a diameter of D ≈ 2.8 nm normalized to the first absorption peak height without a metal tip (black) and with a 5 nm metal tip (magenta). The dots represent the corresponding oscillator strength of individual transitions.
It may be possible to observe such near-field modulation in a colloidal system. Ag nanoparticles (ca. 10 nm in size) can be conjugated to cadmium sulfide nanorods in solution via established linker chemistry employing short linkers. The enhancement of higher-order modes on binding of Ag nanoparticles would be manifested as an increase in the ensemble absorbance of the excitonic peak and a blue shift due to greater enhancement of the higher k modes. For resolving individual transitions and their enhancement in a near-field, one would require low temperature measurements on single nanorods that are currently challenging for probing absorbance spectra.
Conclusions
We described an approach to control and manipulate the optical selections rules in nanometer scale systems by virtue of near-fields generated from a nearby source, i.e., metal nanoparticles or NFSOM tip. Atomistic calculations on a specific metal-tipped semiconductor nanorod system revealed how the near-field would induce an enhancement in the oscillator strength of the dipole-forbidden transitions relative to the dipole-allowed ones. The near-field effect on excitonic transitions is physically rationalized using a simple effective mass model and awaits experimental verification.
Materials and Methods
Absorption Spectrum.
The calculation of the absorption spectrum is based on linear response. To lowest order in the amplitude of the incoming field, E0, one can show that the absorption rate is given by the following equation (see SI Materials and Methods for a full derivation):
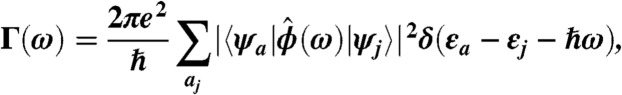 |
[3] |
where εa and εj are the electron and hole eigenvalues, respectively, and ψa(r) and ψj(r) are the corresponding single particle wave functions that are the solutions of the real-space pseudopotential model. The Eq. 3 expression reduces to the well-known dipolar absorption spectrum when ϕ(r,ω) = E0z:
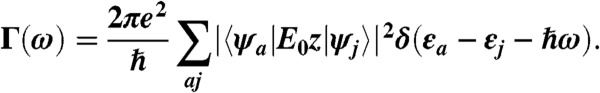 |
[4] |
Electronic Structure.
The electronic structure of the nanorods was described within the real-space screened pseudopotential method (23). The local screened pseudopotentials used in the results shown here were fitted to reproduce the experimental bulk band-gap and effective masses neglecting spin-orbit coupling. The form of the pseudopotential is given in ref. 23 along with the parameterization for CdSe. For CdS, we preformed a parameterization similar to the one describe in ref. 23. Ligand potentials were used to represent the passivation layer.
We studied a series of nanorods with varying aspect ratios (ξ), i.e., Cd256Se(S)255 (ξ = 1), Cd548Se(S)547 (ξ = 2), Cd840Se(S)839 (ξ = 3), Cd1132Se(S)1131 (ξ = 4), Cd1424Se(S)1423 (ξ = 5), Cd1716Se(S)1715 (ξ = 6), Cd2008Se(S)2007 (ξ = 7), Cd2154Se(S)2153 (ξ = 71/2), and Cd2300Se(S)2299 (ξ = 8). Grid size ranged from 64 × 64 × 64 for the smallest nanorod to 64 × 64 × 512 for the largest nanorod depending on its aspect ratio. The diameter of the nanorods was smaller than the experimental value to reduce the computational cost. For CdSe and CdS, the diameter was D = 2.8 and 2.6 nm, respectively. To obtain the lowest transitions and calculate the absorption cross-section, we used the filter-diagonalization approach (23, 24) to filter states near the conduction and valance band edge. Filtering about 300 states was sufficient to obtain converged results for the first peak in the absorption spectrum (SI Materials and Methods).
Near-Field.
To obtain the near-field generated by the metal tip, we followed standard procedures based on solving the relevant Maxwell equations (SI Materials and Methods). For a sphere of radius and dielectric constant ϵ1(ω) embedded in an infinite medium of dielectric constant ϵm(ω) and an external field E0(ω) in the z direction, this equation has a simple solution outside the sphere:
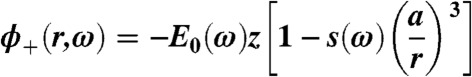 |
[5] |
and inside the sphere:
| [6] |
with
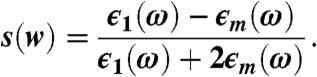 |
[7] |
Supplementary Material
Acknowledgments.
P.K.J. was supported by a Miller Fellowship from the Miller Institute at University of California, Berkeley. D.G. was supported by a National Science Foundation American Competitiveness in Chemistry Postdoctoral Fellowship. E.R. was supported by a visiting Miller Professorship from the Miller Institute at University of California, Berkeley. This work was supported by the Physical Chemistry of Semiconductor Nanocrystals Program, KC3105 of the Director, Office of Science, Office of Basic Energy Sciences, of the United States Department of Energy under contract DE-AC02-05CH11231 (to A.P.A.), by the United States-Israel Binational Science Foundation (R.B.), and by FP7 Marie Curie International Outgoing Fellowships project Hierarchical Junction Solar Cells (E.R. and A.P.A.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1121319109/-/DCSupplemental.
References
- 1.Born M, Wolf E. Principles of Optics. Cambridge, U.K.: Cambridge Univ Press; 2002. [Google Scholar]
- 2.Novotny L, Hecht B. Principles of Nano-optics. Cambridge, U.K.: Cambridge Univ Press; 2006. [Google Scholar]
- 3.Cohen-Tannoudji C, Diu B, Lalöe F. Quantum Mechanics. New York: Wiley Interscience; 1977. [Google Scholar]
- 4.Harris DC, Bertolucci MD. Symmetry and Spectroscopy. New York: Oxford Univ Press; 1978. [Google Scholar]
- 5.Yang N, Tang Y, Cohen AE. Spectroscopy in sculpted fields. Nano Today. 2009;4:269–279. [Google Scholar]
- 6.Moskovits M. Surface-enhanced Raman spectroscopy: A brief perspective. Top Appl Phys. 2006;103:1–17. [Google Scholar]
- 7.Boyd GT, Rasing T, Shen YR. Local-field enhancement on rough surfaces of metals, semimetals, and semiconductors with the use of optical 2nd-harmonic generation. Phys Rev B. 1984;30:519–526. [Google Scholar]
- 8.Hao E, Schatz GC. Electromagnetic fields around silver nanoparticles and dimmers. J Chem Phys. 2004;120:357–366. doi: 10.1063/1.1629280. [DOI] [PubMed] [Google Scholar]
- 9.Jain PK, Xiao YH, Walsworth R, Cohen AE. Surface plasmon resonance enhanced magneto-optics (SuPREMO): Faraday rotation enhancement in gold-coated iron oxide nanocrystals. Nano Lett. 2009;9:1644–1650. doi: 10.1021/nl900007k. [DOI] [PubMed] [Google Scholar]
- 10.Soljacic M, Joannopoulos J. Enhancement of nonlinear effects using photonic crystals. Nat Mater. 2004;3:211–219. doi: 10.1038/nmat1097. [DOI] [PubMed] [Google Scholar]
- 11.Tang Y, Cohen AE. Optical chirality and its interaction with matter. Phys Rev Lett. 2010;104:163901. doi: 10.1103/PhysRevLett.104.163901. [DOI] [PubMed] [Google Scholar]
- 12.Tang Y, Cohen AE. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science. 2011;332:333–336. doi: 10.1126/science.1202817. [DOI] [PubMed] [Google Scholar]
- 13.Curto AG, et al. Unidirectional emission of a quantum dot coupled to a nanoantenna. Science. 2010;329:930–933. doi: 10.1126/science.1191922. [DOI] [PubMed] [Google Scholar]
- 14.Andersen ML, Stobbe S, Sorensen AS, Lodahl P. Strongly modified plasmon-matter interaction with mesoscopic quantum emitters. Nature Phys. 2011;7:215–218. [Google Scholar]
- 15.Zurita-Sánchez JR, Novotny L. Multipolar interband absorption in a semiconductor quantum dot. I. Electric quadrupole enhancement. J Opt Soc Am B. 2002;19:1355–1362. [Google Scholar]
- 16.Jain PK, El-Sayed MA. Surface plasmon coupling and its universal size scaling in metal nanostructures of complex geometry: Elongated particle pairs and nanosphere trimers. J Phys Chem C. 2008;112:4954–4960. [Google Scholar]
- 17.Pendry JB, Martin-Morena L, Garcia-Vidal FJ. Mimicking surface plasmons with structured surfaces. Science. 2004;305:847–848. doi: 10.1126/science.1098999. [DOI] [PubMed] [Google Scholar]
- 18.Hui PM, Stroud D. Theory of Faraday rotation by dilute suspensions of small particles. Appl Phys Lett. 1987;50:950–952. [Google Scholar]
- 19.Mokari T, Sztrum CG, Salant A, Rabani E, Banin U. Formation of asymmetric one-sided metal tipped semiconductor nanocrystal dots and rods. Nat Mater. 2005;4:855–863. [Google Scholar]
- 20.Ash EA, Nicholls G. Super-resolution aperture scanning microscope. Nature. 1972;237:510–512. doi: 10.1038/237510a0. [DOI] [PubMed] [Google Scholar]
- 21.Jain PK, Huang W, El-Sayed MA. On the universal scaling behavior of the distance decay of plasmon coupling in metal nanoparticle pairs: A plasmon ruler equation. Nano Lett. 2007;7:2080–2088. [Google Scholar]
- 22.Jackson JD. Classical Electrodynamics. 3rd Ed. New York: Wiley; 1999. [Google Scholar]
- 23.Rabani E, Hetenyi B, Berne BJ, Brus LE. Electronic properties of CdSe nanocrystals in the absence and presence of a dielectric medium. J Chem Phys. 1999;110:5355–5369. [Google Scholar]
- 24.Toledo S, Rabani E. Very large electronic structure calculations using an out-of-core filter-diagonalization method. J Comp Physiol. 2002;180:256–269. [Google Scholar]
- 25.Wall MR, Neuhauser D. Extraction through filter‐diagonalization of general quantum eigenvalues or classical normal mode frequencies from a small number of residues or a short‐time segment of a signal. I. Theory and application to a quantum‐dynamics model. J Chem Phys. 1995;102:8011–8022. [Google Scholar]
- 26.Sun JW, Buhro WE, Wang LW, Schrier J. Electronic structure and spectroscopy of cadmium telluride quantum wires. Nano Lett. 2008;8:2913–2916. doi: 10.1021/nl801737m. [DOI] [PubMed] [Google Scholar]
- 27.Baer R, Rabani E. Theory of resonance energy transfer involving nanocrystals: The role of high multipoles. J Chem Phys. 2008;128:184710. doi: 10.1063/1.2913247. [DOI] [PubMed] [Google Scholar]
- 28.Chance RR, Prock A, Silbey R. Frequency shifts of an electric-dipole transition near a partially reflecting surface. Phys Rev A. 1975;12:1448–1452. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.