Abstract
We report observation and analysis of the depolymerization filaments of the bacterial cytoskeletal protein FtsZ (filament temperature-sensitive Z) formed on a mica surface. At low concentration, proteins adsorbed on the surface polymerize forming curved filaments that close into rings that remain stable for some time before opening irreversibly and fully depolymerizing. The distribution of ring lifetimes (T) as a function of length (N), shows that the rate of ring aperture correlates with filament length. If this ring lifetime is expressed as a bond survival time, (Tb ≡ NT), this correlation is abolished, indicating that these rupture events occur randomly and independently at each monomer interface. After rings open irreversibly, depolymerization of the remaining filaments is fast, but can be slowed down and followed using a nonhydrolyzing GTP analogue. The histogram of depolymerization velocities of individual filaments has an asymmetric distribution that can be fit with a computer model that assumes two rupture rates, a slow one similar to the one observed for ring aperture, affecting monomers in the central part of the filaments, and a faster one affecting monomers closer to the open ends. From the quantitative analysis, we conclude that the depolymerization rate is affected both by nucleotide hydrolysis rate and by its exchange along the filament, that all monomer interfaces are equally competent for hydrolysis, although depolymerization is faster at the open ends than in central filament regions, and that all monomer–monomer interactions, regardless of the nucleotide present, can adopt a curved configuration.
Keywords: bacterial division, atomic force microscopy, computer simulations, GTP hydrolysis
Bacterial cytoskeletal protein FtsZ (filamenting temperature-sensitive Z) assembles into dynamic polymers on the inner side of the bacterial cytoplasmic membrane in the presence of GTP. Its role in cell division is twofold: recruiting the rest of the proteins involved in the assembly of the septal ring and contributing to generate the force needed for cell rupture. Recent in vitro experiments with artificially membrane-bound FtsZ reconstituted in model systems support the suggestion that FtsZ is capable of generating a contractile force without the need of any other proteins (1, 2). Several theoretical models trying to explain the molecular mechanism by which the GTP-dependent self-assembling polymerization process generates a contractile force have been recently proposed (3–12), but the debate is still open. Existing controversy over the relative contribution of filament curvature and lateral interactions in the constriction process is difficult to resolve until new experimental data determine how GTP hydrolysis is associated to monomer exchange within filaments.
FtsZ is known to polymerize above a critical concentration in the presence of GTP (13). Bulk experiments in solution using a fluorescence signal to follow polymerization (14) have provided indirect evidence of monomer exchange, annealing, and depolymerization of individual filaments. Visualization of filaments adsorbed on a mica surface with atomic force microscopy (AFM) (15, 16) also showed a rich dynamic behavior in which annealing, filament curvature, and lateral interactions played important roles. We now extend the AFM analysis to characterize the depolymerization of isolated individual filaments. We have quantitatively analyzed the behavior of two types of structures: closed rings and open curved filaments. The survival time of closed FtsZ rings and the shortening of open filaments were analyzed using statistical methods. This analysis, combined with computer simulations, allowed estimating the depolymerization velocity of the open filaments and describing the influence of the monomer location within the filament on the depolymerization rate. We conclude that all monomer–monomer interfaces are competent for depolymerization and that each rupture event takes place randomly and independent of its position, excluding any cooperative depolymerization process. We also conclude that depolymerization at the open ends is faster than in central filament regions and that filament curvature is not solely associated with the presence of GDP.
Results
Experimental Results.
FtsZ individual filaments.
Individual FtsZ filaments form on a mica surface exposed to a solution with FtsZ below its critical concentration, even when no filaments form in the solution (13). They assemble due to a local increase in protein concentration on the surface. It has been previously shown that this process is dependent on the surface diffusion of the monomers, and that lowering the temperature or increasing the viscosity of the solution reduces the number of observed filaments (17). The filaments studied were formed exposing mica to a 50 nM protein–GTP solution for 10 min before adding the protein-free imaging buffer also containing 1 mM GTP. It is important to note that samples are imaged in the absence of protein in solution, therefore no protein is available in the bulk to exchange with the filaments. This preparation protocol allowed the formation of short filaments that closed to form stable rings. After the rings opened irreversibly, we measured the depolymerization velocity of the open filaments. The two types of structures, closed rings and open curved filaments, were analyzed separately.
Closed rings.
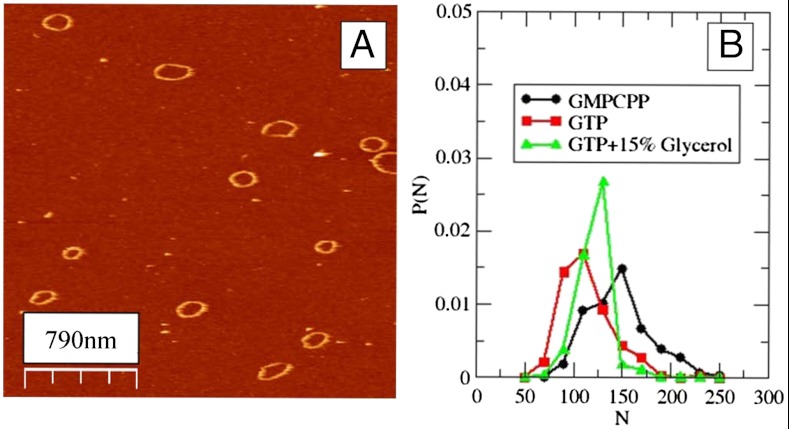
Closed FtsZ rings on the mica can either open transiently at random locations or irreversibly, leading to subsequent filament depolymerization. Reversible opening events were sometimes followed by a loss of material that gave rise to smaller rings. Because depolymerization rate is associated with GTP hydrolysis (13), we explored the behavior of rings formed in the presence of guanosine-5’-[(β, γ)-methyleno]triphosphate (GMPCPP), a slow hydrolyzing GTP analogue (18) and in low-pH solutions, that are also known to decrease GTP hydrolysis rate (19). In both cases, the reduction in the hydrolysis rate produced an increase in ring lifetime. Increasing the viscosity of the imaging solution adding glycerol reduced monomer diffusion and was also efficient in stabilizing the closed rings. Fig. 1 shows some rings and their size distribution under three experimental conditions. The most frequent size observed falls within the expected values considering that the spontaneous curvature of the open filaments described earlier (20), with a preferred angle of 2.4–3.0° between neighbor bonds, would bring the two ends close to each other when N is in the range of 120–150 monomers.
Fig. 1.
(A) AFM image of FtsZ rings formed in presence of GTP at pH 7.5. (B) Size distribution of rings formed with GTP (squares), GMPCPP (circles), and GTP plus 15% of glycerol (triangles).
Fig. 2 illustrates the typical behavior of the rings over time: Openings can happen at different positions in the same filament (Fig. 2A), and some are followed by material loss that reduces the size of the ring (Fig. 2B). Movies showing the behavior of the filaments over time are presented in the SI Text.
Fig. 2.
FtsZ closed rings dynamics. Shape fluctuation, opening, and reannealing at random positions (arrows) are observed for GTP (A) and GMPCPP (B). Opening event followed by a partial depolymerization leading to smaller ring is observed in B.
For each ring, we measure the length (N), lifetime (T) (i.e., the time before it opens irreversibly), and define a bond lifetime (Tb ≡ NT) (see section below). Table 1 summarizes the average values 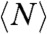 ,
, 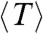 , and
, and 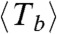 for three populations studied: rings formed with GTP, with GMPCPP, and rings formed with GTP but observed with glycerol present in the imaging buffer. SI Text shows the data for rings observed in low-pH solution. Slow hydrolysis and reduced monomer diffusion are both associated with longer and more stable rings.
for three populations studied: rings formed with GTP, with GMPCPP, and rings formed with GTP but observed with glycerol present in the imaging buffer. SI Text shows the data for rings observed in low-pH solution. Slow hydrolysis and reduced monomer diffusion are both associated with longer and more stable rings.
Table 1.
The number of observed FtsZ rings, their mean size and size dispersion (in number of monomers), and the mean time for which each ring is observed in successive AFM frames are compared for different nucleotide buffers: GTP, GMPCPP, and GTP with 15% glycerol buffers
| Buffer | GTP | GMPCPP | GTP glycerol |
| No. rings | 243 | 365 | 204 |
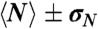 |
103 ± 26 | 137 ± 32 | 112 ± 15 |
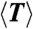 , min , min |
6.5 | 13.1 | 8.9 |
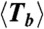 , min , min |
670 | 1,800 | 990 |
|
vo, min-1 |
0.0015 |
0.00056 |
0.0010 |
Depolymerization of open filaments.
Filaments with GTP disappear very fast once opened, usually within 1 min, the time needed to take an AFM image (Fig. 3A). Increasing the scan rate to 40 s per image allowed us to see at least one open filament, but it was not possible to follow the intermediate steps of depolymerization (Fig. 3B). In the presence of GMPCPP, however, the process is slow enough to be observed along several frames (Fig. 3C) (see SI Text).
Fig. 3.
Depolymerization of FtsZ filaments. (A) Shrinkage of a FtsZ closed filament in presence of GTP at pH 7.5—i.e., full GTPase activity and diffusion. (B) Increasing the scan velocity allows observing open filaments in the same biochemical conditions as in A. Slowed depolymerization observed in the presence of GMPCPP (C) or in presence of GTP in an imaging buffer with increased viscosity (D). In all cases, both filament ends lose monomers during depolymerization.
Fig. 3D illustrates that the depolymerization observed when the viscosity of the imaging buffer is increased has the same qualitative behavior (see SI Text). When GTPase hydrolysis is slowed with increasing acidity of the imaging buffer (19), the depolymerization process is comparable (see SI Text).
Quantitative Analysis and Simulation Models.
Length and lifetime of closed rings.
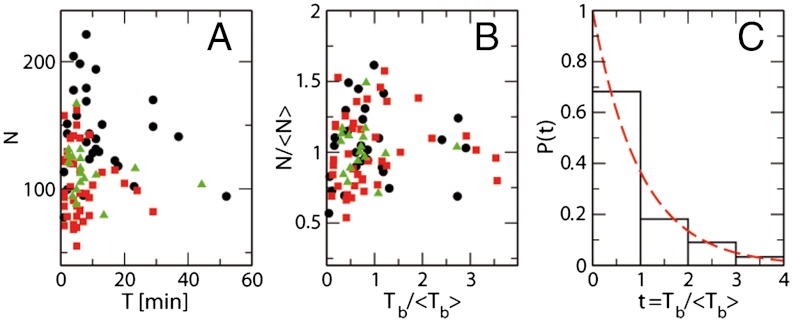
Filaments were parametrized to measure filament length as a function of time as described in detail in the SI Text. The size N (number of monomers) and lifetime T of rings of three different ring populations are presented in Fig. 4A. All three (T,N) distributions are quite broad, spanning in length from 50 to 230 monomers and in ring lifetime from 1 to more than 50 min. The distributions shows that the length is correlated with the lifetime—i.e., longer rings have a shorter lifetime than smaller ones. Rings with N ≈ 100 monomers may last as long as 50 min, whereas rings with N ≈ 200 are never observed for more than 20 min. An explanation for this length-lifetime correlation is that irreversible opening is triggered by independent events occurring at each monomer–monomer interface. Therefore the larger the number of interfaces, the higher the probability of having one rupture to break the ring. To test this random rupture assumption, eliminating the effect of the number of bonds, we define a typical bond survival time Tb ≡ NT. That takes into account the lifetime of a ring, T, and the number of bonds present, N, and reflects the fact that opening of only one bond is enough to trigger the irreversible opening. If this rupture event is stochastic, this bond survival time should have a broad distribution and be independent of filament length. Because the three populations analyzed have different lifetimes and filament lengths, N and Tb were also normalized by the average 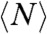 and
and 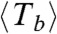 values of each population. This normalization produces the overlap of the three datasets, eliminating the stabilizing effect associated with slow hydrolysis rate and reduced lateral diffusion. The distributions for (
values of each population. This normalization produces the overlap of the three datasets, eliminating the stabilizing effect associated with slow hydrolysis rate and reduced lateral diffusion. The distributions for (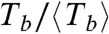 ,
, 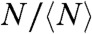 ) shown in Fig. 4B are now uncorrelated, as expected for random events.
) shown in Fig. 4B are now uncorrelated, as expected for random events.
Fig. 4.
Depolymerization of FtsZ rings under different conditions: A shows the (T,N) distribution for the size of each ring N (estimated number of monomers) and its observed survival time T (minutes from the first to the last AFM image in which the ring is observed); black circles, buffer with GMPCPP; red squares, buffer with GTP; green triangles, GTP buffer with 15% glycerol. B shows the distribution (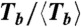 ,
,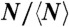 ) for the values of N and Tb ≡ NT, normalized to their mean values, given in Table 1. C presents the histogram for the normalized lifetime per bond
) for the values of N and Tb ≡ NT, normalized to their mean values, given in Table 1. C presents the histogram for the normalized lifetime per bond 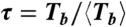 , collecting the data from the three nucleotide buffers in B independently of their size. The red dashed line is P(τ) = exp(-τ), with no fitting parameters, which represents the probability distribution for independent events with unit frequency.
, collecting the data from the three nucleotide buffers in B independently of their size. The red dashed line is P(τ) = exp(-τ), with no fitting parameters, which represents the probability distribution for independent events with unit frequency.
The experimental datasets allow obtaining the rupture rate of one bond as 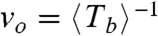 for each population studied, and also allow checking if the irreversible opening of a FtsZ ring of size N behaves like a stochastic process with frequency
for each population studied, and also allow checking if the irreversible opening of a FtsZ ring of size N behaves like a stochastic process with frequency 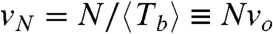 , implying that rupture events occur randomly and independently at each monomer interface (see SI Text for more details on the statistical analysis). The normalized probability for
, implying that rupture events occur randomly and independently at each monomer interface (see SI Text for more details on the statistical analysis). The normalized probability for 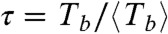 , obtained from the three datasets in Fig. 4B should be very close to the exponential form P(τ) = exp(-τ), with no fitting parameters, which describes a fully random process that happens with unit frequency (in the time units normalized by
, obtained from the three datasets in Fig. 4B should be very close to the exponential form P(τ) = exp(-τ), with no fitting parameters, which describes a fully random process that happens with unit frequency (in the time units normalized by 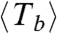 ) as shown in Fig. 4C. This behavior implies that the filaments do not show any kind of aging or memory effect.
) as shown in Fig. 4C. This behavior implies that the filaments do not show any kind of aging or memory effect.
Table 1 summarizes the data extracted from the analysis of the survival time of the closed rings and shows the monomer–monomer bond breaking frequencies vo found for each experimental condition. GMPCPP reduces it to less than half the value obtained for GTP, which correlates well with the known reduction of the hydrolysis rate of GMPCPP. Additional experiments modulating the GTP hydrolysis rate by lowering the pH are shown in the SI Text. Low pH also reduces vo threefold at pH below 6.5, in accordance with the measured decrease in GTPase activity (19) (see SI Text). From this quantitative analysis of ring lifetimes, we conclude that, under our experimental conditions, with no monomer exchange in and out of the rings, the rupture frequency between protein monomers is random, it correlates both with hydrolysis rate and monomer lateral diffusion, and it is the only parameter required to explain the time evolution of the rings.
Depolymerization rate of open filaments.
The length versus time data of 22 open filaments were used to quantify the depolymerization process by measuring the “instantaneous” depolymerization velocity—i.e., the difference in the estimated number of monomers between two consecutive AFM frames. The histogram (Fig. 5) has a broad distribution and includes apparent growth events, in which the estimated length N increases between an image and the following one. Because there is no protein in the imaging buffer, these events are most probably artifacts of our estimation for N.
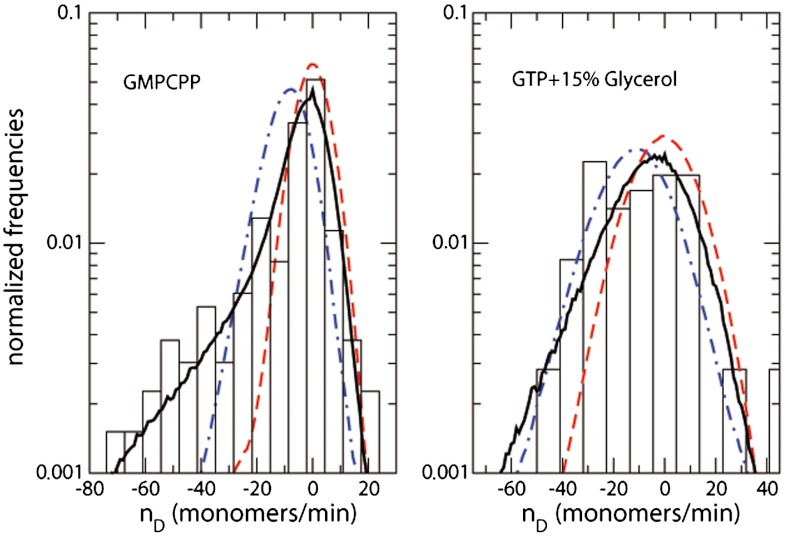
Fig. 5.
Histograms of depolymerization velocities, in estimated number of monomers between consecutive AFM images taken at 1-min intervals, for GMPCPP buffer (Left) and GTP with 15% glycerol buffer (Right). The black full lines are the simulation results obtained with 105 biased fragmentations (see SI Text). Blue dash-dotted lines are the simulation results for unbiased fragmentations, with the frequency vo measured for closed FtsZ rings. Red dashed lines are the results for one-by-one monomer depolymerization, with frequency fitted to reproduce the observed mean value.
Filaments shrink at a mean rate of 9.3 and 11.8 monomers per minute, respectively, for GMPCPP and GTP with 15% glycerol. Filaments in the presence of GTP depolymerize at least 10 times faster, that is, more than 100 monomers per minute, the time needed to take an AFM image, making it technically impossible to measure the depolymerization velocity. The shape of the histogram of the depolymerization velocities can provide additional information to the mean depolymerization rate (see SI Text). The histogram for the filaments grown with GMPCPP is asymmetric. On the positive side (increasing lengths), there is a sharp decay that may be well fitted by a Gaussian and interpreted as the result of the noise coming from numerical estimation of the instantaneous filament length from the AFM images. On the negative side (depolymerization), the velocity distribution has a slowly decaying tail, so that the AFM images taken at 1-min intervals may show the loss of up to 70 monomers. The depolymerization events of filaments with GTP observed in the presence of 15% glycerol are noisier than those with GMPCPP and produce a broader histogram with much weaker (or maybe completely lacking) asymmetry.
The analysis of the closed rings, in which all of the monomer–monomer interfaces are equivalent, indicated that these bonds break independently with a certain frequency correlated with the nucleotide hydrolysis rate. If we extend this hypothesis to open filament, we would expect that the depolymerization of an initially long filament would proceed as a fragmentation process in which any of the bonds would be irreversibly broken with the same frequency vo, equivalent to the one obtained from the analysis of ring rupture and listed in Table 1. Once the filament is fragmented in two pieces, the fragmentation would proceed on each segment independently, until all the pieces are too small to be observed in the AFM images. However, this interpretation does not agree with the experimental results. If a random fragmentation processes with a rupture frequency vo is applied to open filaments, the computer model described below gives mean depolymerization velocities of 1.36 monomers per minute for GMPCPP and 0.98 monomers per minute for GTP on filaments observed in the presence of 15% Glycerol. These velocities are significantly slower than the 9.3 and 11.8 monomers per minute measured, indicating that the direct extension from the breaking of rings to shrinkage of open filaments does not explain the observed data.
The opposite view to the fragmentation process at random positions would be to assume that the depolymerization occurs by removing only one monomer from the filament end at a time. To get the observed mean depolymerization velocities, monomers at the ends of the filaments would have to leave at a rate of 4 to 5 per minute—i.e., about 104 faster than the events leading to the breaking of a ring. Under this assumption, and in absence of other sources of noise, the observed distribution of instantaneous velocities between two AFM images would be very narrow and symmetric ( see SI Text). Adding some extra noise, we could get the broader Gaussian presented by the dash-dotted lines in Fig. 5, which could be acceptable for GTP with glycerol, but clearly fails to reproduce the strong asymmetry of the histograms for the GMPCPP buffer. Neither of these two extreme interpretations, depolymerization by fragmentation process nor by individual monomer release, reproduces the shape of the histogram of depolymerization velocities observed.
Model and computer simulations of fragmentation processes.
The bond breaking frequency of rings, the mean depolymerization velocity for open filaments, and the asymmetry of the instantaneous shrinkage velocities may only be explained if we assume that an open filament has different breaking frequencies depending on the location of the bond. Bonds between monomers within the filament have a lower breaking frequency and bonds connecting the monomers at the ends have a higher breaking frequency.
To check if this scenario can explain our experimental results, we have run Langevin computer simulations with a filament model that had been previously developed to study FtsZ filaments (20) and is explained in more detail in the SI Text.
The model, which treats protein monomers as beads in a chain linked by elastic springs, can mimic filament fragmentation. Simulations reveal that the distance, although more significantly, the relative orientation between monomers adjacent to a rupture event, undergo rapid changes (see SI Text).
The overall rupture frequency used in the computer simulations is explained in the SI Text. The parameter v1 represents the rupture frequency of short filaments (bonds at filament ends), whereas the value of vo extracted from the analysis of the rings (Table 1) gives the breaking frequency for long fragments (bonds within the filament). The results of the simulations, with the optimal fitted values for v1 and using vo reproduce very accurately the asymmetry of the velocity histograms. The full line in the left panel of Fig. 5 represents the curve for v1/vo = 30 ± 5, which fits both the histograms of filaments in GMPCPP and in GTP plus glycerol buffer, indicating that the bonds in short filaments rupture that short filaments rupture 30 times faster than the bonds in closed rings.
Discussion
The association between nucleotide exchange or hydrolysis and depolymerization has been difficult to study experimentally, in spite of its relevance, to fully understand polymer dynamics. We have now been able to observe the depolymerization of single FtsZ filaments. We have analyzed our data using statistical methods that have provided not only average kinetic information but also insight into how the depolymerization takes place. A short discussion on the advantages of using this approach as compared to standard kinetic analysis is included as SI Text.
It is clear from our data that nucleotide hydrolysis rate correlates with the rate at which monomers are released. Filament rings increase their lifetime and open filaments decrease their depolymerization velocity under low GTPase hydrolyzing conditions. However, there is a more than 1,000-fold difference between the hydrolysis rate and the filament rupture times observed, considering GTPase activities measured in solution (21). Because in our experiments there is no monomer exchange between the filaments and the bulk, a plausible explanation is the presence of a nucleotide hydrolysis-exchange cycle in which hydrolysis and substitution of the nucleotide occurs many times before an irreversible rupture event takes place. Evidence for this cycle comes from the fact that both decreasing the hydrolysis rate or increasing the solution viscosity retard depolymerization. Higher viscosity keeps the appropriate orientation between open ends after a hydrolysis event for longer times, decreasing the probability of an irreversible rupture in the time needed for the nucleotide exchange, having therefore an equivalent effect to decreasing hydrolysis rate. Depolymerization experiments carried out in solution (14) have also determined that GTPase hydrolysis rate is faster than depolymerization, but in such bulk experiments monomer exchange and monomer release cannot be isolated as independent processes, and therefore their association to GTP hydrolysis or exchange is ambiguous. Biochemical data suggesting nucleotide exchange into protofilaments are available (14, 21–24), supporting our interpretation that both nucleotide exchange and hydrolysis are determining the observed depolymerization dynamics.
Two additional observations support our suggestion that hydrolysis products within the filament are being substituted by fresh GTP from the bulk before any monomer release takes place. When GTP is removed from the buffer, filaments disappear too quickly to be observed over time. On the other hand, all interfaces behave equivalently along the full lifetime of the ring. Some of the rings formed in the presence of GTP can be observed for more than 10 min. Assuming a GTPase hydrolysis rate on the order of eight GTP hydrolyzed per minute per FtsZ monomer (21), after 10 min, if no nucleotide exchange were possible, the filament would accumulate GDP at most of the interfaces. We see no evidence that the interaction between monomers changes, as would be expected if the GDP generated were not replaced by GTP.
The quantitative analysis of the depolymerization of open filaments led to another important conclusion: The rupture rate between two monomers depends on the location of the monomers interface. Bonds located at the center of the filament rupture at a slower rate than bonds located at the end. We cannot follow directly the fast rupture rate of the filament because our experimental time resolution does not allow distinguishing a sequential loss of 10 independent monomers from a single fragmentation of a 10 monomer piece. However, we extract the information from comparing the velocity histogram distribution with the computer simulation results. From the mean depolymerization rate and the strong asymmetry of the histogram, we can discard both a fragmentation with a slow rupture rate vo at random locations and a sequential depolymerization of single monomers from the filaments ends with a fast rupture rate v1. A size-biased fragmentation, approximately 30 times more effective for short filaments than the uniform slow fragmentation process, is what best describes the observations. Because there are more possible fragmentations of long pieces than of small ones, the mean depolymerization rate of open filaments ends up being about 10 times faster than the estimate from the vo value obtained from the rings.
The assumption that filament ends hydrolyze faster has also been suggested by other groups. Molecular modeling studies indicate that the effective hydrolysis rate is larger at monomers located near filament ends than it is between monomers located within the filament (25). Both effects, higher hydrolysis rate and faster monomer diffusion at the ends, could contribute to give a faster irreversible separation of the end monomer with a frequency v1 much larger than the vo found for monomer–monomer interactions in the central part of the filaments and associated to the irreversible opening of rings.
Combining the information provided by the study of the resilient closed rings and the depolymerization of the open filaments allows us to reach yet another important conclusion: FtsZ filaments show no sign of cooperative depolymerization. Tubulin, the related eukaryotic cytoskeletal protein, shows dynamic instability (26), a cooperative depolymerization process that is not observed here for FtsZ filaments. All monomer–monomer interfaces are equally competent for annealing, opening or closing randomly. These results are consistent with recent biochemical data that have also shown that all the GTP-bound sites within FtsZ filaments are noninteracting and catalytically active (27).
Associating the GTPase hydrolysis cycle to filament depolymerization has remained a challenge difficult to address from bulk steady-state experiments. It has been suggested (14) that the mechanisms that contribute to FtsZ dynamic behavior include random fragmentation within the protofilament following GTP hydrolysis, and that dissociation of subunits occurs either at the end or within the filament, mainly at GDP containing subunits, allowing also for annealing of fragments of different protofilaments. Our data qualitatively refine the picture. We have confirmed that the hydrolysis events within a filament are indeed random, independent from each other, and that rupture can occur, although at different rates, both within and at the filament ends.
Because there is no change in the curvature of the rings along the full nucleotide hydrolysis-exchange cycle, another clear result is that monomers within filaments are equivalent and that, regardless of their GTP or GDP content, all are capable of sustaining a curved configuration. This structural plasticity, understood as a structural state of the polymer not associated to the chemical state of its bound nucleotide (28) has been previously described for tubulin and actin. We observe that it is also relevant in FtsZ polymers and should be considered in future theoretical models to explain the force generation mechanisms.
Finally, the data presented here describing how individual filaments depolymerize help to understand the more complex situation found in vivo. Recent experiments describing the behavior of FtsZ filaments attached to supported lipid bilayers (29) indicate that the essential traits of the dynamic behavior of the FtsZ filaments observed on mica (15) are preserved on lipid surfaces, in spite of the formation of higher order aggregates. Accordingly, experimental evidence shows that the FtsZ ring in cells retains a dynamic behavior (30). It is therefore expected that the dynamic character of the filaments that allows for filament rupture and annealing in vitro will play an important role in the functional force-generating mechanism in vivo.
Materials and Methods
Protein Purification and Assay.
Escherichia coli FtsZ was purified by the calcium-induced precipitation method as described previously. The protein concentration was measured using the bicinchoninic acid assay (Pierce), with spectrophotometrically calibrated FtsZ standards (31).
AFM Imaging.
A 50 nM solution of FtsZ in Tris•HCl 50 mM, KCl 500 mM, MgCl2, 5 mM pH 7.5 buffer in the presence of 1 mM GTP was incubated on a freshly cleaved mica surface for 10 min. Excess protein was removed and images of the adsorbed protein were taken under buffer at different pH (50 mM citrate buffer, KCl 500 mM, MgCl2 5 mM adjusted for pH 5, 6.5, and 7.5). Experiments done in the presence of glycerol were carried out by adding 15% glycerol to the imaging buffer after the filaments had been formed on the mica surface. Images were taken in jump mode (32) optimizing conditions to allow taking one image per minute.
Filament Shape Parametrization.
Filaments that were stable and isolated enough to assure that their dynamic behavior was not affected by the proximity of neighboring filaments were parametrized and analyzed. Filaments were described in polar coordinates using the harmonics series
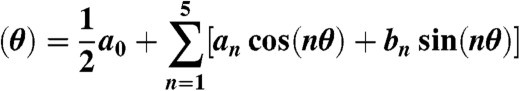 |
[1] |
truncated at the fifth term in order to have enough flexibility to adjust any filament. The detailed analytical protocol is presented in the SI Text.
Supplementary Material
Acknowledgments.
The authors acknowledge Mercedes Jiménez and Jesús Mingorance for providing materials and useful discussions. We also acknowledge funds from COMBACT S-BIO-0260/2006- (Comunidad de Madrid; to M. Vicente and G.R.); NOBIMAT-M S2OO9/MAT·1507 (Comunidad de Madrid; to M. Vélez); DIVINOCELL FP7 HEALTH-F3-2009-223431 (European Commision; to M. Vicente, G.R., and M. Vélez); Plan Nacional BIO2008-04478-C03-00 (Ministerio de Ciencia e Innovación, Spain; to M. Vicente, G.R., and M. Vélez), CONSOLIDER INGENIO 2010 CSD2007-00010 (Ministerio de Ciencia e Innovación; to M. Vélez), and the Comunidad Autónoma de Madrid for fellowships to P.M.-G.; FIS2010-22047-C05-01 (Ministerio de Ciencia e Innovación, to P.T.) and MODELICO-S2009/ESP-1691 (Comunidad de Madrid, to P.T.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1204844109/-/DCSupplemental.
References
- 1.Osawa M, Erickson HP. Inside-out Z rings-constriction with and without GTP hydrolysis. Mol Microbiol. 2011;81:571–579. doi: 10.1111/j.1365-2958.2011.07716.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Osawa M, Anderson DE, Erickson HP. Reconstitution of contractile FtsZ rings in liposomes. Science. 2008;320:792–794. doi: 10.1126/science.1154520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Erickson HP. Modeling the physics of FtsZ assembly and force generation. Proc Natl Acad Sci USA. 2009;106:9238–9243. doi: 10.1073/pnas.0902258106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Allard JF, Cytrynbaum EN. Force generation by a dynamic Z-ring in Escherichia coli cell division. Proc Natl Acad Sci USA. 2008;106:145–150. doi: 10.1073/pnas.0808657106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lan G, Daniels BR, Dobrowsky TM, Wirtz D, Sun SX. Condensation of FtsZ filaments can drive bacterial cell division. Proc Natl Acad Sci USA. 2009;106:121–126. doi: 10.1073/pnas.0807963106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Surovtsev IV, Morgan JJ, Lindahl PA. Kinetic modeling of the assembly, dynamic steady state, and contraction of the FtsZ ring in prokaryotic cytokinesis. PLoS Comput Biol. 2008;4:e1000102. doi: 10.1371/journal.pcbi.1000102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Páez A, et al. Simple modeling of FtsZ polymers on flat and curved surfaces: Correlation with experimental in vitro observations. PMC Biophys. 2009;2:8. doi: 10.1186/1757-5036-2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ghosh B, Sain A. Origin of contractile force during cell division of bacteria. Phys Rev Lett. 2008;101:178101. doi: 10.1103/PhysRevLett.101.178101. [DOI] [PubMed] [Google Scholar]
- 9.Mingorance J, Rivas G, Vélez M, Gómez-Puertas P, Vicente M. Strong FtsZ is with the force: Mechanisms to constrict bacteria. Trends Microbiol. 2010;18:348–356. doi: 10.1016/j.tim.2010.06.001. [DOI] [PubMed] [Google Scholar]
- 10.Sun SX, Walcott S, Wolgemuth CW. Cytoskeletal cross-linking and bundling in motor-independent contraction. Curr Biol. 2010;20:R654–R665. doi: 10.1016/j.cub.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fischer-Friedrich E, Gov N. Modeling FtsZ ring formation in the bacterial cell anisotropic aggregation via mutual interactions of polymer rods. Phys Biol. 2011;8:026007. doi: 10.1088/1478-3975/8/2/026007. [DOI] [PubMed] [Google Scholar]
- 12.Drew DA, Koch GA, Vellante H, Talati R, Sanchez O. Analyses of mechanisms for force generation during cell septation in Escherichia coli. Bull Math Biol. 2009;71:980–1005. doi: 10.1007/s11538-008-9390-6. [DOI] [PubMed] [Google Scholar]
- 13.Osawa M, Anderson DE, Erickson HP. Dynamic assembly of FtsZ regulated by GTP hydrolysis. EMBO J. 1998;17:462–469. doi: 10.1093/emboj/17.2.462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen Y, Erickson HP. FtsZ filament dynamics at steady state: Subunit exchange with and without nucleotide hydrolysis. Biochemistry. 2009;48:6664–6673. doi: 10.1021/bi8022653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mingorance J, et al. Visualization of single Escherichia coli FtsZ filament dynamics with atomic force microscopy. J Biol Chem. 2005;280:20909–20914. doi: 10.1074/jbc.M503059200. [DOI] [PubMed] [Google Scholar]
- 16.Páez A, Tarazona P, Mateos-Gil P, Vélez M. Self-organization of curved living polymers: FtsZ protein filaments. Soft Matter. 2009;5:2625–2637. [Google Scholar]
- 17.Hamon L, et al. Mica surface promotes the assembly of cytoskeletal proteins. Langmuir. 2009;25:3331–3335. doi: 10.1021/la8035743. [DOI] [PubMed] [Google Scholar]
- 18.Hyman AA, Salser S, Drechsel DN, Unwin N, Mitchison TJ. Role of GTP hydrolysis in microtubule dynamics: Information from a slowly hydrolyzable analogue GMPCPP. Mol Biol Cell. 1992;3:1155–1167. doi: 10.1091/mbc.3.10.1155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mendieta J, et al. Structural and functional model for ionic (K+/Na+) and pH dependence of GTPase activity and polymerization of FtsZ the prokaryotic ortholog of tubulin. J Mol Biol. 2009;390:17–25. doi: 10.1016/j.jmb.2009.05.018. [DOI] [PubMed] [Google Scholar]
- 20.Hörger I, et al. Langevin computer simulations of bacterial protein filaments and the force-generating mechanism during cell division. Phys Rev E Stat Nonlin Soft Matter Phys. 2008;77:011902. doi: 10.1103/PhysRevE.77.011902. [DOI] [PubMed] [Google Scholar]
- 21.Romberg L, Mitchison TJ. Rate-limiting guanosine 5-´triphosphate hydrolysis during nucleotide turnover by FtsZ a prokaryotic tubulin homologue involved in bacterial cell division. Biochemistry. 2004;43:282–288. doi: 10.1021/bi035465r. [DOI] [PubMed] [Google Scholar]
- 22.Mingorance J, Rueda S, Gómez-Puertas P, Valencia A, Vicente M. Escherichia coli FtsZ polymers contain mostly GTP and have a high nucleotide turnover. Mol Microbiol. 2001;41:83–91. doi: 10.1046/j.1365-2958.2001.02498.x. [DOI] [PubMed] [Google Scholar]
- 23.Huecas S, et al. The interactions of cell division protein FtsZ with guanine nucleotides. J Biol Chem. 2007;282:37515–37528. doi: 10.1074/jbc.M706399200. [DOI] [PubMed] [Google Scholar]
- 24.Tadros M, González JM, Rivas G, Vicente M, Mingorance J. Activation of the Escherichia coli cell division protein FtsZ by a low-affinity interaction with monovalent cations. FEBS Lett. 2006;580:4941–4946. doi: 10.1016/j.febslet.2006.07.083. [DOI] [PubMed] [Google Scholar]
- 25.Martin-Garcia F, et al. Molecular dynamics simulation of GTPase activity in polymers of the cell division protein FtsZ. FEBS Lett. 2012 doi: 10.1016/j.febslet.2012.03.042. (in press) [DOI] [PubMed] [Google Scholar]
- 26.Wade R. On and around microtubules: An overview. Mol Biotechnol. 2009;43:177–191. doi: 10.1007/s12033-009-9193-5. [DOI] [PubMed] [Google Scholar]
- 27.Salvarelli E, Krupka M, Rivas G, Vicente M, Mingorance J. Independence between GTPase active sites in the Escherichia coli cell division protein FtsZ. FEBS Lett. 2011;585:3880–3883. doi: 10.1016/j.febslet.2011.10.046. [DOI] [PubMed] [Google Scholar]
- 28.Kueh HY, Mitchison TJ. Structural plasticity in actin and tubulin polymer dynamics. Science. 2009;325:960–963. doi: 10.1126/science.1168823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mateos-Gil P, et al. FtsZ polymers bound to lipid bilayers through ZipA form dynamic two dimensional networks. Biochim Biophys Acta Biomembr. 2012;1818:806–813. doi: 10.1016/j.bbamem.2011.12.012. [DOI] [PubMed] [Google Scholar]
- 30.Stricker J, Maddox P, Salmon ED, Erickson HP. Rapid assembly dynamics of the Escherichia coli FtsZ-ring demonstrated by fluorescence recovery after photobleaching. Proc Natl Acad Sci USA. 2002;99:3171–3175. doi: 10.1073/pnas.052595099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rivas G, et al. Magnesium-induced linear self-association of the FtsZ bacterial cell division protein monomer. J Biol Chem. 2000;275:11740–11749. doi: 10.1074/jbc.275.16.11740. [DOI] [PubMed] [Google Scholar]
- 32.Moreno-Herrero F, et al. Scanning force microscopy jumping and tapping modes in liquids. Appl Phys Lett. 2002;81:2620–2622. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.