Folding helical proteins in explicit solvent using dihedral-biased tempering

Abstract

Using a single-trajectory-based tempering method with a high-temperature dihedral bias, we repeatedly folded four helical proteins [α₃D (PDB ID: 2A3D, 73 residues), α₃W (1LQ7, 67 residues), Fap1-NR_α (2KUB, 81 residues) and S-836 (2JUA, 102 residues)] and some of the mutants in explicit solvent within several microseconds. The lowest root-mean-square deviations of backbone atoms from the experimentally determined structures were 1.9, 1.4, 1.0, and 2.1 Å, respectively. Cluster analyses of folding trajectories showed the native conformation usually occupied the most populated cluster. The simulation protocol can be applied to large-scale simulations of other helical proteins on commonly accessible computing platforms.

Molecular dynamics (MD) allows one to study protein folding (1–5) in molecular details. It is, however, computationally demanding if we model a protein accurately using an all-atom representation and simulate it in explicitly solvent. Recent advances in simulation methods and improved computer hardware have made it possible to fold a protein up to about 30 to 80 residues (6–17).

In this study, we report folding simulations of four helical proteins of 67 to 102 amino acid residues, along with their mutants, via a dihedral-biased tempering method. The method couples accelerated dihedral dynamics (10, 18, 19) with a fast motion at a high temperature through a single-trajectory-based tempering method reported previously (12). As the dihedral bias was only added at higher temperatures, we were still able to recover unbiased room temperature properties. This method allowed us to study several interesting nonnative conformations in addition to the native one.

We simulated four proteins in Protein Data Bank (PDB): α₃D (PDB ID: 2A3D, 73 residues) (20, 21), α₃W (1LQ7, 67 residues) (22, 23), Fap1-NR_α (2KUB, 81 residues) (24) and S-836 (2JUA, 102 residues) (25) in a few microseconds. The first three are parallel three-helix bundles, and the last is a parallel four-helix bundle. Among the four, only Fap1-NR_α is a natural domain; the rest are artificially designed proteins.

Results

Overview of Folding of Helical Proteins.

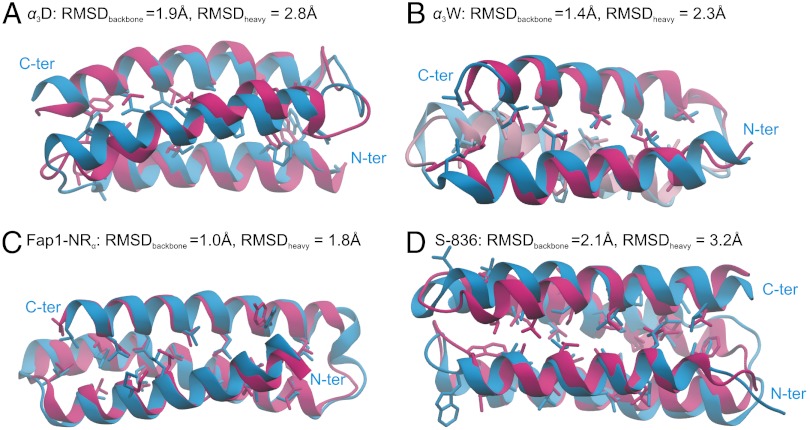
Protein sequences, simulation conditions, and parameters for the dihedral bias are listed in Tables S1, S2, and S3, respectively. In Fig. 1, we show the trajectory frames with the lowest backbone root-mean-square deviations (RMSDs) 1.9 (α₃D), 1.4 (α₃W), 1.0 (Fap1-NR_α), and 2.1 Å (S-836) from the respective experimental structures, which will be referred to as “native” structures even for the designed proteins. By comparison, control simulations using regular MD starting from the native conformations yielded higher average RMSDs (3.2, 2.2, 1.5, and 3.2 Å, respectively) at 300 K, suggesting that the native conformations were stably reached.

Fig. 1.

Best folded structures (blue) of four proteins: (A) α₃D, (B) α₃W, (C) Fap1-NR_α, and (D) S-836 compared with the experimentally (NMR) determined structures (red).

Without the experimental structure, cluster analyses (see Methods and SI Text) showed that the native conformation occupied the largest cluster in most trajectories for α₃D, α₃W, and S-836 (see Table S3). For Fap1-NR_α, the native conformation was found in the second largest cluster, possibly due to limited sampling and/or force field inaccuracy (see SI Text for a discussion).

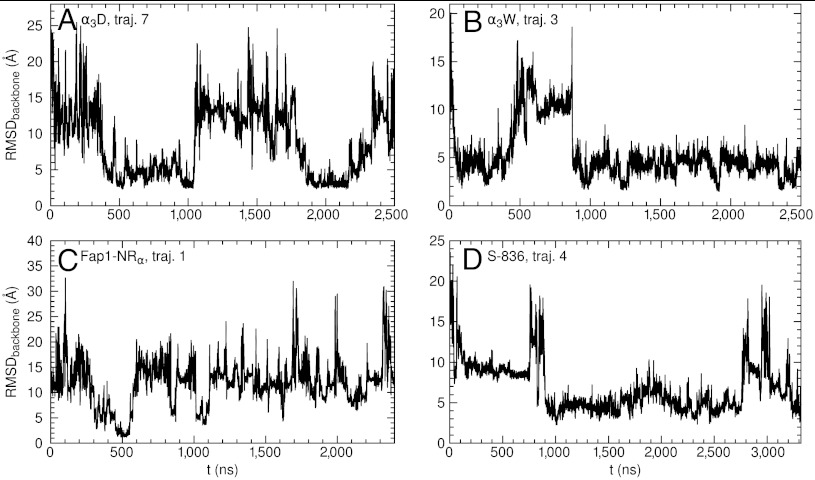
For each protein, we show the time series of RMSD for a typical trajectory in Fig. 2. All simulations started from fully extended conformations (Fig. S1) with large RMSDs. Folding and unfolding events, as indicated by the rises and falls of RMSD, typically occurred on a time scale of 0.5 to 2 µs. We have accumulated around 10 folding events in each of α₃D, α₃W, and S-836, although longer and/or more simulations may be needed to further improve statistics.

Fig. 2.

The backbone root-mean-square deviation (RMSD) from the experimentally determined structure versus time in a typical simulation trajectory of (A) α₃D, (B) α₃W, (C) Fap1-NR_α, (D) S-836.

Since the simulation method used a variable temperature, only a fraction of trajectory frames were pertinent to the room temperature. We only reported results after reweighted to 300 K using the multiple histogram method (26–28; see SI Text).

Geometry of a Parallel Helix Bundle.

Helical proteins are geometrically interesting, as they present different ways of packing helices. Here we discuss two features in packing helices by using the three proteins α₃D, α₃W, and S-836 as examples (we omitted Fap1-NR_α as it shares the same overall geometry with α₃W).

The first feature is the packing “chirality.” If a parallel three-helix bundle protein structure is viewed as three connected rods, after the first two helices are aligned, the third one can be packed against either side of the plane extended by the former two. We call the bundle right-handed if the first helix, when viewed along the middle helix from N to C terminus, can be rotated clockwise to overlap with the third one by an angle less than 180°; otherwise, we call the bundle left-handed. A three-helix bundle of either chirality exists; α₃D is right-handed, while α₃W and Fap1-NR_α are left-handed.

Another packing feature is the helix orientation. Although two successive helices are usually aligned antiparallel, a parallel alignment via a long loop is also possible.

In our trajectories, we found several compact but less stable nonnative conformations, which differed from the native one by the packing chirality or helix orientation. We wished to see what determines the natural geometry.

α₃D.

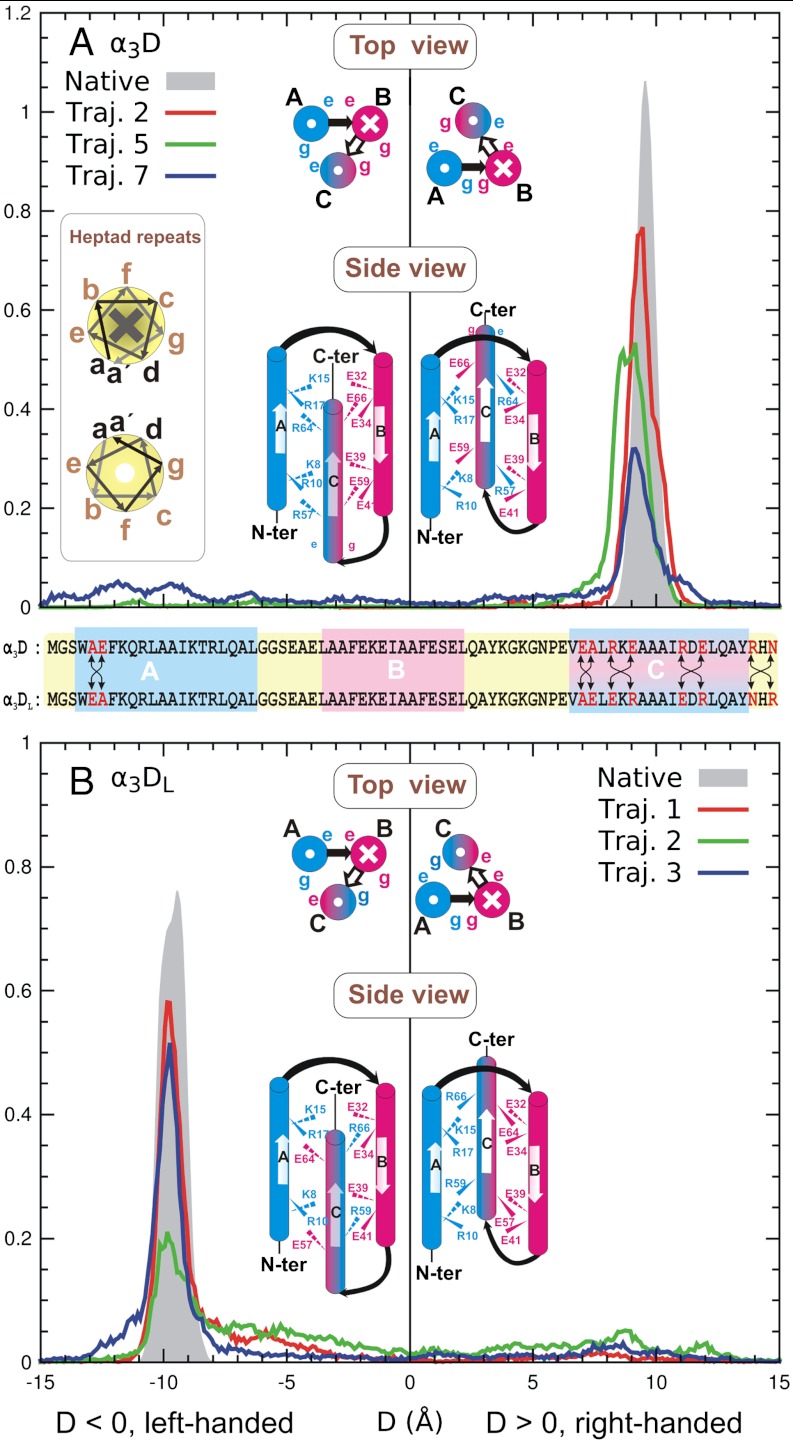
We started with the first three-helix bundle, α₃D (20, 21). A typical trajectory is shown in Fig. S2A. The three helices are labeled as A, B, and C from N to C terminus. In Fig. 3A, we show the distributions of the chiral distance D (defined in SI Text, positive for a right-handed bundle, negative a left-handed one) from three independent folding trajectories, as well as a 300 K regular MD trajectory starting from the native structure. The distributions were dominated by a right-handed (native) peak around D = 9 ∼ 10 Å, coinciding with that at D = 9.7 Å from the native simulation. The widths of the peak still differed among the trajectories, however.

Fig. 3.

The packing-chirality D distributions at 300 K of (A) α₃D and a mutant (B) α₃D_L. In each panel, the shaded peak was obtained from a 300 K regular MD simulation of the respective native conformation. For each protein, interaction patterns of charged residues are also shown schematically in top and side views, in which the right and left sides represent the right-handed and left-handed conformations, respectively. For α₃D (A), only the right-handed (native) conformation exists; the left-handed conformation is hypothetical. But the opposite is true for the mutant α₃D_L (B). Inset of A: helix heptad. In the top views and heptad illustration, crosses and dots in circles mean pointing into and out of the paper, respectively. The sequences of the two proteins are compared in the middle of the figure.

The dominance of the right-handed conformation can be explained by a favorable interhelical charge interaction (20). In the protein, residues in all three helices follow the heptad repeat a - b - c - d - e - f - g (see Fig. 3A, Left, Inset), in which the a and d residues are hydrophobic and the e and g ones charged or polar. The charge interactions among the e and g residues of different helices help secure the skeleton.

For α₃D, the e and g residues on helix A are all positively charged, while those on helix B are negatively charged; on helix C, the e residues are positively charged but the g ones are negatively charged. In the center diagram of Fig. 3A, we show schematically the distributions of these residues in the two opposite chiral conformations (Right, native; Left, hypothetical) in both top and side views. In the right-handed native conformation (the right panel), the positively charged e residues (Arg57 and Arg64) on helix C contact with the negatively charged g residues (Glu39 and Glu32) on helix B, and the negatively charged g residues (Glu59 and Glu66) on helix C with the positively charged e residues (Lys8 and Lys15) on helix A; both are favorable. By contrast, in the left-handed conformation, the e and g residues on helix C have to contact unfavorably with their counterparts on helices A and B with the same charges.

We further show that the packing chirality can be reversed by a mutation, in which we flipped the charges on the e and g residues of helix C through two local swaps: R57E-E59R and R64E-E66R (R57E means mutating Arg57 to Glu57). We also made three local swaps (A5E-E6A, E54A-A54E, and R71N-N71R) to help stabilize the left-handed conformation. The mutant is referred to as α₃D_L. A sequence comparison with α₃D is shown in the middle of Fig. 3.

We simulated the mutant α₃D_L in three trajectories (Figs. S2B and S3). As shown in Fig. 3B, the left-handed conformation became dominant with a signature peak at D = -9.7 Å, while the right-handed one almost vanished. Cluster analyses confirmed that the left-handed conformation occupied the largest cluster in 300 K.

We further investigated the local stability of the mutant α₃D_L in comparison with that of the original α₃D. The cluster center from trajectory 1 was extracted and energy minimized as the putative native conformation of α₃D_L, as illustrated in Fig. S4A. We then ran a separate 300 K regular MD simulation starting from this point for local properties (the local chiral distribution was shown as the shaded peak in Fig. 3B). The average RMSD among all trajectory frames from the native simulation was 2.0 Å, which was comparable to that of α₃D, 2.1 Å, suggesting a similar conformational stability. Further, as shown in Table S4, the hydrophobic contact number, interhelical distances, and angles were similar to the native conformation of α₃D. Finally, the side chain χ₁ (C-C_α-C_β-C_γ) dihedrals of α₃D and α₃D_L had similar rotameric distributions, as shown in Fig. S5 A and B, as well as similar rotameric entropy of the hydrophobic core, as shown in Table S5. Thus, the mutations might not affect the stability of the hydrophobic core significantly, and the charge interaction should be responsible for the chirality change.

The comparison of α₃D and α₃D_L also suggested that the stability of the native right-handed conformation of α₃D was limited by the energy of forming a few favorable pairs of charged residues. Other energy contributions, such as hydrophobic interactions, were unlikely to inhibit the chirality flip.

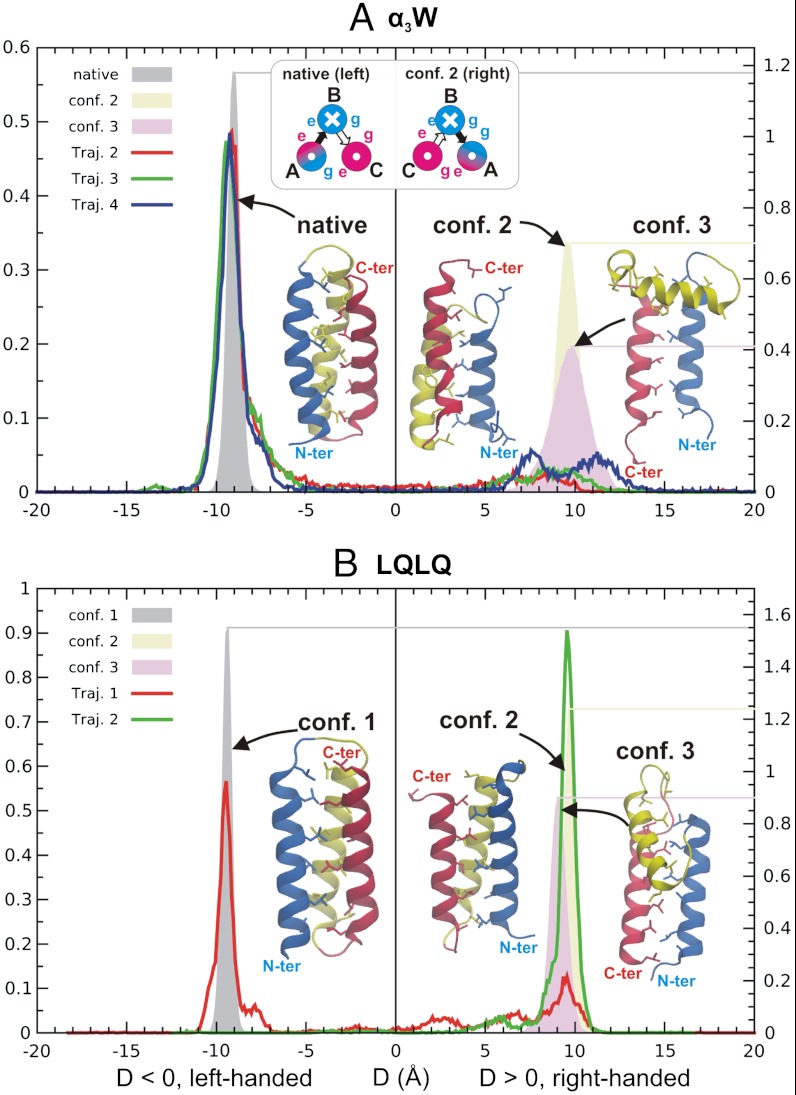
α₃W. We now turn to the second protein α₃W (PDB ID: 1LQ7) (22, 23), which was previously simulated in implicit solvent (29–31). However, our trajectories revealed in addition to the native conformation two compact, geometrically different (albeit less populated) conformations.

Like α₃D, α₃W is a parallel bundle of three helices, again labeled as A, B, and C from N to C terminus. Its strategy to secure the chirality is similar to that of α₃D (22): the heptad pattern is also strictly followed in all three helices; the e and g residues on helix B are positively charged; those on helix C are negatively charged; and the e and g residues on helix A are negatively and positively charged, respectively. As shown in Fig. 4A, Upper, Inset, the arrangement now favors the left-handed conformation.

Fig. 4.

The packing-chirality D distributions at 300 K of (A) α₃W and (B) a mutant LQLQ with a symmetric sequence. The native and two nonnative conformations are also shown in either case. The colors of the three helices are blue, yellow, and red, sequentially, from N to C terminus. The shade peaks (right vertical scales) in both panels were obtained from 300 K regular MD simulations starting from the representative structures.A, Upper Inset for charge interactions is similar to that in Fig. 3A or B.

The chiral distribution computed from the folding trajectories indeed showed a prominent left-handed (D < 0) peak as well as a suppressed right-handed (D > 0) one, as seen in Fig. 4A. In fact, the right-handed peak covered two different conformations, both of which had corresponding clusters under cluster analyses (300 K, cluster centers also shown in Fig. 4A). We ran respective 300 K MD simulations starting from the two nonnative conformations as well as the native one. The chiral distributions of the three conformations are shown as shaded peaks in Fig. 4A.

The first nonnative conformation (conf. 2) had the opposite chirality to the native one. Its metastability was achieved by sliding two helices along the parallel axis, which somewhat relieved unfavorable charge interactions (see Fig. S6). The conformation had similar interhelical distances and angles as the native one, but a lowered contact number [from 49 (native) to 40] among hydrophobic residues, as shown in Table S4.

The second nonnative conformation (conf. 3) differed from both the native one and conf. 2 by a reversely oriented helix C (see Fig. 4A). It was stabilized through a few interhelical hydrophobic and charged interactions, as shown in Fig. S7A.

We further demonstrate that if all charged residues on the helices were turned to polar or neutral ones, the protein could indeed switch among conformations of different geometries. We simulated a highly symmetric three-helix bundle, named LQLQ, in which all a and d residues were Leus and all b, c, e, f, and g residues were Glns in two independent trajectories. Cluster analyses revealed three clusters, which we refer to as conf. 1, 2, and 3, as shown in Fig. 4B.

Due to the symmetric sequence, conf. 1 and 2 (left- and right-handed, respectively) were similar in all geometric measures except the opposite chirality, as shown in Table S4. They represented the two most populated clusters with similar populations. Conf. 3 (a smaller cluster) was similar to, but more compact than, the conf. 3 in α₃W, with the middle helix B being almost parallel, instead of orthogonal, to the other two helices. Note helix B was closer to helix C, not A, although the two choices appeared to be symmetric; we propose a possible explanation in Fig. S7B.

Additionally, we simulated another mutant LALQ in which the b and c residues were Alas instead Glns with similar results (Fig. S8), suggesting some generality of LQLQ in modeling a symmetric three-helix bundle. However if the e, f, and g residues were also replaced Alas, helices in the resulting mutant LALA tended to be bent (see Fig. S9), suggesting that the polar and/or charged residues with long side chains might help maintaining a straight skeleton.

S-836.

The last protein is the four-helix bundle S-836 (PDB ID: 2JUA) (25). The four helices are labeled as A, B, C, and D from N to C terminus. In five trajectories (the total simulation time was 17 μs), the first four reached the native conformation, while the last sampled two different nonnative ones.

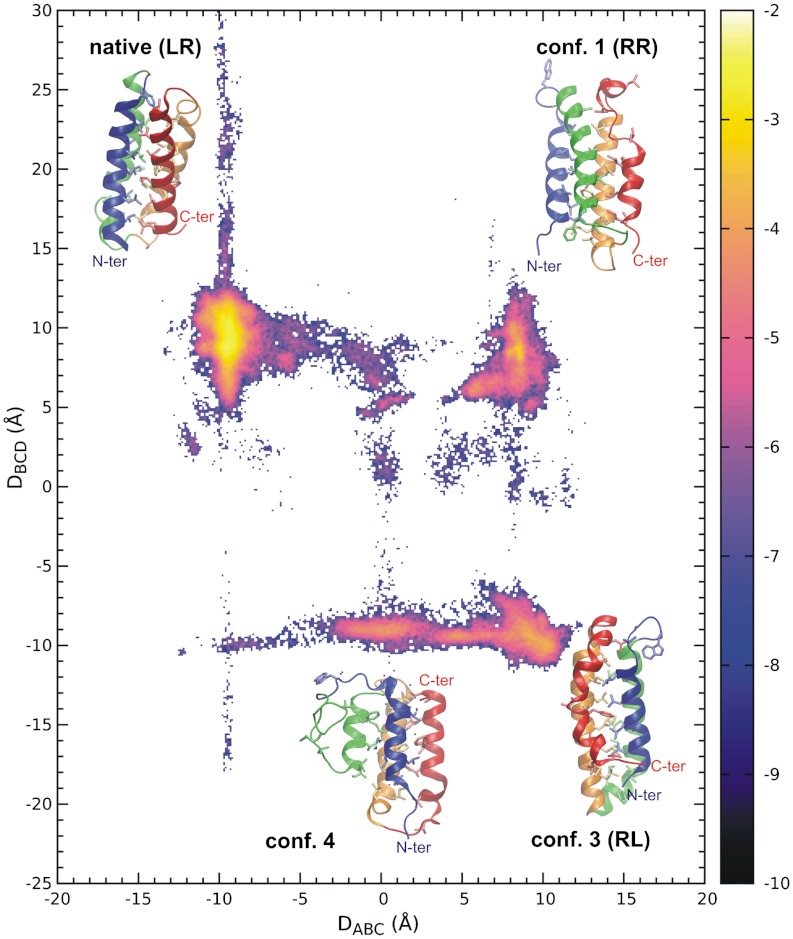
To describe the geometry of the protein, we first extended the packing chirality for a three-helix bundle to a four-helix one. We view the four helices as two successive three-helix groups, A-B-C and B-C-D, each of which is thus equivalent to a three-helix bundle and has its own chirality. We partition the conformation space to four quadrants according to the signs of the two chiral distances D_ABC and D_BCD, denoted as LR (D_ABC < 0, D_BCD > 0), RR (D_ABC > 0, D_BCD > 0), RL (D_ABC > 0, D_BCD < 0) and LL (D_ABC < 0, D_BCD < 0). A quadrant can also be represented by either the native (LR) conformation or some hypothetic one that differs from the native only by chirality; e.g., the representative RR conformation differs from the native only by the chirality of the A-B-C helix group.

We computed the joint distribution of D_ABC and D_BCD after combining data from all trajectories. As shown in Fig. 5, the distribution revealed four major clusters. The four corresponding conformations were the native one (LR), conf. 2 (RR) and 3 (RL), and conf. 4, which differed from conf. 3 by a reversely oriented helix A. Although the competing conformations exist, the native one still occupied the most populated cluster in the first four folding trajectories, and the population ratios to the first runner-up clusters were 2.1, 3.8, 1.1, and 1.9, respectively.

Fig. 5.

The logarithm of the packing-chirality distribution of S-386 at 300 K with representative conformations at the four most populated clusters. The colors of the four helices are blue, green, orange, and red, sequentially, from N to C terminus.

Except conf. 4 (which is not a simple chiral image of the native), the chiral conformations could be sorted as LR (native) > RR and RL (conf. 2 and 3) > LL (missing) by their populations. We attempt to explain the order by the pairing pattern of charged residues, as shown in Fig. S10. The missing LL conformation was possibly due to inescapable repulsion between His83, His86, Lys90, His94 on helix D, and Lys32, His36 on helix B (all His are positively charged). Helices A and D in the RL conformation encountered a similar but less severe problem, causing a kink in helix D to avoid direct repulsion between His86 and Lys17. Unfavorable interactions between helices B and D in the RR conformation could bend or dislocate helix D. The LR (native) conformation appeared to have the best pairing pattern, although unfavorable contacts exist; e.g., Glu91 and Asp11.

In nature, four-helix bundles adopting the RR, RL, and LL conformations do exist. In fact, the majority [e.g., cytochrome ć (PDB ID: 3ZTM) (32) and cytochrome b₅₆₂ (PDB ID: 1QPU) (33)] adopt the RL conformation, the opposite of the native LR conformation of S-836. Two examples of the RR and LL conformations are the C-terminal domain of KaiA (PDB ID: 1Q6A) (34) and domain I of the transcription factor TFIIS (PDB ID: 1EO0) (35), respectively.

Additional results of the simulated proteins are discussed in the SI Text and Figs. S11–S17.

Conclusions

We have shown the usefulness of the single-trajectory-based tempering with a dihedral bias in studying helical proteins in explicit solvent. We were able to fold, within a few microseconds, four helical proteins (with the native conformation usually found in the largest cluster in simulation trajectories) as well as their mutants.

Our trajectories showed that a parallel helix bundle, especially one with a symmetric sequence, often has competing conformations that differ from the native one only by packing chirality and/or helix orientation. Similarly, the existence of competing conformations was previously reported for the Rop-dimer and its mutants (36–38). While the ability to identify the native geometry is essential in studying helical proteins, the competing conformations can help to design new proteins, either as targets or as pitfalls to avoid (39).

Despite continuous improvement, the current force field might have yet reached perfection. As suggested by Best and Hummer (40), the current AMBER force field still underestimates both the enthalpy of hydrogen bonds (rendering helical conformations less energetically favorable) and the entropy of unfolded states. Our sampling strategy, which used a helical bias and a high-temperature motion, could hopefully alleviate both problems.

Methods

We describe the principles of computational methods below; details are supplied in the SI Text. The source code can be downloaded from http://sigler.bioch.bcm.tmc.edu/MaLab/.

Dihedral-biased Tempering.

Tempering is a technique (12, 41–48) that accelerates sampling by occasionally raising and lowering the temperature. In this study, we adopted a single-trajectory-based tempering method reported previously (12) for computing efficiency. We then added a dihedral bias on top of it to facilitate simulations of helical proteins.

In the tempering method, temperature T is a continuous variable in (T_L,T_H) covering the room temperature T₀. Here, T_L is slightly below T₀, while T_H(T_H > T₀) accelerates the system motion. Tempering preserves the Boltzmann distribution at any temperature cross-section such that the corresponding generalized ensemble is simply a superposition of canonical ensembles of the temperature range.

We now introduce a bias potential V to the generalized ensemble through a temperature-dependent Hamiltonian; i.e., the energy function, H(T) = H₀ + (T/T₀ - 1)V, where H₀ is the unbiased Hamiltonian. Since V has the maximal magnitude at T_H, but is zero at the room temperature T₀, the new Hamiltonian is reduced to the original one at T = T₀, and unbiased room temperature T₀ properties can thus be recovered through a modification of the multiple histogram method (26–28).

We let the bias potential V target the two backbone dihedral angles [i.e., φ (C-N-C_α-C) and ψ(N-C_α-C-N)], as they critically influence protein dynamics (10, 18, 19). It is parameterized in terms of three intrinsic dihedral modes (see Fig. S18 and Table S6), one of which corresponds to the helical conformation. The magnitudes of the modes are adjustable in each trajectory. The bias potential V applies uniformly to all except glycine and proline residues.

The method was coded to GROMACS 4.0.7 (49). We used a modified version (40) of AMBER03 (50, 51) as the force field (the modification slightly reduced helical content), TIP3P (52) as the water model, the particle-meshed Ewald (PME) method (53) for long-range electrostatic interaction, and the velocity-rescaling method for thermostat (54); SETTLE (55) and the parallel LINCS (56) were used as constraint algorithms for waters and proteins, respectively.

The verifications of the methods are shown in SI Text; see also Figs. S19 and S20.

Although the method is designed for helical proteins, extensions to other types of proteins might be achieved via a random trial of various bias potentials, as discussed in the SI Text. To confirm a folding, we can compare several independent trajectories to see if a common structure is reached.

Clustering Method.

We used a deterministic clustering method. The method finds a balance between the intracluster distance (the distance of two protein structures is defined as their backbone RMSD after alignment; it is then averaged over all pairs of frames within the cluster) and the total number of clusters. It also allows each frame to carry the weight from the multiple histogram method (26–28) to filter out frames irrelevant to 300 K.