Structural distributions from single-molecule measurements as a tool for molecular mechanics

Abstract

A mechanical view provides an attractive alternative for predicting the behavior of complex systems since it circumvents the resource-intensive requirements of atomistic models; however, it remains extremely challenging to characterize the mechanical responses of a system at the molecular level. Here, the structural distribution is proposed to be an effective means to extracting the molecular mechanical properties. End-to-end distance distributions for a series of short poly-L-proline peptides with the sequence P_nCG₃K-biotin (n = 8, 12, 15 and 24) were used to experimentally illustrate this new approach. High-resolution single-molecule Förster-type resonance energy transfer (FRET) experiments were carried out and the conformation-resolving power was characterized and discussed in the context of the conventional constant-time binning procedure for FRET data analysis. It was shown that the commonly adopted theoretical polymer models—including the worm-like chain, the freely jointed chain, and the self-avoiding chain—could not be distinguished by the averaged end-to-end distances, but could be ruled out using the molecular details gained by conformational distribution analysis because similar polymers of different sizes could respond to external forces differently. Specifically, by fitting the molecular conformational distribution to a semi-flexible polymer model, the effective persistence lengths for the series of short poly-L-proline peptides were found to be size-dependent with values of ~190 Å, ~67 Å, ~51 Å, and ~76 Å for n = 8, 12, 15, and 24, respectively. A comprehensive computational modeling was carried out to gain further insights for this surprising discovery. It was found that P₈ exists as the extended all-trans isomaer whereas P₁₂ and P₁₅ predominantly contained one proline residue in the cis conformation. P₂₄ exists as a mixture of one-cis (75%) and two-cis (25%) isomers where each isomer contributes to an experimentally resolvable conformational mode. This work demonstrates the resolving power of the distribution-based approach, and the capacity of integrating high-resolution single-molecule FRET experiments with molecular modeling to reveal detailed structural information about the conformation of molecules on the length scales relevant to the study of biological molecules.

1. Introduction

Compared to small molecules, our understanding of the reactivity of larger and more complicated macromolecules, such as proteins and poly-peptides, is severely limited. One major reason is that the conformation of a macromolecule in solution is continually reconfigured by random thermal forces in ways that cannot yet be predicted from first principles. Continuum mechanics, which has been used to describe the relationship between forces and displacements in macromolecules, represents a coarse-grained physical picture (both in time and spatial extent) where the atomistic details of the molecule are not explicitly considered. In this framework, mechanical properties such as elasticity, plasticity, and persistence length are used to describe the energetics associated with the constantly changing molecular conformation and approximate the equilibrium distribution of molecular conformation, which is ultimately determined by the atomic details according to statistical mechanics. Considering complex molecules via the view of continuum mechanics bypasses the atomic-level details and turns the prediction of molecular responses into a relatively simple problem. A notable example is the success of using persistence length to describe and predict the force-extension response of long oligonucleotides. The mechanical view of molecular conformation thus provides an outstanding framework to investigate biomolecular systems [1], such as mechano-chemical coupling in single-domain enzymes [2] and in understanding and expanding the scope of force-dependent chemistry [3, 4].

A direct way to measure the mechanical properties of molecules is by exerting forces on a single molecule and measuring the resulting displacements. Popular single-molecule force methods include the laser tweezers [5–7], the magnetic tweezers [8], and the atomic force microscopy (AFM) [9]. More recently, a chemical kinetics method was proposed [10] that could potentially resolve the mechanical properties in smaller-scale molecules such as peptides and proteins. In those experiments, short polymers are used to serve as force-inducers for small-molecule chemical reactions.

Here, we attempt to employ an alternative approach to characterize the mechanical properties of molecules, namely from the spatial distribution of their structures. The motivation is that the structural distribution is a manifestation of the mechanical responses to thermal random forces. This force-free strategy is distinctive from the aforementioned approaches of applying external forces and extracting mechanical properties from the corresponding force-extension curves. For example, using the stiff-chain model [11], the effective persistence length between two well-defined points in a linear polymer can be determined from the experimentally measured distance distribution between them. This information will in turn permit one to deduce the molecular elasticity modulus and predict the behavior of similar polymers with different sizes. The distribution-based approach for determining mechanical properties have been used to measure the persistence lengths of μm-sized actin [12] and microtubule filaments [13]. Yet, application to single molecule-level mechanics has not been pursued. We demonstrate the feasibility of this approach using a series of short poly-L-proline peptides and illustrate how the measured distributions of end-to-end distances reveal their molecular behaviors and mechanical properties. Short poly-L-proline peptides were chosen as a model system for their direct relevance to protein signaling motifs and their historical roles as molecular rulers. Moreover, the long inter-conversion time between trans and cis proline isomers (vide infra) gives an additional advantage at the technical level since the isomerization timescale of seconds [14] and experimental timescale of milliseconds [15] are well separated and the analysis and interpretation of experimental data can be greatly simplified [16, 17].

2. Background

The poly-L-proline-II helix conformation—first identified in poly-L-proline peptides from which it derives its name [18, 19]—is unique in that the ω-dihedral angle of the peptide backbone adopts a trans configuration rather than the more commonly observed ω-cis isomer. In addition, the poly-L-proline-II helix involves no intra-molecular hydrogen bonds and is thought to behave as a relatively rigid rod on short length scales [20]. The poly-L-proline II backbone ω-dihedral angle has been observed for non-proline residues including short non-prolyl peptides [21–23] and denatured proteins [24]. Poly-L-proline II is also known to be an important configuration of proline-rich peptides, such as structural proteins and those involved in signal transduction [25–27].

The presumed rigidity of poly-L-proline peptides has produced interest to both theorists [14, 20, 28] and experimentalists [29–36] as model systems for validating and calibrating measurements and developing molecular understanding of peptide conformation in solution. It has been found, however, that poly-L-proline peptides are not perfectly rigid; many studies have shown evidence that they adopt more compacted structures compared to the fully extended forms predicted from the crystal structure and a perfectly rigid rod model [20, 33, 34, 37]. Despite continued interest in this system since the initial report of the crystal structure more than 50 years ago, a consensus on the physical origin of the observed compaction of poly-L-proline in solution at room temperature has yet to emerge. The two commonly invoked models for the shorter-than predicted end-to-end distances include intrinsic flexibility of the proline helix [14, 20, 33, 38] and formation of kinks due to cis-isomers interspersed in the otherwise trans-proline structure [28, 31, 32, 34, 39].

Förster-type resonance energy transfer (FRET) experiments have been intimately linked with poly-L-proline since short proline peptides were first used as a “molecular ruler” by Stryer and Haugland to demonstrate the characteristic 1/R⁶ distance dependence for energy transfer [29]. Though the peptides used were shorter than the then-estimated persistence length of poly-L-proline, the measured distances were less than predicted from the model assuming a perfectly rigid poly-L-proline structure [20]. Stryer and Haugland attributed the discrepancy to overestimating the calculated Förster radius (R₀) since it was empirically found that a shorter R₀ could adequately fit the measured data [29]. In recent years, poly-L-proline molecular ruler experiments have been revisited with advanced ensemble [30, 31] and single-molecule fluorescence techniques [32–35]. In many of these experiments, the measured end-to-end distances were shorter than predicted by a perfectly rigid, all-trans poly-L-proline model. These deviations have variously been attributed to non-ideal energy transfer in very short poly-L-prolines [30, 35], flexibility of the proline helix [30, 33, 35], or the presence of cis-isomers in an otherwise all-trans poly-L-proline-II helix [31, 32, 34].

Single-molecule FRET, because it can in principle reveal the entire end-to-end distance distribution rather than the ensemble-averaged mean distance [40], can be used to provide more detailed information about the structure of poly-L-proline peptides in solution. The earliest single-molecule experiments on poly-L-proline were continuations of the original “molecular ruler” experiments [33–35]. Consistently, these experiments yielded end-to-end distances for poly-L-proline peptides that were less than expected for a perfectly rigid type-II proline helix. This observation has been explained using a modified energy-transfer formula [33], or attributed to short persistence lengths using the worm-like chain polymer model [34].

Isomerization to ω-cis isomeric state can also lead to shorter end-to-end distances of poly-L-proline. While Watkins et al. [34], inspired by the pioneering works of Mattice and Mandelkern on long polyproline polymer chains [37, 41], first pointed out the importance of considering interspersed cis isomers in short poly-L-proline peptides, the exact nature of how cis isomers might contribute to the observed distance discrepancies remained unclear. Subsequently, two groups further considered trans-cis isomerization as the source of shortened distances observed in FRET experiments on poly-L-proline, supporting the picture put forth by Watkins et al.. Doose et al. [31] systematically investigated a series of poly-L-proline peptides (quencher-Pn-tryptophan, n = 1–10) and argued that the existence of sub-populations disqualified poly-L-proline as a distance standard on the molecular scale. The most convincing evidence to date for the existence of cis isomers in poly-proline peptides was provided by Best et al., who have investigated this possibility using a combination of single-molecule FRET (on P₂₀G), NMR (on P₈G and P₂₀G), and molecular dynamics simulations [32]. It should be mentioned that the existence of cis isomers does not rule out the compatibility with polymer models; in fact, such isomers offer a very nice molecular interpretation for the freely jointed chain and the self-avoiding chain models, as well for the buckling phenomenon in mechanics.

3. Approach

For succinctness, only the approach is outlined in the main text; details of the experimental setup, methods, materials, and molecular modeling can be found in Supplementary Information. Three commonly used theoretical models are considered: the worm-like chain (WLC), the freely jointed chain (FJC), and the self-avoiding chain (SAC). These polymer models contain distinctly different physical pictures for poly-L-proline flexibility. The WLC describes a continuously flexible rod such as a trans poly-L-proline with torsional flexibility in the peptide backbone. In contrast, the FJC and SAC describe a polymer with discrete kinks such as a trans poly-L-proline II helix with interspersed cis isomers, but with the distinction that the former allows chain segments to overlap in space whereas the latter does not. Though these models assume infinitely long polymers, they have been conventionally applied to systems of all lengths, including short poly-L-proline peptides [30, 32–34]. On the other hand, Doose et al., based on their observed sub-populations in short poly-L-proline peptides, cautioned against the use of the continuous WLC model for describing the distributions of end-to-end distances [31].

In the present work, we first show that all three models are able to quantitatively describe the observed average end-to-end distance progression along a series of poly-L-proline peptides of different lengths. That is, the widely used end-to-end distance alone does not discriminate among these three models—a serious problem that has also been noted in a recent paper by O’Brien et al.[42]—underscoring the experimental challenge of resolving competing physical pictures. Here, we reason that the microscopic physical characteristics distinguishing these models will manifest themselves in the shape of the end-to-end distance distribution.

In practice, this approach requires the measurement of the entire distance distribution quantitatively using single molecule FRET with the photon-counting noise removed in a model-free manner. Otherwise, the telltale features in the distribution would be masked by the counting noise. The model-free distributions afford an unbiased evaluation of single-molecule experimental results—after all, one would like to discover the unknown features of the distribution rather than modeling them (see Supplementary Information for further discussion, including resolution of multiple distribution modes). Though technically challenging, several significant advances since the initial report [34] have made the present work possible. They include automated single-molecule spot localization and photon arrival time registration with confocal detection to minimize manual location uncertainties [15], rigorous statistical tests for unbiased trajectory selection [43, 44], and good statistics by virtue of the larger number of molecules included in the analysis. The high-resolution method has made it possible to provide the first direct experimental evidence showing that adenylate kinase from E. coli can assume both the open and closed conformations in the absence of substrates [15], the molecular details of which are currently being actively pursued by several theoretical and computational groups [45–55]. The roles of local unfolding of a hinge in this enzyme has discussed in a mutation study [49] and has been shown most recently to alter the closed-to-open transition via all-atom molecular dynamics simulations [56]. Indeed, again using the high-resolution single-molecule method, the kinetic rates of large-amplitude conformational changes in the protein tyrosine phosphatase B from M. tuberculosis have been shown to be regulated by the local folding/unfolding transition of a helix [57].

The fully automated photon-by-photon single-molecule microscopes (Ref. [34] and Supplementary Information) were used to measure the FRET conformational distribution of a series of poly-L-proline peptides immobilized on polyethylene glycol (PEG) passivated quartz cover slips. The poly-L-proline peptides are P_nCG₃K-biotin with n = 8, 12, 15, and 24, where the donor dye (AlexaFluor-555) was attached to the N-terminus and the acceptor (AlexaFluor-647) to the C-terminus. Fluorescence spectra and lifetime data were measured at the single-molecule level and compared with ensemble-averaged data in solution to verify that spectroscopic signatures were not altered by immobilization and proximity to surface (see Supplementary Information) [58]. Single-molecule polarization modulation experiments were performed to demonstrate that there was sufficient orientational randomization of the dye-proline complexes on the experimental timescale (see Supplementary Information) [15, 43]. This criteria has been reasoned to be sufficient to justify the orientation factor κ² = 2/3 assumption in the Förster radius (R₀) calculation at the single-molecule level [17]. These experiments strongly suggest that there are no adverse interactions between the quartz substrate and dyes, nor between the peptide and the dyes. The photon-by-photon method—which includes time-stamped data acquisition and statistical analysis—allows removal of broadening due to photon-counting noise from experimental end-to-end distance distributions, providing the highest resolution allowed by information theory.

The experimentally obtained distributions, accumulated from more than 200 single-molecule traces (see Supplementary Information), were then compared with predictions from statistical polymer models. The results, to be discussed in the next section, show that none of the three models examined agree with the distributions of end-to-end distances of short poly-L-proline peptides—a result that is not unexpected considering the various assumptions involved—establishing that conformation distribution is a powerful parameter for discriminating theoretical models. In fact, by fitting the distribution of lengths for each proline to a semiflexible polymer mode, it was found to our surprise that the effective persistence length depends on the size of the poly-L-proline. Finally, in order to gain specific insights into structural details of poly-L-proline peptides in solution, the experimentally measured distributions were compared with the configurations sampled by molecular modeling.

4. Materials and Methods

4.1. Materials

Peptides with the sequence PnCG3K-biotin, where n = 8, 12, 15 and 24, were synthesized using standard Fmoc chemistry as described previously [34]. AlexaFluor 555-C₅ N-succinimidyl ester and AlexaFluor 647-C₂ maleimide (Invitrogen) were attached to the N-terminus amine and cysteine thiol, respectively, for use as donor and acceptor probes in FRET experiments. Labeling reactions were carried out in PBS with 1-mM peptide and a 5-fold excess of each dye. Labeled poly-L-proline peptides were purified on a Bio-Gel P4 drip column (Bio-Rad) equilibrated with 10-mM triethyl ammonium bicarbonate (TEAB) to remove unreacted dye. TEAB was prepared by bubbling CO₂ through triethylamine in water. Salt-free poly-L-proline samples were produced by lyophilization. Labeling efficiency of the poly-L-proline was determined to be nearly quantitative though MALDI mass spectrometry.

4.2. Steady-State FRET

Ensemble, steady-state FRET measurements were performed according to the method of acceptor quenching of the donor [15, 59]. Fluorescence measurements were collected on a Fluoromax spectrometer (Jovin-Yvon). Donor excitation was performed at 500 nm and acceptor at 600 nm. Slit widths were configured to give a 4-nm spectral resolution.

4.3. Single-Molecule FRET

Details of the experimental setup and procedure have been described in previous publications [15, 34, 57] but will be briefly summarized here. Labeled peptides were immobilized on a biotin-PEG derivatized quartz cover slip (Technical Glass Products Inc.) through biotin-streptavidin chemistry and experiments were performed on home-built, networked single-molecule confocal microscopes [15]. Continuous-wave solid-state doped-pumped Nd:YAG lasers (Coherent Compass 315M) were used as light source. Individual photon arrival times were collected on single-photon counting avalanche photodiodes (Perkin Elmer AQR-14). Four server-based single-molecule microscopes were automated in order to locate the centroid of fluorescence emission (assuming a 2-D Gaussian) from raster-scanned images for subsequent photon-by-photon data acquisition. Automation is important because it eliminates most operator-related localization error and affords better quality data with consistent signal-to-background ratio.

Data analysis was performed as described previously [15, 34, 44, 57, 60, 61]; however, for completeness, it will be summarized here. Raw intensity-versus-time trajectories were analyzed according to the maximum information method (MIM) [60]. Single-molecule probability density functions (PDFs) were calculated using Gaussian kernel density estimation from distances calculated by the MIM. Maximum-entropy deconvolution (MaxEnt) was used to remove broadening in the distribution arising from photon-counting noise [34]. The uncertainties of deconvoluted probability distributions were estimated using the bootstrap method. The distributions tended to converge when calculated from at least 200 individual trajectories, as was done here as well as in previously published experimental work [15, 57].

Single-molecule data was also analyzed with constant-time binning in order to compare the results of this common data analysis procedure with the results from the more advanced maximum information method. In constant-time binning method, the energy transfer efficiency (E) in each bin was calculated according to E = n_a /(n_a + γn_d) are the number of photons in the acceptor and donor n_a and n_d channel respectively and γ was an experimentally determined correction factor to account for differences in quantum yield and experimental collection efficiencies between the two fluorophores [62]. The photon counts per bin (n_a and n_d) were corrected for background by subtracting the mean background count rate determined from the region of the trajectory in which both dyes have bleached. A further correction for crosstalk was applied using the bulk spectra of the dyes and the transmittance of the band pass filters used in the experimental setup.

4.4. Molecular Modeling

The molecular models of poly-L-proline containing single cis isomers were constructed using the internal coordinate facilities of CHARMM [63]. Each isomer was constructed independently and a restraint potential is added to keep ω at the desired value. The restraint potential is in the form of E_dihe = k[1–cos(ω)] where k = 5000.0 kcal mol⁻¹. The CHARMM22 [64] all-atom force field with the CMAP cross terms [64, 65] was used to compute the potential energy. The generalized Born with a simple switching (GBSW) implicit solvent model [66–68] provided model solvation forces and energies. The molecular structure was then energy minimized with the restraint on ω on for 100 steepest descent and 3000 adopted basis Newton-Raphson minimization steps in CHARMM. These energy-minimized structures for each scanned cis ω angle were used as the basis for the model results used in Fig. 7.

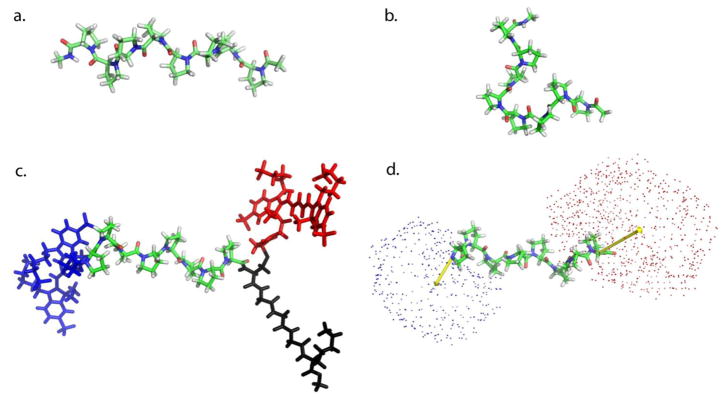
Figure 7.

Computation modeling of poly-L-proline with cis-isomers. (a) Structure of poly-L-proline p₈ in an all-trans conformation. (b) Structure of poly-L-proline P₈ with a cis isomer at between the 4^th and 5^th proline residues. (c) Simulation of all trans poly-L-proline P₈ with dyes attached. N-terminal donor is colored blue, c-terminal acceptor is colored red and the CGGGK-biotin linker is in black. (d) Results of simulations showing mean dye orientation (yellow vector) superimposed on all-trans poly-L-proline P₈. The position of the center atom of each dye from simulations is represented as a small sphere (blue, donor; red. acceptor).

To develop a molecular model of all-trans poly-L-proline P₈ with the dye molecules attached, we used models for AlexaFluor-555 and AlexaFluor-647 previously developed for use with simulations of adenylate kinase [15]. The structure for the acceptor dye, AlexaFluor 647, was obtained from the US Patent database [69]. Since the chemical structure of the donor dye is not available, a structure similar to that of the acceptor dye was assumed with two fewer -CH- groups in the alkene chain, drawing analogies from Cy3-Cy5 dyes. Force fields of the dye molecules were constructed using standard CHARMM geometries and point charges of the constituent residues. In the absence of explicit solvent, electrostatics were treated with a distance-dependent dielectric, with electrostatic energies proportional to 1/R².

The model Alexa Fluor 555 dye was attached via the succinimide group to the N-terminal proline, and the Alexa Fluor 647 dye was attached to a C-terminal cysteine residue. Both linkers contain six dihedral angles of sp³ hybridized bonds between the proline and the dye molecule, with low barriers to rotation. To scan through possible configurations of these linkers, a constraint was placed on each angle of the form E_dihe = k[1–cos(φ–φ₀)] where k = 500 kcal mol⁻¹ and φ₀ = 180º, −60º, or 60º. Each configuration of dihedral angles was energy minimized with the dihedral constraints for 500 steepest descent and 2500 adopted basis Newton-Raphson minimization steps in CHARMM.

The six dihedral angles on each dye molecule yielded the (3⁶)² = 531,441 dye configurations, with 3⁶ = 729 different positions for each dye molecule. For each of the 729 dye positions, the vector between the final proline residue and the center of the dye molecule was calculated, yielding an average vector from the end of poly-L-proline to the dye center. This vector was applied onto the full set of poly-L-proline models to facilitate the comparison between molecular modeling and single-molecule end-to-end distance distributions.

5. Results and Discussion

5.1. Single-molecule analysis of poly-L-proline conformations

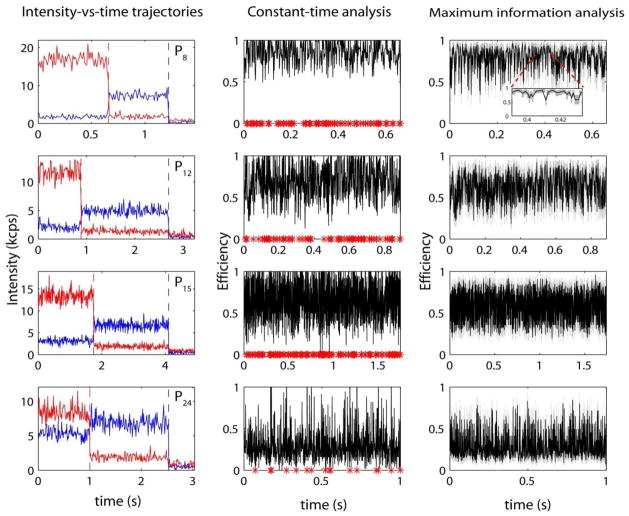
In order to characterize the conformational states of short poly-L-proline peptides, single-molecule FRET experiments have been carried out on peptides of the following sequence: P_nCG₃K-biotin, where n = 8, 12, 15 and 24. Representative single-molecule intensity-versus-time trajectories for each sample are displayed in Figure 1. These data demonstrate many of the characteristics typical of single-molecule experiments: low signal-to-noise ratio, significant photon-counting noise and rapid photo-bleaching of first the acceptor and subsequently the donor chromophores. To extract distance distributions from this data requires a carefully optimized data analysis strategy. Figure 1 also presents a transformation of the raw intensity traces into distances-versus-time traces utilizing two methods of single-molecule data analysis: the simple constant-time binning (CTB) analysis and our own maximum information (MIM) analysis [60]. MIM analysis was performed at a relative error (δR/R₀) of 10%, which translates to a mean time resolution of ~1 ms at the photon count rates obtained in these experiments. An equivalent time resolution was used for constant-time analysis. At this time resolution, up to 20% of the distance measurements in the CTB analysis for poly-proline-P₈ become ill-defined due to inappropriate background and cross-talk corrections. Typically, background correction is performed by subtracting the mean count rate for the region of the trajectory after each dye has bleached from each time bin. However, due to the Poisson statistics governing photon emission and collection in single-molecule experiments, subtraction of the mean background, in which Poisson noise has been mitigated by averaging, can frequently result in negative values for the number of photons in the time bin leading to non-physical efficiency values greater than 1 or less than 0. This has been denoted by a red asterisk on the x-axis of Figure 1. Additionally, since the error associated with each measurement is generally related to the number of photons within each time bin [60]—information which is discarded due to averaging in CTB analysis—the measurement error for each FRET efficiency determination is both unknown and inconsistent. By contrast, the MIM provides a reliable measurement of the distance with known precision. This method relies on photon-by-photon data analysis and ideas from information theory to determine the error bounds for each measurement in both time and distance (denoted by the grey boxes in Figure 1). Rather than binning the data at a constant time interval the MIM creates bins with a constant amount of relative error—an important feature which facilitates visual inspection of single-molecule data and is critical to further advanced statistical analysis. The CTB scheme reveals many transient excursions in the calculated FRET efficiency for the trajectories presented in Figure 1. However, by comparing the CTB results with those from the MIM, it is evident that much of what would be interpreted as millisecond conformational fluctuations are in fact within the experimental noise. This underscores the fact that a quantitative and objective analysis of measurement uncertainties is essential for data interpretation, especially for noisy single-molecule experiments. In other words, one must be cautious in the application and interpretation of CTB analysis at fast time resolutions where these issues are exacerbated due to smaller bins containing fewer photons: troublingly, in this scenario conformational fluctuations are indistinguishable from experimental noise. Photon-counting noise could be mitigated by significantly increasing the bin size used in the analysis, however, only at a tradeoff in time resolution. The MIM, on the other hand, is shown to reliably achieve high time resolutions with accurate, well-characterized measurement error.

Figure 1.

Representative intensity-versus-time traces and the corresponding constant time binning (CTB) analysis and maximum information (MIM) analysis for poly-L-proline peptides of lengths P_n = 8, 12, 15 and 24. Single-molecule intensity-versus-time traces are colored blue for donor emission and red for acceptor emission. Dashed vertical lines represent the time at which each dye irreversibly photo bleaches. Red asterisks on the x-axis of the CTB analysis plot represent measurements where the FRET value is ill-defined (greater than 1 or less than zero). Grey boxes in the MIM analysis represent error in the efficiency and time along the x- and y-axes respectively. All trajectories are analyzed with a time resolution of ~1 millisecond.

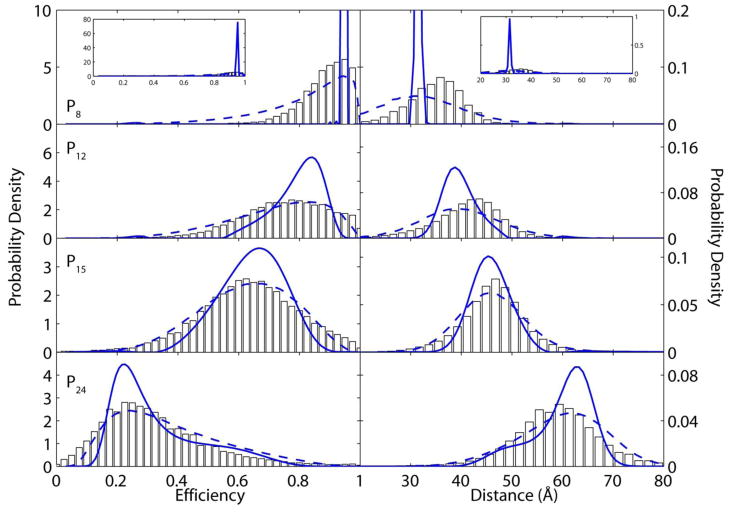
A unique feature of single-molecule FRET experiments is that they can access the underlying distribution of conformational states within a sample rather than simply a single average distance, as is the case for conventional ensemble methods [40]. Figure 2 displays probability density functions (PDFs) calculated for the four proline samples presented in Figure 1 at a mean time resolution of ~4-milliseconds. Each PDF was constructed from more than 200 single-molecule trajectories. Combination of multiple single-molecule time traces is necessary since cis-trans isomerization of proline residues is expected to occur on the timescale of seconds [14] while single-molecule data collection lasts for one second on average. PDFs are calculated according to both CTB analysis (bars) and MIM analysis (dashed blue lines) and displayed as both energy transfer efficiency and distance in Ångströms. Both analysis methods yield similar results: broad, featureless distributions that are difficult to interpret directly. This broadening is caused by photon-counting noise, resulting from the low signal-to-noise ratio of single-molecule fluorescence experiments. Further interpretation of single-molecule PDFs calculated by CTB analysis is commonly achieved by fitting to Gaussian distributions that require an a priori assumption the number of states in the system—yielding potentially biased results since the molecular states are in fact unknown.

Figure 2.

Single-molecule histograms and probability density functions (PDF) for proline peptides of length n = 8, 12, 15 and 24 displayed as both energy transfer efficiency and distance. Histograms created from constant time bin analysis are denoted as white bars. Raw PDFs from maximum information analysis are shown by dashed blue lines. Counting noise-removed PDFs from maximum entropy deconvolution are blue lines with circles. Inset in a. shows the fully deconvoluted PDF. All analyses are presented at a 4-ms mean time resolution.

The known photon-counting uncertainties associated with each measurement in the MIM offers a significant advantage over CTB analysis because experimental noise can be removed from the PDF through maximum entropy deconvolution. This statistically robust technique allows removal of broadening introduced from both experiment and data processing and reveals the true underlying distance distribution in an unbiased, model free manner [34]. In particular, the distance uncertainty due to photon-counting noise can be deconvoluted because of its know Poisson distribution. Deconvoluted PDFs for the poly-L-proline samples are displayed as solid blue lines in Figure 2. These deconvoluted distributions contain detailed information about the conformational states of poly-L-proline peptides, which were otherwise obscured by noise. For instance, it is evident that the conformation of poly-L-proline P₈ is nearly homogeneous as evidenced by its sharply peaked delta function-like distribution. The other poly-L-proline samples investigated have finite widths, which are indicative of a broad distribution of conformations amongst molecules in these experiments. Interestingly, poly-L-proline P₂₄ clearly displays a bimodal distribution with a shoulder towards shorter distances. These detailed insights into the conformational propensities of poly-L-proline are only possible with the advances in automated data acquisition and model-free analysis afforded by the MIM.

5.2. Consistency with ensemble-averaged FRET experiments

The steady-state, ensemble-averaged FRET (red line, Figure 3) was measured for each poly-proline sample and the resulting distances were compared to the mean distance measured by single-molecule methods (blue line, Figure 3). The quantitative agreement between the results of these experiments indicates that neither the behavior of the fluorescent probes or the poly-L-proline molecules is significantly affected by the immobilization strategy, lending additional support for the accuracy of single-molecule measurements. This data also highlights the discrepancy between the experimental distances measured for poly-L-proline and the maximum end-to-end distances expected for an ideal, all-trans poly-L-proline helix (dashed black line, Figure 3). This model was calculated assuming the crystallographic value of a 3.12-Å rise for each proline monomer in the chain [19] and does not take into account the additional distance added by the dye and the dye-linker chemistry. The additional distance contribution from the dye likely explains why poly-L-proline P₈ has a measured distance slightly longer than predicted by the ideal, all-trans case. However, the other poly-L-proline samples investigated are significantly shorter than predicted by the ideal all-trans poly-L-proline model. The compaction is most striking in the case of poly-L-proline P₂₄ where the measured distance is ~15-Å less than the idealized all-trans distance. This deviation from ideal behavior has been widely reported in FRET experiments of poly-L-proline peptides [29, 31–35] and will be the focus of the remainder of the current report.

Figure 3.

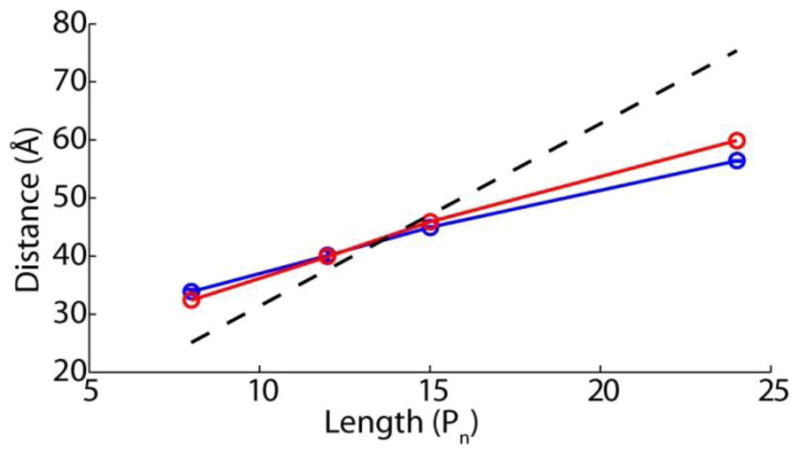
Comparison of steady-state bulk FRET with mean distances from single-molecule experiments (blue curve). For comparison, the predicted end-to-end distances for perfectly rigid poly-L-proline have been included (dashed black line); no correction has been made for additional distance contributions expected from dyes and dye-linkers.

5.3. Mean end-to-end distance cannot distinguish competing theoretical models

Having established the accuracy of high-resolution single-molecule experimental methods, poly-L-proline PDFs can now be used to investigate the structure of these peptides in solution. Of specific interest is that the observed relationship between the mean end-to-end distances does not follow the trend predicted by an all-trans type-II poly-L-proline structure (Figure 3). Three scenarios have been proposed to explain this observation: 1) non-ideal energy transfer resulting in a mis-estimation of Förster radius or distance [30, 33, 35], 2) flexibility of the poly-L-proline helix resulting in a misestimation of persistence length, and 3) introduction of cis-isomers causing discrete kinks in the otherwise all-trans poly-L-proline helix [31, 32, 34]. The experiments presented in the previous section and in Supplementary Information strongly suggest that the first scenario, non-ideal energy transfer due to surface immobilization, is not the cause of the observed discrepancy. The other two scenarios represent two distinct physical pictures for the behavior of the poly-L-proline helix at the microscopic level.

Statistical models are a common framework for describing the behavior of polymers in solution. Although these models are valid only in the limiting case of infinitely long polymers, they are nonetheless frequently applied to short peptides, including short poly-L-proline peptides in solution [30, 32–34]. A potential strategy to contrast these models is to use them to calculate the mean end-to-end distance as a function of poly-L-proline contour length and compare the mean distance profiles with experimental data to discriminate different models. However, with only two fit parameters parameters, persistence length and additional distance from dye linker from FRET probes, as seen in Figure 4, the mean distance predicted by WLC (red line), FJC (green line) and SAC (light blue line) models all adequately describe the mean single-molecule experimental distances as a function of poly-L-proline chain length (blue circles). Therefore, simply comparing mean distance profiles cannot single out a statistical model that describes the structures of short poly-L-proline peptides in solution.

Figure 4.

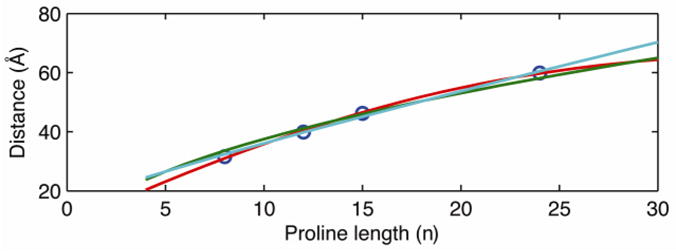
Mean distances alone cannot discriminate different polymer models. Fit of the mean distances from single molecule probability density functions (PDFs, blue circles) from Figure 2 to the mean values predicted by the worm-like chain (WLC, red line), self-avoiding chain (SAC, light blue) and freely jointed chain (FJC, green line) statistical polymer models.

5.4. Conformational distribution as an enabling parameter to discriminate theoretical models

The parameters used to fit the mean distances for the models in Figure 4 can also be used to construct a probability distribution (p(R), see Supplementary Information), which can be compared directly to the experimentally measured PDFs. As shown in Figure 5, compared to the FJC and the SAC models, the WLC model (red line) predicts a relatively narrow distance distribution skewed towards shorter distances. Though the WLC model predicts somewhat similar distribution widths and distances to the experimental data, agreement between theory and data is not definitive. The skewed shape predicted by the WLC model is only seen in the poly-L-proline P₂₄ experimental distribution whereas the rest of the experimental data are rather symmetric. Even in the case of poly-L-proline P₂₄, the agreement with experimental data is only qualitative. The tails of the distribution predicted by the WLC model extend beyond that in the observed PDF by 10 Å. Furthermore, a region predicted to have significant density between 70–80 Å by the WLC model has no population in the measured PDF. The FJC (green line) and SAC (light blue) models both predict a very broad and symmetric distribution of distances that are a poor fit to experimental data. For example, using the parameters from fitting the mean end-to-end distances, both models predict the existence unphysical distances that are too long or short for the investigated poly-L-proline samples. Existence of these non-physical distances in the radial distribution functions for the FJC and SAC models likely arises from their application to short polymers where the underlying assumptions—namely an infinetly long polymer—are no longer applicable. Comparing with single-molecule PDFs reveals that none of the examined statistical models is adequate to describe the end-to-end distance distributions of short poly-L-proline peptides. The results presented in this section thus strike a cautionary note about the hazards of inferring the structural information of short polymers using standard statistical polymer models. Moreover, it is evident that distributions measured by high-resolution single-molecule experiments are a critical parameter in characterizing the mechanical properties of molecules. It would otherwise be challenging, if not impossible, to differentiate different statistical models solely based on ensemble data or even the usual shot-noise inundated single-molecule end-to-end distributions.

Figure 5.

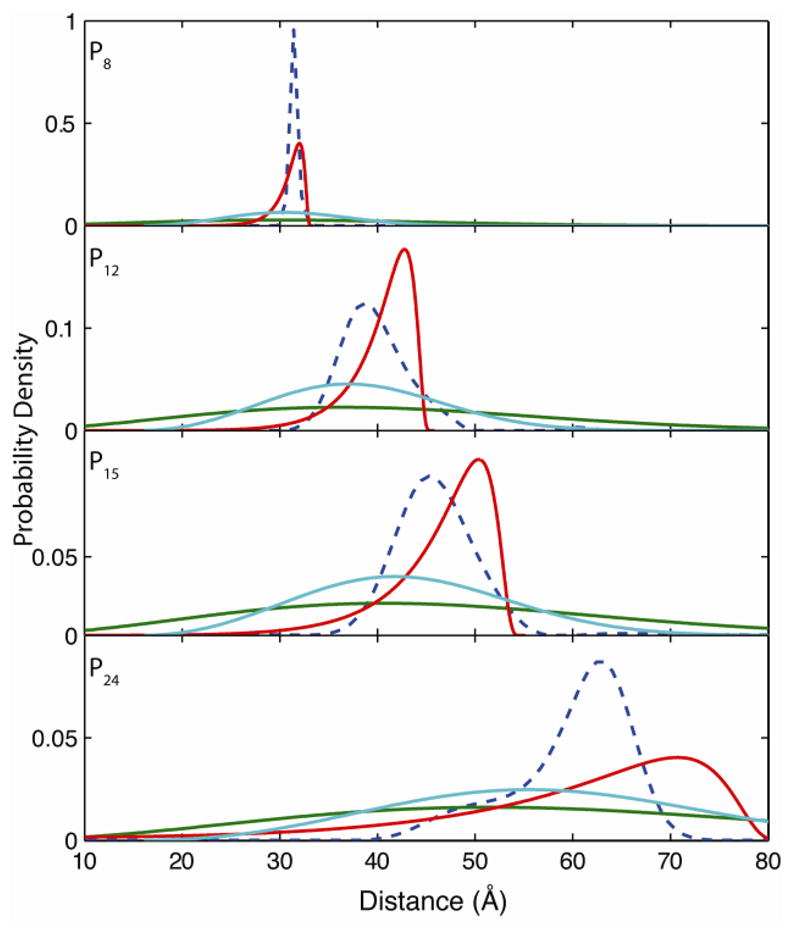
Distance distribution as an effective measure to discriminate different polymer models. Distance distributions predicted by WLC (red), SAC (light blue), and FJC (green) polymer models using fitting parameters from Figure 4 and compared to experimental PDFs (dashed blue line). All models predict broader distributions than observed experimentally with the FJC and SAC models predicting physically unreasonable distances.

5.5. Length-dependent flexural rigidity of short poly-L-proline peptides

For each poly-L-proline length, it is possible to obtain the effective persistence length l_p and the apparent contour length L_eff by fitting the measured distribution to the numerical solution of the worm-like chain model that are amenable to all lengths [70]. The results are summarized in Figure 6. As expected, the effective contour length increases with the number of proline units. The most likely values for the effective persistence lengths and the uncertainties associated with those values were estimated using the bootstrap simulation on the experimentally measured distributions and the uncertainties of them. The most likely persistence length of P₈ was found to be 190 Å with a 68% confidence interval of (lower-bound 110 Å, upper-bound 310 Å). The uncertainties are relatively high because of the limited data points in P₈. Interestingly, the persistence length derived from single-molecule data for P₈ is consistent with the previous estimation of 220 Å for all-trans poly-L-proline peptides [71–73]. The effective persistence length precipitously drops to 67 Å (33 Å, 150 Å) and 50.6 Å (48.8 Å, 52.0 Å) for P₁₂ and P₁₅, respectively. Within the experimental error, the effective persistence lengths for these two proline sizes are indistinguishable. Interestingly, from P₁₅ to P₂₄, the effective persistence length increases from 50.6 Å to 75.6 Å (73.5 Å, 78.7 Å). Length dependent persistence length has been reported previously for microtubules[13] as well as by analysis of crystal structures of proteins, DNA and RNA [74, 75]. In these cases, an increase in persistence length is attributed to increasing number of non-local interactions with chain length. Though intra-chain hydrogen bonding is not predicted to be present in poly-proline peptides, steric considerations and volume exclusion could be predicted to dominate non-local interactions.

Figure 6.

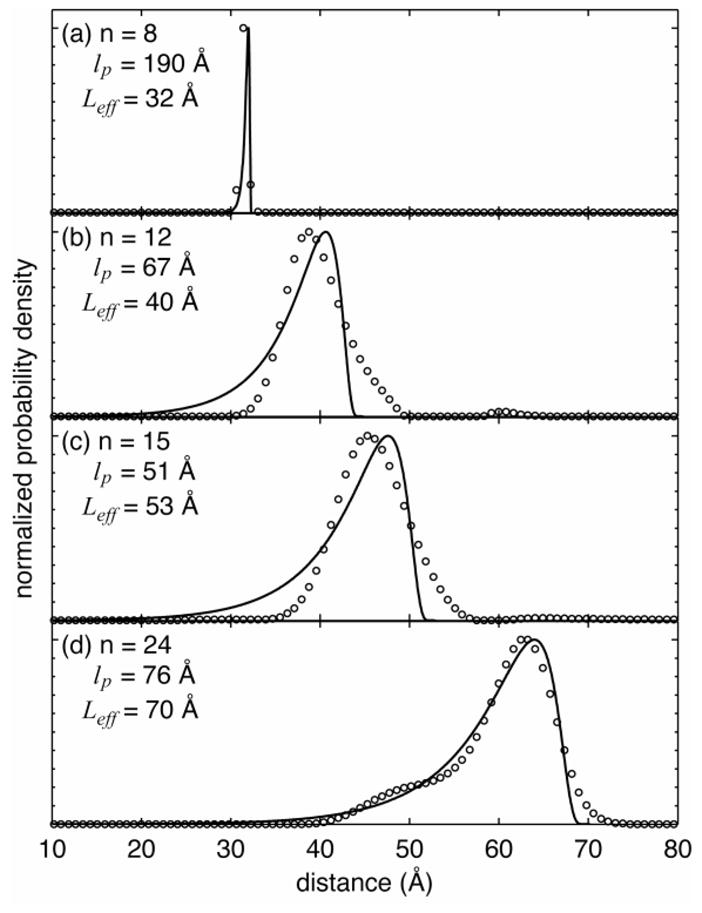
Chain-length-dependent flexural rigidity revealed by molecular conformation distributions. The open circles are experimental data and the solid lines are fits to the full-width half-maximum of the semi-flexible chain model, from which the effective persistence lengths (l_p ) and apparent contour lengths ( L_eff ) were estimated.

5.6. Insights from comparison with molecular modeling

In order to formulate a physical picture, molecular models of poly-L-proline containing single cis isomers were constructed (see Supplementary Information for computational details). Figure 7 presents sample energy-minimized structures of two poly-L-proline P₈ isomers. Figure 7a shows the all-trans configuration and Figure 7b shows the configuration after introducing a single cis ω angle at position 4. Figure 7b illustrates the shortened end-to-end distance expected when a trans-to-cis isomerization occurs at a single proline ω angle. Energy minimized poly-L-proline molecular models were constructed for the all peptide constructs used in single molecule experiments with a cis ω isomer at each residue position of the peptide backbone. An additional set of molecular models was also constructed for each poly-L-proline peptide to determine the structure when two cis ω residues are present.

The end-to-end distances represented by poly-L-proline molecular models cannot be directly compared with single-molecule FRET experiments due to the distance added to the experimental measurements by the dye and dye-linker. For instance, the measured distance for poly-L-proline P₈ by single-molecule FRET is 32 Å while the maximum end-to-end distance predicted by the all-trans P₈ model is 23 Å (Figure 3), presumably due to the additional distance contribution added by the dye itself. In order to better compare molecular models with single-molecule experiments, a molecular model of all-trans poly-L-proline P₈ with the dye molecules attached was also developed (Figure 7c, see Supplementary Information for details). Since single-molecule polarization experiments indicated that the dyes are freely rotating on the experimental timescale (see Supplementary Information Figure S3), we assume that the main contribution to the inter-dye distance arises from configurational and steric considerations rather than from long-lived, stable interactions between dye and peptide. In order to address this contribution, an ensemble of allowable configurations of the attached dye was scanned by rotating each sp³ hybridized bond in the dye linker through the three lowest energy rotamers followed by energy minimization. Since each dye molecule attached to the end of the poly-L-proline has a total of six sp³ hybridized bonds, a total of (3⁶ = 729)² = 531, 441 possible dye configurations were scanned. The average position of each dye was then calculated by taking the spatial mean of the central methine atom in the cyanine-like moiety of the dye over the entire ensemble of allowed configurations. Figure 7d shows the results of this calculation superimposed on an all-trans poly-L-proline P₈ structure. The positions of each dye in the 729 permutated configurations are shown as a cloud of points in Figure 7d. The yellow arrow represents the mean dye vector calculated from the full ensemble of 531,441 configurations. These mean dye vectors are then projected onto the full set of poly-L-proline models generated by scanning cis-isomers in order to facilitate comparison between molecular modeling and single-molecule end-to-end distance distributions.

The end-to-end distances of cis-isomer scanning calculations are used to label the experimentally measured single-molecule PDFs (blue curves) in Figure 8. Without considering the relative free-energy differences of the scanned cis-isomers, the end-to-end distances calculated from all energy-minimized structures are assembled as histograms in Figure 8: the all-trans poly-L-proline in red, cis scanning with a single cis-isomer are white and a double cis-isomer scanning is grey. The histograms of calculated distances are not to directly compare with the actual population of the end-to-end distances of proline isomers with single-cis or dual-cis configurations but to illustrate the extent by which the end-to-end distance can vary due to the presence of one or two cis ω angles. Furthermore, the calculated energetics of minimized isomers are not drastically different, mostly within 2% of the average potential energy using an implicit solvent model. The approximation that all energy minima of the single- and dual-cis isomers of poly-L-proline are equally populated certainly needs to be refined if a quantitative comparison with single-molecule experiments is desired.

Figure 8.

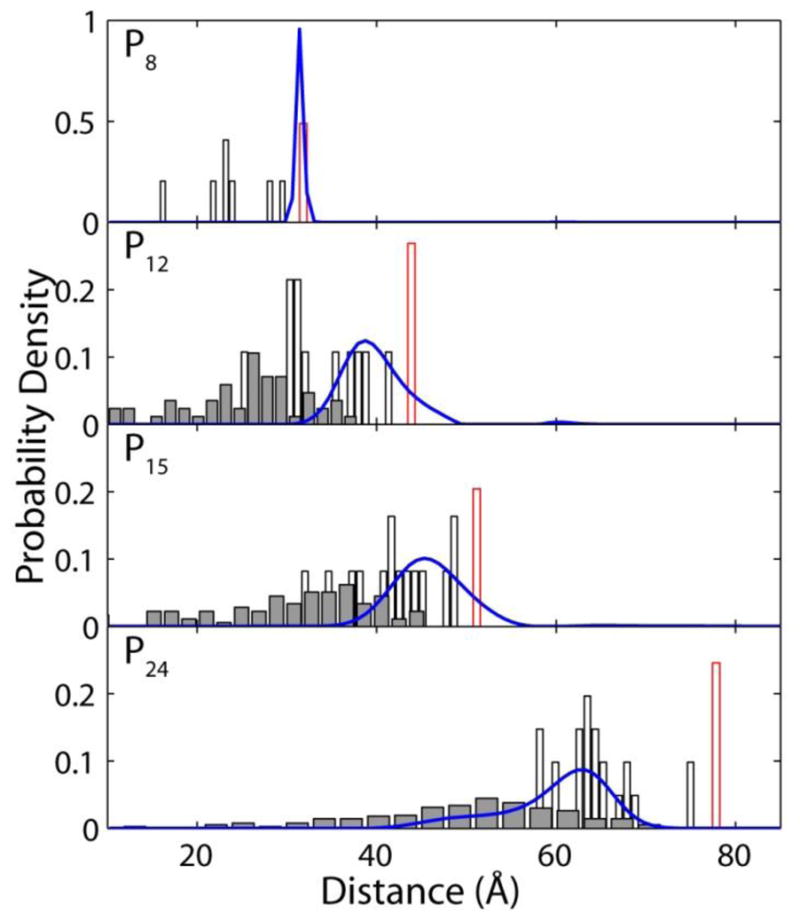
Single-molecule probability density functions compared with results of molecular dynamics simulations. White bars represent distances predicted from poly-L-proline peptides with a single cis-isomer, red outlines represents the predicted distances for all trans poly-L-proline and grey bars represent simulations with two cis isomers. Additional distance correction was made in addition to the end-to-end proline distance to account for distance added by dye and linkers as discussed in the text. Results emphasize the non-statistical distribution of cis-isomers in short poly-L-proline peptides.

Despite the simplification and approximation employed in our molecular modeling strategy to probe the cis-isomer structures of poly-L-proline, it provides several important insights for interpreting the PDFs measured from single-molecule experiments. For instance, the optimized molecular structures of the isomers of poly-L-proline P₈ indicate that the all-trans isomer is in very close agreement with the distances measured by single-molecule experiments without any adjustable parameter. The calculated end-to-end distances of the two isomers with a cis ω configuration at the N- and C-terminal proline residues also agree with the measured distances. Therefore, the structural picture afforded by molecular modeling and the measured PDF suggests that the shortest poly-L-proline P₈ peptide examined with single-molecule experiments prefers only the most extended conformations while internal cis-isomers within the proline chain are not likely. This result is also consistent with the semiflexible model discussed in the previous section, which suggests that P₈ exhibits a persistence length of ~190 Å, on the same ~200-Å order as previously reported persistence length for all-trans poly-L-proline peptides.

By contrast, comparison of the molecular models with the single-molecule results for longer poly-L-proline samples suggests a significant population of structures containing cis ω isomers at internal residues. While the end-to-end distances calculated from the all-trans molecular structures of poly-L-proline P₁₂ and P₁₅ overlap with the experimental distribution, the end-to-end distances of isomer models with a single cis ω are closer to the peak of the experimental distribution shown in Figure 8. This result suggests that the solution structure of P₁₂ and P₁₅ contains a dominant portion of isomers with at least a single cis ω angle. Though some of the molecular structures containing double cis-isomers for P₁₂ and P₁₅ overlap with the experimentally measured distribution, most of the double-cis structures have significantly shorter end-to-end distances experimental values. Therefore, the population of isomers with double cis ω angles in P₁₂ and P₁₅ is likely very small.

Poly-L-proline P₂₄, the longest proline studied, also shows the most surprises. Comparing the measured distribution of end-to-end distances and those calculated from molecular structures suggests that P₂₄ is unlikely to access the all-trans conformation. The experimentally measured distribution only extends to 70 Å while the calculated all-trans distance is nearly 80 Å. On the other hand, the experimentally measured end-to-end distance distribution predominantly overlaps with the calculated distances from molecular structures containing a single cis-proline residue. Furthermore, there is a significant population of more compact conformations of P₂₄, as evidenced by the shoulder in the single-molecule PDF. This shoulder coincides quite well with the distances calculated from molecular models containing two cis ω isomers. Therefore, the experimental distance distribution for P₂₄ can only be described by a mixture of configurations including both one and two cis isomers. By fitting the single-molecule PDF to two Gaussians we can estimate that ~75% of the P₂₄ molecules contain a single cis isomer while ~25% contain two cis isomers. This simple picture estimates that the overall fraction of the total residues in poly-L-proline P₂₄ with cis ω isomers is ~5% in buffer, which is in reasonable agreement with previous NMR estimates of 2–3% in D₂O [32, 39].

The comparison of proline molecular models with single-molecule experiments reveals specific structural features of poly-L-proline in solution. While the shortest poly-L-proline P₈ favors a nearly all-trans structure without internal cis ω isomers, these structures apparently become more favorable in longer peptides as observed for P₁₂, P₁₅ and P₂₄. Only the longest poly-L-proline P₂₄ studied shows evidence of a significant population of molecules containing two cis ω isomers, while at this length the all-trans isomer is likely to be rarely visited.

5.7. The physical picture for short poly-L-proline peptides

The physical picture for short poly-L-proline peptides that emerges from the above discussion refines our original model (cf. Figure 11 in [34]). For very short lengths, P_n<=8, the proline peptide can be very well regarded as all trans with an effective persistence length comparable to 200 Å. At longer chain lengths, n = 12 and 15, the otherwise all-trans proline peptides have a significant likelihood of one cis isomer. The flexibility of the polyproline with a cis isomer is the primary reason why the effective persistence lengths for P₁₂ and P₁₅—a manifestation of the distribution of different conformations on the 4-ms experimental timescale—are significantly shorter compared to that for P₈. As the chain length becomes longer, the probability for the molecule to acquire more than one cis residue becomes greater. P₂₄, for example, likely acquires two cis residues at room temperature while the majority of P₂₄ (75%) exists with one cis residue with a distribution mode at ~62 Å. To understand the increase in the effective persistence length of P₂₄ compared to that of P₁₅, we note that the effective persistence length of P₂₄ is deduced primarily from the one-cis distribution (cf. Figure 6) and reflects the mechanical strength of the one-cis isomer of P₂₄. Assuming a random distribution of the cis isomer location in P₂₄, The extent of consecutive all-trans repeats in the one-cis P₂₄ isomers is expected to be greater than that in P₁₅, and therefore exhibiting a greater effective persistence length. While it seems reasonable to suggest that poly-L-proline persistence length would approach a limiting value at longer chain lengths, data from this work does not permit a strong statement on this issue.

6. Conclusions

In this work, we propose to use conformational distributions to characterize the mechanical properties of individual molecules. This approach is demonstrated by using the high-resolution and model-free single-molecule FRET measurements. A series of poly-L-proline peptides is analyzed to illustrate the unique capability of this approach to establish the accuracy of statistical models to predict mechanical properties of short polymers at the molecular scale. We first show that the mean end-to-end distances, as commonly used in the past, cannot distinguish competing theoretical models. We then show that the conformational distribution provides rich information that permits discrimination of theoretical models. Importantly, the idea of using the conformational distribution as a tool for molecular-level mechanics uncovers the previously unknown chain-length-dependent flexural rigidity in poly-L-proline peptides. By integrating experimental observations with a comprehensive set of molecular modeling, we depict a structural picture explaining the roles of cis residues and ω-angle isomerization in the chain-length-dependent persistence length in poly-L-proline peptides. The present work thus demonstrates the power of using the conformational distribution for resolving the mechanical properties of macromolecules as well as highlighting the potential of combining high-resolution single-molecule methods and molecular modeling to provide previously unattainable molecular insight. Looking forward, the results provide an approach to achieving a predictive understanding of protein molecular machines.

Research Highlight.

A mechanical view provides an attractive alternative for predicting the behavior of complex systems since it circumvents the resource-intensive requirements of atomistic models; however, it remains extremely challenging to characterize the mechanical responses of a system at the molecular level. Here, the structural distribution is proposed to be an effective means to extracting the molecular mechanical properties. End-to-end distance distributions for a series of short poly-L-proline peptides with the sequence PnCG3K-biotin (n = 8, 12, 15 and 24) were used to experimentally illustrate this new approach. High-resolution single-molecule Förster-type resonance energy transfer (FRET) experiments were carried out and the conformation-resolving power was characterized and discussed in the context of the conventional constant-time binning procedure for FRET data analysis. It was shown that the commonly adopted theoretical polymer models—including the worm-like chain, the freely jointed chain, and the self-avoiding chain—could not be distinguished by the averaged end-to-end distances, but could be ruled out using the molecular details gained by conformational distribution analysis because similar polymers of different sizes could respond to external forces differently. Specifically, by fitting the molecular conformational distribution to a semi-flexible polymer model, the effective persistence lengths for the series of short poly-L-proline peptides were found to be size-dependent with values of ~190 Å, ~67 Å, ~51 Å, and ~76 Å for n = 8, 12, 15, and 24, respectively—the first experimental evidence of such behavior on the molecular level. A comprehensive computational modeling was carried out to gain further insights for this surprising discovery. It was found that P8 exists as the extended all-trans isomaer whereas P12 and P15 predominantly contained one proline residue in the cis conformation. P24 exists as a mixture of one-cis (75%) and two-cis (25%) isomers where each isomer contributes to an experimentally resolvable conformational mode. This work demonstrates the resolving power of the distribution-based approach, and the capacity of integrating high-resolution single-molecule FRET experiments with molecular modeling to reveal detailed structural information about the conformation of molecules on the length scales relevant to the study of biological molecules.