Improved MR-based characterization of engineered cartilage using multiexponential T₂ relaxation and multivariate analysis

Abstract

Noninvasive monitoring of tissue quality would be of substantial use in the development of cartilage tissue engineering strategies. Conventional MR parameters provide noninvasive measures of biophysical tissue properties and are sensitive to changes in matrix development, but do not cleanly distinguish between groups with different levels of matrix development. Furthermore, MR outcomes are nonspecific, with specific changes in matrix components resulting in changes in multiple MR parameters. To address these limitations, we present two new approaches for evaluation of tissue engineered constructs using MR, and apply them to immature and mature engineered cartilage after 1 week and 5 weeks of development, respectively. First, we applied multiexponential T₂ analysis for quantification of matrix macromolecule-associated water compartments. Second, we applied multivariate support vector machine (SVM) analysis using multiple MR parameters to improve detection of degree of matrix development. Classification of samples based on individual MR parameters, T₁, T₂, k_m, or ADC, showed that the best classifiers were T₁ and k_m, with classification accuracies of 85% and 84%, respectively. SVM analysis improved accuracy to 98% using the combination (k_m, ADC). These approaches were validated using biochemical and Fourier transform infrared imaging spectroscopy analyses, which showed increased proteoglycan and collagen with maturation. Monoexponential T₂ values decreased with maturation, but without further specificity. Much more specific information was provided by multiexponential analysis. The T₂ distribution in both immature and mature constructs was comparable to that of native cartilage. The analysis also showed that proteoglycan-bound water increased significantly during maturation, from a fraction of 0.05±0.01 to 0.07±0.01. In summary, multivariate SVM and multiexponential T₂ analysis provide improved sensitivity to changes in matrix development and specificity to matrix composition in tissue engineered cartilage. These approaches show substantial potential for evaluation of engineered cartilage tissue as well as extension to other tissue engineering constructs.

Introduction

Development of techniques to repair damaged cartilage has been the subject of extensive research (1-3). However, long-term outcomes have remained disappointing, so that development of functional engineered replacement tissues for cartilage remains an important avenue of investigation.

Successful growth of an engineered replacement for cartilage requires appropriate stimuli to yield tissue with molecular, biochemical and biomechanical properties which approach those of native tissue (4). Engineered cartilage would ideally have the appropriate amounts of the primary matrix components, type II collagen and aggrecan, and water, and exhibit structural organization that promotes proper functional characteristics. However, there remains no consensus as to the optimal approach to achieve these goals when engineering cartilage replacement tissue.

A key component in the design of optimal cartilage tissue engineering strategies will be development of appropriate methods for evaluating engineered constructs. Standard techniques such as biochemical assays and histology are invasive and destructive. This precludes longitudinal evaluation, limiting the ability to monitor the constructs during development and modify growth conditions.

MRI has emerged as a non-invasive modality that permits in vivo evaluation of engineered tissue constructs during growth. Although previous studies have established correlations between MRI parameters such as T₁, T₂, magnetization transfer (MT) and apparent diffusion coefficient (ADC) and biochemical properties of tissue engineered constructs (4-7), these parameters are highly nonspecific measures of matrix composition. For instance, T₁ and T₂ were both found to significantly correlate with GAG, collagen and water content in engineered cartilage (5,6) showing a lack of specificity for any single matrix component. Similarly, magnetization transfer rate, k_m, although primarily sensitive to collagen content (6), is also correlated with GAG concentration in cell-seeded gelatin sponges (8). T₂, although readily measured, varies as a function of macromolecular content, tissue orientation, and hydration (7,9-11). Thus, individual conventional MRI parameters are sensitive but nonspecific to matrix macromolecular composition.

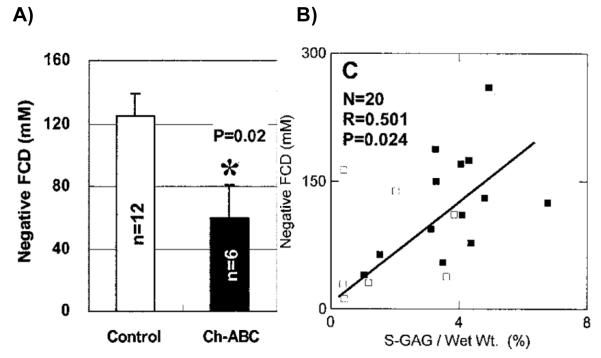
There are additional complications in the use of MRI outcome measures as a surrogate for tissue status. Relationships between MR parameters and cartilage pathology have been extensively documented, and analysis of parameter means between control and experimental or disease groups indicates whether there is a statistically significant difference in that parameter. Such group differences have been found in many circumstances. However, these measurements are of limited specificity; there can be a great deal of overlap observed between values measured in normal cartilage and degraded cartilage. This has been observed in the setting of cartilage tissue engineering as well. Using chondrocyte-seeded hollow fiber bioreactors, we have previously observed significant differences in dGEMRIC-derived fixed charge density (FCD) measurements between normal and chondroitinase-ABC treated tissue (Figure 1A) (5). However, the diagnostic usefulness of this observation is highly limited, as is seen from examining the FCD values of individual samples. In Figure 1B, showing the relationship between FCD and sGAG, there is a large overlap between FCD values for the control and the chondroitinase-ABC treated constructs. This raises the important question of whether MR parameter outcome measures can be used to detect, in an individual subject, the presence of disease, such as degenerative changes in the cartilage matrix.

Figure 1.

dGEMRIC derived fixed charge density (FCD) from chondrocyte-seeded hollow fiber bioreactors from (5). A) Mean FCD for control versus chondroitinase-ABC-treated cartilage. B) FCD versus biochemically-determined GAG content.

For these reasons, new approaches to the analysis of tissue engineered cartilage by MRI would be of substantial value. We have approached this problem from two main vantage points.

First, we have used multiexponential transverse relaxation analysis to probe the water microenvironments in developing cartilage in order to assess their mobility and relative size. Relaxation distributions can be obtained through multiexponential analysis using the nonnegative least squares algorithm (12). Since different matrix macromolecules have inherently different molecular mobility, assignment of these water compartments to matrix components can be guided by their relaxation rates. Multiexponential transverse relaxation analysis has applied to a number of tissues, including muscle (13), bone (14), intervertebral disc (15), neural tissue (16,17), and cartilage (18,19). Previously, we have demonstrated a correspondence between specific water fractions and matrix components in native cartilage (20,21). In the present work, we extend this approach to an engineered cartilage tissue system. We identify water compartment fractions and associate them with underlying matrix and scaffold components. In particular, we assign water fractions to our polyglycolic acid (PGA) scaffold material, collagen, proteoglycan, and bulk water.

Our second approach is to implement multivariate analysis of the developing tissue using multiple MR imaging parameters. Given the different physical basis for the various MRI outcome measures, we expect such multivariate analysis to increase our ability to characterize matrix development and tissue quality. Our previous work demonstrated the improvement resulting from multivariate analysis as compared to conventional univariate analysis when distinguishing between normal and degraded cartilage (22). However, our use of a Gaussian mixture model, while effective, requires relatively strict assumptions regarding the underlying structure of the data. In the present work, we extend the multivariate approach using the support vector machine (SVM) classification paradigm (23). The support vector machine has been used in a variety of biomedical classification problems, including distinguishing benign from cancerous tumors and identifying stages of cancer progression (24,25). In this work, we demonstrate its ability to improve accuracy of classifying samples at different stages of matrix development.

To demonstrate these approaches to MR evaluation of engineered cartilage, we use chondrocyte-seeded scaffolds made of PGA, a commonly used scaffold material. MR measurements were made at after 1 and 5 weeks of culture, representing immature and mature constructs, respectively. We use the complementary technique of Fourier transform infrared imaging spectroscopy (FT-IRIS) to obtain quantitative maps of collagen and proteoglycan distribution across the samples. FT-IRIS provides this molecule-specific data with high spatial resolution and has previously been used to assess macromolecular distribution in developing cartilage (26-28) and thus serves as an appropriate technique for comparison with multiexponential T2 analysis. Finally, we also interpret our results in terms of biochemical analyses of sGAG and water content.

Materials and Methods

Fabrication of cartilage constructs

Chondrocytes were isolated from cartilage harvested from immature bovine stifle joints after an 18hr-digestion using 0.15% collagenase type II (Worthington Biochemicals Co., Lakewood, NJ) in Dulbecco’s modified Eagle’s medium (DMEM, Invitrogen) supplemented with antibiotics. The digest was filtered through a 100 μm nylon filter; the isolated chondrocytes were washed twice with phosphate buffered saline (PBS, Invitrogen). Total cell count and viability were determined using the Trypan blue dye exclusion assay.

PGA fibrous felts (2 mm-thick, Biomedical Structures) were cut into 6 mm disks. The PGA disks were sterilized by immersion in 70% ethanol for 8 hours, rinsed in sterile PBS and dried overnight in a laminar flow hood. 3.5 inch-long, 16-gauge needles (Fisher Scientific) were fixed to silicone stoppers and placed in the mouths of spinner flasks. The needle-stopper-flask assembly was steam-sterilized for 30 min at 121°C. PGA disks were threaded onto the needles and placed 4 mm apart using silicon tubing spacers. For preconditioning, the PGA disks were placed in culture medium in spinner flasks and stirred in a humidified incubator for 18 hours. A suspension of chondrocytes was then injected via the sidearm of the flasks and stirred for 48 additional hours. The final concentration was 15 × 10⁶ cells per scaffold.

Constructs were cultured for up to 5 weeks in DMEM-filled six-well plates with 10% fetal bovine serum, 2 mM glutamine (Invitrogen), 0.2% penicillin/streptomycin (Invitrogen), 0.25 μg/ml fungizone (Invitrogen), 50 μg/ml gentamicin (Invitrogen), 0.1 mM non-essential amino acids, 0.4 mM L-proline (Sigma) and 50 μg/ml L-ascorbic acid-2-phosphate (Sigma). Culture media was changed three times per week.

In order to account for signal originating from the PGA scaffold and distinguish it from matrix deposition, preconditioned empty PGA scaffolds were prepared and stored in an incubator for three days and analyzed.

MRI measurements

MR data were acquired at 4°C using a 9.4T/105-mm Bruker Avance III spectrometer (Bruker Biospin GmbH, Rheinstetten, Germany).

Non-localized T2 measurements

Each sample was placed into an NMR tube containing Fluorinert (catalog number F-4758, Sigma-Aldrich, St. Louis, MO, USA) to maintain sample hydration and eliminate MR signal contamination by bath solution. Relaxation data were obtained with a 5 mm solenoid coil using a non-localized CPMG pulse sequence with a two-step phase cycle 90_{(x, x)}/180_{(y, -y)}, and with sampling of a single point from the top of each echo. Acquisition parameters included TE/TR = 90 μs/10 s, 16,384 echoes, and number of excitations (NEX) = 64. SNR ranged from 8,983 to 20,283.

MR imaging

Experiments were performed with a 30-mm proton birdcage resonator. Up to six samples were threaded onto a tube through a 2.5 mm hole, and inserted into each well of a susceptibility-matched four-well sample holder containing Fluorinert. Images were taken from 0.5 mm-thick sagittal slices through the center of each of the 4 wells, permitting all samples within each well to be imaged simultaneously (Figure 2). T₂ data were acquired using a 64-echo CPMG pulse sequence with TR/TE = 5 s/12.8 ms. T₁ imaging data were acquired using a progressive saturation spin-echo sequence with TE = 12.8 ms, with TR ranging between 100 ms and 15 s in 12 steps. Magnetization transfer (MT) imaging data were obtained using the same spin-echo sequence preceded by a 6 kHz off-resonance saturation pulse of amplitude B₁ = 12 μT and pulse length t_p incremented from 0.1 to 4.6 s in 8 steps. Other MRI parameters included BW = 50 kHz, NEX = 2, FOV = 4.0 × 1.5 cm (read × phase encode), matrix size = 256 × 128, and resolution = 156 × 117 μm.

Figure 2.

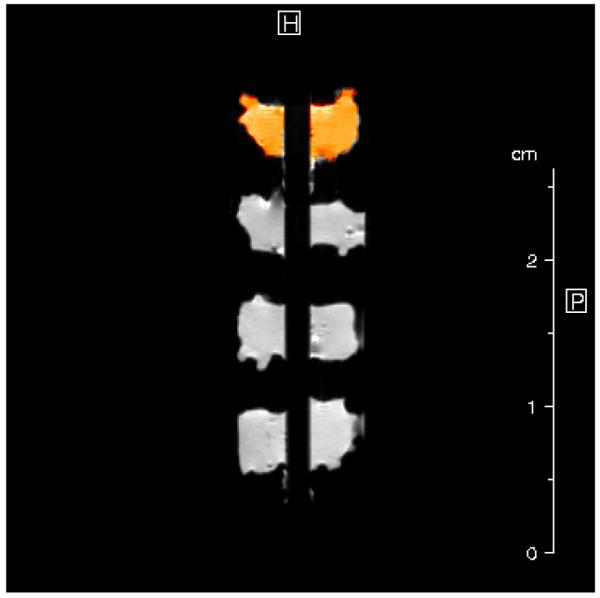
Mid-sagittal MR image of four engineered cartilage constructs threaded on a hollow tube, stacked vertically in one well of the four-well sample holder. The orange highlighted region represents the selected region of interest (ROI) of the top sample for MR parameter determination.

Signal intensity was averaged over all pixels in a region of interest (ROI) covering an entire PGA construct (Figure 2). Averaged intensities were then fit to appropriate three-parameter monoexponential functions to obtain T₁, T₂, MT ratio (MTR), and the magnetization transfer rate k_m for each sample.

Fitting of T₂ relaxation data

The non-negative least squares (NNLS) approach was used for multiexponential T₂ analysis as previously described (19). This approach makes no a priori assumptions about the number of relaxation components present. 80 possible T₂ values were logarithmically spaced over the interval [0.01, 3000] ms. Regularization of NNLS fits was performed such that the chi-squared (χ²) value from the regularized fit was 101% of the χ² from the non-regularized fit (29). The first moments and associated fractions for each T₂ component were calculated. These T₂s and component fractions were interpreted in terms of matrix composition. All fitting routines were implemented in MATLAB (MathWorks, Natick, MA, USA).

Simulation of T₂ Relaxation Data

Analysis of simulated data using the parameters corresponding to the non-localized experiments, TE = 90μs and 16,384 echoes, was performed to ensure the reliability of our results. Data were simulated based on the average experimental values for the component T₂s and weights (see below) using the following expression (19):

$$y(n\cdot \mathit{TE})=B+y_0\sum _{m=1}^M{w}_m\cdot e^{-(n\cdot \mathit{TE})∕T_{2,m}}+\epsilon (0,\sigma ),$$ (1)

where y(n ·TE) is the amplitude of the n^th echo, B is a baseline offset, y₀ is the overall signal amplitude, w_m is the fractional weight of the m^th T₂ component, and ε(0,σ) is additive Gaussian noise with mean 0 and standard deviation σ. SNR, defined as y₀ /σ, was set to the average of the values obtained for three day (unseeded), immature, and mature samples, which were 12,204, 11,348, and 15,060, respectively. The reliability, accuracy, and precision of the results for component T₂s and weights were evaluated over 100 trials for each SNR value. Reliability was defined as correctly identifying the number of T₂ components, accuracy was defined by percent error of the derived T₂s and weights, and precision was defined as the coefficient of variation (CV) of the identified component T₂ values and associated weights over the 100 trials.

Assessment of classification accuracy

Classification according to tissue maturity was performed based on the quantitative imaging data. 48 total samples (n=24 for immature samples and n=24 for mature samples) were randomly divided into a training set (equal to 2/3 of the total) and validation set (equal to the remaining 1/3 of the total) (30). To reduce potential bias introduced by a particular random selection of the training set, 100 independent realizations of random training set selection were performed for each analysis. Two classification approaches were applied to the data: i) assignment based on arithmetic means (9) and ii) the support vector machine. Both analyses were performed using the e1071 package written in the R language (31).

Classification accuracy, defined as the number of samples correctly assigned divided by the total number of samples, is taken as the average over the 100 trials as specified and was calculated independently for the training and validation sets.

Assignments using arithmetic means of individual MRI parameters

The mean value of a specified MRI parameter was calculated for immature and mature samples in the training set. Each sample in the validation set was then classified as immature or mature, depending on which of these two means its MRI parameter value was closer to. Classification accuracy was reported for both training and validation sets, with the training set accuracy indicating the maximal ability of arithmetic means to distinguish sample maturity status.

Assignments using multiparametric SVM clustering

The SVM algorithm as applied in this work defines a decision hyperplane between two groups of points, with each point representing a sample, with position x, defined by sample characteristics in a multiparametric feature space (32). The hyperplane is expressed as the inner product of the feature space coordinates x and a normal vector wwhich defines the perpendicular to the hyperplane, with an offset b from the origin, that is, it is defined by w · x − b = 0 . The oriented hyperplane maximizes the separation 2/∥w∥ between the two groups. The optimization problem is approached using the method of Lagrange multipliers, with constraints w · x − b = ±1 defining the margin between the two groups. Although completely accurate separation between the two groups may not be possible, imposition of a penalty function for misclassified samples results in a well-posed problem. An adjustable parameter, C, defines the penalty associated with misclassified samples. A larger value of C increases the penalty for misclassification, and therefore results in a narrower margin between support vectors of the two groups to be distinguished. This, however, results in a less generalizable discriminant function that can lead to a decrease in performance in a validation set as compared to the training set. In accordance with the SVM algorithm as implemented in the e1071 package, training set data were transformed from their original space, as defined by the MRI parameters selected to describe the samples, into a higher dimensional feature space in which the optimal separating hyperplane could be determined by solving a convex optimization problem (32). This is achieved through use of a kernel function that defines a dot product within the transformed feature space (33). We selected the widely-used Gaussian radial basis function, K(X, X’) = ex p∥X(−X’ ∥²/ σ) , which depends upon a single adjustable parameter, σ , defining its extent and curvature (34,35). The values for σ and C were determined by the criterion of minimizing the classification error (36). Finally, an estimate of the probability that a data point belongs to one of the two classes defined by the SVM decision hyperplane can be calculated from a sigmoidal distance function that equals 0.5 for points on the decision hyperplane and approaches ± 1 with increasing directed distance from the decision hyperplane (32,37).

Fourier Transform Infrared Imaging Spectroscopy (FT-IRIS)

After imaging, PGA constructs were embedded in paraffin and thin sections (9 μm) were obtained and mounted directly onto low e slides (Kevley Technologies, OH). Tissue sections were deparaffinized in Xylene and air-dried for data acquisition. Spectra and images of the entire sections were obtained using the Perkin Elmer Spotlight 400FTIR Imaging system (Perkin Elmer, Shelton, CT) with 8 wavenumber (cm⁻¹) spectral resolution in the range of 4000 to 748 cm⁻¹ using 2 co-added scans. Quantitative analysis of integrated peak areas was performed using ISys 5.0 software (Malvern, UK). The integrated area of the amide I (AM I) (1660-1720 cm⁻¹), and PG (988-1100 cm⁻¹) bands were used to monitor the quality and distribution of collagen and proteoglycan in the constructs (38). Spectra were baseline-corrected, and images were created based on the integrated area of AM I and PG. These maps were generated with a pixel resolution of 25 μm.

The absorbance measurements by FT-IRIS in this study were performed on dry mounted samples. This is in contrast to MRI measurements which are performed on hydrated samples, and, in the case of multiexponential analysis, are reported as proportions of total observable water. To allow for more quantitative comparisons between these two modalities, we normalized the IR-derived matrix content of each sample by its biochemically-derived water weight divided by the total sample wet weight (20).

Biochemical Analysis for sGAG Content

BNC samples were weighed while wet, and then again after being dried at room temperature overnight in a vacuum. They were then digested in buffer containing 1 mg/ml proteinase k (Sigma-Aldrich, St. Louis, MO, USA) and 100 mM ammonium acetate. The 1,9-dimethylmethylene blue assay (DMMB) was performed on the digests to determine sulfated glycosaminoglycan content (39). Absorbances at 525 nm were measured with a SPECTRAmax 340PC³⁸⁴ spectrometer (Molecular Devices, Sunnyvale, CA, USA). Values were converted to sGAG content through comparison with chondroitin sulfate C standards (Sigma-Aldrich, St. Louis, MO, USA).

Results

Tissue Engineered Constructs

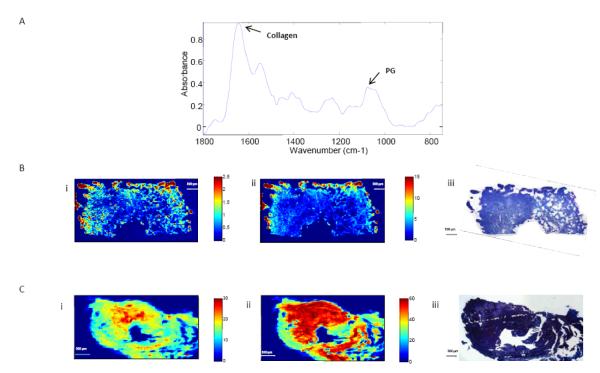
Figure 3A shows typical infrared spectra obtained from engineered cartilage with the absorbances associated with collagen and PG indicated. The corresponding images (Figures 3B & 3C) show the spatial distribution of these absorbances, and illustrate an increase in matrix deposition for both collagen and proteoglycan with culture time. The IR images also reflect the heterogeneity in matrix deposition in both the immature and mature samples. Immature samples showed greater collagen and PG content around the edges of the scaffold and much lower concentrations near the center. Mature samples also showed heterogeneous matrix distribution, with matrix being more centrally concentrated than in the immature samples.

Figure 3.

A) Representative infrared spectrum indicating specific spectral features for collagen and proteoglycan (PG). (B) Representative FT-IRIS image from half of an immature engineered cartilage construct showing the distributions of (i) PG and (ii) collagen normalized by biochemically-derived water content. (B,iii) Representative Alcian blue and H&E staining from the corresponding sample. The central void through which the sample was affixed onto the hollow support tube is seen as a semicircle along the bottom of the image. (C) Representative FT-IRIS image of an entire mature engineered cartilage showing the distribution of (i) PG and (ii) collagen normalized by biochemically derived water content. (C,iii) Representative Alcian blue and H&E staining from the corresponding sample. The central void for mounting onto the support tube is seen in the center of the image.

Biochemical and FT-IRIS results are presented in Table 2. As mentioned above, the FT-IRIS data are normalized by water content for comparison to MRI results. FT-IRIS showed significant increases in PG and AM I between the immature and mature groups, reflecting an increase in proteoglycan and collagen deposition with culture time. Biochemically-derived sGAG also increased during maturation. The water content was greatest in PGA-only scaffolds with a value of 94%. Both the PGA-only and immature samples showed significantly lower water content than mature samples, indicating a reduction of water content with matrix deposition.

Table 2.

Biochemical- and Fourier transform infrared imaging spectroscopy (FT-IRIS)- derived matrix content of engineered cartilage samples used for multiexponential T2 analysis

Sample	Biochemistry		FT-IRIS Measurements
Condition	Water	sGAG	PG	AM I
Immature	0.93±0.008 (n = 8)	0.019±0.011 (n = 8)	0.645±0.183 (n = 8)	2.562±0.789 (n = 8)
Mature	0.91±0.011 (n = 8)*	0.030±0.009 (n = 8)*	5.954±1.841 (n = 5)*	16.744±2.817 (n = 5)*

Biochemical and FT-IRIS results (mean ± standard deviation). Biochemical results are reported as weight fractions (mg/mg) normalized by total wet sample weight. FT-IRIS results are reported as the ratio of the integrated signal from the respective wavenumbers normalized by the biochemically-derived water content.

^*indicates p<0.05.

Multiexponential T₂ Simulations

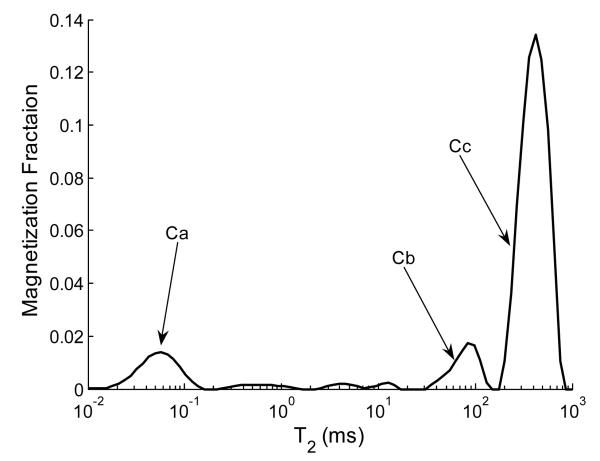
Figure 4 shows a typical T₂ distribution from a mature sample. As seen, three distinct relaxation components (C_a, C_b, and C_c) are present. These components were consistently detected in all samples. As will be discussed in more detail below, these are assigned respectively to collagen-bound, PG-bound, and relatively unbound water pools. In immature samples, rather than a single C_b, two components were consistently detected with T₂s of ~40ms and ~130ms instead of the single component with a T₂ of ~100ms seen in mature samples. For the purpose of comparison between time points, we report the combination of these two components as C_b. While simulations for immature samples were performed using both of these smaller components which comprise C_b, accuracy and precision are reported in terms of the total area. In engineered cartilage grown on collagen I scaffolds, we have previously observed the appearance of multiple components within a relatively narrow range of relaxation times, representing different degrees of mobility assigned to PG-bound water (40). The appearance of multiple components was ascribed to polydispersity of PG.

Figure 4.

Typical T₂ distribution from a mature engineered cartilage sample showing components C_a, C_b, and C_c. The smaller peaks between C_a and C_b were detected in all samples to varying degrees but did not display magnetization fractions large enough for reliable quantification.

Table 1 shows the accuracy and precision of relaxation components determined from simulations based on the average non-localized experimental SNR for each group, and input relaxation values and fractions corresponding to experimentally-derived results. Component weights w_b and w_c were accurate to within 10% for all groups. C_a showed larger errors in both w_a (~15-25%) and T_2,a (~10-15%); these errors are attributed to the rapid T₂ of this component relative to the echo time of the acquisition (i.e. T_2,a = 60 μs and TE = 90 μs). The reliability was 100% for all groups, indicating the robustness of identifying the correct number of components for the given experimental SNR and component T₂s and fractions.

Table 1.

Estimated accuracy and precision of T₂s and associated weights expressed as percent error

Condition		T2,a (ms)	T2,b (ms)	T2,c (ms)	wa (%)	wb (%)	wc (%)
PGA	Input value	0.07	----	896.87	0.05	----	0.95
	Accuracy (%)	11.34	----	−0.58	−15.60	----	0.86
	Precision (%)	0.99	----	0.00	1.98	----	0.11
1 Week	Input Value	0.06	88.93	673.91	0.06	0.04	0.89
	Accuracy (%)	10.66	12.11	−0.43	−18.94	9.15	1.29
	Precision (%)	3.94	1.24	0.02	7.72	1.01	0.22
5 Week	Input Value	0.06	94.35	479.65	0.06	0.06	0.86
	Accuracy (%)	14.18	3.23	−0.21	−25.04	6.69	1.29
	Precision (%)	1.71	0.20	0.01	3.15	0.34	0.22

Each sample condition was simulated with 100 noise realizations based on the average experimental SNR of each group and using the appropriate group average T₂s and associated weights as input values. Accuracy is defined as percent error. Precision is reported as the coefficient of variation (CV), defined as the standard deviation over 100 noise realizations divided by the corresponding input parameter value x 100. Reliability was 100% for all groups. Input simulation values for the T₂ components in ms and their (% magnetization) were as follows. PGA scaffold: C_a = 0.07 (5), C_c = 896.87 (95), SNR = 12,204; 1 Week: C_a = 0.06 (6), C_b = 88.93 (4), C_c = 673.91 (89), SNR = 11,348; and 5 Week: C_a = 0.06 (6), C_b = 94.35 (6), C_c = 479.65 (86), SNR = 15,060.

Multiexponential T₂ analysis

Table 3 shows the results of monoexponential T₂ analysis and multiexponential T₂ analysis. The latter is presented as the T₂ and weight fractions for each component. Monoexponential T₂ decreased with culture time, consistent with previous studies which show a non-specific decrease in T₂ with matrix development (4,7). In the multivariate analysis, T_2,a and T_2,b did not change with maturation, consistent with unchanging mobility of the fractions closely associated with collagen and PG. However, T_2,c decreased significantly with increasing culture time, indicating greater motional restrictions within the pool of less-bound water with increased matrix development. &&&

Table 3.

Mono- and multiexponential T₂ analysis results for PGA constructs.

		Component T2s			Component Fractions
Condition	T2,mono	T2,a	T2,b	T2,c	wa	wb	wc
PGA (N=3)	839 ± 36	0.066 ± 0.021	---	897 ± 45	0.05 ± 0.01	---	0.94 ± 0.02
Immature (N=8)	559 ± 29	0.063 ± 0.012	89 ± 7	674 ± 40	0.06 ± 0.01	0.05 ± 0.01	0.88 ± 0.02
Mature (N=8)	417 ± 39	0.063 ± 0.007	85 ± 9	480 ± 56	0.06 ± 0.02	0.07 ± 0.01	0.85 ± 0.02

T₂ values obtained from monoexponential (T_2,mono) and multiexponential (T_2,i) fits with corresponding weights (w_i) from non-negative least squares (mean ± standard deviation).

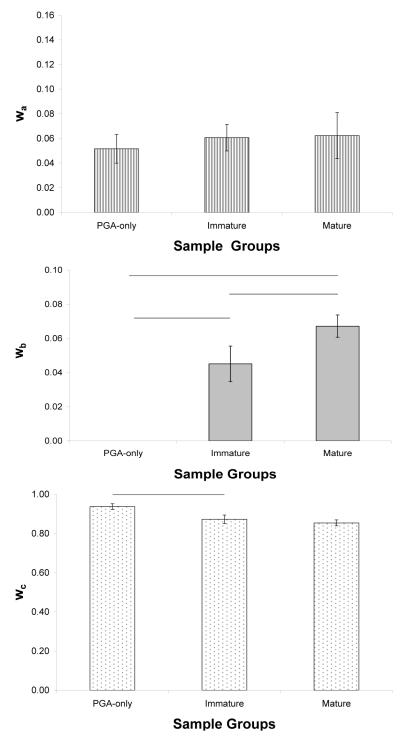
C_a is assigned to collagen because T_2,a relaxes on a time scale that is consistent with collagen bound water (41,42). The fraction w_a corresponding to T_2,a showed no significant change with maturation (Figure 5A). The presence of the component C_a in PGA-only (unseeded) samples indicates its association with tightly-bound scaffold water. There was no significant difference in w_a between the PGA-only samples and chondrocyte-seeded samples. We attribute this lack of change partly to the increase in overestimation of this fraction with culture time. Specifically, w_a was overestimated by ~16%, ~19%, and ~25% in PGA-only, immature and mature samples, respectively. As mentioned above, the fraction of this component is difficult to detect due to its rapid relaxation time relative to the echo spacing.

Figure 5.

Component weight fractions for empty PGA scaffolds, immature and mature engineered cartilage. A) There are no differences in w_a between groups. B) w_b was not detected in PGA scaffolds and showed an increase between immature and mature groups. C) There was a decrease in the bulk water fraction, w_c, between PGA scaffolds and immature samples and a slight but insignificant decrease in w_c between immature and mature samples. Horizontal bars indicate p < 0.05.

C_b, the component previously assigned to PG-bound water in native cartilage (19), was not detected in the PGA-only scaffolds (Figure 5B). However, there was a significant increase in its associated fraction, w_b, during maturation of seeded constructs, consistent with the increase in biochemical and FT-IRIS derived PG content.

C_c was consistently the largest relaxation component. Given this, and its large value, we assign this to bulk water. The unseeded PGA-only scaffolds had the greatest w_c (Figure 5C). The substantial decrease seen with seeding reflects the development of a larger pool of PG-bound water with maturation progresses.

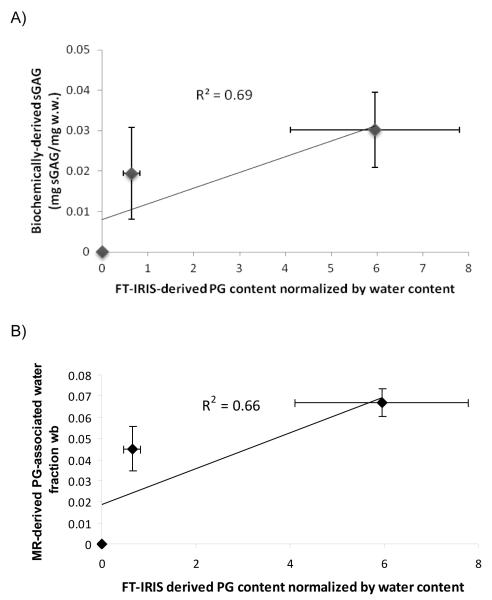
Figure 6A shows the correlation between the average values of FTIR-derived PG content in PGA-only, immature, and mature groups, and the corresponding biochemical values for PG. This serves to validate the use of FTIR analysis in this setting. Similar results were achieved for the correlation between group values of w_b and FTIR-determined PG (Figure 6B).

Figure 6.

A) Biochemically-derived PG content plotted against FT-IRIS-derived PG content normalized by water content (R² = 0.69). B) MR-derived PG water fraction w_b plotted against FT-IRIS-derived PG content normalized by water content (R² = 0.66).

Univariate and SVM Classification

Table 4 shows the classification accuracy over the 100 iterations of random simple splits using MRI univariate arithmetic means and using MRI multivariate SVM. The univariate results represent, in effect, the conventional approach to interpretation of MR parameter results. As shown, for the univariate analyses, classification accuracy in the validation sets was essentially indistinguishable from that in the training sets. k_m and T₁ where the best univariate classifiers both showing comparable classification accuracy. Classification accuracy according to any of the multivariate combinations using the SVM approach was superior to that achieved with any of the univariate classifiers both in the training set and, more importantly, in the validation set. In this study, the best bivariate classifier was (k_m, ADC), with no further improvement seen in adding a third or fourth MR outcome measure.

Table 4.

Classification accuracy of immature and mature constructs using univariate analysis and support vector machine multivariate analysis.

	Training	Validation
T1	0.858 ± 0.046	0.836 ± 0.069
T2	0.838 ± 0.042	0.819 ± 0.072
km	0.862 ± 0.039	0.850 ± 0.074
ADC	0.787 ± 0.062	0.758 ± 0.081
(T1, T2)	0.962 ± 0.032	0.913 ± 0.065
(T1,km)	0.998 ± 0.009	0.959 ± 0.053
(T1, ADC)	0.940 ± 0.029	0.893 ± 0.060
(T2,km)	1.000 ± 0.000	0.971 ± 0.037
(T2, ADC)	1.000 ± 0.000	0.878 ± 0.073
(km, ADC)	1.000 ± 0.000	0.978 ± 0.042
(T1, T2, km)	0.981 ± 0.016	0.948 ± 0.051
(T1, T2, ADC)	0.966 ± 0.024	0.921 ± 0.057
(T1, km, ADC)	1.000 ± 0.000	0.958 ± 0.056
(T2, km, ADC)	1.000 ± 0.000	0.936 ± 0.058
(T1, T2, km, ADC)	0.980 ± 0.019	0.948 ± 0.044

Samples (N = 48) were randomly split into a training set (n = 36) and a validation set (n = 12) for each classification iteration. Accuracy is reported as the average from 100 iterations.

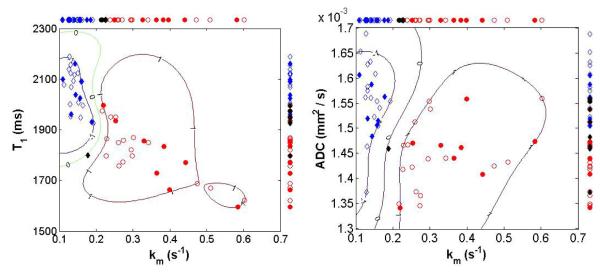
In figure 7, immature and mature samples are plotted according to pairs of MR parameters. The pairs used are (T₁, k_m) and (ADC, k_m). For illustrative purposes, a random sample selection from a single iteration of the simple split procedure (2/3 of the 48 samples for a training set and 1/3 of the 48 sample for a validation set) is displayed. The decision hyperplane constructed by the SVM algorithm in the training set is labeled by the contour curve of level zero, on which the locus of points have an equal probability of being assigned to the immature or mature groups. Points are assigned to the immature or mature group based on their location with respect to the decision hyperplane. In Figure 7A, based on the parameter pair (k_m, T₁), all samples were correctly classified with exception of an immature cultured sample from the validation set. Similar classification performance was obtained using the parameter pair (k_m, ADC) (Figure 7B), with again only one validation set sample being misclassified.

Figure 7.

Typical scatter plots for bivariate combinations of MR imaging parameters. Results for univariate classification based on simple means are shown along the top and right sides of each plot, respectively. ADC and km shows good separation between immature and mature sample groups. Diamond symbols: immature samples; Circle symbols: mature samples; Open symbols: training set; Solid symbols: validation set; Black solid symbols: misclassified samples in the validation set. The loci labeled −1 and +1 represent contours defined by the support vectors for immature and mature samples, respectively. The support vector margin is signified by the contour labeled zero.

Discussion

MRI is increasingly used to assess development of engineered tissue, with a goal of relating noninvasive measurements to the biophysical and biochemical status of the tissue (4-7). Several MR parameters have been used for this: T₂ is sensitive to tissue hydration, collagen content, and collagen orientation with respect to the main magnetic field (4,43); ADC is particularly sensitive to macromolecular content and hydration (44); the dGEMRIC index is sensitive to PG content (5); and magnetization transfer rate (k_m) primarily reflects collagen content (7). Heteronuclear studies have also been performed, with the Na⁺ signal intensity being sensitive to local PG content (45). All of these measurements exhibit utility in certain circumstances. Relationships between MR parameters and cartilage matrix development have been documented, and analysis of parameter means between various stages of development (4) or control and experimentally treated groups (44) indicates whether there is a statistically significant difference in a particular parameter. Such group differences have been found in many circumstances. However, these measurements are of limited specificity; there can be a great deal of overlap in parameter values measured for different groups, including groups representing different stages of development. For example, we observe such an overlap in individual MR parameter values between immature and mature samples (Figure 7) in spite of the statistically significant differences between group mean MR parameter values (data not shown).

Development and optimization of tissue engineering strategies remains an area of intense interest; the ability to nondestructively detect differences in tissue quality and maturity would be of substantial benefit towards this. However, the ability to discriminate between different stages of cartilage development in engineered cartilage tissue using MR parameters has received little attention. This would ideally entail the development of an objective classification technique. To establish and validate such a classification approach, assignments would be made according to a pre-established algorithm, after which sensitivity and specificity of the procedure can then be calculated based on known sample characteristics. After validation, the algorithm would be applied to unknown samples. This procedure can be carried out for any MR parameter; therefore, an initial goal of uniparametric analysis as applied to tissue engineering would be to identify which of the several available MR parameters is best able to discriminate between different stages of matrix development. Of the standard parameters, T₂ is perhaps the most widely-used. This may be due to the speed and simplicity of T₂ measurements and the fact that T₂ is sensitive to several tissue parameters. However, without formal evaluation, the advantage of one parameter over another for detection of engineered cartilage matrix development remains speculative. Finally, we note that it would be of substantial interest and practical importance if an MR parameter could be identified that performed well in a variety of settings; of course, in an actual experimental protocol, one would not have the luxury of testing all parameters against a gold standard to determine the optimal one.

In the present study, classification results based on univariate MR parameter means indicated that T₁ and k_m performed the best and provided virtually identical classification accuracy, with the average of sensitivity and specificity equaling 0.85. This is generally consistent with our previous studies of native cartilage in which T₁ performed best as a univariate classifier for discriminating between normal and pathomimetically-degraded cartilage, although in that previous work k_m was substantially worse than T₁. For instance, in comparisons between normal and mildly trypsin-degraded cartilage, T₁ showed ~0.65 classification accuracy as compared to the value of ~0.51 obtained for k_m (22). The usefulness of T₂ also differed between these studies. In the present work, T₂ performed well in comparison to the other MR parameters, with an accuracy of 0.82. However, in the previous study of degraded cartilage, it performed poorly with a classification accuracy of ~0.54; this is in comparison to an accuracy of ~0.65 for T₁ mentioned above (22).

Multiparametric classification

Beyond this evaluation of single MR parameters, there remains the overall problem of cartilage classification and characterization given the limited specificity of MR outcome measures. A conventional approach to this is multivariate, or multiparametric, statistical analysis. While others have performed “multiparametric studies” of cartilage in which samples or subjects have been evaluated using several MRI parameters individually (46), actual multiparametric statistical methods have not to our knowledge been previously applied to cartilage. However, such work has been explored in other applications of MRI. Automated sharp and fuzzy classification of brain tissue into grey matter, white matter, CSF, and partial-volumed mixtures of these tissue types was performed using a variance minimization approach similar to Fischer linear discriminant analysis (47). The MR parameters used for classification were T₁, T₂, and proton density. Results compared favorably with operator-dependent classification. Fuzzy k-means clustering was also used in a two dimensional feature space consisting of 1st and 2nd echoes from a dual-echo sequence to classify brain tissue (48). Results were comparable to operator-dependent methods. Another application to brain was in the definition of tissue boundaries for experimental stroke in the rat (49). The multiparametric ISODATA clustering approach, a variation on k-means clustering, was implemented using a feature space consisting of proton density, T₂-weighted, and T₁ data. Using histologic analysis as the gold standard, the ISODATA approach was superior to ADC, DWI, or T₂-weighted images in segmentation of ischemic lesions. This approach was also used successfully for identification of breast lesions in human subjects (50). In another application to cancer, k-means clustering in the feature space of ADC, T₂, and proton density was applied to a model of human colorectral malignancy (51). Regions of viable tumor tissue, necrotic tissue, and adipose tissue were successfully segmented, and response to therapy was also monitored using the multispectral approach. A model that is much more flexible than either linear discriminant analysis or k-means clustering is the MCLUST approach, which establishes a Gaussian mixture model in feature space. This was successfully applied to segmentation and detection of malignant breast tissue in human patients (52).

The difficulty in establishing normative values for individual MR parameters may be unsolvable, given the dynamic range of MR outcome measures across the range of engineered cartilage matrix characteristics. An additional complication is the use of different scaffold materials, rendering comparisons between culture systems difficult. Indeed, we observe this when comparing the results obtained using PGA constructs in the present work with other cartilage tissue engineering systems. Cartilage samples using PGA scaffolds from the current study showed similar amounts of matrix deposition compared with other cartilage tissue engineering scaffold systems used in our lab. For instance, we have previously reported sGAG content of 0.045 and 0.062 mg sGAG/mg wet sample weight in scaffold-free bioreactor tissue cultured for 2 weeks and 3 weeks, respectively (7). Samples used in the MR imaging experiments of the current study showed sGAG amounts of 0.016 and 0.095 mg sGAG/mg wet weight after 1 and 5 weeks of culture, respectively. In terms of dry weight, we found sGAG content of 0.25 and 0.35 mg sGAG/mg dry weight in engineered cartilage grown in a collagen I scaffold for 1 week and 4 weeks, respectively (4). The results for the samples used in the MR imaging experiments of the current study were comparable, with values of 0.25 and 0.31 mg sGAG/mg dry weight, respectively. In spite of the similarities in sGAG content between these different cartilage matrix systems, the MR imaging parameter values differ greatly. For instance, T₁ values in the scaffold-free bioreactor tissue were 3125 and 2510 ms for 2 week and 3 week samples, respectively (7). This is much longer than the T₁ values obtained for the constructs developing on PGA scaffolds in the current study, which were 2046 and 1812 ms for 1 week and 5 weeks of development, respectively. Even shorter values were obtained on constructs developing on collagen I scaffolds, with T₁ values of 1663 and 1592 ms for samples cultured for 1 week and 4 weeks, respectively (4). Although we only compare T₁ values here, the T₂ values and k_m values varied just as widely. The large differences in MR parameters among these constructs with fairly similar degrees of matrix deposition highlights the influence which scaffold material has in MR parameter characterization; this greatly complicates the interpretation of MR parameter values.

In the current work, we critically assess the ability to discriminate between immature and mature engineered cartilage. As expected, we found large differences in matrix development between immature and mature samples, as verified with biochemical and FT-IRIS quantitative measures. This therefore represents, if anything, relatively straightforward classification problem. However, projections of univariate MR parameters in Figure 7 shows overlapping points. This finding motivates the use of a multivariate classification approach. Indeed, the multidimensional plots in Figure 7 show the way in which these two groups are better separated in 2-dimensional space.

The combination of k_m and ADC showed the best validation set classification accuracy out of all parameter combinations in the present study, with the average of sensitivity and specificity equaling 0.98. This is a substantial improvement on the classification accuracy obtained using k_m alone. Other pairs that included km showed comparable results, with (T₁, k_m) and (T₂, k_m) showing classification accuracies of 0.96 and 0.97, respectively. We note that this result is somewhat different from our previous findings on native cartilage explants, in which (T₁, k_m) was the best univariate classifier. However, again, the differences between the accuracy obtained with (k_m, ADC), (T₂, k_m), and (T₁, k_m) in the present study are slight. We have previously found minimal or no improvement in classification upon the addition of a 3d or 4th parameter (22). Consistent with this, combinations which included more than two parameters do not show any improvement in classification accuracy in the present study of engineered tissue.

Multiexponential T₂ analysis

In the present work, in addition to exploring increased specificity in the classification of developing cartilage through use of multivariate statistical methods, we sought to improve the sensitivity of MR-derived measures to specific matrix components through the use of multiexponential T₂ analysis. This approach is based on the fact that different water compartments within tissue would be expected to exhibit different transverse relaxation rates due (primarily) to differing water mobility within the compartments. We obtain a distribution of relaxation times which represent the mobility of water compartments in the tissue through the use of the nonnegative least squares algorithm (12). Multiexponential transverse relaxation time analysis has been applied to other tissues, most prominently to determine brain myelin fraction (53,54). Although there are other approaches (55), the most convenient and physically intuitive way to model non-monoexponential T₂ decay is with multiple exponentials. This can be performed in two basic ways. The tissue can be modeled by a pre-specified number of exponentials, each representing a discrete tissue compartment; while this may be the most straightforward approach, it suffers from the severe drawback of constraining at the outset the number of tissue water compartments that will be found by the analysis. An increasingly popular alternative is to implement the nonnegative least squares (NNLS) algorithm (12); this is a constrained optimization approach with the constraint reflecting the fact that none of the relaxation components can contribute negatively to the signal. NNLS does not require any assumption about the number of relaxation components comprising the data. In the case of cartilage, the components of interest are the collagen and PG macromolecules, and the bulk water compartment. Given the polydispersity of the PG fraction (56), the multiexponential approach with NNLS analysis therefore appeared very suitable for cartilage matrix analysis.

Simulation results

It is well-established that both experimental and biophysical factors influence the ability to accurately detect and quantify multiple water components through non-negative least squares analysis of T₂ relaxation data. These factors include the signal-to-noise ratio (SNR), echo time (TE), the number of echoes, the number of T₂ components, and the respective T₂s and weight fractions of these components (19,21). Thus, the analysis of simulated multiexponential T₂ decay data is an important step for reliable interpretation of experimental data.

Our results from the current study are consistent with our previous work which shows reduced accuracy in components whose T₂s are close to or less than the echo time (21). For example, in our simulations, which used an echo time of 90 μs, we found the largest errors in C_a, with an input T₂ value of ~60 μs. Also, T_2,a is consistently underestimated and w_a is consistently overestimated.

The effect of additional relaxation components on reliability of multiexponential analysis is seen by examining the simulation results for C_a. The accuracy and precision in determining T_2,a and w_a are less favorable in the seeded scaffolds, for both the immature and mature groups, as compared to the results for the unseeded PGA-only group. This is a direct result of the larger number of simulation input components in the engineered cartilage groups. The reduction in accuracy and precision with addition of components is well documented in other work (21).

The effect of component size on the reliability of the analysis is seen in the results obtained for C_b. Simulation results indicated increased accuracy of T_2,b and w_b determination as maturation progressed, concomitant with an increase in the simulation input value of w_b. This result is consistent with previous simulation results showing improved accuracy of w_b determination as the ratio w_b/w_c increases towards unity (21). In both that previous analysis and the current work, we find that w_b is underestimated.

Experimental results

As discussed, individual MRI parameters are limited in that they model complex biophysical properties with a single parameter. For instance, conventional T₂ measurements are determined using a single relaxation time constant; however, this time constant is a weighted average of the time constants of multiple tissue microenvironments. In native cartilage, the T₂ of water associated with proteoglycan molecules ranges from 15-80 ms (57) whereas the T₂ of water associated with the more rigid collagen molecules ranges from 30-100 μs (14,41,42). The largest pool of water exists is the most slowly relaxing and, based on its relatively large value of T₂, is only loosely associated with the matrix. Monoexponential T₂ is preferentially influenced by this dominant bulk water component, rendering the interpretation of specific changes in matrix composition in native or engineered cartilage using monoexponential T₂ virtually impossible. These considerations are reflected in our data; the smaller components C_a and C_b have little influence on the monoexponential T₂, so that its decrease with matrix development is largely driven by changes in bulk water mobility and provides minimal information about the developing matrix.

In the current study, we found that the T₂ distribution of cartilage engineered on a PGA scaffold was similar to that of native cartilage. First, as expected, the component with the largest weight fraction, C_c, exhibits the longest T₂. In native cartilage, we have tentatively assigned this component as bulk water loosely associated with the matrix. In the present study, this component was dominant in both empty PGA scaffolds and in chondrocyte-seeded scaffolds. The proportional size of this component with respect to total detected water was found to be larger than in native cartilage, consistent with the greater water content in these engineered constructs compared with native cartilage. Second, there was the consistent finding of a moderate-sized component, C_b, which relaxes somewhat more rapidly than the bulk component. As previously mentioned, in native cartilage we have tentatively assigned this component as PG-associated water based on its relaxation time and the known motional characteristics of PG (57), as well as the correspondence of this component with biochemically-derived PG content in normal (20) and degraded cartilage (21). We observed a similar relationship between PG and this component in engineered constructs, as seen in Figure 6. Also, consistent with this assignment of C_b to PG-associated water, this component was absent in the unseeded scaffolds (Table 3). Finally, in both native and engineered cartilage we found a rapidly relaxing component, C_a, with T₂ ranging from ~30 to several hundred microseconds (data not shown). In native cartilage, this component is consistent in fraction size and relaxation time with the known abundance and mobility of collagen (58-61). In the current study, we tentatively assign this component to both tightly-bound PGA-associated water and tightly-bound collagen-associated water. The association with PGA-associated water is supported by the presence of this component in the PGA-only scaffold. The lack of variation of the weight fraction, w_a, of this rapidly relaxing component between groups suggests its association with collagen-bound water. In particular, we interpret this as resulting from the simultaneous degradation of the PGA scaffold (62) and the increase in collagen formation, as measured using FT-IRIS (Table 2). We note that we have also observed this rapidly relaxing component in unseeded collagen I scaffolds (40).

In order to accurately quantify a given relaxation component in the setting of realistic SNR, it is necessary to use an echo time on the order of or shorter than its T₂. We therefore performed our experiments using a nonlocalized CPMG sequence, with sampling at echo maxima. This permitted much more rapid sampling of the decay curve than would be possible with a typical imaging sequence; in this sense, improving identification of underlying water compartments and detection of short T₂ components comes at the expense of spatial resolution. However, improved detection of relaxation components is especially important for systems which have not been previously studied by this technique, and the loss of spatial information is of relatively less importance in tissue systems which are presumed to be relatively uniform in their microstructure. In contrast, nonlocalized experiments would be much less informative in heterogeneous tissues such as articular cartilage, which exhibits a distinct layered structure. In this case, the presence of spatial varying matrix and water compartments would greatly complicate the interpretation of the relaxation components in terms of tissue microstructure. Recognizing the importance of articular cartilage studies, and the potential importance of investigating structured engineered constructs, we have also implemented localized multiexponential relaxation time analyses (21) as well as actual imaging approaches (20).

The incorporation of FT-IRIS analysis in this work and in previous studies (20,21) has been very important in validating our MR approaches. FT-IR provides measurements that are highly specific to cartilage matrix components and degeneration (26-28). FT-IRIS couples an FT-IR spectrometer to an optical microscope with an array detector, permitting spatially-selective evaluation of matrix components within tissue sections that are typically on the order of a few microns thick, with an in-plane spatial resolution of ~9 microns. Thus, FT-IRIS has been used to evaluate the quality of repair and degenerative tissue at a molecular level with high spatial resolution (27). However, FT-IRIS requires extensive sample preparation when used in transmission mode, while in reflectance mode it samples tissue characteristics within a few microns only of the surface. Thus, FT-IRIS is largely complementary to MR, but forms a very suitable modality for comparison with our emerging MR methods.

In conclusion, MR parameters vary with the biochemical composition of engineered cartilage, but in a nonspecific way. Univariate classification based on individual MR parameters, exhibits limited accuracy due to large overlap of MR outcomes between groups. Use of multiparametric support vector machine discriminant analysis results in substantial improvement in classification accuracy, permitting much more accurate detection of sample maturation. This approach can be applied to detect maturation in developing constructs. Further, conventional MR parameters are generally sensitive to tissue composition and status, but vary in a nonspecific way; they reflect multiple physical and chemical properties. Therefore, parameter changes can be ascribed to a variety of tissue level changes. In contrast, multiexponential transverse relaxation analysis can define specific microstructural components in cartilage, providing a much more direct measure of matrix components. These two approaches, multivariate SVM analysis and multiexponential relaxation analysis, provide improvements in sensitivity to changes in matrix development and specificity to matrix composition in the evaluation of developing tissue engineered constructs.

Abbreviations

PG

proteoglycan

GAG

glycosaminoglycan

sGAG

sulfated glycosaminoglycans

FT-IRIS

Fourier transform infrared imaging spectroscopy

SVM

support vector machine

NNLS

non-negative least squares

SNR

signal-to-noise ratio

DMEM

Dulbecco’s modified eagle’s medium

DPBS

Dulbecco’s phosphate buffered saline

DMMB

1,9-dimethylmethylene blue assay

FT-IR

Fourier transform infrared

mid-IR

mid-infrared

CPMG

Carr-Purcell-Meiboom-Gill experiment

NEX

number of excitations

MT

magnetization transfer

CV

coefficient of variation

SD

standard deviation

ANOVA

analysis of variance

C_a, C_b, and C_c

observed multiexponential T₂ components

w_a, w_b, and w_c

magnetization fractions associated with observed T₂ components

ROIs

regions of interest