Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2012 Mar 8;159(1):27–39. doi: 10.1104/pp.112.194662

Computational Method for Quantifying Growth Patterns at the Adaxial Leaf Surface in Three Dimensions1,[W],[OA]

Lauren Remmler 1, Anne-Gaëlle Rolland-Lagan 1,*
PMCID: PMC3366717  PMID: 22402928

Abstract

Growth patterns vary in space and time as an organ develops, leading to shape and size changes. Quantifying spatiotemporal variations in organ growth throughout development is therefore crucial to understand how organ shape is controlled. We present a novel method and computational tools to quantify spatial patterns of growth from three-dimensional data at the adaxial surface of leaves. Growth patterns are first calculated by semiautomatically tracking microscopic fluorescent particles applied to the leaf surface. Results from multiple leaf samples are then combined to generate mean maps of various growth descriptors, including relative growth, directionality, and anisotropy. The method was applied to the first rosette leaf of Arabidopsis (Arabidopsis thaliana) and revealed clear spatiotemporal patterns, which can be interpreted in terms of gradients in concentrations of growth-regulating substances. As surface growth is tracked in three dimensions, the method is applicable to young leaves as they first emerge and to nonflat leaves. The semiautomated software tools developed allow for a high throughput of data, and the algorithms for generating mean maps of growth open the way for standardized comparative analyses of growth patterns.

The highly regulated organization of tissues into functional shapes during morphogenesis is a crucial and intriguing process (Coen et al., 2004; Strutt, 2005; Tsukaya, 2006). Changes in shape and size as an organ develops are driven by spatial and temporal variations in growth parameters, such as the rate and directionality of tissue expansion and tissue rotation (for review, see Coen et al., 2004). Characterizing these growth parameters at a sufficient spatial and temporal resolution would be instrumental in uncovering the mechanisms responsible for the generation of organ shapes.

Leaves are a good system in which to study the process of morphogenesis, given their relatively thin structure that can be approximated as a three-dimensional (3D) surface, visual accessibility, and the absence of cell migration (Cosgrove, 2005). Early efforts to measure leaf growth involved drawing ink dots on the adaxial leaf surface to delineate a grid of small rectangles whose deformations over time could be used to calculate regional growth rates (Avery, 1933; Richards and Kavanagh, 1943). Other studies since then have employed the same concept of quantifying growth at the adaxial leaf surface by tracking ink marks (Maksymowych, 1962; Saurer and Possingham, 1970; Poethig and Sussex, 1985; Granier and Tardieu, 1998; Wang et al., 2011) or vein intersections (Maksymowych, 1959; Erickson, 1966; Wolf et al., 1986; Walter and Schurr, 1999; Taylor et al., 2003; Walter et al., 2003). Recently, digital image sequence analysis tools have been developed to automatically track the displacement of identifiable features in successive images of a leaf (Schmundt et al., 1998; Ainsworth et al., 2005; Wiese et al., 2007).

One important limitation of existing tracking methods is that they cannot be used to study early stages of leaf development in which major growth and developmental processes occur. This is because drawing or printing ink dots on the leaf surface (Avery, 1933; Richards and Kavanagh, 1943; Maksymowych, 1962; Poethig and Sussex, 1985; Granier and Tardieu, 1998; Wang et al., 2011) or threading or clipping weights through the leaf margins, as required for the digital image sequence analysis setup (Schmundt et al., 1998; Ainsworth et al., 2005; Wiese et al., 2007), require that the leaf be relatively large, and vascular features (Maksymowych, 1959; Erickson, 1966; Wolf et al., 1986; Walter and Schurr, 1999; Taylor et al., 2003; Walter et al., 2003) are not visible at early stages of development.

Another significant limitation of existing methods and computations is that they are only applicable to flat or flattened leaves. In the past decade, there has been increased interest in more geometrically complex leaf shapes, such as such those with stronger curvatures, rolling, ruffling, wrinkling, and twisting, but, as many researchers have pointed out, methods to study the growth of such 3D surfaces are not available at present (Piazza et al., 2005; Tsukaya, 2006; Cronk, 2009; Micol, 2009; Walter et al., 2009).

Finally, previous leaf growth studies have not been able to produce average leaf growth information at high spatial resolution. Even within leaves of the same genotype at the same developmental stage, there is variation in leaf size and growth, so in order to make quantitative comparisons of leaf growth between mutant and wild-type plants, plants grown in different environmental conditions, or plants of different ecotypes, for example, it would be very useful to have a method for producing mean spatial maps of growth parameters from a number of samples.

Here, we present a novel technique and computational tools that allow for a detailed analysis of spatial growth patterns at the adaxial surface of a leaf in three dimensions from an early stage of development. The computational tools involve largely automated image analysis and point-tracking algorithms, as well as programs for averaging results of several samples, to compute and display average leaf shapes and spatial maps of mean growth pattern parameters. The technique may be applied to characterize growth in other organs and organisms. The algorithms developed are available at http://mysite.science.uottawa.ca/arolland/.

RESULTS

In this study, we monitor the growth of the first rosette leaf in 35 Arabidopsis (Arabidopsis thaliana) plants from 7 to 19 days after sowing (DAS). More information on the data set can be found in Supplemental Materials and Methods S1 and Supplemental Figure S1A. Here, we first present the results of the data acquisition and computational methodology and then describe the growth parameter data obtained.

Using Fluorescent Particles as Landmarks to Track Leaf Growth

To track growth, fluorescent microparticles are applied topically to the adaxial surface of the leaves. Particles are applied as soon as the leaf surface is exposed, typically at 7 DAS (i.e. DAS7), when the leaves are as small as 500 μm in length. The application method is gentle, noninvasive, and does not disturb leaf development (Supplemental Fig. S1B). The particles settle onto the leaf cuticle and move with the leaf surface as it grows (Supplemental Fig. S1C), so leaf growth can be quantified by tracking particle divergence.

Imaging the Leaf and Fluorescent Particles

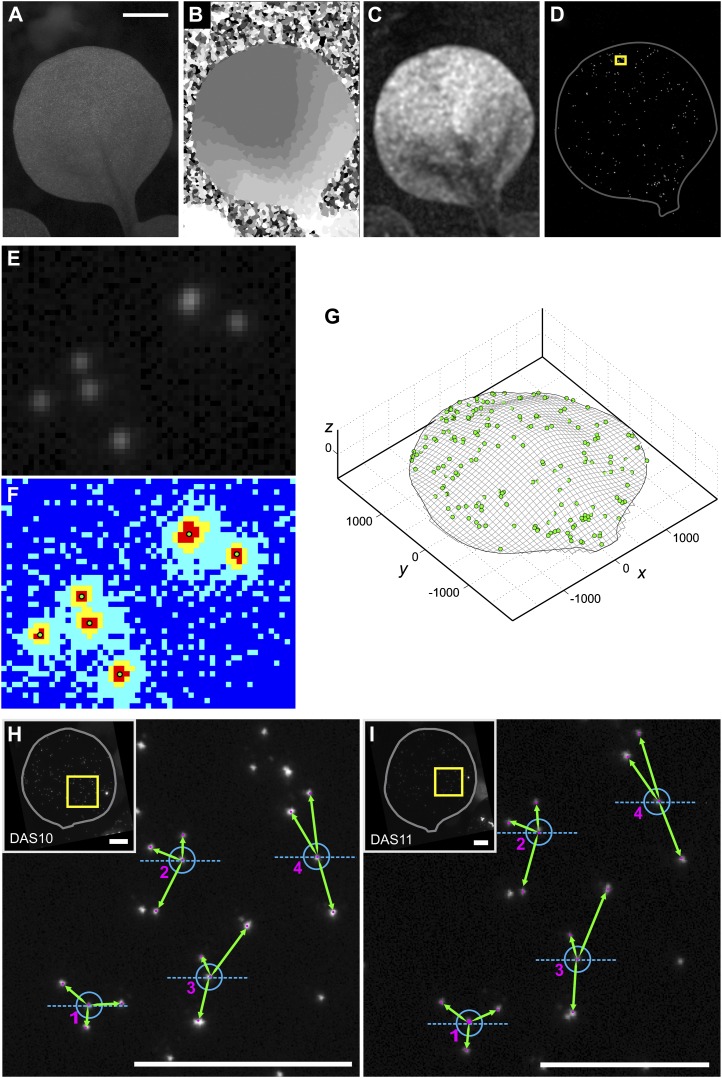
Each leaf is imaged every 24 h with a motorized fluorescence macroscope (for details, see “Materials and Methods”). We first acquire a z-stack (a series of images at different focal planes) of a leaf under reflected bright-field lighting and then a second stack under fluorescent lighting. The microscopy software saves details such as the vertical step size between focal planes in the z-stack and the resolution of the images. The bright-field stack is used to obtain a multifocus montage image of the leaf (Fig. 1A), a depth map of the leaf surface (Fig. 1B), and a confidence map of the depth map computations (Fig. 1C). The fluorescence stack is used to produce a multifocus image of the fluorescent particles (Fig. 1D). All computational steps that follow are performed using our custom-made software developed in Matlab (see “Materials and Methods”).

Figure 1.

Figure 1.

Open in a new tab

Acquiring and extracting data. A to D, Leica LAS Montage Module images generated from z-stack images of a leaf. We use the bright-field z-stack to obtain a multifocus montage (A), a depth map (B), and a confidence map for the depth map (C). We use the fluorescence z-stack to obtain a multifocus montage image of the fluorescent particles on the leaf (D). In D, the image is enhanced to improve the visibility of the particles in the publication-sized figure, the leaf outline is plotted for clarity, and the yellow rectangle indicates the region magnified in E and F. Bar in A = 1 mm. E and F, Illustration of the particle digitization algorithm. E shows a zoomed-in region of the fluorescence montage image. The algorithm applies a k-means clustering function that sorts the pixel values into four groups: typically, the dark parts of the image (dark blue), the very faintly glowing areas around the particles (light blue), the brighter glowing areas around the particles (yellow), and the brightest parts of the image, the fluorescent particles (red). The x, y coordinates of particles, shown as green dots, are defined as the centroid of clusters of the brightest pixels (F). G, Digital reconstruction of the leaf surface and particles in three dimensions after extracting z-coordinates from the depth map. Axes units are in μm. H and I, Illustration of the pattern-matching algorithm. We show the particles on a leaf at two successive time points, DAS10 (H) and DAS11 (I). The insets show the fluorescent montage images (rotated so that the leaves are oriented vertically), and the yellow rectangles indicate the areas shown on the main panels. The neighbor patterns of four particles are shown, with the green arrows illustrating the neighbor distances and orientation (measured relative to the axis in blue). Matches between the two time points, indicated by the numbering, are identified by the program based on these unique neighbor patterns. Bars in H and I = 1 mm. For more information, see Supplemental Figure S1.

Extracting the 3D Leaf Surface

If the leaf being imaged is not touching other leaves, the two-dimensional projection of the leaf outline can be obtained automatically from the bright-field multifocus leaf image through the use of an image texture analysis function (for details, see Supplemental Fig. S2). Alternatively, the outline can be obtained by digitally tracing it on the bright-field multifocus leaf image. The 3D outline and topography of the leaf are then extracted from the depth map. The 3D leaf surface is recorded as a mesh fitted over the area enclosed by the leaf outline, using the depth map to determine the z-coordinates of each point on the grid (Supplemental Video S1). The leaf coordinates are then centered and aligned so that the leaf blade is centered at the origin of a Cartesian coordinate system, the proximodistal axis of the leaf coincides with the y axis, and the x-y plane corresponds to the regression plane fitted to the leaf surface.

Digitizing Particles Semiautomatically

A k-means clustering function (Seber, 2008) is applied to the multifocus fluorescence image (Fig. 1, E and F) to automatically identify which pixels in the image are bright enough to be considered the fluorescence of a particle. Particle x, y coordinates are identified as the centroid of interconnected bright pixels. Depending on the quality of the image and the distribution of particles, this will typically identify 80% to 100% of the particles. Any bead missed by the algorithm can be manually added by the user. The z-coordinates of the particles are retrieved from the vertical height of the 3D leaf surface at each particle’s x, y position. Figure 1G shows an extracted leaf surface and its associated particles in three dimensions.

Tracking Particles Semiautomatically

Digital image sequence analysis software (Bernd, 1997) is not applicable to particle tracking in our study due to the large displacement of particles between successive images. To make our procedure capable of high throughput, we developed a set of programs for semiautomatic tracking of points with large displacements due to growth deformations. This involves two algorithms. A pattern-recognition algorithm first identifies a particle at successive time points based on the relative positions of its neighboring particles, as illustrated in Figure 1, H and I. The pattern-recognition algorithm typically matches 80% to 100% of the particles. These initial matches are then used by a warping and matching algorithm to estimate the tissue deformation between time points and thereby identify any remaining particles based on their relative positions on the leaf. Matches need to be verified by the user, and in cases where matching is not successful, the default parameters of the matching programs can be adjusted by the user. Further details of both algorithms are provided in Supplemental Materials and Methods S1.

Computing Growth Strains in Three Dimensions

To subdivide the surface into small regions that can be tracked over time, we apply a Delaunay triangulation function to connect all of the particle coordinates on the leaf to each other through nonintersecting triangles, using the same triangulation on matched particles over successive time points. Now, instead of tracking the movement of particles per se, we are tracking the changes in size, shape, and orientation of triangular regions over time. Using singular value decomposition (SVD) formulas, as explained by Goodall and Green (1986), we are able to compute a variety of growth parameters. SVD allows us to calculate, for each triangle, the direction of maximal growth, the rotation, and the scaling factors p and q. p is the scaling factor along the maximal direction of growth, and q is the scaling factor along the minimal direction of growth, which by the laws of mechanics is oriented orthogonally to the maximal direction of growth. We compute the relative growth (RG) for each triangle as the percentage increase in area over the course of 1 d (24 h):

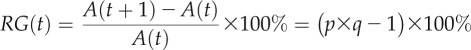graphic file with name PP_194662E01_LW.jpg

where RG(t) is the percentage increase in area from day t to day t+1, A(t) is the area of the triangle at day t, A(t+1) is the area of the triangle at day t+1, and p and q are the scaling factors along the maximal and minimal directions of growth over the course of 1 d.

Growth anisotropy, a measure of how preferentially growth occurs along the maximal direction of growth, is computed from the ratio of the scaling factors (p/q). An anisotropy value of 1 indicates that growth is occurring evenly in all directions, and higher values indicate that growth occurs predominantly along a main direction.

The SVD calculations are not directly applicable to 3D landmarks. To compute growth strain parameters from 3D coordinates, we developed an algorithm to first rotate the triangle coordinates onto a two-dimensional plane, compute growth using SVD, and then reorient the results in the true 3D position by applying the inverse of the flattening rotations. Further details are provided in Supplemental Materials and Methods S1.

To display a given growth parameter from one time point to the next, we plot the parameter value of each triangular region on the first of the two time points using a color map. For instance, to display leaf RG from DAS10 to DAS11, we plot the RG values on the DAS10 leaf. An example of a map of RGs of one leaf over time is shown in Figure 2A. These results can be plotted and viewed in three dimensions, as shown in Supplemental Video S2.

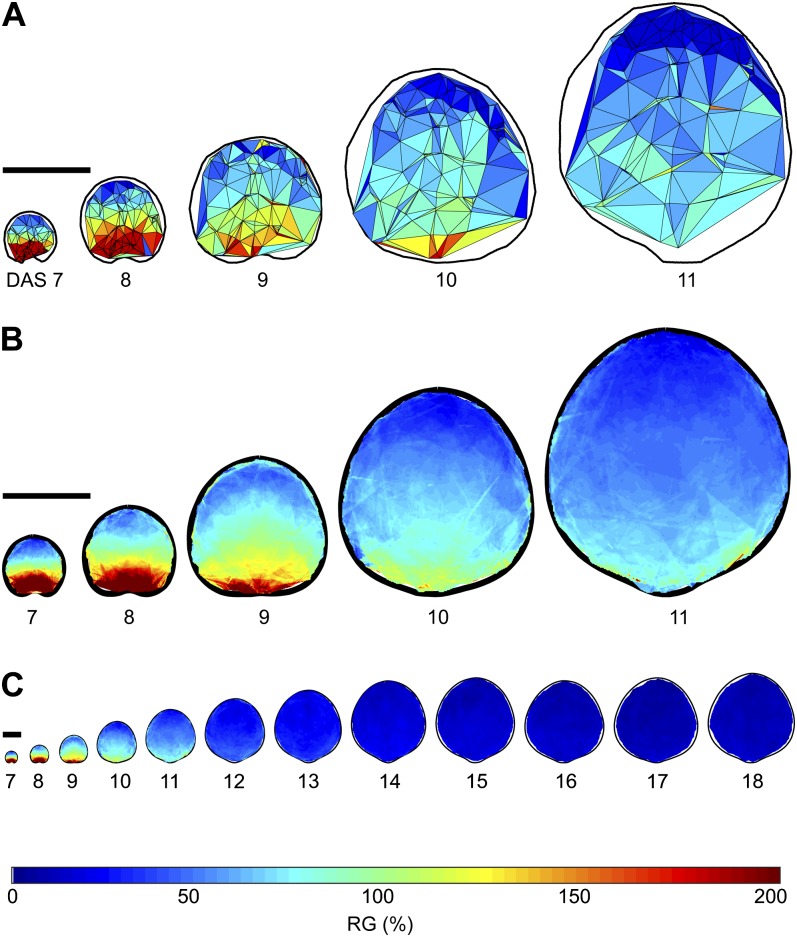
Figure 2.

Figure 2.

Open in a new tab

Spatial maps of RGs over time. A, Spatial maps of RG for one leaf for DAS7 to DAS11. The color of each triangle indicates the percentage increase in area over the course of 1 d, according to the color scale below. B, Mean spatial maps of RG for DAS7 to DAS11 based on the average of 12 to 23 samples per time point. C, Mean spatial maps of RG for all time points quantified in this study, DAS7 to DAS18. Bars = 1 mm. For more information, see Supplemental Figure S2.

Making Mean Spatial Growth Maps

Because there is inherent variability in growth patterns between samples, we use warping procedures adapted from Rolland-Lagan et al. (2009) to generate mean growth maps and related se maps based on multiple samples for each time point. In particular, we track the growth of the first leaf in several plants and for each time point calculate the average leaf outline of the samples. Growth data for each sample can then be mapped to the average leaf shape through warping. As all samples for a given time point are overlaid, we can then calculate average growth parameters for each point on the average leaf surface. This yields mean growth parameter maps for each time point and reveals the average behavior of tissue. The number of samples used in the mean map calculations varies in space and time (Supplemental Fig. S3A), with most areas and most time points having 12 to 15 samples. To illustrate the result of combining data from multiple samples, in Figure 2B we show the mean RG spatial maps for the same time points (DAS7–DAS11) and on the same size and color scale as that of the RG maps shown for the individual leaf sample in Figure 2A. Spatial means of the scaling factors, RG, anisotropy, and associated se values of the means are displayed as surface color maps on the mean leaf shape, and angles of the maximal direction of growth and the rotation of tissue are displayed as lines, with the orientation of a line indicating the direction of growth or rotation. We only display mean values on the surface maps for locations where the number of samples is at least three.

Relative Growth Values Follow a Tip-to-Base Gradient and Decrease over Time

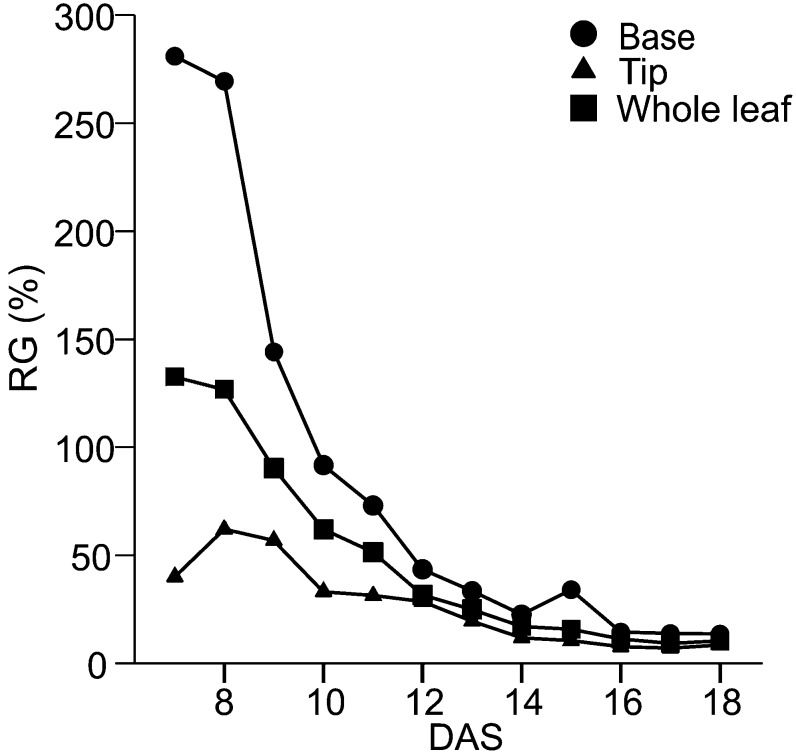
In Figure 2C, we show the mean maps of RG for all of the time points analyzed. Temporally, we see that growth slows down over the course of development and that the changes in the mean leaf size accordingly become much smaller at later time points. To further evaluate temporal changes in leaf growth, we took the average of all the values in the top and bottom quarters of the mean spatial maps for each DAS and plotted them over time (Fig. 3). Overall, growth appears to be declining at an exponential rate, and the decline in RG at the leaf base is much higher than the decline in RG at the leaf tip at earlier time points, with the difference in growth rates between leaf base and leaf tip decreasing over time.

Figure 3.

Figure 3.

Open in a new tab

RGs of the whole leaf and leaf base and tip over time. The values for the whole leaf are computed from the average of all the values across the mean spatial map of RG. The values for the leaf base and tip are computed from an average of the bottom and top quarters of the mean RG spatial map, respectively.

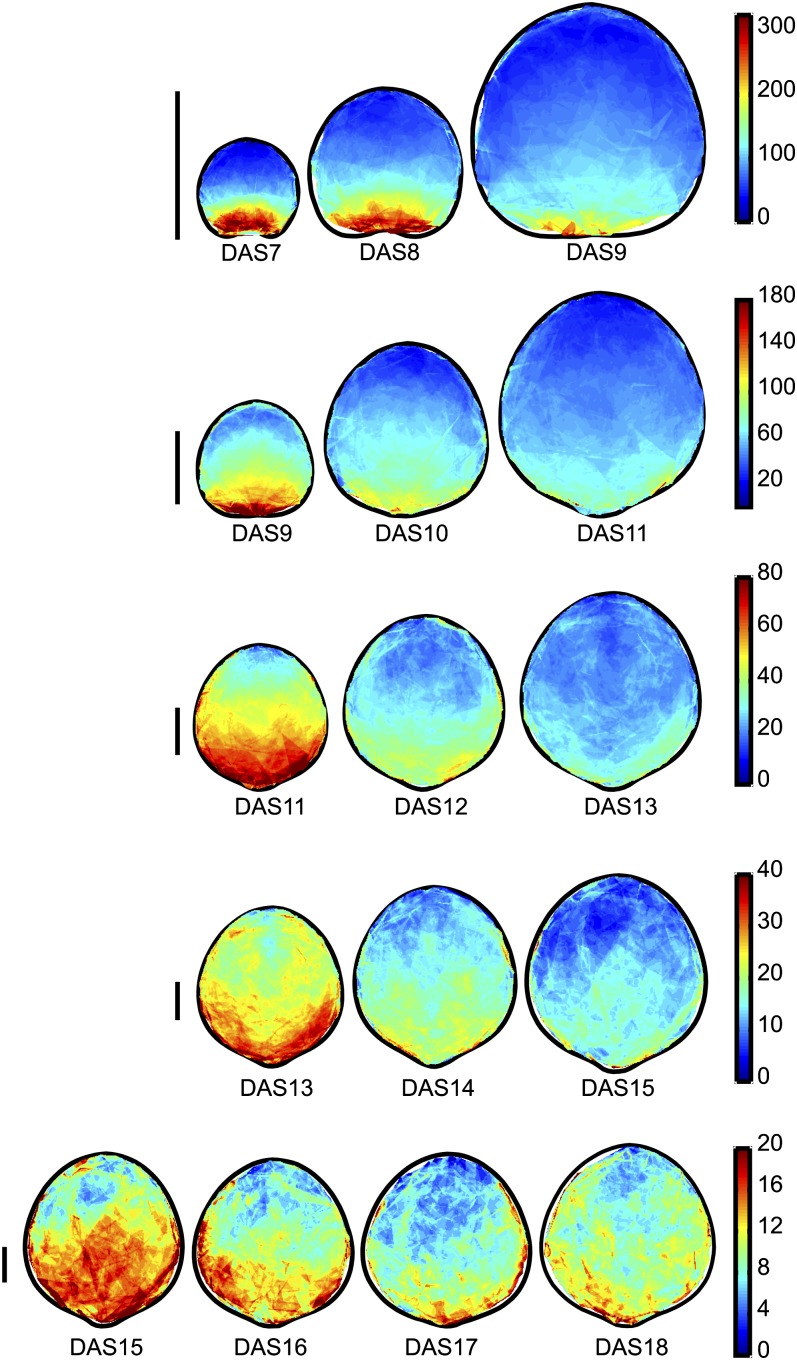
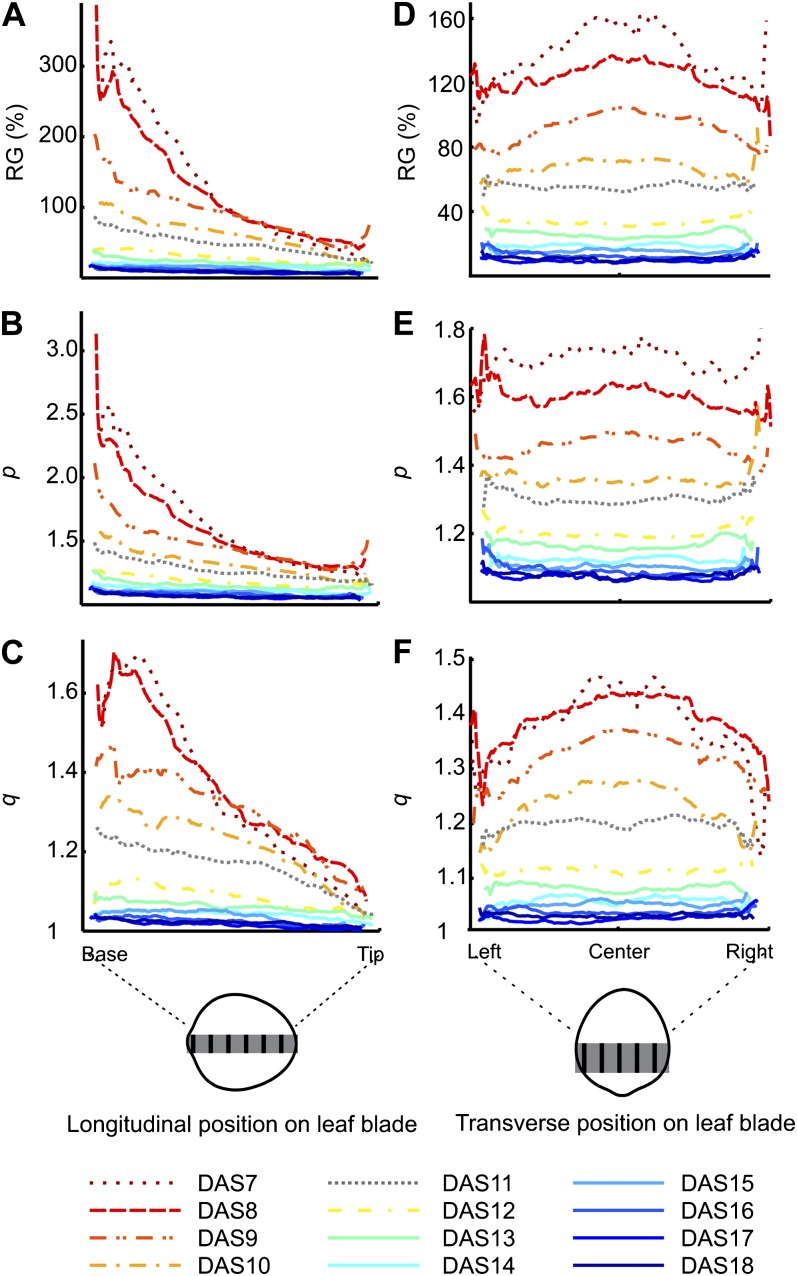
Since the leaf size and range of RGs change drastically over time, in Figure 4, we separate the growth maps into groups of three (DAS7 to -9, DAS9 to -11, DAS11 to -13, DAS13 to -15, and DAS15 to -18) and show RG for each group using a different color scale. This shows a clear proximodistal growth gradient, with RG highest at the base and lowest at the tip for all time points. To better assess and describe the proximodistal growth gradient, we take a strip of values along the midrib of the mean RG maps and plot the average of the values in that strip at each position along the leaf proximodistal axis (Fig. 5A). This shows that the slope of the growth gradient decreases significantly over time.

Figure 4.

Figure 4.

Open in a new tab

Mean spatial maps of RG for DAS7 to DAS18, with groups of time points on different color scales. RG (percentage increase in area over the course of 1 d) values are indicated by the color according to the color scales shown on the right. The time points are divided into groups of three (with each group overlapping by 1 DAS), each shown on a different line on a different color scale (right), so that the spatial and temporal patterns can be seen clearly. Bars on the left = 1 mm.

Figure 5.

Figure 5.

Open in a new tab

Proximodistal and transverse patterns of growth parameters. A to C, Proximodistal gradient of RG (A), p (B), and q (C). As illustrated in the diagram below the graphs, we take a strip of values along the midline of the mean spatial maps (in gray) and plot the average of the values in that strip at each position along the leaf proximodistal axis (i.e. averaging occurs along the direction of the black lines within the gray strip). D to F, Transverse gradient shapes of RG (D), p (E), and q (F). As illustrated in the diagram below the graphs, we take a strip of values across the width of the mean spatial maps (in gray) and plot the average of the values in that strip at each position along the leaf transverse axis (i.e. averaging occurs along the direction of the black lines within the gray strip).

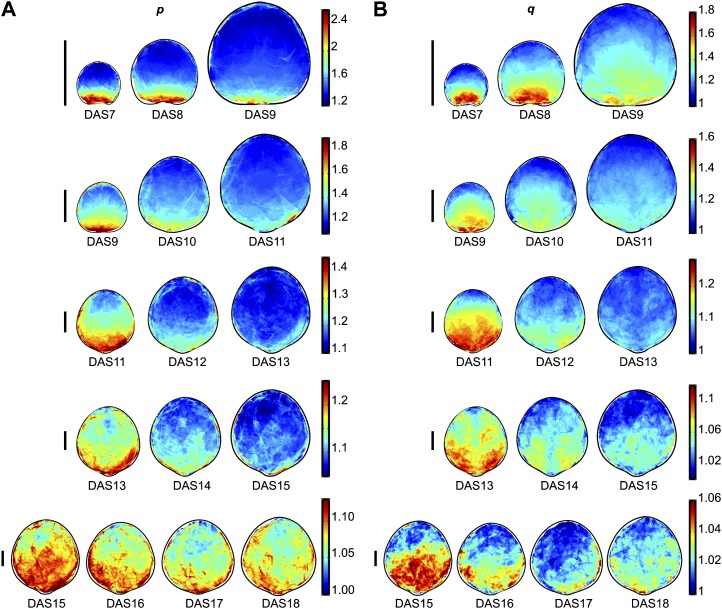
The scaling factors in the direction of maximal and minimal growth, p (Fig. 6A) and q (Fig. 6B), respectively, both follow the same trend as RG, with values decreasing over time and decreasing from base to tip. p and q also decline faster at early time points and decline by a greater amount at the base than at the tip over the course of development (Supplemental Fig. S4, A and B). The proximodistal gradients of p and q are slightly different, as p follows an exponential decline from base to tip (Fig. 5B) while q declines more linearly (Fig. 5C).

Figure 6.

Figure 6.

Open in a new tab

Mean spatial maps of scaling factors p (A) and q (B), representing growth along the maximal and minimal directions of growth, respectively. The time points are divided into groups of 3 to 4 d (with each group overlapping the previous group by 1 d), each shown on a different line on a different color scale (right) so that the spatial and temporal patterns can be seen clearly. The maps are scaled to the relative mean leaf sizes for each DAS, and the bars on the left = 1 mm. Color scales indicate the scaling factor along the maximal (A) or minimal (B) direction of growth over the course of a 1-d interval. For more information, see Supplemental Figure S3.

The Shape of the Growth Gradient Isolines Is Initially Downward Curving But Becomes Straighter over Time and Differs between p and q

The two-dimensional shape of gradients on maps can be assessed visually by identifying isolines, i.e. lines along which parameter values are the same. The RG gradient isolines have a downward-curving shape for DAS7 through DAS10, and then in DAS11 to DAS13 appear to take on a straighter and even slightly upward-curving shape. From DAS13 onward, the gradient still exists but the shape of the gradient becomes much less distinctive. The relative se of the mean RG (Supplemental Fig. S3B) is generally higher at those later time points, ranging from 1% to 10% for DAS7 to DAS11 and from 10% to 30% for DAS12 to DAS18, except for areas around the leaf perimeter, where the relative se is high due to lower sample coverage.

To better assess our observations about the shape of the RG gradient isolines, we took a section along the width of the mean maps and plotted the average of the values at each transverse position in that strip as a function of the position along the leaf transverse axis (Fig. 5D). Here, we can clearly see that the RG gradient is downward curving for DAS7 to DAS10, with values highest at the middle of the leaf and lowest at the sides. At later time points, it seems to be the opposite, although the difference between values at the middle and sides of the leaf is very small. We carried out the same assessment for the maps of p and q and found that they do not have the same gradient shape as each other. For p, the gradient appears to be very slightly downward curving from DAS7 to DAS9 and slightly upward curving from DAS13 onward (Fig. 5E). The difference in q between the middle and sides of the leaf, on the other hand, is much more dramatic and shows a very strong downward curvature for DAS7 to DAS11, with values at the middle being up to approximately 15% higher than at the sides. From then on, the gradient shape of q appears to be relatively straight (Fig. 5F). These observed gradient shapes are statistically significant (Supplemental Table S1; Supplemental Fig. S4, C and D).

Another interesting pattern is seen in spatial maps of q (Fig. 6B), but not p, for DAS11 to DAS14. We see lower values along the middle of the leaf, corresponding to the position of the midvein, and particularly in DAS13 we also see two “branches” of lower values extending out fairly symmetrically from the midvein at about 45°.

Anisotropy Is Strongest at the Leaf Base and Leaf Perimeter and Decreases over Time

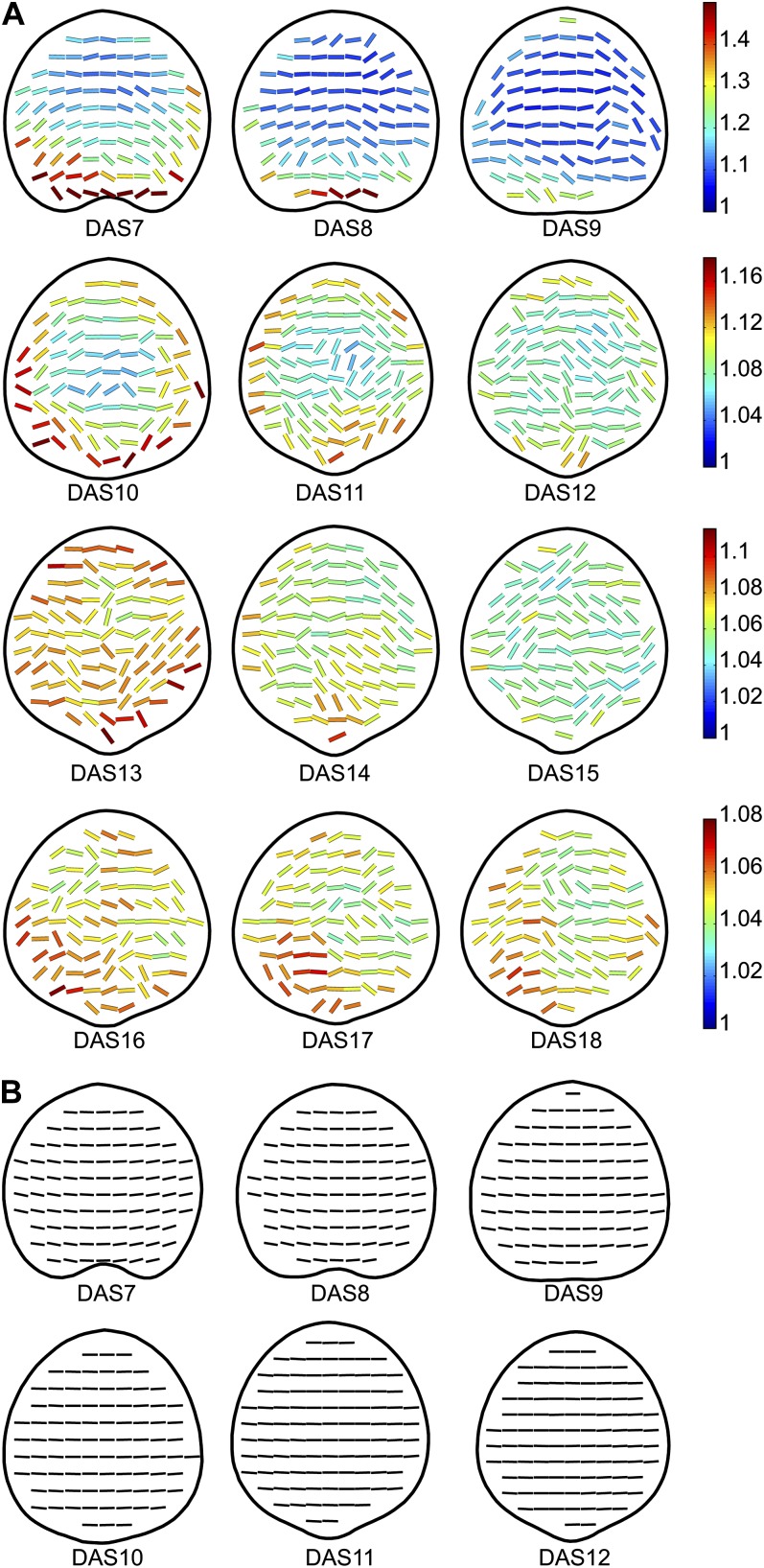
Figure 7A shows spatial maps of the angles of the maximal direction of growth, colored according to anisotropy. Like relative growth values, growth anisotropy values also decrease over time. Spatially, growth anisotropy appears to follow a gradient where the values are highest at the base and perimeter of the leaf. However, the base and perimeter also correspond to the areas with higher relative se values (up to 15%) at the earlier time points (Supplemental Fig. S5A). This gradient becomes less distinctive after DAS12, while the relative se of anisotropy is very low, generally under 2%.

Figure 7.

Figure 7.

Open in a new tab

Mean spatial maps of growth directionality and tissue rotation. A, Mean spatial maps of anisotropy and main growth direction for DAS7 to DAS18. The orientation of each line represents the direction of maximal growth at that point, and the color of the line indicates the growth anisotropy (p/q) as per the color scales on the right. B, Mean spatial maps of tissue rotation for DAS7 to DAS12. The orientation of the lines represents the rotation of the tissue measured from the positive x axis, with horizontal lines corresponding to no rotation (0°). For more information, see Supplemental Figure S4.

The Main Direction of Growth Varies in Space

The maximal direction of growth seems to follow a gradient where it is fairly horizontal in central regions of the leaf and bends in outer regions to be more in line with the angle of the nearest leaf margin, with the exception of areas where the leaf margin is parallel to the proximodistal axis of the leaf, in which case the angle of principal direction is oriented perpendicularly to the leaf margin. Another exception to this rule appears to exist from DAS11 to DAS14, where the main direction of growth along the midline of the leaf seems to align more closely with the proximodistal axis of the leaf. At DAS13, the main direction of growth is also aligned along two branches extending at about 45° on each side of the leaf midline. In order to assess the variability in growth directions at each point of the leaf, we can calculate circular variance. Circular variance provides a measure of the spread of angles, ranging from 0 to 1, with values close to 0 indicating a tighter clustering of the values around the mean (Zar, 1996). The circular variance of the mean growth directions is fairly high (Supplemental Fig. S5B), with most values in the range of 0.2 to 0.8 at DAS7, 0.4 to 0.8 at DAS8 to DAS9, and 0.6 to 0.8 at the remaining time points.

Tissue Rotates Upward at the Outer Edges of the Leaf by an Angle That Decreases over Time

Mean spatial maps of the rotation of tissue are shown in Figure 7B. Tissue at the leaf tip and along the center does not rotate, while tissue on the left rotates slightly clockwise and tissue on the right rotates slightly counterclockwise. The amount of rotation decreases over time, with rotation of up to ±15° at DAS7, ±12° at DAS8, and ±10° at DAS9. At later time points, the angles of rotation become very small. The circular variance of the rotation angles is very low (mostly in the range of 0–0.05) for all time points (Supplemental Fig. S5C).

DISCUSSION

In this paper, we have presented a novel technique for quantifying leaf growth patterns in vivo over several days without disturbance to the plant. Growth can be followed from a much earlier stage of development than has previously been possible, and various growth parameters can be computed from 3D coordinates of landmarks. Leaf growth phenotypes can be quantified relatively quickly using several semiautomated custom computational tools, and mean spatial growth maps can be generated to analyze and compare the mean leaf growth patterns of several groups of plants. In the following, we discuss the results we obtained as well as the method itself.

Changes in the Growth Gradient Shape over Time Suggest Possible Mechanisms for the Control of Leaf Growth and Shape

Our results showed that the RGs across the leaf decrease over time and have a very distinct proximodistal gradient, with values highest at the base and lowest at the tip. At early time points, isolines in the growth gradient have a very clear downward-curving pattern. This suggests that the signal that gives rise to the gradient is a growth-promoting/maintaining signal originating from the leaf base. At approximately DAS11, the shape of the isolines in the growth gradient becomes straighter or even upward curving. This change in gradient shape over time may reflect interplay between a growth-promoting signal originating from the leaf base from early time points onward and a growth-inhibiting signal originating from the leaf tip at later time points. Interestingly, the KLUH gene has been shown to be expressed at the leaf base during early development and was proposed to generate a proximodistal concentration gradient of a mobile growth factor in the leaf (Anastasiou et al., 2007; Kazama et al., 2010). On the other hand, the cell division patterns in leaves of the snapdragon (Antirrhinum) cincinnata mutant support the existence of a growth-repressing signal originating from the leaf tip (Nath et al., 2003).

The isolines of the growth gradient may affect the 3D curvature of the leaf. A downward-curving growth gradient indicates that at any point along the proximodistal axis of the leaf, the sides of the leaf grow slower than the center. This should lead to an increased curvature of the leaf across the transverse axis during the days where the gradient is clearly downward curving; this concept is exaggerated in the Arabidopsis peapod mutant, whose dome-shaped leaf phenotype is explained by excess growth of the lamina but not the perimeter (White, 2006). By the same token, as the growth gradient becomes straighter or upward curving, the leaf transverse curvature should decrease. The relationship between growth gradients and leaf shape, including leaf curvature, will be discussed in more detail in a related paper.

Differences in the Patterns of p and q Support the Hypothesis That Expansion in the Maximal and Minimal Directions of Growth Are Regulated Independently

The proximodistal gradient and the shape of the gradient isolines differed between the scaling factors p and q, with p having a more exponential decline in values from base to tip compared with the more linear decline of q, and p having relatively straight gradient isolines throughout development in comparison with the very strongly downward-curving gradient isolines of q in early development. Since p and q are directly implicated in the calculation of the relative growth and anisotropy, the patterns we observe in p and q may simply be the result of mechanisms controlling growth and anisotropy. However, such differences in their patterns could also indicate that p and q are under the control of different signals that may diffuse at different rates in the leaf and originate from different positions. This offers support to the hypothesis of Baskin (2005) that expansion in the maximal and minimal directions are regulated by distinct molecular mechanisms.

Based on narrow-leaf mutants with reduced cell expansion in the mediolateral axis and short-leaf mutants with reduced cell elongation in the proximodistal axis, Tsuge et al. (1996) have similarly proposed that leaf expansion involves independent processes controlling cell elongation along the leaf length and leaf width. However, our results on the anisotropy and direction of growth show that growth orientation varies spatially and does not occur distinctly along the length and width axes of the leaf. Therefore, it may be more appropriate to consider effects on expansion in the maximal and minimal growth directions, like Baskin (2005), rather than along the leaf width and length specifically. It would be interesting to quantify the growth patterns in these mutants to see how those differ from the wild type in terms of growth direction, p, and q.

A Polarizing Substance May Control Growth Directionality

Kennaway et al. (2011) recently outlined three possibilities regarding the control of growth directionality in developing tissues. The first possibility is that directions of growth are defined in the leaf tissue early in development and remain fixed locally, in which case any change in the pattern of growth directions at the whole organ level would reflect rotation of the tissue within the organ. Alternatively, growth orientation could be set globally through external information, such as gravity. In this case, the pattern of growth directions at the whole organ level would remain the same as the organ develops. Lastly, growth direction may be governed by a polarizing substance that continues to diffuse through the tissue throughout growth. If this were the case, it would be impossible to predict the growth direction pattern without knowing details such as the source and diffusion coefficients of the proposed substance. Our results do not support the first two possibilities, because changes in growth orientation patterns do not correspond to tissue rotation (Supplemental Fig. S5, D and E), and although there are some general trends in the direction of growth that remain consistent, the pattern does not remain exactly the same over time. Therefore, our results are more consistent with the idea that growth direction is governed by a polarizing substance. Growth directionality may also be influenced by mechanical forces in the leaf, which is discussed in the next section in the context of the vascular system.

Growth Patterns Suggest Growth Differences between Vascular and Nonvascular Tissue

Digital image sequence analysis studies have reported lower growth in leaf vascular tissue compared with surrounding nonvascular tissue (Christ, 2005; Wang et al., 2011). Moreover, it has been suggested that there are tensile stresses along veins (Bohn et al., 2002; Corson et al., 2009) and that growth direction can be dictated by mechanical stresses in the tissue (Hamant et al., 2008). It is likely, therefore, that growth in vascular tissue is oriented along vascular paths. In our study, we did not quantify growth at a sufficiently high spatial resolution to clearly distinguish vascular regions in individual samples, and since venation patterns vary, the vascular and interveinal regions of the different samples would not be perfectly aligned in the making of the mean spatial maps. However, at DAS11 to DAS14, q (but not p) values are lower along the midline of the leaf (where the midvein is located) and along two lines extending out on each side of the midline, which may correspond to the positions of secondary veins. Maps of anisotropy and growth direction further show that the maximal direction of growth tends to be oriented along those same presumed vein positions. These results suggest that once veins have differentiated (Scarpella et al., 2006), growth in the vasculature occurs preferentially along vascular paths and that growth along vein width is reduced compared with growth along the minimal direction of growth in the surrounding tissue.

Accuracy and Reliability of the Method and Results

The nearly perfect bilateral symmetry of the growth patterns we observed provides strong evidence for the accuracy, robustness, and reliability of the method described. Moreover, the growth patterns we observed are consistent with other leaf growth analyses, which have shown a similar proximodistal gradient in growth rates in Arabidopsis (Wiese et al., 2007) as well as in other species, such as tobacco (Nicotiana tabacum; Avery, 1933; Poethig and Sussex, 1985; Walter and Schurr, 1999; Walter et al., 2003), sunflower (Helianthus annuus; Granier and Tardieu, 1998), grape (Vitis vinifera; Wolf et al., 1986), spinach (Spinacia oleracea; Saurer and Possingham, 1970), cocklebur (Xanthium pensylvanicum; Maksymowych, 1959; Erickson, 1966), ivy (Hedera helix; Wang et al., 2011), and poplar (Populus spp.; Taylor et al., 2003). An exception to this pattern was shown in soybean (Glycine max; Ainsworth et al., 2005), where no spatial gradient was observed, leading the authors to conclude that the mechanisms of leaf growth in soybean may be different from that in other species. The soybean study followed growth from when the leaves were already 30 mm in length. Therefore, it would be interesting to see whether a growth gradient is detectable in the soybean leaf at earlier time points, as our results show that the proximodistal growth gradient in Arabidopsis leaves becomes less steep as they mature.

Measurements of growth directionality in leaves were provided by Richards and Kavanagh (1943) and Erickson (1966). These measurements were made at relatively late stages of development, when growth was nearly isotropic, although Richards and Kavanagh (1943) did show that leaf growth becomes more isotropic over time, which concurs with our findings.

While a spatial pattern is still discernible in the mean RG maps for the later stages, it is less clear and se values are higher. This could reflect more variation in growth among samples at the later time points, as we also saw that the leaf sizes diverge more as they mature. However, when we looked at spatial maps of individual samples, we also saw much “patchier” patterns at later time points, with regions of high relative growth interspersed with regions of lower relative growth, compared with clearer gradients at the earlier time points. This patchiness has also been noted to some extent in other leaf growth analyses (Christ, 2005; Wiese et al., 2007). Christ (2005) hypothesized that this could be associated with patchy stomatal conductance, as spatial variation in stomatal openings could result in small spatial heterogeneities in turgor pressure and thus growth. We propose that this increased patchiness at later time points could also be associated with the differentiation of cells as the leaf matures, as different cell types may have different cell wall properties that could respond differently to growth cues. This theory is supported by a recent study showing that stomatal guard cells follow substantially different growth dynamics than those of neighboring epidermal pavement cells (Asl et al., 2011). Changes in the flux or position of growth signal sources in the leaf blade over time (Aloni et al., 2003) could also play a role.

Limitations and Future Improvements

Our microscopy setup and experimental techniques cannot be used to monitor growth before the leaf surface is exposed. Those earlier stages correspond to periods when cell divisions are occurring throughout the leaf primordium (Kazama et al., 2010) and therefore would be particularly interesting to capture. The computational methods presented could be adapted to quantify growth in those earlier stages using other 3D microscopy systems, such as confocal microscopy, optical projection tomography, or selective plane illumination (for review, see Ntziachristos, 2010).

As the microscopy setup presented requires that landmarks be visible from one vantage point, it cannot be used to quantify growth in severely wrinkled leaves or those that have curved under themselves. However, depending at which stage the leaf curling/wrinkling occurs, it may be possible to at least identify the alterations in growth patterns that lead to the curvature/folds.

The leaf shape and surface extraction, particle digitization, and particle-tracking algorithms have been mostly automated, but we note that they do need to be visually verified by the user and, in some cases, manually adjusted. We are working toward a fully automated analysis for future versions of the programs.

3D length and width measurements follow a logarithmic curve similar to what has been observed in other studies. A slight drop in leaf size at DAS16 appears to be due to the fact that the leaves of our secondary data set, collected a few weeks after the original data set (see Supplemental Fig. S1A and Supplemental Materials and Methods S1), continued to grow from DAS14 to DAS15 at a higher rate than the original data set. Although temperature, humidity, and light are controlled in our laboratory, it has been shown that even small variations in growing conditions and handling of plants can lead to significant differences in leaf growth phenotypes (Massonnet et al., 2010). Therefore, in order to compare growth patterns from data sets collected at different times, we suggest growing a set of wild-type plants along with the set of plants being analyzed. Simple two-dimensional measurements of leaf area or leaf width of those wild-type plants over time could then be used to generate a reference growth curve to be compared between experiments for calibration purposes.

Ease of Use and Wider Applicability of the Methods and Computational Tools

The methods and software presented allow for easy, high-throughput phenotyping of spatiotemporal leaf growth patterns for the largest range of developmental stages to date.

The processing time is relatively short and makes it feasible to capture growth information for many leaves over many time points. The data acquisition time depends on which developmental stages are to be followed, with each imaging session taking roughly 2 h for 15 leaves. Running through the programs, from image analysis to the generation of mean spatial maps, for 15 leaves over 10 time points, for example, would take less than 40 h. A real-time demonstration for one sample tracked from one time point to the next is shown in Supplemental Video S3.

In this study, we used a line of plants lacking trichomes to make it easier to extract the leaf surface and particle 3D coordinates, but we have developed tools to automatically crop trichomes out of the depth map while preserving the leaf surface data (Supplemental Materials and Methods S1; Supplemental Fig. S6) and tested that particle location can be extracted even in the presence of trichomes. Thus, average leaf growth patterns can be quantified for wild-type and mutant plants in a wide variety of species, opening the way for standardized comparative analyses of growth patterns. We expect that such analyses will be instrumental in elucidating the mechanisms of growth pattern formation and the control of leaf shape.

Our analysis was performed on the first rosette leaves of Arabidopsis, as they are the first leaves to appear and are commonly used to compare the morphology of leaf shape in wild-type and mutant plants (Pérez-Pérez et al., 2011). However, the same technique can also be used to track growth in later leaves if desired, as leaf overlap is usually minimal (Leister et al., 1999). If necessary, any leaves obstructing the view can be moved out of the way during imaging.

The tracking and growth-computing software we presented could be adapted to quantify growth at the surface of other organs or organisms, as long as they are visually accessible and have recognizable landmarks (applied topically, naturally occurring, or genetically engineered). The software for computing average growth maps could also be used on growth pattern data sets collected using other methods (Dumais and Kwiatkowska, 2002).

CONCLUSION

The method outlined in this paper makes it possible to describe average spatiotemporal growth patterns at the 3D surface of leaves. Mean spatial maps of growth parameters from multiple samples show clear spatiotemporal patterns, which may reflect the influence of morphogenetic signals. For instance, if a signal promoting or restricting growth is produced at a given position on the leaf and during a given time, any disruption to its localization or timing will be reflected in the leaf growth patterns. Generating mean growth maps from multiple samples will make it possible to perform standardized comparative analyses of growth patterns between wild-type and mutant plants and/or between species, and under different environmental conditions. Such comparative analyses may shed light on the morphogenetic mechanisms controlling leaf growth and shape. Similar approaches to the ones presented in this paper could also be applied to explore the control of morphogenesis in other organs and organisms.

MATERIALS AND METHODS

Plant Materials and Growth Conditions

In this study, we used Arabidopsis (Arabidopsis thaliana) ecotype Landsberg erecta glabra1-1, available from the Arabidopsis Biological Resource Center as seed stock number cs64. We follow the growth of one of the first two rosette leaves on each plant, chosen randomly, as is standard practice (Scarpella et al., 2006), since they develop almost simultaneously.

Seeds are surface sterilized and imbibed at 4°C in the dark for 4 d, then sown in autoclaved Pro-Mix potting soil (Premier) with five plants per 3- × 3-inch pot, and grown under an ArabiSun lighting system (Lehle Seeds), with 27-W mercury bulbs providing a light intensity of 150 μmol m−2 s−1, on a 16/8-h light/dark cycle, with watering as needed to keep the soil moist. The light shelves and microscope are in the same room, in which the temperature is maintained at 22°C and humidity at 25% to 30%. To image the leaves, each pot is removed from the light shelves (during the light phase of the cycle) and placed on the microscope stage, then it is returned to the light shelves after imaging (which takes a maximum of 25 min per pot).

Plants with similar germination times and sizes are used for analysis. We use one group to track growth from DAS7 to DAS12, a second to track DAS12 to DAS18, and a third to obtain additional information for DAS10 to DAS14 (for further details, see Supplemental Materials and Methods S1).

Particles and Application Technique

We use 6.2- and 29.6-μm SPHERO Fluorescent Yellow Particles (Spherotech), using the former on smaller leaves (up to DAS14) and the latter on larger leaves. We start by making strong and weak dilutions of the particles in distilled water: approximately 2 and 10 μL mL−1 for the 6.2-μm particles and 40 and 200 μL mL−1 for the 29.6-μm particles. If allowed to sit for several minutes, the particles will fall to the bottom of the solution, at which point most of the water can be removed from the top and replaced with fresh water, to help remove any chemicals present in the original particle solution. After this, the solutions are vortexed frequently before and during application to prevent settling and clumping of the particles. A syringe with a 28-gauge needle is used to apply the particle solution to the leaf surface, starting with the weaker solution. If the desired leaf can be fully covered by a spherical droplet of the solution, the particles are left to settle onto the leaf surface (approximately 20 min). At this time, the droplet of water can be removed by touching it with a piece of tissue or drawing it off with the syringe, allowing any remaining water to evaporate. More information about the particle application technique can be found in Supplemental Materials and Methods S1.

Microscopy and Image Acquisition

Z-stack images are obtained with a Leica Z16 APO A MacroFluo motorized fluorescence macroscope using a Leica DFC350 camera (Leica Microsystems). The Leica Application Suite Montage Module (Leica Microsystems) is used to generate the multifocus images and depth map. To visualize the fluorescent yellow particles, we use a GFP filter cube (excitation filter BP 470/40, dichromatic mirror 500, suppression filter BP 525/50), with the intensity of the fluorescent light source kept as low as possible. Further details on image acquisition settings are available in Supplemental Materials and Methods S1.

Software and Computations

All custom-written programs are developed in Matlab version 2010a(Mathworks), using many Matlab built-in functions as well as functions from the Matlab Image Processing Toolbox and Statistics Toolbox. Statistical analyses are performed using IBM SPSS 18 software. Further details on the software we developed can be found in Supplemental Materials and Methods S1. The software demonstration in Supplemental Video S3 is made with Adobe Captivate 5.5 (Adobe Systems).

Supplemental Data

The following materials are available in the online version of this article.

Supplementary Material

Supplemental Data
supp_159_1_27__index.html (1.4KB, html)

Acknowledgments

We thank Rebecca Assaf for sharing data from a sister project used for the early development of some computational tools, Mona Hosseini-Abardeh for her participation in early stages of this work, Alice Szymanski for assistance with the collection of a preliminary data set, Ruth Stadler and Norbert Sauer for providing seeds of the AtSuc2prom:GFP plants used for Supplemental Figure S1C, Sophie Chiasson-Gould for providing the image used in Supplemental Figure S6, Konrad Gajewski for help with gradient description terminology, and Alp Oran for his assistance with creating the software demonstration file shown in Supplemental Video S3.

References

  1. Ainsworth EA, Walter A, Schurr U. (2005) Glycine max leaflets lack a base-tip gradient in growth rate. J Plant Res 118: 343–346 [DOI] [PubMed] [Google Scholar]
  2. Aloni R, Schwalm K, Langhans M, Ullrich CI. (2003) Gradual shifts in sites of free-auxin production during leaf-primordium development and their role in vascular differentiation and leaf morphogenesis in Arabidopsis. Planta 216: 841–853 [DOI] [PubMed] [Google Scholar]
  3. Anastasiou E, Kenz S, Gerstung M, MacLean D, Timmer J, Fleck C, Lenhard M. (2007) Control of plant organ size by KLUH/CYP78A5-dependent intercellular signaling. Dev Cell 13: 843–856 [DOI] [PubMed] [Google Scholar]
  4. Asl LK, Dhondt S, Boudolf V, Beemster GTS, Beeckman T, Inzé D, Govaerts W, De Veylder L. (2011) Model-based analysis of Arabidopsis leaf epidermal cells reveals distinct division and expansion patterns for pavement and guard cells. Plant Physiol 156: 2172–2183 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Avery GS., Jr (1933) Structure and development of the tobacco leaf. Am J Bot 20: 565–592 [Google Scholar]
  6. Baskin TI. (2005) Anisotropic expansion of the plant cell wall. Annu Rev Cell Dev Biol 21: 203–222 [DOI] [PubMed] [Google Scholar]
  7. Bernd J. (1997) Digital Image Analysis. Springer, New York [Google Scholar]
  8. Bohn S, Andreotti B, Douady S, Munzinger J, Couder Y. (2002) Constitutive property of the local organization of leaf venation networks. Phys Rev E Stat Nonlin Soft Matter Phys 65: 061914. [DOI] [PubMed] [Google Scholar]
  9. Christ MM. (2005) Temporal and spatial patterns of growth and photosynthesis in leaves of dicotyledonous plants under long-term CO2- and O3-exposure. PhD thesis. Heinrich Heine University, Duesseldorf, Germany [Google Scholar]
  10. Coen E, Rolland-Lagan AG, Matthews M, Bangham JA, Prusinkiewicz P. (2004) The genetics of geometry. Proc Natl Acad Sci USA 101: 4728–4735 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Corson F, Adda-Bedia M, Boudaoud A. (2009) In silico leaf venation networks: growth and reorganization driven by mechanical forces. J Theor Biol 259: 440–448 [DOI] [PubMed] [Google Scholar]
  12. Cosgrove DJ. (2005) Growth of the plant cell wall. Nat Rev Mol Cell Biol 6: 850–861 [DOI] [PubMed] [Google Scholar]
  13. Cronk Q. (2009) The Molecular Organography of Plants. Oxford University Press, Oxford [Google Scholar]
  14. Dumais J, Kwiatkowska D. (2002) Analysis of surface growth in shoot apices. Plant J 31: 229–241 [DOI] [PubMed] [Google Scholar]
  15. Erickson RO. (1966) Relative elemental rates and anisotropy of growth in area: a computer programme. J Exp Bot 17: 390–403 [Google Scholar]
  16. Goodall CR, Green PB. (1986) Quantitative analysis of surface growth. Bot Gaz 147: 1–15 [Google Scholar]
  17. Granier C, Tardieu F. (1998) Spatial and temporal analyses of expansion and cell cycle in sunflower leaves: a common pattern of development for all zones of a leaf and different leaves of a plant. Plant Physiol 116: 991–1001 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hamant O, Heisler MG, Jönsson H, Krupinski P, Uyttewaal M, Bokov P, Corson F, Sahlin P, Boudaoud A, Meyerowitz EM, et al. (2008) Developmental patterning by mechanical signals in Arabidopsis. Science 322: 1650–1655 [DOI] [PubMed] [Google Scholar]
  19. Kazama T, Ichihashi Y, Murata S, Tsukaya H. (2010) The mechanism of cell cycle arrest front progression explained by a KLUH/CYP78A5-dependent mobile growth factor in developing leaves of Arabidopsis thaliana. Plant Cell Physiol 51: 1046–1054 [DOI] [PubMed] [Google Scholar]
  20. Kennaway R, Coen E, Green A, Bangham A. (2011) Generation of diverse biological forms through combinatorial interactions between tissue polarity and growth. PLoS Comput Biol 7: e1002071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Leister D, Varotto C, Pesaresi P, Niwergall A, Salamini F. (1999) Large-scale evaluation of plant growth in Arabidopsis thaliana by non-invasive image analysis. Plant Physiol Biochem 37: 671–678 [Google Scholar]
  22. Maksymowych R. (1959) Quantitative analysis of leaf development in Xanthium pensylvanicum. Am J Bot 46: 635–644 [Google Scholar]
  23. Maksymowych R. (1962) An analysis of leaf elongation in Xanthium pensylvanicum presented in relative elemental rates. Am J Bot 49: 7–13 [Google Scholar]
  24. Massonnet C, Vile D, Fabre J, Hannah MA, Caldana C, Lisec J, Beemster GTS, Meyer RC, Messerli G, Gronlund JT, et al. (2010) Probing the reproducibility of leaf growth and molecular phenotypes: a comparison of three Arabidopsis accessions cultivated in ten laboratories. Plant Physiol 152: 2142–2157 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Micol JL. (2009) Leaf development: time to turn over a new leaf? Curr Opin Plant Biol 12: 9–16 [DOI] [PubMed] [Google Scholar]
  26. Nath U, Crawford BC, Carpenter R, Coen E. (2003) Genetic control of surface curvature. Science 299: 1404–1407 [DOI] [PubMed] [Google Scholar]
  27. Ntziachristos V. (2010) Going deeper than microscopy: the optical imaging frontier in biology. Nat Methods 7: 603–614 [DOI] [PubMed] [Google Scholar]
  28. Pérez-Pérez JM, Rubio-Díaz S, Dhondt S, Hernández-Romero D, Sánchez-Soriano J, Beemster GTS, Ponce MR, Micol JL. (2011) Whole organ, venation and epidermal cell morphological variations are correlated in the leaves of Arabidopsis mutants. Plant Cell Environ 34: 2200–2211 [DOI] [PubMed] [Google Scholar]
  29. Piazza P, Jasinski S, Tsiantis M. (2005) Evolution of leaf developmental mechanisms. New Phytol 167: 693–710 [DOI] [PubMed] [Google Scholar]
  30. Poethig RS, Sussex IM. (1985) The developmental morphology and growth dynamics of the tobacco leaf. Planta 165: 158–169 [DOI] [PubMed] [Google Scholar]
  31. Richards OW, Kavanagh AJ. (1943) The analysis of the relative growth gradients and changing form of growing organisms: illustrated by the tobacco leaf. Am Nat 77: 385–399 [Google Scholar]
  32. Rolland-Lagan AG, Amin M, Pakulska M. (2009) Quantifying leaf venation patterns: two-dimensional maps. Plant J 57: 195–205 [DOI] [PubMed] [Google Scholar]
  33. Saurer W, Possingham JV. (1970) Studies on the growth of spinach leaves (Spinacea oleracea). J Exp Bot 21: 151–158 [Google Scholar]
  34. Scarpella E, Marcos D, Friml J, Berleth T. (2006) Control of leaf vascular patterning by polar auxin transport. Genes Dev 20: 1015–1027 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Schmundt D, Stitt M, Jähne B, Schurr U. (1998) Quantitative analysis of the local rates of growth of dicot leaves at a high temporal and spatial resolution, using image sequence analysis. Plant J 16: 505–514 [Google Scholar]
  36. Seber GAF. (2008) Cluster Analysis: Multivariate Observations. John Wiley & Sons, Hoboken, NJ, pp 347–394 [Google Scholar]
  37. Strutt D. (2005) Organ shape: controlling oriented cell division. Curr Biol 15: R758–R759 [DOI] [PubMed] [Google Scholar]
  38. Taylor G, Tricker PJ, Zhang FZ, Alston VJ, Miglietta F, Kuzminsky E. (2003) Spatial and temporal effects of free-air CO2 enrichment (POPFACE) on leaf growth, cell expansion, and cell production in a closed canopy of poplar. Plant Physiol 131: 177–185 [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Tsuge T, Tsukaya H, Uchimiya H. (1996) Two independent and polarized processes of cell elongation regulate leaf blade expansion in Arabidopsis thaliana (L.) Heynh. Development 122: 1589–1600 [DOI] [PubMed] [Google Scholar]
  40. Tsukaya H. (2006) Mechanism of leaf-shape determination. Annu Rev Plant Biol 57: 477–496 [DOI] [PubMed] [Google Scholar]
  41. Walter A, Roggatz U, Schurr U. (2003) Expansion kinematics are an intrinsic property of leaf development and are scaled from cell to leaf level at different nutrient availabilities. Plant Biol 5: 642–650 [Google Scholar]
  42. Walter A, Schurr U. (1999) The modular character of growth in Nicotiana tabacum plants under steady-state nutrition. J Exp Bot 50: 1169–1177 [Google Scholar]
  43. Walter A, Silk WK, Schurr U. (2009) Environmental effects on spatial and temporal patterns of leaf and root growth. Annu Rev Plant Biol 60: 279–304 [DOI] [PubMed] [Google Scholar]
  44. Wang L, Beyer ST, Cronk QC, Walus K. (2011) Delivering high-resolution landmarks using inkjet micropatterning for spatial monitoring of leaf expansion. Plant Methods 7: 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. White DW. (2006) PEAPOD regulates lamina size and curvature in Arabidopsis. Proc Natl Acad Sci USA 103: 13238–13243 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Wiese A, Christ MM, Virnich O, Schurr U, Walter A. (2007) Spatio-temporal leaf growth patterns of Arabidopsis thaliana and evidence for sugar control of the diel leaf growth cycle. New Phytol 174: 752–761 [DOI] [PubMed] [Google Scholar]
  47. Wolf SD, Silk WK, Plant RE. (1986) Quantitative patterns of leaf expansion: comparison of normal and malformed leaf growth in Vitis vinifera cv. Ruby Red. Am J Bot 73: 832–846 [Google Scholar]
  48. Zar JH. (1996) Biostatistical Analysis, Ed 3. Prentice Hall, Englewood Cliffs, NJ, pp 591–614 [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Data
supp_159_1_27__index.html (1.4KB, html)
supp_pp.112.194662_194662supplemental.pdf (1.5MB, pdf)
supp_pp.112.194662_194662SUPPLEMENTAL_MATERIAL.doc (23.5KB, doc)
Download video file (975.4KB, mov)
Download video file (673.1KB, mov)
Download video file (15MB, mov)

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES