Normalization and analysis of cDNA microarrays using within-array replications applied to neuroblastoma cell response to a cytokine

Abstract

The quantitative comparison of two or more microarrays can reveal, for example, the distinct patterns of gene expression that define different cellular phenotypes or the genes that are induced in the cellular response to certain stimulations. Normalization of the measured intensities is a prerequisite of such comparisons. However, a fundamental problem in cDNA microarray analysis is the lack of a common standard to compare the expression levels of different samples. Several normalization protocols have been proposed to overcome the variabilities inherent in this technology. We have developed a normalization procedure based on within-array replications via a semilinear in-slide model, which adjusts objectively experimental variations without making critical biological assumptions. The significant analysis of gene expressions is based on a weighted t statistic, which accounts for the heteroscedasticity of the observed log ratios of expressions, and a balanced sign permutation test. We illustrated the use of the techniques in a comparison of the expression profiles of neuroblastoma cells that were stimulated with a growth factor, macrophage migration inhibitory factor (MIF). The analysis of expression changes at mRNA levels showed that ≈99 genes were up-regulated and 24 were reduced significantly (P <0.001) in MIF-stimulated neuroblastoma cells. The regulated genes included several oncogenes, growth-related genes, tumor metastatic genes, and immuno-related genes. The findings provide clues as to the molecular mechanisms of MIF-mediated tumor progression and supply therapeutic targets for neuroblastoma treatment.

DNA microarrays measure the expression of thousands of genes in a single hybridization experiment by using oligonucleotide or cDNA probes. Although the technique has been widely used for monitoring mRNA expression in many areas of biomedical research (1), large experimental variations pose challenges to the analysis of the resulting data. Issues about normalization, the analysis of gene effects, and experimental designs have been systematically addressed (2–13). Yet, there are still a number of important problems in these areas that need to be studied.

The normalization of microarray data is required because of the variations in experimental conditions such as the efficiency of dye incorporation, concentration of DNA on arrays, amount of mRNA, variability in reverse transcription, washing process, and batch variation, among others. Proper normalization is critical for revealing relevant biological results. Yet, the normalization methods (3–6) require certain critical biological or statistical assumptions. For example, a popular method of global normalization (5) assumes that there is no print-tip block effect and no intensity effect. Without such an assumption, the global normalization method is statistically biased. But such an assumption is not valid for many situations, as documented in refs. 3, 4, and 6. The “lowess” method in ref. 3 significantly relaxes the above assumption, but it is assumed that the average expression levels of up- and down-regulated genes at each intensity level are about the same in each print-tip block. Tseng et al. (4) relax this assumption to only a subset of more conservative genes based on a rank invariant selection method. Such a biological assumption is not always granted, especially when cells are treated with some reagents (14). In an attempt to relax further the above biological assumption, Huang et al. (6) introduce a semilinear model to account for the intensity effect and use data from other arrays to obtain an aggregated estimate. The method is expected to work well when the gene effect is the same across arrays and the number of arrays is large. All of the above biological and statistical assumptions can be removed by using within-array replications. We develop a method to estimate the intensity and print-tip effects by aggregating information from the replications. This process allows us to estimate the intensity effect and print-tip effect without the above biological assumptions, which is particularly useful in situations in which cells are treated. After removing the effects of intensity and print-tip blocks, one can further apply the global normalization method to reduce the dye effect.

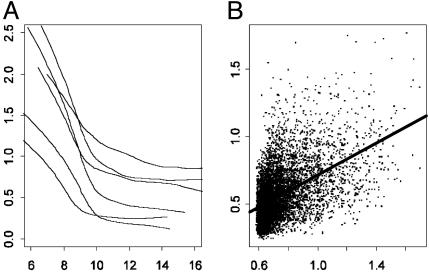
Various statistical methods (3, 4, 9, 10) have been introduced to assess the gene effect, but they have not accounted for the impact of heteroscedasticity: the expression ratios that are associated with high intensity tend to be more stably measured. In addition, experimental errors vary across arrays (see Fig. 6). We assess such a degree of heteroscedasticity and use a weighted t statistic to evaluate the effects of genes. Our analysis shows that this method yields statistically significant and biologically meaningful results.

Fig. 6.

(A) Estimated SD curves 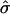in model 3, as a function of log intensities for six experiments. (B) The average of predicted SDs versus the SE for each gene. The correlation is ≈0.51.

The techniques were applied to the cDNA microarrays of neuroblastoma cells stimulated by a growth factor, macrophage migration inhibitory factor (MIF). Neuroblastoma is the second most common pediatric solid cancer and is responsible for ≈15% of all childhood cancer deaths (15). The clinical hallmark of neuroblastoma is marked heterogeneity, with the likelihood of tumor progression varying widely according to the stage, age at diagnosis, and anatomical site. MIF has emerged to play a central role in the control of the host inflammatory and immune responses. In addition to MIF's potent effects on the immune system, several reports have linked it to fundamental processes that control cell proliferation, cell survival, angiogenesis, and tumor progression (16). Recently, the overexpression of MIF was found in several human cancers (17, 18). However, the precise role of MIF in tumorigenesis remains unclear. Understanding the genes that are affected by MIF in neuroblastoma may provide approaches to screening and identifying molecular targets for the treatment of patients.

Materials and Methods

Neuroblastoma Cell Line Culture and Stimulation Assay. This study investigated human neuroblastoma cell line SK-N-AS. Cells were maintained in Eagle's MEM that was supplemented with 10% FBS and antibiotics (GIBCO). For stimulation experiments, cells were first seeded at 1 × 10⁶/ml in flask and then incubated in MEM that was supplemented with 10% FBS for 24 h. The cells were then washed with PBS and treated with different concentrations of recombinant human MIF for 24 h.

DNA and RNA Isolation. Total RNA was isolated from cells with or without MIF treatment by using TRIzol Reagent (GIBCO), according to the manufacturer's instructions. Finally, the quality and quantities of RNA samples were verified at agarose gel electropheresis.

cDNA Microarrays. cDNA clones of the Sequence Validated Human cDNA Library (ResGen, Invitrogen) were amplified by PCR using primers that were complementary to the vector sequences. The purified PCR products were then robotically arrayed onto polylysine-coated microarray slides, on which the DNAs were immobilized by UV light. Of the cDNA microarrays described here, 19,968 contained sequence-validated human cDNAs, generally with insert sizes of 0.25–2.5 kb. Among them, 111 cDNA clones were printed twice on each slide.

Expression Array Analyses. Twenty-five micrograms of total RNA was reverse-transcribed with oligo(dT) primer (5′-TTT TTT TTT TTT TTT TTT TTV N-3′) and Superscript II Reverse Transcriptase (GIBCO/BRL), in the presence of Cy5-dCTP and Cy3-dCTP (Amersham Pharmacia), respectively. After purification through a Microcon-30 filter (Amicon), the Cy3- and Cy5-labeled cDNA probes were mixed with 40 μg human Cot-1 DNA (GIBCO), 20 μg yeast tRNA (GIBCO), and 20 μg poly d(A) (Sigma). The mixture was concentrated to 16 μl with a Microcon-30 filter (Amicon). After denaturation, 16 μl of 2× hybridization solution (50% formamide, 10× SSC, 0.2% SDS) was added into the mixture and incubated for at least 20 min at 42°C. The mixture was then hybridized onto the prewarmed (42°C) slides for 18 h at 42°C. After hybridization, the slides were scanned (Scan Array Lite, GSI Lumonics, Billerica, CA). Images were analyzed by using genepix pro 4.0 software (Axon Instruments, Foster City, CA).

For each cDNA spot, the local background was subtracted from the total signal intensities of Cy5 and Cy3. The ratio of net fluorescence from the Cy5-specific channel to that from the Cy3-specific channel was calculated for each spot and represents the expression of the cDNA in the cells treated with MIF relative to the expression in the cells without treatment. Six independent experiments were performed to reduce variations related to labeling and hybridization efficiencies among the experiments.

Results

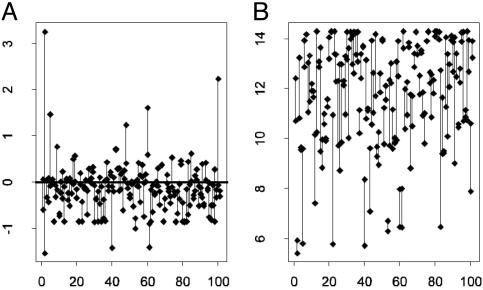
Replications and Preprocessing. Among 19,968 genes on an array, there are 111 replicated clones (Fig. 1). These provide valuable information for removing the effects of print-tip block and intensity. However, because of experimental errors, the actual number of available pairs of replication in six arrays ranges from 82 to 101.

Fig. 1.

Log ratios (A) and intensities (B) for pairs of clones replicated in an array connected by lines (the horizontal axis is the index of pairs). These provide useful information for normalization without making critical biological assumptions. The x axes are the indices of the pairs.

Following ref. 3, we first computed the log intensity A = 0.5 log₂(G * R) and log ratio M = log₂G/R, with R and G being the red (Cy3) and green (Cy5) intensities, respectively. For simplicity, A is referred to as the intensity. The median intensities are actually very stable among the six replications: the median intensities among six arrays are ≈10% different from each other. We first normalized the six arrays so that they had the same median intensity as the median intensity of the six aggregated arrays. This does not change the ratios and normalization results, but facilitates our presentation and analysis.

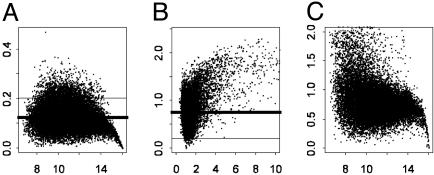
The intensities and ratios are not available at certain spots for each given array. The spots with average log intensities <6 were regarded as missing (only ≈3% of such genes). Genes with less than four replications were not considered, which filtered out ≈12% of the genes. The repeatability of the expressions of mRNA can be measured by the coefficient of variation (CV), which is the SD of intensity divided by the average for each gene in six replications: the higher the CV, the lower the repeatability. Genes with high CVs (1.5 SD above the median CV) were regarded as unreliable measurements and were deleted. This process filtered out another 8% of the genes (Fig. 2A). The effects of the remaining 15,266 genes treated by MIF were compared to those without treatment. The intensities (A) instead of ratios as in ref. 4 were used to compute the CVs because the former can be more reliably computed (Fig. 2). This is because the average intensities are much larger than the averages of ratios, which are close to one for many genes. Furthermore, the CVs that are based on ratios are closely related to t test statistics (to be defined) and those with low repeatability will be automatically filtered out in the process of analysis of the gene effect.

Fig. 2.

CVs computed based on intensities (A) and ratios (B), which are a measure of repeatability. The median CVs in A is 0.12 (thick bar), which is much lower than that in B (0.75). Genes with CVs above thin bar in A were filtered. (A) The average intensities against the CV based on intensities. (B) The average ratios against the CV based on ratios. (C) The average intensities versus the CV based on ratios.

Within-Array Normalization. For each array, let M_gi and A_gi be the measurement of M and A for gene g in replication i. For those with replications, let I be the total number of replications. In our study, I = 2. To take into account the print-tip effect, let c and r be the associated column and row of the print-tip block where the cDNAs reside. To examine the intensity and print-tip effect, we introduce the following semilinear in-slide model

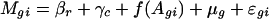[1]

for all genes in an array. Here, β_r and γ_c are the effects of the print-tip block, f is the intensity effect, and μ_g is the gene effect. For identifiability, the parameters β, γ, and f all have mean zero. Because gene effects μ_g are completely unknown, any gene without replication provides no information about the print-tip and the intensity effects. However, those genes with replications provide relevant information. Let 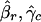, 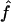and f̂ be the estimated parameters (to be detailed below) from genes with replications. Then, for each gene without replication, the normalized log ratio is

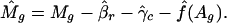[2]

According to model 1, this is the observed log ratio after taking out the effects of print-tip and intensity.

The semilinear in-slide model 1 is similar to those used in refs. 3 and 6. In ref. 3, for each print-tip (so that parameters β and γ can be set to zero), model 1 is fitted. To be able to identify the intensity effect, Dudoit et al. (3) implicitly made an important biological assumption: the average of μ_g is zero for those genes with A_g that are approximately the same. In an effort to remove this biological assumption, Huang et al. (6) aggregated information from other arrays. However, the gene effects are assumed to be the same across arrays.

The parameters in the semilinear in-slide model can be estimated by the following Gauss-Seidel or back-fitting algorithm (19, 20). For genes with replication in an array, we iterate the following steps:

• Initialize the print-tip and intensity effects as zero.

• Given an estimate of the print-tip and intensity effects, the gene effect can be estimated by

  

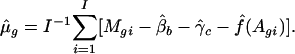
• Given the gene and intensity effects, the parameters β and γ can be estimated by ordinary least squares.

• Given the gene and print-tip effects, the intensity effect can be estimated by lowess (21) or more generally local linear fit (20), by smoothing the partial residuals 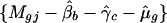on intensities {A_gj}.

• Iterate the last three steps until convergence.

In our implementation, it took us only a couple of iterations to get the algorithm to converge. Statistically, when the number of replicated genes is large, the print-tip and intensity effect can be estimated with good accuracy. However, as expected, the gene effects can be accurately assessed only when the number of replicated arrays is sufficiently large.

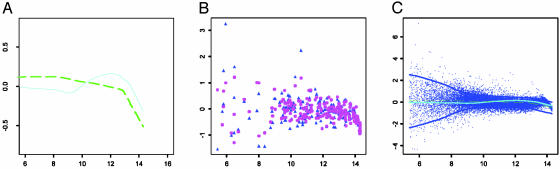
Fig. 3 depicts the normalization for one of the arrays. Presented in Fig. 3A are the intensity effects that are estimated by our method (green curve) and the lowess method (3) (cyan curve).∥

Fig. 3.

(A) The intensity effects f estimated based on the data in Fig. 1 (cyan curve) and estimated by the method in ref. 3 (green curve). (B) The unnormalized (blue) and normalized (pink) ratios for the genes with replications vs. their intensities. (C) Normalized log ratios (vs. their intensities) with intensity and print-tip effect removed for a given array, along with the lowess estimate of SDs (blue curves); two other curves are reproduced from A.

Global Normalization. After removing the effects of the print-tip block and intensity, we normalize each slide so that its median log ratio is zero. This eliminates the biases of conventional global normalization without removing those effects. This is equivalent to adding an intercept term in 1.

Estimation of In-Slide Variability. The ratios of expressions for genes with low intensity tend to have a large variability (Fig. 3C). Further, the intensities for the same gene can also vary substantially across experiments (see Fig. 6A). Therefore, the simple average of the gene effects across arrays is not an efficient method. The presence of heteroscedasticity also makes it difficult to compute P values. The degree of heteroscedasticity should be estimated and its impact should be removed in the analysis of the gene effect.

For each array, let M̂_g be the normalized log ratio for gene g in the pool of 15,266 candidate gene sets. We model the heteroscedasticity with the following model

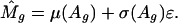[3]

The function μ can be estimated by the lowess method (3, 19), resulting in an estimate 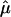. Let 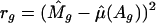be the squared residuals. An application of the lowess method to smooth the pairs {(A_g, r_g)} results in an estimate of the function 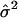(Fig. 3C). This method is statistically efficient (22). Thus, for each gene, in addition to the normalized ratio Â_g, we obtained a weight 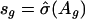, which indicates the reliability of the measured log ratio M_g in an array.

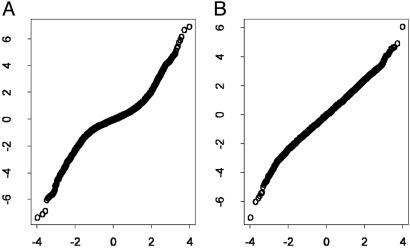
To examine the effect of the weight, we use the quantile-quantile plot to determine the normality of unstandardized log ratios M̂_g and standardized log ratios 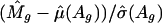for an array. Fig. 4A shows that log ratios are not normally distributed because of the heteroscedasticity, yet the standardization mitigates this effect (Fig. 4B).

Fig. 4.

Quantile–quantile plot for log ratios Â_g (A) and standardized log ratios. The standardization is effective as the quantile–quantile plot appears more linear. The x axes are the quantiles of the standard normal distribution, and y axes are the quantiles of log ratios.

Analysis of Treatment Effects. After normalization, a commonly used method to evaluate treatment effects is the two-sample t statistic (3) or its variants (6, 9, 10). For each gene g, in the presence of heteroscedasticity s_gj in slide j, we applied the weighted least-squares technique with weights 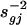to the problem:

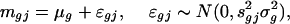where m_gj is the log ratio (after normalization) for gene g at the jth array. This results in an estimated ratio

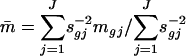and weighted t statistic

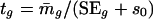[4]

where 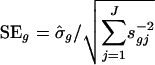with weighted sample SD 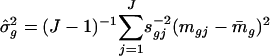. The constant s₀ is used here to guard against the zero denominator (9). When s_g = 1, the weighted t statistic reduces to the classical t statistic.

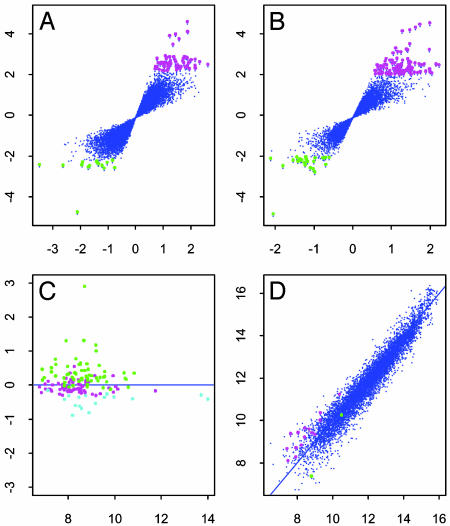
We applied both weighted and ordinary t tests to examine the effect of MIF treatment on genes. Fig. 5 depicts the results with α = 0.001. Table 1 summarizes the results. The weighted t test has a better ability to assess the effect of genes. In fact, the weighted t statistic is, in general, larger than the ordinary t statistic (Fig. 5C) and hence identifies more significant genes (Table 1) with smaller P values.

Fig. 5.

The gene effect is studied by using the ordinary t test (A) and the weighted t test (B). The test statistics are plotted against their average log ratios. Genes with P values <0.001 are marked with magenta (up-regulated) and green (down-regulated). (C) Average log intensity versus log₂(weighted t stat/ordinary t stat) for the genes with P values <0.001 by one of the t tests. Magenta, cyan, and green spots are the genes identified by both methods, ordinary t test only, and weighted t test, respectively. (D) The average of log intensities with MIF treatment versus those without MIF treatment. Up-regulated and down-regulated genes, identified by the weighted t test, are indicated by magenta and green, respectively.

Table 1. No. of genes that are up-regulated or down-regulated after MIF treatment.

	α = 5%			α = 1%			α = 0.5%			α = 0.1%			α = 0.05%			α = 0.01%			α = 0.005%			α = 0.001%
Methods	Up	Down	FDR, %	Up	Down	FDR, %	Up	Down	FDR, %	Up	Down	FDR, %	Up	Down	FDR, %	Up	Down	FDR, %	Up	Down	FDR, %	Up	Down	FDR, %
t test	842	823	45.9	279	200	31.9	174	90	28.9	62	16	19.6	49	9	13.2	12	1	11.7	6	1	10.7	5	1	2.5
Weighted t test	963	546	50.1	338	131	32.1	234	73	24.9	99	24	12.4	62	11	10.5	13	1	10.9	13	1	5.4	5	1	2.5

Balanced Sign Permutation and P Values. Instead of using the two-sample permutation idea (9), to keep the correlation structure among genes and heteroscedasticity within each array, we used a balanced sign permutation. For example, after reverting the treatment and control in slides 4, 5, and 6 as the control and treatment (multiplying their log ratios by –1), there is no treatment effect among six arrays. From such a reversion, 15,266 t test or weighted t test statistics were obtained. There are 20 examples of such a balanced sign permutation. The pool of these 20 × 15,226 test statistics forms an estimate of the null distribution of the test statistics (23). Hence, the P values were obtained.

We applied the multiple comparison techniques of refs. 23 and 24 to select significant genes and obtained unsatisfactory results. This result was because the effects of genes are corrected. In addition, with the number of genes in an order of 15,000, the multiple comparison method requires calculating tail probability in an order of 10^–6, which cannot be accurately estimated. Following ref. 9, instead of controlling the false discovery rate (FDR), we estimate it. For a weighted t statistic, with α = 0.001, we would expect to have 15.3 false positive genes. Hence, the FDR of the weighted t statistic is ≈12.4% (see Table 1). The choice of α = 0.001 for our presentation is based on the consideration of FDR and the number of significant genes.

Global Changes in Gene Expression in Response to MIF. MIF induces biological effects in target cells by changing the expression of a subset of genes. RNA was isolated from neuroblastoma cell line SK-N-AS that was treated with MIF for 24 h. The number of genes with significant changes in expression in response to MIF is shown in Table 1. A total of 99 (0.65%) genes were up-regulated and 24 (0.16%) were reduced (P <0.001) in MIF-stimulated neuroblastoma cells. Genes that displayed increased or decreased expression included a number of structural genes, genes involved in cell proliferation, cell cycle regulation, transcription factors, and known growth factor receptors and immune-related genes (Table 2). Furthermore, activating transcription factor 5 (25) and HNK-1 sulfotransferase (26) have been reported to play roles in controlling the development of the nervous system. In addition, a group of genes are known to be tumor related, such as kruepel-subfamily C2H2-type zinc finger protein (27), tumor differentially expressed 1 (28), inter-α-trypsin inhibitor heavy chain (29), fatty acid synthase (30), and ribosomal protein S27 (31). Cell division cycle 34, tumor differentially expressed 1, and casein kinase 1-encoded proteins (32) are also reported to be involved in cell proliferation. Finally, type IV collagen and inter-α-trypsin inhibitor heavy chain may be associated with tumor metastasis. Hagedorn et al. (33) and Krecicki et al. (34) suggested that loss of type IV collagen is an absolute indication for tumor metastasis. Our previous study showed that MIF could trigger neuroblastoma cell migration (data not shown), and the current data revealed that type IV collagen can be down-regulated by MIF (Table 2), suggesting that MIF enhances tumor cell migration probably by decreasing type IV collagen. In summary, we used a global gene expression strategy to identify genes that are affected by MIF in neuroblastoma. These genes represent good candidates for future analysis.

Table 2. Selected genes regulated by MIF.

Gene ID	Description	Fold change	P value
H20743	Cell division cycle 34	4.33	0.0000
N36994	Kruepel-subfamily C2H2-type zinc finger protein	3.66	0.0001
AA456325	Tumor differentially expressed 1	2.70	0.0001
AA452119	Toll-related protein	2.26	0.0002
AA677388	Inter-α-trypsin inhibitor heavy chain	2.41	0.0002
AA669272	Casein kinase 1	3.91	0.0002
AA027266	Tranglutaminase	2.43	0.0003
AA464711	Complement component 3A receptor 1	-3.19	0.0004
AA884709	Cytochrome P450	2.80	0.0004
AA418008	Growth factor independent 1	2.33	0.0004
AA132964	IL-22 receptor	2.35	0.0004
AA083478	Tripartite motif-containing 22	-2.59	0.0006
H50323	Fatty acid synthase	3.07	0.0007
H68555	Collagen, type IV	-2.60	0.0007
T94611	NKG2 type II integral membrane protein	2.80	0.0008
R16195	HNK-1 sulfotransferase	-1.63	0.0008
AA457474	Receptor activity modifying protein 2	1.95	0.0009
AA416782	Orthopedia (Drosphila) homolog	2.13	0.0009
AA857413	Ribosomal protein S27	2.04	0.0010
T90841	Activating transcription factor 5	2.22	0.0010

Discussion

Normalization is important for cDNA microarray data analysis. It reduces the effects of blocks, intensity, and slides. Global normalization is a popular method used in microarray analysis. However, because of the block and intensity effects, such a method can suffer from substantial biases, making it hard to reveal the biological effect of treatments. Several useful ideas have already been introduced to overcome the drawback (3, 4, 6). They are very powerful when their biological assumptions are granted.

The semilinear in-slide model is a powerful approach for removing the intensity and block effects. It requires virtually no biological assumptions and does not assume the identical gene effects across arrays. When the latter is imposed, the statistical efficiency in estimating the intensity effect and print-tip block effect can be improved somewhat by aggregating information on estimating the gene effects from other arrays. The effects of intensity and block can be efficiently removed when the number of clones with replications is large within an array. With the number of genes in the order of tens of thousands in an array, it is not difficult to print hundreds of replicated clones. With such an order of replicated genes, the intensity and block effects can be very effectively removed. After the removal, the global normalization can be carried out to remove the slide effect.

It is evident (Fig. 6) that expression ratios are heteroscedastic within and across arrays. When the intensity is large, the variability of the ratios gets small. Even in the region (e.g., A ≥10) where it tends to be constant in each array, the variability still varies across different arrays (Fig. 6A). The measurement errors across arrays need to be standardized. Thus, a weighted version of the t statistic such as 4 is needed to obtain a correct P value and efficiently test whether there is any treatment effect.

Because of the large number of genes to be analyzed, the traditional multiple comparison techniques in statistics need to be applied carefully. This poses challenges to the control of FDR. First, the treatment effects on mRNA expressions can be correlated. Second, with the number of multiple comparisons in the order of tens of thousands, the probability calculation largely depends on the model assumption. Robustness to the model assumption is a critical issue, and one should try to estimate the FDR. Significance analysis of microarrays (9) is a powerful approach. However, it does not take care of the correlation and heteroscedastic structure within and across arrays. The balanced sign permutation overcomes this drawback and provides a useful method for computing the P value.