Noncrossing quantile regression curve estimation

Summary

Since quantile regression curves are estimated individually, the quantile curves can cross, leading to an invalid distribution for the response. A simple constrained version of quantile regression is proposed to avoid the crossing problem for both linear and nonparametric quantile curves. A simulation study and a reanalysis of tropical cyclone intensity data shows the usefulness of the procedure. Asymptotic properties of the estimator are equivalent to the typical approach under standard conditions, and the proposed estimator reduces to the classical one if there is no crossing. The performance of the constrained estimator has shown significant improvement by adding smoothing and stability across the quantile levels.

1. Introduction

Quantile regression has become a useful tool to complement a typical least-squares regression analysis (Koenker, 2005). Modelling of the median as opposed to the mean is much more robust to outlying observations. Additionally, examining the effect of the predictors on other quantiles can yield a clearer picture regarding the overall distribution of a response. In particular, in numerous instances, interest focuses on the effect of the predictors on the tails of a distribution, in addition to, or instead of, the centre. Quantile regression is used to model the conditional quantiles of a response. Applications of quantile regression come from diverse areas, including economics, public health, meteorology and surveillance.

However, when an investigator wishes to use quantile regression at multiple percentiles, the quantile curves can cross, leading to an invalid distribution for the response. Given a set of covariates, it may turn out, for example, that the predicted 95th percentile of the response is smaller than the 90th percentile, which is impossible.

Consider a recent application of quantile regression to model tropical cyclone intensity (Jagger & Elsner, 2009). The goal is to model the maximum wind speed for near-coastal tropical cyclones occurring near the US coastline based on climatological variables. Of particular interest is the upper tail of the distribution, as these are the storms that may cause major damage. Jagger & Elsner (2009) used quantile regression to examine the upper tail behaviour as a function of four large-scale climate conditions. A sample of 422 tropical cyclones is used to model the maximum wind speed in terms of the climate covariates: the North Atlantic Oscillation Index, the Southern Oscillation Index, the Atlantic sea-surface temperature and the average sunspot number.

With the focus being on the upper quantiles of the wind speed distribution, those corresponding to category 4 and 5 hurricanes, consider using these data to fit a quantile regression at the set of percentiles (0.25, 0.5, 0.75, 0.9, 0.95, 0.99). The fitted slopes of the quantile functions give the effects of the covariates at the various levels of cyclone intensity. One particular issue with fitting the upper quantiles is the lack of data, so fitting individual quantile curves can be even more problematic.

For example, if one were to examine the fitted quantiles for these data, the upper quantiles cross not far from the mean. Due to the crossing, for instance, the practitioner would be forced to claim that when the North Atlantic Oscillation Index is one standard deviation below its mean and the other three are one standard deviation above, the 90th percentile of the distribution of wind speeds is larger than the 95th percentile. In addition, as further discussed in the analysis later, inference regarding the significant predictors changes dramatically from one quantile to the next. For example, predictors that appear highly significant in both the 90th percentile and the 99th percentile may not appear significant at the 95th percentile. Although this is possible, much of it can be attributed to the fact that the quantile functions are estimated separately.

This problem is well known, but no simple and general solution currently exists. For linear quantile regression, Koenker (1984) considered parallel quantile planes to avoid the crossing problem. Cole (1988) and Cole & Green (1992) assumed that a suitable transformation would yield normality of the response and proceeded to obtain nonparametric estimates of the transformation along with the location and scale, which then fully determine the quantile functions.

Similarly, He (1997) proposed a method to estimate the quantile curves while ensuring non-crossing. However, the approach assumes a heteroscedastic regression model for the response, which allows the predictors to affect the distribution of the response via a location and scale change of an underlying base distribution. Although this is a flexible model, the predictors may affect the response distribution in a less structured manner, which may not be captured by this model. Furthermore, since the procedure is a sequential algorithm, the distributional properties of the estimator are unclear. Simulation has also shown that even when the assumed heteroscedastic model is correct, the estimation procedure does not necessarily improve upon the unconstrained quantile regression estimator in finite samples. Wu & Liu (2009) have recently proposed an algorithm to ensure noncrossing, by fitting the quantiles sequentially and constraining the current curve to not cross the previous curve. One drawback of this algorithm is its dependence on the order that the quantiles are fitted. Neocleous & Portnoy (2008) discuss interpolation of the typical regression quantiles to ensure that, asymptotically, the probability of crossing will tend to zero for the full quantile process.

The crossing problem persists for nonlinear quantile curves. Several authors have proposed to first estimate the conditional cumulative distribution function via local weighting, and then invert it to obtain the quantile curve. Hall et al. (1999), Dette & Volgushev (2008) and Chernozhukov et al. (2009) enforce the noncrossing via this approach by modifying the estimate of the conditional distribution function. This indirect approach is used if interest is purely in estimation of the conditional quantile. However, when interest also focuses on quantifying the effects of the predictors, the quantile curves are typically modelled via a parametric form, such as linear predictor effects, and a direct estimation approach is required.

In this paper, a direct correction to the quantile regression optimization problem is used to ensure noncrossing quantile curves for any given sample. The approach is also extended to nonparametric quantile curves.

2. Noncrossing quantile regression

2.1. Alleviating the crossing problem

Let x = (x₁, . . . , x_p)^T, and denote z = (1, x^T)^T. Let 𝒟 ⊂ R^p, be a closed convex polytope, represented as the convex hull of N points in p-dimensions. Interest focuses on ensuring that the quantile curves do not cross for all values of the covariate x ∈ 𝒟. Although the region of interest for noncrossing is assumed to be bounded, the covariate space itself may still be unbounded. If noncrossing were desired in linear quantile regression on an unbounded domain in any covariate direction, the result will be parallel lines, yielding the constant slope, location-shift model.

Assuming a linear quantile model, the τth conditional quantile of the response is given by $z_i^{\text{T}}{\beta }_{\tau }$, i.e. $\text{pr}\left(y_i⩽z_i^{\text{T}}{\beta }_{\tau }|x_i\right)=\tau$. The classical estimator of the regression coefficients for this quantile function is given by

$${\widehat{\beta }}_{\tau }={\text{arg}\hspace{0.17em}\text{min}}_{\beta }\sum _{i=1}^n{\rho }_{\tau }\left(y_i-z_i^{\text{T}}\beta \right),$$ (1)

where ρ_τ (u) = u{τ − I (u < 0)} is the so-called check function.

A typical quantile regression analysis will solve (1) separately for each of the q desired quantile levels, τ₁ < … < τ_q, to get $\widehat{\beta }(\tau )={\left({\widehat{\beta }}_{{\tau }_1}^{\text{T}},\dots ,{\widehat{\beta }}_{{\tau }_q}^{\text{T}}\right)}^{\text{T}}$. Without any restriction, these resulting regression functions will often cross in finite samples, and hence the resulting conditional quantile curve for a given x will not be a monotonically increasing function of τ. Recall that z = (1, x)^T. Then, formally, nonmonotonicity of the resulting estimated quantile function at a given point x is given by $z^{\text{T}}{\widehat{\beta }}_{{\tau }_t}<z^{\text{T}}{\widehat{\beta }}_{{\tau }_{t-1}}$ for at least one t ∈ (2, . . . , q). For a simple example, it often turns out to be the case that the intercept is not an increasing function of τ, hence at x = 0 the quantile function is nonmonotone. This becomes even more problematic with a larger number of predictors as the curves have a much larger space in which they may cross. When q increases, crossing also becomes much more likely.

To alleviate the crossing issue, it is proposed to estimate the quantiles simultaneously under the noncrossing restriction. Specifically, the optimization problem becomes

$$\begin{array}{ccc}\hfill \widehat{\beta }(\tau )& =\hfill & {\text{arg}\hspace{0.17em}\text{min}}_{\beta }\sum _{t=1}^{q}w\left({\tau }_t\right)\sum _{i=1}^n{\rho }_{{\tau }_t}\left(y_i-z_i^{\text{T}}{\beta }_{{\tau }_t}\right)\hfill \\ \hfill \text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}{z}^{\text{T}}{\beta }_{{\tau }_t}& ⩾\hfill & z^{\text{T}}{\beta }_{{\tau }_{t-1}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x\hspace{0.17em}\in \hspace{0.17em}𝒟,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t=2,\dots ,q,\hfill \end{array}$$ (2)

for some weight function, w(τ_t), such that w(τ_t) > 0 for all t = 1, . . . , q.

Without the restriction, the solution to (2) is exactly the solution to (1) regardless of the choice of weight function w(τ_t). In fact, a direct consequence of this formulation is that if the classical estimator obeys the noncrossing constraint for a given dataset, the resulting estimator will be the classical estimator. Furthermore, the asymptotic distribution of the estimator, as discussed in the next section, will not depend on the choice of weight function. A convenient practical choice of weight function is to equally weight the terms, i.e. w(τ_t) = 1 for all t. This is the choice used in the examples.

Since the domain is the convex hull of N points, it suffices to enforce the noncrossing restriction at each vertex. Letting (z₁, . . . , z_N) denote the set of vertices, then any point in the region can be expressed as ${\sum }_{k=1}^N{c}_k{z}_k$ with ${\sum }_{k=1}^N{c}_k=1$ and each c_k ⩾ 0. If $z_k^{\text{T}}{\beta }_{{\tau }_t}⩾z_k^{\text{T}}{\beta }_{{\tau }_{t-1}}$ for all k = 1, . . . , N, it follows that ${\sum }_{k=1}^N{c}_k{z}_k^{\text{T}}{\beta }_{{\tau }_t}⩾{\sum }_{k=1}^N{c}_k{z}_k^T{\beta }_{{\tau }_{t-1}}$. This can then be solved via standard linear programming with N * (q − 1) linear constraints, where N is the number of vertices and q is the number of quantiles. This may result in a large number of constraints.

However, it will now be shown that if the domain of interest can be reduced to [0, 1]^p, constraints at each of the 2^p vertices are unnecessary, and only a total of q − 1 constraints are needed rather than N (q − 1). Any domain of interest, for which there exists an invertible affine transformation that maps to [0, 1]^p, can be used so that the transformation is performed, and then transformed back after the estimation, while retaining the noncrossing property. This has the potential to simplify computation a great deal. Hence, one may wish to approximate the desired domain by one of this form. The remainder of the article will focus on the domain 𝒟 = [0, 1]^p.

To ensure noncrossing everywhere, consider the transformation from β_τ1, . . . , β_τq to γ_τ1, . . . , γ_τq, where γ_τ1 = (γ_0,τ1, γ_1,τ1, . . . , γ_p,τ1)^T = β_τ1 and γ_τt = (γ_0,τt, γ_1,τt, . . . , γ_p,τt)^T = β_τt − β_τt−1 for t = 2, . . . , q.

The constraint in (2) is equivalent to z^Tγ_τt ⩾ 0 for all x ∈ 𝒟 and all t = 2, . . . , q. Break each γ_j,τt into its positive and negative parts, so that ${\gamma }_{j,{\tau }_t}={\gamma }_{j,{\tau }_t}^{+}-{\gamma }_{j,{\tau }_t}^{-}$, where both ${\gamma }_{j,{\tau }_t}^{+}$ and ${\gamma }_{j,{\tau }_t}^{-}$ are nonnegative, and only one may be nonzero. With this reparameterization, noncrossing can be easily ensured on 𝒟 = [0, 1]^p. Using this parameterization, the constraint in (2) becomes simply that

$${\gamma }_{0,{\tau }_t}-\sum _{j=1}^p{\gamma }_{j,{\tau }_t}^{-}⩾0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(t=2,\dots ,q).$$ (3)

This gives the point that is the worst-case scenario for each t, having x_j = 1 when γ_j,τt < 0, and x_j = 0 when γ_j,τt > 0. Since this point is in 𝒟, noncrossing must be enforced there, and hence (3) is a necessary condition. Since this point is the worst case, all other points in 𝒟 = [0, 1]^p will then automatically satisfy the constraint for each t = 2, . . . , q, and hence (3) is also a sufficient condition.

After reparameterization, the problem is thus reduced to a linear programming problem, which can be solved via standard software. The linear program is extremely sparse and thus the use of a sparse matrix representation is more efficient. For computation, the linear programming has been implemented via use of the SparseM package (Koenker & Ng, 2003) in the R software platform (R Development Core Team, 2010), and the code is available from the first author.

2.2. Asymptotic properties

Consider a set of percentiles τ₁ < … < τ_q, such that τ_t ∈ [ε, 1 − ε] for all t, with 0 < ε < 1/2. For the asymptotic properties, the set (τ₁, . . . , τ_q) is allowed to change with n, if desired. In particular, one may wish to consider a denser set as the sample size increases. Assume that the linear quantile regression model holds with true parameter β⁰(τ), so that the ${\tau }_t^{\text{th}}$ quantile of the conditional distribution for the response is given by $z^{\text{T}}{\beta }_{{\tau }_t}^0$. Specifically, $F_{Y_i|x}^{-1}\left({\tau }_t\right)=z^{\text{T}}{\beta }_{{\tau }_t}^0$ for i = 1, . . . , n, where F_Yi|x denotes the conditional distribution function for observation i. Let β̃(τ) be the classical quantile regression estimator obtained by solving (1) separately for each τ_t, and let β̂(τ) be the constrained noncrossing version obtained via (2).

The following theorem shows that, regardless of the choice of a weight function, the estimator obtained via (2) is asymptotically equivalent to the typical quantile regression estimator. The following conditions are assumed.

• Condition 1. The weights w(τ_t) > 0 for all t = 1, . . . , q.

• Condition 2. The matrix $n^{-1}{\sum }_{i=1}^n{x}_i{x}_i^{\text{T}}$ is positive definite.

• Condition 3. The conditional distributions have densities, f_Yi|x, that are differentiable with respect to Y_i for every x and each i = 1, . . . , n.

• Condition 4. There exist constants a > 0, b < ∞ and c < ∞ such that

  $$\begin{array}{ll}a⩽f_{Y_i|x}\left\{F_{Y_i|x}^{-1}(\tau )\right\}⩽b,\hfill & |f_{Y_i|x}^{(1)}\left\{F_{Y_i|x}^{-1}(\tau )\right\}|⩽c,\hfill \end{array}$$

  uniformly for x ∈ 𝒟, ε ⩽ τ ⩽ 1 − ε, and i = 1, . . . , n, where $f_{Y_i|x}^{(1)}$ denotes the derivative of f_Yi|x with respect to Y_i.

The first condition ensures that the chosen weight function is appropriate to estimate the desired quantile curves. The remaining conditions allow a uniform Bahadur representation of the classical quantile regression estimator, as in Neocleous & Portnoy (2008), which ensures that ${\tilde{\beta }}_{\tau }-{\beta }_{\tau }^0=O_p\left(n^{-1/2}\right)$ uniformly in ε ⩽ τ ⩽ 1 − ε.

Theorem 1. Let β̂(τ) and β̃(τ) be the constrained and unconstrained estimators, respectively, for the set of quantiles τ₁ < … < τ_q, such that n^1/2 min_t (τ_t+1 − τ_t) → ∞. Then for any u ∈ 𝔕^pq,

$$\left|\text{pr}\left[n^{1/2}\left\{\widehat{\beta }(\tau )-{\beta }^0(\tau )\right\}⩽\hspace{0.17em}u\right]-\text{pr}\left[n^{1/2}\left\{\tilde{\beta }(\tau )-{\beta }^0(\tau )\right\}⩽u\right]\right|\hspace{0.17em}\to 0,$$

so that the constrained estimator has the same limiting distribution as the classical quantile regression estimator.

Based on Theorem 1, inference for the n^1/2-consistent constrained quantile regression can be achieved by using the known asymptotic results for classical quantile regression. In particular, appropriate asymptotic standard errors can be computed via the quantile regression sandwich formula (Koenker, 2005, Sec. 3.2.3).

3. Extension to nonparametric quantile curves

3.1. Quantile curves

Consider the model with a single predictor x ∈ [0, 1]. Without assuming that the quantiles vary linearly with x, a nonparametric fit is often performed via quantile smoothing splines. When the quantiles are curves, the crossing problem becomes even more pronounced, as the curves are more likely to cross.

Taking the approach of quantile smoothing splines (Koenker et al., 1994), the constrained joint quantile smoothing spline estimate can be formulated as the set of functions ĝ_τ1, . . . , ĝ_τq ∈ 𝒢 that minimizes

$$\begin{array}{l}\sum _{t=1}^{q}w\left({\tau }_t\right)\sum _{i=1}^n{\rho }_{{\tau }_t}\left\{y_i-g_{{\tau }_i}(x_i)\right\}+\sum _{t=1}^q{\lambda }_{{\tau }_t}V\left({g^{\prime }}_{{\tau }_t}\right)\hfill \\ \text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}{g}_{{\tau }_t}(x)⩾g_{{\tau }_{t-1}}(x),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x\hspace{0.17em}\in [0,1],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t=2,\dots ,q,\hfill \end{array}$$ (4)

where V (g′) is the total variation of the derivative of the function g. For twice continuously differentiable g, we have $V(g^{\prime })={\int }_0^1\left|g^{″}(x)\right|dx$. In general,

$$V(g^{\prime })=\underset{P}{\text{sup}}\sum _{i=0}^{N_P-1}\left|g^{\prime }\left(x_{i+1}\right)-g^{\prime }\left(x_i\right)\right|dx,$$ (5)

where the supremum is taken over the set of all possible partitions P of [0, 1], and N_P denotes the number of endpoints that defines the partition P.

Following Pinkus (1988) and Koenker et al. (1994), consider the expanded second-order Sobolev space,

$$𝒢=\left\{g:g(x)=a_0+a_{1}x+{\int }_0^1(x-y)+d\mu (y),\hspace{0.17em}\hspace{0.17em}V(\mu )<\infty ,a_i\in \hspace{0.17em}\Re ,i=0,1\right\},$$

where μ is a measure with finite total variation. This space includes the usual Sobolev space of functions having second derivative with finite L₁ norm and absolutely continuous first derivative, while also including the limiting piecewise linear functions. As discussed in Pinkus (1988), this expansion is necessary to ensure that the interpolating function that minimizes the total variation resides in the function space 𝒢. For piecewise linear functions, the supremum in (5) occurs when the partition coincides with the breakpoints of the function.

Theorem 2. The set of functions ĝ_τ1, . . . , ĝ_τq ∈ 𝒢 minimizing (4) subject to the noncrossing constraint consists of noncrossing linear splines with knots at the data points.

This implies that it suffices to consider the problem in terms of a linear spline basis, for which the total variation is a linear function of the coefficients. Hence, as in Koenker et al. (1994), the smoothing spline problem is a linear programming problem. It will now be shown that the noncrossing quantile constraint can be directly incorporated into this framework while retaining the linear programming problem.

Let {B_j (x)} for j = 1, . . . , k_n + 1 denote the linear B-spline basis with k_n internal knots and endpoints at 0 and 1. Then ${\widehat{g}}_{{\tau }_t}(x)={\widehat{\beta }}_{0,{\tau }_t}+{\sum }_{j=1}^{k_n+1}{\widehat{\beta }}_{j,{\tau }_t}{B}_j(x)$. Using the analogous parameterization as in the previous section in terms of differences in the coefficients across quantile levels, i.e. γ_τ1 = β_τ1 and γ_τt = β_τt − β_τt−1 for t = 2, . . . , q, it follows that ${\widehat{g}}_{{\tau }_t}(x)-{\widehat{g}}_{{\tau }_{t-1}}(x)={\widehat{\gamma }}_{0,{\tau }_t}+{\sum }_{j=1}^{k_n+1}{\widehat{\gamma }}_{j,{\tau }_t}{B}_j(x)$ for any x. Hence the differences across quantiles is simply written in terms of a linear B-spline basis.

Considering the differences across successive quantiles as a linear spline with knots at each data point, it follows that it is necessary and sufficient to enforce the nonnegative constraint at the knots. Nonnegativity at each knot will imply nonnegativity between the knots due to the linearity. The form of the linear B-spline basis allows for a convenient parameterization, since at each knot a single basis function takes the value 1 while the remaining are 0. Hence at x_j, where x_j is the value at knot j, the difference across the successive quantiles is given by ĝ_τt (x_j) − ĝ_τt−1 (x_j) = γ̂_0,τt + γ̂_j,τt. Hence, letting ${\gamma }_{j,{\tau }_t}={\gamma }_{j,{\tau }_t}^{+}-{\gamma }_{j,{\tau }_t}^{-}$ be the coefficients parameterized as above, it is necessary and sufficient to improve ${\gamma }_{0,{\tau }_t}-{\text{max}}_j\left({\gamma }_{j,{\tau }_t}^{-}\right)⩾0$ for each t = 2, . . . , q. This can be turned into a linear programming problem using the constraints ${\gamma }_{0,{\tau }_t}-{\gamma }_{j,{\tau }_t}^{-}⩾0$ for each t = 2, . . . , q and j = 1, . . . , k_n + 1.

Using the linear B-spline basis, the total variation penalty is simply a linear function of the basis coefficients. Hence, the full optimization problem given by (4) is again a linear programming problem, and computation can be done efficiently using the sparse matrix representation as before.

3.2. Tuning the procedure

Koenker et al. (1994) and He & Ng (1999) suggest the use of a Schwartz-type information criterion for choosing the regularization parameter in quantile smoothing splines. For each individual quantile curve, this criterion is

$$\text{SIC}\hspace{0.17em}\left({\lambda }_{{\tau }_t}\right)=\text{log}\left[n^{-1}\sum _{i=1}^n{\rho }_{{\tau }_t}\left\{y_i-{\widehat{g}}_{{\tau }_t}^{{\lambda }_{{\tau }_t}}\left(x_i\right)\right\}\right]+{(2n)}^{-1}{p}_{{\lambda }_{{\tau }_t}}\text{log}(n),$$ (6)

where $g_{{\tau }_t}^{{\lambda }_{{\tau }_t}}$ denotes the estimated function for that choice of λ_τt, while p_λτt is the number of interpolated data points, i.e. those with zero residuals, and serves as a natural measure of the complexity of the model. The full set of tuning parameters for the individual quantile curves minimizes the joint Schwartz-type criterion,

$${\text{SIC}}_J(\lambda )=\sum _{t=1}^q{w}_{*}\left({\tau }_t\right)\text{log}\hspace{0.17em}\hspace{0.17em}\left[n^{-1}\sum _{i=1}^n{\rho }_{{\tau }_t}\left\{y_i-{\widehat{g}}_{{\tau }_t}^{{\lambda }_{{\tau }_t}}\left(x_i\right)\right\}\right]+{\left(2n\right)}^{-1}\text{log}(n)\sum _{t=1}^q{p}_{{\lambda }_{{\tau }_t}},$$ (7)

for any choice of weights w_*(τ_t) > 0. The weights, w_*(τ_t), may differ from those in the loss function due to the log scale. However, in the case of w(τ_t) = 1, as in the examples, it is natural to also choose w_*(τ_t) = 1.

For the proposed joint noncrossing quantile smoothing spline, the joint Schwartz-type criterion (7) is used to select the tuning parameters. If the individual quantile smoothing splines chosen via the separate sic criteria (6) do not cross, then the joint quantile smoothing spline will be exactly this set.

One could instead choose the logarithm of the full objective function, i.e. taking the logarithm outside the double summation, instead of summing the individual pieces. However, the proposed criterion in (7) will guarantee that the individual quantile smoothing splines agree with the joint noncrossing smoothing spline when the former are noncrossing. The alternative criterion will not necessarily maintain this desirable property. In addition, simulation results have shown that (7) seems to exhibit better empirical performance.

In the joint quantile smoothing spline, there are separate tuning parameters for each quantile curve, resulting in a q-dimensional tuning parameter selection problem. However, experience, as shown in the simulations, has shown that a single tuning parameter performs sufficiently well in controlling the overall smoothness of the set of curves, while still allowing for varying degrees of smoothness among the curves themselves.

If a full q-dimensional tuning is desired, a directed search can proceed as follows.

Algorithm 1.

• Step 1. Fit the joint smoothing spline with a single tuning parameter, i.e. set λ_τ1 = … = λ_τq and find the value that minimizes the sic_J criterion.

• Step 2. Vary λ_τ1 on a grid around the current value and minimize the sic_J criterion keeping the remaining λ_τt values fixed at the current value. Take this as the new tuning parameter vector.

• Step 3. Continue to update sequentially in this fashion, until no further improvement is possible.

While this algorithm is not guaranteed to find the global minimizer, it will at least converge to a local minimizer, starting from the optimal solution for the single tuning parameter case.

4. Simulation study

4.1. Linear quantile regression

The proposed method is now compared to classical quantile regression without the noncrossing assumption. Additionally, the method is compared to the approach of He (1997), which assumes a location-scale heteroscedastic error model. Each of the examples is a special case of the heteroscedastic error model as in He (1997):

$$\begin{array}{ll}{y}_i={\beta }_0+{\beta }^{\text{T}}{x}_i+\left({\gamma }_0+{\gamma }^{\text{T}}{x}_i\right){\epsilon }_i,\hfill & x_{ij}~U(0,1),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\epsilon }_i~N(0,1).\hfill \end{array}$$

For all examples, the intercepts are set to β₀ = γ₀ = 1. In each example, six quantile curves, τ = 0.1, 0.3, 0.5, 0.7, 0.9, 0.99, are fitted to the data, either separately for the classical quantile regression approach or simultaneously for the proposed approach. The method of He (1997) estimates the location and scale parameters in the model directly, and then uses them to estimate the quantile curves. For each example, 500 datasets are simulated. The three examples are as follows.

• Example 1. The sample size is n = 100, with p = 4 predictors, and parameters β = (1, 1, 1, 1)^T, and γ = (0.1, 0.1, 0.1, 0.1)^T.

• Example 2. The sample size is n = 100, with p = 10 predictors, and parameters β = (1, 1, 1, 1, 0^T)^T, and γ = (0.1, 0.1, 0.1, 0.1, 0^T)^T.

• Example 3. The sample size is varied with n = (100, 200, 500), with p = 7 predictors, and parameters β = (1, 1, 1, 1, 1, 1, 1)^T and γ = (1, 1, 1, 0, 0, 0, 0)^T.

To illustrate the crossing problem, for the first example, out of the 500 generated datasets, 491 of them had at least one crossing in the domain.

The results from the examples are given in Table 1. Presented are the empirical root mean integrated squared errors in estimation of the curves for each of τ = 0.5, 0.9, 0.99 given by $\text{RMISE}\hspace{0.17em}=\hspace{0.17em}{\left[n^{-1}{\sum }_{i=1}^n{\left\{{\widehat{g}}_{\tau }\left(x_i\right)-g_{\tau }\left(x_i\right)\right\}}^2\right]}^{1/2}$, where ĝ_τ is the estimated function and g_τ is the true function. In this case, the functions g and ĝ are linear, while in the next section they are nonlinear. The table presents the average root mean integrated squared errors over the 500 datasets along with their estimated standard errors. The results for the other quantiles are similar, and are thus omitted. However, by fitting simultaneously, it is guaranteed that they will not cross.

Table 1.

Average root mean integrated squared error (×100) over 500 simulated datasets, with standard error in parentheses

		Example 1			Example 2
	τ = 0.5	τ = 0.9	τ = 0.99	τ = 0.5	τ = 0.9	τ = 0.99
NCRQ	30.1 (0.44)	40.7 (0.59)	72.9 (0.88)	42.9 (0.43)	53.2 (0.52)	89.7 (0.84)
RQ	31.2 (0.46)	42.9 (0.65)	86.1 (0.96)	47.9 (0.45)	66.5 (0.64)	121.3 (0.95)
RRQ	31.2 (0.46)	48.6 (0.70)	92.7 (2.01)	47.9 (0.45)	76.3 (0.70)	147.3 (2.34)
		Example 3,	n = 100		Example 3,	n = 200
	τ = 0.5	τ = 0.9	τ = 0.99	τ = 0.5	τ = 0.9	τ = 0.99
NCRQ	75.9 (0.92)	99.8 (1.19)	179.7 (2.04)	56.4 (0.66)	74.6 (0.91)	132.3 (1.62)
RQ	82.1 (0.99)	116.7 (1.36)	226.5 (1.85)	60.0 (0.69)	82.1 (0.99)	162.2 (1.74)
RRQ	82.1 (0.99)	133.0 (1.52)	250.7 (4.72)	60.0 (0.69)	91.5 (1.04)	158.9 (2.50)
		Example 3,	n = 500
	τ = 0.5	τ = 0.9	τ = 0.99
NCRQ	35.8 (0.41)	47.0 (0.55)	92.5 (1.14)
RQ	37.1 (0.42)	49.7 (0.57)	109.0 (1.28)
RRQ	37.1 (0.42)	56.7 (0.65)	96.0 (1.33)

NCRQ, proposed noncrossing regression quantiles; RQ, classical regression quantiles; RRQ, restricted regression quantiles of He (1997).

In each of the settings considered, the proposed constrained approach gives significantly better estimation for all quantiles. This is probably because the constraints add some smoothness and stability across the quantile curves. Since the true curves do not cross, it is expected that the constrained estimates would perform better. This improvement is greater in the tails, as there is less data, hence the smoothing effect of the constraint allows for the borrowing of strength. In addition, the improvement is much more pronounced for Example 2, due to the presence of the extra irrelevant predictors.

By varying the sample size in Example 3, as expected, the differences become smaller as the sample size grows, due to the consistency of the classical estimators. However, even with n = 500 some statistically significant improvement still remains, as seen by the differences in root mean integrated squared errors relative to their reported standard errors. The estimator of He (1997), although based on the heteroscedastic model, does not exhibit better performance than the typical estimator except in the extreme quantiles in the larger sample case. This phenomenon was also observed by Wu & Liu (2009), and probably occurs because it requires implicit nonparametric estimation of the quantiles of the residuals, which may be unstable for smaller sample sizes.

Examples with other set-ups, including covariates generated from Gaussian distributions, gave similar results, and are thus omitted.

4.2. Nonparametric quantile regression

For nonparametric quantile regression, the proposed method is compared with quantile smoothing splines and quantile regression splines. Quantile smoothing splines result in penalized linear splines, as in the proposed method, but with each curve fitted independently. Quantile regression splines start with linear splines and perform knot selection. Both methods are implemented in the R package COBS (Constrained B-Spline Smoothing, He & Ng, 1999; Ng & Maechler, 2007). This package also allows the user to specify qualitative constraints on each individual quantile curve, such as monotonicity or convexity. This constraint on the curves refers to constraining the quantile curve for a particular value of τ, not as a function across values of τ as would be needed to ensure noncrossing. To ease the computational burden, the COBS package, by default, implements the quantile smoothing splines with 25 knots instead of knots at each data point. The user may specify more or less knots, if desired. The same choice of a reduced set of knots is used for computational convenience for the proposed joint smoothing spline in the simulation study.

Each of the two examples is again a special case of the heteroscedastic error model,

$$y_i=f\left(x_i\right)+g\left(x_i\right){\epsilon }_i,$$

for some functions f and g. The covariate is again generated as U (0, 1) and ε_i ∼ N (0, 1) with n = 100. The two examples are given as follows.

• Example 4. The mean function is f(x) = 0.5 + 2x + sin(2πx − 0.5), and the variance function is g(x) = 1.

• Example 5. The mean function is f(x) = 3x, and the variance function is g(x) = 0.5 + 2x + sin(2πx − 0.5).

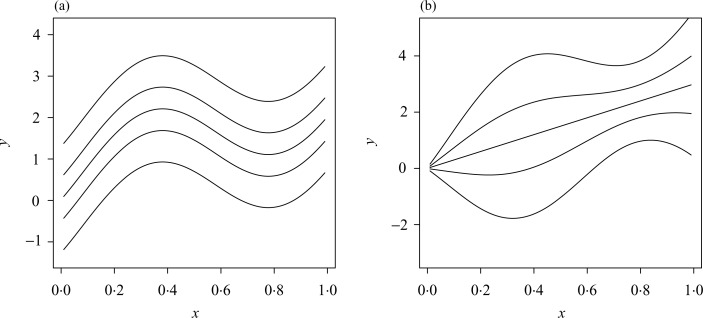
Example 4 results in the quantile curves simply being a shift in the intercept as shown in Fig. 1(a). Example 5 results in the quantile curves having various degrees of smoothness, with the median being linear, and more curvature exhibited in the extreme quantile curves, as shown in Fig. 1(b).

Fig. 1.

Plot of the true conditional quantile functions for Example 4 (a) and Example 5 (b). The five curves from bottom to top represent τ = 0.1, 0.3, 0.5, 0.7, 0.9.

For the nonparametric fits, the 0.99 quantile was not used, as it is too extreme for a nonparametric estimate based on a sample of size 100. Hence the set of quantiles, τ = 0.1, 0.3, 0.5, 0.7, 0.9 was fitted. Table 2 shows the results for τ = 0.5, 0.7, 0.9 for the two examples over the 500 simulated datasets for each example. The lower quantiles are analogous due to symmetry. Overall, the proposed method compares favourably to the traditional quantile splines, in terms of integrated squared error. For comparison, the proposed method is computed using a single tuning parameter as well as using a separate tuning parameter for each quantile level. In both examples, the single tuning parameter exhibits a performance very similar to the full q-dimensional tuning.

Table 2.

Average root mean integrated squared error (×100) over 500 simulated datasets, with standard error in parentheses

	Example 4			Example 5
	τ = 0.5	τ = 0.7	τ = 0.9	τ = 0.5	τ = 0.7	τ = 0.9
NCRQ	25.7 (0.21)	25.9 (0.21)	31.8 (0.31)	26.4 (0.33)	32.2 (0.34)	48.5 (0.60)
NCRQ (single)	24.6 (0.19)	25.3 (0.19)	32.3 (0.34)	26.6 (0.34)	31.7 (0.32)	49.9 (0.62)
RQ (RS)	29.8 (0.18)	30.6 (0.21)	35.2 (0.31)	24.7 (0.42)	36.3 (0.43)	52.2 (0.73)
RQ (SS)	27.1 (0.19)	27.6 (0.21)	34.7 (0.31)	21.8 (0.35)	34.2 (0.39)	53.4 (0.90)

NCRQ, proposed noncrossing regression quantiles; NCRQ (single), proposed approach with a single tuning parameter; RQ (RS), classical regression splines with knot selection; RQ (SS), classical regression smoothing splines via regularization.

4.3. Varying the choice of quantiles

Assume that the linear quantile regression model holds for a given quantile of interest. Since the proposed noncrossing approach is based on simultaneous estimation of a set of quantile curves, the estimate for the quantile of interest will change depending on the included quantiles. For example, if interest focuses on the median, one can add any number of additional quantiles to the median. Based on the results of Theorem 1, the asymptotic distribution will not be affected by the number of quantiles added. However, adding additional quantiles can improve the finite sample results via adding stability to the estimation.

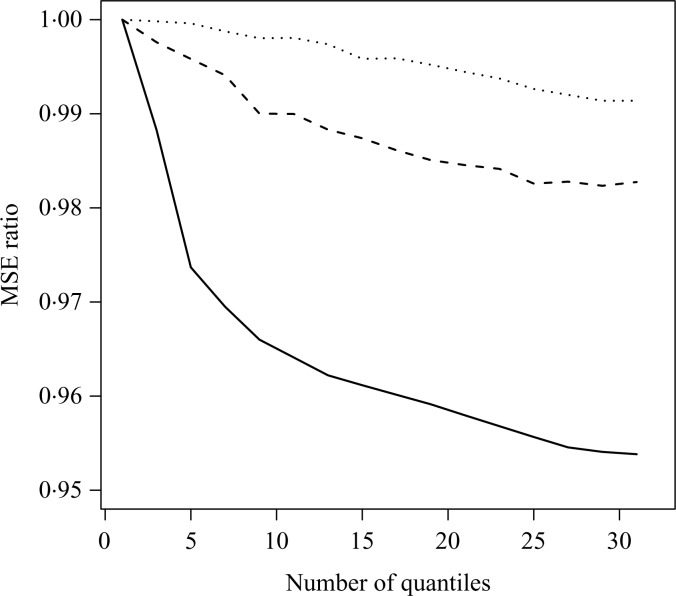
Figure 2 plots mean squared error in estimating the slope at the median for a univariate model as a function of the number of included quantiles for each of sample sizes n = 50, 100 and 200. The median regression estimate was computed on 5000 datasets based on an increasingly dense sequence of equally spaced quantiles. The y-axis represents the ratio of mean squared error to that of using only the median. The use of more quantiles seems to help stabilize the estimation.

Fig. 2.

Plot of mean squared error in estimation of the slope at the median as a function of the number of included quantiles, for sample sizes n = 50 (solid line), n = 100 (dashed line), and n = 200 (dotted line). Each curve is scaled so that the mean squared error is reported as a ratio relative to that of using only median regression.

It is natural to assume that if all quantiles are linear, adding more would give better results. Figure 2 was generated via the model in Example 5, so that only the median is linear. However, even with the misspecification, there is a gain in accuracy, probably because quantiles near the median are still close to linear, and help stabilize the estimation. This phenomenon was observed in other scenarios, including those focused on extreme quantiles. In practice, we recommend adding quantiles in a neighbourhood of the quantile of interest until the estimation appears to stabilize.

5. Analysis of hurricane data

The noncrossing quantile regression approach is now applied to the tropical cyclone data. The data consist of a sample of 422 tropical cyclones occurring near the US coastline over the period 1899–2006. Jagger & Elsner (2009) used linear quantile regression to model the maximum wind speed of each cyclone as a function of four climate covariates: the North Atlantic Oscillation Index, the Southern Oscillation Index, the Atlantic sea-surface temperature and the average sunspot number. The climate covariates are constant within a single year to represent the yearly large-scale climate conditions. The North Atlantic Oscillation Index is the preseason and early-season average of the May and June values. The other three are obtained by averaging over the peak season of August through October. The particular focus is on the upper quantiles, as these extreme hurricane-strength storms are of considerable importance.

Following Jagger & Elsner (2009), quantile regression is applied to these data at the quantiles 0.25, 0.5, 0.75, 0.9, 0.95, 0.99. Table 3 shows the parameter estimates for the intercept along with the four slope parameters for the three upper quantiles from both a classical quantile regression fit and the proposed noncrossing fit. As in Jagger & Elsner (2009), included are pointwise 90% confidence intervals. In the other three quantiles, the results for both methods are similar.

Table 3.

Coefficient estimates for the intercept and the four climate covariates for the hurricane data at upper quantiles, with 90% confidence intervals

	Unconstrained			Constrained
	τ = 0.9	τ = 0.95	τ = 0.99	τ = 0.9	τ = 0.95	τ = 0.99
INT	109.15* (85.01, 133.29)	120.06* (88.26, 151.86)	134.65* (119.41, 149.89)	107.83* (84.56, 131.11)	117.95* (91.16, 144.74)	140.63* (121.44, 159.83)
NAO	−5.03* (−9.91, −0.14)	−0.95 (−6.38, 4.49)	1.43 (−1.58, 4.44)	−4.93* (−9.61, −0.26)	−3.06 (−8.04, 1.93)	−3.06 (−6.54, 0.43)
SOI	5.74* (0.40, 11.09)	1.23 (−5.75, 8.21)	−3.98* (−7.44, −0.51)	5.21* (0.02, 10.39)	3.32 (−2.62, 9.27)	−2.80 (−7.10, 1.50)
SST	6.16* (1.34, 10.97)	4.19 (−1.65, 10.03)	−0.73 (−3.52, 2.06)	5.17* (0.57, 9.77)	5.17* (0.12, 10.22)	3.21 (−0.48, 6.90)
SUN	3.48 (−1.21, 8.17)	1.95 (−2.60, 6.50)	6.19* (2.86, 9.52)	3.16 (−1.43, 7.75)	3.16 (−1.17, 7.49)	3.16 (−0.52, 6.84)

INT, intercept; NAO, North Atlantic Oscillation Index; SOI, Southern Oscillation Index; SST, Atlantic sea surface temperature; SUN, average sunspot number;

^*,statistically significant coefficients at α = 0.1.

Of particular note is the smoothing of the coefficients in the extreme quantiles. This smoothing stabilizes the inference and avoids some of the possibly spurious associations, such as the significance of the sunspot number in the 99th percentile but not in any of the other upper quantiles. The confidence intervals for both methods were obtained using the asymptotic normality and using the kernel method to estimate the inverse density needed for the standard errors (Powell, 1991; Koenker, 2005).

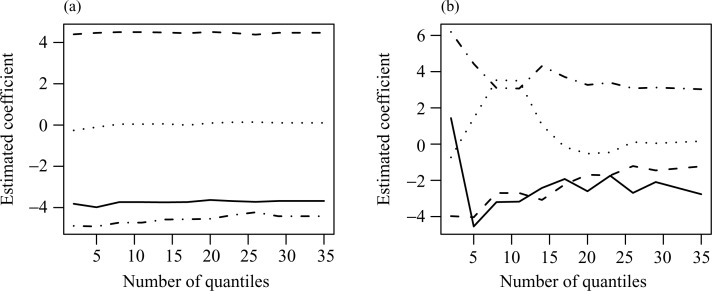
As the estimates will change depending on the number and location of included quantiles, a sensitivity analysis is performed. The coefficient estimates for the median and 0.99 quantile regressions are examined as a function of an increasing number of quantiles. Figure 3 plots the estimated coefficients for each of the four slopes for the median (a) and the 0.99 quantile (b). Initially, only the two quantiles were fitted. Then quantiles were sequentially added until a grid spacing of 0.05 was obtained, with a grid spacing of 0.01 bracketing the median, from 0.45 to 0.55, and a spacing of 0.01 from 0.9 to 0.99, to ensure a more saturated region around the quantiles of interest. The median is much less sensitive, while the 0.99 quantile is clearly highly sensitive. Once 14 quantiles are included, the inference regarding significant predictors remains unchanged upon adding more quantiles, and is the same as that reported in Table 3. This is at the point in the sensitivity analysis that the 0.95 quantile is first added between the 0.9 and the 0.99 quantiles.

Fig. 3.

Plot of the estimated slope coefficients at the median (a) and the 0.99 quantile (b) as the number of included quantiles is increased. NAO, North Atlantic Oscillation Index (solid line); SOI, Southern Oscillation Index (dashed line); SST, Atlantic sea surface temperature (dotted line); SUN, average sunspot number (dotted/dashed line).

Appendix

Proof of Theorem 1

Let Ẑ_n and Z̃_n denote n^1/2{β̂(τ) − β⁰(τ)} and n^1/2{β̃(τ) − β⁰(τ)}, respectively. Then |pr(Ẑ_n ⩽ u) − pr(Z̃_n ⩽ u)| = |pr(Ẑ_n ⩽ u|Ẑ_n ≠ Z̃_n) − pr(Z̃_n ⩽ u|Ẑ_n ≠ Z̃_n)| pr(Ẑ_n ≠ Z̃_n).

Since the first term in the product is bounded by 1, it suffices to show that pr(Ẑ_n ≠ Z̃_n) → 0, or pr(Ẑ_n = Z̃_n) → 1.

Due to the formulation of the estimator, the event Ẑ_n = Z̃_n is equivalent to the event that the classical quantile regression estimator maintains its appropriate ordering. To show that the probability of this event goes to 1, consider the difference in the classical estimator at successive quantiles, n^1/2(z^Tβ̃_τt+1 − z^Tβ̃_τt). It will be shown that this difference must be positive with probability tending to 1 for every t = 1, . . . , q.

The difference can be written as

$$n^{1/2}\left(z^{\text{T}}{\tilde{\beta }}_{{\tau }_{t+1}}-z^{\text{T}}{\beta }_{{\tau }_{t+1}}^0\right)-n^{1/2}\left(z^{\text{T}}{\tilde{\beta }}_{{\tau }_t}-z^{\text{T}}{\beta }_{{\tau }_t}^0\right)+n^{1/2}\left(z^{\text{T}}{\beta }_{{\tau }_{t+1}}^0-z^{\text{T}}{\beta }_{{\tau }_t}^0\right).$$

Under the assumed regularity conditions, the classical quantile regression estimator, β̃(τ), is n^1/2-consistent. Hence, it follows that the first two terms are O_p(1) for any t.

By the mean value theorem, it follows that $z^{\text{T}}{\beta }_{{\tau }_{t+1}}^0-z^{\text{T}}{\beta }_{{\tau }_t}^0=\left({\tau }_{t+1}-{\tau }_t\right)\frac{\partial }{\partial \tau }{z}^{\text{T}}{\beta }_{\tau }^0{|}_{\tau =\tau *}$, where τ_t ⩽ τ^* ⩽ τ_t+1. Now, regularity condition (3) yields that $\frac{\partial }{\partial \tau }{z}^{\text{T}}{\beta }_{\tau }^0={\left\{f_{Y_i|x}\left(F_{Y_i|x}^{-1}(\tau )\right)\right\}}^{-1}⩾1/b$ for any τ ∈ (0, 1). Hence $n^{1/2}\left(z^{\text{T}}{\beta }_{{\tau }_{t+1}}^0-z^{\text{T}}{\beta }_{{\tau }_t}^0\right)⩾n^{1/2}\left({\tau }_{t+1}-{\tau }_t\right)/b$. By assumption, the right-hand side diverges. This leads to the third term dominating in the difference with probability tending to 1, and thus the difference will be positive.

Proof of Theorem 2

Assume that g̃_τ1 , . . . , g̃_τq ∈ 𝒢 is the minimizing set of functions. Now consider any particular τ_t. The value of the loss function, the first term in (4), only depends on the values of g_τt at the data points. Hence any other g_τt such that g_τt (x) = g̃_τt (x) at the data points will yield the same value for the loss function. So it suffices to consider the problem of finding the interpolator of the set of points {g̃_τt (x_i)}, which minimizes the total variation. The solution to this interpolation problem is given by a linear spline with knots at the given set of x_i (Fisher & Jerome, 1975; Pinkus, 1988). Denote this solution by ĝ. Clearly, since the set of g̃ are noncrossing, they maintain the proper ordering at each of the data points, so the interpolating splines ĝ will not cross.