A hybrid approach to protein differential expression in mass spectrometry-based proteomics

Abstract

Motivation: Quantitative mass spectrometry-based proteomics involves statistical inference on protein abundance, based on the intensities of each protein's associated spectral peaks. However, typical MS-based proteomics datasets have substantial proportions of missing observations, due at least in part to censoring of low intensities. This complicates intensity-based differential expression analysis.

Results: We outline a statistical method for protein differential expression, based on a simple Binomial likelihood. By modeling peak intensities as binary, in terms of ‘presence/absence,’ we enable the selection of proteins not typically amenable to quantitative analysis; e.g. ‘one-state’ proteins that are present in one condition but absent in another. In addition, we present an analysis protocol that combines quantitative and presence/absence analysis of a given dataset in a principled way, resulting in a single list of selected proteins with a single-associated false discovery rate.

Availability: All R code available here: http://www.stat.tamu.edu/~adabney/share/xuan_code.zip.

Contact: adabney@stat.tamu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

A key goal of quantitative mass spectrometry-based proteomics is statistical inference on differential protein expression. Quantitative information is derived from spectral peak intensities that are identified as having come from one of a protein's constituent peptides. Statistical procedures for differential protein expression are naturally constructed in the context of regression or ANOVA, or as a ‘rollup’ problem (Polpitiya et al., 2008).

However, intensity-based procedures are challenged by the presence of widespread missing intensities. It is typical for 20–40% of the total collection of attempted measurements to be missing; that is, in a matrix with all identified peptides in the rows, samples in the columns, 20–40% of the matrix cell entries are empty. With standard regression or ANOVA procedures, peptides with missing values must either be removed from the analysis, or their missing values must be imputed. There will typically be very few peptides with no missing values, so filtering peptides in this way results in a much less informative dataset. Furthermore, previously-published reports indicate that the vast majority of missing values are the results of censoring of absent or low-abundance peptides (Wang et al., 2003). This means that simple imputation routines are not appropriate (Little and Rubin, 2002).

Parametric imputation and other specialized methodology can be employed to enable intensity-based inference with lessened information loss (Karpievitch et al., 2009). However, some information loss is inevitable. In particular, ‘one-state’ (or nearly so) peptides, those for which there are many observed intensities in one comparison group but few in another comparison group, are not amenable to an intensity-based analysis; not limited to the two-class problem. As a result, such peptides are typically filtered out of an intensity-based analysis. A protein that is always present in a diseased state, say, and never in the healthy state would be of great biological interest, so it is unfortunate if our statistical methodology cannot identify such a protein.

An alternative to an intensity-based analysis is a ‘presence/absence’ analysis, in which peak intensities are digitized into binary measurements depending on whether a peak was observed or not. This is analogous to the spectral counting approach in MS/MS studies (Zybailov et al., 2005), where a peptide is quantified by the number of fragmentation spectra assigned to it. Data collected in our laboratory do not necessarily have MS/MS fragmentation data associated with it, instead being obtained according to the accurate mass and time tag pipeline (Smith et al., 2002; Zimmer et al., 2006). Still, we have information on whether or not a particular peptide was observed in each sample.

While presence/absence analysis is better-suited to finding one-state proteins, it necessarily has less statistical power to detect abundance differences in proteins with little to moderate missingness. Ideally, protein differential expression analysis would simultaneously target proteins of both types, resulting in a single list of differentially expressed proteins, with a single-associated false discovery rate (FDR). A hierarchical Bayesian model would be well-suited to this purpose, but such techniques are complex, computationally intensive and less amenable to high-throughput pipelines.

We present a hybrid analysis protocol that consists of two stages: (i) intensity-based analysis, and (ii) a presence/absence analysis. The results of each are merged to create a single collection of ‘interesting’ proteins, to which we use novel methodology to apply a single FDR. This enables the researcher to extract more information from a quantitative proteomic dataset than would be achievable by either approach alone, while still maintaining an interpretable measure of overall statistical confidence. For the proposed hybrid analysis protocol, we demonstrate the following: (i) resulting FDR estimates are conservative; (ii) one-state proteins are consistently selected as differentially expressed; and (iii) the number of differentially expressed proteins selected at a specified FDR exceeds that either intensity-based or presence/absence analysis alone.

2 METHODS

2.1 Data

2.1.1 Diabetes

These data are as previously described, containing label-free proteomic measurements on human patients with and without Type II diabetes (Karpievitch et al., 2009).

2.1.2 Filtering based on peptide detectability

To minimize the number of sibling peptides with large missingness proportion differences, we use PeptideSieve (Mallick et al., 2007) to filter peptides whose amino acid sequences are unlikely to be detected by MS. In all 554 peptides are filtered out before carrying on any further analysis.

2.1.3 Simulation

We carried out simulation studies as follows, to investigate the operating characteristics of our methodology at both peptide and protein levels. Peptide-level data were generated from a Binomial model, under the same conditions as the diabetes data (two comparison groups with 10 samples in each); the Binomial model is appropriate, since presence/absence data can be viewed as success/failure of independent Bernoulli trials. Presence probabilities in group one took the values on p₁=0.2, 0.3, 0.4, 0.5. Half of the group-two peptides were assigned the same presence probabilities as their group-one counterparts. In the other half, differential presence probabilities were created, with probability differences (comparing group two to group one) of p_d=p₂−p₁=0.1, 0.2,···, 0.9−p₁. Separate simulations were carried out for each of the group-one presence probability values with even replications on different p_d settings.

Similarly, for protein-level data, the number of peptides per protein was randomly selected to range between 1 and 30. Protein-level presence probabilities also took the values p₁=0.2, 0.3, 0.4, 0.5 and p_d=p₂−p₁=0.1, 0.2,···, 0.9−p₁. For each constituent peptide, the group-one peptide-level presence probability equaled the protein-level probability multiplied by a randomly-selected number between 0 and 1 (to allow for different levels of detectability for peptides of the same protein). Peptide-level differential presence probabilities were handled as described for the peptide-level simulation above.

Finally, to simulate data for use by the hybrid method, with both peak intensities and presence/absence indicators, we randomly generated intensities from a Normal distribution with parameters chosen to mimic the diabetes data. Missingness proportions took the values 10, 20, 30 and 40%, with missingness created by censoring the lowest corresponding percentages of peptide intensities. As in the above simulations, half of the peptides/proteins were given differential expression, now defined in terms of mean intensity levels. Differential intensity magnitudes took both low-magnitude values of 1, 2, as well as high-magnitude values of 5, 10, all on the log scale.

2.2 Logistic model for protein presence/absence

Logistic regression is a natural analysis method for presence/absence data, given their binary nature. Specifically, let Y_ijkl be the indicator for whether a peak was observed for peptide j of protein i in comparison group k and sample l. Then, we can say Y_ijkl ~ Binomial(1, p_ijk) for l=1, 2,…, n_k, where n_k is the number of samples in comparison group k. A simple logistic regression model would then be

(1)

Here, Prot_i represents the overall (across all comparison groups) log odds of peak presence for protein i, Pep_ij is the effect of peptide j of protein i (assumed to be the same across all k comparison groups), and Grp_ik is the protein-level effect of comparison group k in protein i. Usual sum-to-zero constraints apply; namely, ∑_j=1^m_i Pep_ij=0 and ∑_k=1^K Grp_ik=0 for i=1, 2,…, M, where M is the total number of proteins in the data.

For the purposes of comparing protein presence probabilities across comparison groups, the parameters of interest are the Grp_ik, i=1, 2,…, M. For example, in the diabetes data, K=2, with k=1, 2 corresponding to the diabetic and control groups, respectively. Hence, Grp_i1 − Grp_i2 is the log odds ratio for protein i, comparing diabetics to controls. Testing for a difference in presence probabilities corresponds to testing the null hypothesis that Grp_i1 − Grp_i2=0; given the model's sum-to-zero constraints, this is equivalent to the null hypothesis that Grp_i1=Grp_i2=0. Of course, the model is not restricted to the two-class case and can naturally be generalized to the K-class case, in which the corresponding null hypothesis is that Grp_i1=Grp_i2=···=Grp_iK.

Unfortunately, logistic regression is not well-suited in practice to the analysis of presence/absence data. In particular, biologically-interesting proteins are liable to be missed entirely, due to inherent limitations of the methodology. Consider a ‘one-state’ protein, present in all samples for one comparison group, absent in all samples for the other comparison groups. From a biological perspective, this would be a very interesting protein. However, in logistic model, the p-value for such a protein will tend to be reported as nearly equal to one, meaning that the protein would not be selected as differentially expressed under any reasonable criteria.

A simple scenario illustrates this problem. Consider a ‘one-state’ protein with just a single peptide. In logistic regression, the assumed variance-covariance matrix for regression coefficients is (X′WX)⁻¹, where X is the model matrix, and W is diagonal with entries p_k(1 − p_k), with p_k the presence probability in comparison group k, k=1, 2. For comparison groups in which no peaks were observed, the estimated value of p_k is zero, making the corresponding entry in W equal to zero. This results in an overestimation of the standard error for the group effect model term, hence an understatement of statistical significance for that protein's group effect. In the diabetes data, for example, ‘one-state’ proteins are assigned p-values of one.

2.3 Exact peptide-level tests

In light of the logistic regression limitations, we propose an exact procedure for testing for differences in presence/absence between two comparison groups. Let y_jk·=∑_l=1ⁿ y_jkl be the number of observed peaks for peptide j in comparison k, k=1, 2. We use T_j=|y_j1· − y_j2·| as the peptide-level test statistic. Based on the Binomial probability model, the exact sampling distribution of T_j under the null hypothesis H₀ of no difference in presence probabilities can be written as

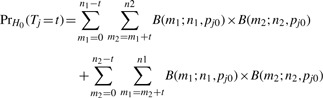where B(m; n, p) is the Binomial PMF at m, with n trials and probability of success p and p_j0 is the shared probability of peak presence for both groups. Thus, based on an observed statistic of t_j, the p-value is ∑_t≥t Pr_H0(T_j = t). In practice, we need only to estimate the shared presence probability under the null hypothesis, p_j0, to approximate the p-value for a given peptide. We estimate p_j0 with a pooled sample proportion, resulting in 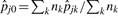, where 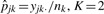, K=2.

As an example, consider a ‘one-state’ peptide, present in all samples of one group but in no samples of the other group, in the diabetes data. Whereas logistic regression reports a p-value of one, the exact test correctly highlights the peptide as statistically significant. Specifically, the test statistic T_j equals 10, and 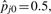, so the p-value is computed as 2×B(10; 10, 0.5)×B(0; 10, 0.5) < 0.0001

2.4 Bootstrap protein-level tests

For inference at the protein level, there is the added challenge of multiple peptides belonging to the same protein. To incorporate all sibling peptides into a single test for differential presence probabilities, we use the following test statistic:

(2)

where i is protein index, j is peptide index and k is comparison group index, i=1, 2,…, M, j=1, 2,…, m_i, k=1,···, K, K=2. The statistic in (2) is a weighted average of observed presence difference on each sibling peptide. For the weighting term κ_ij, we use κ_ij=y_ij··/∑_j y_ij··

A parametric bootstrap procedure (Efron and Tibshirani, 2002) is used to approximate the sampling distribution of the T_Mi under null hypothesis setting as follows. First the Binomial parameters p_ijk are estimated, for which two approaches are considered. The first approach simply uses the sample proportion for peptide j of protein i in comparison group k being present, which needs 2×m_i parameter estimation per protein. Alternatively, we approaching the problem by inducing some structure between the p_ijk, assuming that p_ijk=p_ik×d_ij, where p_ik is the overall presence probability for protein i in comparison group k, and d_ij is the ‘detectability’ probability (the probability that a particular ion species is detected by the LC-MS instrument) for peptide j of protein i. This assumption of structure translates to an assumption that the detectability of a peptide does not differ between comparison groups. Since detectability is a function of chemical composition rather than abundance (Mallick et al., 2007), this seems a reasonable assumption. After introducing the structure assumption the number of parameters per protein to be estimated reduces from K×m_i to K+m_i.

With the second approach, the presence probability p_ik of protein i in group k is estimated by averaging the presence proportion of its top 10% most prevalent peptides (rounded up to the nearest integer number of peptides).

The rationale here is that, for these most prevalent peptides, the detectability probability will be close to one, making p_ijk≈p_ik. Then 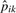is used to estimate d_ij as 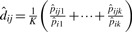, where 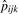and 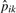are the sample presence proportions. Clearly, this estimation approach will work best for proteins with several peptides detected; with few peptides, the above calculation may be based on the single most-abundant peptide. Still, we point to the Results section as evidence of adequate performance overall.

Since we have 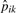and 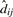, according to the equation p_ijk = p_ik×d_ij, the null sampling distribution of our test statistic could be generated by parametric bootstrap. Under the null hypothesis setting, the presence probabilities of protein i across K comparison groups are the same and set to be p_i0. In two group case, p_i0=p_i1=p_i2 and 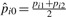. Thus, for peptide j of protein i in group k, n_k zeroes or ones are generated from the Binomial distribution with probability 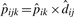, k = 1, 2. We run B bootstrap iterations and compute the test statistic (2), T_Mb in each iteration. The p-value is then computed as the proportion of bootstrap test statistic values being as or more extreme as our observed T_Mi value:

2.5 FDR estimation

The FDR associated with a list of features selected at a p-value cutoff c_p (Storey and Tibshirani, 2003) is the expected number of false positives F out of the total number of selected features S:

(3)

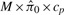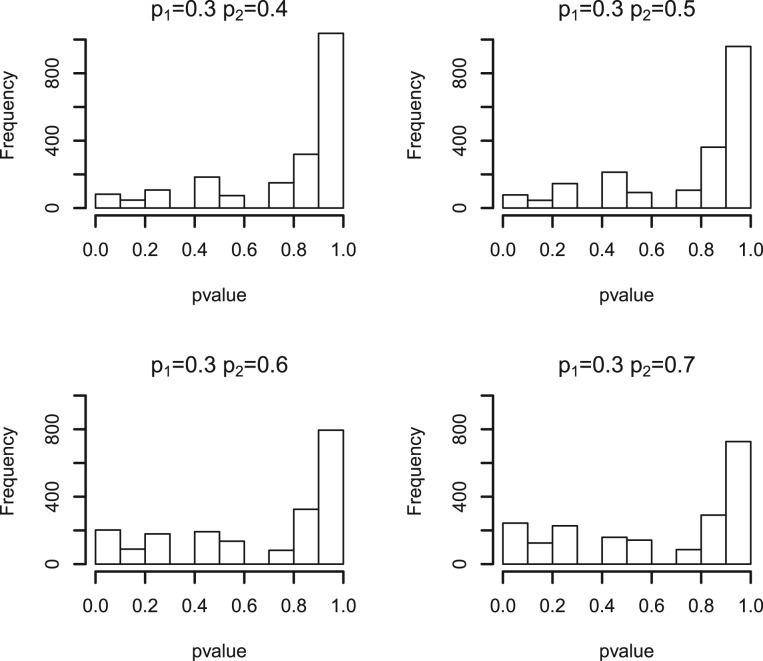
The denominator can be replaced simply with the observed number of selected features. The traditional approach to estimate the numerator is to exploit the expected uniform sampling distribution of the null p-values (Storey and Tibshirani, 2003). In particular, we can estimate E [ F_cp ] by , where M is the total number of features and 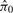is the estimated proportion of null features out of the total M features. However, as our test statistic is discrete, its null sampling distribution is not necessarily Uniform. As an example, Figure 1 shows a simulated null sampling distribution for peptide-level test statistics, in which the shape of the null sampling distribution is quite non-Uniform and could depend on many factors, including the number of peptides of a protein, the sample size of each comparison group and the overall number of observed peaks of a protein. With discrete test statistics, standard FDR estimates will tend to be conservative (Benjamini and Hochberg, 1995; Benjamini and Yekutieli, 2001). There is some published work aimed specifically at FDR estimation with discrete test statistics (Gilbert, 2005; Pounds and Cheng, 2006).

Fig. 1.

P-value histograms of simulated null peptides with shared presence probabilities of 0.2, 0.3, 0.4, 0.5 across each comparison group. The null sampling distribution is non-uniform, due to the discrete nature of the test statistic

2.5.1 Peptide-level FDR estimation

A more general way to describe the estimate of the numerator in Equation (3) is as a weighted sum of calculations from the estimated null p-value distribution:

where w_j is a weight (number between 0 and 1), and 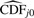is the estimated cumulative distribution function (CDF) for null features. In the case of a continuous test statistic, the null p-value distribution is known to be U(0, 1), so no actual estimation of CDF_j0 is required. Since the right-tail probability of the U(0, 1) distribution at c_p is equal to c_p, we would simply have 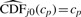for all j. The weights w_j would ideally be selected in a way to give prominence to (take values closer to one for) null peptides. With a continuous test statistic, since 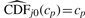for all j, we can replace the w_j with an estimate of the number of null features, rather than having to weight each feature individually. Thus, with the traditional estimate of the numerator in Equation (3), the w_j are replaced with 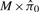. Again, our challenge in the present context is that our peptide-level test statistic is not continuous. With this in mind, we derive a peptide-level FDR estimate by proceeding from the more general formulation above. Specifically, we specify peptide-specific weights w_j and use the assumed Binomial nature of presence/absence observations to derive estimates of the null p-value CDF for each peptide, as follows.

The estimate of CDF_j0 is derived from an estimate of the null probability mass function (PMF) for peptide j, which is assumed to be Binomial:

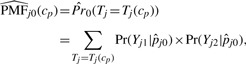where 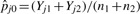is a pooled estimate of presence probability for peptide j under the null hypothesis that p_j1 = p_j2. For the w_j, we use

This corresponds to calling a peptide null if its estimated null PMF is greater than its PMF estimated without restricting that the null hypothesis be true. We therefore estimate the peptide-level FDR as

In what follows, we refer to an ‘unweighted’ FDR estimate as that resulting from setting all w_j equal to one.

2.5.2 FDR estimates for multi-peptide proteins

Our simulation studies indicate that for most settings, the p-value of the test statistic for multi-peptide protein (2) is approximately uniformly distributed under null hypothesis setting, especially when there are moderate overall levels of presence (data not shown) and moderate number of sibling peptides in a protein. Because of this, we use the standard (Storey and Tibshirani, 2003) method for FDR estimation. ‘Namely, at p-value cutoff c_p, we estimate the FDR as which could also be seen as a uniform weight across proteins 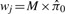across all proteins’.

where M is the total number of proteins, and 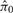is the estimated proportion of null proteins, We estimate π₀ by fitting a smooth lowess curve to the values of 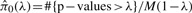, then choosing 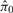as the fitted value of the smooth curve as λ→1 (Storey and Tibshirani, 2003).

2.5.3 Weighted FDR estimation for mixed single and multi-peptide proteins

In practice, both single-peptide proteins and multi-peptide proteins are usually mixed in a dataset, for which we have developed p-value and FDR estimation separately. The two sets of p-value are left as is whereas a unified FDR estimate needs to be generated based on the pooled set of p-values. The numerator of FDR for mixed case is given by summing up the estimation of expected number of false positive features for single-peptide protein and multi-peptide proteins, as indicated in the above two sections, and the denominator is the number of selected features based on the p-value pool.

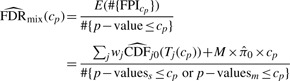where p-values_s are the p-values for single-peptide proteins and p-values_m are those for multi-peptide proteins; the ‘#’ notation is used to indicate ‘number of’.

2.6 Hybrid analysis incorporating both presence/absence and intensity measurements

The above methodology has dealt only with presence/absence data, from which peak intensity measurements are excluded. The rationale for simplifying peak intensity measurements to presence/absence is that it better enables discovery of ‘one-state’ (or similar) proteins. However, statistical information is lost by throwing out intensity measurements, which would translate to decreased statistical power to detect differentially expressed proteins that differ in terms of abundance but not presence/absence. Thus, we would ideally incorporate both peak intensity and presence/absence information into a differential expression analysis. One simple way to do this is to carry out separate intensity-based and presence/absence-based analysis, select proteins at a specified FDR from each analysis, then report the union of the two resulting protein lists. However, while we might intuitively expect a small FDR for the resulting list of proteins, we will not generally be able to assign an actual FDR estimate. In what follows, we derive a FDR estimate for the union list of differentially expressed proteins. Thus, taken together, the methodology presented here allows the researcher to select a list of differentially expressed proteins, some based on intensity and others based on presence/absence, to which an overall FDR estimate can be assigned.

We use a single p-value threshold c_p for both intensity measurements and presence/absence; so, a protein is selected if either of its intensity-based and presence/absence p-values are less than c_p. Intensity-based p-values are derived from regression models and censored likelihoods from our prior work (Karpievitch et al., 2009). Let p–value_b and p–value_p correspond to the binary presence/absence and peak intensity measurements, respectively. The FDR for a hybrid analysis can then be estimated by

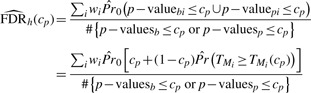We set the weight w_i equal to the average of the binary weight and the uniform weight derived from Storey and Tibishirani's FDR estimation scheme in the intensity-based method (Karpievitch et al., 2009).

3 RESULT

3.1 Simulation data

Table 1 shows Type I error and power for the proposed presence/absence methodology applied to simulated single-peptide and five-peptide proteins. As would be expected, we have greater power to detect differential expression when there are multiple peptides in a protein. The pool of number of peptides of a protein is 5, 10, 15, 20, 25, the presence probability of proteins take value among p₁=0.2, 0.3, 0.4, 0.5 and p_d=p₂−p₁=0.1,···, 0.9−p₁, peptide detectablity is set to vary among 0.9, 0.7, 0.5, 0.1, 0.01.

Table 1.

Peptide-level error rates and power with p₁=0.2, 0.3, 0.4, 0.5 and p_d=0.0, 0.1,…, 0.7

No. of pep = 1
pd=p2−p1	p1=0.2	p1=0.3	p1=0.4	p1=0.5
pd=0.0	0.053	0.051	0.050	0.047
pd=0.1	0.069	0.065	0.058	0.048
pd=0.2	0.133	0.122	0.120	0.110
pd=0.3	0.240	0.232	0.210	0.182
pd=0.4	0.381	0.365	0.353	0.348
pd=0.5	0.512	0.461	0.430	*
pd=0.6	0.720	0.677	*	*
pd=0.7	0.874	*	*	*
No. of pep = 5
pd=0.0	0.051	0.052	0.050	0.054
pd=0.1	0.196	0.158	0.136	0.096
pd=0.2	0.486	0.404	0.388	0.352
pd=0.3	0.778	0.734	0.710	0.692
pd=0.4	0.960	0.924	0.910	0.908
pd=0.5	0.994	0.990	0.990	*
pd=0.6	1.000	1.000	*	*
pd=0.7	1.000	*	*	*

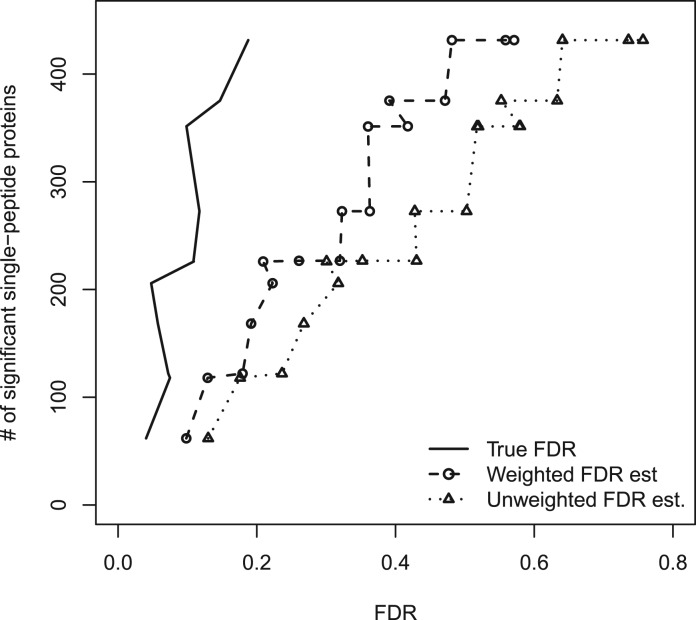
Figure 2 shows the number of significant single-peptide proteins versus FDR, based on the proposed peptide-level presence/absence methodology. The particular simulation scenario displayed in the figure has p₁ = 0.3, with a random mixture of differential presence/absence, ranging over p_d = 0.1, 0.2,…, 0.6. The unweighted FDR estimate is very conservative, resulting in many fewer significant peptides at a given FDR estimate, relative to the true FDR curve. The binary weighting improves this somewhat, resulting in greater power while maintaining conservative FDR estimation. In the Supplementary Materials, we include similar figures for a variety of p1 and pd values. We also include simulation-based comparisons with the Benjamini–Hochberg estimator (Benjamini and Hochberg, 1995) and that of Pounds and Cheng (Pounds and Cheng, 2006); the simulations suggest that our proposed FDR estimates are more powerful across the board, likely the result of our estimators having been developed specifically for the presence/absence problem.

Fig. 2.

Numbers of significant single-peptide proteins versus FDR for the proposed peptide-level methodology, on simulated data with p₁=0.3 and a mixture of differential presence/absence levels. The weighted FDR estimate is conservative

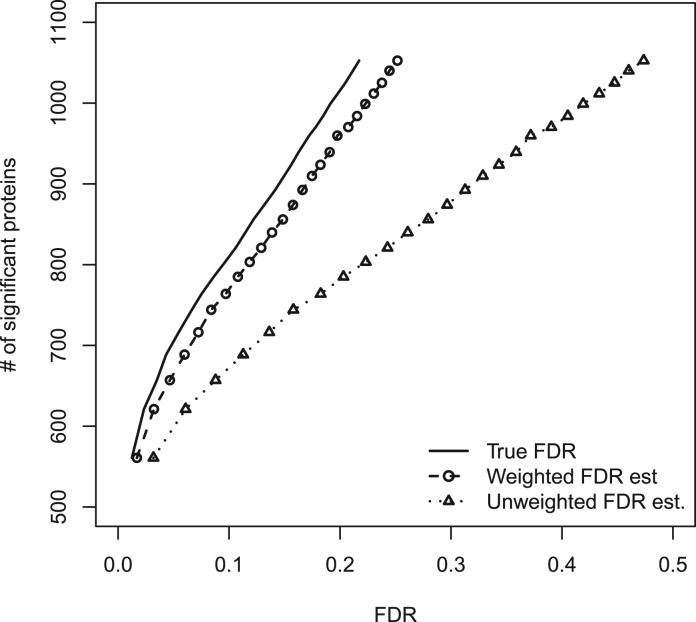
Figure 3 shows the number of significant five-peptide proteins versus FDR, based on the proposed protein-level presence/absence methodology. The simulation scenario in this figure is similar to that in Figure 2, now with each protein having five constituent peptides. In this case, ‘weighting’ is carried out using the standard 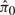estimate, again resulting in conservative FDR estimation. The pictures for different values of p₁, as well as for different numbers of constituent peptides, are not qualitatively different (data not shown). Furthermore, the Storey–Tibshirani FDR estimator on which these results are based has been shown to be quite powerful relative to other estimators, including the Benjamini–Hochberg estimator (Storey, 2002).

Fig. 3.

Numbers of significant five-peptide proteins versus FDR for the proposed protein-level methodology, on simulated data with p₁=0.3 and a mixture of differential presence/absence levels. The weighted FDR estimate is conservative

Our final simulation contains a combination of single- and multi-peptide proteins, a variety of differential expression magnitudes, with a sample size of 10 in each of the 2 comparison groups. In this case, peak intensities were simulated, from which presence/absence data were obtained, to reflect the intended real-world setting in which both intensity-based and binary presence/absence information is available. Table 2 compares the proposed hybrid approach with both our ‘qualitative’ (presence/absence-based) and previously-published ‘quantitative’ (intensity-based) (Karpievitch et al., 2009) methodology. The table shows numbers of differentially expressed proteins at an estimated FDR of 0.05, for a variety of simulation settings (varying the proportion of missing data as well as the amount and magnitude of differential expression). The hybrid approach consistently results in greater numbers of significant proteins, at a given FDR, than either of the presence/absence- or intensity-based approaches. Thus, by combining a traditional intensity-based analysis with a presence/absence analysis, we are able to supplement our findings with additional proteins of interest; these would potentially include ‘one-state’ proteins.

Table 2.

Number of identified features at estimated FDR level of 0.05 obtained from binary-based method, intensity-based method and hybrid method under a variety of simulation settings

Low magnitude		25%	dif			50%	dif
Method/Miss (%)	10	20	30	40	10	20	30	40
Quantitative	313	313	166	174	697	630	488	136
Qualitative	218	263	301	299	490	587	612	641
Hybrid	358	387	326	356	743	685	657	609
High magnitude		25%	dif			50%	dif
Quantitative	422	349	281	114	1010	900	668	547
Qualitative	491	514	530	519	812	998	1011	1033
Hybrid	525	537	539	503	1036	1080	1055	1084

The hybrid approach consistently results in greater numbers of differentially expressed proteins.

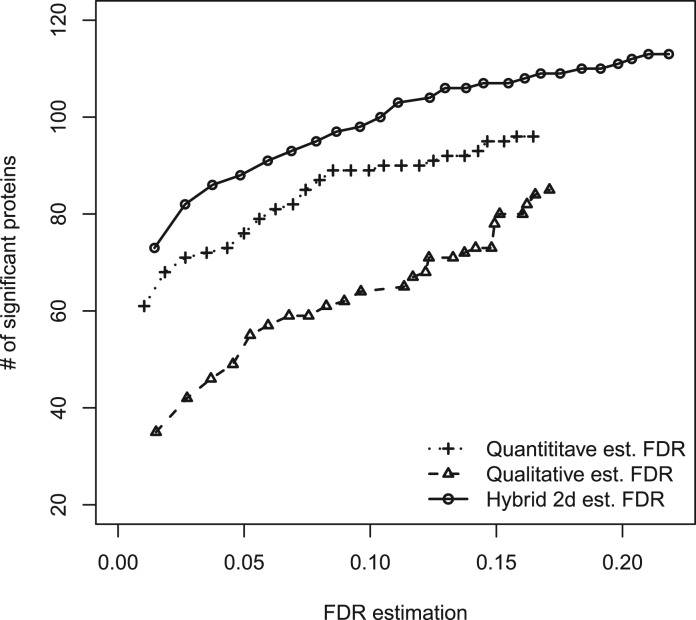
3.2 Diabetes data

The original dataset is comprised of 177 proteins and 1396 peptides. Figure 4 compares the proposed hybrid approach with presence/absence- and intensity-based approaches. The hybrid approach consistently results in greater numbers of differentially expressed proteins, at a given FDR. In this case, this is largely due to the presence/absence method supplementing the intensity-based method with proteins that were filtered out of the analysis due to too many missing values. Seventeen proteins were selected by the presence/absence method but not by the intensity-based method. Of these, several have known relevance to diabetes: a ketohexokinase isoform (IPI00216136.1) (Cirillo et al., 2009), a clusterin isoform (IPI00291262.3) (Daimon et al., 2011), a c8 beta chain complement component (IPI00294395.1) (Zhang et al., 2011), apolipoprotein E (IPI00021842.1) (Bach-Ngohou et al., 2002), apolipoprotein C-III (IPI00021857.1) (Juntti-Berggren et al., 2004), and apolipoprotein C-I (IPI00021855.1) (van der Ham et al., 2009).

Fig. 4.

Numbers of significant proteins versus FDR estimation on diabetes dataset by presence/absence-based method, intensity-based method and hybrid method.

4 DISCUSSION

The proposed presence/absence-based methodology is designed to enable the detection of ‘one-state’ (or similar) proteins that are not amenable to traditional intensity-based methods. Furthermore, we have proposed a hybrid approach that combines both intensity- and presence/absence-based analysis of a dataset, together with FDR estimation of the combined list of differentially expressed proteins. The proposed hybrid approach was demonstrated to outperform either of the intensity- or presence/absence-based methods alone.

An obvious limitation to our work is its applicability to only two comparison groups. A regression-based implementation would be more generalizable, and we intend to pursue this in our future work. The choices of weights in the peptide-level and hybrid methods could undoubtedly be improved upon as well; all FDR estimates are quite conservative.

Funding: NIH National Center for Research Resources (RR18522), National Institute of Allergy and Infectious Diseases NIH/DHHS through Interagency agreement Y1-AI-8401 and Award No. U54AI081680, and in part on work supported by Award No. KUS-C1-016-04, made by King Abdullah University of Science and Technology (KAUST). Work was performed in the Environmental Molecular Science Laboratory, a national scientific user facility sponsored by the US Department of Energys Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory in Richland, Washington. Pacific Northwest National Laboratory is operated by Battelle Memorial Institute for the US Department of Energy under contract DE-AC05-76RL0 1830.

Conflict of Interest: none declared.