A rule of seven in Watson-Crick base pairing of mismatched sequences

Abstract

Sequence recognition through base pairing is essential for DNA repair and gene regulation but the basic rules governing this process remain elusive. In particular, the kinetics of annealing between two imperfectly matched strands is not well characterized despite its potential importance in nucleic acids-based biotechnologies and gene silencing. Here we use single molecule fluorescence to visualize the multiple annealing and melting reactions of two untethered strands inside a porous vesicle, allowing us to quantify precisely the annealing and melting rates. The data as a function of mismatch position suggest that seven contiguous base pairs are needed for rapid annealing of DNA and RNA. This phenomenological rule of seven may underlie the requirement of seven nucleotides complementarity to seed gene silencing by small non-coding RNA and may help guide performance improvement in DNA and RNA-based bio- and nano-technologies where off-target effects can be detrimental.

Introduction

Double helix formation¹ of nucleic acids has been under investigation for over six decades. Thermodynamic parameters have been determined from compiled data of temperature-induced melting of DNA duplex and theoretical analysis^2,3, allowing the prediction of melting temperatures T_m with 2°C accuracy. The equilibrium constant, K_d, defined as the ratio of the rates of melting, k_off, and annealing, k_on, can also be determined. However, the determinants of individual rates are still poorly understood due to the difficulty in directly observing the annealing and melting reactions.

k_on could be deduced from changes in diffusion times^4–6, from fluorescence resonance energy transfer (FRET) analysis in bulk^7,8, through relaxation analysis following electric shock⁹ or temperature jumps^10–12 and by nuclear magnetic resonance¹³. Recently, single molecule techniques have enabled the determination of opening and closing rates for DNA and RNA hairpins^12,14,15 or oligonucleotides tethered inside membrane pore proteins¹⁶ but not the observation of freely diffusing intermolecular reaction. Moreover, single molecule mechanical studies gave extrapolated zero-force k_off 100–10,000 folds different from the fluorescence-based estimate¹⁷. In none of the previous studies was the effect of base pair mismatches on the annealing and melting kinetics examined despite the likelihood that the kinetics may play an important role in a variety of cellular processes where two slightly mismatched oligonucleotides interact.

Here, we aimed to quantify precisely the effect of a single base pair mismatch on the annealing and melting rates between two untethered DNA or RNA. We developed an assay based on single molecule FRET¹⁸ that can directly observe multiple rounds of melting and annealing reactions of a pair of DNA or RNA strands freely diffusing inside a porous vesicle. Confinement by the vesicle ^19,20,21,22 enables us to observe single molecule reactions even when the K_d is as high as 100 μM, which cannot be achieved by conventional methods. We observe that a single base pair mismatch can cause over 3 orders of magnitude change in K_d depending on the mismatch position. k_off increased gradually as the mismatch was placed closer to the middle of the sequence whereas k_on exhibited a response more like a step function to the mismatch position such that preventing 7 contiguous base pairs resulted in up to 100 times lower annealing rate. These results suggest that at least 7 contiguous Watson-Crick base pairs are necessary for rapid duplex formation.

Results

Kinetics of the full 9 bp DNA-DNA interaction

First, we designed two 9 nt long, complementary DNA strands (Fig. 1a) with T_m near room temperature^2,3,23,24 and void of secondary structures and dinucleotide repeats. The two DNA strands are end-labeled fluorescently with Cy3 (donor) and Cy5 (acceptor) so that their proximity can be detected using FRET. We used a vesicle encapsulation method described earlier which allows exchange of ions while keeping the nucleic acid oligomers within²¹ (see Methods section). Only those vesicles with fluorescence intensities and subsequent (single step) photo-degradation consistent with one donor and one acceptor were included in the analysis.

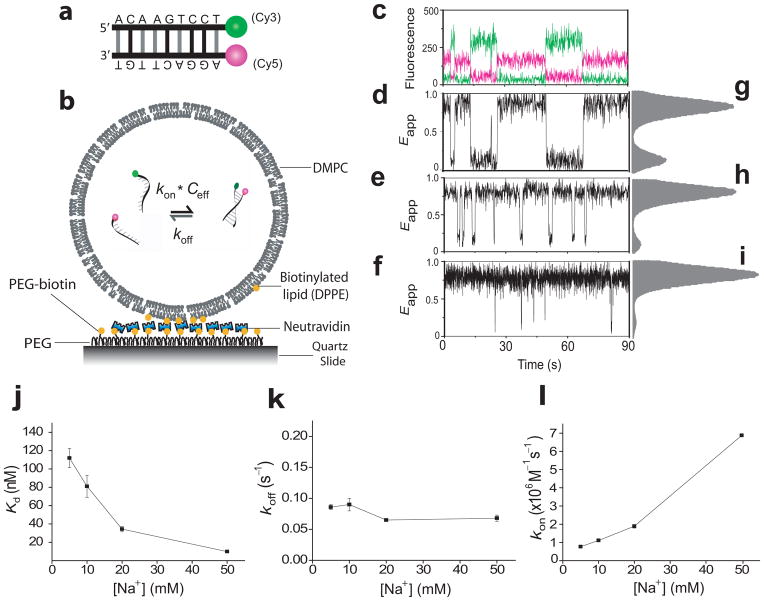
Figure 1.

Single-molecule porous vesicle encapsulation assay. (a) Schemes for the 9 bp DNA duplex and (b) DNA encapsulation; (c–l) Salt dependent dynamics for 9 bp DNA in 200 nm vesicles: single molecule time traces (c, d, e, f), and histograms from over 100 vesicles (g, h, i), at 5 mM (c, d, g), 20 mM (e, h), and 50 mM Na⁺ (f, i). K_d, k_off, and k_on vs [Na⁺] (j, k, l); 541 vesicles were used to calculate the rates in j, k and l. All error bars represent standard error from triplicate experiments at 23 °C. In c, green curve denotes the donor intensity and red the acceptor intensity.

Figure 1 shows single vesicle time traces and apparent FRET efficiency (E_app) histograms obtained under various NaCl concentrations, each condition representing at least three different preparations of encapsulated samples. The lower salt conditions show two clear peaks centered around E_app = 0.85 and 0.1 (Figs. 1g–i), corresponding to the annealed and melted states, respectively. Time trajectories of single molecule FRET (Figs. 1d–f) show repetitive transitions between two E_app states due to multiple annealing and melting transitions. Via dwell time analysis, we determined the average dwell times of the high and low E_app states, τ_high and τ_low, respectively. k_off is given by τ_high⁻¹ whereas k_on is obtained as (τ_low c_eff)⁻¹. The effective concentration c_eff is given by 6/N_Aπd³_, where d is the vesicle diameter in decimeter estimated as the filter diameter used in the vesicle preparation (see Methods section) and N_A is Avogadro’s number.

K_d≡ k_off/k_on decreases by an order of magnitude when [Na⁺] increases from 5 mM to 50 mM (Fig. 1j). K_d vs. [Na⁺] agrees well with a logarithmic function derived from the unified thermodynamic database for 10 mM to 50 mM salt concentrations¹⁹ (Supplementary Fig. 1a–b), and also for the lowest concentration, 5 mM, after accounting for the effects of buffer electrolyte (Supplementary Fig. 1c). This dependence of K_d on salt is therefore attributable to the well known trend^2,10–12 of increased duplex stability with increasing ionic strength. The salt-dependence of k_on and k_off, measured independently in this study, reveal that the salt effect on K_d mostly originates from rapidly increasing k_on (Fig. 1l) consistent with previous NMR studies¹³, and we see relatively little variation in k_off (Fig. 1k). The large dependence of k_on on salt concentration is attributable to effective charge screening of the electro-negative DNA backbone.

Potential effects of the fluorescent labels were tested by comparing with a construct with the labels on the opposite ends of the duplex. The cyanine dyes stack on the terminal base pair of the duplex²⁵, with possible stabilization of the double stranded DNA. At 10 mM Na⁺, k_on for the original 9 bp duplex with labels at the same side is 1.1 (± 0.1)×10⁶ M⁻¹s⁻¹ (Fig. 1l) which is well within the range of previous estimates of 10⁴ to 10⁷ M⁻¹s⁻¹ for duplexes varying from 8 bp to 20 bp (ref. 4–6,13). k_off under the same condition is 0.1 (±0.01) s⁻¹ (Fig. 1k). When the dyes were positioned at opposite ends, we indeed observed a factor of 2 decrease in k_off (0.05 (±0.01) s⁻¹ vs. 0.10 (±0.01) s⁻¹) while k_on remained unaffected (1.0 (±0.1) ×10⁶ M⁻¹s⁻¹ vs. 1.1 (±0.1) ×10⁶ M⁻¹s⁻¹) (Supplementary Fig. 2). The effect of fluorescent labeling therefore must be negligible compared to the orders of magnitude variations we report below for mismatched sequences.

Effect of single base pair mismatches on DNA

We introduced a single base pair mismatch by changing the A-T base pair at one end of the 9 bp duplex into T-T mismatch, and observed a factor of ~ 2.5 increase in K_d (Fig. 2a). The decrease in stability is mostly due to a factor of 3.5 increase in k_off (Fig. 2b). There is however an increase by a factor of 1.5 in k_on (Fig. 2c), which we cannot explain.

Figure 2.

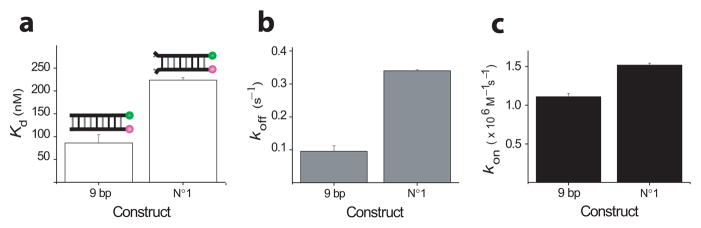
The effect of terminal base pair mismatch. (a) K_d, (b) k_off, and (c) k_on at 10 mM Na⁺; A total of 309 vesicles were used to calculate the rates in this figure.

We then proceeded to characterize the effect of a mismatch at each of the nine possible positions. The constructs were designed similarly to the 1^st bp mismatch above by changing a single base from the original 9 bp sequence; for example in the 2^nd bp the original C-G was changed to G-G mismatch (Fig. 3a and Supplementary Table 1). For each construct, the experiments were first attempted in 200 nm diameter vesicles, but as the mismatch makes the DNA-DNA interactions weaker, some duplexes were not well captured at the lower concentrations required for capturing < 1 duplex per vesicle; in those cases, we increased the DNA concentrations and used vesicles of smaller diameters (100, 50, and 30 nm). The same DNA construct in different vesicle sizes shows similar τ_high (and therefore similar k_off) values but very different τ_low values. However, after adjusting for the different vesicle volumes, we obtained nearly identical k_on values (Supplementary Fig. 3).

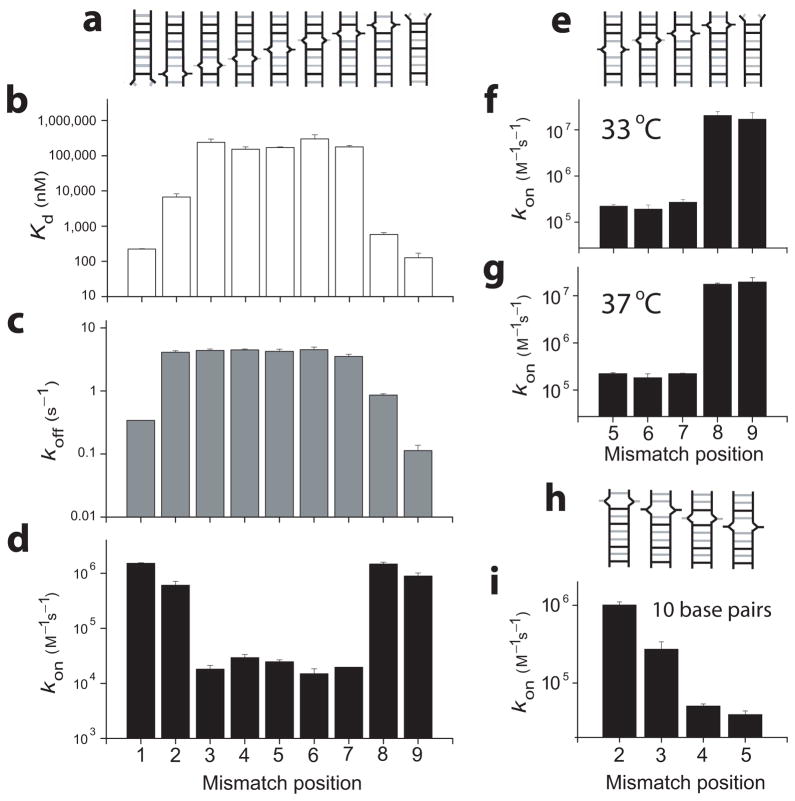
Figure 3.

The effect of DNA mismatch position. (a, e) Schemes of mismatched constructs; (b) K_d, (c) k_off, and (d) k_on were measured at 23 °C, 10 mM Na⁺; (e) For mismatch positions 5 through 9, k_on was additionally measured at 33 °C, 150 mM Na⁺ and (f) at 37 °C, 200 mM Na⁺; A total of 723 vesicles were used for b, c, and d, 937 vesicles in f, 511 vesicles in g, and 697 vesicles in i.

Depending on the position of a single bp mismatch, there is a variation by over a factor of 3,000 in K_d with the mismatch having a bigger negative impact on the duplex stability when it is closer to the middle (Fig. 3b). The equilibrium constant K_d is higher than 100 μM for the middle mismatches, which would have made it difficult to perform kinetic analysis using conventional single-molecule methods. A relative high penalty cost of a middle mismatch compared to an end mismatch is consistent with observations from previous thermodynamic analyses^26,27. We note that changing the middle construct (mismatch position 5) from a G-G to a C-C mismatch resulted in a duplex that we were unable to capture with adequate encapsulation yield even in our smallest vesicle size, likely because the middle C-C mismatch is more disruptive than the corresponding G-G mismatch as shown by previous thermodynamic analyses^27,28.

The variation in k_off was ~ 30 fold, and the general trend shows a gradual, bell-shaped variation, peaking with a mismatch toward the middle of the duplex (Fig. 3, Supplementary Fig. 4). The only outlier from the symmetric bell shape is the 2^nd bp mismatch which showed a four times higher k_off compared to the reciprocal mismatch on the 8^th bp; this effect may arise from the fact that the 2^nd bp is the only G-C pair in the first half of the duplex.

The k_on vs mismatch position result shows the most striking effect (Fig. 3d). For mismatches on the 1^st and 2^nd bp, k_on is of the same order of magnitude as with the full 9 bp construct (~ 10⁶ M⁻¹s⁻¹), but moving the single mismatch to the 3^rd bp reduced k_on by a factor of ~ 100. The same observation is made comparing the mismatches on the other end of the duplex: for the mismatch on the 9^th and 8^th bp comparable k_on values are measured, then a factor of ~ 100 decrease in k_on for the mismatch on the 7^th bp. The position of this transition remained the same at different conditions: room temperature with 10 mM Na⁺ (Fig. 3d), 33 °C with 150 mM Na⁺ (Fig. 3f), and 37 °C with 200 mM Na⁺ (Fig. 3g), and after testing for possibly missed transitions using a hidden Markov analysis on the FRET trajectories²⁹ (Supplementary Fig. 4i–k).

Furthermore, there is little variation of k_on for mismatches between the 3^rd and the 7^th bp. Overall, DNA constructs with mismatches on the 1^st, 2^nd, 8^th, and 9^th bp (with 7 or more contiguous base pairs) have up to two orders of magnitude higher k_on than the constructs with a mismatch position between the 3^rd and 7^th bp (< 7 contiguous base pairs). These results suggest 7 bp cooperativity during duplex formation (but not during melting), whereby a single mismatch that prevents 7 contiguous base pairs results in the lowest annealing rate. The necessity for at least 7 contiguous base pairs remains valid over a range of biologically relevant temperature and salt conditions.

As a further test of the apparent requirement of 7 contiguous base pairs for rapid annealing, we designed 10 nt constructs of unrelated sequence. When a single mismatch reduces the maximal contiguity to 6 bp or 5 bp we obtained the lowest annealing rate k_on ~10⁴ M⁻¹s⁻¹ (Fig. 3i), and k_on increased by about one order of magnitude with 7 bp contiguity (see Supplementary Figure 4 for k_off and K_d). The lowest annealing rate was achieved when the mismatch is at least 4 nt away from the end in contrast to the 9 nt constructs which gave the lowest annealing rate when the mismatch is placed at the 3^rd nt from the end, indicating that the rule of seven does not arise from an end effect. In the case of the 10 nt sequence, however, 8 bp contiguity further increased the annealing rate by a factor of ~ 3, suggesting that 7 contiguous base pairs are necessary but not always sufficient for the highest annealing rate.

Effect of single base pair mismatches on RNA

The rule of seven, suggested by our measurements on DNA, is reminiscent of the empirical observation that mammalian targets of micro RNA (miRNA) can be predicted by searching for conserved 7 nt matches ^30–32 and that messenger RNAs are under selective evolutionary pressure to conserve (targets) or avoid (non-targets) 7 nt binding sites that match miRNAs seed sequence ^33,34. In the canonical model for miRNA target recognition^35,36 the target recognition is suggested to be driven by Watson-Crick base pair interactions of residues 2 to 8 of the 5′ portion of the miRNA, and consequently the protein in the silencing complex is assigned the role of preorganizing the geometry so as to favor the optimal presentation of this heptameric core for hybridization³⁰. If the naked RNA molecules themselves require 7 contiguous base pairs for rapid annealing, we may deduce that the proteins in the silencing complex may have evolved to utilize such an intrinsic property of nucleic acids alone. We therefore tested if there exists a large difference in annealing rate between 7 and 6 contiguous base pairs in the case of RNA using a well-known miRNA as an example.

We synthesized the 8 nt sequence corresponding to miR125 seed in human, a homolog to Lin-4 in C. Elegans³⁷, labeled with Cy5 at the 3′ end. Its complementary target sequence derived from human p53 gene³⁸, with the 1^st bp mismatched (U-U) and 7 contiguous bp, was labeled at the 5′ end with Cy3 (#1RNA_7cont.bp). It was compared with the second construct with a (C-U) mismatch in the 2^nd bp (#2RNA_6cont.bp, see Supplementary Table 1).

Figure 4 shows the average rates obtained from the spontaneous melting and annealing of individual RNA duplexes at 5mM Na⁺ inside porous vesicles. In terms of K_d, the 7 contiguous bp RNA is a factor of ~ 450 times more stable than 6 contiguous bp RNA (Fig. 4a). k_off values were 0.014 (±0.004) s⁻¹ for 7 bp RNA and 0.14 (±0.03) s⁻¹ for 6 bp RNA, exhibiting difference of a factor of 10 (Fig. 4b). The predominant difference in stability between the two RNA constructs, however, comes from a difference of a factor of 45 in k_on, with 3.4 (±0.8)×10⁶ M⁻¹s⁻¹ for 7 bp RNA, and 7.6 (± 1.2)×10⁴ M⁻¹s⁻¹ for 6 bp RNA (Fig. 4c). These results support further the requirement of 7 contiguous Watson-Crick base pairs for rapid annealing of two oligonucleotides.

Figure 4.

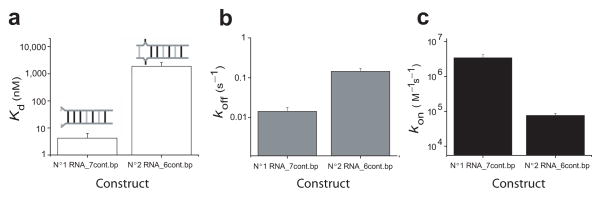
The effect of mismatch position on RNA. (a) K_d, (b) k_off, and (c) k_on for 8 bp RNA constructs with 7 and 6 contiguous base pairs at 23 °C, 5 mM Na⁺; A total of 228 vesicles were used to calculate the rates in this figure.

Discussion

In the ‘zipper-up’ model³⁹, DNA annealing is said to proceed first through a slow nucleation step followed by microseconds time scale zipping. One implication of the model, the so-called ‘all or none’ aspect requiring that the strands should be either fully annealed or fully unzipped within our 30 ms time resolution, is consistent with the 2-states nature of the single molecule FRET trajectories observed. However, thermodynamic estimation suggests that 2 to 3 base pairs should be enough for this nucleation step in the zipper-up model³⁹. Therefore, we do not believe that this model is directly applicable to the 7 bp cooperativity observed in this study.

A heptamer core was previously postulated as the optimal compromise in miRNA target recognition: a larger core would impose topological difficulties for the silencing complex whereas a smaller core would result in a drop in the initial Watson-Crick base pairing interaction. Recent crystal structures of Argonaute yielded a picture consistent with this model, with the protein prearranging the core residues in A-form helix⁴⁰. In vivo investigation has shown that 6 mer seed match was not sufficient for miRNA regulation even when inserted in multiple copies in the 3′ UTR of messenger RNAs, whereas a single insertion of a 7 mer was sufficient for gene silencing⁴¹. However, previous studies could not test if such a difference was intrinsically due to a systematic drop in the formation rate of miRNA-mRNA helix or due to the effect of the proteins in the silencing complex. Our results suggest that specificity in the microRNA target recognition may arise from the intrinsic properties of oligonucleotides themselves that require 7 contiguous base pairs for rapid annealing.

Many questions remain to be addressed, particularly regarding the origin of the 7 bp cooperativity and the limits of its validity. Different approaches providing more atomistic details, for example using molecular dynamics simulation, may prove useful in elucidating the molecular mechanism. A key advantage of our porous vesicle encapsulation assay is that the oligonucleotides are untethered, and therefore free to adopt any preferred geometry during the double helix formation. However, the method is laborious compared to measurements using tethered oligonucleotides. Although we have tested three unrelated sequences in DNA and RNA, these represent a tiny fraction of the sequence space and we do not know yet whether similar rules will hold for oligonucleotides longer than 10 nt. New technical developments to improve the co-encapsulation efficiency or to parallelize the experiments may improve the data throughput, allowing us to sample a much bigger sequence space and to test the validity and generality of the rule more thoroughly.

It is possible that other instances of 7 bp cooperativity occur in other cellular processes, for example during transcription initiation and termination. Moreover, understanding the rules governing the rate of duplex formation in the presence of a mismatch should also be useful for hybridization based applications in biotechnology where off-target effects can be detrimental. Examples include improvement on target specificity of small interference RNA (siRNA), DNA-based computing, DNA-based nanotechnologies and microarrays. In many cases, the overall hybridization efficiency would be governed by the annealing kinetics (k_on) instead of the thermodynamic stability (e.g. T_m, as most commonly considered) because even in the presence of mismatches, melting can be slower than the relevant time scale.

Methods

The encapsulation and single molecule detection methods were as described previously²¹ with the following optimizations.

Vesicle Encapsulation

Lipid films were prepared by mixing biotinyl cap phosphoethanolamine with dimyristoyl phosphatidylcholine (DMPC) dissolved in chloroform (1:100 molar ratio) then dried in vacuum for ~ 1 h. The lipids were hydrated with solution containing DNA or RNA according to the following specifications:

• Solution condition for DNA encapsulations: 500 mM NaCl, 10 mM MgCl₂, and 25 mM Tris pH 8.0

• Solution condition for RNA encapsulations: 500 mM NaCl, and 25 mM Tris pH 8.0 (MgCl₂ absence intentional, and special care was taken to minimize potential RNase contamination during sample preparation).

• Oligo concentrations:

  • For the full 9 bp, 9 bp with dyes on separate ends, #1, #9 DNA constructs: successful encapsulations were conducted at 400 nM oligo concentrations (for extrusion with 200 nm filter pores) or 3.2 μM oligo concentrations (for extrusion with100 nm filter pores).

  • For N°2 and #8 DNA constructs: successful encapsulations were conducted at 3.2 μM oligo concentrations (for extrusion100 nm filter pores).

  • For N°3, N°4, N°5, N°6, N°7 DNA constructs: successful encapsulations were conducted with 6.4 μM oligo concentrations (for extrusion with either 50 nm or 30 nm filter pores)

  • For N°1RNA_7cont.bp construct: successful encapsulations were conducted with 100 nM oligo concentration (for extrusion with 200 nm filter pores)

  • For N°2RNA_6cont.bp construct: successful encapsulations were conducted with 1 μM oligo concentration (for extrusion with 50 nm filter pores)

After hydration, the mixture of lipid and nucleic acids was frozen in liquid nitrogen and thawed about 7 times to create large unilamellar vesicles. The solution was then processed through an extrusion set with a filter with small pores to create the small unilamellar vesicles of the desired size (see specifications above for the filter pore sizes used for each construct). Dynamic light scattering measurements gave vesicle size estimates that are in line with the filter pore diameter used (Supplementary Fig. 3). The effective co-encapsulation yield (defined as the fraction of vesicles detected with a pair of donor and acceptor among all vesicles with any signal) was ~ 20% for 200nm and 100 nm vesicles. The co-encapsulation yield for 50 nm and 30 nm depended on the stability of the construct used and was more variable; only those preparations with 10% or better yield were included in the analysis. Higher co-encapsulation yield may be obtained if stock-level concentrations of labeled DNA could be used to match the expected local concentrations after encapsulation: for example ~ 25 μM for 50 nm vesicles, and ~ 117 μM for 30 nm vesicles. However, in practice, such high concentrations of labeled DNA and RNA were unreasonable due to high cost.

All lipids, extrusion sets and vesicle size filters were obtained from Avanti Polar Lipids, Inc (Alabaster, AL 35007). All oligonucleotides (DNA and RNA) were custom-designed and purchased from Integrated DNA Technology (Coralville, IA 52241). Additional information on DNA and RNA design is available online as Supplementary Table 1.

Single Molecule detection and analysis

We used total internal reflection fluorescence microscopy for imaging as described previously²¹. Imaging solution contains 1 mg/ml glucose oxidase, 0.04 mg/ml catalase, 0.8% dextrose, and saturated trolox (~ 3 mM) in 50 mM Tris. Because the transition temperature of DMPC is at room temperature, coexistence of liquid and gel phases of the lipids would result in membranes with pores wide enough for exchanging ions and small molecules but small enough to keep larger biomolecules like DNA oliomers inside the vesicles²¹. All solution exchanges were made at room temperature. Data acquisition was performed under various salt and temperature conditions as indicated in the text and figure captions.

We calculated the apparent FRET efficiency by E_app= I_A/(I_D+I_A) where I_D and I_A are the emission intensity of the donor and acceptor, respectively. Since multiple molecules may be confined in the same vesicle, the criterion set to determine the rates of bi-molecular interactions was that only vesicles with fluorescence consistent with one donor and one acceptor were selected; any additional criteria (e.g. encapsulation yield for successful experiment) were as described in the manuscript. To obtain the transition rates from repetitive reactions inside vesicles, we selected the region where both donor and acceptor were photoactive in the individual traces. E_app of the selected region was then regarded as a two-state trajectory with a midpoint cutoff at E_app ~ 0.5, and the individual dwell times were extracted for each low E_app (< 0.5) and high E_app (> 0.5) residence. The kinetic rates for each condition were calculated from the average dwell times, obtained from multiple vesicles. Alternatively, a previously described hidden Markov model²⁹ has been adopted to test for events which might be missed because of short dwell times. For all rate calculations, the vesicle diameter is estimated to be the pore size of filter selected for vesicle extrusion (200 nm, 100 nm, 50 nm, or 30 nm).